Modeling and analysis of forced vibrations in transversely isotropic thermoelastic thin beams

Abstract

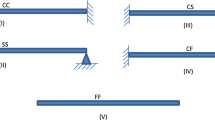
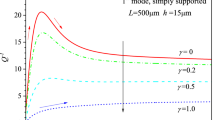
In this paper, the transverse vibrations in a homogenous, transversely isotropic, thermoelastic thin beams due to time varying patch loads have been investigated. The governing equations of motion for classical elasticity and heat conduction for non-Fourier (non-classical) process have been integrated to model the transverse vibrations in a homogenous, transversely isotropic thin beam in closed form by employing Euler–Bernoulli beam theory. The axial ends of the beam are assumed to be at either clamped–clamped or clamped-free/cantilever conditions. The model equation governing transverse vibrations in a thermoelastic thin beam has been solved analytically by employing Laplace transform technique with respect to space and time variables. In order to obtain deflection and other quantities in the physical domain, the inversion of Laplace transform in the time domain has been performed by using the calculus of residues. The variational iteration method along with Durbin technique has also been employed to solve the model equation for comparison and validation purpose. The expressions for deflection and response ratio in the physical domain have been computed numerically with the help of MATLAB software for a silicon carbide micro-beam. The computed results have been presented graphically. The obtained analytic results are envisioned to be easy to implement for engineering analysis and designs of resonators (sensors), modulators, actuators and radio frequency filters.

Appendix

The values of the coefficients A _i and B _i, i = 1,2 of expressions (32) and (33) are given by

$$ A_{1} = A_{1}^{1} (\cosh \,\eta - \cos \,\eta )\, - A_{1}^{2} (\sinh \,\eta - \sin \,\eta ) $$

$$ A_{1}^{1} = \sinh \,\eta \left( {1 - \frac{{\hat{a} + \hat{b}}}{2}} \right)\,\sinh \,\eta \left( {\frac{{\hat{a} - \hat{b}}}{2}} \right) - \sin \,\eta \left( {1 - \frac{{\hat{a} + \hat{b}}}{2}} \right)\,\sin \,\eta \left( {\frac{{\hat{a} - \hat{b}}}{2}} \right) $$

$$ A_{1}^{2} = \cosh \,\eta \left( {1 - \frac{{\hat{a} + \hat{b}}}{2}} \right)\,\sinh \,\eta \left( {\frac{{\hat{a} - \hat{b}}}{2}} \right) + \cos \,\eta \left( {1 - \frac{{\hat{a} + \hat{b}}}{2}} \right)\,\sin \,\eta \left( {\frac{{\hat{b} - \hat{a}}}{2}} \right) $$

(76)

$$ A_{2} = A_{2}^{1} (\cosh \,\eta + \cos \,\eta )\, - A_{2}^{2} (\sinh \,\eta + \sin \,\eta ) $$

$$ A_{2}^{1} = \sinh \,\eta \left( {1 - \frac{{\hat{a} + \hat{b}}}{2}} \right)\,\sinh \,\eta \left( {\frac{{\hat{a} - \hat{b}}}{2}} \right) - \sin \,\eta \left( {1 - \frac{{\hat{a} + \hat{b}}}{2}} \right)\,\sin \,\eta \left( {\frac{{\hat{b} - \hat{a}}}{2}} \right) $$

$$ A_{2}^{2} = \cosh \,\eta \left( {1 - \frac{{\hat{a} + \hat{b}}}{2}} \right)\,\sinh \,\eta \left( {\frac{{\hat{a} - \hat{b}}}{2}} \right) + \cos \,\eta \left( {1 - \frac{{\hat{a} + \hat{b}}}{2}} \right)\,\sin \,\eta \left( {\frac{{\hat{a} - \hat{b}}}{2}} \right) $$

(77)

$$ B_{1} = A_{1}^{1} (\sinh \,\eta + \sin \,\eta )\, - A_{1}^{2} (\cosh \,\eta - \cos \,\eta ) $$

(78)

$$ B_{2} = A_{2}^{1} (\sinh \,\eta - \sin \,\eta )\, - A_{2}^{2} (\cosh \,\eta + \cos \,\eta ) $$

(79)