Interactions of propagating waves in a one-dimensional chain of linear oscillators with a strongly nonlinear local attachment

Abstract

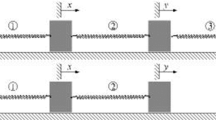
We study the interaction of propagating wavetrains in a one-dimensional chain of coupled linear damped oscillators with a strongly nonlinear, lightweight, dissipative local attachment which acts, in essence, as nonlinear energy sink—NES. Both symmetric and highly un-symmetric NES configurations are considered, labelled S-NES and U-NES, respectively, with strong (in fact, non-linearizable or nearly non-linearizable) stiffness nonlinearity. Especially for the case of U-NES we show that it is capable of effectively arresting incoming slowly modulated pulses with a single fast frequency by scattering the energy of the pulse to a range of frequencies, by locally dissipating a major portion of the incoming energy, and then by backscattering residual waves upstream. As a result, the wave transmission past the location of the NES is minimized, and the NES acts, in effect, as passive wave arrestor and reflector. Analytical reduced-order modeling of the dynamics is performed through complexification/averaging. In addition, governing nonlinear dynamics is studied computationally and compared to the analytical predictions. Results from the reduced order model recover the exact computational simulations.

Appendix

The kernels appearing in (4) are defined in terms of the previously identified normalized variables as follows,

$$G_{m} \left( \tau \right) = \frac{1}{\varOmega }e^{{ - \frac{\varepsilon \varLambda \tau }{{2\left( {1 + \varepsilon } \right)}}}} \quad\,\int\limits_{0}^{\tau } {J_{0} \left[ {\left( {\alpha^{2} - \frac{{\varepsilon^{2} \varLambda^{2} }}{{4\left( {1 + \varepsilon } \right)^{2} }}} \right)^{1/2} \left( {\tau^{2} - v^{2} } \right)^{1/2} } \right]J_{2m}\quad \left( {\frac{{2D^{1/2} }}{\varOmega }v} \right)dv \, } \quad \alpha = \frac{{\omega_{1} }}{\varOmega }, \quad \frac{D}{{\varOmega^{2} }} = \frac{1 + \varepsilon }{2} - \frac{{\alpha^{2} }}{2} = \frac{{1 - \alpha^{2} }}{2} + O\left( \varepsilon \right) $$

(9)

where $J_{k} ( \bullet )$ is the Bessel function of the first kind and of the mth order, and $G_{ - m} \left( \tau \right) = G_{m} \left( \tau \right),\,\,\,m = 1,\;2, \ldots$.

To derive this expression we consider the reduced set of equations (5) and note that correct to $O\left( \varepsilon \right)$ the first equation governing the motion of the center of mass of the NES and the 0th particle of the chain is a linear non-homogeneous ordinary differential equation which can be explicitly solved to yield:

$$ v\left( \tau \right) = \frac{{DF_{p} }}{{\varOmega^{2} }}\int\limits_{0}^{\tau } {\left[ {G_{1 - p} (\xi ) + G_{1 + p} (\xi )} \right]\sin \left( {\tau - \xi } \right)d\xi } + O\left( \varepsilon \right) $$

(10)

This approximation when substituted into to the second of Eq. (5) governing the relative oscillation between the NES and the 0th particle yields a single nonlinear integro-differential equation that replaces the infinite set of Eq. (2) correct to $O\left( \varepsilon \right)$:

$$ w^{\prime\prime} + \varLambda w^{\prime} - \frac{(1 + \varepsilon )}{{\varOmega^{2} }}\frac{{f_{NES} ( - \varepsilon^{1/2} w)}}{{\varepsilon^{3/2} }} = \frac{{d^{2} }}{{d\tau^{2} }}\left\{ {\frac{{DF_{p} }}{{\varOmega^{2} }}\int\limits_{0}^{\tau } {\left[ {G_{1 - p} (\xi ) + G_{1 + p} (\xi )} \right]\sin \left( {\tau - \xi } \right)d\xi } } \right\} + O\left( \varepsilon \right) w(0 + ) = w^{\prime}(0 + ) = 0$$

(11)

We will refer to (11) as the ‘reduced system.’ It is clear that in its present form (11) cannot be analytically treated for general ranges of the system parameters. However, we will show that this restriction can be alleviated under the assumption of weak coupling between adjacent particles in the chain. To this end, we need to rescale the coefficients of the linear coupling stiffnesses in the chain according to $D \to \varepsilon^{1/2} D$. From the physical point of view, in the limit of weak coupling between particles the impulsive response of the chain takes the form of a slowly modulated wavetrain with a single ‘fast’ normalized frequency equal to unity (which in physical units corresponds to the grounding frequency $\omega_{1}$ of each oscillator of the chain). The time scale of the slow modulation is directly related to the weak coupling in the chain. In turn, this enables a slow-fast partition of the governing dynamics, as well as averaging with respect to the single fast frequency; the resulting slow modulation equations fully capture the leading-order scattering of propagating waves with the NES, and provides us with a methodology for analytically studying (to first order) the effectiveness of the NES as passive wave arrestor. Later in our analysis we will relax the assumption of weak coupling in the chain in order to study the performance of the NES for the case of strong coupling. In that case, however, our study will be entirely numerical, as it won’t be amenable to slow-fast partition of the dynamics and analytical treatment.

For the case of weak coupling, the response $v\left( \tau \right)$ (cf. expression (10)) is of $O(\varepsilon^{1/2} )$. Considering the mathematical structure of $G_{m} (\xi ),\,\,m = 1 \pm p$ in (10), and taking into account integral expressions for the Bessel functions of the first kind [40] we obtain the following alternative integral representation,

$$ G_{m} \left( \tau \right) = \frac{1}{\pi \,\varOmega }e^{{ - \frac{\varepsilon \varLambda \tau }{{2\left( {1 + \varepsilon } \right)}}}} \,\int\limits_{0}^{\pi } {\,\frac{{\cos \left( {m\theta } \right)}}{\omega \left( \theta \right)}} \sin \left[ {\omega \left( \theta \right)\tau } \right]\,\,d\theta $$

(12)

where, for weak coupling between particles of the chain, the frequency $\omega \left( \theta \right)$ is defined by:

$$ \omega \left( \theta \right) = \frac{1}{\varOmega }\left[ {\omega_{1}^{2} + 4\varepsilon^{1/2} D\left( {\sin \frac{\theta }{2}} \right)^{2} } \right]^{1/2} $$

(13)

Expanding $\omega \left( \theta \right)$ and $\varOmega^{ - 1}$ in terms of the small parameter $\varepsilon$ yields the following asymptotic approximations,

$$1 - \omega^{2} \left( \theta \right) = \frac{{2\varepsilon^{1/2} D}}{{\omega_{1}^{2} }}\cos \theta - \varepsilon \left( {1 + \frac{{4D^{2} }}{{\omega_{1}^{4} }}\cos \theta } \right) + O\left( {\varepsilon^{3/2} } \right) \frac{1}{\varOmega } = \frac{1}{{\omega_{1} }} - \frac{{\varepsilon^{1/2} D}}{{\omega_{1}^{3} }} + O\left( \varepsilon \right) $$

(14)

which, when substituted into (12) yields the following asymptotic approximation for $G_{m} \left( \tau \right)$:

$$G_{m} \left( \tau \right) = \underbrace {{L_{m} (\varepsilon^{1/2} \tau )}}_{Slow\,part}\underbrace {{{}_{{}}e^{j\tau }_{{}} }}_{Fast\,\,part} +\,cc, L_{m} (\varepsilon^{1/2} \tau ) \equiv \frac{1}{2j}\left[ {\frac{1}{{\pi \omega_{1} }} - \frac{{\varepsilon^{1/2} D}}{{\pi \omega_{1}^{3} }} + O(\varepsilon )} \right]\,\,e^{{ - \frac{\varepsilon \varLambda \tau }{{2\left( {1 + \varepsilon } \right)}}}} \,\,\int\limits_{0}^{\pi } {\,\left\{ {\left[ { - \frac{{\varepsilon^{1/2} D}}{{\pi \omega_{1}^{3} }}\cos \theta + O(\varepsilon )} \right]\cos \theta \,e^{{j\varepsilon^{1/2} \tau \left[ { - \frac{D}{{\pi \omega_{1}^{3} }}\cos \theta + O(\varepsilon )} \right]}} } \right\}} \,d\theta $$

(15)

Hence, in the limit of weak coupling between particles of the chain the kernels $G_{m} \left( \tau \right)$can be expressed in terms of a fast oscillation with unit normalized frequency modulated by the slow (complex) modulation $L_{m} (\varepsilon^{1/2} \tau )$, with $(cc)$ denoting complex conjugate.

Considering now the right hand side of Eq. (11) and substituting (15), in the limit of small coupling between particles we express it as,

$$ \frac{{d^{2} }}{{d\tau^{2} }}\left\{ {\frac{{\varepsilon^{1/2} DF_{p} }}{{\varOmega^{2} }}\int\limits_{0}^{\tau } {\left[ {G_{1 - p} (\xi ) + G_{1 + p} (\xi )} \right]\sin \left( {\tau - \xi } \right)d\xi } } \right\} + O\left( \varepsilon \right) = \frac{{d^{2} }}{{d\tau^{2} }}\left\{ {\frac{{\varepsilon^{1/2} DF_{p} }}{{\pi \,\varOmega^{3} }}\,\,\int\limits_{0}^{\pi } {\,\frac{{\left[ {\cos (p - 1)\theta + \cos (p + 1)\theta } \right]}}{{\omega (\theta )\,\left[ {1 - \omega^{2} (\theta )} \right]}}\,\,\left[ {\cos \omega (\theta )\tau - \omega (\theta )\sin \tau } \right]d\theta } } \right\} + O\left( \varepsilon \right) = \underbrace {{A_{p} (\varepsilon^{1/2} \tau )}}_{Slow\,part}\underbrace {{{}_{{}}e^{j\tau }_{{}} }}_{Fast\,\,part} +\,cc $$

(16)

where the slowly varying complex modulation $A_{m} (\varepsilon^{1/2} \tau )$ is expressed asymptotically as:

$$ A_{p} (\varepsilon^{1/2} \tau ) = \frac{{jF_{p} }}{{2\omega_{1} }}\,e^{ - jp\pi /2} \,J_{p} \left( {\frac{{D\varepsilon^{1/2} \tau }}{{\omega_{1}^{2} }}} \right) + O(\varepsilon^{1/2} ),\,\,\,\,p \le - 2 $$

(17)

Note the asymptotic expression (17) correctly confirms that $A_{p} (0 + ) = 0$, i.e., it is consistent with the initial conditions of the problem.

Substituting (16) and (17) into the reduced system (11) brings it in the following asymptotic form:

$$ w^{\prime\prime} + \varLambda w^{\prime} - \frac{(1 + \varepsilon )}{{\varOmega^{2} }}\frac{{f_{NES} ( - \varepsilon^{1/2} w)}}{{\varepsilon^{3/2} }} = \frac{{jF_{p} }}{{2\omega_{1} }}\,e^{ - jp\pi /2} \,J_{p} \left( {\frac{{D\varepsilon^{1/2} \tau }}{{\omega_{1}^{2} }}} \right)\,\,e^{j\tau } + cc + O\left( {\varepsilon^{1/2} } \right) w(0 + ) = w^{\prime}(0 + ) = 0 $$

(18)

This equation models the leading-order nonlinear dynamic interaction between modulated waves propagating in the impulsively excited chain and the NES attached at the 0th particle.