Dynamic modelling of thin plate made of certain functionally graded materials

Abstract

The aim of the contribution is to formulate a macroscopic mathematical model describing the dynamic behaviour of a certain composite thin plates. The plates are made of two-phase stratified composites with a smooth and a slow gradation of macroscopic properties along the stratification. The formulation of mathematical model of these plates is based on a tolerance averaging approach (Woźniak, Michalak, Jędrysiak in Thermomechanics of microheterogeneous solids and structures, 2008). The presented general results are illustrated by analysis of the natural frequencies for two cases of plates: a plate band and an annular plate. The spatial volume fractions of the two different isotropic homogeneous components are optimized so as to maximize or minimize the first natural frequency of the plate under consideration.

1 Introduction

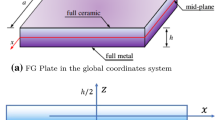
The object of the analysis is a composite thin plate with the apparent properties smoothly varying along a preferred direction in the plate midplane. Considerations are restricted to the two-phased of the functionally graded—type composites. The plate is made of two different isotropic homogeneous materials (Fig. 1). In this case we say that the aforementioned functionally graded materials are longitudinally graded, i.e. the effective properties of the considered plates are smooth and slowly-varying along the layering in the plate midplane.

Fig. 1

Fragment of plates midplane with longitudinally graded microstructure: (a) microscopic level, (b) macroscopic level

The aim of the contribution is to derive and apply a macroscopic model describing dynamic behaviour of thin plates made of composites which have the λ-periodic microstructure along ξ ¹-coordinate but slowly varying apparent properties in the perpendicular direction of ξ ²-axis. The generalized period λ of inhomogenity is assumed to be sufficiently small when compared to the measure of the domain of argument ξ ¹ (Fig. 1). Thus we deal with plates having space-varying periodic microstructure. The above gradation will be referred to as the longitudinal gradation.

The effective properties of the plate are constant in the ξ ¹-direction and varying in the ξ ²-direction. Since effective properties of this plate are graded in space then we deal here with a special case of a functionally graded material (FGM), Suresh, Mortensen [18].

Functionally graded materials are a new class of composite materials where composition of each material constituent determines continuously and smoothly varying apparent properties of composite. The dynamic analysis of functionally graded rectangular plates (FGP) are to be found in many papers. We can mention here as examples some of these papers. Chen et al. [3] analyzed nonlinear vibration of an initially stressed functionally graded plates (FGP). The material properties of the FGP are assumed to be temperature-dependent and graded through the thickness. In the paper of Gupta and Kumar [5] an analysis of thermal effect on vibration of non-homogeneous visco-elastic plate of linearly varying thickness has been discussed. Batra and Jin [2] studied free vibrations of a functionally graded anisotropic plate with the objective of maximizing one of its first five natural frequencies. The gradation of material properties through the thickness is attained by varying the fiber orientation angle. Tyliokwski [21] analyzed parametric vibrations of FGP subjected to in plane time-dependent forces. Material properties vary continuously in the thickness direction according to volume fraction power law distribution. In the paper Orakdöğen et al. [14] an finite element analysis of FGP multi-layered composite plate for coupling effect of extension and bending has been discussed. The volume fraction of material properties is graded in the thickness direction and was defined by using two power-law functions. The studies concerned with dynamic analysis of FGM circular and annular plates are limited. They are mentioned here some papers: Malekzadek et al. [9] presented analysis of free vibration of functionally graded annular plates on elastic foundation. Temperature-dependent material properties are graded through the thickness. The equations of motion are derived using the Hamilton’s principle based on the first-order shear deformation theory (FSDT). In the paper of Prakash and Ganapathi [16] the asymmetric free vibration and thermoelastic stability of the FGM circular plates using finite element method have been analyzed. Material properties are graded in the thickness direction according to a simple power law distribution. In the paper of You et al. [22], an analytical solution is developed to determine deformations and stresses in circular disks made of FGM subjected to internal and/or external pressure. The governing equations are derived from basic equations of axisymmetric, plane stress problem in elasticity. The mechanical properties of materials are the functions of the radial coordinate. Tornabene and Viola [20] analyzed a dynamic behaviour of functionally graded parabolic and circular panels and shells of revolution. The first-order shear deformation theory (FSDT) is used to study these structures. The two-constituent shells are graded through the thickness. Two different power law distributions are considered for the ceramic/metal volume fraction. The solution is given by means of the generalized differential quadrature methods. The majority of above mentioned studies are concerned with analysis functionally graded plates where material properties vary continuously through the plate thickness. In contrast to these papers, the plates under consideration have effective properties varying in the midplane of the plates.

The exact equations describing dynamics behaviour of the FGM-plates comprise highly-oscillating and non-continuous coefficients. The modeling problem is how to describe microheterogeneous plate by certain averaged equations with functional but smooth and slowly varying coefficients. For the above problem we can apply homogenization technique for equations with non-uniformly oscillating coefficients, cf. Jikov et al. [6]. However, because the formulation of averaged models by using the asymptotic homogenization is rather complicated from the computational point of view, these asymptotic methods are restricted to the first approximation. Hence, averaged model obtained by using this method neglects the effect of the microstructure size on the overall response of the FGM-plate. The formulation of the macroscopic mathematical model for the analysis of dynamic behaviour of the plates under consideration will be based on the tolerance averaging technique. The general modelling procedures of this technique are given by Woźniak et al. in book [24]. Application of the tolerance averaging technique to the analysis of periodic composites or structures were presented, e.g. for laminates by Matysiak and Nagórko [10], for porous media by Dell’Isola et al. [4], for honeycomb composites by Wierzbicki and Wożniak [23], for stability analysis of thin biperiodic cylindrical shells by Tomczyk [19], for investigation of dynamic behaviour of different periodic plates; by Baron [1] for medium-thickness plates, by Jędrysiak [7] for thin elastic plates interacting with an elastic periodic foundation, by Michalak et al. [12] for dynamic modeling of elastic wavy plates, by Michalak [11] for plates with initial geometrical periodical imperfections interacting with a periodic elastic foundation. In the book edited by Woźniak et al. [24] the list of references on this subject can be found. The approach, based on the tolerance averaging technique, to formulate an averaging model for functionally graded stratified media was proposed by Michalak et al. [13], Jędrysiak and Woźniak [8], Rychlewska and Woźniak [17].

The aim of this contribution is two-fold. First, to formulate a non-asymptotic model of the FGM-plate under consideration. This model takes into account the effect of the microstructure size on the dynamic behaviour of the FGM-plate. Second, to investigate a free-vibration problem in the framework of a non-asymptotic model.

2 Preliminaries

The object of our considerations are rectangular plates of microstructures shown on Fig. 1a or annular plates with microstructure given in Fig. 2a. Let us introduce the orthogonal curvilinear coordinate system Oξ ¹ ξ ² ξ ³ in the physical space occupied by a plate under consideration. The time coordinate will be denoted by t. Sub- and super-scripts i,k,l run over 1,2,3 and α,β,δ run over 1,2. Setting x≡(ξ ¹,ξ ²) and z=ξ ³ it is assumed that the undeformed plate occupies the region Ω≡{(x,z):−h/2≤z≤h/2,x∈Π}, where Π is the plate midplane and h is the plate thickness.

Fig. 2

Fragment of annular plates midplane with longitudinally graded microstructure: (a) microscopic level, (b) macroscopic level

The model equations for the dynamic behaviour of the plate will be obtained in the framework of the linear approximated theory for thin elastic plates. Let w(ξ ^α,t),p(ξ ^α,t),μ stand for the midplane deflection, loadings and the mass density related to plate midplane. Denoting by g _αβ the metric tensor, by ε _αβ a Ricci tensor, by ∂ _α =∂/∂ξ ^α and by vertical line before the subscripts the covariant derivative, we obtain strain-deflection relations

(1)

The strain energy averaged over the plate thickness is given by

(2)

where

and kinetic energy by

(3)

In order to derive governing equations we shall define Lagrangian

(4)

Introducing the action functional

(5)

we can write the following Euler-Lagrange equations

(6)

This direct description leads to plate equations with discontinuous and highly oscillating coefficients, which are too complicated to be used in the analysis of dynamics problems.

3 Modelling concepts

Introduce the polar coordinates system Oξ ¹ ξ ² so that the undeformed midplane of annular plate occupies the region Π≡[0,φ]×[R ₁,R ₂]. Let λ, 0<λ≪φ, be known microstructure parameter. Denote Π_Δ as a subset of Π of points with coordinates determined by conditions (ξ ¹,ξ ²)∈(λ/2,φ−λ/2)×(R ₁,R ₂). An arbitrary cell with a center at point with coordinates (ξ ¹ ξ ²) in Π_Δ will be determined by Δ(ξ ¹,ξ ²)=(ξ ¹−λ/2,ξ ¹+λ/2)×{ξ ²}. At the same time, the thickness h of the plate under consideration is supposed to be constant and small compared to the microstructure parameter λ.

In order to derive averaged model equations of longitudinally graded plates we apply the tolerance averaging approach, see Woźniak et al. [24]. We mention some basic concepts of this technique, as a tolerance parameter, a tolerance periodic function, a slowly varying function, a highly oscillating function, an averaging operator.

The main concept of the tolerance averaging approach is that values of functions belonging to region Π can be determined only within to certain accuracy δ. Let δ stand for an arbitrary positive number and X be a linear normed space. Tolerance relation ≈ for a certain δ is defined by

(7)

where δ is said to be the tolerance parameter.

Let ∂ ^k f be the k-th gradient of function f=f(x), x∈Π, k=0,1,…,α (α≥0), ∂ ⁰ f≡f. Function f∈H ^α(Π) is called the tolerance periodic function (with respect to cell Δ and tolerance parameter δ), $f \in \mathit{TP}_{\delta}^{\alpha}(\Pi,\Delta)$, if for k=0,1,…,α, the following conditions hold

(8)

Function $\tilde{f}^{(k)}(\mathbf{x}, \cdot)$ is referred to as the periodic approximation of ∂ ^k f in Δ(x),x∈Π, k=0,1,…,α.

Function F∈H ^α(Π) is called the slowly varying function (with respect to the cell Δ and tolerance parameter δ), $F \in SV_{\delta}^{\alpha} (\Pi,\Delta)$, if

(9)

It can be observed that periodic approximation $\tilde{F}^{(k)}$ of ∂ ^k F(⋅) in Δ(x) is a constant function for every x∈Π. If $F \in SV_{\delta}^{\alpha} ( \Omega,\Delta)$ then

Function ϕ∈H ^α(Π) is called the highly oscillating function (with respect to the cell Δ and tolerance parameter δ), $\phi\in HO_{\delta}^{\alpha} (\Pi,\Delta)$, if

(10)

and for k=1,…,α these functions satisfy conditions

(11)

If α=0 then we denote $\tilde{f} \equiv\tilde{f}^{(0)}$.

Let by φ(⋅) denote a highly oscillating function, $\varphi\in HO_{\delta}^{2}(\Pi,\Delta)$, defined on $\bar{\Pi}$, continuous together with gradient ∂ ¹ φ. Its gradient ∂ ² φ is a piecewise continuous and bounded. Function φ(⋅) is called the fluctuation shape function of the 2-nd kind, if it depends on λ as a parameter and satisfies conditions:

• 1. ∂ ^k φ∈O(λ ^α−k) for k=1,…,α,α=2,

• 2. 〈φ〉(x)≈0 for every x∈Π_Δ.

Set of all fluctuation shape functions of the 2-nd kind is denoted by $FS_{\delta}^{2}(\Pi,\Delta)$. Condition (2) can be replaced by 〈ρφ〉(x)≈0 for every x∈Π_Δ, where ρ>0 is a certain tolerance periodic function.

The important concept of the modelling technique is the averaging operation

(12)

for every ξ ¹∈[λ/2,φ−λ/2], ξ ²∈[R ₁,R ₂].

The starting point of the modeling procedure is a decomposition of displacement field w(ξ ¹,ξ ²,t)

(13)

The first modeling assumption, related to the above decomposition, states that w ⁰(⋅,ξ ²,t),V _A (⋅,ξ ²,t) are slowly varying functions together with all partial derivatives. Functions $w^{0}( \cdot,\xi^{2},t) \in SV_{\delta}^{2}(\Omega,\Delta)$, $V_{A}( \cdot,\xi^{2},t) \in SV_{\delta}^{2}(\Omega,\Delta)$ are the basic unknowns of the modelling problem. Functions g ^A(⋅) are known, dependent on the microstructure length parameter λ, fluctuation shape functions.

The second modelling assumption of tolerance averaging approximation states that terms O(λ) in the course of averaging can be neglected, see Woźniak et al. [24]. Under this approximation for an arbitrary integrable function f, slowly varying function F and fluctuation shape function g, we have

(14)

4 Averaging description

The tolerance averaging approach can be applied to (1)–(5) by using decomposition of displacement field w(ξ ¹,ξ ²,t). Substituting the right-hand sides of (13) into (4), (5) and using the tolerance averaging approximation we obtain

(15)

where the averaged Lagrangian (4) has the form

(16)

Tolerance model

Applying the principle of stationary action to Lagrangian (16) we obtain the following system equations for w ⁰(⋅),V _A (⋅)

(17)

Coefficients in the above equations are smoothly varying in contrast to coefficients in Euler-Lagrange equations for action functional $\mathcal{A}(\cdot)$. The model (17) have the physical sense only if w ⁰(⋅,t),V _A (⋅,t) are slowly varying functions with respect to ξ ¹-coordinate. This condition determines the range of the physical applicability of the proposed model.

Homogenized model

For the purely formal point of view the homogenized model equations can be obtained directly from the tolerance model equations by neglecting terms which are linear with respect to λ ⁿ, for n=1,2,… . This formal procedure has nothing in common with the limit passage λ→0 since the period λ remains constant in the course of the modelling. It means that in (17) we neglected the underlined terms. The homogenized model equations have the form

(18)

It can be observed that V _A (⋅,t) can be eliminated from (18)

(19)

Denoting

(20)

we arrive from (18) the following equation

(21)

Equations (20), (21) represent the homogenized model of the composite plate under consideration. It has to be emphasized that for the homogenized model only averaged deflection w ⁰(⋅,t) can be taken as the basic unknown.

5 Applications

We shall investigate free vibrations of two types of plates with inhomogeneous microstructure. We assume that composite plates are made of two different isotropic homogeneous materials. The crucial point of the tolerance modelling technique is a determination of fluctuation shape functions (FSF). In a dynamic processes system of FSF; g ^A(⋅), A=1,…,N, can be assumed as a representing eigenvibrations form of free vibrations of the cell Δ(ξ ^α), ξ ^α∈Π. We restrict our analysis to the simplest case N=1 in which we take into account only the lowest free vibration mode. The calculation of the exact form of fluctuation shape function for the plates under consideration is very difficult, hence we apply approximate form of this function in our consideration. For one dimensional cell under consideration Δ(ξ ¹,ξ ²), ξ ¹,ξ ²∈Π as the fluctuation shape function, we assume function

(22)

The function C(ξ ²) will be derived from condition 〈μg〉=0.

5.1 Plate band

Free vibrations of a cantilever plate band with microstructure given in Fig. 3 will be considered in this subsection.

Fig. 3

The microstructure of cantilever plate band

Tolerance model

After a simple manipulation we obtain from (17) the following system of two differential equations describing dynamic behaviour of the plate band

(23)

Equations (23) represent a system of two partial differential equations for the averaged deflection w ⁰(⋅,t) and fluctuation amplitude V(⋅,t).

(24)

Substituting (24) into (23) we obtain equations for $\tilde{w}^{0}(x_{2})$ and $\tilde{V}(x_{2})$

(25)

Since g(⋅)∈O(λ ²), the inertial module 〈μgg〉 and the underlined terms depend on the microstructure length parameter λ, hence aforementioned equations describe the microstructure length-scale effect on the natural frequencies of the plate under consideration.

Homogenized model

Using (21) we derive equation for the homogenized model

(26)

The basic unknown is averaged deflection w ⁰(⋅,t). Similarly as in a tolerance model we look for a solution to (26) in the form of a function with separable variables

(27)

Substituting (27) into (26) we obtain equations for $\tilde{w}^{0}(x_{2})$

(28)

The above equation represents the single partial differential equation for the averaged deflection $\tilde{w}^{0}(x_{2})$.

Equations (25), (28) have smooth and slowly varying functional coefficients. Hence in most cases solutions to specific problems for longitudinally graded plates have to be obtained using approximate methods. In order to obtain the solution of (25) and (28) the finite difference method will be used.

Numerical calculations

For verification the obtained averaged model equations we will compare values of the first vibration frequency from the tolerance model with these values from the finite element method. In Fig. 4 there are shown ratios of the first vibration frequency obtained from the tolerance model ω ₁ to the same obtained from finite element method $\hat{\omega}_{1}$. The span L of the plate band is taken as a parameter. With the rise of the span the gradation of the effective properties is slower and the ratio of the frequencies is decreasing to 1.0. From Fig. 4 we can see that differences between values of the first vibration frequency for tolerance model and the same for a finite element method are smaller than 7%.

Fig. 4

Comparison of the values of the first vibration frequency obtained from tolerance model with those from FEM; the span L of the plate band is taken as a parameter

The aim of numerical calculations is to derive free vibrations frequencies for different volume fractions of the two component of the composite plate under considerations. In Fig. 5 are presented results for composite plate with steel beams and aluminum matrix.

Fig. 5

The first free vibrations frequency versus non-dimensional parameter d ₁/λ: ▲—d ₂/λ=1, ■—d ₂/λ=0, - - - - steel plate, — aluminum plate

Material properties assigned to steel and aluminum are as follows: steel—E=210 GPa, ρ=7800 kg/m³, v=0.3; aluminum—E=69 GPa, ρ=2720 kg/m³, v=0.3.

These diagrams show that the first free vibration frequency of a longitudinally graded cantilever plate could be greater or smaller than those of a steel and aluminum plate. For plate band on the span L=3 m with d ₂/λ=1.0 and d ₁/λ=0.0 (more aluminum on clamped boundary) the first frequency is 20% and 18% lower than the first frequency of a steel and aluminum plate, respectively. For plate band with d ₂/λ=0.0 and d ₁/λ=1.0 (more steel on clamped boundary) the first frequency is 25% and 32% higher than the first frequency of a steel and aluminum plate, respectively. From Fig. 5 we can confirm that composite which has only steel fraction on clamped boundary and only aluminum fraction on free boundary, make the first frequency largest. Similar results are given by Qian and Batra in paper [15] where we have deal with functionally graded cantilever plate made of steel and aluminum composite. In that paper a volume fraction of an aluminum constituent is expressed as power function of x ₂-coordinate and the effective properties of composite are deduced by Mori-Tanaka technique.

5.2 Annular plate

We shall investigate a simple problem of natural polar-symmetrical vibrations of an annular plate simply supported on its boundary. The fragment of midplane of this plate is shown in Fig. 6.

Fig. 6

Fragment of midplane of annular plate with longitudinally graded microstructure

Tolerance model

Setting w ⁰=w ⁰(ρ,t), V=V(ρ,t) we obtain from (17) the following system of equations of motion described in polar coordinate system (ξ ¹=φ,ξ ²=ρ)

(29)

where we have denoted $\tilde{B}^{2222} = B^{2222}$, $\tilde{B}^{1122} =\rho^{2}B^{1122}$, $\tilde{B}^{1111} = \rho^{4}B^{1111}$.

Homogenized model

Denoting $D_{r}(\rho) =B_{\mathit{eff}}^{2222}$, $D_{\varphi} (\rho) =\rho^{4}B_{\mathit{eff}}^{1111}$, $D_{r\varphi} (\rho) =\rho^{2}B_{\mathit{eff}}^{1122}$ we obtain from (21) equation of motion for the homogenized model of annular plate

(30)

The above equation represents one partial differential equation for the averaged displacement w ⁰(⋅,t) and has the form similar to equation of motion of circular plate with cylindrical orthotropy.

Numerical calculations

Substituting (24) into (29), (30) we derive equations with functional coefficients; hence in order to obtain the solution of these equations the finite difference method will be used.

In Fig. 7a–c are presented results for annular plate made from steel-aluminum composite. In Fig. 7a there are shown diagrams of the first free vibrations frequency for the annular plate with an inner radius R ₁=4 m, while in Fig. 7b and Fig. 7c for the annular plate with an inner radius R ₁=8 m and R ₁=12 m respectively. Figure 7d shows diagram of the first free vibrations frequency for the band plate. The span of all plates is equal R ₂−R ₁=3 m. The diagrams show value of first natural frequencies versus volume fraction of the beams where the ■—line relates to beams from aluminium, while ▲—line relates to beams from steel. These diagrams show that also for simply support longitudinally graded annular plate, the first free vibration frequency can be greater or smaller than that of a steel and aluminum plate. Let’s notice that, the biggest differences are for plate with smaller inner radius Fig. 7a (for volume fraction of beams equal 70% there are 16% lower than aluminum plate and 20% higher than steel plate, respectively). When the inner radius of plate rises, annular plate tends to band plate and these phenomena slowly disappear. For an annular plate with an inner radius R ₁=12 m (Fig. 7c) we can see that the first free vibrations frequency for composite plate is almost completely between frequencies for steel and aluminium plate.

Fig. 7

(a) The first free vibrations frequency for annular plate with inner radius R ₁=4 m. ▲—composite with aluminum matrix and steel beams, ■—composite plate with steel matrix and aluminum beams, - - - - aluminum plate, — steel plate. (b) The first free vibrations frequency for annular plate with inner radius R ₁=8 m. ▲—composite with aluminum matrix and steel beams, ■—composite plate with steel matrix and aluminum beams, - - - - aluminum plate, — steel plate. (c) The first free vibrations frequency for annular plate with inner radius R ₁=12 m. ▲—composite with aluminum matrix and steel beams, ■—composite plate with steel matrix and aluminum beams, - - - - aluminum plate, — steel plate. (d) The first free vibrations frequency for annular plate with inner radius) R ₁=∞ (band plate). ▲—composite with aluminum matrix and steel beams, ■—composite plate with steel matrix and aluminum beams, - - - - aluminum plate, — steel plate

6 Conclusions

In this study, in contrast to the majority FGM plates with stochastic microstructure, the plate with a deterministic but space-varying microstructure has been considered. The main feature of considered micro-stratified plates is that the effective properties are slowly varying along the layering. The results obtained in this contribution justify formulating the following conclusions:

• 1. The composite thin plates having functionally graded material structure in a certain direction and micro-periodic in a perpendicular direction are described by equations of motion involving only smooth coefficients. These coefficients vary in the midplane of the plate, are slowly varying in the preferred direction and constant in a perpendicular direction. The material properties of majority FGM plates are assumed to be graded through the thickness of the plate.

• 2. Since the proposed model equations have smooth and slowly varying functional coefficients then in most cases solutions to specific problems for functionally graded plates under consideration have to be obtained using numerical methods.

• 3. It is shown that the obtained averaged model equations make possible to find the compositional profile of a two-component longitudinally graded plate so that the first natural frequency is greater or smaller than that of each component plate. The similar results only for FGM rectangular plates are given in paper [15].

• 4. The general tolerance model (17) (as well as (23) for plate band and (29) for annular plate) describe effect of microstructure size on the dynamic behaviour of the functionally graded plate.