Abstract
The paper presents the author’s method of numerical modelling multi-body systems of a rail vehicle class. The method exploits dynamics of relative motion, which describes perturbations in general motion of the vehicle. Quite a few original elements are included in the author’s approach. This approach is compared to other possibilities of describing dynamics of multi-body systems in relative motion. The author’s method makes use of Kane’s equations that are opposed in the paper to the Newton-Euler approach that is used most often in the analogous applications. Numerical implementation of the theoretical results is also presented and a sample of the corresponding numerical analysis. Both these show the particular way to model dynamics of such systems efficiently and what consequences might be of the simplification in the description of relative motion. This appears to be more important than it is usually believed, particularly when accelerating or breaking the vehicle.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper concerns the dynamics of discrete mechanical systems in relative motion. The methods of modelling being discussed arise from needs of the rail vehicle dynamics. These needs come out from description of the dynamics relative to the frames moving along track centre line, from significant dimension of the vehicle-track systems, and from need of automatic generation of equations of motion (AGEM) for such systems. Recently many issues of the rail vehicle dynamics can be resolved with the commercial software packages as ADAMS, MEDYNA, SIMPACK, VAMPIRE and many others [1, 2] that build equations of motion automatically. Therefore many people think wrongly that there is no need to build such equations and the corresponding software individually and hence this issue became out of date. In the authors opinion most of the engineering problems can be treated in this way, while many advanced research problems of the rail vehicle dynamics cannot. This is mainly because of the so called black-box problem that makes it impossible to arbitrary user to get the insight into the code of the package and to make direct changes in this code. In research such possibility is the necessity very often. Consequently, there is no any problem to cite very many recent publications were their authors needed to build their own models and simulation software in order to perform their studies, e.g. [3–18]. This encourages the author of this paper to present the method he uses.
General review of options for the description of multi-body system (MBS) in relative motion is made in the paper. It makes the background for presenting the author’s own method. This method is based on Kane’s equations [19–21], in the version adapted to description of relative motion. It is opposed to Newton-Euler formalism (e.g. [22, 23]) used most often in computer applications of such type [24]. The considerations are of general character as long as possible. At the advanced stage however, it is possible to increase numerical efficiency in applications specialised to rail vehicles by exploitation of the specific features of such systems. Next the author’s software for computer generation of equations of motion and example of the numerical analysis with its use are presented.
In the present paper we treat in fact the systems of an open structure [25–28]. Example of such system S is shown in Fig. 1. It is composed of n bodies B j of mass centres C j (where j=1,…,n) and interconnecting elements. It is assumed for the systems of closed structure, which sometimes correspond to rail vehicle systems, that they can be represented by the appropriate open systems, however completed with the so called closing constraints [25, 27, 28]. We also confine ourselves to systems of rigid bodies, leaving out of consideration systems with the flexible bodies [20, 27, 29]. The systems composed of rigid bodies (discrete systems) are those most often used in modelling railway vehicle motion (dynamics). Quite often also the track model supplemented to vehicle model in order to consider both systems jointly is of discrete type.
The aim of current paper is first of all to represent the methods used by present author to model the systems of rail vehicle or rail vehicle-track class. These methods originate in dynamics of relative motion, of the bases known. On the other hand, however, the set of presented methods includes many original components by present author. These original constituents can be presented in the points as follows.
-
Derived and used in the method the general equations of relative motion for MBS, which are based on the Kane’s equations concept. They represent the Kane’s equations adapted to description of multi-body systems in the moving reference frames.
-
Derived and used in the method the equations of relative motion based on Huston’s results, suitable in the AGEM approach. Except extension of these results for dynamics of relative motion the extension from scleronomic (or free) systems to rheonomic systems is done through that derivation.
-
Derived and used in the method the general formulae that enable to build the adapted equations for holonomic and non-holonomic system, based on the equations for the free system. These formulae can also be applied selectively to particular type of the forces (inertia, external, and imaginary ones) rather than to the whole equations. It was shown that such approach is particularly effective for the systems of rail vehicle class.
-
Formulated and applied the general method for determining the components of linear and angular velocities of transportation. These kinematical quantities are indispensable when considering mechanical systems in motion relative to moving reference systems. Besides, this method was applied to several shapes of transition curves (TCs) for which the corresponding components were determined. The circular curve (CC) and straight track (ST) are special cases of the 3-d curve (TC with its superelevation ramp) and their components were also determined.
-
Numerical implementation of theoretical results listed above in the simulation software. Numerical implementations represent the software for particular 2-axle non-traction vehicles and the software in AGEM’s type where structure and dimension of the vehicle model can change.
-
Extensive verification of the method through simulation studies with the software as described above. Number of the problems studied in such a way runs into tens. Their most recent examples are given further on.
In most cases the original elements specified above were discussed individually. When the author happened to discuss some of them together they were presented partly at most. In the configuration presented in this article they are presented for the first time. Such joint presentation makes a new contribution because of two facts. First, it is impossible to identify the method by present author basing on very many sources on quite different topics. One should not expect the reader to read all these sources and combine them in the single coherent method. Note that these sources: treat particular issues in detail (comprehensively), some are in the author’s native language, and many do not refer to the complete modelling method as presented here at all. Second, here the information is carefully selected. Thanks to it the modelling method as a whole, rather than comprehensive details of the particular issues, is presented to the reader.
The advantage of the presented material is its completeness. Both the dynamical and kinematical issues of modelling the systems in view are treated in present article. This gives a chance for the reader to eventually adopt (become familiar with) the presented methods, basing on the single publication. In fact, the kinematical part of the considerations gives a chance to use the method in practice. Without presenting it, the really objective assessment of the discussed methods would be doubtful. Therefore, presentation of the method in the single source is one of this paper’s aims.
2 Methods describing dynamics of multi-body systems in relative motion and their connection with railway vehicle dynamics
In spite of rough similarity of rail vehicle to other moving objects, such as the rest of vehicles (e.g. road and off-road ones), airplanes and so on, two specific features distinguish its dynamics. The first one is description of phenomena in wheel-rail contact. The methods of that description are useful nowhere else. Therefore, if one wants the model and software to cover rail vehicles then one has to supplement more versatile elements with the specific ability of wheel-rail contact description.
The second distinguishing feature concerns the subject being considered in rail vehicle dynamics. Contrary to other objects, the subject for considerations is rarely absolute motion in relation to the Earth (i.e. relative to system A in Fig. 2). Here, there is no selection of motion trajectory or its freedom, as for motor cars on road or airplanes in space respectively, but there is the motion predefined in advance by the existing shape of the track. Thus, most often one is not interested in the known predefined motion (called the basic one). Instead he is interested in the perturbations of some ideal motion (basic motion) along track centre line. If reference systems in type of A′ (Fig. 2) follow the basic motion, then description of motion in relation to these systems is actually description of the perturbations (vehicle oscillations) [16, 22, 30].
Figure 2 represents the same as in Fig. 1 system S of n rigid bodies B j , however with the interconnecting elements omitted just to reduce details number. The OXYZ co-ordinate system denoted by A is the fixed (absolute) system. The systems O 1j xyz denoted by \(A'_{j}\) represent reference systems moving along track centre line (or trajectories parallel to it), which correspond to particular bodies B j (j=1,…,n). In case of general body B j the subscript j can alternatively be omitted for convenience. Note also that there is no absolute need for each body B j to have its own moving reference system \(A'_{j}\). In general, the bodies can also share them quite arbitrarily if it is eventually useful. The vectors r j , \(\boldsymbol{r}'_{j}\), and r o1j represent the radius vectors of mass centres C j in A and in A′, and origin O 1j of A′ in A, respectively.
Description of motion in the systems moving along track centre line, that is a space curve in general, generates some difficulties in comparison to description in the fixed (inertial) systems. In the most general view there are three possibilities of describing the perturbations understood as above, which are in one’s disposal and in practical use. And so, description of motion in the (absolute) reference system is possible. Then, however, one needs possibility to deduct given basic motion (transportation) from absolute motion to determine the perturbations. Alternatively, the dynamics of an object can be directly the dynamics of relative motion [22, 30, 31], i.e. in moving (non-inertial) reference systems. Except the above two possibilities there exists also the third one. Here, equations describe absolute motion, while co-ordinates taken (at least some) refer to motion in relation to moving reference frames. It is obvious that differently constructed equations correspond to these three possibilities [31].
Possibility 1
Co-ordinates relative to inertial reference system in type of A (Fig. 2) and any formalism valid for motion relative to A (absolute motion).
where: fd—operator representing any formalism; B—inertia forces of motion in A; Z—external forces; \(x,\dot{x}\)—co-ordinates and velocities, respectively; u(t), v(t), w(t)—given functions of time representing displacements, velocities, and accelerations of transportation, i.e. of A′ relative to A.
Possibility 2
Co-ordinates relative to non-inertial reference system in type of A′ (Fig. 2) and any formalism adapted to description in A′ (direct methods of the dynamics of relative motion).
where: B′—inertia forces in motion relative to A′; P—imaginary forces (inertia forces arising from and depending on the transportation); fp—imaginary forces operator, appropriate for selected formalism.
Possibility 3
Co-ordinates relative to A′, as well as any formalism valid in A. In practice it is variational principle or formalism directly based on it.

where fz—operator for variational principle.
As (1)–(3) are recorded in the most general form possible, thus their deeper discussion is a must. Let us start it with the equalities on the very left-hand sides of (1)–(3). In fact they represent dynamical equations of motion. In case of (3) equations of motion are supplemented with the algebraic kinematical relations. They relate absolute and relative variables (displacements, velocities and accelerations). These kinematical relations must be substituted into the differential equations in order to solve them. The mentioned equations of motion can be either vectorial or scalar (matrix) in their form. The vectorial equations have to be transformed into the scalar ones, when one is going to solve them with respect to the co-ordinates and velocities adopted. Obviously, the scalar equations take a form of the second order ordinary differential equations.
Now let us discuss the braces on right-hand sides of the equations of motion (after the arrows). They represent both the linear and the angular direct solutions of the equations of motion. These are displacements (co-ordinates) and velocities, relative to inertial (OXYZ) or/and to non-inertial (O 1j xyz) systems. In case of (1) the direct solution x(t), \(\dot{x}(t)\) is further processed in order to get relative displacements (co-ordinates) x′(t) and velocities \(\dot{x}'(t)\). One can note that the same kinematical relations as those used in (3) enable to do it. Unlike (1), in case of (2) and (3) relative co-ordinates x′(t) and velocities \(\dot{x}'(t)\) are the direct solution of the equations of motion.
Third, the differential equations have got typical physical interpretation of the dynamical equations of motion. This becomes obvious when meaning of forces B, B′, Z and P is taken into account. As explained above the first two represent inertia forces, the third external forces, and the last one imaginary forces. The operators fd, fp and fz do not change that interpretation. Just mentioned operators indicate that mentioned forces must be expressed in accelerations, velocities, and co-ordinates adopted in accordance with the formalism chosen. In particular, these could be Cartesian co-ordinates, generalised co-ordinates, generalised velocities, quasi-velocities, and so on. The general form of formulae (1)–(3) makes the equations of motion valid for both unconstrained and constrained systems. When the constraints exist in the system, then operators fd, fp and fz represent also the operations necessary to take account of them, appropriate for the formalism in use. These operations are quite typical (identical with those for the absolute motion analysis) and will be explained further on, when example equations of motion are presented. Then information on parameters the forces B, B′, P and Z depend on is also given.
It is rather clear that some formalisms are better and some worse suited to the roles corresponding to Possibilities 1–3. The literature analysis shows that number of applications (numerical implementations) in the particular roles is quite different and their type as well. These problems are continued in the next subsection and at the beginning of Sect. 3.
2.1 Application of the methods based on equations of absolute motion
Current subsection refers to application of Possibilities 1 and 3 formulated above. Note, that for both cases equations of motion, precisely their initial forms respectively in (1) and (3), are the same. Substantial differences exist however, that we treat below.
Within Possibility 1, the equations of motion are solved first and next deduction of functions defining transportation s(t), v(t) and w(t) from the solution is made. As an effect we get a chance to determine co-ordinates, velocities, and even accelerations in relation to moving reference systems. Such procedure does not find many supporters and is the most rare in applications concerning rail vehicle systems. The examples can be found in [1, 32]. It is like that probably because the co-ordinates and velocities we obtain directly from integration of the equations are not those rail vehicle dynamics is interested in. Secondly, it seems that such way of obtaining the co-ordinates and velocities can lead to the biggest errors. The cause could be very big possible difference in values of co-ordinates and velocities in absolute (inertial) and relative (non-inertial) systems.
Within Possibility 3, prior the equations of motion are solved, relationships linking up absolute and relative quantities through functions s(t), v(t) and w(t) are introduced into some of these equations. The equations being subject to such operation become equations of relative motion. They are not, however, general equations of relative motion with terms dependent on transportation explicitly recorded (separated), as it is in (2). They are valid for the particular case only, defined with the given s(t), v(t), w(t) functions. Each time these functions change, the equation must be build from the beginning and the absolute motion determined. It is some disadvantage of this method additionally intensified if one is interested in the easy determination of imaginary forces (for instance centrifugal ones) and moments. On the other hand, the advantage here is identical initial form of the equations related to absolute and relative motion. This advantage manifests especially when we need to analyse systems where partially absolute and partially relative motions are of interest. Some versatility visible here is one of the reasons for use of Possibility 3 by many MBS formalisms exploited in commercial packages that are capable of analysing relative motion, e.g. [22, 25, 33–35].
At the end note that there are the sources where interest in motion relative to the track-based moving reference frames is expressed, nevertheless no particular method of the description is chosen, e.g. [36].
2.2 The methods based on equations of relative motion represented in literature
Current subsection is a review for the literature examples of usage of Possibility 2 formulated at the beginning of Sect. 2. No works by the author of present article are embodied, however. And so, in the early monographic works treating MBS formalisms, e.g. [25, 30], the starting point for the equations of relative motion are vectorial equations for a single free rigid body. Let us exploit their form related to [37], however exactly as it is presented in [38].


where: \(\boldsymbol{r}'_{C}\)—radius vector of mass centre C of body in O 1 xyz system; m, J—body mass and inertia tensor with respect to mass centre C; \(\boldsymbol{v}'_{C}\), \(\boldsymbol{a}'_{C}\)—velocity and acceleration of C in relative motion (relative to O 1 xyz); ω′, ε′—body’s angular velocity and acceleration in relative motion; a o1, ω, ε, R C , T C —absolute acceleration of origin O 1 (relative to OXYZ), angular velocity and acceleration of transportation (i.e. of O 1 xyz in OXYZ), resultant of external forces acting on body and resultant of external torques acting on body with respect to the centre C; and E, ϑ—unit tensor and the trace of J, so ϑ=J 11+J 22+J 33.
While deriving (4) and (5) the fundamental relationships were used that enable to express the absolute kinematical variables through the relative ones. The absolute acceleration p C of mass centre C can be expressed as a following sum (e.g. [19, 37])
Above, the undefined third addend is the acceleration caused by the angular acceleration ε of A′, the forth addend represents centrifugal acceleration due to rotation of A′, and the last addend is the Coriolis acceleration. Besides, if we denote absolute angular velocity and acceleration of B with respect to A by θ and α then they can be expressed as follows [39]


where (d′ω′/dt) indicates local time differentiation of ω′ with respect to A′. In order to get (4) the relationship (6) was introduced into the original vector form of Newton dynamical equation. In order to get (5) the relationships (7) and (8) were introduced into the original vector form of the Euler dynamical equation. It is seen that final form of (4) is the direct result of the operations described above. Unlike (4), in order to get final form of (5) intensive manipulation and use of the identity known in the tensor calculus were necessary.
Next, making use of (4) and (5), matrix form of the equations is recorded. In some recent monographs (e.g. [34, 35]) such matrix form is recorded directly without explicit reference to equations in type of (4) and (5). Explicitly the passage from vector to matrix representation of the equations of relative motion was done in [25]. The set of the equations as in [25], however including the term missed for spherical motion there, has got the form as given below.


In the analogous equations represented in [34, 35] the relationship (7) is used and some manipulation done in the equation of spherical motion. Matrices in (9) and (10) have got their counterparts in vectors and tensors present in (4) and (5). Obviously, some vector bases have to be chosen to express these matrices. In particular, in case of (9) they can be are expressed for the basis matching the transportation system O
1
xyz (Fig. 1). In case of (10) they can be expressed in the body-fixed reference frame. For any of the bases i
m
(m=1,2,3) and arbitrary vector c that means c=(i
m
)T
c, and for dyadic \(\breve{\mathbf{J}}\) that means \(\breve{\mathbf{J}} = (\boldsymbol{i}_{m})^{\mathrm{T}}\mathbf{J}\boldsymbol{i}_{m}\). At the same time c=[c
α
], J=[J
αβ
] where (α,β=1,2,3), and  represents skew-symmetric matrix of arbitrary vector b=(i
m
)T
b.
represents skew-symmetric matrix of arbitrary vector b=(i
m
)T
b.
If we denote  (i=1,…,6;j=1,2,3) and
(i=1,…,6;j=1,2,3) and

then (9) and (10) recorded jointly take a form of the dynamical equations, as in [22, 25].
where Q is matrix of inertia forces and Λ is matrix of external (active) forces. Matrix of inertia I is not symmetric in general. The variables are represented in matrices x I, x II here. Kinematical equations for these variables are as follows: \(\dot{\mathbf{x}}_{\mathrm{I}}=\mathbf{X}_{\mathrm{I}}(\mathbf{x}_{\mathrm{I}},\mathbf{x}_{\mathrm{II}})=\hat{\mathbf{X}}_{\mathrm{I}}(\mathbf{x}_{\mathrm{I}})\mathbf{x}_{\mathrm{II}}= \mathbf{K}(\mathbf{x}_{\mathrm{I}})\mathbf{x}_{\mathrm{II}}\). Note that physical interpretation of these variables has much in common with that for the original Newton-Euler equations. The difference is their definition with respect to the moving (non-inertial) reference frames but not with respect to the absolute (inertial) reference frames. The common feature is that in case of the dynamic equations for the mass centre translational motion, the relative translational velocity components are still the generalized velocities. In case of the dynamic equations of rotational motion with respect to the mass centre, the relative rotational velocity components are still quasi-velocities. In order to emphasize relative sense of these variables let us use the following identities: \(\mathbf{x}_{\mathrm{I}} \equiv \mathbf{x}'_{\mathrm{I}}\), \(\mathbf{x}_{\mathrm{II}} \equiv \mathbf{x}'_{\mathrm{II}}\), \(\dot{\mathbf{x}}_{\mathrm{I}}\equiv\dot{\mathbf{x}}'_{\mathrm{I}}\), and \(\dot{\mathbf{x}}_{\mathrm{II}}\equiv\dot{\mathbf{x}}'_{\mathrm{II}}\). Here and further on superscript “′” is used to distinguish the relative variables.
Note that (12) possess the general form that is the same for the relative and absolute variables, i.e. relative to the absolute and relative reference frames. For the absolute systems simply Q 1 and some terms in explicit form of Q 2 vanish. Hence, further considerations in [25, 34] are performed without distinguishing both this cases, i.e. without any next comments on the relative motion or more specifically the relative dynamics. Due to subject of this paper we will do differently. Now, we will built the explicit equations (explicit multi-body formalisms) for description of motion relative to moving reference frame(s). Such explicit equations are also derived (presented) in [22, 30], however the concept of notation is different there.
When it is needed, it is possible to extend the considerations and change the variables, of the interpretation as described above, for any set of the generalized co-ordinates and velocities that describes univocally state of the system in relative motion. Number of these new variables has to be the same as before. General form of (12) remains still valid when we introduce arbitrary generalised co-ordinates \(\mathbf{w}'_{\mathrm{I}}\) and velocities \(\mathbf{w}'_{\mathrm{II}}\). When assuming that K(x I) is non-singular,
and kinematical equations
it can be recorded that


After introduction of (14) into (12) matrix equation the system takes the form
where

The system considered till now is a single free rigid body. Assume now, that holonomic and non-holonomic constraints appear of the implicit form
It is a well known fact (e.g. [25]) that after differentiation of the first item in (17) with respect to time we obtain the constraints on the velocity level linear in velocities (velocity variables). It is also known that in case of the mechanical problems non-holonomic constraints are linear in velocities, too. These facts are often used to represent both types of the constraints in the unified form. Here, assuming number of all constraints equal to r, it can be done as below

where Φ is constraints matrix (r×6n) and γ is column matrix (r×1) that vanishes for stationary constraints. In such circumstances the matrix equation of motion can be recorded. Thus it is
where λ is column matrix (r×1) of Lagrange’s multipliers λ=[λ 1 λ 2⋯λ r ]T and \(\hat{\boldsymbol{\Lambda}}_{z}\) represents a vector of the generalized constraint reaction (passive) forces that act in the directions defined by the w II variables.
When one wants to solve (15) or (19) then one should note that \(\hat{\mathbf{I}}\) is not symmetrical matrix in general case. This problem can be handled by left-hand side multiplication of these equations (all their terms on both sides) through the transpose matrix Ω T. Then on the left-hand side the modified symmetrical matrix \(\breve{\mathbf{I}} = \boldsymbol{\Omega}^{\mathrm{T}}\hat{\mathbf{I}} =\boldsymbol{\Omega}^{\mathrm{T}}\mathbf{I}\boldsymbol{\Omega}\) appears and \(\breve{\mathbf{I}} ^{ - 1}\) can be determined. The operation of this multiplication is simple so there is no need to present other terms of the equations explicitly, here.
To describe relative motion of the constrained system by the reduced matrix equation in generalised independent co-ordinates \(\mathbf{y}'_{\mathrm{I}}\) and velocities \(\mathbf{y}'_{\mathrm{II}}\), (19) need to be converted. First, the constraint forces \(\hat{\boldsymbol{\Lambda}} _{z}\) have to vanish. Second, variables \(\mathbf{w}'_{\mathrm{I}}\) and \(\mathbf{w}'_{\mathrm{II}}\) need to be replaced with \(\mathbf{y}'_{\mathrm{I}}\) and \(\mathbf{y}'_{\mathrm{II}}\). Third, number of the equations shell be reduced. It is shown for absolute systems in many publications, also in [25, 30], that such conversion is possible. Now, we will adopt these results for the needs of the relative motion dynamics. It was shown that general solution of (18) is necessary to achieve the goal. It leads to the explicit constraint equations at the velocity level. A big challenge is usually the derivation of such explicit constraint equations, which are often obtained from the implicit form (17). The derivation is usually possible for the case of simple (linear in velocities) non-holonomic constraints, and not for the general (non-linear) ones as introduced in (17). As non-holonomic constraints in the railway systems do not happen in practice, we can assume that such operation is possible. Then the matrix representation of the explicit constraint algebraic equations on the velocity level is as follows

It is here the proper place to remind that for the system subjected to the holonomic and non-holonomic constraints number of the independent co-ordinates and velocities differ. That is why in general case dimension of the \(\mathbf{y}'_{\mathrm{I}}\) vector is bigger than of the \(\mathbf{y}'_{\mathrm{II}}\) vector by the number of the non-holonomic constraints. Also number of y I variables is smaller than of w I by the number of the holonomic constraints, while number of y II variables is smaller than of w II by the total number of the constraints.
The corresponding equations of motion in independent generalized velocities (state-space equations) with variables \(\mathbf{w}'_{\mathrm{I}}\), \(\mathbf{w}'_{\mathrm{II}}\) replaced with \(\mathbf{y}'_{\mathrm{I}}\), \(\mathbf{y}'_{\mathrm{II}}\) are
Now inertia matrix \(\tilde{\mathbf{I}}\) is symmetrical thanks to left-hand side multiplication by  within (21). Make note the following relationships are present in (21):
within (21). Make note the following relationships are present in (21):

Kinematical equations linking state variables y I and y II up, which correspond to (21) can be expressed in the form \(\dot{\mathbf{y}}'_{\mathrm{I}} = \mathbf{Y}_{\mathrm{I}}(\mathbf{y}'_{\mathrm{I}},\mathbf{y}'_{\mathrm{II}})=\hat{\mathbf{Y}}_{\mathrm{I}}(\mathbf{y}'_{\mathrm{I}})\mathbf{y}'_{\mathrm{II}}\). When solving (21) in the presence of non-holonomic constraints their equations ought to be enclosed in the system. For example they can be extracted from (18) or taken as the second item in (17).
The equations presented so far treated the single body. It was shown in [25] that forms of (12), (15), (19) and (21) can be generalised for any number of bodies. In terms of notation it is trivial and does not move us forward from the point of view of imaginary forces and torques form.
Let us now discuss form of the imaginary forces in the just presented equations. In spite of illusory separation of the imaginary forces and torques (i.e. those dependent on the transportation) in (12), (15), (19) and (21), the corresponding Q terms do not contain just the forces and torques dependent on transportation. This is because Q 2 contains matrices dependent on absolute angular velocity θ=ω+ω′ and on ω×ω′, being a sum and vector product of the transportation and relative angular velocities, respectively. It results in Q 2 being a mixture of imaginary forces with non-linear kinematics terms, e.g. [34]. Adoption of generalised co-ordinates can intensify such mixing, what is explicitly seen in the second items of (16) and (22). Consequently, it is impossible (at least difficult) to extract the imaginary forces’ terms from the equations for such their representation. For instance, calculation of wheelsets’ gyroscopic moments, connected with their rotation during vehicle motion, is not possible without the additional measures. Not as drastic example, but still similar, is the centrifugal forces in Q 1. The reason is calculation of the matrix being a sum of the terms within brackets in (9) before the multiplication by inertia matrix is done. The imaginary forces and torques happen sometimes to be a matter of interest in railway vehicle dynamics, however (e.g. [16, 40]). As we can see, adoption of computationally optimal form of (9) and (10) cannot be always treated as the ideal one.
Equations just presented form the recipe for computer generation of dynamical equations of relative motion with the use of multi-body formalisms originated from the Newton-Euler equations. Note that building the equations is operation on the matrices present in (9)–(22). In order to perform it, these matrices have to be calculated first. This calculation is possible after unit vector bases connected with reference systems are chosen. At the same time, the bases for Newton equations (linear motions) and Euler equations (rotations) can be different. It means in case of numerical generation of equations that each launch of the software requires repetition of: vector bases’ selection, calculation of all matrices for these bases, and finally operations on these matrices in order to build equations. It is seen that building the equations are the operations on objects dependent on the selected vector bases. It will be shown further on that such feature does not concern the method by present author.
In view of numerical applications, at least two facts should be reminded related to solving the presented equations. Firstly, in case of (19) it is significant number of the equations. It arises from number of co-ordinates utilised in a formalism, called the maximum number in [1, 2, 24, 41], and from number of equations of constraints. Secondly, it is solving the set of differential-algebraic equations (DAE) in case of (19). It still presents quite a big trouble in general case [24, 42]. Within the domain of rail vehicles [43] refers to it. Discussion of that issue exceeds the framework of this paper. In conclusion, if constraint reaction forces are of no interest and no non-holonomic constraints exist, then it is better to use the formalisms employing the independent co-ordinates. Their number is called in [1, 2, 24, 41] the minimum number, and accordingly reduced number of the ordinary differential equations (ODEs) describes the system.
3 The author’s method exploiting adapted Kane’s equations for computer modelling systems of rail vehicle class
Equations of motion valid in absolute reference frames can be adapted, so as they enable to describe multi-body system in moving reference frames (co-ordinate systems). Then they can be applied according to Possibility 2 defined at the beginning of Sect. 2. In other words direct methods of the dynamics of relative motion can be utilised. Example of such adaptations was shown in Sect. 2.2. Below we refer to the adaptation of Kane’s equations, with main emphasis on their form suitable in the AGEM.
The formal adaptation of original Kane’s equations, i.e. in the vectorial form, was performed by the author twice. It was done in his D.Sc. thesis and in [39]. Obtained equations of relative motion make it possible to describe any discrete system composed of particles and rigid bodies. At the same time, description of the systems composed exclusively of the particles and exclusively of the bodies is possible. Despite the same result, different methods of the derivation were applied in both cases. In the thesis, the starting point was original Kane’s equations for a system of particles. In [39] that was Jourdain’s principle for a system of rigid bodies. Both used formalisms are obviously valid in inertial reference systems. Fundamental for the derivation, no matter which method is used, was determination of the relative partial velocities [39]. Invoke this result now for so called simple non-holonomic system [19] of n rigid bodies.


where: \(\boldsymbol{v}'_{j}\), \(\boldsymbol{\omega}'_{j}\)—relative velocity of the centre C j and angular velocity of body j (in A′); u 1,…,u l —independent quasi-velocities; j—body indicator (j=1,…,n); l—degrees of freedom number; \(\hat{\boldsymbol{v}}'_{j_{\rho}}\), \(\hat{\boldsymbol{\omega}}'_{j_{\rho}}\)—correspondingly, ρ-th relative non-holonomic partial velocity of mass centre C j of body j relative to \(A'_{(j)}\) and ρ-th relative non-holonomic partial angular velocity of body B j relative to \(A'_{(j)}\), being the functions of generalised co-ordinates q 1,…,q k ; k—number of independent co-ordinates q; \(\hat{\boldsymbol{v}}'_{j_{t}}, \hat{\boldsymbol{\omega}}'_{j_{t}}\)—free terms, being the functions of time t; \(\boldsymbol{r}'_{j}\), \(\boldsymbol{\varphi}'_{j}\)—radius vector of C j with respect to origin of \(A'_{(j)}\) system and vector of infinitesimal rotation of B j with respect to \(A'_{(j)}\); and “^”—indicator of non-holonomic system variable.
Here let us base on Jourdain’s principle that the virtual power of reaction forces and moments resulting from constraints vanishes. The virtual velocity of rigid body’s mass centre and virtual angular velocity of any rigid body B j in the absolute reference system are


where δ is symbol of variation, \(\boldsymbol{v}_{j_{\rho}}\), \(\boldsymbol{\theta} _{j_{\rho}}\) denote partial velocities of mass centre and partial angular velocities of the j-th body. Jourdain’s principle for the system of n rigid bodies can be expressed as follows:
The new denotations mean: m j —mass of the body j, a j —absolute acceleration of the centre C j (in A), ε j —absolute angular acceleration of body j, and J j inertia tensor of body j.
If the quasi-velocities u ρ are taken in a specific way, i.e. relative to noninertial system of A′ type (Fig. 2), then (27) still holds. Then, however, relative partial velocities appear in (25), (26) since relative velocities \(\boldsymbol{v}'_{j},\boldsymbol{\omega} '_{j}\) are those of interest and those dependent on such specific generalized velocities. Note, that according to Fig. 2 the absolute position of mass centre C j and consequently the absolute velocity of C j are as follows:


Substituting (29) in (25), and then (7), for j-th body, in (26) one can write for translational and angular virtual velocities, respectively:


Substituting (30) and (31) in (27) one can write

For any set of l independent variations δu 1,δu 2,…,δu l , (32) is valid if and only if the l equations given below are satisfied.

After introduction of (6)–(8) for each body j in these l equations and manipulation analogous to that explained below (8) one can obtain the adapted Kane’s equations in the form as follows.

where new denotations: \(\boldsymbol{a}'_{j}\)—relative acceleration of the centre C j (in A′); \(\boldsymbol{\varepsilon}'_{j}\)—relative angular acceleration of body j; a o1j , ω j , ε j —linear acceleration and angular velocity and acceleration of transportation, i.e., of \(A'_{j}\) relative to A, respectively; R j , T j —general denotation of resultants of forces and torques; E, ϑ j —unit tensor and first invariant of J j .
First four terms in (34) have got their absolute counterparts in the original Kane’s equations, i.e. in those valid in inertial systems. The first two are forces and torques of inertia, respectively, coming out from relative motion, i.e. motion relative to the reference systems of A′ type (see Fig. 2). The third and forth terms are external (active) forces and torques, identical with those in inertial system. The fifth and sixth terms have got no counterparts and are of the correction character. They include imaginary forces and torques of inertia, which depend on the transportation. Note also, that despite presence of vectors and tensors of rank two in (34) these equations are in fact the scalar ones, since calculation of the scalar products is the last performed operation.
Equations obtained on the basis of (34) are equations of relative motion, which can be built with use of the formal steps typical for the Kane’s method [19, 20], and which are valid for non-holonomic system. Solving these equations is possible only with equations of non-holonomic constraints [39]. It can be demonstrated [39], like for inertial systems, that here also the case of non-holonomic system is the most general one. The cases of holonomic and free systems are its special cases. Therefore (34) is valid also for such systems. The basic difference consists in adoption of relative partial velocities adequately to the case. It can be seen that (34) have got the form not suitable for a computer generation of equations.
If we combine in (34) forces and torques of the same type then we will get notation that refers to original matrix form of Kane’s equations [19, 20]
Consequently, the sum of scalar products of forces by linear- and of torques by angular relative non-holonomic partial velocities in (34) contributes to generalised forces of inertia in relative motion \(\hat{F}_{\rho} ^{*}\). The sum of analogous products for external forces and torques contributes to generalised external forces \(\hat{F}_{\rho}\). Finally, the sum of analogous products for imaginary forces and torques contributes to the generalised imaginary forces \(\hat{F}_{\rho}^{**}\).
In spite of matrix notation, (35) has not found its place in the computer modelling. It is like that because they are a direct outcome of the vectorial notation of (34). They are not a recipe, that enables to realise operations on components of all vectors and tensors in direct and easy way, what is indispensable in the computer generation of equations of motion.
3.1 The method for computer generation of equations of relative motion
The key element while obtaining adapted Kane’s equations, in the form suitable in computer generation of equations, is expressing the relative velocity \(\boldsymbol{v}'_{j}\) of mass centre and relative angular velocity \(\boldsymbol{\omega}'_{j}\) of j-th body in relative partial velocities. Starting from (23) and (24) one can get [39]


where \(\hat{v}'_{j\rho m}\), \(\hat{\omega}'_{j\rho m}\) are components of relative linear and angular partial velocities \(\hat{\boldsymbol{v}}'_{j_{\rho}}\), \(\hat{\boldsymbol{\omega}}'_{j_{\rho}}\), called alternatively their coefficients. Note explicit dependence of coefficients \(\hat{v}'_{jtm}\), \(\hat{\omega}'_{jtm}\) on time t. Indicators m define directions of unit vectors \(\boldsymbol{i}_{m}^{(j)}\) (m=1,2,3) for axes of reference systems, where \(\boldsymbol{v}'_{j}\) and \(\boldsymbol{\omega} '_{j}\) are expressed.
Relationships (36) and (37) make it possible to convert scalar components in (35), that arise directly from (34), into the following form:



where: \(R^{*}_{jm}\), R jm , \(R^{**}_{jm}\), \(T^{*}_{jm}\), T jm , \(T^{**}_{jm}\)—components in transportation systems (moving reference frames defined by \(\boldsymbol{i}_{m}^{(j)}\)) of resultant forces \(\boldsymbol{R}_{j}^{*}\), R j , \(\boldsymbol{R}_{j}^{**}\) and torques \(\boldsymbol{T}^{*}_{j}\), T j , \(\boldsymbol{T}^{**}_{j}\). In the very last forms of relationships (36)–(40) summing up over repeated indices was used. It enabled to eliminate some sum signs. We use this type of notation also in (41)–(44) and (46).
In order to shorten a process of building the equations let us make use of the correction character of imaginary forces, explained under (34). As a consequence, we can adopt form of external forces and forces of inertia valid in inertial systems, replacing only the absolute variables (in OXYZ) with the relative ones (in O 1 xyz). According to the above we can make use of the results presented by Huston for the inertial (absolute) systems, e.g. [33, 44], and next supplement them with the imaginary forces. Thus we can write down
and


where J jsm and J jsw are components of inertia tensor of the body j and e abc is permutation symbol. Compared to the original Huston’s result some important differences are present in (43). First, index (′) was used to indicate relative variables. Second, the record was completed with correction forces of inertia \(\hat{F}_{\rho}^{**}\) (imaginary forces and torques). Third, terms in the last three rows of (43) are extension of the original equations to rheonomic systems and vanish for scleronomic systems. This extension was originally carried out in [39]. It arises from use of \(\boldsymbol{v}'_{j}\) and \(\boldsymbol{\omega} '_{j}\) as in (36) and (37) in the derivation process. They include coefficients \(\hat{v}'_{jtm}\), \(\hat{\omega}'_{jtm}\) explicitly dependent on time and which are valid for rheonomic systems. Originally, expressions for \(\boldsymbol{v}'_{j}\) and \(\boldsymbol{\omega} '_{j}\) do not include such coefficients and are valid for scleronomic systems. Step by step derivation of (41)–(43), i.e. their formal adaptation, is presented in [39]. Its essential element is differentiation of (36) and (37) in order to define the accelerations of bodies, the linear ones \(\boldsymbol{a}'_{j}\) of mass centres and the angular ones \(\boldsymbol{\varepsilon}'_{j}\).
The supplement to (10) are the kinematical equations. Their general form is

that is valid in scleronomic and rheonomic systems. This form simplifies for scleronomic systems as last terms of the sum vanish, i.e. p σ (q,t)=0.
Equations (41)–(43) supplemented with final form of (39) enable computer generation of external and inertial forces and torques in relative motion. The necessary effort is identical with that for the inertial systems. Now, let us present imaginary forces and torques in the form corresponding to (39), (41)–(43), so that their computer generation is also possible. In order to do it let us extract generalised imaginary forces from (34). After some manipulation it is:

According to [37] the terms of the generalized forces are called as follows: the first term are inertia forces of translation, the second and third terms represent centrifugal forces of inertia, the forth and fifth ones are inertia forces of rotation, and the sixth and seventh ones are gyroscopic forces. Now, substituting (36) and (37) into (45) and using matrix calculus yields an expression we are interested in.

Formulae (41)–(43) and (46) express generalised forces, including imaginary ones, explicitly by quasi-velocities. All components in the mentioned equations are defined for directions defined by \(\boldsymbol{i}_{m}^{(j)}\). These components represent vectors and tensors present in (34). Discussed formulae are extension of Huston results, e.g. [33, 44], to rheonomic systems and to description in non-inertial (moving) reference systems [39].
3.2 General comments on using the methods based on the Kane’s equations
Presented form of the adapted Kane’s equations might be to some people a little discouraging. This is because of inherent complexity of (34), (41)–(43) and (46), especially when compared to (19) and (21). It is going to be explained below that this first impression is misleading and some important advantages come out from the equations as presented. To take advantage of these advantages the equations have to be used in the software. Eventual fully matrix form of the equations would probably kill the advantages Kane’s equations possess. Such a form would only shorten the notation in the paper rather than is necessary while building the software for computer generation of equations of motion. Note also, that useful elements of the matrix formulation are in fact already present in the formulae provided. For example these are (38)–(41). Also many of the quantities present in the discussed equations are represented in the software as arrays that in general also represent matrices.
Quite fundamental feature (34) and (41)–(43) possess is the same general form for free, holonomic and non-holonomic systems. For a holonomic system k=l, while for a free one k=l=6n; where n is number of rigid bodies in the system. The cases distinguish from each other in the form of matrix of partial velocities’ coefficients \(\hat{v}'_{j\rho m}\), \(\hat{\omega}'_{j\rho m}\). In case of free and holonomic systems equations (41) and (44) are sufficient to find the solution. In case of non-holonomic system (k−l) equations of non-holonomic constraints supplement (41) and (44).
Equation (41) together with (42), (43) and (46) is the recipe for computer generation of dynamical equations of motion. This recipe is valid for any unit vector basis since it comes out directly from vectorial counterpart (34). It is seen from (41)–(43) and (46) that building the equations consists of operations on the components of vectors and tensors present there. Thanks to it, record of quantities in the form dependent on the taken vector bases, takes place at the very end of process of building the equations. It is not at the very beginning like in the formalisms based on Newton-Euler equations presented in Sect. 2.2. Just described advantage of Kane equations, distinctive for this formalism, is the reason for frequent use of that type of equations in the software for computer generation of equations of motion.
Besides, the methods exist for Kane equations of determining constraint reaction forces. We mean two methods described in [19] and [33, 43], respectively. They make possible both the overall determination and the selective determination of the constraint forces. However, the method in [33, 43] is better suited in the first case, while in [19] is better for the second case. Note also, that Newton-Euler equations transformed into (19) enable just the overall determination of constraint forces. The methods for Kane equations are suitable in numerical implementation due to their arrangement and clarity. Moreover, when determining the constraint forces differential equations of motion are solved independently of algebraic equations, what is not the case for Newton-Euler equations. Discussed methods can be applied only if any of the external forces acting on the system does not depend on the constraint reaction forces. If it is not the case, there are no general methods suitable for separating the differential and algebraic equations in case of numerical applications. Unfortunately, in rail vehicles the tangential wheel-rail contact forces depend on the normal forces (being in fact the constraint reaction forces). So, use of the described methods for the mentioned types of forces and for simultaneous numerical generation of equations of motion of rail vehicles is not possible.
3.3 Utilising specificity of systems of a rail vehicle class
Despite above explained general advantages, it does not mean that (41)–(43) and (46) have no weak points at the closer look. It can be expected that especially the last one of the mentioned equations has got certain disadvantages [39] connected with its numerical efficiency. One can see that determination of imaginary forces according to (46) means carrying out operations on components of vectors and tensors. In case of big systems it is many quite complex, but also recurrent operations. For instance, matrices of \(\hat{v}'_{j\rho m}\), \(\hat{\omega}'_{j\rho m}\) coefficients are large 3-dimensional objects multiplied by themselves in some of (46) components. Any simplification in numerical calculation of imaginary forces is therefore desirable, here.
In this context, the alternative method was proposed by the author. Originally it was formulated as a theorem. Here, as in [31, 39], we shall confine ourselves to analytical formulae that constitute base of its proof. In order to get to these formulae we shall start from demonstration of relationships between relative partial velocities for non-holonomic, holonomic and free systems.
Let us impose q=6n−k holonomic constraints on system of n free rigid bodies and next m=k−l non-holonomic constraints on the holonomic system. If both types of constraints are linearly dependent on quasi-velocities, then expressing dependent quasi-velocities u σ through independent ones u ρ we obtain


where: k, l—numbers of degrees of freedom for holonomic and non-holonomic systems; A σρ , B σρ and C σ , D σ —functional coefficients of generalised co-ordinates q 1,…,q k and time t. Introducing denotation “∼” for free system variables let us express formulae (23) and (24) for such a system. In this case free terms depending on time equal zero.


In case of holonomic system formulae (23) and (24) take the following forms:


Substituting now formula (47) in (49) yields:

Comparison of (53) to (51) enable to record the relation between relative linear partial velocities of holonomic and of free systems. At the same time analogous steps can be applied to (47) and (50) for relative angular velocities. Thus


Introduce now formula (48) into (51). It yields

Comparison of (56) to (23) enable to record the relation between relative linear partial velocities of non-holonomic and of holonomic systems. At the same time analogous steps can be applied to (48) and (52) for relative angular velocities. Hence:


Let us now search for relation between arbitrary type of generalised forces for free and holonomic systems. Take any of the generalised forces (38)–(40), leaving out index for a given force type, and substitute (54) and (55) in it. In instance of the holonomic system replacement of \(\hat{\boldsymbol{v}}'_{j_{\rho}}\), \(\hat{\boldsymbol{\omega}}'_{j_{\rho}}\) and l for \(\boldsymbol{v}'_{j_{\rho}}\), \(\boldsymbol{\omega} '_{j_{\rho}}\) and k, respectively, is also needed. Thus we get

Utilising definitions (38)–(40), the forces for holonomic system can now be expressed by those for free system as follows
Analogously to (60), generalised forces for non-holonomic system can be expressed by those for holonomic system. Again we have to take any of the generalised forces (38)–(40), and next substitute (57) and (58) in it. We get

Finally introduce (60) into (61) in order to express forces for non-holonomic system by those for free one. Hence it is

It is seen in (62) that generalised forces of any type for non-holonomic or holonomic system are linear combinations of forces of the corresponding type for free system. Quantities A sρ , B σρ and A sρ B σρ take a role of coefficients in this relationship, while equations of constraints (47) and (48) are their origin. Advantage of use of (62), referring to significant increase in numerical efficiency and simpler algorithmization of numerical generation of equations, are described in [39]. We will return to them briefly in Sect. 5. It is worthy of notice that expressing forces for constraint system by forces for free system can simplify if the forces in free system are analogous for each body. This condition is easily satisfied [31, 39] for the systems in rail vehicle type. It is also worthy to realise that (62) refers any type of the forces, so complete equations of motion of constraint system can be expressed as linear combinations of equations for free system.
Result shown above is an effect of the operations carried out on Kane’s equations, however it can be generalised. Generalised forces are in fact projections of forces and torques on directions of generalised co-ordinates and velocities or quasi-velocities. In Kane’s approach these co-ordinates and velocities can be chosen arbitrarily. So it is obvious that (62) is valid if directions of these projections coincide with axes of Cartesian and body fixed reference frames. Consequently it is seen that Newton-Euler (N-E) equations can be utilised to build the equations for the free system. Next equations for constraint system can be obtained according to (62) or (60). Such an approach is true for any formalism coming out directly from N-E equations and for those exploiting generalised forces. It can be used selectively to determine the imaginary forces in order to adapt the equations to non-inertial systems. It can also be used comprehensively to build complete equations of motion. Since (62) easily undergoes algorithmization [31, 39], so this generalized result can be also numerically implemented.
4 Kinematical elements of computer modelling relative motion with regard to needs of rail vehicles
No matter which possibility of relative motion description from Sect. 2 is chosen, in any instance there is a need to define s(t), v(t) and w(t) functions that characterise transportation. It is seen in (4), (5) and (34) that a matter of interest in this context are components of vectors a o1, ω,ε. It shall appear later that velocity v and its components are of practical importance, too.
In order to calculate mentioned components let us introduce known in differential geometry natural system O 1 x n y n z n (the Frenet’s trihedron). It is related to transportation system O 1 xyz as shown in Fig. 3. Track centre line that defines position of both these systems origin O 1, being a 3-dimensional curve in general, is drawn with dash-dot line in Fig. 3. Describe it in the absolute OXYZ system with use of parametric equations as follows:
where l is natural parameter equal to curve running length, measured e.g. from origin of the OXYZ. If “′” represents derivative with respect to l, then basic quantities characterising curve given by (63), i.e. curvature κ and torsion τ, can be expressed in the following way:


From point of view of purely kinematical considerations (63) may be quite arbitrary. From point of view of proper shape of a railway track, however, some demands are formulated. First are demands for boundary conditions for adjacent points of track sections of different shape (straight sections, circular curves, and transition curves). Additionally for transition curves so called consistency conditions hold. They require the same courses (functions) of curvature κ, superelevation ramp 2z, and unbalanced lateral acceleration. All these demands are well known in literature, e.g. [31, 45].
Note, that vectors v, a o1 of velocity and acceleration of translatory motion for origin O 1 of transportation system are tangent to track centre line. They are tangent to O 1 x axis at the same time. Taking account of identity for axes O 1 x n ≡O 1 x (see Fig. 3) components of the mentioned vectors in natural and transportation systems can be expressed as follows


where v, a are instantaneous velocity and acceleration of natural system origin. It is worthy of notice that validity of (66) and (67) spreads on arbitrarily defined change of v=v(t) or v=v(l) (including v=const) and change of a corresponding to it, since a=dv/dt. It can be agreed, that if functions l=l(t) and v are known then problem of v,a o1 components is solved. Note, that they do not depend on the curve shape.
Determination of components for vectors ω,ε of angular velocity and acceleration of transportation is much more complex. Making use of κ and τ, the vector ω F of angular velocity of natural system O 1 x n y n z n can be expressed through components in this system
where t, b, n are versors of tangential, binormal and normal axes (of O 1 x n y n z n ), respectively.
In view of O 1 x n ≡O 1 x and tangency of these axes to the curve, the angular velocity ω expressed by components ω t , ω n , ω b in natural system can differ from above expressed velocity ω F for tangential component only. Consequently, the remaining components stay unchanged. So,
General form of vector for angular acceleration of transportation ε, expressed by components ε t , ε n , ε b in natural system, is represented by relationship as follows.

The final form in (70) was obtained by: differentiation of (69), use of local differentiation with respect to natural system, and components of ω F given in (68). The last two rows in (70) define components ε t , ε n , ε b . Note that in order to determine them, the components ω t and ω b have to be known. Component ω b is given in (69), while missing component ω t is time derivative of angle γ t (see Fig. 3) of O 1 xyz system rotation around tangential direction t.
Formulae (69) and (70) define vectors ω, ε univocally by components in the natural system. It is the most universal representation and we could stop with it. However, for vectors v,a o1 also components in transportation system O 1 xyz were determined. Considering further application of the obtained results, the determination of ω,ε components in O 1 xyz, as it was done for v,a o1, gives possibility of direct substituting all the components into equations of motion expressed in the transportation system. Such equations are the most commonly used form of equations in railway vehicle dynamics. Therefore below we give the recipe for transformation of components ω t , ω n , ω b and ε t , ε n , ε b into components ω x , ω y , ω z and ε x , ε y , ε z , respectively. Corresponding direction cosine matrix arises from Fig. 3. Thus for any vector c one can write

All considerations and relationships we obtained hitherto in this subsection are of general nature. Let us exploit now properties of the track used by rail vehicles. Note at the beginning that values of angle β (Fig. 3) are very small [16, 31]. Consequently values of angle γ t differ just slightly from values of angle γ that corresponds to track superelevation, i.e. γ t ≅γ. Thus the following relationship can be recorded
To make use of (72) it is necessary to determine angle γ. It is given as follows
where z(l) is change of track centre line vertically (a half value of the superelevation ramp [45]) and b is half of the track gauge. The approximate relation in (73), which is utilised in practice, can be applied thanks to real values of angle γ≤6∘.
Small values of angle β enable to draw similar conclusion for angles φ t , φ (Fig. 3) as for angles γ, γ t , that is to say φ t ≅φ. Angle φ can be reckoned [31] basing on the formula:
Carrying out matrix multiplication according to (71) and taking account of γ t ≅γ,φ t ≅φ, ω n =0 for velocities and of γ t ≅γ, φ t ≅φ for accelerations one obtains components of ω and ε:

In case one is interested in components of ω, ε for other directions, one should proceed analogously starting from determination of the corresponding direction cosine matrix.
It is seen that in order to perform numerically efficient calculation of ω x , ω y , ω z and ε x , ε y , ε z it is enough to apply (75), making use of (73) and (74) at the same time. Calculation of the necessary values of ω t , ω n , ω b and ε t , ε n , ε b ought to be done according to (69), (70), and (72).
Above given formulae are valid in any conditions of motion, i.e. in straight track, circular curve, and transition curve (no matter what shape the last have). It was shown in [16, 31] that cases of the circular curve and straight track, representing one- and two-dimensional curves, can be treated as the special cases of three-dimensional curve (railway transition curve with superelevation ramp). In work [31] both the parametric equations of railway transition curves were presented as well as explicit form of the components for the 3-rd order parabolic, cosine, and sinusoidal transition curves. The components for circular curve and straight track were presented, too.
One may conclude that elaboration of the software for numerical calculation of components in accordance with (75) for quite arbitrary shape of the track centre line is not easy. On the other hand, introduction of the analytical results obtained traditionally [31] into simulation programmes, which is an alternative here, does not seem laborious. It arises from small number of the real transition curve types. Eventual non standard track shapes demand supplementary determination of the components and the corresponding extension in the software, however.
5 Numerical implementation of the theoretical results
Author of present article is co-author of software package ULYSSES for computer (automatical) generation of equations of motion. Some details about this software and corresponding references can be found in [31, 39]. It is aimed at rail vehicles, nevertheless it possess ability for other objects to be modelled in the relative motion. This package is numerical implementation of theoretical results from Sect. 3.
A core of the package is TITAN programme of scheme shown in Fig. 4. Subroutines mentioned there accomplish the following tasks. The CONTFORC procedure calculates wheelsets’ external forces (contact, track flexibility and gravitational ones). The GRAVFO adds gravitational forces other than those affecting wheelsets. The IMAGFORC calculates imaginary forces. The procedure calculating forces in flexible connections between the bodies is named GENSIL.
Notice in Fig. 4, that in case of inertia forces (non-linear kinematics terms) they are calculated directly, taking account of all bodies and the constraints, in accordance with (42) and (43). In case of external and imaginary forces it is done differently. They are reckoned for the free system at first. In instance of the imaginary forces (46) is applied, though in a simplified form that matches single free rigid body. This step is repeated as many times as the number of bodies in the system is. Last of all account is taken of the system’s constraints in conformity with (60). This formula is used as non-holonomic constraints are unusual in rail vehicle systems and consequently capabilities of the programme were limited to the holonomic constraints.
Described algorithm gives some numerical benefits in terms of the efficiency. Namely, it is possible to count the generalized correction forces, in full range of their calculation, with use of the same subroutines for each of the bodies treated as free. Consequently, we obtain vector (matrix) of the generalized forces for the free system. Next, to match the constrained system, we reduce this vector using (60) to determine the corresponding reduced components. Building the reduced vector is highly optimised in the code by copying the unchanged components directly into this vector and by avoiding the multiplication by those of A sρ coefficients which equal zero. Furthermore, this idea was extended to the external forces, so in fact the summed vector of the generalized external and correction forces is processed in such a way (Fig. 4). The method just described is much more efficient than ordinary multiplication of transpose of Jacobian matrix by the vector of forces for a free system, which can be used as an equivalent here.
Another advantage in terms of efficiency can be seen by an analysis of the components \(v'_{j\rho m}\), \(\omega '_{j\rho m}\), where (j=1,…,n), (ρ=1,…,l), (m=1,2,3). For non-holonomic (holonomic) and free systems of rigid bodies each corresponding matrix has got n×l(k)×3 and n×6n×3=18n 2 such components, respectively. In case of the free bodies, however, one can consider each body separately. Then for the single body (n=1) number of the components in each \(v'_{\rho m} ,\omega '_{\rho m}\) matrix equals 6×3=18, while for n bodies it equals 18×n=18n, respectively. As the equations for the system of free bodies, either treated together or separately, have to be the same it is obvious that (18n 2−18n) among all 18n 2 components for the bodies treated together must be equal to zero. Since number of constraints in case of railway vehicle models is not great, so majority of these zero components will be preserved in the reduced matrices \(v'_{j\rho m},\omega '_{j\rho m}\). The efficient way to avoid multiplication by these zero components, according to (39) and (40), is calculation of the forces with use of (60) or (62). For the systems of dimension corresponding to a single rail vehicle, such avoiding these unnecessary multiplication is less complicated and time consuming than check of a factor value before multiplication or use of techniques for spare matrices multiplication.
6 Application of computer methods of modelling in simulation of rail vehicle motion
It is obvious that models of railway vehicle dynamics, also those being built numerically, are mainly created to project behaviour of real objects. The most common and relatively cheep solution for such projection are numerical simulations. The applications of simulation of rail vehicle motion could be grouped as follows: traditional, in research and engineering issues; in animation of rail vehicle motion; in professional simulators of rail vehicles; and in computer games. Scope of simulation applications by present author was presented in [31]. They all concern the research issues. Decent sample of such studies is Sect. 6.1 as well as some are represented in [16–18, 40]. They treat for example: railway vehicle lateral stability in a curved track [18, 40]; optimisation of shape of railway transition curves [17]; and importance of imaginary forces in rail vehicle dynamics in a curved track [16, 40].
6.1 Sample of the author’s numerical analysis of railway vehicle dynamics
The question being presented here was chosen as that of strong relation to theoretical results treated earlier in present article. The example is use of the ULYSSES package in numerical (simulation) studies on influence of complete and incomplete inclusion of imaginary forces and torques in description of rail vehicle dynamics. The main idea of these studies is comparison of the simulation results from the complete dynamical model and the model with the imaginary terms omitted. Differently to the earlier studies [39], current ones [16, 40] refer to transient states of motion (vehicle accelerating and braking). There is no chance to present the results comprehensively in this article. Therefore we shall limit to sample of the results, which reveals univocally that this problem may be of practical nature. More results of such type are presented and discussed in [16, 40]. The discussion is performed in [16] of importance of all the imaginary forces terms. It is specified clearly which of them and in what conditions should never be neglected.
Figure 5 represents courses of the selected omitted torque. Its omission is the cause for the differences shown in Fig. 6. Figure 6 illustrates spectacular differences in simulation results from both models. It represents car body yaw co-ordinate (angle of rotation around vertical axis) for 2-axle freight car. Parameters of this model and details of the real object are given in [18, 40]. The model passes the route composed in continuation of straight track, short transition curve, and circular curve. The solid line refers to complete model, while dashed one to the model with the imaginary torque omitted. Values of accelerations (vehicle speeds up here) are given in the figures in brackets in [m/s2]. The differences shown in Fig. 6 arise from omission of imaginary torque about vertical axis acting on the vehicle body. The disparity in solutions visible in Fig. 6 is a result of the author’s intentional simplifications in modelling the relative motion. In many applications by other authors similar simplifications happen quite often. They are usually done without complete knowledge what consequences of particular simplifications might occur, however. Publications [1, 30, 46, 47] can be mentioned as the examples where such simplifications could be identified.
7 Conclusion
The survey of the methods present in literature, which utilise the dynamics of multi-body systems in relative motion was done. The survey is limited by this paper’s needs, however. The methods under consideration are applied to computer modelling dynamics of rail vehicles. At first, the methods that originate in Newton-Euler MBS formalisms were of interest. With these methods as background and in contrast with them, the author’s approach was presented with many original elements. General method of describing discrete multi-body systems in relative motion was elaborated within this approach, which can be used in computer generation (or analytical derivation) of equations of motion. It is based on the Kane’s approach. An alternative method of building the equations for the systems of rail vehicle type was also shown, distinguished by higher numerical efficiency. The general method of determining the components of linear and angular velocities and accelerations of transportation is presented. These quantities are necessary in any method considering the relative motion, not only in that used by the present author. Basing on these results, the software was built to automatic generation of equations of motion (AGEM) for MBS in relative motion. Despite its generality it is specialized to rail vehicles. The selected sample of the author’s results from simulation studies was also shortly discussed. These numerical studies showed that rigorous modelling the relative motion in railway vehicle dynamics is of much higher significance that it is commonly believed [16, 40]. This refers especially to vehicle motion in transition curves and in particular with variable velocity (accelerating or braking) [16]. The most important term in this respect are inertia forces of rotation (as defined below formula (45)) present in the equations describing vehicle body’s rotational motions.
The author hopes that this paper can make the help and inspiration to all those who need to build their own rail vehicle simulation software. In case of the research purposes such needs are more numerous than it is sometimes believed.
8 Notations
- A, OXYZ :
-
inertial co-ordinate system attached to the earth (absolute system);
- A′, O 1 xyz :
-
non-inertial moving co-ordinate system following the transportation (transportation system)—track surface oriented;
- A σρ ,A sρ ,B σρ :
-
functional coefficients in equations of constraints expressing dependant velocities by the independent ones, for holonomic (A) and non-holonomic (B) constraints;
- a o1, \(\textbf{a}_{o1}\),:
-
linear acceleration of transportation for A′, i.e. acceleration of A′ in A, and its matrix representation, respectively;
- a o1j , \(\textbf{a}_{o1j} \) :
-
linear acceleration of transportation for j-th A′, i.e. acceleration of \(A'_{j}\) in A; and its matrix representation, respectively;
- \(\boldsymbol{a}'_{C}\), a′, \(\boldsymbol{a}'_{j} \) :
-
relative (i.e. in A′) acceleration of mass centre C of rigid body and C j of j-th body;
- a,ε :
-
values of linear and angular accelerations of transportation in general, respectively;
- B, B′:
-
inertia forces of motion in A and in A′, respectively; additionally for body(ies), corresponding moments of forces come within this definition;
- B, B j :
-
rigid body and j-th rigid body, respectively;
- b :
-
half of a track gauge;
- C, C j :
-
mass centres of rigid body and j-th rigid body, respectively;
- E, e abc :
-
unit tensor and permutation symbol, respectively;
- \(F_{\rho} ^{*}\), F ρ , \(F_{\rho} ^{**}\) :
-
generalised forces of inertia (with respect to A′), generalised external forces, and generalised imaginary forces (inertia forces depending on transportation), respectively;
- \(\tilde{F}_{\rho}\), F ρ , \(\hat{F}_{\rho}\) :
-
generalised forces of any type for free, holonomic and non-holonomic systems, respectively;
- fd, fz :
-
operators representing any formalism and variational principle, respectively;
- fp :
-
imaginary forces’ operator, appropriate for the formalism selected;
- I, \(\hat{\mathbf{I}}\) , \(\breve{\mathbf{I}}\), \(\tilde{\mathbf{I}}\) :
-
non-symmetrical (the first two) and symmetrical (the last two) matrices of inertia;
- J, ϑ :
-
inertia tensor of rigid body and first invariant of J, i.e. ϑ=J 11+J 22+J 33;
- j :
-
rigid body indicator (j=1,…,n);
- J :
-
moment of inertia and components of the inertia tensor J;
- K, G, H :
-
functional matrices;
- k, l :
-
number of system’s degrees of freedom; in case of l also natural parameter equal to curve running length (measured from origin of OXYZ system);
- k, p :
-
when used as indices trailing and leading wheelsets’ indicators, respectively;
- l 0 :
-
track section length or total length of transition curve;
- m :
-
rigid body mass; direction index of unit vectors \(\boldsymbol{i}_{m}^{(j)}\) (m=1,2,3) for axes of reference systems, where \(\boldsymbol{v}'_{j}\) and \(\boldsymbol{\omega}'_{j}\) are expressed;
- n :
-
number of rigid bodies;
- O 1 x n y n z n :
-
natural system (moving trihedral system)—track centre line oriented;
- P, P(v,w):
-
imaginary forces (inertia forces arising from and depending on transportation); additionally for body(ies), corresponding moments of forces come within this definition;
- P ψb :
-
imaginary torque around O 1 z the transportation system axis;
- p C ,p :
-
absolute acceleration of rigid body mass centre C;
- Q, \(\hat{\mathbf{Q}}\), \(\tilde{\mathbf{Q}}\) :
-
matrices of inertia forces;
- R C , R C :
-
resultant vector of external (active) forces acting in body mass centre C and the corresponding column matrix of these forces, respectively;
- \(\boldsymbol{R}_{j}^{*}\), R j , \(\boldsymbol{R}_{j}^{**}\) :
-
resultant vectors of inertia, external and imaginary forces, respectively;
- \(\boldsymbol{r}'_{C}\), r′, \(\boldsymbol{r}'_{j}\) :
-
radius vector of mass centre C of rigid body and C j of j-th body in A′ system;
- r, r j :
-
radius vector of mass centre C of rigid body and C j of j-th body in A system;
- r o1, r o1j :
-
radius vector of origin of A′ system and of j-th \(A'_{j}\) system, respectively;
- s(t), v(t), w(t):
-
given functions of time representing displacements, velocities, and accelerations of basic motion (of transportation in kinematics), i.e. for motion of A′ in A;
- T C , T C :
-
resultant moment of external forces with respect to body mass centre C and the corresponding column matrix of these forces, respectively;
- \(\boldsymbol{T}_{j}^{*}\), T j , \(\boldsymbol{T}_{j}^{**}\) :
-
resultant vectors of inertia, external and imaginary torques, respectively;
- t, b, n :
-
versors of tangential, binormal and normal axes of O 1 x n y n z n system, respectively;
- t, b, n :
-
directions of tangential, binormal and normal axes of O 1 x n y n z n system, respectively; also used as indices; in case of t also time;
- u, u π , u ρ :
-
generalised quasi-velocities (nomenclature from [37]) or generalised velocities (nomenclature from [19]);
- \(\boldsymbol{v}'_{C}\), v′, \(\boldsymbol{v}'_{j}\) :
-
relative velocity of mass centre C of rigid body and C j of j-th body;
- \(\mathbf{v}'_{C}\), \(\mathbf{r}'_{C}\) :
-
matrix representations of vectors \(\boldsymbol{v}'_{C}\) and \(\boldsymbol{r}'_{C}\), respectively;
- \(\boldsymbol{v}'_{j_{\rho}}\), \(\boldsymbol{\omega}'_{j_{\rho}}\) :
-
relative holonomic linear and angular partial velocities;
- \(\tilde{\boldsymbol{v}}_{j_{\rho}}\), \(\tilde{\boldsymbol{\omega}}'_{j_{\rho}}\) :
-
relative linear and angular partial velocities for free system of bodies;
- \(\hat{\boldsymbol{v}}'_{j \rho}\), \(\hat{\boldsymbol{\omega}}'_{j \rho}\) :
-
relative non-holonomic linear and angular partial velocities;
- v,a :
-
values of instantaneous velocity and acceleration of natural system’s origin O 1 (in direction t tangent to track centre line);
- \(\hat{v}'_{j\rho m}\), \(\hat{\omega}'_{j\rho m}\) :
-
components of relative partial velocities \(\hat{\boldsymbol{v}}'_{j_{\rho}}\), \(\hat{\boldsymbol{\omega}}'_{j_{\rho}}\), called alternatively their coefficients;
- \(\hat{v}'_{jtm}\), \(\hat{\omega}'_{jtm} \) :
-
coefficients, as above but those explicitly dependent on time;
- \(\mathbf{w}'_{\mathrm{I}}\), \(\mathbf{w}'_{\mathrm{II}}\) :
-
matrix representations of equations’ relative generalised variables chosen arbitrarily, co-ordinates and velocities, respectively;
- x I, x II, \(\mathbf{x}'_{\mathrm{I}}\), \(\mathbf{x}'_{\mathrm{II}}\) :
-
matrix representations of relative variables in Newton-Euler equations adapted to description of relative motion, co-ordinates (I) and velocities (II);
- \(\mathbf{y}'_{\mathrm{I}}\), \(\mathbf{y}'_{\mathrm{II}}\) :
-
matrix representations of equations’ relative independent generalised variables, co-ordinates and velocities, respectively;
- x, \(\dot{x}\) :
-
absolute linear and angular co-ordinates and velocities; (i.e. in OXYZ system); x used as index indicates longitudinal direction in O 1j xyz systems;
- x′, \(\dot{x}'\) :
-
relative linear and angular co-ordinates and velocities; (i.e. in O 1j xyz systems);
- x(l), y(l), z(l):
-
co-ordinates of 3-dimensional curve in the absolute system; in case of railway track z(l) is a change of track centre line vertically (a half value of the superelevation ramp [45]);
- y,z :
-
indices denoting corresponding directions of transportation system O 1 xyz axes;
- Z :
-
external (active) forces; additionally in case of body(ies), corresponding moments of forces come within this definition;
- α :
-
absolute angular acceleration of rigid body;
- δ :
-
symbol of variation;
- ε, ε j :
-
angular acceleration of transportation, i.e. of A′ and \(A'_{j}\) relative to A, respectively;
- ε′, \(\boldsymbol{\varepsilon}'_{j}\) :
-
relative angular acceleration of rigid body and of rigid body j, respectively;
- ψ b :
-
yaw angle of vehicle body;
- φ, β :
-
orientation angles of natural system O 1 x n y n z n with respect to horizontal plane;
- γ :
-
variable angle corresponding to track superelevation ramp;
- γ t , φ t :
-
rotation angles around t, the tangent to track centre line, of transportation system O 1 xyz and natural system O 1 x n y n z n , respectively;
- κ, τ :
-
curvature and torsion of 3-dimensional curve, respectively;
- Λ, \(\hat{\boldsymbol{\Lambda}}\), \(\tilde{\boldsymbol{\Lambda}}\) :
-
matrices of external forces;
-
θ,
 :
: -
absolute angular velocity of rigid body and the corresponding matrix;
- ρ, σ :
-
indicators for vectors and scalars, related to ρ-th and σ-th velocity (or degree of freedom), respectively;
-
Ω, Φ,
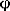 :
: -
functional matrices (Φ—constraints matrix);
- ω, ω j :
-
angular velocity of transportation, i.e. of A′ and \(A'_{j}\) relative to A, respectively;
- ω F :
-
angular velocity of natural system;
- ω′, \(\boldsymbol{\omega}'_{j}\) :
-
relative angular velocity of rigid body and of j-th rigid body, respectively;
-
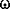 ,
, 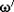 ,
,  ,
, 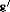 :
: -
matrix representations of vectors ω, ω′, ε, ε′, respectively;
- ω, ε :
-
components of vectors ω and ε, respectively; most often accompanied with single index defining direction of the component; in case of two indices the first indicates particular rigid body.
References
Kortum W, Sharp RS, de Pater A (1991) Application of multibody computer codes to vehicle system dynamics. Report to 12th IAVSD symposium on a workshop and resulting activities. Soc for Eng and Scientific Education, Oberpfaffenhofen
Schiehlen W (ed) (1990) Multibody systems handbook. Springer, Berlin
Cammoro R, Escalona JL (2010) Application of moving shape functions method to curved railroad tracks. In: Topping BHV, Adam JM, Pallarés FJ, Bru R, Romero ML (eds) Proceedings of the tenth international conference on computational structures technology. Civil-Comp Press, Stirlingshire, Paper 8. doi:10.4203/ccp.93.8
Cheng YC, Lee CK (2010) Stability analysis of high-speed railway vehicle using half-car model. Int J Heavy Veh Syst 17(2):139–158
Long X-Y, Wei Q-C, Zeng F-Y (2010) Dynamical analysis of railway transition curves. P I Mech Eng F-J Rai 224(F1):1–14
Wang D-H, Liao W-H (2009) Semi-active suspension systems for railway vehicles using magnetorheological dampers: part I. System integration and modelling. Veh Syst Dyn 47(11):1305–1325
Wang D-H, Liao W-H (2009) Semi-active suspension systems for railway vehicles using magnetorheological dampers: part II. Simulation and analysis. Veh Syst Dyn 47(12):1439–1471
Cheng YC, Yang C-J, Jiang C-P (2010) Dynamics analysis of high speed railway vehicles excited by earthquake forces. In: Proceedings of international conference on modelling, identification and control (IMIC 2010), Okayama, pp 94–99
Fan W-T, Wu W-F (2010) Stability analysis and derailment evaluation of rail vehicles. Int J Heavy Veh Syst 13(3):194–211
Lee S-Y, Cheng Y-C (2008) A new dynamic model of high-speed railway vehicle moving on curved tracks. J Vib Acoust 130(1):011009
Long X-Y, Wei Q-C, Wang Y-J (2008) Simulation and analysis of high-speed train running quality affected by route alignment condition. In: Proceedings of international conference on intelligent computation technology and automation (ICICTA 2008), Changsha, pp 708–712
Nath Y, Yayadev K (2005) Influence of yaw stiffness on the nonlinear dynamics of railway wheelset. Commun Nonlinear Sci 10:179–190
Hoffmann M (2006) Dynamics of European two-axle freight wagons. PhD thesis, Technical University of Denmark, Informatics and Mathematical Modelling, Lyngby, Denmark
Handoko YA (2006) Investigation of the dynamics of railway bogies subjected to traction/braking torque. PhD thesis, Central Queensland University, Center for Railway Engineering, Australia
Li C-H (2009) Hunting stability analysis of tilting vehicle system moving on curved tracks. MSc thesis, National Kaohsiung First University of Science and Technology, Department of Mechanical and Automation Engineering, Taiwan
Zboiński K (2011) The importance of kinematics accuracy in modelling the dynamics of rail vehicle moving in a curved track with variable velocity. Int J Heavy Veh Syst 18(4):411–446
Zboinski K, Woznica P (2010) Formation of railway transition curves based on advanced dynamic vehicle models. In: Topping BHV, Adam JM, Pallarés FJ, Bru R, Romero ML (eds) Proceedings of the tenth international conference on computational structures technology. Civil-Comp Press, Stirlingshire, Paper 6. doi:10.4203/ccp.93.6
Zboiński K, Dusza M (2010) Self-exciting vibrations and Hopf’s bifurcation in non-linear stability analysis of rail vehicles in a curved track. Eur J Mech A, Solids 29(2):190–203
Kane TR, Levinson DA (1985) Dynamics: theory and applications. McGraw-Hill, New York
Amirouche F (2006) Fundamentals of multibody dynamics. Birkhauser, Boston
Parsa K (2007) The Lagrangian derivation of Kane’s equations. Trans Can Soc Mech Eng 31(4):407–420
Shabana AA, Zaazaa KE, Sugiyama H (2008) Railroad vehicle dynamics: a computational approach. CRC Press/Taylor and Francis, Boca Raton/London
Shabana AA (2005) Dynamics of multibody systems, 3rd edn. Cambridge University Press, Cambridge
Flores P, Ambrosio J, Claro JCP, Lankarani HM (2008) Kinematics and dynamics of multibody systems with imperfect joints: models and case studies. Springer, Berlin
Roberson RE, Schwertassek R (1988) Dynamics of multibody systems. Springer, Berlin
Featherstone R (2008) Rigid body dynamics algorithms. Springer, New York
Ambrosio JAC, Eberhard P (2009) Advanced design of mechanical systems: from analysis to optimisation. Springer, New York
Schiehlen W, Valasek M (2003) Virtual nonlinear multibody systems. Kluwer Academic, Dordrecht
Bauchau OA (2011) Flexible multibody dynamics. Springer, Dordrecht
Popp K, Schiehlen W (1993) Fahrzeugdynamik. Teubner, Stuttgart
Zboinski K (2004) Numerical and traditional modelling of dynamics of multi-body system in type of a railway vehicle. Arch Transp 16(3):81–106
Gimenez JG, Martin LM, Pascal JP, Maupu JL (1991) IAVSD railway benchmark #2. SIDIVE and VOCO solutions. In: Proc 12th IAVSD symp. Vehicle Syst Dyn 20(suppl): 172–184
Huston R (1990) Multibody dynamics. Butterworth-Heinemann, New York
Schiehlen W, Eberhard P (2004) Technische dynamik: modelle fur regulung und simulation. Teubner, Stuttgart
Schiehlen W (2007) Vehicle and guideway modelling: suspension systems. In: Schiehlen W (ed) Dynamical analysis of vehicle systems. Springer, New York
Iwnicki S (ed) (2006) Handbook of railway vehicle dynamics. CRC Press/Taylor and Francis, Boca Raton/London
Lurie AI (1961) Analiticeskaja mechanika. FizMatGIZ, Moscow
Kisilowski J, Knothe K (eds) (1991) Advanced railway vehicle system dynamics. WNT, Warsaw
Zboinski K (2001) Relative kinematics exploited in Kane’s approach to describe multibody system in relative motion. Acta Mech 147(1–4):19–34
Zboinski K (2010) Selected problems of non-linear (non-smooth) dynamics of rail vehicles in a curved track. In: Thomsen PG, True H (eds) Non-smooth problems in vehicle systems dynamics. Springer, Berlin, pp 87–99
Forehand DIM, Cartmell MP, Khanin R (2005) The theory and application of classical Eulerian code. Int J Mech Eng Educ 33(2):149–176
Laulusa A, Bauchau OA (2008) Review of classical approaches for constraint enforcement in multibody systems. J Comput Nonlinear Dyn 3(1):011004
Jaschinski A, Kortum W, Rentrop P (1992) Multibody dynamics software and numerical simulation of high-speed vehicles. In: Proc of CSME forum “transport 1992+”, 1992, III. Montreal, pp 720–726
Josephs H, Huston RL (2002) Dynamics of mechanical systems. CRC Press, Boca Raton
Esveld C (1989) Modern railway track. MRT-Productions, Duisburg
Andersson E, Nilstam NG, Ohlsson L (1995) Lateral track forces at high speed curving. Comparison of practical and theoretical results of Swedish high speed train X2000. In: Proc 14th IAVSD symposium. Vehicle Syst Dyn 25(suppl): 37–52
Berghuvnd A, Stensson A (1998) Dynamic behaviour of ore wagons in curves at Malmbanan. Veh Syst Dyn 30(3–4):271–283
Acknowledgements
Scientific work financed in part as research project no. N N509 403136 in the years 2009–2011 from funds for science of Ministry of Science and Higher Education, Warsaw, Poland.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Zboinski, K. Modelling dynamics of certain class of discrete multi-body systems based on direct method of the dynamics of relative motion. Meccanica 47, 1527–1551 (2012). https://doi.org/10.1007/s11012-011-9530-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-011-9530-1











 :
: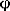 :
: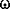 ,
, 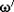 ,
,  ,
, 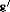 :
: