1 Introduction

The linear theory of elasticity is of paramount importance in the stress analysis of steel, which is the commonest engineering structural material. To a lesser extent, linear elasticity describes the mechanical behavior of the other common solid materials, e.g. concrete, wood and coal. However, the theory does not apply to the behavior of many of the new synthetic materials of the elastomer and polymer type, e.g. polymethyl-methacrylate (Perspex), polyethylene and polyvinyl chloride. The linear theory of micropolar elasticity is adequate to represent the behavior of such materials. For ultrasonic waves i.e. for the case of elastic vibrations characterized by high frequencies and small wavelengths, the influence of the body microstructure becomes significant, this influence of microstructure results in the development of new type of waves are not in the classical theory of elasticity. Metals, polymers, composites, solids, rocks, concrete are typical media with microstructures. More generally, most of the natural and manmade materials including engineering, geological and biological media possess a microstructure. Agarwal [1, 2] studied respectively thermo-elastic and magneto-thermo-elastic plane wave propagation in an infinite non-rotating medium. Some problems in thermo-elastic rotating media are due to Schoenberg and Censor [3], Puri [4], Roy Choudhuri and Debnath [5, 6] and Othman [7, 8]. Othman [9, 10] studied the effect of rotation in a micropolar generalized thermoelastic and thermo-viscoelasticity half space under different theories. The propagation of plane harmonic waves in a rotating elastic medium without thermal field has been studied. It was shown there that the rotation causes the elastic medium to be dispersive and an isotropic. These problems are based on more realistic elastic model since earth, moon and other planets have angular velocity.

Eringen and Şuhubi [11] and Eringen [12] developed the linear theory of micropolar elasticity. Othman [13] studied the relaxation effects on thermal shock problems in elastic half space of generalized magneto-thermoelastic waves under three theories.

Eringen [14] introduced the theory of microstretch elastic solids. This theory is a generalization of the theory of micropolar elasticity [12, 15] and a special case of the micromorphic theory. The material points of microstretch elastic solids can stretch and contract independently of their transformations and rotations. The microstretch is used to characterize composite materials and various porous media [16]. The basic results in the theory of micro stretch elastic solids were obtained in the literature [17–20].

The theory of thermo-microstretch elastic solids was introduced by Eringen [16]. In the frame-work of the theory of thermomicrostretch solids Eringen established a uniqueness theorem for the mixed initial-boundary value problem. The theory was illustrated through the solution of one dimensional waves and compared with lattice dynamical results. The asymptotic behavior of solutions and an existence result were presented by Bofill and Quintanilla [21]. A reciprocal theorem and a representation of Galerkin type were presented by De Cicco and Nappa [22].

De Cicco and Nappa [23] extended a linear theory of thermomicrostretch elastic solids that permits the transmission of heat as thermal waves at finite speed. The theory is based on the entropy production inequality proposed by Green and Laws [24]. In [23], the uniqueness of the solution of the mixed initial-boundary-value problem is also investigated. The basic results and an extensive review on the theory of thermomicrostretch elastic solids can be found in the book of Eringen [17].

The coupled theory of thermoelasticity has been extended by including the thermal relaxation time in the constitutive equations by Lord and Shulman [25] and Green and Lindsay [26]. These theories eliminate the paradox of infinite velocity of heat propagation and are termed generalized theories of thermo-elasticity. Othman and Lotfy [27] studied two-dimensional problem of generalized magneto-thermoelasticity under the effect of temperature dependent properties. Othman and Lotfy [28] studied transient disturbance in a half-space under generalized magneto-thermoelasticity with moving internal heat source. Othman and Lotfy [29] studied the plane waves in generalized thermo-microstretch elastic half-space by using a general model of the equations of generalized thermo-microstretch for a homogeneous isotropic elastic half space. Othman and Lotfy [30] studied the generalized thermo-microstretch elastic medium with temperature dependent properties for different theories. Othman and Lotfy [31] studied the effect of magnetic field and inclined load in micropolar thermoelastic medium possessing cubic symmetry under three theories. The normal mode analysis was used to obtain the exact expression for the temperature distribution, thermal stresses, and the displacement components.

In the recent years, considerable efforts have been devoted to the study of failure and cracks in solids. This is due to the application of the latter generally in industry and particularly in the fabrication of electronic components. Most of the studies of dynamical crack problem are done using the equations of coupled or even uncoupled theories of thermoelasticity [32–35]. This is suitable for most situations where long time effects are sought. However, when short time is important, as in many practical situations, the full system of generalized thermoelastic equations must be used [16].

The purpose of the present paper is to obtain the normal displacement, temperature, normal force stress, and tangential couple stress in a microstretch elastic solid under the effect of rotation. The normal mode analysis used for the problem of generalized thermo-microstretch for an infinite space weakened by a finite linear opening Mode-I crack is being solved for the considered variables. The distributions of the considered variables are represented graphically. A comparison is carried out between the temperature, stresses and displacements as calculated from the generalized thermoelasticity (L-S) and (CD) theories for the propagation of waves in semi-infinite microstretch elastic solids.

2 Formulation of the problem

Following Eringen [17], Lord and Şhulman [25], the constitutive equations and field equations for a linear isotropic generalized thermo-microstretch elastic solid in the absence of body forces are obtained, we consider rectangular coordinate system (x,y,z) having origin on the surface y=0 and z-axis pointing vertically into the medium. The thermoelastic plate is rotating uniformly with an angular velocity Ω=Ωn, where n is a unit vector representing the direction of the axis of rotation. The basic governing equations of linear generalized thermoelasticity with rotation in absence of body forces and heat sources are

figure a
(1)
(2)
(3)
(4)
(5)
$$ m_{il}=\alpha\varphi_{r,r}\partial_{il}+\beta\varphi_{i,l}+\gamma\varphi_{l,i},$$
(6)
$$ \lambda_{{i}} = \alpha_{0} \varphi_{{i}}^{*},$$
(7)
$$ {e} = \frac{\partial{u}}{\partial{x}} + \frac{\partial {w}}{\partial{z}}.$$
(8)

The state of plane strain parallel to the xz-plane is defined by

$$ \everymath{\displaystyle}\begin{array}{@{}l}{u}_{1} = {u} (x,z,t),\qquad {u}_{2} = 0,\qquad {u}_{3} = w(x,z,t),\\ [2mm]\varphi_{1} = \varphi_{3} =0,\qquad \varphi_{2} = \varphi_{2}(x,z,t),\\ [2mm]\varphi^{*} = \varphi^{*}(x,z,t),\qquad \Omega= (0,\Omega,0).\end{array}$$
(9)

The field equations (1)–(4) reduce to

(10)
(11)
(12)
(13)
(14)

where

$$ \everymath{\displaystyle}\begin{array}{@{}l}\hat{\gamma} = (3\lambda+ 2\mu+ k) \alpha_{{t}_{1}},\qquad \\[2mm]\hat{\gamma}_{1} = (3\lambda+ 2\mu+ k)\alpha_{{t}_{2}}\quad \mbox{and}\quad \\[2mm]\nabla^{2} = \frac{\partial^{2}}{\partial {x}^{2}} + \frac {\partial^{2}}{\partial {z}^{2}}.\end{array}$$
(15)

The constants \(\hat{\gamma}\) and \(\hat{\gamma}_{1}\) depend on mechanical as well as the thermal properties of the body and the dot denote the partial derivative with respect to time.

Equations (10)–(14) are the field equations of the generalized thermo-microstretch elastic solid, applicable to the (L-S) theory, and the classical coupled theory (CD), as follows:

(1) The equations of the coupled thermo-microstretch (CD) theory, when

$$ {n}_{0} = 0,\qquad {n}_{1} = 1,\qquad \tau_{0} = 0.$$
(16)

Equations (10), (11), (13) and (14) has the form

(17)
(18)
(19)
(20)

The constitutive relation can be written as

$$ \sigma_{{xx}} = \lambda_{0}\varphi^{*}+ (\lambda+ 2\mu+ k) \frac{\partial {u}}{\partial{x}} + \lambda \frac{\partial {w}}{\partial {z}} - \hat{\gamma} {T},$$
(21)
$$ \sigma_{{zz}} = \lambda_{0}\varphi^{*}+ (\lambda+ 2\mu+ k) \frac{\partial{w}}{\partial{z}} + \lambda \frac{\partial{u}}{\partial{x}} - \hat{\gamma} {T},$$
(22)
$$ \sigma_{{xz}} = \mu\frac{\partial{u}}{\partial {z}} + (\mu+ k)\frac{\partial {w}}{\partial{x}} + {k}\varphi_{2},$$
(23)
$$ \sigma_{{zx}} = \mu\frac{\partial{w}}{\partial {x}} + (\mu+ k)\frac{\partial {u}}{\partial{z}} + k\varphi_{2},$$
(24)
$$ {m}_{{xy}} = \gamma \frac{\partial\varphi _{2}}{\partial {x}},$$
(25)
$$ {m}_{{zy}} = \gamma \frac{\partial\varphi _{2}}{\partial z},$$
(26)

where

$$ \everymath{\displaystyle}\begin{array}{@{}rcl}{c}_{3}^{2} &=& \frac{2\alpha_{0}}{3\rho j},\qquad {c}_{4}^{2} = \frac{2\lambda_{1}}{9\rho j},\\[4mm]{c}_{5}^{2}&=& \frac{2\lambda_{0}}{9\rho j},\qquad {c}_{6}^{2} = \frac{2\hat{\gamma }_{1}}{9\rho j}.\end{array}$$
(27)

(2) Lord-Shulman (L-S) theory, when

$$ {n}_{1} = {n}_{0} = 1,\qquad \tau_{0} >0.$$
(28)

Equations (10), (11) and (13) are the same as (17), (18) and (19) and (14) has the form

(29)

(3) The corresponding equations for the generalized micropolar thermoelasticity without stretch can be obtained from the above mentioned cases by taking:

$$ \alpha_{0} = \lambda_{0} =\lambda_{1} = \varphi^{*} = 0.$$
(30)

For convenience, the following non-dimensional variables are used:

$$ \everymath{\displaystyle}\begin{array}{@{}l}\bar{x}_{{i}} = \frac{\omega^{*}}{{c}_{2}} {x}_{{i}},\qquad \bar{u}_{{i}} = \frac{\rho c_{2}\omega^{*}}{\hat{\gamma}T_{0}} {u}_{{i}},\qquad \bar{t} =\omega^{*}{t} ,\\[4mm]\bar{\tau}_{0} = \omega^{*}\tau_{0},\qquad \bar{\nu}_{0} = \omega^{*}\nu_{0},\qquad \bar{T} = \frac{{T}}{{T}_{0}} ,\\[4mm]\bar{\sigma}_{{ij}} =\frac{\sigma_{{ij}}}{\hat{\gamma}T_{0}} ,\qquad \bar{m}_{{ij}} = \frac {\omega^{*}}{{c}_{2}\hat{\gamma}T_{0}}{m}_{{ij}},\\[4mm]\bar{\varphi}_{2} = \frac{\rho c_{2}^{2}}{\hat {\gamma }T_{0}}\varphi_{2},\qquad \bar{\lambda}_{3} = \frac{\omega^{*}}{{c}_{2}\hat{\gamma}T_{0}}\lambda_{3},\qquad \bar{\varphi}^{*} = \frac{\rho c_{2}^{2}}{\hat{\gamma}T_{0}}\varphi^{*},\\[4mm]\omega^{*} = \frac{\rho C_{{E}}{c}_{2}^{2}}{{K}},\qquad \bar{\Omega} =\frac{\Omega}{ \omega^{*}},\qquad {c}_{2}^{2} = \frac{\mu}{\rho}.\end{array}$$
(31)

Using (31), (10)–(14) become (dropping the dashed for convenience)

(32)
(33)
(34)
$$ \biggl( \frac{{c}_{3}^{2}}{{c}_{2}^{2}}\nabla^{2} -\frac{c_{4}^{2}}{\omega^{*2}} - \frac{\partial^{2}}{\partial t^{2}}\biggr)\varphi^{*} -\frac{c_{5}^{2}}{\omega^{*2}} e + a_{9}T = 0,$$
(35)
(36)

Assuming the scalar potential functions φ(x,z,t) and ψ(x,z,t) defined by the relations in the non-dimensional form:

$$ u = \frac{\partial\varphi}{\partial x} + \frac {\partial \psi }{\partial z},\qquad w =\frac{\partial\varphi}{\partial z} - \frac{\partial\psi}{\partial x},$$
(37)
$$ {e} = \nabla^{2}\varphi.$$
(38)

Using (37) in (32)–(36), we obtain.

(39)
(40)
$$ \biggl[\nabla^{2} - 2 a_{4} - a_{5}\frac{\partial^{2}}{\partial t^{2}}\biggr] \varphi_{2} - a_{4}\nabla^{2}\psi= 0,$$
(41)
$$ \biggl[a_{6}\nabla^{2} - a_{7} -\frac{\partial^{2}}{\partial {t}^{2}}\biggr]\varphi^{*} - a_{8}\nabla^{2}\varphi+ a_{9}T = 0,$$
(42)
(43)

where

$$ \everymath{\displaystyle}\begin{array}{@{}l}c_{1}^{2} = \frac{\lambda+ 2\mu+ {k}}{\rho},\qquad {a}_{0} =\frac{c_{2}^{2}}{c_{1}^{2}},\\[4mm]a_{1} = \frac{\lambda_{0}}{\lambda+2\mu+ k},\qquad a_{2}= \frac{\rho c_{2}^{2}}{\mu+ k},\\[4mm]a_{3} = \frac{{k}}{\mu+ k},\qquad a_{4} =\frac{{k} c_{2}^{2}}{\gamma\omega^{*2}},\qquad a_{5} =\frac{\rho jc_{2}^{2}}{\gamma},\\[4mm]{a}_{6} =\frac{c_{3}^{2}}{c_{2}^{2}},\qquad {a}_{7} = \frac{c_{4}^{2}}{\omega^{*2}},\qquad {a}_{8} =\frac{c_{5}^{2}}{\omega^{*2}},\\[4mm]a_{9} = \frac{2\hat{\gamma }_{1}{c}_{2}^{2}}{9\hat{\gamma} j\omega^{*2}},\qquad \varepsilon = \frac{\hat{\gamma}^{2} T_{0}}{\rho\omega ^{*}K},\qquad \varepsilon_{1} = \frac{\hat{\gamma} \hat{\gamma }_{1}T_{0}}{\rho\omega^{*}K}.\end{array}$$
(44)

3 Normal mode analysis

The solution of the considered physical variables can be decomposed in terms of normal mode as the following form:

(45)

where \([ \bar{\varphi} , \bar{\psi },\bar{\varphi}^{*}, \bar{\varphi}_{2},\bar{\sigma }_{{il}},\bar{m}_{{il}},\bar{T}](x)\) are the amplitude of the functions ω is a complex and a is the wave number in the z-direction.

Using (45), then (39)–(43) become respectively

$$ \bigl( {D}^{2} - A_{1}\bigr)\bar{\varphi} -{a}_{0} \bar{T} + a_{1} \bar{\varphi}^{*} +A_{2}\bar{\psi} = 0,$$
(46)
$$ \bigl( {D}^{2} - {A}_{3}\bigr)\bar{\psi} -a_{3} \bar{\varphi}_{2} - A_{2}\bar{\varphi} = 0,$$
(47)
$$ \bigl( {D}^{2} - {A}_{4}\bigr) \bar{\varphi}_{2} - {a}_{4}\bigl({D}^{2} -{a}^{2}\bigr)\bar{\psi} = 0,$$
(48)
$$ \bigl( a_{6}{D}^{2} - A_{5}\bigr)\bar{\varphi}^{*} - {a}_{8}\bigl({D}^{2} -{a}^{2}\bigr)\bar{\varphi} + a_{9}\bar{T} = 0,$$
(49)
(50)

where \({D} = \frac{\partial}{\partial x}\),

$$ A_{1} = a^{2} + {a}_{0}\bigl(\omega^{2} - \Omega^{2}\bigr),$$
(51)
$$ A_{2} = 2\Omega{a}_{0} \omega,\qquad A_{2}^{*} = 2\Omega{a}_{2} \omega,$$
(52)
$$ A_{3} = a^{2} + {a}_{2}\bigl(\omega^{2} - \Omega^{2}\bigr),$$
(53)
$$ A_{4} = {a}^{2} + 2a_{4} +a_{5}\omega^{2},$$
(54)
$$ A_{5} = {a}^{2}a_{6} +a_{7} + \omega^{2},$$
(55)
$$ A_{6} = \omega( {n}_{1} + \tau_{0}\omega),$$
(56)
$$ {A}_{7} = \varepsilon\omega( n_{1} +n_{0}\tau_{0}\omega).$$
(57)

Eliminating \(\bar{\varphi}_{2},\bar{\psi},\bar{\varphi},\bar{T}\) and \(\bar{\varphi}^{*}\) between (46) and (50), we get the following tenth order ordinary differential equation satisfied by \(\bar{\varphi}_{2},\bar{\psi},\bar{\varphi},\bar{T}\) and \(\bar{\varphi}^{*}\)

(58)

Equation (58) can be factorized as

(59)

where

$$ A = [ {g}_{3} + a_{6}g_{1} +a_{6}A_{1} + a_{0}a_{6}A_{7}- a_{1}a_{8}]/a_{6},$$
(60)
(61)
(62)
(63)
(64)
$$ \everymath{\displaystyle}\begin{array}{@{}l}{g}_{1} = {A}_{3} + {A}_{4} +{a}_{3}{a}_{4},\qquad {g}_{2} ={A}_{3}{A}_{4} + {a}^{2}a_{3}{a}_{4},\\[2mm]{g}_{3} = {A}_{5} + {a}_{6}{A}_{6}^{*},\qquad {g}_{4} ={A}_{5}{A}_{6}^{*} - \varepsilon_{1}\omega{a}_{9} ,\\[2mm]{g}_{5} = {a}_{8}(A_{6}^{*} +{a}^{2}) - {a}_{9}{A}_{7},\\[2mm]{g}_{6} ={a}^{2}({a}_{8}{A}_{6}^{*} +{a}_{9}{A}_{7}),\\[2mm]{g}_{7} ={A}_{7}({A}_{5} - {a}^{2}{a}_{6}) +\varepsilon_{1}\omega a_{8},\\[2mm]{g}_{8} = {a}^{2}(A_{5}A_{7} -\varepsilon_{1}\omega a_{8}),\quad {A}_{6}^{*} ={a}^{2} + A_{6}.\end{array}$$
(65)

The solution of (58), has the form

$$ \bar{\varphi} = \sum_{{n} = 1}^{5}{M}_{{n}}(a,\omega) e^{ -{k}_{{n}}x},$$
(66)
$$ \bar{\psi} = \sum_{{n} = 1}^{5}M'_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(67)
$$ \bar{\varphi}_{2} = \sum_{{n} = 1}^{5}M''_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(68)
$$ \bar{\varphi}^{*} = \sum_{{n} = 1}^{5}M'''_{{n}}(a,\omega)e^{ - {k}_{{n}}x},$$
(69)
$$ \bar{T} = \sum_{{n} = 1}^{5}M''''_{{n}} (a,\omega) e^{ -{k}_{{n}}x},$$
(70)

where M n (a,ω), \(M'_{{n}}(a,\omega)\), \(M''_{{n}}(a,\omega)\), \(M'''_{{n}}(a,\omega)\) and \(M''''_{{n}}(a,\omega)\) are some parameters depending on a and \(\omega . {k}_{{n}}^{2}\) (n=1,2,3,4,5) are the roots of the characteristic equation of (59).

Using (66)–(70) into (39) and (43) we get the following relations

$$ \bar{\psi} = \sum_{{n} = 1}^{5}{a}_{{n}}^{*}{M}_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(71)
$$ \bar{\varphi}_{2} = \sum_{{n} = 1}^{5}{b}_{{n}}^{*}{M}_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(72)
$$ \bar{T} = \sum_{{n} = 1}^{5}{c}_{{n}}^{*}{M}_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(73)
$$ \bar{\varphi}^{*} = \sum_{{n} = 1}^{5}{d}_{{n}}^{*}{M}_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(74)

where

$$ a_{n}^{*} = \frac{A_{2}(k_{n}^{2} - A_{4})}{(k_{n}^{4} -g_{1}k_{n}^{2}+ g_{2})},$$
(75)
$$ b_{n}^{*} = \frac{a_{4}A_{2}(k_{n}^{2} -a^{2})}{(k_{n}^{4} -g_{1}k_{n}^{2} + g_{2})},$$
(76)
$$ c_{n}^{*} = \frac{{a}_{6}A_{7}k_{n}^{4} - g_{7}k_{n}^{2} +g_{8}}{a_{6}k_{n}^{4} - g_{3}k_{n}^{2} + g_{4}},$$
(77)
$$ d_{n}^{*} = \frac{{a}_{8}k_{n}^{4} - g_{5}k_{n}^{2} +g_{6}}{a_{6}k_{n}^{4} - g_{3}k_{n}^{2} + g_{4}}.$$
(78)

4 Application

The plane boundary subjects to an instantaneous normal point force and the boundary surface is isothermal, the boundary conditions at the vertical plan y=0 and in the beginning of the crack, at x=0 as in Fig. 1 are:

Fig. 1
figure 1

Displacement of an external Mode-I crack

Full size image

(1) Mechanical boundary condition is that the surface of the half-space are

$$ \sigma_{{zz}} = - p(x),\quad \vert x \vert< a,$$
(79)
$$ \sigma_{{xz}} = 0, \quad - \infty< x < \infty,$$
(80)
$$ {m}_{{xy}} = 0, \quad - \infty< x < \infty,$$
(81)
$$ \lambda_{z} = 0, \quad - \infty< x < \infty.$$
(82)

(2) Thermal boundary condition is that the surface of the half-space subjects to a thermal shock problem

$$ \everymath{\displaystyle}\begin{array}{@{}l}{T} = {f}({x}), \quad| {x} | < {a}\quad \mbox{and} \quad \frac{\partial {T}}{\partial {z}} = 0 \quad| {x} | > {a} .\end{array}$$
(83)

Using (31), (37), (39)–(43) with the non-dimensional boundary conditions and using (66)–(70), we obtain the expressions of displacement components, force stress, coupled stress and temperature distribution for microstretch generalized thermoelastic medium as follows:

$$ \bar{u} = \sum_{{n} = 1}^{5}\bigl(i {a} {a}_{{n}}^{*} - {k}_{{n}}\bigr)M_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(84)
$$ \bar{w} = \sum_{{n} = 1}^{5}\bigl(ia - {a}_{{n}}^{*}{k}_{{n}}\bigr)M_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(85)
$$ \bar{\sigma}_{zz} = \sum_{{n} = 1}^{5}{s}_{{n}}{M}_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(86)
$$ \bar{\sigma}_{xz} = \sum_{{n} = 1}^{5}{r}_{{n}}{M}_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(87)
$$ \bar{m}_{xy} = \sum_{{n} = 1}^{5}{q}_{{n}}{M}_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(88)
$$ \bar{T} = \sum_{{n} = 1}^{5}{c}_{{n}}^{*}{M}_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(89)
$$ \bar{\lambda}_{z} = \sum_{{n} = 1}^{5}{p}_{{n}}{M}_{{n}}(a,\omega) e^{ - {k}_{{n}}x},$$
(90)

where

$$ \everymath{\displaystyle}\begin{array}{@{}rcl}{s}_{{n}} &=& f_{1}d_{n}^{*} + i af_{2}({i}{a} -{a}_{{n}}^{*}{k}_{{n}})\\[2mm]&&{}-f_{3}{k}_{{n}}(i {a}{a}_{{n}}^{*} - {k}_{{n}}) -{c}_{{n}}^{*},\\[2mm]{q}_{{n}} &=& -{f}_{7}b_{n}^{*}k_{n},\qquad p_{{n}} = {f}_{8}d_{n}^{*},\\[2mm]{r}_{{n}} &= &iaf_{4}(iaa_{{n}}^{*} -{k}_{{n}}) - {k}_{{n}}f_{5}({ia} -{a}_{{n}}^{*}{k}_{{n}}) +f_{6}{b}_{{n}}^{*},\\[2mm]{f}_{1} &=&\frac{\lambda_{0}}{\rho c_{2}^{2}},\qquad {f}_{2} = \frac{\lambda+2 \mu+ k}{\rho c_{2}^{2}},\\[4mm]{f}_{3} &=& \frac{\lambda}{\rho c_{2}^{2}},\qquad {f}_{4} = \frac{\mu}{\rho c_{2}^{2}},\qquad {f}_{5} = \frac{\mu+ k}{\rho c_{2}^{2}},\\[4mm]{f}_{6} &=&\frac{k}{\rho c_{2}^{2}}, \qquad {f}_{7} = \frac{\gamma\omega ^{*^{2}}}{\rho c_{2}^{4}}\quad \mbox{and} \quad {f}_{8} = \frac{\alpha _{0}\omega^{*}}{\rho c_{2}^{3}}.\end{array}$$
(91)

Applying the boundary conditions (79)–(83) at the surface x=0 of the plate, we obtain a system of five equations. After applying the inverse of matrix method

(92)

We obtain the values of the five constants M n , n=1,2,3,4,5. Hence, we obtain the expressions of displacements, force stress, coupled stress and temperature distribution for microstretch generalized thermoelastic medium.

5 Numerical results and discussions

In order to illustrate our theoretical results obtained in preceding section and to compare these in the context of various theories of thermoelasticity, we now present some numerical results. In the calculation process, we take the case of magnesium crystal (Eringen, 1964) as material subjected to mechanical and thermal disturbances. Since, ω is the complex constant, then we taken ω=ω 0+iζ. The other constants of the problem are taken as ω 0=−2, ζ=1 and the physical constants used are:

The variation of the components of displacement u and w, temperature distribution T, normal stress σ zz , tangential stress σ xz , tangential couple stress m xy and microstress λ z with distance x at the plane z=1, a=1, f=1 and p=2 for (CD) and (L-S) theories have been shown by solid and dashed lines respectively for generalized thermo-microstretch elastic (GTMSE) medium with rotation (Ω=0.2) and without rotation (Ω=0.0). These distributions are shown graphically in Figs. 2–8 for thermal sources for t=0.1. Distributions of displacement u and w, temperature distribution T, normal stress σ zz , tangential stress σ xz and tangential couple stress m xy with distance x at the plane z=1, t=0.1, a=1, f=1 and p=2 for (CD) and (L-S) theories have been shown by solid, and dashed lines respectively for generalized micropolaer thermoelasticity elastic (GMTE) medium (without microstretch constants). Distributions are shown graphically in Figs. 9–14 for thermal sources (a mode-I crack). Figures 15–22 show the comparison between the temperature T, displacement component w, the force stresses components σ zz , σ xz , the tangential coupled stress m xy and the microstress λ z , the case of different three values of z, (namely z=1, z=0.9 and z=0.8) under GL theory. We notice that the results for the temperature, the displacement and stress distribution when the relaxation time is including in the heat equation are distinctly different from those when the relaxation time is not mentioned in heat equation, because the thermal waves in the Fourier’s theory of heat equation travel with an infinite speed of propagation as opposed to finite speed in the non-Fourier case. This demonstrates clearly the difference between the coupled and the generalized theories of thermoelasticity.

Fig. 2
figure 2

Temperature distribution at different rotation for GTMSE medium

Full size image

1. For generalized thermo-microstretch elastic (GTMSE) medium at Ω=0.2 and Ω=0.0, are shown graphically in Figs. 2–8. For the value of z, namely z=0.1, were substituted in performing the computation. It should be noted (Fig. 2) that in this problem, the crack’s size, x is taken to be the length in this problem so that 0≤x≤0.4 (for Ω=0.0) and 0≤x≤0.7 (for Ω=0.2), z=0 represents the plane of the crack that is symmetric with respect to the z-plane. It is clear from the graph that T has maximum value at the beginning of the crack (0≤x≤1 (for Ω=0.2)), it begins to fall just near the crack edge (2.5≤x≤3.5), where it experiences sharp decreases (with maximum negative gradient at the crack’s end). The value of temperature quantity converges to zero with increasing the distance x.

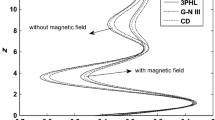
Figure 2 shows that in two theories (CD) and (L-S) the values of temperature for Ω=0.0 are small compared to those for Ω=0.2 in the ranges 0≤x≤1.1 and 4≤x≤6.5, large in the range 1.1≤x≤4 while the values are converge to zero for x>8.

Behavior of displacement component u in the (CD) and (L-S) theories for the two different values of rotation is similar, as shown in Fig. 3. Values of displacement for Ω=0.0 are large compared to those for Ω=0.2 in the ranges 0≤x≤1.5 and 4.8≤x≤8 but large in the range 1.5≤x≤4.8, while the values are converge to zero for x≥8.

Fig. 3
figure 3

Normal displacement distribution at different rotation for GTMSE medium

Full size image

Figure 4 displacement component w in the (CD) and (L-S) theories for the two different values of rotation is similar, values of displacement for Ω=0.2 are large compared to those for Ω=0.0 in the ranges 0≤x≤1.8 but small in the range 1.8≤x≤4.5, while the values are converge to zero for x≥8. From this figs., we note that Fig. 3, the horizontal displacement, u, begins with decrease then smooth increases again to reach its maximum magnitude just at the crack end. Beyond it u falls again to try to retain zero at infinity. Figure 4, the vertical displacement w, we see that the displacement component w always starts from the zero (for Ω=0.2) value and terminates at the zero value. Also, at the crack end to reach minimum value, beyond reaching zero at the double of the crack size (state of particles equilibrium).

Fig. 4
figure 4

Displacement distribution at different rotation for GTMSE medium

Full size image

The displacements u and w show different behaviours, because of the elasticity of the solid tends to resist vertical displacements in the problem under investigation. Both of the components show different behaviours, the former tends to increase to maximum just before the end of the crack. Then it falls to a minimum with a highly negative gradient. Afterwards it rises again to a maximum beyond about the crack end.

Figure 5 depicted that in all theories (CD) and (L-S) the values of normal stress σ zz for Ω=0.2 are large compared to those for Ω=0.0 in the range 0≤x≤3.8 and small in the range 3.8≤x≤6.3, while the values are converge to zero for x≥8. The stress component, σ zz reach coincidence with negative value (Fig. 6) and satisfy the boundary condition at x=0, reach the maximum value near the end of crack and converges to zero with increasing the distance x.

Fig. 5
figure 5

Normal stress distribution at different rotation for GTMSE medium

Full size image
Fig. 6
figure 6

Tangential stress distribution at different rotation for GTMSE medium

Full size image

Behavior of tangential stress component σ xz in the theories (CD) and (L-S) is similar for both two different values of rotation, as depicted in Fig. 6 shows that in tow theories the values of rotation for Ω=0.2 are small in the ranges 0≤x≤2.5 and 5.3≤x≤8 compared to those for Ω=0.0; but large in the range 2.5≤x≤5.3, while values are the same for the three theories at x≥8, also Fig. 6, shows that the stress component σ xz satisfy the boundary condition at x=0 and had a different behaviour. It decreases in the start and start decreases (maximum (for Ω=0.2)) in the context of the three theories until reaching the crack end. These trends obey elastic and thermoelastic properties of the solid under investigation.

Behavior of tangential coupled stress m xy in all two theories is opposite for both two different values of rotation constant, as depicted in Fig. 7. shows that in the theories (CD) and (L-S) the values of coupled stress for Ω=0.2 are large in the ranges 0≤x≤2.7 compared to those for Ω=0.0; while the values are the same for the two theories at x≥3. The tangential coupled stress m xy satisfies the boundary condition at x=0. It increases in the start and start decreases in the context of the two theories until reaching the crack end. Figure 8 shows that in the theories (CD) and (L-S) the values of microstress component λ z for Ω=0.2 are opposite and small in the ranges 0≤x≤3 and 6≤x≤8 compared to those for Ω=0.0; but large in the range 3≤x≤6, while values are the same for the three theories at x≥8. The values of microstress for λ z satisfy the boundary condition at x=0, begins with increase (for Ω=0.0) then decreases again to reach its minimum magnitude just near the crack end, beyond reaching zero at the double of the crack size (state of particles equilibrium).

Fig. 7
figure 7

Tangential couple stress distribution at different rotation for GTMSE medium

Full size image
Fig. 8
figure 8

Microstress distribution at different rotation for GTMSE medium

Full size image

2. For generalized micropolaer thermoelasticity elastic (GMTE) medium in the presence (Ω=0.2) and absence (Ω=0.0) of rotation constant are shown graphically in Figs. 9–14. Figure 9 shows that for both the two theories the values of temperature in the (GMTE) medium are small for Ω=0.2 (the general behavior) compared to those in the case of Ω=0.0.

Fig. 9
figure 9

Temperature distribution at different rotation for GMTE medium

Full size image

Behavior of displacement component u for the (CD) and (L-S) theories shown in Fig. 10, the values normal displacement u in the (GMTE) medium are small for Ω=0.2 (the general behavior) compared to those in the case of Ω=0.0.

Fig. 10
figure 10

Normal displacement distribution at different rotation for GMTE medium

Full size image

Figure 11 values of normal component of displacement w are small when Ω=0.0 compared to those in the case of Ω=0.2 (the general behavior).

Fig. 11
figure 11

Displacement distribution at different rotation for GMTE medium

Full size image

Figure 12 when we compare the values of frequency of normal stress in the presence of rotation (Ω=0.2) are small compared to those in the absence (Ω=0.0) of rotation in the ranges 0≤x≤1.5 and 3.8≤x≤6.5; large in the ranges 1.5≤x≤3.8 and x≥6.5, while values are the same for the theories at x>9.

Fig. 12
figure 12

Normal stress distribution at different rotation for GMTE medium

Full size image

Figure 13 Values of tangential stress component σ xz for Ω=0.0 are small compared to those for Ω=0.2 in the ranges 0≤x≤1.2 and 3.8≤x≤7 but large in the range 1.2≤x≤3.8, while values are the same for the three theories at x>9.0.

Fig. 13
figure 13

Tangential stress distribution at different rotation for GMTE medium

Full size image

Figure 14 shows that in two theories the values of coupled stress m xy for Ω=0.2 are small compared to those for Ω=0.0 (the general behavior).

Fig. 14
figure 14

Tangential couple stress distribution at different rotation for GMTE medium

Full size image

3. Figures 15–22 show the comparison between the temperature T, displacement component w, the force stresses components σ zz ,σ xz , the tangential coupled stress m xy and the microstress λ z , the case of different three values of z (namely z=1, z=0.9 and z=0.8) under GL theory. It should be noted (Fig. 15) that in this problem. It is clear from the graph that T has increases to maximum value at the beginning of the crack; it begins to fall just near the crack edge, where it experiences sharp decreases (with maximum negative gradient at the crack’s end). Graph lines for both values of z show different slopes at crack ends according to z-values. In other words, the temperature line for z=1 has the highest gradient when compared with that of z=0.9 and z=0.8 at the second of the range. In addition, all lines begin to coincide when the horizontal distance x is beyond the double of the crack size to reach the reference temperature of the solid. These results obey physical reality for the behaviour of copper as a polycrystalline solid (it should be noted (Fig. 16)).

Fig. 15
figure 15

Variation of temperature distribution T for different vertical distances, under GL theory

Full size image
Fig. 16
figure 16

Variation of temperature distribution T for different vertical distances, under GL theory (3D)

Full size image

Figure 17, the vertical displacement w, despite the peaks (for different vertical distances z=1, z=0.9 and z=0.8)) occur at equal value of x, the magnitude of the maximum displacement peak strongly depends on the vertical distance z. it is also clear that the rate of change of w increases with decreases z as we go farther apart from the crack. On the other hand, Fig. 18: (3D) shows atonable increase of the vertical displacement w, near the crack end to reach minimum value beyond x=3 reaching zero at the double of the crack size (state of particles equilibrium).

Fig. 17
figure 17

Variation of displacement distribution w for different vertical distances, under GL theory

Full size image
Fig. 18
figure 18

Variation of displacement distribution w for different vertical distances, under GL theory (3D)

Full size image

Figure 19, the vertical stresses σ zz . Graph lines for both values of z show different slopes at crack ends according to z-values. In other words, the σ zz component line for z=1 has the highest gradient when compared with that of z=0.9 and z=0.8 at the edge of the crack. In addition, all lines begin to coincide when the horizontal distance x is beyond the double of the crack size to reach zero after their relaxations at infinity. Variation of z has a serious effect on both magnitudes of mechanical stresses. These trends obey elastic and thermoelastic properties of the solid under investigation.

Fig. 19
figure 19

Variation of stress distribution σ zz for different vertical distances, under GL theory

Full size image

Figure 20, shows that the stress component σ xz satisfy the boundary condition, the line for z=0.8 has the highest gradient when compared with that of z=0.9 and z=1 (the general behavior) and converge to zero when x>5. These trends obey elastic and thermoelastic properties of the solid.

Fig. 20
figure 20

Variation of stress distribution σ xz for different vertical distances, under GL theory

Full size image

Figure 21, the tangential coupled stress m xy it increases in the start and start decreases (minimum) in the context of the three values of z until reaching the crack end, for z=1 has the highest gradient when compared with that of z=0.8 and z=0.9 at the edge of the crack. All lines begin to coincide when the horizontal distance x is beyond the edge of the crack x>3.

Fig. 21
figure 21

Variation of tangential couple stress m xy for different vertical distances, under GL theory

Full size image

Figure 22, shown the values of microstress for λ z it decreases in the start and start increases (maximum) in the context of the three values of z until reaching nearly the crack end, for z=0.8 has the highest gradient when compared with that of z=0.9 and z=1 at the edge of the crack. All lines begin to coincide when the horizontal distance x is beyond the double of the crack size to reach zero after their relaxations at infinity.

Fig. 22
figure 22

Variation of microstress λ z for different vertical distances, under GL theory

Full size image

6 Conclusions

  1. 1.

    The curves in the context of the (CD) and (L-S) theories decrease exponentially with increasing x, this indicate that the thermoelastic waves are unattenuated and nondispersive, where purely thermoelastic waves undergo both attenuation and dispersion.

  2. 2.

    The presence of microstretch plays a significant role in all the physical quantities.

  3. 3.

    The curves of the physical quantities with (L-S) theory in most of figures are lower in comparison with those under (CD) theory.

  4. 4.

    Analytical solutions based upon normal mode analysis for themoelastic problem in solids have been developed and utilized.

  5. 5.

    A linear opening mode-I crack has been investigated and studied for copper solid.

  6. 6.

    Temperature, radial and axial distributions were estimated at different distances from the crack edge.

  7. 7.

    The stresses distributions, the tangential coupled stress and the values of microstress were evaluated as functions of the distance from the crack edge.

  8. 8.

    Crack dimensions are significant to elucidate the mechanical structure of the solid.

  9. 9.

    Cracks are stationary and external stress is demanded to propagate such cracks.

  10. 10.

    It can be concluded that a change of volume is attended by a change of the temperature while the effect of the deformation upon the temperature distribution is the subject of the theory of thermoelasticity.

  11. 11.

    The value of all the physical quantities converges to zero with an increase in distance x and all functions are continuous.

  12. 12.

    The presence of rotation plays a significant role in all the physical quantities.