Skip to main content
SpringerLink
Log in

Vibrations of nonhomogeneous orthotropic rectangular plates with bilinear thickness variation resting on Winkler foundation

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

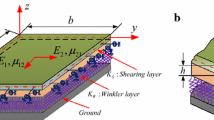
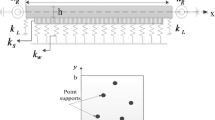
Free transverse vibrations of nonhomogeneous orthotropic rectangular plates with bilinear thickness variation resting on Winkler foundation are presented here using two dimensional boundary characteristic orthogonal polynomials in the Rayleigh-Ritz method on the basis of classical plate theory. Gram-Schmidt process has been used to generate orthogonal polynomials. The nonhomogeneity of the plate is assumed to arise due to linear variations in elastic properties and density of the plate material with the in-plane coordinates. The two dimensional thickness variation is taken as the Cartesian product of linear variations along the two concurrent edges of the plate. Effect of nonhomogeneity parameters, aspect ratio and thickness variation together with foundation parameter on the natural frequencies has been illustrated for the first three modes of vibration for four different combinations of clamped, simply supported and free edges correct to four decimal places. Three dimensional mode shapes for specified plate for all the four boundary conditions have been plotted. A comparison of results in special cases with published one has been presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

x,y,z :

Cartesian coordinate system

X,Y :

Non-dimensionalized variables

a,b :

Length and breadth of the plate

t :

Time

w(x,y,t):

Displacement at the point (x,y) at time t

\(\bar{W}(x,y)\) :

Maximum transverse displacement at the point (x,y)

E x ,E y :

Young’s moduli in proper directions

G xy :

Shear modulus

υ x ,υ y :

Poisson’s ratios in x and y directions

h(x,y):

Thickness

E 1, E 2, ρ 0,G 0 :

Material constants

α,β,γ 1,γ 2,δ 1,δ 2 :

Nonhomogeneity parameters

ψ 1,ψ 2 :

Thickness parameters

K f :

Foundation parameter

p 1,p 2,p 3,p 4 :

Non-negative integers

N :

Positive integer

V max ,T max  :

Maximum strain and kinetic energies of the plate

U f,max  :

Maximum strain energy stored in foundation

ω :

Circular frequency

j,k :

Integers used in displacement approximation

d k :

Unknowns used in displacement approximation

a jk :

Coefficients in (7)

φ k :

Orthogonal polynomials

\(\hat{\phi} _{k}\) :

Orthonormal polynomials

C:

Clamped edge

S:

Simply supported edge

F:

Free edge

\(\frac{a}{b}\) :

Aspect ratio

Ω:

Non-dimensionalized frequency parameter

δ jk :

Kronecker delta

References

  1. Bert CW, Malik M (1996) Free vibration analysis of tapered rectangular plates by differential quadrature method: a semi-analytical approach. J Sound Vib 190(1):41–63

    Article  ADS  Google Scholar 

  2. Bhardwaj N, Gupta AP, Choong KK (2007) Effect of elastic foundation on the vibration of orthotropic elliptic plates with varying thickness. Meccanica 42(4):341–358

    Article  MATH  Google Scholar 

  3. Bhat RB (1985) Natural frequencies of rectangular plates using characteristic orthogonal polynomials in Rayleigh-Ritz method. J Sound Vib 102(4):493–499

    Article  ADS  Google Scholar 

  4. Bhat RB, Laura PAA, Gutierrez RG, Cortinez VH, Sanzi HC (1990) Numerical experiments on the determination of natural frequencies of transverse vibrations of rectangular plates of non-uniform thickness. J Sound Vib 138(2):205–219

    Article  ADS  Google Scholar 

  5. Chakraverty S, Ragini Jindal, Agarwal VK (2007) Vibration of nonhomogeneous orthotropic elliptic and circular plates with variable thickness. J Vib Acoust 129(2):256–259

    Article  Google Scholar 

  6. Chakraverty S, Petyt M (1999) Vibration of nonhomogeneous plates using two-dimensional orthogonal polynomials as shape functions in the Rayleigh-Ritz method. J Mech Eng Sci 213(7):707–714

    Google Scholar 

  7. Civalek Ö (2006) Harmonic differential quadrature-finite differences coupled approaches for geometrically nonlinear static and dynamic analysis of rectangular plates on elastic foundation. J Sound Vib 294(4–5):966–980

    Article  ADS  Google Scholar 

  8. Civalek Ö (2007) Nonlinear analysis of thin rectangular plates on Winkler-Pasternak elastic foundations by DSC-HDQ methods. Appl Math Model 31(3):606–624

    Article  MathSciNet  MATH  Google Scholar 

  9. Civalek Ö, Acar MH (2007) Discrete singular convolution method for the analysis of Mindlin plates on elastic foundation. Int J Press Vessels Piping 84(9):527–535

    Article  Google Scholar 

  10. Dickinson SM, Li EKH (1982) On the use of simply supported plate functions in the Rayleigh-Ritz method applied to the flexural vibration of rectangular plates. J Sound Vib 80(2):292–297

    Article  ADS  Google Scholar 

  11. Grossi RO, Laura PAA (1980–1981) Transverse vibrations of orthotropic rectangular plates with thickness variation in two directions and with edges elastically restrained against rotation. Fibre Sci Technol 14(4):311–317

    Article  Google Scholar 

  12. Gupta AK, Tripti Johri, Vats RP (2010) Study of thermal gradient effect on a non-homogeneous orthotropic rectangular plate having bidirection linearly thickness variation. Meccanica 45(3):393–400

    Article  MathSciNet  Google Scholar 

  13. Gupta AK, Tripti Johri, Vats RP (2007) Thermal effect on vibration of non- homogeneous orthotropic rectangular plate having bi-directional parabolically varying thickness. In: Proceedings of international conference on engineering & computer science, San Francisco, USA

    Google Scholar 

  14. Gutierrez RH, Laura PAA, Sanzi HC, Elvira G (1995) Vibrations of a rectangular plate of non-uniform thickness partially embedded in a Winkler medium. J Sound Vib 185(5):910–914

    Article  ADS  MATH  Google Scholar 

  15. Huang M, Ma XQ, Sakiyama T, Matuda H, Morita C (2005) Free vibration analysis of orthotropic rectangular plates with variable thickness and general boundary conditions. J Sound Vib 288(4–5):931–955

    Article  ADS  Google Scholar 

  16. Huang MH, Thambiratnam DP (2001) Analysis of plates resting on elastic supports and elastic foundation by finite strip method. Comput Struct 79(29–30):2547–2557

    Article  Google Scholar 

  17. Kobayashi H, Sonoda K (1991) Vibration and buckling of tapered rectangular plates with two opposite edges simply supported and the other two edges elastically restrained against rotation. J Sound Vib 146(2):323–337

    Article  ADS  Google Scholar 

  18. Lal R, Dhanpati (2007) Transverse vibrations of non-homogeneous orthotropic rectangular plates of variable thickness: A spline technique. J Sound Vib 306(1–2):203–214

    Article  ADS  Google Scholar 

  19. Lal R, Dhanpati, Kumar Y (2008) Buckling and vibration of non-homogeneous orthotropic rectangular plates of varying thickness under biaxial compression. Int J Appl Math Mech 4(4):93–107

    Google Scholar 

  20. Lal R, Yajuvindra Kumar, Gupta US (2010) Transverse vibrations of nonhomogeneous rectangular plates of uniform thickness using boundary characteristic orthogonal polynomials. Int J Appl Math Mech 6(14):93–109

    Google Scholar 

  21. Lam KY, Wang CM, He XQ (2000) Canonical exact solutions for Levy-plates on two-parameter foundation using Green’s functions. Eng Struct 22(4):364–378

    Article  Google Scholar 

  22. Laura PAA, Larrondo HA, Cortinez VH, Avalos DR (1991) Transverse vibrations of rectangular plates of non-uniform thickness subjected to a uniform state of in-plane stress. J Sound Vib 151(1):175–180

    Article  ADS  Google Scholar 

  23. Leissa AW (1969) Vibration of plates. NASA SP, vol 160. US Government Printing Office, Washington

    Google Scholar 

  24. Leissa AW (1973) Free vibrations of rectangular plates. J Sound Vib 31(3):257–293

    Article  ADS  MATH  Google Scholar 

  25. Leissa AW (1977) Recent research in plate vibrations 1973–1976: classical theory. Shock Vib Dig 9(10):13–24

    Article  Google Scholar 

  26. Leissa AW (1978) Recent research in plate vibrations 1973–1976: complicating effects. Shock Vib Dig 10(12):21–35

    Article  Google Scholar 

  27. Leissa AW (1981) Plate vibration research 1976–1980: classical theory. Shock Vib Dig 13(9):11–22

    Article  Google Scholar 

  28. Leissa AW (1981) Plate vibration research 1976–1980: complicating effect. Shock Vib Dig 13(10):19–36

    Article  Google Scholar 

  29. Leissa AW (1987) Recent studies in plate vibrations 1981–1985, part I, classical theory. Shock Vib Dig 19(2):11–18

    Article  Google Scholar 

  30. Leissa AW (1987) Recent studies in plate vibrations 1981–1985, part II, complicating effects. Shock Vib Dig 19(3):10–24

    Article  Google Scholar 

  31. Liew KM, Lim MK (1993) Transverse vibration of trapezoidal plates of variable thickness: symmetric trapezoids. J Sound Vib 165(1):45–67

    Article  ADS  MATH  Google Scholar 

  32. McFadden TT, Bennett FL (1991) Construction in cold regions. Wiley, New York

    Google Scholar 

  33. Hsu M-H (2006) Vibration characteristics of rectangular plates resting on elastic foundations and carrying any number of sprung masses. Int J Appl Sci Eng 4(1):83–89

    Google Scholar 

  34. Hsu M-H (2010) Vibration analysis of orthotropic rectangular plates on elastic foundations. Compos Struct 92(4):844–852

    Article  Google Scholar 

  35. Mizusawa T (1986) Natural frequencies of rectangular plates with free edges. J Sound Vib 105(3):451–459

    Article  ADS  Google Scholar 

  36. Raju KK, Rao GV (1994) Mode shape change in the stability problem and its effect on the vibration behaviour of simply supported orthotropic rectangular plates on an elastic foundation. J Sound Vib 175(5):693–699

    Article  ADS  MATH  Google Scholar 

  37. Saha KN, Kar RC, Datta PK (1997) Dynamic stability of a rectangular plate on non-homogeneous Winkler foundation. Comput Struct 63(6):1213–1222

    Article  MATH  Google Scholar 

  38. Sanzi HC, Laura PAA, Degreco VBH (1988) Numerical experiments on the determination of the fundamental frequency of transverse vibration of non-uniform rectangular plates. J Sound Vib 123(2):382–386

    Article  Google Scholar 

  39. Singh B, Chakraverty S (1994) Flexural vibration of skew plates using boundary characteristic orthogonal polynomials in two variables. J Sound Vib 173(2):157–178

    Article  ADS  MATH  Google Scholar 

  40. Tameroglu SS (1996) Vibrations of clamped rectangular plates on elastic foundations subjected to uniform compressive forces. J Eng Mech 122(8):714–718

    Article  Google Scholar 

  41. Tomar JS, Gupta AK (1985) Effect of thermal gradient on frequencies of an orthotropic rectangular plate whose thickness varies in two directions. J Sound Vib 98(2):257–262

    Article  ADS  MATH  Google Scholar 

  42. Tomar JS, Gupta DC, Vinod Kumar (1984) Natural frequencies of a non homogeneous isotropic elastic infinite plate of variable thickness resting on elastic foundation. Meccanica 19(4):320–324

    Article  MATH  Google Scholar 

  43. Wang Y, Wang Z-M (2008) Transverse vibration of viscoelastic rectangular plate with linearly varying thickness and multiple cracks. J Sound Vib 318(4–5):1005–1023

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Roorkee, Roorkee, 247 667, India

    Yajuvindra Kumar & R. Lal

Authors
  1. Yajuvindra Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Lal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yajuvindra Kumar.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kumar, Y., Lal, R. Vibrations of nonhomogeneous orthotropic rectangular plates with bilinear thickness variation resting on Winkler foundation. Meccanica 47, 893–915 (2012). https://doi.org/10.1007/s11012-011-9459-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-011-9459-4

Keywords

Search

Navigation