Skip to main content

Advertisement

SpringerLink
Log in

New analytical approach to energy pumping problem in strongly nonhomogeneous 2dof systems

  • Original Paper
  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

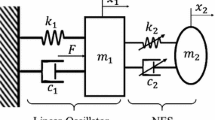
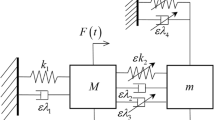
We present new analytical approach to the problem of energy pumping in strongly non- homogeneous nonlinear two-degree-of-freedom (2DOF) systems with single anchor spring under condition of initial impact. Energy pumping is a passive, almost irreversible transfer of mechanical energy from the main substructure of the system to the light auxiliary attachment. The mechanism of energy pumping in the system under consideration is a resonance capture. The approach is based on application of Laplace transformation to the principal asymptotic approximation of the equations of motion in complex form and using the power expansion of the solution in terms of time. Obtained temporal dependence of the system energetic characteristics gives a tool for estimation of energy pumping efficiency. In particular, we show that the system without an anchor spring in attachment is more efficient than the system with such a spring. Numerical simulations confirm the analytical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Gendelman O (2001) Transition of energy to a nonlinear localized mode in a highly asymmetric system of two oscillators. Nonlin Dyn 25:237–253

    Article  MATH  Google Scholar 

  2. Vakakis AF (2001) Inducing passive nonlinear energy sinks in linear vibrating systems. ASME J Vibr Acoust 123:324–332

    Article  Google Scholar 

  3. Gendelman O, Manevitch LI, Vakakis AF, M’Closkey R (2001) Energy pumping in nonlinear mechanical oscillators I: Dynamics of the underlying Hamiltonian systems. ASME J Appl Mech 68:34–41

    Article  MathSciNet  MATH  Google Scholar 

  4. Vakakis AF, Gendelman O (2001) Energy pumping in nonlinear mechanical oscillators II: Resonance capture. ASME J Appl Mech 68:42–48

    Article  MathSciNet  MATH  Google Scholar 

  5. Manevitch LI, Gendelman O, Musienko AI, Vakakis AF, Bergman L (2003) Dynamic interaction of a semi-infinite linear chain of coupled oscillators with a strongly nonlinear end attachment. Physica D 178:1–18

    Article  ADS  MathSciNet  MATH  Google Scholar 

  6. Vakakis AF, Manevitch LI, Musienko AI, Kerschen G, Bergman LA (2005) Transient dynamics of a dispersive elastic wave guide weakly coupled to an essentially nonlinear end attachment. Wave Motion 41:109–132

    Article  MathSciNet  MATH  Google Scholar 

  7. Gendelman OV, Gorlov DV, Manevitch LI, Musienko AI (2005) Dynamics of coupled linear and essentially nonlinear oscillators with substantially different masses. J Sound Vibr 286:1–19

    Article  ADS  Google Scholar 

  8. Manevitch LI (2001) The description of localized normal modes in a chain of nonlinear coupled oscillators using complex variables. Nonlin Dyn 25:95–109

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. N. N. Semenov Institute of Chemical Physics, Russian Academy of Sciences, ul. Kosygina 4, 119991, Moscow, Russia

    Leonid I. Manevitch & Andrey I. Musienko

  2. LGM, URA CNRS 1652, Ecole Nationale des Travaux Publics de l’Etat, 3 Rue Maurice Audin, 69518, Vaulx-en-Velin Cedex, France

    Claude-Henri Lamarque

Authors
  1. Leonid I. Manevitch
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andrey I. Musienko
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Claude-Henri Lamarque
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Andrey I. Musienko.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Manevitch, L.I., Musienko, A.I. & Lamarque, CH. New analytical approach to energy pumping problem in strongly nonhomogeneous 2dof systems. Meccanica 42, 77–83 (2007). https://doi.org/10.1007/s11012-006-9021-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-006-9021-y

Keywords

Search

Navigation