Pairwise Markov Models and Hybrid Segmentation Approach

Abstract

The article studies segmentation problem (also known as classification problem) with pairwise Markov models (PMMs). A PMM is a process where the observation process and underlying state sequence form a two-dimensional Markov chain, it is a natural generalization of a hidden Markov model. To demonstrate the richness of the class of PMMs, we examine closer a few examples of rather different types of PMMs: a model for two related Markov chains, a model that allows to model an inhomogeneous Markov chain as a conditional marginal process of a homogeneous PMM, and a semi-Markov model. The segmentation problem assumes that one of the marginal processes is observed and the other one is not, the problem is to estimate the unobserved state path given the observations. The standard state path estimators often used are the so-called Viterbi path (a sequence with maximum state path probability given the observations) or the pointwise maximum a posteriori (PMAP) path (a sequence that maximizes the conditional state probability for given observations pointwise). Both these estimators have their limitations, therefore we derive formulas for calculating the so-called hybrid path estimators which interpolate between the PMAP and Viterbi path. We apply the introduced algorithms to the studied models in order to demonstrate the properties of different segmentation methods, and to illustrate large variation in behaviour of different segmentation methods in different PMMs. The studied examples show that a segmentation method should always be chosen with care by taking into account the purpose of modelling and the particular model of interest.

1 Introduction

1.1 Pairwise Markov Models

Let $\mathcal{X}$ and $\mathcal{Y}$ be discrete sets and let $\{Z_t\}_{t=1}^{\infty }=\{(X_t,Y_t)\}_{t=1}^{\infty }$ be a homogeneous Markov chain taking values in $\mathcal{Z}\subset \mathcal{X}\times \mathcal{Y}$. This will be assumed in the whole article if not specified otherwise. Here the state space $\mathcal{Z}$ can be a proper subset of $\mathcal{X}\times \mathcal{Y}$. Following the terminology proposed by W. Pieczynski (see, e.g. Pieczynski (2003), Derrode and Pieczynski (2004), Lanchantin et al. (2011), Lapuyade-Lahorgue and Pieczynski (2012), Boudaren et al. (2012), Derrode and Pieczynski (2013), and Gorynin et al. (2018)), we call the process $Z=(X,Y)$ a pairwise Markov chain or a pairwise Markov model (PMM). The name reflects the fact that although the processes X or Y might lack the Markov property, conditionally on X (or on Y) the process Y (or X) is an inhomogeneous Markov chain (see Proposition 2.1 in Pieczynski (2003)). It turns out that the two-dimensional structure makes PMMs very useful and flexible allowing to consider many stochastic models as a homogeneous Markov chain. Probably the most known model falling into the class of PMMs is the hidden Markov model (HMM), where Y is a Markov chain and given $Y_1,\ldots ,Y_n$, the observations $X_1,\ldots ,X_n$ are conditionally independent. In HMMs, the distribution of $X_t$ conditional on $Y_1,\ldots ,Y_n$ depends solely on $Y_t$ (sometimes the dependence on $Y_{t-1}$ is allowed as well). However, the class of PMMs is much larger compared to HMMs, allowing also for conditionally dependent observations and models where Y is not a Markov chain.

In this article, we examine closer a few rather different PMM models. Although these models serve different purposes, we show how the unified PMM framework becomes useful and simplifies analysis. The first model, studied in Subsection 3.1, presents a parametric class of PMMs where both marginal processes are Markov chains with given transition matrices and the parameters allow to model dependence structure between the marginal chains. Such a model can be useful in random sequence analysis in computational molecular biology or linguistics, because it provides a relatively simple model for dependent Markov chains. For such applications the property that both marginal processes are Markov chains is natural, although typically in PMMs at least one of the marginal processes does not have the Markov property. The close examination of that model allows us to present an example of a PMM where Y (and also X) is a Markov chain without having the so-called HMM-DN property (see Sect. 2 for definition of the HMM-DN property). To our best knowledge, such an example has not been published before. Our second model in Subsection 3.2 – a regime-switching model – allows to embed an inhomogeneous Markov chain into a PMM, and thus an inhomogeneous Markov chain can be considered as a conditional marginal process of a homogeneous PMM. In particular, suppose that X is a stochastic process that in a certain random time-period behaves as a homogeneous Markov chain, but then the transition matrix changes. After the change, X evolves again as a Markov chain but now with another transition matrix, and after a certain random time-period the matrix changes again. Such a model can be considered as a PMM (X, Y), where the Y-process is a Markov chain that governs the time periods – regimes – for different transition matrices and the X-process is the observed one. We argue that given a realization of Y, X is an inhomogeneous Markov chain, but unconditionally it lacks the Markov property. Although the regime-switching model has been successfully applied in signal and image processing, to our best knowledge it lacks a mathematically rigorous treatment and we try to fill in that gap. The third model in Subsection 3.3 allows to consider a semi-Markov process as a PMM and the fourth model in Subsection 3.4 combines the regime-switching model and semi-Markov model into one. In the regime-switching model the regime process Y is a Markov chain, thus the times Y spends in a particular regime are geometrically distributed. Replacing Y by a semi-Markov PMM, let it be (U, V), allows us to generalize the regime-switching model so that the intra-regime times do not have necessarily geometrical distributions. Hence the resulting model (X, (U, V)) is actually a three-dimensional Markov chain known as a triplet Markov model, see e.g. Lanchantin and Pieczynski (2004), Benboudjema and Pieczynski (2007), Lanchantin et al. (2011), Lapuyade-Lahorgue and Pieczynski (2012), Boudaren et al. (2012), and Gorynin et al. (2018). Besides the unified theoretical analysis of the PMM model, the main practical advantage of the PMM approach is that due to the Markov property, all the classical HMM tools (forward-backward algorithms, EM training etc) are applicable. In this article we focus on segmentation problem with PMMs.

1.2 Segmentation Problem, Outline and Ojectives of the Article

Suppose that a researcher has a realization $x_1,\ldots ,x_n$ of observations $X_1,\ldots ,X_n$ and the objective is to estimate the unobserved class variables $Y_1,\ldots ,Y_n$. We shall call estimation of unobserved class variables a segmentation problem (also known as classification, denoising or decoding). The standard solutions of the segmentation problem are either a state sequence that maximizes the conditional probability $P(Y_1=y_1,\ldots ,Y_n=y_n|X_1=x_1,\ldots ,X_n=x_n)$ over all sequences $(y_1,\ldots ,y_n)$ – the so-called Viterbi path – or a sequence which maximizes the probability $P(Y_t=y|X_1=x_1,\ldots ,X_n=x_n)$ over all possible states y for every $t\in \{1,\ldots ,n\}$ separately. This pointwise estimator is called the pointwise maximum a posteriori (PMAP) path. Since the Viterbi and forward-backward algorithms apply for any PMM, both the Viterbi and PMAP path can be easily found. However, both these solutions have their limitations. The PMAP path is guaranteed to maximize the expected number of correctly estimated classes (accuracy), but it might have a zero (conditional) probability, hence it can be inadmissible. The Viterbi path, on the other hand, might be rather inaccurate in terms of pointwise classification errors. These deficiencies are well known in the literature and were pointed out already by L. Rabiner in his seminal tutorial (Rabiner 1989). As a remedy against inadmissible PMAP paths, he proposed to replace the PMAP path with a state path that maximizes the expected number of correctly estimated state blocks of length k, $k\ge 2$, we shall call these state path estimators Rabiner k-block paths. Since inadmissibility is mostly caused due to impossible transitions in the model and any impossible transition automatically results in a wrongly estimated block, it is natural to hope that any k-block path should minimize such impossible transitions, especially for larger k. However, Rabiner k-block paths can still be inadmissible and this might happen quite easily. Often various counterexamples consider two-block paths, but our example in Subsection 5.3 shows that even 5-block paths can be inadmissible.

To deal with the problem of inadmissibility more efficiently, a family of hybrid path estimators was defined in Lember and Koloydenko (2014). The idea behind the hybrid paths mimics partly the Rabiner k-block idea, but instead of block length k, a hybrid path depends on a regularization parameter $C\ge 0$ and any hybrid path is guaranteed to be admissible. We shall see in Sect. 4 that when $C=k-1$, then for smaller integer values k the corresponding hybrid path can be considered as an analogue of the k-block path. Hybrid paths interpolate between PMAP and Viterbi paths: for $C=0$ the hybrid path equals the PMAP path and from certain C on the hybrid path equals the Viterbi path. This means that there exists a constant $C_o$ (depending on the model and data) such that the hybrid path becomes Viterbi when $C>C_o$.

The class of PMMs is large and in practice several subclasses are of interest. In Sect. 2, we present main classes of PMMs and recall the main properties of different classes. In particular, we show how the different subclasses correspond to the factorization of the transition matrix. A special attention is devoted to the question, when is one of the marginal processes a Markov chain. Section 3 is devoted to the presentation and study of our four main model examples. In Sect. 4, we briefly recall the decision-theoretical foundations of segmentation theory and define the class of hybrid classifiers. All classifiers considered in the article would be solely of theoretical interest if it would be difficult to compute them. In Lember and Koloydenko (2014) it was shown that for HMMs the hybrid paths can be easily found by a dynamic programming algorithm that combines the Viterbi algorithm and the forward-backward recursions. Proposition 4.2 shows that the same algorithm holds for PMMs so that the hybrid paths can be found with complexity $O(|\mathcal{Y}|n)$, the complexity is independent of C. The algorithm for the Rabiner k-block paths has complexity $O(|\mathcal{Y}|^{k-1}n)$ (Proposition 4.3). This means that for bigger blocks Rabiner k-block paths are very time-consuming to calculate. In Sect. 5, several simulations and numerical examples to illustrate segmentation with PMMs are presented. Numerical studies are mainly motivated by the following research questions and hypotheses:

• 1. Is there a bound on $C_o(x^n)$ that does not depend on n? This question is negatively answered in Subsection 5.1, where it is shown that even for the simplest model studied in Subsection 3.1 such an upper bound does not exist.

• 2. How does $C_o(X^n)$ behave in different models? The counterexample of Subsection 5.1 is alarming, thus the next natural question is whether such an unstable behavior of $C_o$ is typical or due to the particular observation sequence $x^n$? The first part of Subsection 5.2 deals with this question and the simulations confirm that for this particular model, the constant $C_o$ is typically quite independent of $x^n$ and its length n. To understand whether such a stability of $C_o$ characterizes this particular model, in Subsection 5.3 the same analysis is performed with the regime-switching model defined in Subsection 3.2. The results show that for the studied parameter combinations $C_o(X^n)$ is highly varying.

• 3. How different are hybrid paths corresponding to different regularization parameters C? Hybrid paths naturally interpolate between the Viterbi and PMAP path. When these two paths are very different from each other, one could expect a larger variety also between different hybrid paths. To illustrate this, in Subsection 5.1 all hybrid paths corresponding to one particular observation sequence for our first model from Subsection 3.1 are calculated (Fig. 1).

• 4. How different are the hybrid and Rabiner k-block paths? This research question is driven by the analogy of the hybrid and k-block paths, hence it is natural to ask how much they actually differ. Subsection 5.2 studies this question for our first model (from Subsection 3.1) and Subsection 5.3 for the regime-switching model (from Subsection 3.2).

• 5. Hybrid path is a remedy against inadmissibility. As pointed out above, the PMAP path can be inadmissible and so can the Rabiner k-block path. The natural question is whether the inadmissibility is just a theoretical threat or it might really happen in practical models? And when this becomes an issue, is a hybrid path a good replacement? To answer these questions, in Subsection 5.3 segmentation is studied for the regime-switching model with some impossible regime changes. This is a model of big practical importance and it turns out that with certain model parameter combinations, for all the 100 generated observation sequences the PMAP paths were inadmissible, even the majority of the Rabiner 5-block paths were inadmissible (Table 3). When replacing the PMAP path with the 2-block hybrid path, the accuracy decreases slightly, but obviously all the paths become admissible.

Throughout the article we assume that the observation alphabet $\mathcal{X}$ is discrete. The reason for making this assumption is to reduce mathematical technicalities. In real segmentation problems $\mathcal{X}$ is often uncountable, say $\mathcal{X}=\mathbb {R}^d$. All ideas and algorithms of this note carry on to the uncountable $\mathcal{X}$ as well, just the notation and proofs would be more technical. For formal definition of PMMs, the Viterbi algorithm and related concepts in the case of general $\mathcal{X}$, see Lember and Sova (2020, 2021a, 2021b).

Fig. 1

Studied state path estimates for one observation sequence in Example 5.2. From top to down: true underlying state path, PMAP, hybrid block paths for $k=2,\ldots ,14$, Rabiner block paths for $k=2,\ldots ,14$, Viterbi

2 Subclasses and Properties of PMMs

Recall that $\mathcal{X}$ and $\mathcal{Y}$ are discrete sets and $\{Z_t\}_{t=1}^{\infty }=\{(X_t,Y_t)\}_{t=1}^{\infty }$ is a homogeneous Markov chain taking values in $\mathcal{Z}\subset \mathcal{X}\times \mathcal{Y}$. In what follows, we shall denote by p various probabilities like transition probabilities $p(z_{t+1}|z_t)=p(x_{t+1}, y_{t+1}|x_t,y_t)=P(X_{t+1}=x_{t+1},Y_{t+1}=y_{t+1}|X_{t}=x_{t},Y_{t}=y_{t})$, joint distributions $p(x_s,\ldots ,x_t)=P(X_s=x_s,\ldots ,X_t=x_t)$ etc. We use abbreviation $x_s^t=(x_s,\ldots ,x_t)$ and when $s=1$, we write $x^t$ instead of $x_1^t$. We denote $p_t(y|x^n)=P(Y_t=y|X^n=x^n)$. As usual in a discrete setting, any conditional probability implies that the probability of the condition is strictly positive. Sometimes we abuse the notation a bit by writing $p(x_{t+1}=x|x_t=x')$ instead of $P(X_{t+1}=x|X_t=x')$ etc.

Pairwise Markov models is a large class of stochastic models that can be classified via the properties of transition probabilities $p(z_{t+1}|z_t)$. When the transition probabilities factorize as

$$\begin{aligned} p(z_{t+1}|z_t)=p(y_{t+1}|y_t)p(x_{t+1}|y_{t+1}), \end{aligned}$$

then we have an HMM. Clearly HMMs is a very narrow subclass of PMMs. A broader subclass of PMMs is the class of Markov switching models, see Cappé et al. (2005), where the observations are not conditionally independent any more:

$$\begin{aligned} p(z_{t+1}|z_t)=p(y_{t+1}|y_t)p(x_{t+1}|y_{t+1},x_{t}). \end{aligned}$$

Thus, HMMs is a special case of Markov switching models. A more general class of models where Y is a Markov chain is the class of hidden Markov models with dependent noise (HMM-DN), see Derrode and Pieczynski (2013), where the transition probabilities factorize as follows:

$$\begin{aligned} p(z_{t+1}|z_t)=p(y_{t+1}|y_t)p(x_{t+1}|y_{t+1}, y_t,x_{t}).\end{aligned}$$

(1)

Hence the class of Markov switching models is a special class of HMM-DNs. Observe that (1) is equivalent to

$$\begin{aligned} p(y_{t+1}|z_t)=p(y_{t+1}|y_t). \end{aligned}$$

(2)

Since (1) is an important property, we shall examine it a bit closer. Suppose $\mathcal{Z}=\mathcal{X}\times \mathcal{Y}$. Let $|\mathcal{X}|=k\le \infty$ and $|\mathcal{Y}|=l\le \infty$ and let the kl elements of $\mathcal{X}\times \mathcal{Y}$ be ordered as follows:

$$\begin{aligned} \mathcal{X}\times \mathcal{Y}=\{(\chi _1,\gamma _1),\ldots ,(\chi _k,\gamma _1),(\chi _1,\gamma _2),\ldots ,(\chi _k,\gamma _2),\ldots ,(\chi _1,\gamma _l),\ldots , (\chi _k,\gamma _l)\}. \end{aligned}$$

Then Z is an HMM-DN if and only if the $kl\times kl$ transition matrix factorizes as follows:

$$\begin{aligned} \left( \begin{array}{cccc} p_{11}\cdot A_{11}&{} p_{12}\cdot A_{12} &{} \ldots &{} p_{1l}\cdot A_{1l} \\ p_{21}\cdot A_{21}&{} p_{22}\cdot A_{22} &{} \ldots &{} p_{2l}\cdot A_{2l} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ p_{l1}\cdot A_{l1}&{} p_{l2}\cdot A_{l2} &{} \ldots &{} p_{ll}\cdot A_{ll} \\ \end{array} \right) , \end{aligned}$$

(3)

where $p_{ij}=P(Y_{t+1}=\gamma _j|Y_t=\gamma _i)$ and $A_{ij}$ are the following transition matrices:

$$\begin{aligned} A_{ij}=\left( \begin{array}{ccc} a^{(ij)}_{11} &{} \cdots &{} a^{(ij)}_{1k} \\ \cdots &{} \cdots &{} \cdots \\ a^{(ij)}_{k1} &{} \cdots &{} a^{(ij)}_{kk} \\ \end{array} \right) , \quad a^{(ij)}_{u v}=P(X_{t+1}=\chi _v|Y_{t+1}=\gamma _j,Y_{t}=\gamma _i, X_t=\chi _u). \end{aligned}$$

If Z is a Markov switching model, then the probability $a_{uv}^{(ij)}$ is independent of i and then in (3),

$$\begin{aligned} A_{ij}=A_j, \quad A_j=(a^{(j)}_{uv}),\quad a^{(j)}_{uv}=P(X_{t+1}=\chi _v|Y_{t+1}=\gamma _j, X_t=\chi _u). \end{aligned}$$

When Z is an HMM, then $a^{(ij)}_{uv}$ is independent of both i and u implying that all the rows in $A_j$ are equal.

The property in (2) that defines HMM-DNs and holds for all their subclasses has important implications. Since it obviously implies that $p(y_{t+1}^n|z_t)=p(y_{t+1}^n|y_t)$, we see that the conditional distribution of $x_t$ given the whole sequence $y^n$ depends only on $y^t$:

$$\begin{aligned} p(x_t|y^n)={p(x_t,y^t)p(y_{t+1}^n|x_t,y_t)\over p(y^t)p(y_{t+1}^n|y_t)}={p(x_t,y^t)p(y_{t+1}^n|y_t)\over p(y^t)p(y_{t+1}^n|y_t)} = p(x_t|y^t).\end{aligned}$$

(4)

In particular, it follows that

$$\begin{aligned} p(x_t|y_t^n)=p(x_t|y_t). \end{aligned}$$

(5)

If the stationary model happens to be such that (2) holds for the time-reversed chain, that is $p(y_{t-1}|z_t)=p(y_{t-1}|y_t)$, then clearly $p(x_t|y^n)=p(x_t|y_t^n)$. Therefore, if the model is HMM-DN and the time-reversed chain is HMM-DN as well, then it must hold that $p(x_t|y^t)=p(x_t|y^n)=p(x_t|y_t^n)$, implying that $p(x_t|y^n)=p(x_t|y_t)$. Hence the conditional distribution of $x_t$ given the whole sequence $y^n$ depends solely on $y_t$. Any HMM has this particular property, but in the case of HMMs in addition the X-variables are conditionally independent of Y, that is $p(x^n|y^n)=\prod _{t=1}^n p(x_t|y_t)$. Another implication of (2) is that the conditional transition probabilities $p(x_{t+1}|x_t,y^n)$ depend only on $y_t$ and $y_{t+1}$, but not on $y_{t+2}^n$. Indeed, when (2) holds, then

$$\begin{aligned} p(x_{t+1}|x_t,y^n)&={p(x_{t+1},x_t,y^n)\over p(x_t,y^n)}={p(x_t,y^t)p(z_{t+1}|z_t)p(y_{t+2}^n|y_{t+1})\over p(x_t,y^t)p(y_{t+1}|z_t)p(y_{t+2}^n|y_{t+1},z_t)}\nonumber \\ {}&=p(x_{t+1}|x_t,y_t,y_{t+1}), \end{aligned}$$

(6)

because $p(y_{t+2}^n|y_{t+1},z_t)=\sum _{x_{t+1}}p(y_{t+2}^n|x_{t+1},y_{t+1},z_t)p(x_{t+1}|y_{t+1},z_t)=p(y_{t+2}^n|y_{t+1}).$ Without (2) this probability might depend on $y_{t+2}^n$, i.e. for any PMM, $p(x_{t+1}|x_t,y^n)=$ $p (x_{t+1}|x_t,y_t^n)$.

Preserving the Markov Property

A question raised already in the very first papers about PMMs was when is the Y-process unconditionally a Markov chain, see Pieczynski (2003). It is easy to see that when Z is an HMM-DN, then Y is a Markov chain. Indeed, under (2) we have for any $t\ge 2$:

$$\begin{aligned} p(y_{t+1}|y^t)&=\sum _{x_t\in \mathcal{X}}p(y_{t+1}|x_t,y^t)p(x_t|y^t)=\sum _{x_t\in \mathcal{X}}p(y_{t+1}|x_t,y_t)p(x_t|y^t)\\ {}&=\sum _{x_t\in \mathcal{X}}p(y_{t+1}|y_t)p(x_t|y^t)=p(y_{t+1}|y_t). \end{aligned}$$

Here the second equality follows from the Markov property and the third equality follows from (2). Hence the matrix $(p_{ij})$ in representation (3) is the transition matrix of the Markov chain Y. Since a Markov switching model is a special case of HMM-DNs, then under that model Y is a Markov chain as well. It should be noted that for an HMM-DN model, Y is a Markov chain for any initial distribution. It has been an open question whether being an HMM-DN is also a necessary property for Y being a Markov chain. The following proposition shows that under a special condition it is indeed so.

Proposition 2.1

Let t be fixed and let $(y_{t-1},y_t,y_{t+1})$ be a state triplet such that $y_{t+1}=y_{t-1}$ and $p(x_t|y_t,y_{t-1})=p(x_t|y_t,y_{t+1})$ for every $x_t$. Then the Markov property $p(y_{t+1}|y^t)=$ $p(y_{t+1}|y_t)$ implies that (1) holds.

Proof

Take $(y_{t-1},y_t,y_{t+1})$ such that $p(y_{t-1},y_t,y_{t+1})>0$ and $y_{t+1}=y_{t-1}$. The Markov property implies $p(y_{t+1}|y_t,y_{t-1})=p(y_{t+1}|y_t)$. Then

$$\begin{aligned} p(y_{t+1}|y_t,y_{t-1})&=\sum _{x_t\in \mathcal{X}} p(y_{t+1}|x_t,y_{t},y_{t-1})p(x_t|y_{t},y_{t-1})\\ {}&=\sum _{x_t\in \mathcal{X}} p(y_{t+1}|x_t,y_{t})p(x_t|y_{t},y_{t-1})\\ {}&=\sum _{x_t\in \mathcal{X}} p(y_{t+1}|y_{t}){p(x_t|y_t,y_{t+1})\over p(x_t|y_t)} p(x_t|y_{t},y_{t-1})\\ {}&=p(y_{t+1}|y_{t})\sum _{x_t\in \mathcal{X}}{p(x_t|y_t,y_{t+1})\over p(x_t|y_t)}p(x_t|y_{t},y_{t-1}). \end{aligned}$$

Hence, the equality $p(y_{t+1}|y_t,y_{t-1})=p(y_{t+1}|y_t)$ implies that

$$\begin{aligned} \sum _{x_t\in \mathcal{X}}{p(x_t|y_t,y_{t+1})\over p(x_t|y_t)}p(x_t|y_{t},y_{t-1})=1.\end{aligned}$$

(7)

By the assumption, $p(x_t|y_t,y_{t+1})=p(x_t|y_{t},y_{t-1})$ for every $x_t$. We now show the following implication: if p and q are probability measures on $\mathcal{X}$ so that

$$\begin{aligned} \sum _{x\in \mathcal{X}} {p(x)\over q(x)}p(x)=1, \end{aligned}$$

then $p(x)=q(x)$ for every x. It follows from Jensen’s inequality that

$$\begin{aligned} \ln \Big (\sum _{x\in \mathcal{X}} {p(x)\over q(x)}p(x)\Big )\ge \sum _{x\in \mathcal{X}} \ln \big ({p(x)\over q(x)}\big )p(x),\end{aligned}$$

(8)

the equality holds if and only if $p(x)=q(x)$ for every $x\in \mathcal{X}$. The right-hand side of (8) is the Kullback–Leibler divergence between p and q, hence non-negative. The left-hand side is 0 by the assumption. Thus it follows that $p=q$. Therefore also $p(x_t|y_t,y_{t+1})=p(x_t|y_t)$ holds for every $x_t$ and multiplying both sides by $p(y_t,y_{t+1})$ gives

$$\begin{aligned} p(y_{t+1}|x_t,y_t)p(x_t,y_t)=p(x_t,y_t,y_{t+1})=p(x_t|y_t)p(y_t,y_{t+1})=p(x_t,y_t)p(y_{t+1}|y_t), \end{aligned}$$

thus (1) holds. $\blacksquare$

Proposition 2.1 is basically Proposition 2.3 in Pieczynski (2003), the difference is that stationarity is assumed in Pieczynski (2003). Therefore, Proposition 2.1 here is more general. Observe also that the proof in Pieczynski (2003) does not use Jensen’s inequality and is therefore more complicated. A more general proposition in the context of triplet Markov chain models is considered in Lanchantin et al. (2011), p. 165. That proposition considers a stationary and reversible triplet Markov chain and specifies conditions under which different marginal chains or pairs of marginal chains remain Markovian. The assumptions of Proposition 2.1 are satisfied when Z is a stationary and reversible Markov chain. Thus, for a stationary and reversible Z, the marginal process Y is Markovian if and only if Z is an HMM-DN. We shall now argue that when the chain is not reversible, then the HMM-DN property is not necessary for Y having (unconditionally) the Markov property. Let $Z_1,\ldots ,Z_n$ be an HMM-DN. Then $Y_1,\ldots ,Y_n$ is a Markov chain (for any initial distribution). After reversing the time the Markov property preserves, and thus in the reversed chain Y remains to be a Markov chain. A more formal argument is the following:

$$\begin{aligned} p(y_{t-1}|y_t^n)&=\sum _{x_t} p(y_{t-1}|x_t,y_t^n)p(x_t|y_t^n){\mathop {=}\limits ^{(5)}}\sum _{x_t} p(y_{t-1}|x_t,y_t^n)p(x_t|y_t)\\ {}&=\sum _{x_t} p(y_{t-1}|x_t,y_t)p(x_t|y_t)=p(y_{t-1}|y_t). \end{aligned}$$

Thus, when the reversed chain is not an HMM-DN, then we have an example of a PMM (X, Y) which is not an HMM-DN but Y is a Markov chain. When in addition Z is stationary but not reversible, then the reversed chain is stationary and therefore also homogeneous. As a consequence, it is possible to construct a homogeneous and stationary PMM such that (1) fails (the model is not an HMM-DN), but the marginal process Y is a Markov chain. It should be noted that for such (homogeneous) examples the property that Y is Markovian depends on the initial distribution – when the initial distribution is not the stationary distribution, the Markov property of a marginal chain might fail. In Subsection 3.1 we shall present an example of such a model.

3 Some Examples of Discrete PMMs

3.1 The Related Markov Chains Model

Usually in pairwise Markov models the X-process is not a Markov chain even if Y is. The PMM considered in this section is, however, deliberately constructed so that besides Y also the X-chain were a Markov chain. In particular, the model is an HMM-DN (so that Y is a Markov chain) and it is also an HMM-DN when the roles of X and Y are changed. In what follows, the latter property shall be referred to as HMM-DN by X and it implies that X is a Markov chain as well. For simplicity we consider the two-letter alphabets $\mathcal{X}=\{1,2\}$ and $\mathcal{Y}=\{a,b\}$. Let $P_X$ and $P_Y$ be the transition matrices of X and Y, respectively (all entries positive):

$$\begin{aligned} P_X= \left( \begin{array}{cc} p &{} 1-p \\ q &{} 1-q \\ \end{array} \right) , \quad P_Y= \left( \begin{array}{cc} p' &{} 1-p' \\ q' &{} 1-q' \\ \end{array} \right) . \end{aligned}$$

Given these matrices, we construct a parametric family of PMMs with the state space $\mathcal{X}\times \mathcal{Y}$ so that the marginal processes X and Y were both Markov chains with these transition matrices. The parameters allow to tune the dependence between the X- and Y-sequence. In particular, a certain combination of parameters will yield the case where X and Y are independent Markov processes, and another combination will provide the maximal dependence case. A PMM fulfilling these requirements has the following transition matrix:

(9)

where $\lambda _i,\mu _i, i=1,2$ are parameters satisfying the following conditions:

$$\begin{aligned}&\lambda _1 \in \left[ \max \left\{ {p'+p-1\over p},0\right\} , \min \left\{ {p' \over p},1\right\} \right] , \quad \lambda _2 \in \left[ \max \left\{ {q'+p-1\over p}, 0 \right\} ,\min \left\{ {q' \over p}, 1\right\} \right] , \\&\mu _1\in \left[ \max \left\{ {p'+q-1\over q}, 0\right\} ,\min \left\{ {p'\over q},1 \right\} \right] , \quad \mu _2 \in \left[ \max \left\{ {q'+q-1\over q}, 0\right\} , \min \left\{ {q'\over q}, 1 \right\} \right] . \end{aligned}$$

The conditions above ensure that all probabilities are in [0, 1]. The transition matrix in (9) is of form (3) with $(p_{ij})=P_Y$, and after changing the roles of X and Y it has the same form with $(p_{ij})=P_X$. Hence (X, Y) is an HMM-DN as well as HMM-DN by X. Therefore, X and Y are both Markov chains with transition matrices $P_X$ and $P_Y$. The parameters have the following meaning:

$$\begin{aligned}&\lambda _1=P(Y_{t+1}=a|Y_t=a, X_t=1, X_{t+1}=1),\quad \lambda _2=P(Y_{t+1}=a|Y_t=b, X_t=1, X_{t+1}=1),\\&\mu _1=P(Y_{t+1}=a|Y_t=a, X_t=2, X_{t+1}=1),\quad \mu _2=P(Y_{t+1}=a|Y_t=b, X_t=2, X_{t+1}=1). \end{aligned}$$

Due to the representation in (3) it is clear that any PMM that is an HMM-DN and also HMM-DN by X must have a transition matrix like (9). However, it does not necessarily mean that the transition matrix in (9) is the only possibility for both X and Y being Markov chains, because the marginal processes might be Markov chains even if the model is not an HMM-DN and HMM-DN by X. As we shall see, an example of such a model is the (time) reversed model of Z with the transition matrix in (9). Indeed, reversing the time does not change the Markov property of marginal processes, but it might spoil the HMM-DN properties. Let us remark that sometimes it is useful to rewrite the last two columns of (9) by introducing artificial parameters $\theta _i$ and $\rho _i$, $i=1,2$, see the Appendix.

The PMMs with transition matrix (9) were introduced in Lember et al. (2018) to model dependencies between two-state Markov chains, see also Lember and Sova (2020). The model can be generalized to the case with bigger alphabets, for such a generalization with $P_X=P_Y$, see Avans (2021). Observe that when $\lambda _1=\mu _1=p'$, $\lambda _2=\mu _2=q'$ and the initial distribution factorizes as $\pi (1,a)=\pi _X(1)\pi _Y(a)$, where $\pi _X$ and $\pi _Y$ denote the initial distributions of X and Y, then X and Y are independent Markov chains because then $p(x_{t+1},y_{t+1}|x_t,y_t)=p(x_{t+1}|x_t)p(y_{t+1}|y_t).$ In what follows, we shall consider closer the case with $p'=p$ and $q'=q$, i.e. $P_X=P_Y$. Then taking $\lambda _1=\mu _2=1$ and choosing the initial distribution $\pi$ so that $\pi (1,a)=\pi (2,b)=0.5$, we get the maximal dependence between X and Y: $Y_t=a$ if and only if $X_t=1$ for any $t\ge 1$. Similarly, when $q=1-p$, the choice $\lambda _2=\mu _1=0$ with $\pi (1,b)=\pi (2,a)=0.5$ yields the other case of maximal dependence: $X_t=1$ if and only if $Y_t=b$.

Reversibility of the Related Markov Chains Model

Let us consider the case with $p=p'\in (0,1)$ and $q=q'\in (0,1)$, i.e. $P_X=P_Y$. We aim to find the conditions that ensure the reversibility of Z. Recall that any two-state Markov chain with positive transition probabilities is always reversible. Thus, for the time-reversed Z, the marginal processes X and Y remain to be Markov chains with the same transition matrices $P_X$ and $P_Y$. Suppose now that the reversed chain is an HMM-DN and also HMM-DN by X. Then, as noted above, it must have the transition matrix as in (9) with some parameters $\lambda ^R_i$ and $\mu ^R_i$, $i=1,2$. The elements on the main diagonal of the original and reversed transition matrix always coincide. Therefore, if the reversed chain has a transition matrix of the form in (9), then all its parameters should be the same as the parameters of the original chain, i.e. $\lambda ^R_i=\lambda _i$ and $\mu ^R_i=\mu _i, i=1,2.$ In other words, our model is reversible if and only if it is an HMM-DN as well as HMM-DN by X. The necessary and sufficient conditions for that property to hold are the following:

$$\begin{aligned} p_{11}^R+p_{13}^R=p, \quad p_{31}^R+p_{33}^R=p, \quad p_{21}^R+p_{23}^R=q, \quad p_{41}^R+p_{43}^R=q, \end{aligned}$$

(10)

$$\begin{aligned} p_{11}^R+p_{12}^R=p, \quad p_{21}^R+p_{22}^R=p, \quad p_{31}^R+p_{32}^R=q, \quad p_{41}^R+p_{42}^R=q. \end{aligned}$$

(11)

In the formulas above $(p^R_{ij})$ stands for the transition matrix of the reversed chain, the state space $\mathcal{X}\times \mathcal{Y}$ is encoded as $\{1,2,3,4\}$ (i.e. $(1,a)=1$, $(1,b)=2$, $(2,a)=3$, $(2,b)=4$). The equalities in (10) are necessary and sufficient for the reversed chain being an HMM-DN and the equalities in (11) are necessary and sufficient for the reversed Z being an HMM-DN by X. For calculating $(p^R_{ij})$, one needs to know the unique stationary distribution $(\pi _1,\pi _2,\pi _3,\pi _4)$ of Z that for our model is given by

$$\begin{aligned} \pi _1&=\pi (1,a)=\pi (1)c,\quad \pi _2=\pi (1,b)=\pi (1)(1-c)=\pi (2,a)=\pi _3,\\ \pi _4&=\pi (2,b)=1-\pi (1)(2-c), \end{aligned}$$

with

$$\begin{aligned} \pi (1)={q\over 1-p+q},\quad \text{ and } \quad c=\pi (a|1)={ p(\lambda _2-\mu _2)+q(\mu _1-\mu _2)+\mu _2\over q(\mu _1-\mu _2)+p(\lambda _2-\lambda _1)+1}. \end{aligned}$$

(12)

The distribution in (12) is the unique stationary distribution unless $p+q=1$ and $\lambda _1\!=\!\mu _2\!=\!1,$$\lambda _2=\mu _1=0$. With $p_{ij}^R=(\pi _j/\pi _i)p_{ji}$, we can now verify that all equations in (10) hold if and only if

$$\begin{aligned} c=\frac{q\mu _1}{q\mu _1+p(1-\lambda _1)}, \end{aligned}$$

(13)

and all equations in (11) hold if and only if

$$\begin{aligned} c=\frac{\lambda _2}{\lambda _2-\lambda _1+1}. \end{aligned}$$

(14)

It can be concluded that (13) and (14) are necessary and sufficient conditions for the time-reversed chain being an HMM-DN and HMM-DN by X; or equivalently that these are necessary and sufficient conditions for the reversibility of Z. An example of a set of parameters such that (13) and (14) hold is for example: $p=0.55$, $q=0.8$, $\lambda _1=0.3$, $\lambda _2=0.65$, $\mu _1=0.446875$, $\mu _2=0.8894737$.

Suppose now that (13) fails. Then the reversed chain is not an HMM-DN, but the marginal process Y of the reversed chain is still a Markov process. Hence we have an example of a PMM such that Y is a Markov chain, but the model is not an HMM-DN. For an example of such a chain consider (9) with $p=0.55$, $q=0.8$, $\lambda _1=0.52$, $\lambda _2=0.8$, $\mu _1=0.6$, $\mu _2=0.9$. The transition matrices of the original and reversed chains are

$$\begin{aligned}\mathbb {P} =\left( \begin{array}{cccc} 0.286 &{} 0.264 &{} 0.264 &{} 0.186\\ 0.440 &{} 0.110 &{} 0.360 &{} 0.090\\ 0.480 &{} 0.320 &{} 0.070 &{} 0.130\\ 0.720 &{} 0.080 &{} 0.080 &{} 0.120 \end{array} \right) , \mathbb {P}^R = \left( \begin{array}{cccc} 0.2860000 &{} 0.2247273 &{} 0.2451570 &{} 0.2441157\\ 0.5168932 &{} 0.1100000 &{} 0.3200000 &{} 0.0531068\\ 0.5168932 &{} 0.3600000 &{} 0.0700000 &{} 0.0531068\\ 0.5485923 &{} 0.1355759 &{} 0.1958318 &{} 0.1200000 \end{array} \right) .\end{aligned}$$

In this example both conditions (13) and (14) fail and one can see that the reversed chain is indeed neither HMM-DN nor HMM-DN by X. However, both marginal chains remain Markov chains with the same transition matrices ($p=0.55$, $q=0.8$). This example shows that the marginal process might be a Markov chain without the HMM-DN property. However, the original chain (corresponding to $\mathbb {P}$) is such that Y is a homogeneous Markov chain for any initial distribution, but the reversed chain (corresponding to $\mathbb {P}^R$) has the same property only under the stationary initial distribution.

3.2 Regime-Switching Model

The model studied in the present subsection allows to present an inhomogeneous Markov chain as a conditional marginal process of a homogeneous PMM. Such models have been successfully used in segmentation of non-stationary images, see Lanchantin and Pieczynski (2004), Lanchantin et al. (2011), and Boudaren et al. (2012). Suppose we would like to model the process X which during certain random time-periods evolves as a homogeneous Markov chain with different transition matrices. Thus, the transition matrices of X can be different in different periods, but since these periods are random, the process can lack the Markov property. Suppose we consider three different transition matrices $P_A$, $P_B$ and $P_C$ on a state space $\mathcal{X}$. The process X starts as a Markov chain with one of the three matrices, then after a certain random time-period the transition matrix changes and during the next time period the process evolves as a Markov chain with the new transition matrix. After a certain time period the matrix changes again and so on. To consider such a model as a homogeneous Markov chain, we embed X into a PMM (X, Y), where the Y-process takes values in $\mathcal{Y}=\{A,B,C\}$ and we interpret A, B, C as regimes. Inside a current regime $a\in \mathcal{Y}$, the transition probability $x_t\rightarrow x_{t+1}$ is determined by the matrix $P_a$: for every $y^n\in \mathcal{Y}^n$ such that $y_t=y_{t+1}=a$ and $\forall i,j\in \mathcal{X}$,

$$\begin{aligned} P(X_{t+1}=j|X_t=i,Y^n=y^n)=P(X_{t+1}=j|X_t=i,Y_t=a,Y_{t+1}=a)=P_a(i,j). \end{aligned}$$

(15)

Thus, $P_A$, $P_B$ and $P_C$ are the transition matrices on $\mathcal{X}\times \mathcal{X}$ inside every regime defined by (15). Let $P_Y$ denote the transition matrix of regimes:

$$\begin{aligned} P_Y=\left( \begin{array}{ccc} r_A &{} r_{AB} &{} r_{AC} \\ r_{BA}&{} r_B &{} r_{BC} \\ r_{CA} &{} r_{CB} &{} r_C \\ \end{array} \right) . \end{aligned}$$

Since (15) is the same as (6), we know that for (15) to hold it suffices to construct (X, Y) so that it would be an HMM-DN, i.e. the transition matrix of (X, Y) must factorize as in (3). Thus, the transition matrix of (X, Y) must be as follows:

$$\begin{aligned} \mathbb {Q} = \left( \begin{array}{ccc} r_A P_A &{} r_{AB} P_{AB} &{} r_{AC} P_{AC} \\ r_{BA} P_{BA} &{} r_B P_B &{} r_{BC} P_{BC} \\ r_{CA} P_{CA} &{} r_{CB} P_{CB} &{} r_C P_{C}\\ \end{array} \right) , \end{aligned}$$

where the matrices $P_{AB}$, $P_{AC}$, $P_{BA}$, $P_{BC}$, $P_{CA}$ and $P_{CB}$ define the transitions of the X-process when the regime changes. For example, $P_{AB}(i,j)=P(X_{t+1}=j|X_t=i,Y_t=A,$$Y_{t+1}=B).$ We shall call these matrices inter-regime matrices. In practice, the process is often supposed to stay in the same regime for quite a long time, thus the off-diagonal elements of the regime transition matrix $P_Y$ are close to zero, (Lanchantin et al. 2011). In this case the choice of the inter-regime matrices has a little influence, but they should be specified and in principle there are infinitely many possibilities for doing it. On the other hand, there is only one way to choose the inter-regime matrices so that the overall PMM were a Markov switching model, namely by choosing $P_{AB}=P_{CB}=P_B$, $P_{BA}=P_{CA}=P_A$, $P_{AC}=P_{BC}=P_C$. With this choice, the transition probability $i\rightarrow j$ under regime change is specified by the new regime, that is for every $a\in \mathcal{Y}$,

$$\begin{aligned} P_{aB}(i,j)&=P(X_{t+1}=j|X_t=i,Y_t=a,Y_{t+1}=B)\\ {}&=P(X_{t+1}=j|X_t=i,Y_t=B,Y_{t+1}=B), \end{aligned}$$

and we can see that inter-regime transitions are indeed independent of $Y_t$. Of course, one can choose the inter-regime matrices so that the old regime specifies transitions ($P_{AB}=P_{AC}$$=P_A$, $P_{BA}=P_{BC}=P_B$, $P_{CA}=P_{CB}=P_C$) or for example so that all inter-regime matrices are equal. There are many other meaningful options. For example, one can take all rows of $P_{AB}$ to be equal to the stationary distribution of $P_B$, all rows of $P_{AC}$ to be equal to the stationary distribution of $P_C$ and so on. Such a choice results in the following desirable property for the stationary distribution $(\pi (i,a))$ of (X, Y): the stationary distribution is given by $\pi (i,a)$$=\pi ^Y(a) \pi ^X_a(i),\,a\in \mathcal{Y}, i\in \mathcal{X}$, where $\pi ^Y$ is the stationary distribution of the regime transition matrix $P_Y$, and for any regime $a\in \mathcal{Y}$, $\pi _a^X$ is the stationary distribution of $P_a$. Hence, under stationarity it holds for every regime $a\in \mathcal{Y}$ that $P(X_t=i|Y_t=a)=\pi ^X_a(i)$, $P(X_{t+1}=j,$$X_t=i|Y_t=a,Y_{t+1}=a)=P_a(i,j)\pi _a^X(i)$, $\forall i,j\in \mathcal{X}$. In other words, the proportion of time the observed process X spends in state i during regime a equals to $\pi ^X_a(i)$, and the proportion of pairs (i, j) inside regime a is the same as it would be for a stationary Markov chain with transition matrix $P_a$. We can interpret this property as the observed process X being stationary in every regime. This property – the proportion of pairs (i, j) inside regime a (in PMM (X, Y)) converges to the same limit (namely to $P_a(i,j)\pi _a^X(i)$) as the proportion of pairs (i, j) for a Markov chain X with transition matrix $P_a$ – has great importance in practice. Indeed, in practice often the matrixes $P_a$ and $P_Y$ are constructed based on a training sequence, where the different regimes are known. Then the elements of $P_a$ are obtained just by counting the pairs (i, j) in regime a (in the training sequence) and the elements of $P_Y$ are obtained just by counting the different regimes. Thus, when merging the estimated matrices into one PMM, practitioners desire that the proportion of pairs (i, j) in regime a under the model would converge to the same number as is the corresponding proportion in the training sequence. In this case the model represents the training sequence well. A classical example of such an approach is the so-called CpG islands in genetics. Then $\mathcal{Y}$ consists of two regimes – ‘island’ and ‘normal’ – and $\mathcal{X}=\{T,A,G,C\}$. In the ‘island’ regime, the pair CG is more frequent than normally, in particular the transition probability P(G|C) is much-much greater in the ‘island’ regime compared to the ‘normal’ regime. There are lots of training sequences with known ‘islands’ available, thus the frequency-based estimates of the transition matrices can be obtained, see e.g. Durbin et al. (1998), Chapter 3. When combining these matrices into a single stationary and homogeneous PMM, it is important to guarantee that in the long run the frequencies inside a regime under the model would be the same as in the training sequence. Since the frequencies of the pairs define the ‘islands’, that is actually the most crucial property of the model. As mentioned, this property can be achieved by taking the rows of the inter-regime matrices equal to the stationary distributions (e.g. the rows of $P_{ab}$ would be equal to $\pi _b^X$). We would like to stress that the choice of inter-regime matrices is typically overlooked in the literature.

In Sect. 5 we shall consider the case where $r_{AC}=r_{CA}=0$, i.e. $r_{AB}=1-r_A$ and $r_{CB}=1-r_C$. For example, regimes A, B and C might describe working status of some technical system with many components involved. Then A could correspond to the state where all the components work, B could be the state where at least one of the components is broken and C could be the state where all the components are broken and the system is not working. In this example it is natural to assume that all the components cannot break down at the same time and the broken components cannot be fixed within exactly the same time, thus $r_{AC}=r_{CA}=0$. Moreover, let us assume that the observation space is $\mathcal{X}=\{1,2\}$ and the observations $X_1,X_2,X_3,\ldots$ evolve in regimes A, B and C as Markov chains with transition matrices

$$\begin{aligned} P_A=\left( \begin{array}{cc} 1-\epsilon _1 &{} \epsilon _1 \\ \epsilon _2 &{} 1-\epsilon _2 \\ \end{array} \right) ,\quad P_B= \left( \begin{array}{cc} {\epsilon _2\over \epsilon _1+\epsilon _2} &{} {\epsilon _1\over \epsilon _1+\epsilon _2}\\ {\epsilon _2\over \epsilon _1+\epsilon _2} &{} {\epsilon _1\over \epsilon _1+\epsilon _2} \\ \end{array} \right) ,\quad P_C= \left( \begin{array}{cc} \delta _1 &{} 1-\delta _1 \\ 1-\delta _2 &{} \delta _2 \\ \end{array} \right) . \end{aligned}$$

(16)

The parameters $\epsilon _1$, $\epsilon _2$, $\delta _1$, $\delta _2$ could be chosen so that they are all rather small (less than 0.5). Then regime A corresponds to longer blocks (i.e. the process X jumps less in regime A), the regime B corresponds to HMM (conditionally independent observations) and regime C corresponds to the case of shorter blocks (i.e. the process X jumps more in regime C compared to regime A). In order to stress that the difference between the regimes is solely the dependence structure, one might choose $\epsilon _1$, $\epsilon _2$, $\delta _1$, $\delta _2$ so that the proportion of ones and twos in every regime is equal. Then the following equality must hold:

$$\begin{aligned} {1-\delta _2\over 2-(\delta _1+\delta _2)}={\epsilon _2\over \epsilon _1+\epsilon _2}. \end{aligned}$$

(17)

An Example of HMM-DN by X It is important to realize that when the matrices $P_A$, $P_B$ and $P_C$ are quite similar to each other or the matrix $P_Y$ has certain properties, then it might happen that the X-process is a homogeneous Markov chain. For example, let us consider a model with the following transition matrices:

$$\begin{aligned} P_Y=\left( \begin{array}{ccc} r &{} 1-r &{} 0 \\ {(1-r)/2}&{} r &{} {(1-r)/2} \\ 0 &{} 1-r &{} r \\ \end{array} \right) , \quad P_A=\left( \begin{array}{cc} 1-\epsilon &{} \epsilon \\ \epsilon &{} 1-\epsilon \\ \end{array} \right) , \quad P_C= \left( \begin{array}{cc} \epsilon &{} 1-\epsilon \\ 1-\epsilon &{} \epsilon \\ \end{array} \right) , \end{aligned}$$

$$\begin{aligned} P_B= \left( \begin{array}{cc} {1/2} &{} {1/2}\\ {1/2} &{} {1/2}\\ \end{array} \right) , \quad P_{AB}=\left( \begin{array}{cc} p_{AB} &{} 1-p_{AB} \\ 1-p_{AB} &{} p_{AB} \\ \end{array} \right) , \quad P_{BA}= \left( \begin{array}{cc} p_{BA} &{} 1-p_{BA} \\ 1-p_{BA} &{} p_{BA} \\ \end{array} \right) , \end{aligned}$$

$$\begin{aligned} P_{BC}= \left( \begin{array}{cc} p_{BC} &{} 1-p_{BC} \\ 1-p_{BC} &{} p_{BC} \\ \end{array} \right) , \quad P_{CB}= \left( \begin{array}{cc} p_{CB} &{} 1-p_{CB} \\ 1-p_{CB} &{} P_{CB} \\ \end{array} \right) . \end{aligned}$$

It is shown in Avans (2021) that such a model is HMM-DN by X (hence X is a Markov chain) if and only if the following condition holds:

$$\begin{aligned} {r\over 1-r}\left( {1\over 2}-\epsilon \right) +p_{AB}={p_{BA}+p_{BC}\over 2}=p_{CB}-{r\over 1-r}\left( {1\over 2}-\epsilon \right) . \end{aligned}$$

(18)

Then X is a homogeneous Markov chain with transition matrix

$$\begin{aligned} \left( \begin{array}{cc} \alpha &{} 1-\alpha \\ 1-\alpha &{} \alpha \\ \end{array} \right) ,\quad \text{ where } \quad \alpha =r({1}-\epsilon )+(1-r)p_{AB}. \end{aligned}$$

In particular, when $2{r\over 1-r}({1\over 2}-\epsilon )<1$, then one can choose inter-regime matrices so that (18) holds. The condition $2{r\over 1-r}({1\over 2}-\epsilon )<1$ holds when $\epsilon \approx {1/2}$, so that $P_A\approx P_B\approx P_C$, or when $r\le {1/2}$ (recall that $\epsilon <{1/2}$), making the holding times in regimes A and C relatively short. This example illustrates that for a meaningful PMM the matrices $P_A$, $P_B$ and $P_C$ should not be so similar to each other and the holding times in different regimes should not be very short, otherwise X might turn out to be a homogeneous Markov chain and there is no need to model it with PMMs.

3.3 Semi-Markov Model

A semi-Markov process is a generalization of a Markov chain on an alphabet $\mathcal{X}$ where the sojourn times (times the chain spends in a given state) are not necessarily geometrically distributed. Let the sojourn time distribution for every $a\in \mathcal{X}$ be given by a probability distribution $q_a$, $q_a(k)\ge 0$ for every $k=1,2,\ldots$. After the process has spent a random time with distribution $q_a$ in state a, it jumps to the other state $b\ne a$ with probability $p_{ab}=P(X_{t+1}=b|X_{t+1}\ne a,X_t=a)$. Obviously, $p_{aa}=0$ for every $a\in \mathcal{X}$. These probabilities form the transition matrix $P=(p_{ab})$, which we shall call the jump matrix. There are various ways for considering a semi-Markov chain as a PMM. A common way is to consider a semi-Markov model as an HMM (X, Y), where Y is a Markov chain with transition matrix P and the values of $X_t$ are the sojourn times of $Y_t$. In this representation the distributions $\{q_a, a\in \mathcal{X}\}$ correspond to emission distributions. When a realization of a semi-Markov process is, for example, aaaccccccbbaccccc, then the corresponding HMM representation is $(X_1,Y_1),\ldots , (X_5,Y_5)=(3,a),(6,c),(2,b),(1,a),(5,c)$. Although formally an HMM, nothing is actually hidden in this representation and to restore the original semi-Markov process, both X and Y should be observed. Sometimes (see e.g. Lapuyade-Lahorgue and Pieczynski 2010, 2012), it is useful to consider a semi-Markov process as a marginal process of a PMM $Z=(X,Y)$, where the state space $\mathcal{Z}$ consists of pairs $\mathcal{Z}=\{(a,k): a\in \mathcal{X}, q_a(\ge k)>0\}$, where $q_a(\ge k)=\sum _{i\ge k}q_a(i)$. We see that Y takes values in $\mathbb {N}^+$ and $\mathcal{Z}$ can be a proper subset of $\mathcal{X}\times \mathbb {N}^+$. The possibly infinite transition matrix of Z consists mostly of zeros and is given by

$$\begin{aligned} P(Z_{t+1}=(b,l)|Z_t=(a,k))=\left\{ \begin{array}{ll} 1, &{} \hbox {when}\ b=a,\ l=k-1\ge 1; \\ p_{ab}q_b(l), &{} \hbox {when}\ b\ne a,\ k=1;\\ 0, &{} \hbox {else.} \end{array} \right. \end{aligned}$$

(19)

Thus, when $Z_t=(a,j)$ with $j>1$, then the only possible transition is to $(a,j-1)$. When $j=1$, then $X_{t+1}$ cannot be in state a any more. An example of a realization $z^{17}$ of such a PMM might be

$$\begin{aligned}&(a,3),(a,2),(a,1),(c,6),(c,5),(c,4),(c,3),(c,2),(c,1),\\ {}&(b,2),(b,1),(a,1),(c,7),(c,6),(c,5),(c,4),(c,3), \end{aligned}$$

and we can see that up to the last block the values of $Y_t$ can be actually read from $X_t$. This representation has some advantages over the HMM representation described above, especially when noise is added (the so-called hidden semi-Markov model, see Lapuyade-Lahorgue and Pieczynski 2010, 2012). In Lapuyade-Lahorgue and Pieczynski (2010, 2012), the authors propose a modification of the described PMM model (referred to as a ‘new’ or ‘recent’ semi-Markov model), where the jump matrix might have non-zero elements on the main diagonal, i.e. the condition $p_{aa}=0$ is dropped. It should be noted that when $p_{aa}>0$, then the distribution of the corresponding sojourn time belongs to a rather specific class of distributions. Indeed, when $T_1,T_2,\ldots$ are iid random variables with distribution $q_a(\cdot )$ and $p_{aa}>0$, then the sojourn time in state a can be represented as a random sum $\sum _{i=1}^G T_i,$ where G is independent of $T_1,T_2,\ldots$, and G has a geometric distribution with parameter ($1-p_{aa}$), i.e. $P(G=k)=p_{aa}^{k-1}(1-p_{aa})$, $k=1,2,\ldots$. By analogy with a compound Poisson distribution, let us call the distribution of this random sum as a compound geometric distribution, see Willmot and Lin (2001). The class of compound geometric distributions is obviously larger than the class of geometric distributions (which corresponds to the case $q_a(1)=1$), but it is still quite limited. For example, the distributions with bounded supports (like uniform distributions) do not belong to this class. So the model in (19) is more general than the described modification, because: 1) it allows to use any distribution for sojourn times; 2) the mentioned modification is a special case of (19), obtained by redefining the jump matrix as ${p_{ab}\over 1-p_{aa}}$ for every $b\ne a$, and by taking for $q_a$ the distribution of $\sum _{i=1}^G T_i$, where $G\sim Geom (1-p_{aa})$.

Of course, when compound geometric distribution is of interest, then due to its simplicity the modification is useful in applications. The model given by (19) is an example of a PMM that is neither HMM-DN nor HMM-DN by X. Clearly neither of the marginal processes is a Markov chain. When the jump matrix P has a unique stationary distribution $(\pi _a)$ and all the sojourn times have finite expectations, let them be denoted by $\mu _a<\infty$, then Z has a unique stationary distribution $\pi (a,k)$, where

$$\begin{aligned} \pi (a,k)={\pi _a q_a(\ge k)\over \sum _{b\in \mathcal{X}}\pi _b \mu _b}. \end{aligned}$$

3.4 Semi-Markov Regime-Switching Models

Recall that the regime-switching model introduced in Subsection 3.2 is an HMM-DN, where the regime process Y is a Markov chain with transition matrix $P_Y$. In particular, the sojourn times of regimes are geometrically distributed. If the goal is to model an inhomogeneous Markov chain where the regime sojourn times are not necessarily geometrically distributed, then the two PMMs – semi-Markov and regime-switching model – could be merged into one PMM as follows. Let Y be the semi-Markov PMM considered in the previous Subsection 3.3. Thus the states of Y are pairs (a, k), where a is the regime and k indicates the time left in regime a (including the current t). Let X stand for observations, $X_t$ takes values in $\mathcal{X}=\{1,2,\ldots \}$. As in the regime-switching model, to every regime a there corresponds a $|\mathcal{X}|\times |\mathcal{X}|$ transition matrix $P_a$. In order to specify the model, one has to choose the inter-regime state transition matrices $P_{ab}$ as well. Just as in the regime-switching model, the corresponding PMM (X, Y) can be defined with the following transition matrix:

$$\begin{aligned}&P(X_{t+1}=j,Y_{t+1}=(b,l)|X_{t}=i,Y_{t}=(a,k))\\ {}&=\left\{ \begin{array}{ll} P_{a}(i,j), &{} \hbox {when}\ b=a,\ l=k-1\ge 1; \\ p_{ab}P_{ab}(i,j)q_b(l), &{} \hbox {when}\ a\ne b,\ k=1; \\ 0, &{} \hbox {else;} \\ \end{array} \right. \end{aligned}$$

where $q_a(\cdot )$ denotes the sojourn time distribution for regime a and $(p_{ab})$ is the regime jump matrix. The obtained PMM is an HMM-DN, so when $y^n$ is a realization of $Y^n$ such that $y_{t+1}=(a,k)$, where $k>1$ (implying that $y_t=(a,k+1)$), then it holds that

$$\begin{aligned} P(X_{t+1}=j|X_t=i,Y^n=y^n)&=P(X_{t+1}=j|X_t=i,Y_t=(a,k+1),Y_{t+1}=(a,k))\\ {}&=P_a(i,j). \end{aligned}$$

Observe that in the described model the X-process is a Markov chain inside every regime. Thus, e.g. inside regime a, X is a Markov chain with transition matrix $P_a$. When the chain stays in that regime for quite a long time, then the sojourn time of X being in state $i\in \mathcal{X}$ is ‘almost’ geometrically distributed, meaning that the actual sojourn time distribution depends on the sojourn time of being in regime a and what happens after regime change. However, the regime sojourn times are not necessarily geometrically distributed any more. Let us remark that since Y itself is a PMM, say (U, V), then the obtained PMM can be considered as a three-dimensional Markov chain (X, U, V). Such models are known as triplet Markov models (TMM), see Gorynin et al. (2018). Every TMM can obviously be considered as a PMM by considering two of the three marginal processes as one, thus we can consider the following PMMs: (X, (U, V)), ((X, U), V) or ((X, V), U).

Another generalization of the regime-switching model would be to leave the regime sojourn times to be geometrically distributed and to replace the Markov model inside a regime with a semi-Markov model. Let Y be a Markov chain with states in $\mathcal{Y}$ being regimes, and let the corresponding regime transition matrix be $(r_{ab})$. For every regime $a\in \mathcal{Y}$, let $(p^a_{ij})$ be an intra-regime jump matrix of size $|\mathcal{X}|\times |\mathcal{X}|$, and for every pair $a,b\in \mathcal{Y}$ ($a\ne b$), let $(p^{ab}_{ij})$ be an inter-regime jump matrix of size $|\mathcal{X}|\times |\mathcal{X}|$. Recall that the main diagonal of every jump matrix consists of zeros. For every regime $a\in \mathcal{Y}$, let $q^a_{i}$, $i\in \mathcal{X}$, be a collection of sojourn time distributions so that $q^a_i(k)$ gives the probability that X stays in state i for k time units under regime a. Denoting by $V=(X,U)$ the PMM corresponding to the marginal semi-Markov process, the desired regime-switching semi-Markov process can be represented as a TMM (X, U, Y) with transitions

$$\begin{aligned}&P(V_{t+1}=(j,l),Y_{t+1}=b|V_t=(i,k),Y_{t}=a)\nonumber \\ {}&=\left\{ \begin{array}{ll} 1, &{} \text{ when }\ i=j,\ l=k-1\ge 1,\ a=b; \\ r_{ab}p^b_{ij}q^b_j(l), &{} \hbox {when}\ i\ne j,\ k=1; \\ 0, &{} \hbox {else.} \end{array} \right. \end{aligned}$$

(20)

Of course, when one allows non-zero elements on the main diagonal of the intra-regime jump matrices, but not in the inter-regime jump matrices, then the distribution of sojourn times in state i for regime a is a compound geometric distribution (where $G\sim Geom(1-r_{aa}p^a_{ii})$, because the regime change implies the state change). The described model is (a bit simplified) a noiseless version of the hidden semi-Markov model defined in Lapuyade-Lahorgue and Pieczynski (2012).

4 Segmentation and Risks

The term ‘hidden Markov model’ reflects the situation where the realization of X-chain is observed, but the realization of the Markov chain Y is not observed, hence it is hidden. We now have a more general model – PMM (X, Y) –, but we still assume that a realization $x^n$ of $X^n$ is observed, whilst the corresponding realization of $Y^n$ is unknown. Thus, $x^n$ can be considered as a sample or observations and n is sample size. The segmentation problem consists of estimating the unobserved realization of the underlying process $Y^n$ given observations $x^n$. Formally, we are looking for a mapping $g:\mathcal{X}^n \rightarrow \mathcal{Y}^n$ called a classifier or decoder, that maps every sequence of observations into a state sequence. The best classifier g is often defined via a loss function $L: \mathcal{Y}^n\times \mathcal{Y}^n \rightarrow [0,\infty ],$ where $L(y^n,s^n)$ measures the loss when the actual state sequence is $y^n$ and the estimated sequence is $s^n$. For any state sequence $s^n\in \mathcal{Y}^n$, the expected loss for given $x^n$ is called conditional risk:

$$\begin{aligned} R(s^n|x^n):=E[L(Y^n,s^n)|X^n=x^n]=\sum _{y^n\in \mathcal{Y}^n}L(y^n,s^n)p(y^n|x^n). \end{aligned}$$

The best classifier is defined as a state sequence minimizing the conditional risk:

$$\begin{aligned} g^*(x^n)=\arg \min _{s^n\in \mathcal{Y}^n}R(s^n|x^n). \end{aligned}$$

For an overview of risk-based segmentation with HMMs, see Lember and Koloydenko (2014), Lember et al. (2011), and Yau and Holmes (2013). The two most common loss functions used in practice are the global loss function $L_{\infty }$,

$$\begin{aligned} L_{\infty }(y^n,s^n):=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\ y^n\ne s^n, \\ 0, &{} \hbox {if}\ y^n=s^n, \end{array} \right. \end{aligned}$$

and the loss function $L_1$ obtained with the pointwise loss function $l: \mathcal{Y}\times \mathcal{Y}\rightarrow [0,\infty )$, where $l(s,s)=0$ $\forall s \in \mathcal Y$,

$$\begin{aligned} L_1(y^n,s^n):={1\over n}\sum _{i=1}^n l(y_i,s_i). \end{aligned}$$

(21)

Observe that the loss function $L_{\infty }$ penalizes all differences equally: no matter whether two sequences $a^n$ and $b^n$ differ at one entry or at all entries, the penalty is one. The loss function $L_1$ on the other hand penalizes differences entrywise. The conditional risk corresponding to $L_{\infty }$ and denoted by $R_{\infty }$ is $R_{\infty }(s^n|x^n)=1-p(s^n|x^n)$, thus the best classifier v maps every sequence of observations into sequence $s^n$ with maximum posterior probability:

$$\begin{aligned} v(x^n):=\arg \max _{s^n\in \mathcal{Y}^n}p(s^n|x^n). \end{aligned}$$

Any state path v maximizing $p(s^n|x^n)$ is called the Viterbi path or Viterbi alignment (it might not be unique). The best classifier in the case of $L_1$ in (21) is obtained pointwise: $g^*=(g^*_1,\ldots ,g^*_n)$, where

$$\begin{aligned} g^*_t(x^n)= \arg \min _{s \in \mathcal{Y}}E[l(Y_t,s)|X^n=x^n]= \arg \min _{s\in \mathcal{Y}}\sum _{y\in \mathcal{Y}} l(y,s) p_t(y|x^n).\end{aligned}$$

(22)

If

$$\begin{aligned} l(s,s')=\left\{ \begin{array}{ll} 0, &{} \hbox {if}\ s=s', \\ 1, &{} \hbox {if}\ s\ne s', \end{array} \right. \end{aligned}$$

then the loss function $L_1$ counts pointwise differences between $y^n$ and $s^n$. Thus the corresponding conditional risk measures the expected number of classification errors of $s^n$ given the observations $x^n$ and can be calculated as follows:

$$\begin{aligned} R_1(s^n|x^n):=1-{1\over n}\sum _{t=1}^np_t(s_t|x^n). \end{aligned}$$

It follows that the best classifier under $R_1$ (let us denote it by u) minimizes the expected number of classification errors and it can be calculated pointwise:

$$\begin{aligned} u_t(x^n)=\arg \max _{y\in \mathcal{Y}}p_t(y|x^n),\quad t=1,\ldots ,n. \end{aligned}$$

We will call any such u a pointwise maximum aposteriori (PMAP) path. In PMM literature often the name maximum posterior mode (MPM) is used, see e.g. Pieczynski (2003), Derrode and Pieczynski (2004), Lanchantin et al. (2011), Boudaren et al. (2012), and Gorynin et al. (2018).

4.1 Logarithmic and Hybrid Risks

Define the following logarithmic risks:

$$\begin{aligned} {\bar{R}}_{\infty }(s^n|x^n)&:=-{1\over n}\ln p(s^n|x^n),\quad {\bar{R}}_1(s^n|x^n):=-{1\over n}\sum _{t=1}^n\ln p_t(s_t|x^n), \end{aligned}$$

then the Viterbi path $v(x^n)$ minimizes ${\bar{R}}_{\infty }(\cdot |x^n)$ and the PMAP path $u(x^n)$ minimizes ${\bar{R}}_{1}(\cdot |x^n)$.

The Viterbi path has biggest posterior probability, but it might be inaccurate when it comes to the number of pointwise errors. The PMAP path on the other hand is the most accurate state path in terms of expected number of errors, but it might have very low or even zero posterior probability. In what follows, paths with zero posterior probability are called inadmissible. Often the goal is to find a state path that combines the two desired properties: it has a relatively big likelihood and relatively high accuracy. In Lember and Koloydenko (2014), a family of hybrid paths was defined. A hybrid path operates between the PMAP and Viterbi path and is the solution to the following problem:

$$\begin{aligned} \min _{s^n}[{\bar{R}}_1(s^n|x^n)+C{\bar{R}}_{\infty }(s^n|x^n)]\quad \Leftrightarrow \quad \max _{s^n}\big [\sum _{t=1}^n \ln p_t(s_t|x^n)+C\ln p(s^n|x^n)], \end{aligned}$$

(23)

where ${\bar{R}}_C={\bar{R}}_1(s^n|x^n)+C{\bar{R}}_{\infty }(s^n|x^n)$ is the hybrid risk and $C\ge 0$ is a regularization constant. The case $C=0$ corresponds to the PMAP path and it is easy to see that increasing C increases the posterior probability (${\bar{R}}_{\infty }$-risk) and decreases the accuracy (${\bar{R}}_1$-risk) (see, e.g. Lemma 16 in Lember and Koloydenko (2014)). If C is sufficiently big (depending on the model and $x^n$), then the solution is given by the Viterbi path. We now give an interpretation of the hybrid risk in terms of blocks.

As a remedy against zero-probability PMAP paths, Rabiner (1989) proposed in his seminal tutorial the following: instead of maximizing the sum $\sum _{t=1}^n p_t(s_t|x^n)$ over all $s^n\in \mathcal{Y}^n$, consider blocks of size k and maximize

$$\begin{aligned} p(s_1^k|x^n)+p(s_2^{k+1}|x^n)+\ldots + p(s_{n-k+1}^n|x^{n}). \end{aligned}$$

(24)

The case $k=1$ corresponds to the PMAP path, the bigger k, the ‘closer’ we come to the Viterbi path. This idea can be generalized by defining a k-block loss function as follows:

$$\begin{aligned} l_k: \mathcal{Y}^k \times \mathcal{Y}^k \rightarrow [0,\infty ),\quad L_k(y^n,s^n):={1\over {n-k+1}}\sum _{t=0}^{n-k} l_k(y_{t+1}^{t+k},s_{t+1}^{t+k}). \end{aligned}$$

(25)

For HMMs, the case $k=2$ is studied in Yau and Holmes (2013) under the name Markov loss function. When

$$\begin{aligned} l_k(y_{t+1}^{t+k},s_{t+1}^{t+k})=I_{\{y_{t+1}^{t+k} \ne s_{t+1}^{t+k}\}},\end{aligned}$$

(26)

then minimizing the risk corresponding to the loss function $L_k$ is equivalent to maximizing (24). The case $k=2$ corresponds to the state path that maximizes the expected number of correctly classified pairs (transitions). Unfortunately, the path minimizing the expected $L_k$-loss can still have posterior probability 0 (see the example in Lember and Koloydenko (2014)), therefore we use the following modification of (24). Define for any $k=1,2,\ldots ,n$,

$$\begin{aligned} {\bar{R}}_k(s^n|x^n)&:=-{1\over n}\sum _{t=1-k}^{n-1}\ln p\left( s_{\max (t+1,1)}^{\min (t+k,n)}\big |x^n\right) . \end{aligned}$$

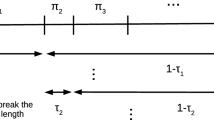
For example, if $k=3$ and $n=7$, then denoting $r(s_{u}^t):=\ln p(s_{u}^t|x^n),$ we have

$$\begin{aligned} -n{\bar{R}}_3(s^n|x^n)=r(s_1)+r(s_{1}^2)+r(s_{1}^3)+r(s_{2}^4)+r(s_{3}^5)+r(s_{4}^6)+r(s_{5}^7)+r(s_{6}^7)+ r(s_7). \end{aligned}$$

Thus, for small k, $-n {\bar{R}}_k(s^n|x^n)$ is basically the sum

$$\begin{aligned} \ln p(s_{1}^k|x^n)+\ln p(s_{2}^{k+1}|x^n)+\cdots +\ln p(s_{n-k+1}^n|x^n). \end{aligned}$$

Let $u_k(x^n)$ minimize ${\bar{R}}_{k}(\cdot |x^n)$. Clearly the PMAP alignment $u(x^n)$ minimizes ${\bar{R}}_{1}(\cdot |x^n)$, hence $u_1(x^n)=u(x^n)$. The connection between hybrid risks and blocks is given by the following proposition.

Proposition 4.1

Let $1<k \le n$, then for every $s^n\in \mathcal{Y}^n$,

$$\begin{aligned} {\bar{R}}_k(s^n|x^n)={\bar{R}}_{\infty }(s^n|x^n)+{\bar{R}}_{k-1}(s^n|x^n). \end{aligned}$$

(27)

Proof

For HMMs the proposition was proved in Lember and Koloydenko (2014) (Theorem 6 and Corollary 7). Let us denote

$$\begin{aligned} \bar{U}_k(s^n|x^n):= \prod _{t=1-k}^{n-1} p \left( s_{\max (t+1,1)}^{\min (t+k,n)} \Big | x^n \right) , \end{aligned}$$

then ${\bar{R}}_k(s^n|x^n)=-1/n \ln \bar{U}_k(s^n|x^n)$. In Lember and Koloydenko (2014) it was shown by applying the Markov property that for any realization $s^n$ of the first order Markov chain, $\bar{U}_k(s^n)=p(s^n)\bar{U}_{k-1}(s^n)$. Since in the case of a PMM (X, Y), $Y^n|x^n$ is a first order (inhomogeneous) Markov chain, the proof immediately holds for PMMs. $\blacksquare$

From Proposition 4.1 it follows that

$$\begin{aligned} {\bar{R}}_k(s^n|x^n)=(k-1){\bar{R}}_{\infty }(s^n|x^n)+{\bar{R}}_{1}(s^n|x^n), \end{aligned}$$

thus when $C=k-1$, the hybrid risk $C{\bar{R}}_{\infty }+{\bar{R}}_1$ is actually the k-block risk ${\bar{R}}_k$. Therefore, the hybrid risk can be considered as a generalization of the k-block risk for non-integer value of C.

For a more detailed discussion about the properties of hybrid classifiers as well as for the discussion of choosing the constant C, see Lember (2023).

4.2 Algorithms for State Path Estimates

The block risks and hybrid risks are meaningful and theoretically justified, but the direct optimization of any risk over $\mathcal{Y}^n$ is beyond computational capacity even for moderate n. Therefore, dynamic programming algorithms similar to the Viterbi one should be applied. For HMMs the algorithm for the hybrid risk was worked out in Lember and Koloydenko (2014). In the present paper we state the dynamic programming algorithm also for PMMs. Let us denote the states of $\mathcal Y$ by $1,\ldots ,l$.

Proposition 4.2

The state path(s) minimizing the hybrid risk

$$\begin{aligned} C{\bar{R}}_{\infty }(s^n|x^n)+B{\bar{R}}_1(s^n|x^n) = -{C \over n} \ln p(s^n|x^n) - {B \over n} \sum _{t=1}^n \ln p_t(s_t|x^n) \end{aligned}$$

(28)

can be found by the following recursion. Define the following scores:

$$\begin{aligned} \delta _1(j)=&\ C\ln p(x_1,j)+B\ln p_1(j|x^n), \quad \forall j \in \mathcal Y,\\ \delta _{t+1}(j)=&\ \max _{i \in \mathcal Y}\Big (\delta _t(i)+C\ln p(x_{t+1},j|x_t,i)\Big )\\ {}&+B\ln p_{t+1}(j|x^n), \quad t=1,\ldots ,n-1,\quad \forall j \in \mathcal Y. \end{aligned}$$

Using the scores $\delta _t(j)$, define the backpointers $\psi _t(j)$ and the terminal state $\psi _n$ as follows:

$$\begin{aligned} \psi _{t}(j)&=\arg \max _{i \in \mathcal Y}\Big [\delta _t(i)+C\ln p(x_{t+1},j|x_t,i)\Big ], \quad t=1,\ldots ,n-1; \\ \psi _n&= \arg \max _{i \in \mathcal Y}\delta _n(i). \end{aligned}$$

The optimal state path $\hat{y}=(\hat{y}_1,\ldots ,\hat{y}_n)$ minimizing the hybrid risk in (28) can be obtained as

$$\begin{aligned} \hat{y}_n= \psi _n, \quad \hat{y}_t=\psi _t(\hat{y}_{t+1}), \quad t=n-1,\ldots ,1. \end{aligned}$$

Proof

The proof of the proposition can be performed using induction. Observe that minimizing (28) over all $s^n$ is equivalent to

$$\begin{aligned}&\max _{s^n} [ C \ln p(s^n,x^n)+ B\sum _{t=1}^n \ln p_t(s_t|x^n)] \\ {}&=\max _{s^n} [ C\ln p(s_1,x_1)+C \sum _{t=2}^n \ln p(s_t,x_t|s_{t-1},x_{t-1})+ B\sum _{t=1}^n \ln p_t(s_t|x^n) ]. \end{aligned}$$

Let

$$\begin{aligned} U(s_1)&=C\ln p(s_1,x_1)+ B \ln p_1(s_1|x^n), \\ U(s^t)&=U(s_1)+ \sum _{u=2}^t \left[ C \ln p(x_u,s_u|x_{u-1},s_{u-1})+ B\ln p_u(s_u|x^n)\right] , \quad t=2,\ldots ,n. \end{aligned}$$

Then

$$\begin{aligned} U(s^{t})=U(s^{t-1}) +C\ln p(x_{t},s_{t}|x_{t-1},s_{t-1})+B\ln p_{t}(s_{t}|x^n), \quad t=2,\ldots ,n, \end{aligned}$$

and we can see directly that $\delta _t(j)$ gives the score of the state path $s^{t}$ that minimizes the hybrid risk and ends in state j, that is

$$\begin{aligned} \delta _t(j)=\max _{s^{t}: \, s_t=j} U(s^{t}). \end{aligned}$$

By induction on t this holds also for $\delta _n(j)$, therefore backtracking from $\psi _n$ gives us the optimal hybrid state path. $\blacksquare$

Observe that the constant B in (28) is redundant, since in practice one can always take $B=1$ and vary the constant C, just like in (23). The reason for adding B to the recursion is that it immediately allows to obtain the Viterbi algorithm by taking $B=0$ and $C=1$.

In the special case of HMM-DN the recursion is

$$\begin{aligned} \delta _{t+1}(y_{t+1})=&\ \max _{y_t}\Big (\delta _t(y_t)+C\ln p(y_{t+1}|y_t)+C\ln p(x_{t+1}|y_{t+1}, y_t,x_t)\Big )\\ {}&+B\ln p_{t+1}(y_{t+1}|x^n) \end{aligned}$$

and for a Markov switching model $p(x_{t+1}|y_{t+1}, y_t,x_t)=p(x_{t+1}|y_{t+1},x_t)$. The algorithm above involves applying forward-backward algorithms to find the probabilities $p_t(y|x^n)$ for every $y\in \mathcal{Y}$ and t. The forward algorithm finds recursively the probabilities $p(x^t,y_t)$:

$$\begin{aligned} p(x^{t},y_{t})=\sum _{y_{t-1}\in \mathcal{Y}}p(x_{t},y_{t}|x_{t-1},y_{t-1})p(x^{t-1},y_{t-1}), \end{aligned}$$

and the backward algorithm finds recursively the probabilities $p(x_{t+1}^n|x_t,y_t)$ as follows:

$$\begin{aligned} p(x_{t+1}^n|x_{t},y_{t})=\sum _{y_{t+1}\in \mathcal{Y}}p(x_{t+1},y_{t+1}|x_{t},y_{t})p(x_{t+2}^n|x_{t+1},y_{t+1}). \end{aligned}$$

In practice the scaled versions of these probabilities are used, see Derrode and Pieczynski (2004). The (scaled) forward-backward algorithms work essentially in the same way as for HMMs, this is all due to the Markov property. Observe that when the model is HMM-DN $\,\text {by}$ X (like in our first example in Subsection 3.1), then by (4), $p(y_t|x^n)=p(y_t|x^t)$, thus $p(y_t|x^n)$ can be obtained by the forward recursion only. The scaled forward recursion in this particular case is simply

$$\begin{aligned} p(y_t|x^t)=\sum _{y_{t-1}}p(y_t|x_t,x_{t-1},y_{t-1})p(y_{t-1}|x^{t-1}). \end{aligned}$$

(29)

For large n, replacing the forward-backward recursion by the forward one might be a big computational advantage. Moreover, when the model is HMM-DN by X and the time-reversed model is HMM-DN by X as well, then for the stationary chain it holds that $p(y_t|x^n)=p(y_t|x_t)$. Therefore, in this case the probabilities $p(y_t|x^n)$ can be found without any forward-backward algorithms, which makes these models especially appealing from the computational point of view.

Rabiner k-block Algorithm In practice it is interesting to compare the state path estimates of the hybrid approach to the Rabiner k-block state path estimates defined in (24). Next we will give the algorithm for computing the Rabiner k-block state path estimates.

Proposition 4.3

The state path(s) minimizing the risk function corresponding to the Rabiner k-block approach and thus, maximizing the sum of probabilities in (24), can be found by the following recursion. Define for every $a\in \mathcal{Y}^{k-1}$ scores $\delta _t(a)$ and backpointers $\psi _t(a)$ as follows:

$$\begin{aligned} \delta _1(a)&= \max _{y_1 \in \mathcal Y} p (y_1,y_2^k=a|x^n), \\ \psi _1(a)&= \arg \max _{y_1 \in \mathcal Y} p (y_1,y_2^k=a|x^n), \\ \delta _t(a)&= \max _{y_t \in \mathcal Y}\left( \delta _{t-1}(y_t,a_1,\ldots ,a_{k-2})+p(y_t,y_{t+1}^{t+k-1}=a|x^n)\right) , \quad t=2,\ldots ,n-k+1, \\ \psi _t(a)&= \arg \max _{y_t \in \mathcal Y}\left( \delta _{t-1}(y_t,a_1,\ldots ,a_{k-2})+p(y_t,y_{t+1}^{t+k-1}=a|x^n)\right) , \quad t=2,\ldots ,n-k+1. \end{aligned}$$

Let $a_{end}=\arg \max _{a\in \mathcal{Y}^{k-1}} \delta _{n-k+1}(a)$. Then the state path $\hat{y}=(\hat{y}_1,\ldots ,\hat{y}_n)$ maximizing (24) can be obtained as

$$\begin{aligned} \hat{y}_{n-k+2}^n=a_{end}, \quad \hat{y}_t=\psi _t(\hat{y}_{t+1}^{t+k-1}),\quad t=n-k+1,\ldots ,1. \end{aligned}$$

Proof

The proof is analogous to the proof of Proposition 4.2. $\blacksquare$

Remark

When $k=2$, the scores have to be calculated just for every $j\in \mathcal Y$, then

$$\begin{aligned} \delta _t(j)= \max _{y_{t} \in \mathcal Y}\left( \delta _{t-1}(y_{t})+p(y_{t},y_{t+1}=j|x^n)\right) , \quad t=2,\ldots ,n-k+1. \end{aligned}$$

5 Behaviour of Different State Path Estimators

Let us now consider the hybrid risk with $B=1$, i.e. the optimization problem in (23). We know that the solution of (23) for $C=0$ corresponds to the PMAP path and the solution for large C corresponds to the Viterbi path. Let $C_o$ be the smallest constant such that the solution of (23) is a Viterbi path for every $C>C_o$. When $\mathcal{Y}$ is finite, then also the set $\mathcal{Y}^n$ is finite, thus $C_o$ surely exists. When $C=C_o$, then (23) has at least two solutions: one of them is the Viterbi path and one of them is not; when $C<C_o$, then none of the hybrid paths is Viterbi. It is also important to observe that in case the Viterbi path is not unique, it is sometimes meaningful to optimize (23) with $C>C_o$ rather than to run the Viterbi algorithm with some tie-breaking rule. Because although different Viterbi paths have the same $\bar{R}_{\infty }$-risk, they might have different $\bar{R}_{1}$-risks, therefore the solution of (23) corresponds to the Viterbi path v that maximizes $\sum _t p(v_t|x^n)$ and has therefore the minimum expected number of classification errors amongst all the Viterbi paths – primus inter pares.

However, when the goal is to find a hybrid path that is neither the Viterbi nor PMAP path, then only the range $(0,C_o)$ for C is of interest. Obviously that range depends on the model, but as we shall see, it might very much depend also on the observation sequence $x^n$ and this dependence can be very unstable even for simplest models. More precisely, we consider the model in Subsection 3.1 and show that for every $M<\infty$, there exists n and observations $x^n$, so that with $x^{n+3}=(x_1,\ldots , x_n,1,1,1)$ it holds that $C_o(x^{n+1})-C_o(x^n)>M$. In other words, adding three more observations increases $C_o$ tremendously.

5.1 Variation of Regularization Constant C

Consider the PMM defined in (9) with parameters $p'=p=6/7$ and $q'=q=8/35$, and $\lambda _1=0.9$, $\lambda _2=0.2$, $\mu _1=0.8$, $\mu _2=0.1$. Then $\theta _1=0.6$, $\theta _2=0.4$ (see the Appendix). Choose the initial distribution $\pi =(\pi (1,a),\pi (1,b),\pi (2,a),\pi (2,b))$ so that

$$\begin{aligned} \pi (a|1)=P(X_1=1,Y_1=a)/P(X_1=1)=0.452328159645=:c_a. \end{aligned}$$

• 1. At first consider the observation sequence

  $$\begin{aligned} x^n=(1,\underbrace{1,2,1}_1,\underbrace{1,2,1}_2,\ldots ,\underbrace{1,2,1}_m), \end{aligned}$$

  thus the sequence has a particular pattern and is of length $n=3m+1$, $m=1,2,\ldots$. Let us denote $\alpha _t(y)=p(y_t=y|x^t)$, then by recursion (29),

  $$\begin{aligned} \alpha _1(a)&= c_a,\quad \alpha _2(a) = \alpha _1(a)\lambda _1 + \alpha _1(b) \lambda _2 =0.5166297...,\\ \alpha _3(a)&= \alpha _2(a)\theta _1 +\alpha _2(b) \theta _2 =0.5033259... \quad \alpha _4(a) = \alpha _3(a) \mu _1 +\alpha _3(b) \mu _2 =c_a,\quad \\ \alpha _5(a)&=\alpha _2(a),\quad \alpha _6(a)=\alpha _3(a),\quad \ldots \end{aligned}$$

  so that $\alpha _t(y)=\alpha _{t-3}(y)$, $y\in \{a,b\}$, $t=4,\ldots ,n$. For this observation sequence $x^n$, the PMAP path and Viterbi path are given by

  $$\begin{aligned} \text{ PMAP }: \quad b\underbrace{aab}_1 \underbrace{aab}_2 \ldots \underbrace{aab}_m, \quad \quad \text{ Viterbi }: \quad bbbbbbb \ldots bbb. \end{aligned}$$

  For any path $y^n$, thus the C-score with $B=1$ (recall (28)) reads as follows:

  $$\begin{aligned} C\ln p(y^n|x^n)+\sum _{t=1}^n\ln p_t(y_t|x^n), \end{aligned}$$

  and the hybrid path corresponding to C maximizes the C-score. In our example, the last hybrid path before Viterbi (when increasing C) is given by

  $$\begin{aligned} y^n=(b,\underbrace{a,b,b}_1, \underbrace{a,b,b}_2, \ldots \underbrace{a,b,b}_m) . \end{aligned}$$

  (30)

  The difference between the C-scores of the Viterbi path and $y^n$ in (30) is given by

  $$\begin{aligned} C\ln p(bbbb\ldots bbb|x^n)-C\ln p(babb\ldots abb|x^n)+\sum _{t=1}^n \ln \alpha _t(b)- \sum _{t=1}^n \ln \alpha _t(y_t) \end{aligned}$$
  $$\begin{aligned} =C \ln { [(1-\lambda _2)(1-\theta _2)]^m \over [\lambda _2(1-\theta _1)]^m } + m \ln {\alpha _2(b)\over \alpha _2(a)} = Cm\ln 6 + m \ln {\alpha _2(b)\over \alpha _2(a)}. \end{aligned}$$

  Thus, if

  $$\begin{aligned} C>{ \ln (\alpha _2(a)/\alpha _2(b)) \over \ln 6}=:C_o, \end{aligned}$$

  then the hybrid path becomes Viterbi, and this holds independently of m or sequence length n. Observe that $C_o=0.0371$ is very small in this example and in terms of block size the hybrid path corresponding to block length $k=2$ would here be equal to the Viterbi path.

• 2. Add now the piece 111 to the end of $x^n$ and consider

  $$\begin{aligned} x^n=(1,\underbrace{1,2,1}_1,\underbrace{1,2,1}_2,\ldots ,\underbrace{1,2,1}_m,1,1,1). \end{aligned}$$

  The PMAP path and Viterbi path are now given by

  $$\begin{aligned} \text{ PMAP }: \quad b\underbrace{aab}_1 \underbrace{aab}_2 \ldots \underbrace{aab}_m aaa, \quad \quad \text{ Viterbi }: \quad aaaaaaa \ldots aaaaaa. \\ \end{aligned}$$

  Let us compare the C-scores of the Viterbi path and constant path $bbbb\ldots b$:

  $$\begin{aligned} C\ln p(b\ldots b|x^n)&+m\sum _{t=1}^3 \ln \alpha _t(b)+\sum _{t=n-3}^n \ln \alpha _t(b)-C\ln p(a\ldots a|x^n)\\ {}&-m\sum _{t=1}^3 \ln \alpha _t(a)-\sum _{t=n-3}^n \ln \alpha _t(a)=C\ln {p(b\ldots b|x^n)\over p(a\ldots a|x^n)}\\ {}&+m\sum _{t=1}^3 \ln {\alpha _t(b)\over \alpha _t(a)}+\sum _{t=n-3}^n\ln {\alpha _t(b)\over \alpha _t(a)}=C\left( \ln {1-c_a\over c_a}+3 \ln {8\over 9}\right) \\ {}&+mD+E, \end{aligned}$$

  where

  $$\begin{aligned} D:=\sum _{t=1}^3\ln {\alpha _t(b)\over \alpha _t(a)}, \,\quad E:=\sum _{t=n-3}^n\ln {\alpha _t(b)\over \alpha _t(a)}=&\ \ln {1-c_a\over c_a} + \ln {\alpha _{n-2}(b)\over \alpha _{n-2}(a)} \\ {}&+ \ln {\alpha _{n-1}(b)\over \alpha _{n-1}(a)}+ \ln {\alpha _{n}(b)\over \alpha _{n}(a)}.\end{aligned}$$

  Observe that $D>0$ and $\ln ((1-c_a)/c_a)+3 \ln (8/9)<0$, thus when

  $$\begin{aligned} C<{mD+E\over \ln (c_a/(1-c_a))+3\ln (9/8)}=:C(m), \end{aligned}$$

  it holds that the Viterbi path is not the hybrid one. Hence $C_o\ge C(m)$ and since C(m) increases with m, so does $C_o$. The computations show that actually $C_o=C(m)$ when $m>8$.

We would like to emphasize that the observed instability of $C_o$ is due to the specific structure of $x^n$. When generating observation sequences randomly from the same model we can see that typically $C_o(x^n)<1$ up to $n=10000$ (slightly increasing with n); for $n=100000$, $C_o(x^n)$ might occasionally exceed 1 and reach up to 3.

5.2 Dissimilarities of Different Hybrid Paths

In this example we continue to study the model (9), but now with the following parameters: $p'=p=0.55$, $q'=q=0.8$, $\lambda _1=0.52$, $\lambda _2=0.8$, $\mu _1=0.6$, $\mu _2=0.9$.

To study the behaviour of the random variable $C_o(X^n)$ as well as hybrid paths, we generated 10 realizations $x^n$ of $X^n$ for $n=100,\, 1000,\,10000,\,100000$. For each observation sequence ($4\times 10=40$ sequences) we performed segmentation with PMAP and Viterbi, and we estimated $C_o$. For most cases $C_o(x^n)\in [12.53,12.55]$, thus the hybrid path corresponding to the block length $k=14$ equals the Viterbi path (for most of the cases). Observe the difference with the previous example, where the same model with another parameter values gave typically much smaller $C_o$. The larger $C_o$ implies that in the present example there is more ‘space’ between the PMAP and Viterbi path and this is due to the very weak dependence between X and Y. The general pattern here is that $C_o(x^n)$ is independent of sequence length; however we also observed that for two studied observation sequences (one of length 10000 and one of length 100000), $C_o(x^n)\in [33.21,33.22]$. It seems that this behaviour depends on some particular subsequences or pieces of $x^n$ and removing that particular piece of observations would result in $C_o\approx 12.5$.

To compare the state path estimates obtained with the PMAP, Viterbi, hybrid and Rabiner k-block algorithms, we studied closer the path estimates for the 10 observation sequences of length 100. Recall that in our model both marginal chains have the same transition matrix and the average block length of ones and twos (or a-s and b-s) is 2.2 and 1.25, respectively. The stationary distribution of X and Y is given by $\pi =(0.8/(0.45+0.8),0.45/(0.45+0.8))$, thus there are almost twice as many ones expected in our observation sequences as twos. In Fig. 1, all the estimated state paths for one observation sequence are presented (in the order from top to down: true underlying state path, PMAP, hybrid block paths for $k=2,\ldots ,14$, Rabiner block paths for $k=2,\ldots ,14$, Viterbi). For better visibility, we have plotted the first 80 states of the path estimates.

We can see how the pattern changes when we move from PMAP to Viterbi: the number of dominating state a (grey) decreases and the number of state b (black) increases. When we study different block lengths to see how information from different neighbourhoods is accounted for, we can see that a larger change compared to PMAP occurs for $k=3$. It is also interesting to observe that the hybrid block estimates are the same for $k=4,\ldots ,10$ (for all the ten observation sequences), thus increasing the block size does not change the path estimate for those k-values.

To get a better overview of the behaviour of the estimated state paths, we present some summary statistics over 100 observation sequences of length $n=100$. For all the observation sequences we estimated the PMAP path, Rabiner and hybrid block paths for $k=2,\ldots ,14$, and the Viterbi path. In Table 1 the averages over 100 sequences of classification errors are presented for the PMAP path, hybrid block paths ($k=2,\ldots ,14$) and Viterbi path.

Table 1 Averages of type I errors, type II errors and total number of classification errors over 100 sequences in Example 5.2 for the PMAP path, hybrid block paths ($k=2,\ldots ,14$) and Viterbi path. In the brackets the corresponding standard deviations are given

In this example we can make two types of classification errors: classify a as b (call it type I error) or classify b as a (type II error). To demonstrate further the difference between the PMAP and Viterbi paths, we present also averages of these classification errors separately. As the theory predicts, the number of classification errors increases with k. However, there is also a clear dependence between k and error types: when k is small ($k=1,2$) then the number of type I errors for this model is small. When k increases and we move towards Viterbi, then the number of type I errors starts to increase and the number of type II errors decreases. Notice also that when we compare the average number of pointwise errors for PMAP and Viterbi, then PMAP is about 10$\%$ better when we consider the total number of errors. The major difference between the results of the two algorithms is what type of errors we make.

In Table 2 the same summary statistics are presented for the Rabiner k-block paths. The general behaviour concerning type I and type II errors is similar for the Rabiner k-block and hybrid paths with $C=k-1$. The major difference is that the Rabiner algorithm gives more varying path estimates for $k=4,\ldots ,10$, which is reflected in a smoother increase/decrease of the averages of type I/type II errors. In column Difference of Table 2 the average number of pointwise differences (and its standard deviation) between the hybrid paths and Rabiner block paths is presented. For $k=12$ the average pointwise difference is 8.91 showing that the Rabiner and hybrid block path estimates can be pretty different (recall that $n=100$).

Table 2 Averages of type I errors, type II errors and total number of classification errors over 100 sequences in Example 5.2 for the PMAP path, Rabiner k-block paths ($k=2,\ldots ,14$) and Viterbi path. In the brackets the corresponding standard deviations are given. In column Difference the average number of pointwise differences (and its standard deviation) between the hybrid block paths and Rabiner block paths is given

5.3 Regime-Switching Model and Inadmissible State Paths

Table 3 Different summary statistics for 100 generated sequence pairs $(x^n,y^n)$ of length $n=1000$ from the model in Example 5.3 with $r_B=0.2,0.4,0.6,0.8$. In columns PMAP and Viterbi, average frequencies (over 100 sequences) of regimes A, B and C are given for the PMAP and Viterbi path. Columns Err(PMAP), Err(Vit) and Err(Hybr2) give the average number of pointwise errors (over 100 sequences) of the PMAP, Viterbi and hybrid 2-block path compared to the true path, the corresponding standard deviations are presented in the brackets. Column Diff(PMAP/Vit) reports the average number of pointwise differences between the PMAP and Viterbi path for the models with different $r_B$, the corresponding standard deviations are given in the brackets. Columns Inadm(PMAP), Inadm(Rab2) and Inadm(Rab5) report the average number of inadmissible transitions in the PMAP, Rabiner 2-block and Rabiner 5-block paths; the number of admissible paths if any is reported in the brackets

The main purpose of this example is to demonstrate possible inadmissibility of PMAP paths and that PMAP and Viterbi can give quite similar results in terms of classification errors. Consider a regime switching model with the following parameters:

$$\begin{aligned} P_Y = \left( \begin{array}{ccc} 0.95 &{} 0.05 &{} 0 \\ (1-r_B)/2 &{} r_B &{} (1-r_B)/2 \\ 0 &{} 0.01 &{} 0.99 \\ \end{array} \right) , \quad \text{ where } \quad r_B=0.2,0.4,0.6,0.8; \end{aligned}$$

let $\epsilon _1=0.2$, $\epsilon _2=0.3$, $\delta _1=0.4$, $\delta _2=0.1$, thus

$$\begin{aligned} P_A=\left( \begin{array}{cc} 0.8 &{} 0.2 \\ 0.3 &{} 0.7 \\ \end{array} \right) ,\quad P_B= \left( \begin{array}{cc} 0.6 &{} 0.4 \\ 0.6 &{} 0.4 \\ \end{array} \right) ,\quad P_C= \left( \begin{array}{cc} 0.4 &{} 0.6 \\ 0.9 &{} 0.1 \\ \end{array} \right) . \end{aligned}$$

Thus, we consider four different values of $r_B$ keeping the rest of the parameters fixed, and study how this affects segmentation results using different state path estimators. For this model (17) holds and the proportion of ones and twos in all the regimes is 0.6 and 0.4, respectively. Observe that the expected number of times the underlying chain is in regime B is according to the stationary distribution for cases $r_B=0.2,0.4,0.6,0.8$ given by 6%, 8%, 11% and 20%, respectively. For given $r_B$, we generated 100 sequence pairs $(x^n,y^n)$ from the corresponding PMM with sequence length $n=1000$, and studied different state path estimates for those sequences. The results of the experiment are summarized in Table 3. In this example regimes A and C are dominating and regime B occurs, especially for $r_B=0.2$ and $r_B=0.4$, very rarely. Since the block lengths of ones and twos in regime A are longer on average compared to regime C, it is quite easy to separate the two regimes based on observations. This means that for smaller $r_B$ classification should be easier and the simulations confirm it – we see that the average number of pointwise errors in the case $r_B=0.2$ is 11% and 12% for PMAP and Viterbi, for $r_B=0.4$ the corresponding numbers are 13% and 14%. When the frequency of regime B increases with increasing $r_B$, the pointwise error rates also increase. For $r_B=0.8$ the error rates of PMAP and Viterbi are 22% and 25%. We can also see that the average number of pointwise differences between the PMAP and Viterbi path for $r_B=0.2,0.4,0.6$ is quite small: 40, 41 and 48, respectively. Thus, one could think that the PMAP and Viterbi path estimates are quite similar but this is not the case. The problem with PMAP paths for this model (with $r_B=0.2,0.4,0.6$) is that the path estimates are inadmissible because of the impossible transitions $1\rightarrow 3$ and $3 \rightarrow 1$. The inadmissibility of PMAP paths is also evident from the low frequencies of regime B in the first 3 rows of column PMAP. The average number of inadmissible transitions in the PMAP paths for each $r_B$ is given in column Inadm(PMAP). To exemplify inadmissibility of Rabiner k-block paths, the average number of inadmissible transitions is presented also for the Rabiner block paths with $k=2$ and $k=5$. We have also counted the number of admissible PMAP, Rabiner 2- and 5-block paths (if any), those numbers are presented in the brackets after the average number of inadmissible transitions. Thus, we can see that for $r_B=0.2$ and $r_B=0.4$, 8 and 4 Rabiner 5-block paths were admissible, respectively. For $r_B=0.8$, only one PMAP path was inadmissible and there were 6 admissible Rabiner 2-block paths. The fact that even Rabiner 5-block paths might be inadmissible is alarming – the intuition suggests that the longer the blocks, the closer the path is to the Viterbi path, but even the blocks of length 5 cannot guarantee admissibility of Rabiner paths in this example.

To conclude: since PMAP paths are inadmissible, in this example with $r_B=0.2,0.4,0.6$, one should use a hybrid path or Viterbi path as a hidden path estimate. When the purpose is to minimize the expected number of pointwise errors, the 2-block hybrid path could be used (the average number of pointwise errors is given in column Err(Hybr2)) or any hybrid path with $C\in (0,1]$ and $B=1$ in (28).

We also studied the distribution of $C_o(X^n)$ for different $r_B$. For each simulated observation sequence we calculated the smallest integer $k_o$ such that for $C\ge k_o$, the hybrid path equals the Viterbi path. Thus $k_o=\lceil C_o \rceil$. Recall that for $k \le n$ the hybrid path with $C=k-1$ can be interpreted as the hybrid k-block path. Table 4 presents the summary statistics of the distribution of $k_o$ (over 100 sequences) for each $r_B$. We can see the values of minimum, first quartile, median, third quartile and maximum in each distribution and these indicate how much $k_o$ varies. Observe the difference with the previous example in Subsection 5.2 – the variation of $C_o$ is tremendous and for $r_B=0.4,0.6,0.8$, the maximum value of $k_o$ is much larger than the sequence length 1000 (the number of observation sequences out of 100 for which $k_o$ is larger than 1000 is 3, 3 and 2, respectively). In particular, $k_o$ might be even more than 9000. This contradicts the naive intuition that when $C>n$, then every hybrid path should be the Viterbi one, because we have reached the maximum block length n.

Table 4 The distribution of the smallest integer $k_o$ in Example 5.3, such that for $C\ge k_o$ the hybrid path equals the Viterbi path

6 Conclusions

The main purpose of this article was to illustrate the richness of the class of PMMs and to investigate the behaviour of hybrid classifiers in discrete PMMs. To demonstrate possibilities of this model class, four different models were presented and studied closer: the related Markov chains model, regime-switching model, semi-Markov model and semi-Markov regime-switching model. The segmentation problem was studied in more detail and exemplified with simulation studies for the first two models. The hybrid classifiers introduced in the article operate between the PMAP and Viterbi path, which are the traditional classifiers used for segmentation in practice. To apply the hybrid algorithm, one has to choose the regularization constant C, from certain $C_o(X^n)$ on the hybrid path becomes Viterbi. We saw that sometimes $C_o(X^n)$ depends mostly on the model and its parameters and not on a particular observation sequence nor sequence length, although for some specific observation sequence from the same model this constant can be highly dependent on n (Example 5.1 and 5.2). But in other models this constant can be sequence-dependent and the variation of $C_o(X^n)$ can be enormous (Example 5.3). Thus, a practitioner who wants to use a hybrid path for segmentation, has to be able to choose a suitable regularization constant C. This choice could be made based on simulation studies if the purpose is to choose C which gives a reasonable balance between the PMAP and Viterbi path (that is C should give a state path estimate with relatively high accuracy and relatively high likelihood). If the aim is to avoid inadmissible PMAP paths but still to minimize the expected number of pointwise errors, a hybrid path with small $C>0$ could be used.

To conclude: our examples demonstrate that a segmentation method (and for hybrid paths the regularization constant C) should always be chosen with care by taking into account the particular aim of the modelling and the model of interest; it is not possible to give any general recommendations or guidelines.

Appendix: Alternative Parametrization of Model (9)

Consider the related Markov chain model in Subsection 3.1, $P_X=P_Y$. Reparametrize the transition matrix

as follows:

where

$$\begin{aligned} \theta _1= {p(1-\lambda _1)\over 1-p},\quad \theta _2={q-p\lambda _2 \over 1-p}, \quad \rho _1={p-q\mu _1 \over 1-q},\quad \rho _2={q(1-\mu _2)\over 1-q}. \end{aligned}$$

Thus, for given p and q, the new parameters $\theta _1$, $\theta _2$, $\rho _1$ and $\rho _2$ are functions of $\lambda _1$, $\lambda _2$, $\mu _1$ and $\mu _2$, respectively. The parameters represent the following probabilities:

$$\begin{aligned}&P(Y_2=a|Y_1=a,X_1=1,X_2=1)=\lambda _1,\quad P(Y_2=b|Y_1=a,X_1=1,X_2=1)=1-\lambda _1, \\&P(Y_2=a|Y_1=b,X_1=1,X_2=1)=\lambda _2,\quad P(Y_2=b|Y_1=b,X_1=1,X_2=1)=1-\lambda _2, \\&P(Y_2=a|Y_1=a,X_1=1,X_2=2)=\theta _1,\quad P(Y_2=b|Y_1=a,X_1=1,X_2=2)=1-\theta _1, \\&P(Y_2=a|Y_1=b,X_1=1,X_2=2)=\theta _2,\quad P(Y_2=b|Y_1=b,X_1=1,X_2=2)=1-\theta _2, \\&P(Y_2=a|Y_1=a,X_1=2,X_2=1)=\mu _1,\quad P(Y_2=b|Y_1=a,X_1=2,X_2=1)=1-\mu _1, \\&P(Y_2=a|Y_1=b,X_1=2,X_2=1)=\mu _2,\quad P(Y_2=b|Y_1=b,X_1=2,X_2=1)=1-\mu _2, \\&P(Y_2=a|Y_1=a,X_1=2,X_2=2)=\rho _1,\quad P(Y_2=b|Y_1=a,X_1=2,X_2=2)=1-\rho _1, \\&P(Y_2=a|Y_1=b,X_1=2,X_2=2)=\rho _2,\quad P(Y_2=b|Y_1=b,X_1=2,X_2=2)=1-\rho _2. \\ \end{aligned}$$

Thus, given an observation sequence $x^n$, the probability of any state sequence $y^n$ is determined by the initial distribution and the transition probabilities above (representing four transition matrices).