Abstract
The stochastic fluid-fluid model (SFFM) is a Markov process \(\{(X_t,Y_t,\varphi _t),t\ge 0\}\), where \(\{\varphi _t,{t\ge 0}\}\) is a continuous-time Markov chain, the first fluid, \(\{X_t,t\ge 0\}\), is a classical stochastic fluid process driven by \(\{\varphi _t,t\ge 0\}\), and the second fluid, \(\{Y_t,t\ge 0\}\), is driven by the pair \(\{(X_t,\varphi _t),t\ge 0\}\). Operator-analytic expressions for the stationary distribution of the SFFM, in terms of the infinitesimal generator of the process \(\{(X_t,\varphi _t),t\ge 0\}\), are known. However, these operator-analytic expressions do not lend themselves to direct computation. In this paper the discontinuous Galerkin (DG) method is used to construct approximations to these operators, in the form of finite dimensional matrices, to enable computation. The DG approximations are used to construct approximations to the stationary distribution of the SFFM, and results are verified by simulation. The numerics demonstrate that the DG scheme can have a superior rate of convergence compared to other methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An unbounded stochastic fluid process \(\{(\widehat{X}_t, \varphi _t),t \ge 0\}\) is a Markov process where the phase \(\{\varphi _t\}\) is a continuous-time Markov chain on a finite state space \(\mathcal {S}\), and the fluid \(\{\widehat{X}_t\}\) varies linearly at rate \(c_{\varphi _t}\). A subset of Markov additive processes, stochastic fluids have been well-analysed in the past two decades. There have been recent generalisations of stochastic fluid processes to a higher dimension: Miyazawa and Zwart (2012) analysed discrete-time multidimensional Markov additive processes, and Bean and O’Reilly (2014) studied the so-called stochastic fluid-fluid model. The latter is the focus of this paper.
An unbounded stochastic fluid-fluid model (SFFM) is a Markov process \(\{(\widehat{X}_t, \widehat{Y}_t, \varphi _t),t \ge 0\},\) where the phase \(\{\varphi _t\}\) is a continuous-time Markov chain on a finite state space \(\mathcal {S}\); \(\{\widehat{X}_t\}\) is the first fluid, which varies linearly at rate \(c_{\varphi _t}\)
and \(\widehat{Y}_t\) is the second fluid, which varies at rate \(r_{\varphi _t}(\widehat{X}_t)\):
Regulated boundaries may also be included for both fluids. To distinguish between unbounded and bounded processes, we use the notations \(\widehat{X}_t\) and \(\widehat{Y}_t\) to denote unbounded processes, and \(X_t\) and \(Y_t\) to denote fluid levels with a regulated lower boundary at 0.
As classic fluid processes, \(\{(\widehat{X}_t, \varphi _t),t \ge 0\}\), or bounded analogues, are used extensively in many areas, such as insurance and environmental modelling, it is clear that stochastic fluid-fluid models have an even wider range of applicability.
An example of application for an SFFM is the modelling of growth and bleaching of coral reefs, as described in (Bean and O’Reilly 2014). In this process, we can model the density of symbiotic zooxanthellae at time t by \(X_t\), with the positive rates \(c_i\) corresponding to the growth of the zooxanthellae, the negative rates to the bleaching. The density, \(X_t\), determines the net rate at which the coral stores the lipids produced by the zooxanthellae. The amount of stored lipids is modelled by \(Y_t\), and the coral dies when the stored lipids run out, that is, \(Y_t = 0\).
Some specifications of stochastic fluid-fluid models have already been analysed; Bean and O’Reilly (2013) and the to-date unpublished work of Bean et al. (Matrix-Analytic Methods for the analysis of Stochastic Fluid-Fluid Models, 2020) study cases where \(\{X_t\}\) and \(\{Y_t\}\) are independent, given \(\{\varphi _t\}\), and Latouche et al. (2013) and O’Reilly and Scheinhardt (2017) study cases where \(\{Y_t\}\) depends on whether \(\{X_t\}\) is above, or below, some specific threshold. Here, we derive approximations to the theoretical operators in (Bean and O’Reilly 2014), which covers a much wider class of models than the specific ones already studied, therefore this work applies to a much larger class of models.
While the analyses in (Bean and O’Reilly 2014; Miyazawa and Zwart 2012) are markedly different, both papers drew inspiration from Neuts’ matrix-analytic approach (Neuts 1981; Latouche and Ramaswami 1999) to obtain the limiting behaviour of these processes, working with operators on function spaces instead of matrices. Thus, their closed-form expressions for the limiting distributions ([Theorem 2] Bean and O’Reilly (2014), [Theorem 4.1] Miyazawa and Zwart (2012)) are given in terms of operators acting on measures, which are not immediately amenable to numerical computations for real-life applications. Only in the simplest cases can the solutions to these operator equations be readily evaluated and, beyond the simplest cases, approximations are needed. One way to numerically handle operators on function spaces is to construct approximations of the operators. To this end, there exist numerical procedures such as finite difference, finite volume, finite element and discontinuous Galerkin (DG) methods (Cockburn 1999; Hesthaven and Warburton 2007). In the context of approximating fluid queues, Bean and O’Reilly (2013) derive an approximation to the process \(\{(X_t,\varphi _t\})\}\) which is a continuous-time Markov chain (specifically, a quasi-birth-and-death process). It turns out that the finite-volume method with an upwind flux, the DG method with a single (constant) basis function in each cell and an upwind flux, and the Markov chain approximation of Bean and O’Reilly (2013) are all equivalent.
In our application to SFFMs, the operators we wish to approximate are acting on a function space of probability densities and therefore our approximation method must respect certain properties of probability densities, such as conservation of probability. This is the case in the DG method (Cockburn 1999).
In this paper, the DG method is used to approximate the operators appearing in (Bean and O’Reilly 2014), and ultimately, the joint stationary distribution of an SFFM. We numerically illustrate the effectiveness of the methodology using an on-off bandwidth-sharing system of two processors (Latouche et al. 2013). In this example, inputs into the processors, \(\{X_t\}\) and \(\{Y_t\}\), are turned on and off by a Markov chain, \(\{\varphi _t\}\); the combined output capacity is fixed and allocated according to the workload of the first, high-priority, processor \(\{X_t\}\). Latouche et al. (2013) evaluate the marginal limiting distribution of the first processor \(\{X_t\}\), and provides bounds for the marginal limiting distribution of the workload of the second processor \(\{Y_t\}\). We verify our DG approximations by comparing them against Monte Carlo simulations, against analytical results obtained, and against our intuitive understanding of the system dynamics. In all considered cases, we find the approximations to be accurate. Further, the numerics also demonstrate a superior rate of convergence over the method of Bean and O’Reilly (2013) whereby the first fluid is approximated by a continuous-time Markov chain.
The paper is organised as follows. In Sect. 2, we give relevant background to present the joint stationary distribution of a stochastic fluid-fluid model. We construct, in Sect. 3, a discontinuous Galerkin scheme to approximate the infinitesimal generator of a stochastic fluid process. Sect. 4 uses this approximation to the infinitesimal generator to construct approximations of the first-return operator, and stationary distribution, of an SFFM. Numerical experiments are reported in Sect. 5. In Appendix 1 we provide a proof that our DG approximations conserve probability. Lastly, since the paper is notationally heavy, we apply the DG method to a small toy example in Appendix 2.
2 Preliminaries
Consider a stochastic fluid-fluid model \(\{(X_t, Y_t, \varphi _t),t \ge 0\}\). We assume that \(X_t, Y_t \in [0,\infty )\) and that there is a regulated boundary at level 0 for both buffers:
for \(i \in \mathcal {S} = \{1,...,N_\mathcal {S}\}\). Let T be the irreducible generator for the finite-state Markov chain \(\{\varphi _t\}\). We denote by \(C := \mathrm {diag}(c_i)_{i \in \mathcal {S}}\) the diagonal fluid-rate matrix for \(\{X_t\}\), and \(R(x) := \mathrm {diag}(r_i(x))_{i \in \mathcal {S}}\) the diagonal fluid-rate matrix of functions for \(\{Y_t\}\).
Remark 2.1
For future reference we require some notation regarding the elements of the model introduced above. We use the notation \(\varvec{u} = (u_h)_{h\in \mathcal H}\) to denote a row-vector, \(\varvec{u}\), defined by its elements, \(u_h\), indexed by \(h\in \mathcal H\), where \(\mathcal H\) is some countable index set. Similarly, \(\varvec{u} = (\varvec{u}_h)_{h\in \mathcal H}\), is a row-vector defined by a collection of row-vectors \(\varvec{u}_h\). The notation \(\varvec{u}_m=(u_h)_{h\in \mathcal H_m}\) refers to the vector containing the subset of elements corresponding to \(\mathcal H_m\subseteq \mathcal H\). When the index set is empty, the resulting vector \(\varvec{u}_m\) is a vector of dimension 0. In cases when the elements have two indices, we order the elements of the vector according to the first index, then the second; i.e. \(\varvec{u} = (u_{g}^h)_{g\in \mathcal G,h\in \mathcal H} = ((u_g^h)_{g\in \mathcal G})_{h\in \mathcal H}\). Here we use the convention that for a vector \(\varvec{u}=(u)_{h\in \mathcal H}\) where the elements \(u\) do not depend on the index \(h\) and \(H\) is some index set, then we repeat \(u\) \(h\)-times; i.e. \(\varvec{u} = (u)_{h\in \mathcal H} =\underbrace{(u,\dots ,u)}_{h-\text{ times }}\). The notation \(U = [u_{gh}]_{g\in \mathcal G, h\in \mathcal H}\) is used to denote a matrix defined by its elements, or sub-blocks, \(u_{gh}\).
Let \(\mathcal S_-=\{i\in \mathcal {S}\mid c_i<0\},\, \mathcal S_+=\{i\in \mathcal {S}\mid c_i>0\},\, \mathcal S_0=\{i\in \mathcal {S}\mid c_i=0\},\, \mathcal S_\nabla =\{i\in \mathcal {S}\mid c_i\le 0\},\, \mathcal S_\Delta =\{i\in \mathcal {S}\mid c_i\ge 0\}\). Define matrices \(C_m:=\mathrm {diag}(c_i)_{i\in \mathcal {S}_m}\), \(m\in \{+,-,0,\nabla ,\Delta \}\), and define the sub-matrices of transition rates \(T_{mn}=[T_{ij}]_{i\in \mathcal S_m,j\in \mathcal S_n}\), \(m,n\in \{+,-,0,\nabla ,\Delta \}\).
For the remainder of this section, we summarise the findings of (Bean and O’Reilly 2014) on the joint stationary distribution of \(\{(X_t, Y_t, \varphi _t),t \ge 0\}\). For each Markovian state \(i \in \mathcal {S}\), we partition the state space of \(X_t\), \([0,\infty )\), according to the rates of change \(r_i(\cdot )\) for the second fluid \(\{Y_t\}\): \([0,\infty ) := \mathcal {F}^{\kern 0.1500em +}_i \cup \mathcal {F}^{\kern 0.1500em -}_i \cup \mathcal {F}^{\kern 0.1500em 0}_i,\) where
For all \(i \in \mathcal {S}\), the functions \(r_i(\cdot )\) are assumed to be sufficiently well-behaved that \(\mathcal {F}^{m}_i\), \(m \in \{+, -, 0\}\), is a finite union of intervals and isolated points.
We assume that the process \(\{(X_t, Y_t, \varphi _t),t\ge 0\}\) is positive recurrent, in order to guarantee the existence of the joint stationary density. Define stationary operators

where \(\mathcal {A} \subset [0,\infty )\).
Then let
 (y) = (
(y) = (
 \(_i(y))_{i \in \mathcal {S}}\) be a vector containing the joint stationary density operators and \(\overline{\mathbb {p}} = (\overline{\mathbb p}_i)_{i \in \mathcal {S}}\) a vector containing the joint stationary mass operators.
\(_i(y))_{i \in \mathcal {S}}\) be a vector containing the joint stationary density operators and \(\overline{\mathbb {p}} = (\overline{\mathbb p}_i)_{i \in \mathcal {S}}\) a vector containing the joint stationary mass operators.
The determination of
 (y) involves two important matrices of operators, \(\overline{\mathbb B}\) and
(y) involves two important matrices of operators, \(\overline{\mathbb B}\) and
 . The operator \(\overline{\mathbb B}\) is the infinitesimal generator of the process \(\{(X_t,\varphi _t)\}\). The operator
. The operator \(\overline{\mathbb B}\) is the infinitesimal generator of the process \(\{(X_t,\varphi _t)\}\). The operator
 is such that \(\overline{\varvec{\mu }}\)
is such that \(\overline{\varvec{\mu }}\)
 \((\mathcal {A})\) is the conditional probability of \(\{Y_t\}\) returning to level zero and doing so when \(X_t \in \mathcal {A}\), given that the initial distribution is \(\overline{\varvec{\mu }}\).
\((\mathcal {A})\) is the conditional probability of \(\{Y_t\}\) returning to level zero and doing so when \(X_t \in \mathcal {A}\), given that the initial distribution is \(\overline{\varvec{\mu }}\).
2.1 Matrix \(\overline{\mathbb B}\) of Operators
Since \(\{(X_t,\varphi _t),t\ge 0\}\) is a Markov process, the evolution of probability can be described by a semigroup. Let \(\mathcal {M}(\mathcal {S} \times \mathbb {R}_{+})\) be the set of integrable complex-valued Borel measures on the Borel \(\sigma\)-algebra \(\mathcal {B}_{\mathcal {S} \times \mathbb {R}_{+}}\). For \(\overline{\varvec{\mu }} \in \mathcal {M}(\mathcal {S} \times \mathbb {R}_{+})\), we can write \(\overline{\varvec{\mu }} = (\overline{\mu _i})_{i \in \mathcal {S}}\). The measures \(\overline{\mu }_i(\cdot )\) represent an initial distribution, \(\overline{\mu }_i(\cdot ) = \mathbb {P}(X_0\in \cdot , \varphi _0 = i)\). Let \(\{\overline{\mathbb V}(t)\}_{t\ge 0},\, \overline{\mathbb V}(t):\mathcal {M}(\mathcal {S} \times \mathbb {R}_{+})\mapsto \mathcal {M}(\mathcal {S} \times \mathbb {R}_{+})\) be the semigroup describing the evolution of probability for \(\{(X_t,\varphi _t),t\ge 0\}\) structured as a matrix of operators, \(\left[ \overline{\mathbb V}(t)\right] _{ij}= \overline{\mathbb V}_{ij}(t)\) where,
Intuitively, the operator \(\overline{\mathbb V}(t)\) maps an initial measure \(\overline{\varvec{\mu }}\) on \((X_0,\varphi _0)\) to the measure \(\mathbb {P}(X_t\in \mathcal A, \varphi _t=j)=:\overline{\mu }_j(t)(\mathcal A)\). The matrix of operators \(\overline{\mathbb B}:=[\overline{\mathbb B}_{ij}]_{i,j\in \mathcal S}\) is the infinitesimal generator of the semigroup \(\{ \overline{\mathbb V}(t)\}\) defined by
with domain the set of measures for which this limit exists. Specifically, the domain of \(\overline{\mathbb B}\) is the set of measures, \(\overline{\varvec{\mu }} = (\overline{\mu }_i)_{i\in \mathcal {S}}\), for which each \(\overline{\mu }_i\) admits an absolutely continuous density on \((0,\infty )\), and can have a point mass at \(0\) if \(i\in \mathcal S_\nabla\); call this set of measures \(\mathcal M_0\). That is, the measures \(\overline{\mu }_i,\, i\in \mathcal {S},\) with \((\overline{\mu }_i)_{i\in \mathcal {S}}\in \mathcal M_0\) are absolutely continuous on \((0,\infty )\) and may have point masses at \(0\) if \(i\in \mathcal {S}_\nabla\). The measure \(\overline{\mu }_i\) cannot have a point mass at 0 if \(i\notin \mathcal S_\nabla\). In the sequel we write \(v_i(x),\, x>0\), as the density of \(\overline{\mu }_i\) and \(q_i\) as the point mass of \(\overline{\mu }_i\) at \(x=0\) (if such a point mass exists).
To use the operators \(\{ \overline{\mathbb V}(t)\}\) and \(\overline{\mathbb B}\) to analyse the fluid-fluid model, Bean and O’Reilly (2014) explicitly track when \((X_t,\varphi _t)\in (\mathcal F_i^m,i)\) for \(i\in \mathcal S,\, m \in \{+,-,0\}\) by partitioning the operators \(\overline{\mathbb V}(t)\) and \(\overline{\mathbb B}\) into \(\overline{\mathbb V}_{ij}^{m n}\) and \(\overline{\mathbb B}_{ij}^{m n}\), for \(i,j\in \mathcal S,\, m,n\in \{+,-,0\}\), where
and \(\left. \overline{\mu }_i\right| _{E}\) is the restriction of \(\overline{\mu }_i\) to \(E\). Similarly, for \(\overline{\mathbb B}_{ij}^{m n},\) \(i,j\in \mathcal S,\, m,n\in \{+,-,0\}\).
We claim that numerical schemes are needed to approximate the analytic operator equations introduced in Bean and O’Reilly (2014). The DG scheme we choose to use here works by first partitioning the state space of the fluid level, \(\{X_t\}\), into a collection of intervals, \(\mathcal {D}_k=[x_k,x_{k+1}]\) then, on each interval, the operator \(\overline{\mathbb B}\) is projected onto a basis of polynomials. So, to help elucidate the connection between the operators \(\{ \overline{\mathbb V}(t)\}\), \(\overline{\mathbb B}\) and their DG approximation counterparts, we take a slightly different approach to partitioning these operators than that taken in Bean and O’Reilly (2014). Rather than partition according to the sets \(\mathcal {F}_i^{\kern 0.1500em m},\,i\in \mathcal {S},\,m\in \{+,-,0\}\), we use the same partition as that in the construction of the DG scheme. By doing so, we can directly correspond elements of the partitioned operators to their approximation counterparts. Since the partition used to construct the DG scheme is finer, then we can always reconstruct the partition in terms of the sets \(\mathcal {F}_i^{\kern 0.1500em m},\,i\in \mathcal {S},\,m\in \{+,-,0\}\).
Let us first partition the space \([0,\infty )\) into \(\mathcal {D}_\nabla = \{0\}\), and non-trivial intervals \(\mathcal {D}_k=[x_k,x_{k+1}]\setminus \{0\},\) with \(x_1=0,\, x_k<x_{k+1},\,k=1,2,...\). The symbol \(\nabla\) is used to refer to sets and quantities which are relevant to boundary at \(x=0\). For \(\varvec{\mu } \in \mathcal {M}_0(\mathcal {S} \times \mathbb {R}_{+})\) we write \(\varvec{\mu } = (\mu ^{k}_i)_{i \in \mathcal {S},k\in \{\nabla ,1,2,...\}},\) where \(\mu ^{k}_i(\cdot ) = \mu _i(\cdot \cap \mathcal {D}_k),\,k=\nabla ,1,2,\dots .\) We also have densities, \(v_i^k(x),\,x>0\), associated with each measure, \(\mu _i^k\). For \(i,j\in \mathcal {S},\,k,\ell \in \{\nabla ,1,2,\dots \}\) define the operators
and the matrices of operators \(\mathbb V^{k\ell }(t) := \begin{bmatrix} \mathbb V_{ij}^{k\ell }(t) \end{bmatrix}_{i,j\in \mathcal S},\,k,\ell \in \{\nabla ,1,2,\dots \}\) and write
Now define \(\mathbb B=\left. \frac{\, \mathrm {d}}{\, \mathrm {d}t}\mathbb V(t)\right| _{t=0}\) as the infinitesimal generator of \(\{\mathbb V(t)\}\), resulting in the tridiagonal matrix of operators
where the blocks \(\mathbb B^{k\ell }:= \begin{bmatrix} \mathbb B_{ij}^{k\ell }(t) \end{bmatrix}_{i,j\in \mathcal S},\,k,\ell \in \{\nabla ,1,2,\dots \}\). The tridiagonal structure arises since, for \(|k-\ell |\ge 2\) (where we take \(\nabla = 0\) if it appears in the differences) it is impossible for \(\{X_t\}\) to move from \(\mathcal D_k\) to \(\mathcal D_\ell\) in an infinitesimal amount of time.
Remark 2.2
We use a blackboard bold font with an overline above the character (e.g. \(\overline{\mathbb B}\) and \(\overline{\mathbb V}(t)\)) to represent theoretical operators derived in (Bean and O’Reilly 2014) which are constructed using the partition in Eq. (1). The operators denoted with an overline play a minor role in the introductory sections of this paper, but do not appear again. We use a blackboard font sans overline (e.g. \(\mathbb V(t)\) and \(\mathbb B\)) to represent the same operators but which are constructed with the finer partition defined by \(\mathcal D_k,\,k=\nabla ,1,2,\dots\). We use the letters \(i,j\in \mathcal S\) to represent states of the phase process, letters \(m,n,\in \{+,-,0\}\) to refer to the partition in terms of the sets in Eq. (1), and the letters \(k,\ell \in \{\nabla ,1,2,...\}\) to refer to the finer partition into sets \(\{\mathcal {D}_k\}_k\). With a slight abuse of notation, whenever we use the dummy variables \(k,\ell\) without qualification we imply \(k,\ell \in \{\nabla ,1,2,\dots \}\), the dummy variables \(m,n\) without qualification imply \(m,n\in \{+,-,0\}\) and the dummy variables \(i,j\) without qualification imply \(i,j\in \mathcal {S}\). E.g. \(\mathbb B_{ij}^{k\ell }\) means \(\mathbb B_{ij}^{k\ell },\, i,j\in \mathcal {S}, k,\ell \in \{\nabla ,1,2,\dots \}\) and \(\mathbb B_{ij}^{mn}\) means \(\mathbb B_{ij}^{mn},\, i,j\in \mathcal {S}, m,n\in \{+,-,0\}\).
By an appropriate choice of the intervals \(\{\mathcal D_k\},\, k\in \{\nabla ,1,2,\dots ,\}\), the partition used in (Bean and O’Reilly 2014) can be recovered. Intuitively, we must ensure that each of the boundaries of \(\mathcal {F}_i^m,\, i\in \mathcal {S},\,m\in \{+,-,0\}\), align with a boundary of a cell \(\mathcal D_k=[x_k,x_{k+1}]\setminus \{0\}\). Then, each set \(\mathcal {F}_i^{\kern 0.1500em m},\, i\in \mathcal {S},\,m\in \{+,-,0\}\), can be written as a union of cells, \(\mathcal D_k,\,k=\nabla ,1,2,\dots\), sans a collection of points which have measure zero for all measures in \(\mathcal M_0\), and this collection of points is inconsequential for the purposes of the approximations presented here.
Formally, to recover the partition used in (Bean and O’Reilly 2014) we choose the intervals \(\mathcal {D}_k\) such that \(l (\mathcal {D}_k\cap \mathcal {F}_i^{\kern 0.1500em m}) \in \{ l (\mathcal {D}_k), 0\}\) for all \(i\in \mathcal {S},\,m\in \{+,-,0\},\,k\in \{\nabla ,1,2,\dots \}\), for all measures \(l \in \mathcal M_0\). That is, we choose \(\mathcal {D}_k\) such that it is contained (up to sets of measure 0 with respect to measures in \(\mathcal M_0\)) within \(\mathcal {F}_i^{\kern 0.1500em m}\) for some \(m\in \{+,-,0\}\) and all \(i\in \mathcal {S}\). We assume such a partition for the rest of the paper. For \(i\in \mathcal {S},\,m\in \{+,-,0\}\), let \(\mathcal K^m_i = \{k\in \{\nabla ,1,2,\dots \}\mid l (\mathcal {D}_k\cap \mathcal {F}_i^{\kern 0.1500em m}) = l (\mathcal {D}_k),\,l\in \mathcal M_0 \}\), so that \(\bigcup \limits _{k\in \mathcal K_i^m} \mathcal {D}_k\) and \(\mathcal F_i^{\kern 0.1500em m}\) are equal up to a set of \(l\)-measure 0 for all \(l\in \mathcal M_0\). Define \(\mathcal K^m = \bigcup \limits _{i\in \mathcal {S}}\mathcal K_i^m\), \(m\in \{+,-,0\}\).
To recover the partition defined by (1) we bundle together the elements of \(\mathbb V(t)\) which correspond to \(\mathcal {F}_i^{\kern 0.1500em m}\) and \(\mathcal {F}_j^{\kern 0.1500em n}\). That is, for \(m,n\in \{+,-,0\}\), define \(\mathbb V_{ij}^{m n}(t)\) as the matrix of operators
Then, for \(i,j\in \mathcal {S},\,m,n\in \{+,-,0\}\), we can write \(\overline{\mathbb V}_{ij}^{mn}(t) = \varvec{1}_{|\mathcal K_i^m|} \mathbb V_{ij}^{m n}(t) \varvec{1}_{|\mathcal K_j^n|}^{\text{ T }}{}\) where \(\varvec{1}_{|\mathcal K_i^m|}\) and \(\varvec{1}_{|\mathcal K_j^n|}\) are row-vectors of 1’s of length \(|\mathcal K_i^m|\) and \(|\mathcal K_j^n|\), respectively, and \({}^{\text{ T }}{}\) denotes the transpose. The same construction can be achieved with \(\mathbb B\).
Let \(\mathcal {S}_k^{\kern 0.1500em +}=\{i\in \mathcal {S}\mid r_i(x)>0,\,\forall x \in \mathcal {D}_k\}\), \(\mathcal {S}_k^{\kern 0.1500em 0}=\{i\in \mathcal {S}\mid r_i(x)=0,\,\forall x \in \mathcal {D}_k\}\), \(\mathcal {S}_k^{\kern 0.1500em -}=\{i\in \mathcal {S}\mid r_i(x)<0,\,\forall x \in \mathcal {D}_k\}\) and \(\mathcal {S}_k^{\kern 0.1500em \bullet} =\{i\in \mathcal {S}\mid r_i(x)\ne 0,\,\forall x \in \mathcal {D}_k\}\) for \(k\in \{\nabla ,1,\dots \}\). For later reference, we need the following constructions. For \(k,\ell \in \{\nabla ,1,2,...\}\)
for \(i,j\in \mathcal {S}\)
and for \(m,n\in \{+,-,0\}\)
We persist with the partition \(\mathcal {D}_k,\,k\in \nabla ,1,2,\dots\) throughout this paper, as this is consistent with the partition used in the DG method, and note that for all the operators defined with this partition, the partitioning used in (Bean and O’Reilly 2014) can always be recovered by the above construction.
We can write \(\mu _i^k\mathbb B_{ij}^{k\ell }(\mathcal A)\) in kernel form as \(\displaystyle \int _{x\in \mathcal {D}_k,y\in \mathcal A}\, \mathrm {d}\mu _i^k(x)\mathbb B_{ij}^{k\ell }(x,dy)\). It is known that
on the interior of \(\mathcal {D}_k\) (Karandikar and Kulkarni 1995). Intuitively, \(v_i^k(y)T_{ij}\, \mathrm {d}y\) represents the instantaneous rate of transition from phase \(i\) to \(j\) in the infinitesimal interval \(\, \mathrm {d}y\), \(v_i^k(y)T_{ii}\, \mathrm {d}y\) represents no such transition occurring, and \(- c_i\frac{\, \mathrm {d}}{\, \mathrm {d}y}v_i^k(y)\, \mathrm {d}y\) represents the drift across the interval \(\, \mathrm {d}y\) when the phase is \(i\).
Translating the results of Bean and O’Reilly (2014) to use the partition \(\{\mathcal {D}_k\}\) we may state that, for all \(i,j\in \mathcal {S}\), \(k\in \{1,2,\dots \}\),
where \(\mathbb 1_{}\) is the indicator function. Intuitively, the first term represents the instantaneous rate of the stochastic transitions of the phase process \(\{\varphi _t\}\), the second term represents the flux out of the right-hand edge of \(\mathcal {D}_k\) which occurs when \(c_i>0\) only, and the last term represents the flux out of the left-hand edge of \(\mathcal {D}_k\) which occurs when \(c_i<0\) only.
The results of Bean and O’Reilly (2014) also imply that,
Intuitively, the first equation represents the flux from \(\mathcal {D}_k\) to \(\mathcal {D}_{k+1}\) across the shared boundary at \(x_{k+1}\) which occurs when \(c_i>0\) only. The second expression represents the flux from \(\mathcal {D}_k\) to \(\mathcal {D}_{k-1}\) across the shared boundary at \(x_{k}\) which occurs when \(c_i<0\) only.
Bean and O’Reilly (2014) also state that, at the boundary \(x=0\), for states \(i\in \mathcal {S}\) with \(c_i\le 0\) such that a point mass at \(0\) is possible, we have
where \(0^+\) is the right limit at \(0\). Otherwise \(\mu _i^{k}\mathbb B_{ij}^{k\ell }=0,\, \text{ for } |k-\ell |\ge 2,\,i,j\in \mathcal S \text{ or } |k-\ell |=1,\,i,j\in \mathcal S,i\ne j\), where we take \(\nabla = 0\) if it appears in the differences, capturing the facts that the process \(\{X_t\}\) is continuous and that drift across boundaries occurs only when \(\{\varphi _t\}\) remains in the same phase.
Note that we have not presented \(\mathbb B\) in its full detail here and refer the reader to (Bean and O’Reilly 2014) for the details. The main goal here is to show how \(\mathbb B\) is used to construct the stationary distribution of the SFFM and to illustrate the link between the operator \(\mathbb B\) and the DG approximation of the same object. As we shall see later, these expressions closely resemble the DG approximations to the same quantities.
2.2 Matrix \(\mathbb D(s)\) of Operators
Let \(b(t) := \int _0^t \left| r_{\varphi _z}(X_z) \right| \, \mathrm {d}z\) be the total unregulated amount of fluid that has flowed into or out of the second buffer \(\{Y_t\}\) during [0, t], and let \(\omega (y) := \inf \{t > 0: b(t) = y\}\) be the first time this accumulated in-out amount hits level y. Note that at the stopping time \(\omega (y)\) it must be that \((X_{\omega (y)},\varphi _{\omega (y)})\in (\mathcal {F}_i^m,i)\) for some \(i\in \mathcal {S}\) and \(m\in \{+,-\}\), i.e. \(m\ne 0\). We define the operators \(\mathbb {U}_{ij}^{k\ell }(y,s): \mathcal {M}_0(\mathcal {D}_{k}\cap \mathcal {F}_i^m) \mapsto \mathcal {M}_0 (\mathcal {D}_\ell \cap \mathcal {F}_j^n)\), for \(k\in \mathcal K_i^+\cup \mathcal K_i^-\), \(\ell \in \mathcal K_j^+\cup \mathcal K_j^-\), and \(i \in \mathcal {S}_k^\bullet ,\,j \in \mathcal {S}_k^\bullet\), by
Then, construct the matrix of operators
The matrix of operators \(\mathbb D(s)\) is the infinitesimal generator of the semigroup \(\{\mathbb U(y,s)\}_{y\ge 0}\) defined by
whenever this limit exists.
Recalling the constructions in Eqs. (4)-(8) and using Lemma 4 of (Bean and O’Reilly 2014) gives the following expression for \(\mathbb {D}(s)\).
Lemma 2.1
For \(y \ge 0\), \(s \in \mathbb {C}\) with Re\((s) \ge 0\), \(i,j \in \mathcal {S}\), \(k\in \mathcal K_i^+\cup \mathcal K_i^-\), \(\ell \in \mathcal K_j^+\cup \mathcal K_j^-\),
where \(\mathbb I\) is the identity operator, and \(\mathbb {R}^{k} := \mathrm {diag}(\mathbb {R}_i^{k})_{i \in \mathcal {S}}\) is a diagonal matrix of operators \(\mathbb {R}_i^{k}\) given by
Also, construct the matrices of operators
2.3 Matrix
 (s) of Operators
(s) of Operators
We denote by
 (s) the matrix of operators with the same dimensions as \(\mathbb D^{+-}\), recording the Laplace-Stieltjes transforms of the time for \(\{Y_t\}\) to return, for the first time, to the initial level of zero as introduced in (Bean and O’Reilly 2014) but constructed with respect to the finer partition \(\{\mathcal {D}_k\}\). Define the stopping time \(\theta (y):= \inf \{t > 0: Y_t = y\}\) to be the first time \(\{Y_t\}\) hits level y, then each component
(s) the matrix of operators with the same dimensions as \(\mathbb D^{+-}\), recording the Laplace-Stieltjes transforms of the time for \(\{Y_t\}\) to return, for the first time, to the initial level of zero as introduced in (Bean and O’Reilly 2014) but constructed with respect to the finer partition \(\{\mathcal {D}_k\}\). Define the stopping time \(\theta (y):= \inf \{t > 0: Y_t = y\}\) to be the first time \(\{Y_t\}\) hits level y, then each component
 \(_{ij}^{k\ell }(s): \mathcal {M}_0(\mathcal D_k) \mapsto \mathcal {M}_0(\mathcal D_\ell ), i,j \in \mathcal {S},\,k\in \mathcal K_i^+\) and \(\ell \in \mathcal K_j^-\), is given by
\(_{ij}^{k\ell }(s): \mathcal {M}_0(\mathcal D_k) \mapsto \mathcal {M}_0(\mathcal D_\ell ), i,j \in \mathcal {S},\,k\in \mathcal K_i^+\) and \(\ell \in \mathcal K_j^-\), is given by

Bean and O’Reilly [Theorem 1] Bean and O’Reilly (2014) give the following result which characterises
 \((s)\).
\((s)\).
Theorem 2.1
For Re \((s) \ge 0\),
 (s) satisfies the equation:
(s) satisfies the equation:

Furthermore, if s is real then
 (s) is the minimal nonnegative solution.
(s) is the minimal nonnegative solution.
2.4 Stationary Distribution
Let
 :=
:=
 (0). We define \(\theta _n := \inf \{t \ge \theta _{n - 1}: Y_t = 0\}\), for \(n \ge 2\), to be the sequence of hitting times to level 0 of \(Y_t\), with \(\theta _1: = \theta (0)\). Consider a discrete-time Markov process \(\{(X_{\theta _n}, \varphi _{\theta _n}),n \ge 1\}\), and for \(i \in \mathcal {S},\,k\in \mathcal K_i^-\) define the measures
(0). We define \(\theta _n := \inf \{t \ge \theta _{n - 1}: Y_t = 0\}\), for \(n \ge 2\), to be the sequence of hitting times to level 0 of \(Y_t\), with \(\theta _1: = \theta (0)\). Consider a discrete-time Markov process \(\{(X_{\theta _n}, \varphi _{\theta _n}),n \ge 1\}\), and for \(i \in \mathcal {S},\,k\in \mathcal K_i^-\) define the measures
 \(_i^k\) as follows
\(_i^k\) as follows
 By (Bean and O’Reilly 2014), the vector of measures
By (Bean and O’Reilly 2014), the vector of measures
 satisfies the following set of equations
satisfies the following set of equations


We reproduce Theorem 2 of (Bean and O’Reilly 2014) below, which gives the joint stationary distribution of \(\{(X_t, Y_t, \varphi _t)\}\). Recall that the joint stationary density operator
 (y) = (
(y) = (
 \(_i(y))_{i \in \mathcal {S}}\) for \(\{(X_t, Y_t, \varphi _t)\}\) and the joint stationary mass operator \({\mathbb p} = (\mathbb p_i)_{i \in \mathcal {S}}\) are defined by (2) and (3), respectively. We can partition
\(_i(y))_{i \in \mathcal {S}}\) for \(\{(X_t, Y_t, \varphi _t)\}\) and the joint stationary mass operator \({\mathbb p} = (\mathbb p_i)_{i \in \mathcal {S}}\) are defined by (2) and (3), respectively. We can partition
 as follows
as follows

where

Similarly, we can write
where \(\mathbb p_i^{k}(\mathcal {A}) = \mathbb p_i(\mathcal {A}\cap \mathcal D_k).\)
Theorem 2.2
The density
 \(^{m}(y)\), for \(m \in \{+,-,0\}\) and \(y > 0\), and the probability mass \(\mathbb {p}^{m}\), for \(m \in \{-,0\}\), satisfy the following set of equations:
\(^{m}(y)\), for \(m \in \{+,-,0\}\) and \(y > 0\), and the probability mass \(\mathbb {p}^{m}\), for \(m \in \{-,0\}\), satisfy the following set of equations:




where \(\mathbb {K} := \mathbb {D}^{++}(0) +\)
 \(\mathbb {D}^{(-+)}(0)\) and z is a normalising constant.
\(\mathbb {D}^{(-+)}(0)\) and z is a normalising constant.
At this point we reiterate that Eqs. (11)-(14) are operator equations and are only amenable to numerical evaluation in the simplest of cases. Sources of this intractability come from, for example, the need to find the inverse operator \(( - \mathbb B^{00})^{-1}\), and the need to find the solution,
 \((s)\), of the operator equation in Theorem 2.1. There is also the complexity of the partition of the operators defined by the sets \(\mathcal F_{i}^m,\, i\in \mathcal {S},\,m\in \{+,-,0\}\) to consider. Therefore, there is the need for approximation schemes such as the DG scheme we introduce next.
\((s)\), of the operator equation in Theorem 2.1. There is also the complexity of the partition of the operators defined by the sets \(\mathcal F_{i}^m,\, i\in \mathcal {S},\,m\in \{+,-,0\}\) to consider. Therefore, there is the need for approximation schemes such as the DG scheme we introduce next.
3 Discontinuous Galerkin Approximation of a Stochastic Fluid Model: Approximating \(\mathbb B\)
Discontinuous Galerkin (DG) methods can be used to approximate the solutions to systems of partial differential equations (PDEs). For a more thorough description of these methods see (Hesthaven and Warburton 2007). The domain of approximation is partitioned into intervals, referred to individually as cells and collectively as a mesh. On each cell, we have a finite element approximation, which constructs a finite-dimensional smooth Sobolev space using piecewise-polynomial basis functions, and then projects the partial differential equations onto this space. This projection leads to a new system of equations, referred to as the weak form of the original system of PDEs. Next, we must approximate the flux operator which moves probability from one cell to another, in a manner similar to the underlying principle of a finite-volume approximation. This method conserves probability, and can handle discontinuities, such as jumps and point masses. Here we construct the DG approximation to the matrix of operators \(\mathbb B\) which we use later to construct a DG approximation to \(\mathbb D(s)\) then
 \((s)\), and ultimately the stationary distribution of an SFFM.
\((s)\), and ultimately the stationary distribution of an SFFM.
3.1 The Partial Differential Equation
We start by introducing the PDE from which we will extract the approximation to the generator \(\mathbb B\).
Let \(f_i(x,t)\) be the joint density of \(\{(X_t, \varphi _t)\}\):
which satisfies the system of partial differential equations
subject to suitable boundary conditions (Bean and O’Reilly 2014). In matrix form,
where \(\varvec{f}(x,t) = \left( f_i(x,t)\right) _{i\in \mathcal S}\). This system of PDEs is closely related to the generator \(\mathbb B\). For \(\mathcal A\subset (0,\infty )\), and assuming \(\varvec{\mu }(t)\) admits a density,
That is, \(f_i(x,t)\) is the density of \(\mu _i(t)\). Then \(\varvec{\mu }(t)\) satisfies the operator differential equation
on the interior of the space \([0,\infty )\). Thus, by approximating the operator on the right-hand side of Eq. (15) we can approximate the infinitesimal operator \(\mathbb B\). The DG method does exactly this, by approximating the operator with a matrix.
3.2 Cells, Test Functions, and Weak Formulation
To begin with, consider an unbounded first fluid level \(\{\widehat{X}_t,t\ge 0\}\), \(\widehat{X}_t\in (-\infty ,\infty )\). We will eventually truncate this space so that we have a finite dimensional approximation; however, this requires a discussion on boundary conditions which we save for later. Let \(\mathcal D_k = [x_k,x_{k+1}],\, k\in \mathbb Z\) partition the domain \((-\infty ,\infty )\). We call the \(\mathcal {D}_k\) cells.
On each cell \(\mathcal {D}_k\) we choose \(N_k\) linearly independent functions \(\{\phi _r^k\}_{r=1}^{N_k}\), compactly supported on \(\mathcal {D}_k\) (i.e. \(\phi _r^k(x)=0\) for \(x\notin \mathcal {D}_k\)) to form a basis for the space \(W_k\), in which we formulate the approximation. Here, as is standard in DG methods (Hesthaven and Warburton 2007), we take \(\{\phi _r^k\}_{r=1}^{N_k}\) to be the space of polynomials of degree \(N_k-1\). It is convenient in this work to take \(\{\phi _r^k\}_{r=1}^{N_k}\) as a basis of Lagrange interpolating polynomials defined by the Gauss-Lobatto quadrature points, since our approximations inherit nice properties from this (Hesthaven and Warburton 2007). However, the constructions presented here are general, and any basis can be used. For the sake of illustration, the reader may think of \(\{\phi _r^k\}_{r=1}^{N_k}\) as the Lagrange polynomials. On each cell \(\mathcal D_k\) we approximate
where \(a_{i,r}^k(t)\) are yet-to-be-determined time-dependent coefficients. We refer to \(u_i^k\) as the local approximation on \(\mathcal {D}_k\), while the global approximation is given by \(\sum \limits _{k\in \mathbb Z}u_i^k\) on the whole domain. The whole approximation space is \(\bigoplus \limits _{k\in \mathbb Z} W_k\).
Let \(\mathcal N_k := \left\{ 1,\dots ,N_k\right\} ,\, k \in \mathbb Z\). For \(k\in \mathbb Z,\) define local row-vectors
Note that we will always use the letter \(r\) to index the basis function within each cell.
The DG method proceeds by considering the weak-formulation of the PDE, which is constructed from the strong-form of the PDE, Eq. (15). In general, to construct the weak-form we need a set of test functions, say \(W\). Now, take the strong form of the PDE, multiply it by some test function \(\psi (x)\in W\), integrate with respect to \(x\), and apply integration by parts to the derivative with respect to \(x\), to get
for \(j\in \mathcal {S}\). It is common to choose \(W\) such that \(\psi (-\infty )=\psi (\infty )=0\), in which case the last term on the right is zero. Requiring (16) to hold for every \(\psi \in W\) gives the weak-formulation of the PDE. For a sufficiently rich set of test functions \(W\) the weak and strong forms of the PDE are equivalent. Solutions to (16) are known as weak solutions and generalise the concept of a solution of the PDE. For example, this may allow discontinuities with respect to \(x\) in the solution – something which is ill-defined for the strong form.
For the purpose of DG, we take the set of test functions to be \(W = \bigoplus \limits _{k\in \mathbb Z} W^k\), the same as the set of basis functions of our solution space. Proceeding as described above, the weak formulation is
since \(\phi _r^k\) is compactly supported on \(\mathcal {D}_k\), for all \(j\in \mathcal S,\,r\in \mathcal N_k\), \(k\in \mathbb Z.\) Now, note that any function \(g(x)\) can be decomposed as \(g(x) = g^{W}(x)+g^\perp (x)\) where \(g^{W}\in W\) and \(g^\perp \in W^\perp\), and \(W^\perp\) is the orthogonal complement of \(W\). Since \(g^\perp\) is orthogonal to \(W\), \(\displaystyle \int _{x}g^\perp (x)\phi _r^k(x)\, \mathrm {d}x=0\) for \(r\in \mathcal N_k,\,k\in \mathbb Z\). Also, note that \(\frac{\, \mathrm {d}}{\, \mathrm {d}x}\phi _r^k(x)\in W\). Using this, we can write
which is equivalent to
Now, \(f_j^W(x,t)\in W\) so, on \(\mathcal D_k\), it can be expressed as \(\varvec{a}_j^k(t) \varvec{\phi }^k(x)^{\text{ T }}{}\), which we now substitute into (17) and repeat this for all test functions \(\phi _r^k(x)\), \(r=1,...,N_k\), to get the following system of equations,
3.3 Mass, Stiffness, and Flux
For \(k\in \mathbb Z\), define local mass and stiffness matrices \(M_k\) and \(G_k\) by
We can write (18) as
It remains to approximate the flux, \(f_j(x,t)\) at the cell edges \(x_k,\,k\in \mathbb Z\), so that we may evaluate the terms \([\kern 0.1500em f_j(x,t)\phi _r^k(x)]_{x=x_k}^{x=x_{k+1}}\), \(r=1,...,N_k,\,k\in \mathbb Z\). This is the key for DG – it joins the local approximations on each cell \(\mathcal {D}_k\), into a global approximation on the whole domain of approximation. The flux is the instantaneous rate (with respect to time) at which density moves across the boundaries \(x_k,\,k\in \mathbb Z\). There are different choices for the flux, and we refer the reader to (Cockburn 1999; Hesthaven and Warburton 2007), and references therein, for some discussion of the topic. Here, we choose the upwind scheme, which, as we shall see, closely resembles the flux terms from the generator \(\mathbb B\). The approximate flux, also known as the numerical flux, is given by
at each \(x=x_k,\,k\in \mathbb Z\). Intuitively, the upwind flux takes the value of the density immediately on the upwind side of each \(x_k\).
Denote by \(x^-\) and \(x^+\) the left and right limits at \(x\), respectively. Assume first \(c_j>0\), then
In matrix form,
where, for \(j\in \mathcal {S}\) with \(c_j>0\), we define \(F_j^{k,k} := -\varvec{\phi }^k(x_{k+1}^-)^{\text{ T }}{}\varvec{\phi }^k(x_{k+1}),\,k\in \mathbb Z\) and \(F_j^{k-1,k} := \varvec{\phi }^{k-1}(x_{k}^-)^{\text{ T }}{}\varvec{\phi }^k(x_{k}),\,k\in \mathbb Z\).
Now proceed similarly for \(c_j<0\) to get the approximation
where, for \(j\in \mathcal {S}\) with \(c_j<0\), we define \(F_j^{k+1,k} := -\varvec{\phi }^{k+1}(x_{k+1}^+)^{\text{ T }}{}\varvec{\phi }^k(x_{k+1}),\,k\in \mathbb Z,\) and \(F_j^{k,k} := \varvec{\phi }^{k}(x_{k}^+)^{\text{ T }}{}\varvec{\phi }^k(x_{k}),\,k\in \mathbb Z\).
The matrices \(F_j^{k-1,k},\,F_j^{k,k},\) and \(F_j^{k+1,k}\) are the local flux matrices. For convenience, we also define the matrices \(F_j^{k,k+1}=0\) for \(c_j<0\) and \(F_j^{k,k-1}=0\) for \(c_j>0\), \(k\in \mathbb Z\).
To write this out as a global system, define the row-vectors
and the block-diagonal matrix
where, for \(k\in \mathbb Z\),
The matrices \(\widetilde{\mathfrak B}^{k\ell }\) are defined by sub-blocks; denote these sub-blocks by \(\widetilde{\mathfrak B}^{k\ell }_{ij}\):
The global system of equations is
3.4 Boundary conditions
To enable computation, this numerical approximation has to take place on a finite interval, which means we must consider a bounded domain and specify boundary conditions. Recall from Sect. 2 that we wish to impose a regulated boundary at \(x=0\). To apply the DG method, we must truncate the state space of the first fluid at some finite interval upper bound, \([0,\mathcal I]\), for some \(\mathcal I<\infty\), and specify the boundary behaviour at \(x=\mathcal I\). Here we consider \(\mathcal I\) to be a regulated boundary. Let us denote the doubly-bounded fluid level by \(\overline{X}_t\). Ultimately, we wish to approximate a fluid-fluid queue where the first fluid level, \(X_t\), is bounded below at 0, only. Thus, the first step in the approximation scheme is to approximate \(X_t\) by \(\overline{X}_t\). The truncation of \(X_t\) to \(\overline{X}_t\) will result in an artificial point mass at the upper bound, which we have to address properly. It is important to choose an \(\mathcal I\) sufficiently large to control the error induced by the artificial upper bound, however, with larger \(\mathcal I\) there comes increased computational burden. We shall further comment on this in Sect. 5, where we report our numerical experiments.
Let \([0,\mathcal {I}]\) be the domain of the approximation, where \(\mathcal {I} < \infty\), and assume there is a regulated boundary for \(\{\overline{X}_t\}\) at \(x=\mathcal I\). We partition the space \([0,\mathcal {I}]\) into \(\mathcal D_\nabla =\{0\},\) \(\mathcal D_\Delta =\{\mathcal I\},\) and \(K\) non-trivial intervals, \(\mathcal {D}_k=[x_k,x_{k+1}]\setminus \{\{0\}\cup \{\mathcal I\}\},\, x_k<x_{k+1},\, k=1,...,K\), \(x_1=0,\,x_{K+1}=\mathcal I\) and define \(h_k := x_{k+1}-x_k\). The notation \(\Delta\) refers to quantities and sets which are relevant to the boundary at \(\mathcal I\).
For states with \(c_i\le 0\), there is the possibility of point mass accumulating at the boundary at \(0\). Denote these point masses by \(q_{\nabla ,i}(t)\) for \(i\in \mathcal S_\nabla\). For states with \(c_i>0\) there is no possibility of a point mass at \(0\). Similarly, for \(c_i\ge 0\) there is the possibility of a point mass at \(\mathcal I\). Denote these point masses by \(q_{\Delta ,i}(t)\), for \(i\in \mathcal S_\Delta\). For states with \(c_i<0\) there is no possibility of a point mass at \(\mathcal I\). Let \(\varvec{q}_\nabla (t)=(q_{\nabla ,i}(t))_{i\in \mathcal {S}_\nabla }\) and \(\varvec{q}_\Delta (t) = (q_{\Delta ,i}(t))_{i\in \mathcal {S}_\Delta }\) and \(\varvec{f}_m(x,t) = (\kern 0.1500em f_i(x,t))_{i\in \mathcal {S}_m}\), \(m\in \{+,-,0\}\).
Let us first consider the boundary at \(\overline{X}_t=0\). Bean and O’Reilly (2014) show the following boundary conditions describe the evolution of probability/density of a stochastic fluid model with a regulated boundary at \(0\);
Equation (21) states that point mass moves between phases according to the sub-generator matrix \(T_{\nabla \nabla }\), and that the flux of probability density into the point masses is \(- \varvec{f}_\nabla (0,t)C_\nabla\). Substituting the DG approximation for \(\varvec{f}_\nabla (0,t)\) into Eq. (21) gives, for \(j\in \mathcal {S}_\nabla\),
Equation (22) describes the flux of probability mass to density upon a transition from a phase in \(\mathcal {S}_\nabla\) to a phase in \(\mathcal {S}_+\). Thus, the flux into the left-hand edge of \(\mathcal {D}_1\) in phase \(j\in \mathcal {S}_+\) is, \(\sum \limits _{i\in \mathcal {S}_\nabla } q_{\nabla ,i}(t)T_{ij}\). Therefore, we can now evaluate
for \(j \in \mathcal {S}_+\). Thus, the DG approximation of the flux into point masses \(q_{\nabla ,j}(t)\) is \(-\varvec{a}_j^1(t)\varvec{\phi }^1(0)^{\text{ T }}{} c_j,\,j\in \mathcal {S}_-\), the rate of transition of point mass within \(\varvec{q}_{\nabla }(t)\) is \(T_{\nabla \nabla }\), and the DG approximation of the transition of point mass to density is \(\sum \limits _{i\in \mathcal {S}_\nabla }q_{\nabla ,i}(t)T_{ij}\varvec{\phi }^1(0),\,j\in \mathcal {S}_+\).
Similarly, for the boundary at \(\overline{X}_t=\mathcal I\) the boundary conditions are
Using the same arguments as above,
for \(j\in \mathcal {S}_\Delta\). Thus, the DG approximation of the flux into the point mass \(q_{\Delta ,j}(t)\) is \(\varvec{a}_j^K(t)\varvec{\phi }^K(0)^{\text{ T }}{} c_j\), \(j\in \mathcal {S}_+\), the rate of transition of point mass within \(\varvec{q}_{\Delta }(t)\) is \(T_{\Delta \Delta }\), and the DG approximation of the transition of point mass to density is \(\sum \limits _{i\in \mathcal {S}_\Delta }q_{\Delta ,i}(t)T_{ij}\varvec{\phi }^K(\mathcal I)\), \(j\in \mathcal {S}_-\).
To include this behaviour in the DG generator we truncate the doubly-infinite matrix \(\widetilde{\mathfrak B}\) at \(k=1\) and \(k=K\), then append \(|\mathcal S_\nabla |\) rows and columns to the top and left, and \(|\mathcal S_\Delta |\) rows and columns to the bottom and right. These represent the point masses \(\varvec{q}_\nabla (t)\) and \(\varvec{q}_\Delta (t)\), respectively. Given the discussion above, the truncated matrix is
where \(\widetilde{\mathfrak B}^{\nabla 1} := T_{\nabla +}\otimes \varvec{\phi }^1(0)\), \(\widetilde{\mathfrak B}^{1\nabla } :=-\mathrm {diag}(c_i\mathbb 1_{(c_i<0)})_{i\in \mathcal {S}}\otimes \varvec{\phi }^1(0)^{\text{ T }}{}\), \(\widetilde{\mathfrak B}^{\Delta K} := T_{\Delta -}\otimes \varvec{\phi }^K(\mathcal I)\) and \(\widetilde{\mathfrak B}^{K,\Delta } := \mathrm {diag}(c_i\mathbb 1_{(c_i>0)})_{i\in \mathcal {S}} \otimes \varvec{\phi }^K(\mathcal I)^{\text{ T }}{},\) and \(\otimes\) is the Kronecker product. Where we have used the same sub-block notation as we have for \(\widetilde{\mathfrak B}\).
After the addition of the boundary conditions, the system of ODEs (20) can now be written as
where \(\widehat{M} = \left[ \begin{array}{ccccc} I_{|\mathcal {S}_\nabla |} &{} &{} &{} &{} \\ &{} I_{N_S}\otimes M_1 &{} &{} &{} \\ &{} &{} \ddots &{} &{} \\ &{} &{} &{} I_{N_S}\otimes M_K &{} \\ &{} &{} &{} &{} I_{|\mathcal {S}_\Delta |} \end{array}\right]\). Define \(B = \widehat{\mathfrak B}\widehat{M}^{-1}\), with the sub-block as we used for \(\widetilde{\mathfrak B}\).
Regarding our notational convention, the matrices in fraktur fonts (e.g. \(\mathfrak B\)) are intermediary constructions that are not directly referred to for the rest of the paper (but do appear again in the appendix). We use regular mathematics fonts to represent
DG approximations to operators, i.e. \(B\) is a DG approximation to \(\mathbb B\) and \(\Psi\) is an approximation to
 .
.
We prove the following result in Appendix 1.
Corollary 3.1
The approximate generator \(B\) conserves probability. That is, for all \(t\ge 0\),
3.5 Putting It All Together
Recall that the ultimate goal for our DG approximation is to approximate the operator \(\mathbb B\). We have that \({ B}^{k\ell }\) is an approximation to \(\mathbb B^{k\ell }\), \(k,\ell \in \{\nabla ,1,...,K,\Delta \}\).
Given we have now truncated the space and added boundaries, let us define \(\mathcal M_{0,\mathcal I}\) as the set of measures, \(\mu _i\), which admit an absolutely continuous density on \((0,\mathcal I)\), may have a point mass at \(x=0\) if \(i\in \mathcal S_\nabla\), and another at \(x=\mathcal I\) if \(i\in \mathcal {S}_{\Delta }\). The set \(\mathcal M_{0,\mathcal I}\) is the domain of the operator \(\mathbb B\) truncated to the interval \([0,\mathcal I]\) with regulated boundaries at \(x=0\) and \(x=\mathcal I\). Also, redefine \(\mathcal K^m_i = \{k\in \{\nabla ,1,...,K,\Delta \}\mid l (\mathcal {D}_k\cap \mathcal {F}_i^{\kern 0.1500em m}) = l (\mathcal {D}_k) \}\) for \(i\in \mathcal {S},m\in \{+,-,0\}\) for all \(l\in \mathcal M_{0,\mathcal I}\).
Approximations \(B^{mn}_{ij}\), \(B_{ij}\), and \(B^{mn}\) to \(\mathbb B^{mn}_{ij}\), \(\mathbb B_{ij}\), and \(\mathbb B^{mn}\), \(i,j\in \mathcal {S},\,m,n\in \{+,-,0\}\), are constructed from the block-matrices \({ B}^{k\ell }_{ij}\), \(i,j\in \mathcal {S}\), \(k,\ell \in \{\nabla ,1,\dots ,K,\Delta \}\), as
4 Application to an SFFM
Given our approximation \(B\) to the generator \(\mathbb B\) we now follow the recipe from (Bean and O’Reilly 2014), replacing the actual generator \(\mathbb B\) with its approximation \({ B}\), to construct approximations, \(\varvec{\pi }\) and \(\varvec{p}\), to the stationary operators,
 and \(\mathbb p\).
and \(\mathbb p\).
It may be convenient to think of our approximations in terms of approximations of kernels. Recall that the operators in (Bean and O’Reilly 2014) can be thought of in terms of kernels. That is, for some function \(\varvec{g} = (g_i(x))_{i\in \mathcal {S}}\), we can write
where \(\mathbb B_{ij}^{k\ell }(x,\, \mathrm {d}y)\) is the kernel of the operator \(\mathbb B_{ij}^{k\ell }\).
Let \(\varvec{a}^\nabla (t):=\varvec{q}_\nabla (t)\) and \(\varvec{a}^\Delta (t):=\varvec{q}_\Delta (t)\), and define basis functions \(\varvec{\phi }^\nabla (x) = \phi ^\nabla _1(x) = \delta (x)\) and \(\varvec{\phi }^\Delta (x) = \phi ^\Delta _1(x) = \delta (x-\mathcal I)\), where \(\delta\) is the Dirac delta function, \(N_\nabla = N_\Delta = 1\), and \(\mathcal N_\nabla = \mathcal N_\Delta = \{1\}\). Also define \(\widehat{M}_\nabla =I_{|\mathcal {S}_\nabla |}\) and \(\widehat{M}_\Delta =I_{|\mathcal {S}_\Delta |}\) and row-vectors
To pose the approximation \(\mathbb B\) in kernel form let \(\varvec{a}_i \varvec{\phi }(x)^{\text{ T }}{}\in W,\,i\in \mathcal {S}\) be the initial density of the process, and \(\varvec{\phi }(x)\varvec{b}_i^{\text{ T }}{}\in W,\,i\in \mathcal {S}\) be a test function. Observe that, from our DG construction earlier and the definition of \(\widehat{M}\),
Thus, we can think of
as an approximation to the kernel \(\mathbb B_{ij}(x,\, \mathrm {d}y)\). This concept can be extended to all the approximations of operators considered in this work.
4.1 Approximating the Operator \(\mathbb R\)
Recall the operator \(\mathbb R^k\) from Lemma 2.1. Essentially, the operator \(\mathbb R^k\) takes an initial measure \(\varvec{\mu }^k\) and multiplies each element by \(1/|r_i(x)|\) on cells \(\mathcal {D}_k\) where \(r_i(x)\ne 0\). In the context of DG the initial distribution is given by \(\varvec{a}_i \varvec{\phi }(x)^{\text{ T }}{}\in W,\,i\in \mathcal {S}\). Thus, for \(k\in \{\nabla ,1,...,K,\Delta \}\) such that \(r_i(x)\ne 0\) on \(\mathcal {D}_k\), we have
Decompose the right-hand side into a component which lies in \(W\) and another orthogonal to W:
where \(\varvec{\rho }^k_i \varvec{\phi }^k(x)^{\text{ T }}{}\in W\), \(g_i^\perp \in W^\perp\). Now, multiply by test functions \(\{\phi _r^k(x)\}_{r=1}^{N_k}\) and integrate over \([0,\mathcal I]\):
since \(g_i(x)^\perp \in W^\perp\). Define the matrix \(M_k^r := \displaystyle \int _{x\in [0,\mathcal I \kern 0.1500em ]} \frac{ \varvec{\phi }^k(x)^{\text{ T }}{}\varvec{\phi }^k(x)}{|r_i(x)|}\, \mathrm {d}x\), then \(\varvec{a}_i^kM_k^r = \varvec{\rho }^k_i M_k,\) which implies \(\varvec{\rho }^k_i = \varvec{a}_i^kM_k^rM_k^{-1}.\) Thus, we have the approximation
Since \(\varvec{a}_i^k\) is arbitrary, we see that we approximate \(\mathbb R_i^k\) by \(R_i^k = M_k^rM_k^{-1},\) and \(\mathbb R^k\) by \(R^k = \mathrm {diag}( R_i^k)_{i\in \mathcal {S}^\bullet _k}\).
In practice, we implement a Gauss-Lobatto quadrature approximation to compute the elements of \(M_k^r\).
4.2 Approximating the Operator \(D\) and the DG Riccati Equation
Recalling Lemma 2.1 and replacing the operators \(\mathbb R^k\) and \(\mathbb B^{\ell m}\), by their approximations we have the following approximation to \(\mathbb D^{mn}(s)\)
Let \(\varvec{\phi }^k(x){M}_k^{-1}\Psi _{ij}^{k\ell }(s)\varvec{\phi }^\ell (y)^{\text{ T }}{}\, \mathrm {d}y\), \(i,j\in \mathcal {S},\) \(k\in \mathcal K_i^+\,, \ell \in \mathcal K_j^-\) be a finite-dimensional approximation of the operator kernel
 \(_{ij}^{k\ell }(s)(x,\, \mathrm {d}y)\), where \(\Psi _{ij}^{k\ell }(s)\) is a matrix of constants for a given \(s\). Construct an approximation to
\(_{ij}^{k\ell }(s)(x,\, \mathrm {d}y)\), where \(\Psi _{ij}^{k\ell }(s)\) is a matrix of constants for a given \(s\). Construct an approximation to
 \((s)(x,\, \mathrm {d}y)\) by
\((s)(x,\, \mathrm {d}y)\) by
where \(\varvec{\phi }^+(x) = (\varvec{\phi }^k(x))_{i\in \mathcal {S}_k^+,k\in \mathcal K^+}\) and \(\varvec{\phi }^-(y) = (\varvec{\phi }^k(y))_{i\in \mathcal {S}_k^-,k\in \mathcal K^-}\) are row-vectors, \(\Psi (s)\) is a matrix of constants for a given \(s\) with the same size as \(D^{+-}\), and \(\widehat{M}_m,\) \(m\in \{+,-,0\}\) is a block diagonal matrix \(\widehat{M}_m = \mathrm {diag}\left( \left( M_k\right) _{i\in \mathcal {S}_k^m}\right) _{k\in \mathcal K^m}\), \(m\in \{+,-,0\}\). Now replace the theoretical kernels in Theorem 2.1 by their DG approximations to get
Multiplying on the left by \(\varvec{\phi }^+(x)^{\text{ T }}{}\) and on the right by \(\varvec{\phi }^-(y)\), integrating over both \(x\) and \(y\), then post-multiplying by \(\widehat{M}^{-1}_-\) gives the following matrix Riccati equation
Thus, we may find \(\Psi (s)\) by solving Eq. (24), using one of the methods in (Bean et al. 2009). Here, we use the Newtons method.
Given the stochastic interpretation of
 \((0)\) we know that
\((0)\) we know that

 \((0)([0,\infty ))=1\) for every vector of measures
\((0)([0,\infty ))=1\) for every vector of measures
 such that
such that
 \(([0,\infty )\varvec{1} = 1\), when an SFFM is recurrent. It appears that this result carries over to the matrix \(\Psi (0)\) giving the property that \(\displaystyle \int _{y\in [0,\mathcal I \kern 0.1500em ]} \Psi (0)\varvec{\phi }^-(y)^{\text{ T }}{}\, \mathrm {d}y = \varvec{1}\). However, we have only observed this numerically and have no proof of this property.
\(([0,\infty )\varvec{1} = 1\), when an SFFM is recurrent. It appears that this result carries over to the matrix \(\Psi (0)\) giving the property that \(\displaystyle \int _{y\in [0,\mathcal I \kern 0.1500em ]} \Psi (0)\varvec{\phi }^-(y)^{\text{ T }}{}\, \mathrm {d}y = \varvec{1}\). However, we have only observed this numerically and have no proof of this property.
4.3 Putting It All Together: Constructing an Approximation to the Stationary Distribution
We find an approximation to the stationary distribution by replacing the theoretical operators in Theorem 2.2 with their approximations. Table 1 defines the notation we use for the DG approximations to stationary operators.
With the notation in Table 1 define row-vectors
Proceeding similarly to the derivation of the Riccati Eq. (24), we can argue that the coefficients \({\varvec{\xi }}\) are the solution to the matrix system
Essentially, we replace the theoretical operators in Eqs. (9) and (10) with their DG counterparts.
Similarly, the coefficients \({\varvec{p}}\) are given by
where \(z\) is a normalising constant. The coefficients \(\varvec{\pi }(y)\) are given by
where \({K} := {D}^{++}(0) + \Psi (0) {D}^{(-+)}(0)\), and z is a normalising constant.
To assist the reader in understanding these constructions and the notation we provide an explicitly worked toy-example in Appendix 2.
5 Numerical Experiments
To illustrate the validity of our discontinuous Galerkin approximation, we perform numerical experiments on a stochastic fluid-fluid model, in a three-pronged approach.
First, we run Monte Carlo simulations, in order to compare the simulated joint density of \(\{(X_t, \varphi _t)\}\) evaluated at the time \(\{Y_t\}\) first returns to the initial level 0 against that which is obtained via the return-probability matrix \(\Psi (0)\). This numerically verifies the accuracy of our proposed approximation for the operator matrix \(\Psi (0)\). Second, we evaluate approximations to the limiting marginal joint density of \(\{(X_t, \varphi _t)\}\) by first approximating the limiting distribution of \(\{(\overline{X}_t,Y_t,\varphi _t)\}_{t\ge 0}\) and then integrating over \(Y_t\). We compare this against the analytical density. Third, we vary the parameters of the second fluid \(\{Y_t\}\) to confirm that the approximating joint density for \(\{(\overline{X}_t, \varphi _t)\}\) does not change, while the marginal limiting distribution for \(\{Y_t\}\) does, both of which are consistent with our intuitive understanding of the chosen example. In all three procedures, we find the approximations to be accurate.
We also analyse different choices for the level of spatial discretisation and the degree of polynomial basis functions, with respect to the order of convergence in relevant error terms.
5.1 An On-Off Bandwidth-Sharing Model
The following example is a modification of the example presented in (Latouche et al. 2013) where it was first analysed. The modification of the example is necessary since, in (Latouche et al. 2013), the model is level dependent; in particular, the rate of change for the process \(\{X_t\}\) at time \(t\) depends on whether \(X_t\) is above, or below, some threshold, \(x^*\).
The modified example we consider here is as follows. Consider a stochastic fluid-fluid \(\{(X_t,Y_t,\varphi _t),t\ge 0\},\) where \(\{X_t\}\) and \(\{Y_t\}\) represent the workloads in Buffers 1 and 2 at time \(t \ge 0\), respectively, both driven by the phase \(\{\varphi _t\},\) which is a Markov chain on the state space \(\mathcal {S} = \{11,10,01,00\}\). Both \(\{X_t\}\) and \(\{Y_t\}\) have a regulated boundary at 0. Here, the state 11 indicates inputs to both buffers being on, the state 00 indicates both being off, the state 10 is when only the first input is on, and the state 01 is when only the second is on. The input of Buffer k is switched from on to off with rate \(\gamma _k\), and from off to on with rate \(\beta _k\), for \(k = 1, 2\). Thus, the infinitesimal generator T for \(\varphi _t\) is given by
The net rates of change for \(X_t\), denoted \(c_i\), are given by
and the net rates of change for \(Y_t\), denoted \(r_i\), are as follows
For our numerical experiments, we use the parameter choices given in (Latouche et al. 2013):
While the true problem has an unbounded domain \([0,\infty )\), the discontinuous Garlekin method requires the domain of approximation to be a finite interval. Here we choose an upper bound of \(\mathcal I=48\) and approximate the process on \([0,\mathcal I \kern 0.1500em]\) with regulated boundaries at \(0\) and \(\mathcal I\). The effect of this truncation can be partly quantified by evaluating \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ X_t > \mathcal I, \varphi _t = i\right]\), \(i\in \mathcal {S}\). We observe that our approximations have an error of at least this amount.
5.2 Numerical Rxperiment for \(\Psi\)
Here we construct an approximation to \(\Psi\) using our DG methodology and compare the results to estimates obtained from Monte Carlo simulation which we treat as the ground truth. We choose the initial distribution of \(\{(X_t,Y_t,\varphi _t)\}\) to be a point mass at \((X_0=5,\, Y_0=0,\, \varphi _0=01)\) and zero elsewhere. Given the initial distribution and the model parameters defined above, we simulate \(10^6\) sample paths until the first return time \(\theta (0)\) and record \((X_{\theta (0)},\varphi _{\theta (0)})\). We then use the samples to estimate the probabilities \(\mathbb {P}\left[ X_{\theta (0)} \le x_k, \varphi _{\theta (0)}=i\right]\), \(x_k=0,0.4,0.8,...,48,\,i\in \mathcal S\) by finding the proportion of samples that lie in these sets. To account for Monte Carlo error we use the bootstrap (\(10^4\) times) to estimate the 95% confidence interval for these estimates. In Fig. 1 the lower and upper red horizontal bars at each point represent these confidence intervals.
We then use the DG methodology with a constant cell width of \(h_k = 0.4,\, k=1,...,120,\) and \(N_k=1\) or \(N_k=2\) basis functions on each cell to estimate the same probabilities. Results are plotted in Fig. 1.
Approximations to the cumulative probabilities \(\mathbb {P}\left[ X_{\theta (0)} \le x_k, \varphi _{\theta (0)}=i\right]\), \(i\in \{00,10\}\) and \(x_k=0,0.4,0.8,...,2,\) obtained by Monte Carlo (red bars), DG with one basis function on each cell (black crosses) and DG with two basis functions on each cell (blue stars). For the Monte Carlo estimate we plot the 95% confidence interval. The cumulative probabilities, \(\mathbb {P}\left[ X_{\theta (0)} \le x_k, \varphi _{\theta (0)}=i\right]\) are constant for \(i\in \{00,10\}\) and \(x_k>1.6\), and are zero for \(\varphi \in \{11,01\}\), as it is impossible for \(\theta (0)\) to occur whilst the process is in these phases; hence, we do not show them here
As shown in Fig. 1, the piecewise-constant DG approximation with one basis function on each cell provides a reasonable approximation, while the piecewise-linear DG approximation with two basis functions on each cell gives an approximation which is almost indistinguishable from the Monte Carlo estimate.
5.3 The Marginal Stationary Distribution of \(X\)
Since Buffer 1, \(\{X_t\}\), is conditionally independent of Buffer 2, \(\{Y_t\}\), given \(\{\varphi _t\}\), we can use results from the existing literature on stochastic fluid flows (da Silva Soares 2005) to obtain the marginal limiting density \(\varvec{\chi }(x) = (\chi _i(x))_{i \in \mathcal {S}}\) of \(\{X_t\}\):
On the other hand, using the methodology of Sect. 3, we can approximate the joint stationary operators
for \(i\in \{11,10,01,00\}\). Then, we marginalise over \(y\) to approximate the marginal stationary distribution \(\varvec{\chi }(x)\)
Let two vectors \({\varvec{\chi }^1}\) and \({\varvec{\chi }^2}\) denote respectively the piecewise-constant and piecewise-linear DG approximations of \(\varvec{\chi }\). We use a mesh with a constant cell width \(h_k=0.4\) for the DG approximation. Figure 2 presents the analytical densities \({\chi }_{i}(x),\,i\in \{11,10,01,00\}\), the piecewise-constant DG approximation, and the piecewise-linear DG approximation.
A plot of the analytic density functions, \(\chi _i(x)\), and the approximations to the density functions \(\chi ^1_i(x),\,\chi ^2_i(x)\), for \(i\in \{11,10,01,00\}\) and \(x\in [0,5]\). The analytic density, \(\chi _i(x)\), is the solid red line with red crosses, \(\chi ^1_i(x)\) the solid green lines and \(\chi ^2_i(x)\) the solid blue line. The analytic density and DG approximation with linear basis functions are indistinguishable. The value of the point masses at \(X=0\) are represented by the height of the circles of the same colour as the corresponding density and have been jittered so that they do not lie on top of each other
The piecewise-linear approximation performs well and is almost indistinguishable from the analytic density, while the piecewise-constant approximation does not perform as well. The piecewise-constant approximation underestimates the point masses and the density at lower values of \(x\), and redistributes this mass in the tails.
5.4 Sensitivity to the Dynamics of \(\{Y_t\}\)
To further confirm that the discontinuous Galerkin approximation \(\Psi (0)\) of the operator
 (0) accurately captures the dynamics of \(\{Y_t\}\), we vary the rate at which the input to this buffer switches off (denoted by \(\gamma _2\)). As we modify this rate, we expect to see a change in the distribution of probability between
(0) accurately captures the dynamics of \(\{Y_t\}\), we vary the rate at which the input to this buffer switches off (denoted by \(\gamma _2\)). As we modify this rate, we expect to see a change in the distribution of probability between
The net input rates for \(\{X_t\}\), \(c_{11}=c_{10}\) and \(c_{01}=c_{00}\), and the proportion of time that the phase process spends in the sets \(\phi _t \in \{11 , 10\}\) and \(\phi _t \in \{01, 00\}\) remains unchanged as \(\gamma _2\) changes. Also, as \(\gamma _2\) increases, the phase process spends proportionally more time in states \(\{10, 00\}\) than in states \(\{11, 01\}\), and thus more time in phases with \(r_i(x)\le 0\). Hence, as \(\gamma _2\) increases, we expect that \(Y_t\) will spend more time at \(Y_t=0\), on average, yet the sum of the densities \(\chi _{11}(x)+\chi _{10}(x)\) and \(\chi _{01}(x)+\chi _{00}(x)\) should remain unchanged.
Regarding our approximations, we keep the mesh (\(h_k=0.4\)) and basis functions (\(N_k=2\)) fixed, and vary \(\gamma _2\) and record the probabilities \(p^0\) and \(p^+\), shown in Table 2. We also plot the densities \(\chi ^2_{11}(x)+\chi ^2_{10}(x)\) and \(\chi ^2_{01}(x)+\chi ^2_{00}(x)\) in Fig. 3. As \(\gamma _2\) increases, the amount of probability in \(p^0\) increases, while the densities \(\chi ^2_{11}(x)+\chi ^2_{10}(x)\) and \(\chi ^2_{01}(x)+\chi ^2_{00}(x)\) remain unchanged, as expected.
Approximations to the density functions \(\chi _{11}(x)+\chi _{10}(x)\) (left) and \(\chi _{01}+\chi _{00}\) (right) on \(x\in [0,8]\) for \(\gamma _2=11\) (green with diamonds), \(\gamma _2=16\) (blue with crosses) and \(\gamma _2=22\) (red with plusses). The coloured circles at \(x=0\) on the right-hand plot represent the point masses and are coloured according to \(\gamma _2=11\) (green), \(\gamma _2=16\) (blue) and \(\gamma _2=22\) (red)
5.5 Numerical Errors
It has been shown that operators such as \(\mathbb {B}\) (defined in Sect. 2.1) under a DG approximation can have an error which converges at the order of \(\mathcal {O}(h_k^{N+2}),\) where \(h_k\) is the discretisation and \(N=N_k\) is the number of basis function on each cell (Hesthaven and Warburton 2007). However, this result cannot be easily translated across to the operator \(\Psi .\) The DG approximation \(\Psi\) is constructed by taking the DG approximation, \(B\), of the operators \(\mathbb {B}\), constructing an approximation, \(D\), to \(\mathbb D\) and then solving the Riccati Eq. (24) with \(D\). We then use the approximation, \(\Psi\), of
 to derive an approximation for the limiting density \(\varvec{\pi }\). With such a construction, it is not known how the error propagates through the process of solving the Riccati equation, and then through further calculations to determine \(\varvec{\pi }\). Determining bounds for the approximation errors of \(\Psi\) and \(\varvec{\pi }\), as functions of the discretisation and basis selection, is a topic for future research.
to derive an approximation for the limiting density \(\varvec{\pi }\). With such a construction, it is not known how the error propagates through the process of solving the Riccati equation, and then through further calculations to determine \(\varvec{\pi }\). Determining bounds for the approximation errors of \(\Psi\) and \(\varvec{\pi }\), as functions of the discretisation and basis selection, is a topic for future research.
As a preliminary step in this direction, we empirically investigate how the approximation error of the marginal limiting density of the fluid \(\{X_t\}\) (see Sect. 5.3) changes with respect to the choice of basis functions and the level of discretisation. Let \([0,\mathcal {I}]\) be the interval on which we approximate the solution, then both the approximations and the analytical solution belong to the space \(\mathcal {S} \times \mathcal {C}^{-1}([0,\mathcal {I}])\), where \(\mathcal {C}^{-1}([0,\mathcal {I}])\) is the set of functions with countably many discontinuities. We compute the error of the approximation as
where \(u_i^k(x)\), \(q_{\nabla ,i}\) and \(q_{\Delta ,i}\), represent the DG approximation to the marginal stationary density of \(\{(X_t,\varphi _t)\}\), and the marginal stationary point masses at \(0\) and \(\mathcal I\), respectively.
A log-log plot of the errors of the approximations versus cell width, \(h=h_k\), are shown in Fig. 4 for piecewise-constant (\(N_k=1\)), piecewise-linear (\(N_k=2\)), piecewise-quadratic (\(N_k=3\)) and piecewise-cubic (\(N_k=4\)) polynomial bases. As log-mesh size decreases the log-error of the approximation decreases linearly. For \(N_k=3\) and \(h=0.2\) and for \(N_k=4\) and \(h=0.8\), a significant amount of the errors of the approximations are from other sources of error such as truncation. Recall that we truncated the problem to the interval \([0,\mathcal I]\) with \(\mathcal I=48\), from which we compute \(\lim \limits _{t\rightarrow \infty } \mathbb {P}\left[ X_t>48\right] \approx 5.83\times 10^{-9}\) as the error due to truncation. Ignoring the approximations where the truncation error is significant, we use least-squares to estimate the slopes of the lines for \(N_k=1\), \(N_k=2\) and \(N_k=3\) to be \(0.871,\, 2.90,\) and \(4.82\), respectively.
In Fig. 5 we plot log-error against \(N_k\), the number of basis functions in each cell. This shows that log-error decreases linearly as the number of basis functions on each cell, \(N_k\), increases. Using least-squares we estimate the slopes of the lines for \(h = 1.6,\,0.8,\,0.4,\,0.2,\,0.1\), and \(0.05\) to be \(-5.46,\, -6.07,\, -7.97,\,-8.38,\, -10.5\) and \(-11.9\), respectively.
To help understand the trade-offs between error, computation time, memory and the overall size of the computational problem, we report, in Table 3, computation statistics for the data in Figs. 4-5. The size of the approximation scheme is quantified by the total number of basis functions required, denoted \(n_\phi\). Computation time and memory requirements are approximately the same for a given problem size, \(n_\phi\); however, the error of the approximation is greatly reduced if a larger number of basis functions is used as opposed to a smaller cell width. For example, using a piecewise-constant approximation, \(N_k=1\), with cell width \(h=0.4\), then \(n_\phi =480\) basis functions are required and the error of this approximation is \(\approx 0.205\). Compare this to the piecewise-cubic approximation, \(N_k=4\), with a cell width of \(h=1.6\) which also requires \(n_\phi =480\) basis function, but achieves an error of \(\approx 4.44\times 10^{-8}\) – an improvement of over 7 orders of magnitude for approximately the same computation effort as measured by run-time or memory.
A log-log plot of errors of approximation for the marginal stationary distribution of \(\{X_i,\varphi _t\}\) for different mesh sizes, \(h\), and number of basis functions, \(N_k\). The error due to truncation at \(\mathcal I=48\) is \(\approx 5.83\times 10^{-9}\) contributes the majority of the error in the approximations with \(N_k=3\) bases and a cell width of \(h=0.2\) and \(N_k=4\) bases and a cell width of \(h=0.8\)
Log-errors of approximation for the marginal stationary distribution of \(\{X_i,\varphi _t\}\) for different mesh sizes, \(h\), and number of basis functions, \(N_k\). The error due to truncation at \(\mathcal I=48\) is \(\approx 5.83\times 10^{-9}\) and contributes the majority of the error in the approximations with \(N_k=3\) bases and a cell width of \(h=0.2\) and \(N_k=4\) bases and a cell width of \(h=0.8\)
The approximation scheme of Bean and O’Reilly (2013) is equivalent to the DG scheme introduce here when \(N_k=1\). The width of the cell, \(h\), corresponds to the parameter ‘\(\Delta x\)’ in Bean and O’Reilly (2013). Further, the finite-volume method with an upwind flux also results in an equivalent approximation. Thus, examining the first column of Table 3 we can observe the numerical performance of these related methods. Comparing the first column of Table 3 to the first row of Table 3 suggests that the DG scheme can converge much faster than these other schemes.
Unfortunately, larger scale analysis of the errors of approximation for \(\Psi\) is computationally prohibitive since the ground truth must be evaluated via Monte Carlo simulation.
6 Conclusions
We proposed the application of the discontinuous Galerkin method to approximate operators associated with stochastic fluid-queues and stochastic fluid-fluid models. Analysis of SFFMs using these operators requires us to partition the operators into regions corresponding to when the second fluid level is increasing, decreasing or constant. The DG method is a natural candidate to approximate these operators due to the cell-based discretisation. By correctly utilising the discretisation of the state space, we used the DG method to approximate the infinitesimal generator of a stochastic fluid model \(\{(X_t,\varphi _t)\}\), ensuring that the necessary partition can be recovered. Furthermore, DG methods are also appealing as they can maintain mass conservation, and high-order schemes can be constructed while maintaining the necessary spatial-discretisation.
Here, we have detailed how one constructs approximations to various operators which arise in the analysis of stochastic fluid-fluid models. We demonstrated this with an application to approximate all the operators needed to construct the joint stationary distribution of a stochastic fluid-fluid models. The DG method also enabled us to obtain other performance measures of stochastic fluid-fluid models that are also analytically presented by operators, such as \(\Psi\).
The numerical results showed that DG approximations of the operator \(\Psi\), as well as the stationary distribution of a SFFM, are accurate and effective. We also verified that the operators and their dynamics were captured accurately. Furthermore, in our example, we observed that adding more regularity in the basis functions was more effective in reducing the error of the approximation than decreasing cell width, for approximately the same computational effort. The numerical illustration also demonstrates that the DG scheme can converge rapidly compared to other methods.
Future work includes determining theoretical error bounds for approximations of the operator \(\Psi\), as well as of the stationary distribution. Another interesting topic for future research is to determine conditions under which the approximation to the stationary distribution is a positive function. It may also be possible to extend the methods presented here to processes with a level-dependent first fluid, such as that in (Latouche et al. 2013).
Code Availability
Code available here: https://github.com/angus-lewis/SFFM.
References
Bean NG, Nielsen BF (2010) Quasi-birth-and-death processes with rational arrival process components. Stoch Models 26(3):309–334
Bean NG, O’Reilly MM, Taylor PG (2009) Algorithms for the Laplace-Stieltjes transforms of first return times for stochastic fluid flows. Method Comput Appl Prob 10:381–408
Bean NG, O’Reilly MM (2013) A stochastic two-dimensional fluid model. Stoch Models 29(1):31–63
Bean NG, O’Reilly MM (2013) Spatially-coherent uniformization of a stochastic fluid model to a quasi-birth-and-death process. Performance Evaluation 70(9):578–592
Bean NG, O’Reilly MM (2014) The stochastic fluid-fluid model: A stochastic fluid model driven by an uncountable-state process, which is a stochastic fluid itself. Stoch Proc Appl 124:1741–1772
Cockburn B (1999) Discontinous Garlekin methods for convection-dominated problems. In: Barth T, Deconink H (eds) Higher-Order Methods for Computational Physics, vol 9. Lecture Notes in Computational Science and Engineering. Springer Verlag, Berlin, pp 69–224
da Silva Soares A (2005) Fluid queues: building upon the analogy with QBD processes. PhD thesis, Université Libre de Bruxelles
Hesthaven JS, Warburton T (2007) Nodal discontinuous Galerkin methods: algorithms, analysis, and applications. Springer Science & Business Media
Karandikar RL, Kulkarni VG (1995) Second-order fluid flow models: Reflected Brownian motion in a random environment. Oper Res 43(1):77–88
Latouche G, Nguyen GT, Palmowski Z (2013) Two-dimensional fluid queues with temporary assistance. In: Latouche G, Ramaswami V, Sethuraman J, Sigman K, Squillante M, Yao D (eds) Matrix-Analytic Methods in Stochastic Models, Springer Proceedings in Mathematics & Statistics, vol 27, Springer Science, New York, NY, chap 9, pp 187–207
Latouche G, Ramaswami V (1999) Introduction to matrix analytic methods in stochastic modeling. ASA-SIAM Series on Statistics and Applied Probability, SIAM, Philadelphia PA
Miyazawa M, Zwart B (2012) Wiener-Hopf factorizations for a multidimensional Markov additive process and their applications to reflected processes. Stoch Syst 2:67–114
Neuts M (1981) Introduction to Matrix Analytic Methods in Stochastic Modeling. The John Hopkins University Press, Baltimore, MD
O’Reilly MM, Scheinhardt W (2017) Stationary distributions for a class of Markov-modulated tandem fluid queues. Stoch Models 33(4):524–550
Acknowledgements
The authors acknowledge the financial support of the Australian Research Council (ARC) through the Discovery Grants DP110101663 and DP180103106. Authors 1-4 also acknowledge the support of the ARC Centre of Excellence for Mathematical and Statistical Frontiers (ACEMS)
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions. Australian Research Council (ARC) Discovery Grants DP110101663 and DP180103106.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethics Approval
Not applicable.
Consent to Participate
Not applicable.
Consent for Publication
All authors consent to the submission of this article to this journal.
Conflicts of Interest
None.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Properties of \(B\)
Recall that the coefficients \({\varvec{a}}_i^k(t)\) can be used to construct an approximate solution to a differential equation at time \(t\) as \(u_i^k(x,t)={\varvec{a}}_i^k(t)\varvec{\phi }^k(x)^{\text{ T }}{}.\) For \(i\in \mathcal {S},\,k\in \{\nabla ,1,...,K,\Delta \},\,r\in \mathcal N_k\), define \(\alpha _{i,r}^k(t) := a_{i,r}^k(t)\displaystyle \int _{x\in \mathcal {D}_k}\phi _r^k(x)\, \mathrm {d}x,\) and row-vectors \(\varvec{\alpha }_i^k(t)=(\alpha _{i,r}^k(t))_{r\in \mathcal N_k}\). Motivated by the fact that we may be interested in approximations of the probabilities \(\mathbb {P}(X(t)\in \mathcal {D}_k,\varphi (t)=i)\) rather than the function \(u_i^k\) itself, we can pose the problem equivalently in terms of the integrals
Define
and matrices
By choosing the basis \(\{\phi _{r}^k\}_{r\in \mathcal N_k,k\in \{1,...,K\}}\) such that \(\int _{x\in \mathcal {D}_k}\phi _r^k(x)\, \mathrm {d}x\ne 0\) for all \(r,k\), then \(P\) is invertible. This is the case for the Lagrange polynomials, but not, for example, for the Legendre polynomials. We can (loosely) interpret the new coefficients \(\alpha _{i,r}^k(t)\) as representing the amount of probability captured by the basis function \(\phi _r^k(x)\) in phase \(i\).
The differential Eq. (23) can be equivalently expressed as \(\frac{\, \mathrm {d}}{\, \mathrm {d}t} \varvec{\alpha }(t) = \varvec{\alpha }(t) { \mathfrak B},\) where
Let
Then
Remark 7.1
One may recognise the structure of \({ {\mathfrak B}}\) as the structure of a quasi-birth-and-death process (QBD), with levels \(k=1,...,K\). This raises the question of whether \({ {\mathfrak B}}\) is indeed a representation of the generator matrix of a QBD, or QBD-like process. In the case of a constant basis function on each cell, i.e. \(N_k=1\) and \(\phi _1^k(x)\propto 1\), \(k=1,...,K\), then \({ {\mathfrak B}}\) is the generator of a QBD: it has zero row-sums, negative diagonal entries, and non-negative off-diagonal entries, the QBD-phase variable is \(\{\varphi _t\}\) and the level is \(k=\nabla ,1,...,K,\Delta\). In fact, if \(h_k\) is the same for every \(k=1,...,K\), then this is the same QBD discretisation of a stochastic fluid process analysed by Bean and O’Reilly (2013). However, for higher-degree polynomials \(\mathfrak B\) is not necessarily the generator of a QBD process. We conjecture that, using polynomial basis functions, then \(N_k=1\) and \(\phi _1^k(x)\propto 1\), \(k=1,...,K\) is the only DG approximation which has an interpretation as a QBD-like process – not even as a QBD-RAP (Bean and Nielsen 2010).
In the following lemma, we use the following properties of the Lagrange interpolating polynomials defined by the Gauss-Lobatto quadrature nodes. Property 1 \(\displaystyle \sum _{s=1}^{N_k} \phi _s^k(x) = {\left\{ \begin{array}{ll} 1&{}x\in \mathcal {D}_k,\\ 0 &{} x\notin \mathcal {D}_k.\end{array}\right. }\)
For \(k\in \{1,...,K\}\), let \(\varvec{e}_n^k\) be a row-vector of length \(N_k\) with a 1 in the \(n\)th position and zeros elsewhere. Property 2 At the cell edges, \(\varvec{\phi }^k(x_k) = \varvec{e}_1^k\) and \(\varvec{\phi }^k(x_{k+1})=\varvec{e}_{N_k}^k\), \(k=1,...,K\).
Lemma 7.1
If \(\{\phi _r^k(x)\}_{r\in \mathcal N_k}\), are chosen as the Lagrange interpolating polynomials on \(\mathcal D_k\), \(k\in \{1,\dots ,K\}\), then the matrix \({ {\mathfrak B}}\) has zero row-sums.
Proof
Let \(\varvec{1}\) and \(\varvec{0}\) be column vectors of ones and zeros, respectively, with an appropriate length depending on the context. Using Property 1, observe that
hence \(M_k^{-1}P_k\varvec{1}=\varvec{1}\). Also
where we have again used Property 1.
Consider first \(c_i>0\). Let \(\varvec{b}\) and \(\varvec{d}\) be arbitrary row-vectors of length \(N_k\) and \(N_{k+1}\), respectively. By Property 2, for \(k=1,...,K-1,\)
Therefore, for \(c_i>0\), we claim
The first sum is zero since \(T\) is a generator of a continuous-time Markov chain. This leaves the other two terms, which, using our previous observations, we get
Similarly, for \(c_i<0\), and row-vectors \(\varvec{b}\) and \(\varvec{d}\) of length \(N_k\) and \(N_{k-1}\), respectively,
Therefore, for \(c_i<0\) and \(k=2,...,K\), using the same arguments as before we have
For the lower boundary,
Also, for \(c_i<0\),
For the upper boundary,
Also, for \(c_i>0\),
Combining all of the above we have shown that the row sums of \({ {\mathfrak B}}\) are zero.
Corollary 7.1
The DG approximation to the generator \(B\) conserves probability. That is, for all \(t\ge 0\),
Proof
Let \(\{\psi _r^k(x)\}_{r\in \mathcal N_k,k\in \{1,...,K\}},\) be a basis for \(span(\phi _r^k(x),r\in \mathcal N_k,k\in \{1,...,K\})\), where \(\{\phi _r^k(x)\}_{r\in \mathcal N_k,k\in \{1,...,K\}}\) are the Lagrange polynomials. Also define \(\psi _1^\nabla (x)=\delta (x)\) and \(\psi _1^\Delta (x)=\delta (x-\mathcal I)\) to capture the point masses at the boundaries. Let us use the same vector notation for the basis \(\psi _r^k(x)\) as we do for \(\phi _r^k(x)\). For \(k\in \{1,...,K\}\), since \(\{\psi _r^k(x)\}_{r\in \mathcal N_k}\) and \(\{\phi _r^k(x)\}_{r\in \mathcal N_k}\) have the same span, then there is a matrix \(V^k\) such that \(\varvec{\psi }^k(x)^{\text{ T }}{} = V^k\varvec{\phi }^k(x)^{\text{ T }}{}\). Trivially, this also holds for \(k=\nabla ,\Delta\).
Let
For a DG approximation, \(B\), constructed from \(\{\psi _r^k\}_{r\in \mathcal N_k,k\in \{\nabla ,1,...,K,\Delta \}}\), it can be shown that \(B\) is similar to \({ {\mathfrak B}}\) with similarity matrix, \(VW\), such that \(B_{ij} = VW{ \mathfrak B}_{ij}W^{-1}V^{-1},\,i,j\in \mathcal {S}\). Therefore,
since \(\displaystyle \int _{x\in [0,\mathcal I \kern 0.1500em]} \varvec{\phi }(x)^{\text{ T }}{}\, \mathrm {d}x =W\varvec{1}\). The row sums of \(\mathfrak B\) are 0, hence
Let \({}^\psi \varvec{a}_i(t)\), \(i\in \mathcal {S}\) denote the coefficients related to the DG approximation constructed with the basis \(\{\psi _r^k\}_{r\in \mathcal N_k,k\in \{\nabla ,1,...,K,\Delta \}}\) (to distinguish them from \(\varvec{a}\) and \(\varvec{\alpha }\) used above). The DE constructed by the DG method is
Integrating over \(x\in [0,\mathcal I \kern 0.1500em]\) and summing over \(j\in \mathcal {S}\) we get
Exchanging the order of operations gives
where the right-hand side is \(0\) due to Eq. (32). This holds for all \(t\ge 0\). The left-hand side of (35) is the rate of change (with respect to time) of the total mass of the system. Since this is \(0\) for all \(t\ge 0\), there is no change in the total mass of the system and thus probability is conserved.
A Toy Example
Here we include a small toy example to show how we construct a DG approximation and to help clarify the notation.
Consider a process \(\{(\overline{X}_t,Y_t,\varphi _t)\}_{t\ge 0}\) with two phases, \(\varphi _t\in \mathcal {S}=\{1,2\}\) and generator matrix \(T\). Let \(\mathcal I = 1.8\), and partition into two intervals \(\mathcal {D}_1=[0,1]\) and \(\mathcal {D}_2=[1,1.8]\), hence \(x_1=0,\,x_2=1,\,x_3=1.8\). We choose a basis of Lagrange polynomials of order 1 to define our approximation space. That is,
The mesh and basis functions are shown in Fig. 6.
We can verify that the matrices \(M\) and \(G\) are given by
The matrix \(P\) is given by
Let \(c_1=1\) and \(c_2=-2\). Then the flux matrices are given by
Suppose that \(r_1(x)>0\) on \(\mathcal {D}_1=\mathcal F_1^{\kern 0.1500em +}\) and \(r_1(x)<0\) on \(\mathcal {D}_2\cup \{1\}=\mathcal F_1^{\kern 0.1500em -}\), and further, that \(r_2(x)<0\) on \(\{0\}\cup \mathcal {D}_1=\mathcal F_2^{\kern 0.1500em -}\) and \(r_2(x)>0\) on \(\mathcal {D}_2=\mathcal F_2^{\kern 0.1500em +}\). Specifically, let
Then, constructing \({ B}\) we get

We also have sub-matrices

and \({ B}_{11}^{-+} = 0_{3\times 2},\, { B}_{12}^{++} = 0_{2\times 2},\, { B}_{12}^{--} = 0_{2\times 3},\, { B}_{21}^{++} = 0_{2\times 2},\, { B}_{21}^{--} = 0_{3\times 3},\, { B}_{22}^{-+} = 0_{3\times 2},\) where \(0_{n\times m}\) denotes a \(n\times m\) matrix of zeros. Furthermore,


Since \(r_1(x)\) and \(r_2(x)\) are constant on each cell then \(R^+\) and \(R^-\) take a particularly simple form. We have

The DG approximations \(D^{m n}(s),\, m,n\in \{+,-\}\) can now be constructed as
For a given value of \(s\), we construct and solve the matrix Riccati equation,
for the matrix \(\Psi (s)\) using, for example, Newtons method (Bean et al. 2009). To obtain the stationary distribution we require \(\Psi (0)\).
Now, to find \({\varvec{\xi }}\), we solve the linear system in Eqs. (9)-(10). The result is a vector which we denote,
where \({\xi }^\nabla _{2}\) is an approximation to \(\lim \limits _{n\rightarrow \infty }\mathbb {P}\left[ \overline{X}_{\theta _n} =0, \varphi _{\theta _n} = 2\right]\) and \({\xi }^\Delta _{1}\) is an approximation to the artificial point mass \(\lim \limits _{n\rightarrow \infty }\mathbb {P}\left[ \overline{X}_{\theta _n} =1.8, \varphi _{\theta _n} = 1\right]\). For \(x\in \mathcal {D}_1\) an approximation to the density of \(\lim \limits _{n\rightarrow \infty }\mathbb {P}\left[ \overline{X}_{\theta _n} \in \, \mathrm {d}x, \varphi _{\theta _n} = 2\right]\), is constructed as \({\xi }_{2,1}^1\phi _1^1(x) + {\xi }_{2,2}^1\phi _2^1(x)\). For \(x\in \mathcal {D}_2\) an approximation to the density of \(\lim \limits _{n\rightarrow \infty }\mathbb {P}\left[ \overline{X}_{\theta _n} \in \, \mathrm {d}x, \varphi _{\theta _n} = 1\right]\), is constructed as \({\xi }_{1,1}^2\phi _1^2(x) + {\xi }_{1,2}^2\phi _2^2(x).\)
Next, given a value of \(y\), we solve the system (25)-(29) to find \({\varvec{p}}= {\varvec{p}}^-\) and \({\varvec{\pi }}(y)\).
For the point masses we have
where \({p}_{2}^\nabla\) is an approximation to \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ \overline{X}_{t} =0, Y_t=0, \varphi _{t} = 2\right]\) and \({p}_{1}^\Delta\) is an approximation to the artificial point mass \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ \overline{X}_t =1.8, Y_t=0, \varphi _{t} = 1\right]\). For \(x\in \mathcal {D}_1\), an approximation to the density of \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ \overline{X}_t \in \, \mathrm {d}x, Y_t = 0, \varphi _{t} = 2\right]\), is constructed as \({p}_{2,1}^1\phi _1^1(x) + {p}_{2,2}^1\phi _2^1(x)\). For \(x\in \mathcal {D}_2\), an approximation to the density of \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ \overline{X}_t \in \, \mathrm {d}x, Y_t = 0, \varphi _{t} = 1\right]\), is constructed as \({p}_{1,1}^2\phi _1^2(x) + {p}_{1,2}^2\phi _2^2(x).\)
Similarly, for \({\varvec{\pi }}^-(y)\), we have
where \({\pi }_{2}^\nabla (y)\) is an approximation to \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ \overline{X}_t =0, Y_t\in \, \mathrm {d}y, \varphi _{t} = 2\right]\) and \({\pi }_{1}^\Delta (y)\) is an approximation to the artificial point mass \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ \overline{X}_t =1.8, Y_t\in \, \mathrm {d}y, \varphi _{t} = 1\right]\). For \(x\in \mathcal {D}_1\) an approximation to the density of \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ \overline{X}_t \in \, \mathrm {d}x, Y_t \in \, \mathrm {d}y, \varphi _{t} = 2\right]\), is constructed as \({\pi }_{2,1}^1(y)\phi _1^1(x) + {\pi }_{2,2}^1(y)\phi _2^1(x)\). For \(x\in \mathcal {D}_2\) an approximation to the density of \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ \overline{X}_t \in \, \mathrm {d}x, Y_t \in \, \mathrm {d}y, \varphi _{t} = 1\right]\), is constructed as \({\pi }_{1,1}^2(y)\phi _1^2(x) + {\pi }_{1,2}^2(y)\phi _2^2(x).\)
For \({\varvec{\pi }}^+(y)\), we have
For \(x\in \mathcal {D}_1\) an approximation to the joint density of \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ \overline{X}_t \in \, \mathrm {d}x, Y_t \in \, \mathrm {d}y, \varphi _{t} = 1\right]\) is constructed as \({\pi }_{1,1}^1(y)\phi _1^1(x) + {\pi }_{1,2}^1(y)\phi _2^1(x)\). For \(x\in \mathcal {D}_2\) an approximation to the density of \(\lim \limits _{t\rightarrow \infty }\mathbb {P}\left[ \overline{X}_t \in \, \mathrm {d}x, Y_t \in \, \mathrm {d}y, \varphi _{t} = 2\right]\) is constructed as \({\pi }_{2,1}^2(y)\phi _1^2(x) + {\pi }_{2,2}^2(y)\phi _2^2(x).\)
In summary, for \(i\in \mathcal {S}\), a global approximation of the joint stationary distribution is
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bean, N., Lewis, A., Nguyen, G.T. et al. A Discontinuous Galerkin Method for Approximating the Stationary Distribution of Stochastic Fluid-Fluid Processes. Methodol Comput Appl Probab 24, 2823–2864 (2022). https://doi.org/10.1007/s11009-022-09945-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11009-022-09945-2



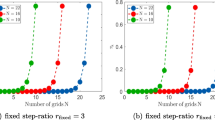

 (s) of Operators
(s) of Operators




