On Lattice Path Counting and the Random Product Representation, with Applications to the E_r/M/1 Queue and the M/E_r/1 Queue

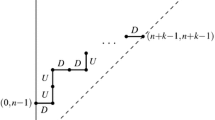
Abstract

We explain how lattice-path counting techniques can be used in conjunction with the random-product representations from Buckingham and Fralix (Markov Process Related Field 21:339–368 2015) to study both the stationary and time-dependent behavior of Markovian queueing systems, and continuous-time Markov chains in general. We illustrate how the approach works by applying it to both the E_r/M/1 queue, and the M/E_r/1 queue. Interestingly, through this approach we show that the stationary distributions, as well as the Laplace transforms of the transition functions associated with both the E_r/M/1 queue and the M/E_r/1 queue, can be expressed explicitly in terms of generalized binomial series from Chapter 5 of the text Concrete Mathematics of Graham, Knuth, and Patashnik.

Appendix

We close this paper by including a brief introduction to generalized binomial series. Many of the results contained in this Appendix can also be found in Graham et al. (1994), but some of our proofs are more probabilistic in nature.

For each integer r ≥ 1, the generalized binomial series $\mathcal {B}_{r}(z)$ is defined (as a formal power series) on page 200 of Graham et al. (1994) as follows:

$$\begin{array}{@{}rcl@{}} \mathcal{B}_{r}(z) = \sum\limits_{k = 0}^{\infty}\frac{1}{1 + rk}{1 + rk \choose k}z^{k}. \end{array} $$

Our usage of generalized binomial series does not allow us to treat them as formal power series, meaning we need to determine where these series converge absolutely. Using the ratio test, one can show that for each integer r ≥ 1, $\mathcal {B}_{r}(z)$ absolutely converges on the open disk U_r, defined as

$$\begin{array}{@{}rcl@{}} U_{r} := \left\{z \in \mathbb{C}: |z| < \frac{(r-1)^{r-1}}{r^{r}}. \right\} \end{array} $$

where we interpret 0⁰ as 1.

The following Lemma will be useful towards establishing the absolute convergence of various series that we encounter in the proofs of our main results.

Lemma A.1

Fix an integerr ≥ 1,and consider the functions$f_{r + 1},g_{r + 1}: [0, \infty ) \rightarrow \mathbb {R}$,defined forρ ≥ 0 as

$$\begin{array}{@{}rcl@{}} f_{r + 1}(\rho) := \frac{(r\rho)^{r}}{(1 + r\rho)^{r + 1}}, ~~~~~ g_{r + 1}(\rho) := \frac{r^{r}\rho}{(r + \rho)^{r + 1}}. \end{array} $$

Bothf_r+ 1andg_r+ 1are continuous on[0,∞), differentiable on(0,∞), and both functions have aunique global maximum atρ = 1:furthermore,

$$\begin{array}{@{}rcl@{}} f_{r + 1}(1) = g_{r + 1}(1) = \frac{r^{r}}{(r + 1)^{r + 1}}. \end{array} $$

Proof

It is easy to verify that both f_r+ 1 and g_r+ 1 are continuous on [0,∞) and differentiable on (0,∞), and that the functions satisfy f_r+ 1(1) = g_r+ 1(1) = r^r/(r + 1)^r+ 1. The key to showing that both f_r+ 1 and g_r+ 1 each have a unique global maximum at ρ = 1 is to show that $f_{r + 1}^{\prime }(\rho )$ and $g_{r + 1}^{\prime }(\rho )$ are both positive when ρ ∈ (0, 1), and both negative when ρ > 1. A quick calculation shows that for ρ > 0,

$$\begin{array}{@{}rcl@{}} f_{r + 1}^{\prime}(\rho) = \frac{r^{2}(r\rho)^{r-1}(1 - \rho)}{(1 + r\rho)^{r + 2}}, ~~~~~ g_{r + 1}^{\prime}(\rho) = \frac{r^{r + 1}(1 - \rho)}{(r + \rho)^{r + 2}} \end{array} $$

which proves the lemma. □

The next result establishes important generalized binomial series identities found on page 200 and 201 of Graham et al. (1994). Not only do we state these identities in the interest of making our paper self-contained, we also give a probabilistic proof that differs from the proofs given in Graham et al. (1994).

Theorem A.1

Fix an integerr ≥ 1.The generalized binomial series$\mathcal {B}_{r}(z)$satisfiesthe following identities for eachz ∈ U_r:(i) for each integera ≥ 1,we have

$$\begin{array}{@{}rcl@{}} \mathcal{B}_{r}(z)^{a} = \sum\limits_{k = 0}^{\infty} \frac{a}{a + rk}\binom{a + rk}{k}z^{k}. \end{array} $$

(1)

Furthermore, (ii)

$$\begin{array}{@{}rcl@{}} \mathcal{B}_{r}(z) = 1 + z\mathcal{B}_{r}(z)^{r} \end{array} $$

(2)

Proof

Formulas (44) and (45) are easy to establish for the case where r = 1: a small amount of algebra shows that for z ∈ U₁,

$$\begin{array}{@{}rcl@{}} \mathcal{B}_{1}(z) = \frac{1}{1-z}. \end{array} $$

Then

$$\begin{array}{@{}rcl@{}} 1 + z\mathcal{B}_{1}(z) = 1 + \frac{z}{1-z} = \frac{1}{1-z} = \mathcal{B}_{1}(z) \end{array} $$

proving (45). Next, note that for each integer a ≥ 1,

$$\begin{array}{@{}rcl@{}} \sum\limits_{k = 0}^{\infty}\frac{a}{a + k}{a + k \choose k}z^{k} = \sum\limits_{k = 0}^{\infty}{a - 1 + k \choose k}z^{k} = \left[\frac{1}{1-z}\right]^{a} = \mathcal{B}_{1}(z)^{a} \end{array} $$

where the second equality is well-known, and follows from applying an induction argument to find the coefficients corresponding to the a-fold convolution of the power series $\mathcal {B}_{1}(z)$. This proves (44).

It remains to prove both (44) and (45) for the case where r ≥ 2. It helps to rewrite (44) and (45) as follows: for each integer a ≥ 1, and each integer r ≥ 1,

$$\begin{array}{@{}rcl@{}} \mathcal{B}_{r + 1}(z)^{a} = \sum\limits_{k = 0}^{\infty}\frac{a}{a + (r + 1)k}{a + (r + 1)k \choose k}z^{k} \end{array} $$

(3)

and

$$\begin{array}{@{}rcl@{}} \mathcal{B}_{r + 1}(z) = 1 + z\mathcal{B}_{r + 1}(z)^{r + 1}. \end{array} $$

(4)

Thus, to prove Theorem A.1, it suffices to instead prove (46) and (47).

We begin by proving (47). From Formula (10) found within Theorem 3.1, we have

$$\begin{array}{@{}rcl@{}} \mu \beta(0)^{r + 1} - (r\lambda + \mu)\beta(0) + r\lambda = 0 \end{array} $$

where we further assume that λ < μ. Using now Theorem 3.2, we observe after some algebra that this equality can alternatively be expressed as

$$\begin{array}{@{}rcl@{}} x_{\mu}x_{\lambda}^{r + 1}\mathcal{B}_{r + 1}(x_{\lambda, \mu})^{r + 1} + x_{\lambda} = x_{\lambda}\mathcal{B}_{r + 1}(x_{\lambda, \mu}) \end{array} $$

or, equivalently,

$$\begin{array}{@{}rcl@{}} x_{\lambda, \mu}\mathcal{B}_{r + 1}(x_{\lambda, \mu})^{r + 1} + 1 = \mathcal{B}_{r + 1}(x_{\lambda, \mu}). \end{array} $$

This equality shows that Eq. 47 must be true. To see why, observe that from Lemma A.1, we may say that given each z ∈ [0,r^r/(r + 1)^r+ 1), we can choose a corresponding λ and μ which satisfies z = f_r+ 1(ρ), where ρ = λ/μ. However, z = f_r+ 1(ρ) = x_λ,μ, which proves (47).

It remains to establish (46). Fix an integer a ≥ 1: then given a fixed integer r ≥ 1, there exists a unique pair of integers j,i satisfying j ≥ 1, 0 ≤ i ≤ r − 1, that further satisfy a = (j − 1)r + i + 1. Then from Eq. 19, we find that

$$\begin{array}{@{}rcl@{}} \beta(0)^{a} = \beta(0)^{(j-1)r+i + 1} = w_{(0,r-1), (j,i)}(0). \end{array} $$

(5)

We can derive an alternative expression for w_{(0,r− 1),(j,i)}(0) using Theorem 2.1: following a line of reasoning nearly identical to that used to derive w_{(0,r− 1),(1,0)}(α) in Theorem 3.2 gives

$$\begin{array}{@{}rcl@{}} w_{(0,r-1),(j,i)}(0) &=& \sum\limits_{k = 0}^{\infty}\frac{a}{a + (r + 1)k}{a + (r + 1)k \choose k}\left( \frac{r\lambda}{r\lambda + \mu}\right)^{a + rk}\left( \frac{\mu}{r\lambda + \mu}\right)^{k} \\ &=& x_{\lambda}^{a} \sum\limits_{k = 0}^{\infty}\frac{a}{a + (r + 1)k}{a + (r + 1)k \choose k}x_{\lambda,\mu}^{k}. \end{array} $$

(6)

Combining Eqs. 48 and 49 and further applying Theorem 3.2 to write β(0) in terms of $\mathcal {B}_{r + 1}(x_{\lambda , \mu })$ gives

$$\begin{array}{@{}rcl@{}} x_{\lambda}^{a}\mathcal{B}_{r + 1}(x_{\lambda, \mu})^{a} = x_{\lambda}^{a} \sum\limits_{k = 0}^{\infty}\frac{a}{a + (r + 1)k}{a + (r + 1)k \choose k}x_{\lambda,\mu}^{k} \end{array} $$

or, equivalently,

$$\begin{array}{@{}rcl@{}} \mathcal{B}_{r + 1} (x_{\lambda, \mu})^{a} = \sum\limits_{k = 0}^{\infty}\frac{a}{a + (r + 1)k} {a + (r + 1)k \choose k}x_{\lambda, \mu}^{k}. \end{array} $$

From this equality, we can argue similarly as we did to establish (47) to say that for each z ∈ [0,r^r/(r + 1)^r+ 1),

$$\begin{array}{@{}rcl@{}} \mathcal{B}_{r + 1}(z)^{a} = \sum\limits_{k = 0}^{\infty}\frac{a}{a + (r + 1)k} {a + (r + 1)k \choose k}z^{k} \end{array} $$

which proves (46). □

Our last Lemma is used in the proof of Theorem 4.3.

Lemma A.2

For each integera ≥ 1,and each integerr ≥ 1,

$$\begin{array}{@{}rcl@{}} \sum\limits_{k = 0}^{\infty}{a + rk \choose k}z^{k} = \frac{\mathcal{B}_{r}(z)^{a}}{1 - r + r\mathcal{B}_{r}(z)^{-1}}. \end{array} $$

(7)

Proof

Proceeding as indicated in Graham et al. (1994), the key to proving this lemma is to first show that for z ∈ U_r

$$\begin{array}{@{}rcl@{}} \sum\limits_{k = 0}^{\infty}{a + rk \choose k}z^{k} = rz\mathcal{B}_{r}(z)^{a - 1}\mathcal{B}_{r}^{\prime}(z) + \mathcal{B}_{r}(z)^{a}. \end{array} $$

(8)

Next, use Eq. 47 to further show that

$$\begin{array}{@{}rcl@{}} \mathcal{B}_{r}^{\prime}(z) = \frac{\mathcal{B}_{r}(z)^{r}}{1 - r + r\mathcal{B}_{r}(z)^{-1}}. \end{array} $$

(9)

Plugging (52) into the right-hand-side of Eq. 51 and simplifying—while making further use of Eq. 47—proves the claim. □

Remark

It should be noted here that identities (44) and (50) still hold when a is a nonpositive integer and r is a positive integer. Furthermore, given a fixed positive integer r, both series still converge absolutely on U_r (as can be verified with the ratio test).

We show how to properly extend identity (44): given any two positive integers a,b, we can say from Eq. 44 that for any integer k ≥ 1,

$$\begin{array}{@{}rcl@{}} \frac{a + b}{a + b + rk}{a + b + rk \choose k} = \sum\limits_{\ell = 0}^{k}\frac{a}{a + r\ell}{a + r\ell \choose \ell}\frac{b}{b + r(k-\ell)}{b + r(k - \ell) \choose k - \ell}. \end{array} $$

A bit of thought shows that when a is fixed, the left and right-hand-sides of this equality are finite-degree polynomials in b. Since these polynomials are equal for each integer b ≥ 1, they must also be equal for each $b \in \mathbb {R}$. In particular, for each integer k ≥ 1 we have

$$\begin{array}{@{}rcl@{}} 0 = \sum\limits_{\ell = 0}^{k}\frac{a}{a + r\ell}{a + r\ell \choose \ell}\frac{-a}{-a + r(k-\ell)}{-a + r(k - \ell) \choose k - \ell} \end{array} $$

which proves, for z ∈ U_r,

$$\begin{array}{@{}rcl@{}} \left[\sum\limits_{k = 0}^{\infty}\frac{-a}{-a + rk}{-a + rk \choose k}z^{k}\right]\left[\sum\limits_{k = 0}^{\infty}\frac{a}{a + rk}{a + rk \choose k}z^{k}\right] = 1 \end{array} $$

or equivalently,

$$\begin{array}{@{}rcl@{}} \sum\limits_{k = 0}^{\infty}\frac{-a}{-a + rk}{-a + rk \choose k}z^{k} = \mathcal{B}_{r}(z)^{-a}. \end{array} $$

This argument shows (44) still holds for each integer a ≤ 0.

The authors of Graham et al. (1994) further claim that these identities hold even when a and r are arbitrary real numbers, but it is not clear to us how/if the radius of convergence of these series change when a and/or r are no longer integers. Fortunately our arguments only require the cases where r and a are integers satisfying r ≥ 2, and a ≥−r.

Lemma 5.2 is used in our proof of Theorems 4.3 and 4.4, but we must ensure that $z_{\lambda }z_{\mu }^{r} \in U_{r + 1}$ first. Here Lemma A.1 is needed: recall that

$$\begin{array}{@{}rcl@{}} z_{\lambda}z_{\mu}^{r} = \frac{\lambda}{\lambda + r\mu + \alpha}\left( \frac{r\mu}{\lambda + r\mu + \alpha}\right)^{r}. \end{array} $$

First, notice that when $\alpha \in \mathbb {C}_{+}$ and λ,μ > 0, we have

$$\begin{array}{@{}rcl@{}} \left|\frac{\lambda + r\mu}{\lambda + r\mu + \alpha}\right| < 1. \end{array} $$

Using this simple observation, we further find that

$$\begin{array}{@{}rcl@{}} |z_{\lambda}z_{\mu}^{r}| < \frac{\lambda}{\lambda + r\mu}\left( \frac{r\mu}{\lambda + r\mu}\right)^{r} = g_{r + 1}(\rho) \leq \frac{r^{r}}{(r + 1)^{r + 1}} \end{array} $$

which proves $z_{\lambda }z_{\mu }^{r} \in U_{r + 1}$. Next, notice that when λ,μ satisfy λ < μ, we have ρ = λ/μ < 1, meaning

$$\begin{array}{@{}rcl@{}} |z_{\lambda}z_{\mu}^{r}| = \frac{\lambda}{\lambda + r\mu}\left( \frac{r\mu}{\lambda + r\mu}\right)^{r} = g_{r + 1}(\rho) < g_{r + 1}(1) = \frac{r^{r}}{(r + 1)^{r + 1}} \end{array} $$

which, again, shows that $z_{\lambda }z_{\mu }^{r} \in U_{r + 1}$ for this case as well.