Skip to main content
SpringerLink
Log in

Option Pricing with Fractional Stochastic Volatility and Discontinuous Payoff Function of Polynomial Growth

  • Published:
Methodology and Computing in Applied Probability Aims and scope Submit manuscript

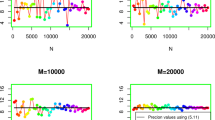
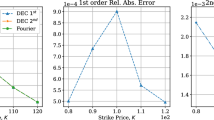
Abstract

We consider the pricing problem related to payoffs of polynomial growth that can have discontinuities of the 1st kind. The asset price dynamic is modeled within the Black-Scholes framework characterized by a stochastic volatility term driven by a fractional Ornstein-Uhlenbeck process. In order to solve the aforementioned problem, we consider three approaches. The first one consists in a suitable transformation of the initial value of the asset price, in order to eliminate possible discontinuities. Then we discretize both the Wiener process and the fractional Brownian motion and estimate the rate of convergence of the related discretized price to its real value whose closed-form analytical expression is usually difficult to obtain. The second approach consists in considering the conditional expectation with respect to the entire trajectory of the fractional Brownian motion (fBm). Here we derive a presentation for the option price which involves only an integral functional depending on the fBm trajectory, and then discretize the fBm and estimate the rate of convergence of the associated numerical scheme. In both cases the rate of convergence is the same and equals n−rH, where n is the partition size, H is the Hurst index of the fBm, and r is the Hölder exponent of the volatility function. The third method consists in calculating the density of the integral functional depending on the trajectory of the fBm via Malliavin calculus and providing the option price in terms of the associated probability density.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Alòs E (2012) A decomposition formula for option prices in the Heston model and applications to option pricing approximation. Finance Stoch 16(3):403–422

    Article  MathSciNet  MATH  Google Scholar 

  • Altmayer M, Neuenkirch A (2015) Multilevel MOnte Carlo quadrature of discontinuous payoffs in the generalized Heston model using Malliavin integration by parts. SIAM J Financial Math 6(1):22–52

    Article  MathSciNet  MATH  Google Scholar 

  • Barndorff-Nielsen OE, Shephard N (2001) Non-Gaussian Ornstein-Uhlenbeck-based models and some of their uses in financial economics. J R Stat Soc Ser B Stat Methodol 63(2):167–241

    Article  MathSciNet  MATH  Google Scholar 

  • Barndorff-Nielsen OE, Shephard N (2002) Econometric analysis of realized volatility and its use in estimating stochastic volatility models. J R Stat Soc Ser B Stat Methodol 64(2):253–280

    Article  MathSciNet  MATH  Google Scholar 

  • Bayer C, Friz P, Gatheral J (2016) Pricing under rough volatility. Quant Finan 16(6):887–904

    Article  MathSciNet  Google Scholar 

  • Bergomi L, Guyon J (2012) Stochastic volatility’s orderly smiles. Risk 25(5):60–66

    Google Scholar 

  • Bertholon H, Monfort A, Pegoraro F (2007) Pricing and inference with mixtures of conditionally normal processes. Direction Générale des études et des relations internationales, Banque de France, pp 1–59

    Google Scholar 

  • Bollerslev T, Mikkelsen HO (1996) Modeling and pricing long memory in stock market volatility. J Econ 73(1):151–184

    Article  MATH  Google Scholar 

  • Carrasco M, Chen X (2002) Mixing and moment properties of various GARCH and stochastic volatility models. Economet Theor 18(1):17–39

    Article  MathSciNet  MATH  Google Scholar 

  • Cheridito P, Kawaguchi H, Maejima M (2003) ORnstein-Uhlenbeck processes. Electron J Probab 8(3):14 (electronic)

    MathSciNet  MATH  Google Scholar 

  • Chronopoulou A, Viens FG (2012) Estimation and pricing under long-memory stochastic volatility. Ann Finance 8(2-3):379–403

    Article  MathSciNet  MATH  Google Scholar 

  • Comte F, Coutin L, Renault E (2012) Affine fractional stochastic volatility models. Ann Finance 8(2-3):337–378

    Article  MathSciNet  MATH  Google Scholar 

  • Cont R, Tankov P (2004) Financial modelling with jump processes. Chapman & Hall/CRC Financial Mathematics Series. Chapman & Hall/CRC, Boca Raton

    MATH  Google Scholar 

  • Fernique X (1975) Regularité des trajectoires des fonctions aléatoires gaussiennes. In: École d’Été de Probabilités de Saint-Flour, IV-1974, vol 480. Springer, Berlin, pp 1–96. Lecture Notes in Math

  • Fouque J-P, Papanicolaou G, Sircar KR (2000) Derivatives in financial markets with stochastic volatility. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  • Funahashi H, Kijima M (2017) Does the Hurst index matter for option prices under fractional volatility. Ann Finance 13(1):55–74

    Article  MathSciNet  MATH  Google Scholar 

  • Heston SL (1993) A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev Financ Stud 6(2):327–343

    Article  MATH  MathSciNet  Google Scholar 

  • Hull JC, White A (1987) The pricing of options on assets with stochastic volatilities. J Financ 42(2):281–300

    Article  MATH  Google Scholar 

  • Kahl C (2008) Modelling and simulation of stochastic volatility in finance. Universal-Publishers

  • Knight J, Satchell S (eds) (2011) Forecasting volatility in the financial markets, 3rd edn. Butterworth-Heinemann, Oxford

    Google Scholar 

  • Kuchuk-Iatsenko S, Mishura Y (2015) Pricing the E,uropean call option in the model with stochastic volatility driven by Ornstein-Uhlenbeck process. Exact formulas Mod Stoch Theory Appl 2(3):233–249

    Article  MATH  Google Scholar 

  • Kyprianou AE, Schoutens W (eds) (2005) Exotic option pricing and advanced Lévy models. Wiley, Chichester

    MATH  Google Scholar 

  • Ledoux M (1996) Isoperimetry and gaussian analysis. In: Lectures on probability theory and statistics, pp 165–294. Springer

  • León JA, Nualart D (1998) Stochastic evolution equations with random generators. Ann Probab 26(1):149–186

    Article  MathSciNet  MATH  Google Scholar 

  • Nicolato E, Venardos E (2003) Option pricing in stochastic volatility models of the O,rnstein-Uhlenbeck type. Math Financ 13(4):445–466

    Article  MATH  Google Scholar 

  • Norros I, Valkeila E, Virtamo J (1999) An elementary approach to a Girsanov formula and other analytical results on fractional Brownian motions. Bernoulli 5(4):571–587

    Article  MathSciNet  MATH  Google Scholar 

  • Nualart D (2006) The Malliavin calculus and related topics. Probability and its Applications (New York), 2nd edn. Springer, Berlin

    MATH  Google Scholar 

  • Palm FC (1996) 7 GARCH models of volatility. Handbook of statistics 14:209–240

    Article  MathSciNet  Google Scholar 

  • Pospíšil J, Sobotka T (2016) Market calibration under a long memory stochastic volatility model. Appl Math Finance 23(5):323–343

    Article  MathSciNet  MATH  Google Scholar 

  • Schobel R, Zhu J (1999) Stochastic volatility with an Ornstein–Uhlenbeck process: an extension. Ann Finance 3(1):23–46

    MATH  Google Scholar 

  • Schweizer M (1995) On the minimal martingale measure and the Föllmer-Schweizer decomposition. Stochastic Anal Appl 13(5):573–599

    Article  MathSciNet  MATH  Google Scholar 

  • Shephard N (1996) Statistical aspects of ARCH and stochastic volatility. Monographs on Statistics and Applied Probability 65:1–68

    Google Scholar 

  • Talagrand M (1994) Sharper bounds for Gaussian and empirical processes. Ann Probab 22(1):28–76

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. The Department of Computer Science Universita degli Studi di Verona - Cà Vignal 2, The University of Verona, Verona, Italy

    Viktor Bezborodov & Luca Di Persio

  2. The Faculty of Mechanics and Mathematics Volodymyrska 64, Taras Shevchenko National University of Kyiv, Kyiv, Ukraine

    Yuliya Mishura

Authors
  1. Viktor Bezborodov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Luca Di Persio
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yuliya Mishura
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yuliya Mishura.

Additional information

The research of Viktor Bezborodov was supported by the Department of Computer Science of the University of Verona, Luca Di Persio was supported by the Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) within the project “Stochastic Partial Differential Equations and Stochastic Optimal Transport with Applications to Mathematical Finance”, and Yuliya Mishura is thankful to the University of Verona for the hospitality during her visit.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bezborodov, V., Di Persio, L. & Mishura, Y. Option Pricing with Fractional Stochastic Volatility and Discontinuous Payoff Function of Polynomial Growth. Methodol Comput Appl Probab 21, 331–366 (2019). https://doi.org/10.1007/s11009-018-9650-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11009-018-9650-3

Keywords

Mathematics Subject Classification (2010)

Search

Navigation