The continuity and estimates of a solution to mixed fractional constant elasticity of variance system with stochastic volatility and the pricing of vulnerable options

Abstract

Stochastic volatility models play an important role in finance modeling. Under a mixed fractional Brownian motion environment, we study the continuity and estimates of a solution to a kind of stochastic differential equations with double volatility terms. Besides, we propose to price the vulnerable option with the discretization method and present the results using a Monte Carlo simulation.

1 Introduction

Most of the existing literature on financial models assumes that the volatility of assets is constant. However, this assumption ignores the return features of volatility clustering, high peak, fat tails, and volatility mean reverting in real markets, which cannot be captured by constant volatility models [1, 2]. To model the volatility smile effectively, one solution is using the stochastic volatility under two cases: (1) the function of stochastic processes is used to describe the volatility [3, 4], and (2) the additional Brownian motion is introduced to describe the stochastic parts of stochastic volatility (SV) models. In this paper, we focus on the second case.

Stochastic volatility models constituted of one stock have been introduced and intensively investigated in the literature. Hull and White [5] first introduce an SV model called the Heston model in which the market volatility follows a mean-reverting Cox–Ingersoll–Ross process. Starting with Xu and Taylor [6], lots of studies show that two-component volatility models outperform one-component ones in the option pricing literature (see [7, 8]). Da Fonseca et al. [9] extend the Heston model to a multifactor specification for the volatility process in a single asset framework. Wang et al. [10] extend the framework of Siu et al. [11] and focus on currency options under a two-factor Markov-modulated stochastic volatility jump-diffusion model. The theoretical development of the SV model is introduced in [12] by studying the following equations:

$$ \textstyle\begin{cases} \mathrm{d}S(t) = \mathit{rS}(t)\,\mathrm{d}t + \sqrt{v(t)} S(t)\,\mathrm{d}{B_{1}}(t), \\ \mathrm{d}v(t) = \kappa (\theta - v(t))\,\mathrm{d}t + {\sigma }(v(t))\,\mathrm{d}{B_{2}}(t), \end{cases} $$

(1.1)

where time variable $t \in (0, T)$, ${B_{1}}(t)$ and ${B_{2}}(t)$ are mutually independent standard Brownian motions, and $r >0$ is the constant risk-free interest rate. Here $v(t)$ is a mean-reverting square-root process, whereas $\kappa > 0$ specifies the speed of adjustment of the volatility toward its theoretical mean $\theta > 0$. Note that $\sigma > 0$ is the second-order volatility, that is, the volatility of volatility. The paper [12] also studies the existence and uniqueness of a strong solution to (1.1). Certain ${L^{p}}$ estimates of (1.1) are proved in [13].

However, all the existing SV models mentioned are based on the Brownian motion with increments following the independent norm distribution. Many works argue that the returns of risky assets have long-range dependence properties, which are expressed by the increment of financial models. Using the Brownian motion to express the stochastic parts without considering its dependency to the financial modeling may have some serious disadvantages [14]. Because of the self-similarity and long-range dependence properties, the fractional Brownian motion becomes a suitable tool in mathematical finance. We refer the readers to [14, 15] for the motivation and references concerning the study of the fractional Brownian motion.

It is worth noting that the SV models shown in the above references constitute one stock. Thus those SV models cannot be used to study vulnerable option shown in Sect. 5, because the vulnerable option is constructed by two stocks.

In this paper, we use the mixed fractional Brownian motion (mfBm), which is a linear combination of a Brownian motion and fractional Brownian motion, to drive the following stock price systems constituted of two stocks:

$$ \textstyle\begin{cases} \mathrm{d}{S_{1}}(t) = r{S_{1}}(t)\,\mathrm{d}t + \sqrt{{V_{1}}(t)} {S_{1}}{(t)^{\alpha _{1}} }\,\mathrm{d}M_{1,1}^{H}(t),& {S_{1}}(0) = {s_{1}}, \\ \mathrm{d}{S_{2}}(t) = r{S_{2}}(t)\,\mathrm{d}t + \sqrt{{V_{2}}(t)} {S_{2}}{(t)^{\alpha _{2}} }\,\mathrm{d}M_{1,2}^{H}(t),& {S_{2}}(0) = {s_{2}}, \end{cases} $$

(1.2)

where the variance processes $\{ {v_{1}}(t), t \ge 0\}$ and $\{ {v_{2}}(t), t \ge 0\}$ are driven by the fractional Cox–Ingersoll–Ross model satisfying

$$\begin{aligned} &\textstyle\begin{cases} \mathrm{d}{V_{1}}(t) = {\kappa _{1}}({\theta _{1}} - {V_{1}}(t))\,\mathrm{{d}}t + {\sigma _{1}}\sqrt{ \vert {V_{1}}(t) \vert } \,\mathrm{d}M_{2,1}^{H}(t), & {V_{1}}(0) = {v_{1}}, \\ \mathrm{d}{V_{2}}(t) = {\kappa _{2}}({\theta _{2}} - {V_{2}}(t))\,\mathrm{ {d}}t + {\sigma _{2}}\sqrt{ \vert {V_{2}}(t) \vert } \,\mathrm{d}M_{2,2}^{H}(t),& {V_{{{2}}}}(0) = {v_{{{2}}}}, \end{cases}\displaystyle \end{aligned}$$

(1.3)

$$\begin{aligned} &\mathrm{d}M_{1,1}^{H}(t) \cdot \,\mathrm{d}M_{1,2}^{H}(t) = \mathrm{ {d}}M_{2,1}^{H}(t) \cdot \mathrm{d}M_{2,2}^{H}(t) = \rho \bigl(\mathrm{ {d}} {t^{2H}} + {\lambda ^{2}}\, \mathrm{d}t\bigr). \end{aligned}$$

(1.4)

Here $M_{1,1}^{H}(t)$, $M_{1,2}^{H}(t)$, $M_{2,1}^{H}(t)$ and $M_{2,2}^{H}(t)$ are mfBm processes, which, together with relative conclusions, will be defined in Sect. 2, and α is an elastic constant. We call this model a mixed factional CEV model. It is not an easy task to show that the solutions to ${V_{1}}(t)$ and ${V_{2}}(t)$ are positive when SV model is driven by mfBm processes. Thus we use $|{V_{1}}(t)|$ and $|{V_{2}}(t)|$ in (1.3) instead of ${V_{1}}(t)$ and ${V_{2}}(t)$ as in the classical SV model.

In this work, we investigate the existence, uniqueness, and continuity of solutions to the dynamic model (1.2)–(1.4). The existence and uniqueness are explained in Sect. 2. In Sect. 3, we study the continuity of the solution to the dynamic model (1.2)–(1.4). In Sect. 4, we price the European option using the discrete type of (1.2)–(1.4) and Monte Carlo simulations.

2 Preliminaries

The mixed fractional Brownian motion is a stochastic process with long memory and plays an important role in the financial modeling. To better understand the rest of the paper, we briefly review some basic concepts and properties of the mixed fractional Brownian motion.

Let H be a constant belonging to $(0,1)$. A fractional Brownian motion (fBm) $\{ {B^{H}}(t), t \ge 0\}$ with Hurst parameter H is a continuous and centered Gaussian process with covariance [16]

$$ R(t,s) = E\bigl[{B^{H}}(t){B^{H}}(s)\bigr] = \frac{1}{2}\bigl({t^{2H}} + {s^{2H}} - \vert t - s \vert ^{2H}\bigr) = \int _{0}^{t} { \int _{0}^{s} {\phi (r,u)\,\mathrm{d}u\,\mathrm{{d}}r} } $$

for $s,t > 0$, where $\phi (r,u) = H(2H - 1)|r - u|^{2H - 2}$. When $H = \frac{1}{2}$, the fBm becomes a standard Brownian motion denoted by $\{ B(t), t \ge 0\}$. A mixed fractional Brownian motion (mfBm) $\{ {M^{H}}(t), t \ge 0\}$ is a linear combination of a Brownian motion (Bm) and a fractional Brownian motion, defined on a filtered probability space $(\varOmega, \mathcal{F},{\mathcal{F} _{t}},P)$ by

$$ M^{H}(t)= \lambda B(t) + {B^{H}}(t), $$

where λ is a real constant, P is a physical probability measure, and $\{ \mathcal{F}_{t}, t \ge 0\}$ denotes the P-completion of the filtration generated by $(B(t), {B^{H}}(t))$. An mfBm $\{ {M^{H}}(t), t \ge 0\}$ has the following properties [12, 13]

• 1. ${M^{H}}(0) = 0$ and $E[{M^{H}}(t)] = 0$ for any $t \ge 0$.

• 2. ${M^{H}}(t)$ is a centered Gaussian process, not a Markovian one for all $H \in (0,1)$.

• 3. $\{ {M^{H}}(t), t \ge 0\}$ has homogeneous increments, that is, the increment ${M^{H}}(t + s) - {M^{H}}(s)$ has the same distribution as ${B^{H}}(t)$ for $s,t \ge 0$.

• 4. The covariance of ${M^{H}}(t)$ and ${M^{H}}(s)$ is given by

  $$ E\bigl[{M^{H}}(t){M^{H}}(s)\bigr] = {\lambda ^{2}} \cdot s \wedge t + R(t,s) \quad\text{for } s,t > 0. $$

• 5. The increments of ${M^{H}}(t)$ are positively correlated if $0.5 < H < 1$, uncorrelated if $H = 0.5$, and negatively correlated if $0 < H < 0.5$.

At the end of this section, we give some notations, function spaces, and conclusions to prove our main results (for details, see [13,14,15]).

Let $\mathcal{S}(\mathrm{{R}})$ be the Schwartz space of rapidly decreasing smooth functions on R with norm

$$ \Vert f \Vert _{H}^{2} = \int _{\mathrm{R}} { \int _{\mathrm{R}} {f(s)f(t)\phi (s,t)\,\mathrm{d}s\,\mathrm{d}t} } < \infty. $$

If we equip $\mathcal{S}(\mathrm{{R}})$ with the inner product

$$ { \langle {f,g} \rangle _{H}} = \int _{\mathrm{R}} { \int _{ \mathrm{R}} {f(s)f(t)\phi (s,t)\,\mathrm{d}s\,\mathrm{d}t} } < \infty , $$

then the completion of $\mathcal{S}(\mathrm{{R}})$, denoted by $L_{H}^{2}(\mathrm{{R}})$, becomes a separable Hilbert space.

Recall that an mfBm is a linear combination of a Bm and fBm. The stochastic integral with respect to a Bm has been studied by many references. We present the fractional Wick–Itô–Skorokhod (fWIS) integral theory.

The stochastic integral with respect to fBm for deterministic functions is easily defined.

Lemma 2.1

If $f, g$ belong to $L_{H}^{2}(\mathrm{{R}})$, then $\int _{\mathrm{{R}}} {f(s)\,\mathrm{d}B_{s}^{H}}$ and $\int _{\mathrm{{R}}} {g(s)\,\mathrm{d}B_{s}^{H}}$ are well-defined zero-mean Gaussian random variables with variances $\Vert f \Vert _{H}^{2}$ and $\Vert g \Vert _{H}^{2}$, respectively, and

$$ E\biggl[ \int _{\mathrm{{R}}} {f(s)\,\mathrm{d}B_{s}^{H}} \int _{\mathrm{{R}}} {g(s)\,\mathrm{d}B_{s}^{H}} \biggr] = { \langle {f,g} \rangle _{H}}. $$

Proof

This lemma is verified in [16]. It can be directly proved by verifying it for simple functions $\sum_{i = 1}^{n} {{a_{i}} {I_{({t_{i}},{t_{i + 1}}]}}}$ and then proceeding with a passage to the limit. □

Definition 2.1

Suppose $Y:\mathrm{R} \to (S)_{H}^{*}$ is a given function such that $Y(t)\diamondsuit {W^{(H)}}(t)$ is dt-integrable in $(S)_{H}^{*}$. Then we define its fractional Wick–Itô–Skorokhod (fWIS) integral $\int _{\mathrm{{R}}} {Y(t)\,\mathrm{d}B_{t}^{H}}$ by

$$ \int _{\mathrm{{R}}} {Y(t)\,\mathrm{d}B_{t}^{H}} = \int _{\mathrm{{R}}} {Y(t)\diamondsuit {W^{(H)}}(t)\, \mathrm{d}t}. $$

In particular, the integral on an interval can be defined as

$$ \int _{0}^{T} {Y(t)\,\mathrm{d}B_{t}^{H}} = \int _{\mathrm{{R}}} {Y(t) {I_{[0, T]}}\,\mathrm{d}B_{t}^{H}}. $$

Here $(S)_{H}^{*}$ is the fractional Hida distribution space, and ♢ stands for the Wick product (for details, see [16]).

Example 2.1

Suppose $Y(t)$ is a step function $Y(t) = \sum_{i = 1}^{n} {{F_{i}}(\omega ){I_{[{t_{i}},{t_{i + 1}})}}(t),}$ where the random variables ${F_{i}}(\omega ) \in (S)_{H} ^{*}$, and a partition π satisfies $0 = {t_{0}} < {t_{1}} < \cdots < {t_{n}} = T$. Then

$$ \int _{0}^{T} {Y(t)\,\mathrm{d}B_{t}^{H}} = \sum_{i = 1}^{n} {{F_{i}}( \omega )\diamondsuit \bigl(B_{{t_{i + 1}}}^{H} - B_{{t_{i}}}^{H}\bigr)}. $$

Let ${L^{p}}({\mathrm{{P}}^{H}}) = {L^{p}}$ be the space of all random variables $F:\varOmega \to \mathrm{R}$ such that

$$ { \Vert F \Vert _{{L^{p}}({\mathrm{{P}}^{H}})}} = E{\bigl[ \vert F \vert ^{p}\bigr]^{ {1 / p}}}< \infty. $$

Definition 2.2

Let $g \in L_{H}^{2}(\mathrm{R})$. The ϕ-derivative of a random variable $F \in {L^{p}}({\mathrm{P} ^{H}})$ in the direction of Φg is defined as

$$ {D_{\varPhi g}}F(\omega ) = \mathop{\lim } _{\delta \to 0} \frac{1}{ \delta } \biggl\{ {F\biggl(\omega + \delta \int _{0}^{\cdot }{(\varPhi g) (u)\,\mathrm{ {d}}u} \biggr) - F(\omega )} \biggr\} , $$

provided that the limit exists in ${L^{p}}({\mathrm{P}^{H}})$. Furthermore, if there is a process $(D_{s}^{\phi }F, s>0)$ such that

$$ {D_{\varPhi g}}F = \int _{\mathrm{R}} {D_{s}^{\phi }F{g_{s}} \,{\mathrm{ {d}}}s} \quad \text{almost surely} $$

for all $g \in L_{H}^{2}(\mathrm{R})$, then F is said to be ϕ-differentiable.

Lemma 2.2

If $g \in L_{H}^{2}(\mathrm{R})$, $F \in {L^{2}}( {\mathrm{P}^{H}})$, and ${D_{\varPhi g}}F \in {L^{2}}({\mathrm{P}^{H}})$, then

$$ F\diamondsuit \int _{\mathrm{R}} {{g_{s}}\,\mathrm{d}B_{s}^{(H)}} = F \int _{\mathrm{R}} {{g_{s}}\,\mathrm{d}B_{s}^{(H)}} - {D_{\varPhi g}}F. $$

3 Moment estimates

In this section, we prove moment estimates and continuity of the solution of the mixed fractional CEV system (1.2)–(1.3) by extending the idea of [13] for a mixed stochastic differential equation.

Lemma 3.1

If X obeys the normal distribution with zero mean, then for any constant $p \ge 1$, there exists a constant ${c_{1}}(p)$, depending only on p, such that

$$ E\bigl[ \vert X \vert ^{p}\bigr] \le {c_{1}}(p)E{ \bigl[ \vert X \vert \bigr]^{p}}. $$

(3.1)

Proof

Let $X \sim N(0,{\sigma ^{2}})$ and $f(x) = \frac{1}{ {\sqrt{2\pi } {\sigma ^{2}}}}\exp \{ - \frac{{{x^{2}}}}{{2{\sigma ^{2}}}}\}$. If $n \ge 2$ is an even number, then it is easy to have

$$ E\bigl[ \vert X \vert ^{n}\bigr] = 2 \int _{0}^{ + \infty } {{x^{n}}f(x)\, \mathrm{d}x} = \frac{2}{ {\sqrt{2\pi {\sigma ^{2}}} }} \int _{0}^{ + \infty } {{x^{n}}\exp \biggl\{ - \frac{x}{{2{\sigma ^{2}}}}\biggr\} \,\mathrm{d}x}. $$

Using $t = \frac{x}{{2{\sigma ^{2}}}}$, we have

$$ E\bigl[ \vert X \vert ^{n}\bigr] = 2 \int _{0}^{ + \infty } {{x^{n}}f(x)\, \mathrm{d}x} = \frac{ {{{(\sqrt{2} )}^{n}}}}{{\sqrt{\pi }}}{\sigma ^{n}} \int _{0}^{ + \infty } {{t^{\frac{{n - 1}}{2}}}\exp \{ - t \} \,\mathrm{d}x}. $$

Recall that $\varGamma (n) = \int _{0}^{ + \infty } {{t^{n - 1}}\exp \{ - t\} \,\mathrm{d}x}$, Thus we use $\varGamma (n) = (n - 1)\varGamma (n - 1)$ and $\varGamma (0.5) = \sqrt{\pi }$ to arrive at

$$ E\bigl[ \vert X \vert ^{n}\bigr] = 2 \int _{0}^{ + \infty } {{x^{n}}f(x)\, \mathrm{d}x} = \frac{ {{{(\sqrt{2} )}^{n}}}}{{\sqrt{\pi }}}{\sigma ^{n}}\varGamma \biggl( \frac{ {n + 1}}{2}\biggr) = (n - 1)!{\sigma ^{n}}. $$

(3.2)

Let $p \ge 1$ be a positive constant. We define

$$ n = \min \{ m|p \le m, m \text{ is an even number}\} . $$

Using the Hölder inequality and combining (3.2), we obtain

$$ E\bigl[ \vert X \vert ^{p}\bigr] \le E{\bigl[ \vert X \vert ^{n}\bigr]^{\frac{p}{n}}} = (n){!^{\frac{p}{n}}} \cdot {\sigma ^{p}}. $$

(3.3)

Now we focus on $E[|X|]$. A change of variable for integral gives

$$\begin{aligned} E\bigl[ \vert X \vert \bigr] &= 2 \int _{\mathrm{R}} {\mathit{xf}(x)\,\mathrm{d}x} = \frac{2}{{\sqrt{2\pi } \sigma }} \int _{\mathrm{R}} {x\exp \biggl\{ - \frac{{{x^{2}}}}{{2{\sigma ^{2}}}}\biggr\} \, \mathrm{d}x} \\ &= \frac{1}{{\sqrt{2\pi } \sigma }} \int _{\mathrm{R}} {\exp \biggl\{ - \frac{ {{x^{2}}}}{{2{\sigma ^{2}}}}\biggr\} \, \mathrm{d} {x^{2}}}. \end{aligned}$$

Letting $t = \frac{{{x^{2}}}}{{2{\sigma ^{2}}}}$ and using integration by substitution, we have

$$ E\bigl[ \vert X \vert \bigr] = \sqrt{{2 / \pi }} \cdot \sigma \int _{\mathrm{R}} {\exp \{ - t \} \,\mathrm{d}t} = \sigma \sqrt{{2 / \pi }}. $$

(3.4)

Combining (3.2), (3.3), and (3.4), the lemma is proved. □

Lemma 3.2

If ${V_{1}}(t)$ is the solution of volatility equation (1.3), then for any $p \ge 2$, we have

$$ E\biggl[ \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \,\mathrm{d}B_{s}^{H}} \biggr\vert ^{p}\biggr] \le {c_{2}}(p,H){H^{p}} {2^{p - 1}} \int _{0}^{T} {E\bigl[ \bigl\vert {V_{1}}(t) \bigr\vert ^{p}\bigr] \,\mathrm{d}t} {+} {c_{3}}(p,H,T), $$

where ${c_{2}}(p,H) = \frac{1}{2}{c_{1}}(p){H^{p}}$ and ${c_{3}}(p,H,T) = \frac{1}{{{2^{p}}}}c(p){H^{p}}{2^{p - 1}}{ ( {\int _{0}^{T} {{t^{2H - 2}}\,\mathrm{d}t} } )^{p}}$.

Proof

For a partition π: $0 = {t_{0}} < {t_{1}} < \cdots < {t_{n}} = t$, let

$$ S\bigl(\sqrt{ \vert {V_{1}} \vert },\pi \bigr) = \sum _{i = 0}^{n - 1} {\sqrt{ \bigl\vert {V_{1}}(t) \bigr\vert } \diamondsuit \bigl(B_{{t_{i + 1}}}^{(H)} - B_{{t_{i}}}^{(H)}\bigr)}. $$

(3.5)

According to the WIS integral with respect to fBm, we have

$$ \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert }\,\mathrm{d}B_{s}^{(H)}} = \mathop{\lim } _{ \vert \pi \vert \to 0} S\bigl(\sqrt{ \vert {V_{1}} \vert },\pi \bigr). $$

(3.6)

Note that, for fixed ${t_{i}}$, ${V_{1}}({t_{i}})$ is a random variable. Using (3.37) in [15], we have

$$\begin{aligned} &\sqrt{ \bigl\vert {V_{1}}({t_{i}}) \bigr\vert } \diamondsuit \bigl(B_{{t_{i + 1}}} ^{(H)} - B_{{t_{i}}}^{(H)}\bigr) \\ &\quad = \sqrt{ \bigl\vert {V_{1}}(t) \bigr\vert } \cdot \int _{\mathrm{{R}}} {{I_{({t_{i}},{t _{i + 1}}]}}} \,\mathrm{d}B_{s}^{(H)} - D_{\varPhi g}^{\phi }\sqrt{ \bigl\vert {V_{1}}({t_{i}}) \bigr\vert } \\ &\quad = \sqrt{ \bigl\vert {V_{1}}(t) \bigr\vert } \cdot \int _{\mathrm{{R}}} {{I_{({t_{i}},{t _{i + 1}}]}}} \,\mathrm{d}B_{s}^{(H)} = \sqrt{ \bigl\vert {V_{1}}(t ) \bigr\vert } \cdot \bigl(B_{{t_{i + 1}}}^{(H)} - B_{{t_{i}}}^{(H)} \bigr). \end{aligned}$$

(3.7)

Substituting (3.7) into (3.5) and using the triangle and Hölder inequalities, we obtain

$$\begin{aligned} E\bigl[ \bigl\vert S\bigl(\sqrt{ \vert {V_{1}} \vert },\pi \bigr) \bigr\vert \bigr] &\le \sum_{i = 0}^{n - 1} {E\bigl[ \bigl\vert {\sqrt{ \bigl\vert {V_{1}}(t) \bigr\vert } \cdot \bigl(B_{{t_{i + 1}}}^{(H)} - B _{{t_{i}}}^{(H)} \bigr)} \bigr\vert } \bigr] \\ &\le \sum_{i = 0}^{n - 1} {\sqrt{E\bigl[ \bigl\vert {{V _{1}}(t )} \bigr\vert \bigr] \cdot E\bigl[ \bigl\vert B_{{t_{i + 1}}}^{(H)} - B_{{t_{i}}}^{(H)} \bigr\vert ^{2}\bigr]} }. \end{aligned}$$

(3.8)

Letting $|\pi | \to 0$ and combining (3.6) and (3.8), we obtain

$$ E\biggl[ \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \,\mathrm{d}B_{s}^{H}} \biggr\vert \biggr] \le \int _{0}^{T} {\sqrt{E\bigl[ \bigl\vert {V_{1}}(t ) \bigr\vert \bigr]} \,\mathrm{d} {t^{H}}}. $$

Using Lemma 3.1, we arrive at

$$\begin{aligned} &E\biggl[ \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \,\mathrm{d}B _{s}^{H}} \biggr\vert ^{p}\biggr] \\ &\quad \le c_{1}(p)E{\biggl[ \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \,\mathrm{d}B _{s}^{H}} \biggr\vert \biggr]^{p}} \le c_{1}(p){ \biggl( { \int _{0}^{T} {\sqrt{E\bigl[ \bigl\vert {V_{1}}(t ) \bigr\vert \bigr]} \,\mathrm{d} {t^{H}}} } \biggr)^{p}}. \end{aligned}$$

(3.9)

Using the Hölder inequality twice, we have

$$\begin{aligned} E\biggl[ \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \,\mathrm{d}B_{s}^{H}} \biggr\vert ^{p}\biggr] &\le c_{1}(p){H^{p}} { \biggl( { \int _{0}^{T} {\frac{1}{2}E\bigl[ \bigl\vert {V_{1}}(t ) \bigr\vert \bigr] + \frac{1}{2}{t^{2H - 2}} \,\mathrm{d}t} } \biggr)^{p}} \\ &\le \frac{1}{{{2^{\mathrm{{p}}}}}}c_{1}(p){H^{p}} { \biggl( { \int _{0}^{T} {E\bigl[ \bigl\vert {V_{1}}(t ) \bigr\vert \bigr]\,\mathrm{d}t} {+} \int _{0}^{T} {{t^{2H - 2}}\, \mathrm{d}t} } \biggr)^{p}}. \end{aligned}$$

Using the inequality ${(a + b)^{p}} \le {2^{p - 1}}({a^{p}} + {b^{p}})$, we get

$$\begin{aligned} & E\biggl[ \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \,\mathrm{d}B _{s}^{H}} \biggr\vert ^{p}\biggr] \\ &\quad\le \frac{1}{{{2^{p}}}}c_{1}(p){H^{p}} {2^{p - 1}} \biggl( { \biggl( { \int _{0}^{T} {E\bigl[ \bigl\vert {V_{1}}(t ) \bigr\vert \bigr]\,\mathrm{d}t} } \biggr)^{p}} + { \biggl( { \int _{0}^{T} {{t^{2H - 2}}\, \mathrm{d}t} } \biggr)^{p}} \biggr). \end{aligned}$$

(3.10)

Recalling that $H \in (0.5,1)$, we have $2H - 2 \in ( - 1, 0)$. This implies that the integral $\int _{0}^{T} {{t^{2H - 2}}\,\mathrm{d}t}$ is convergent. Hence the lemma is proved applying the Hölder inequality to (3.10). □

Theorem 3.1

Let $T > 0$ be fixed. For $p \ge 2$, there are constants ${c_{4}}$ and ${c_{5}}$, depending on λ, p, $\sigma _{i}$, ${\kappa _{i}}$, $H,{v_{i}}$, T, such that

$$ E\Bigl[\mathop{\sup } _{t \in [0,T]} { \bigl\vert {{V_{i}}(t )} \bigr\vert ^{p}}\Bigr] \le {c_{i + 3}},\quad i = 1, 2. $$

Proof

Here we only prove the case $i = 1$. Since for any $t \in [0, T]$,

$$ {V_{1}}(t) = {v_{1}} + \int _{0}^{t} {{\kappa _{1}}\bigl({ \theta _{1}} - {V_{1}}(s)\bigr)\,\mathrm{d}s} + {\sigma _{1}} \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert }} \,\mathrm{d}M_{2,1}^{H}(s), $$

using the Young inequality, we have for any $p \ge 2$ that

$$ { \bigl\vert {{V_{1}}(t)} \bigr\vert ^{p}} \le {3^{p - 1}}\bigl( \vert {v_{1}} \vert ^{p} + {A_{1}} + {A_{2}}\bigr), $$

(3.11)

where ${A_{1}} = \kappa _{1}^{p}{ \vert {\int _{0}^{t} {\theta - {V _{1}}(s)\,\mathrm{d}s} } \vert ^{p}}$, ${A_{2}} = \sigma _{1}^{p} { \vert {\int _{0}^{t} {\sqrt{|{V_{1}}(s)|} } \,\mathrm{d}M_{2,1} ^{H}(s)} \vert ^{p}}$.

Now, we compute $E[{A_{1}}]$ and $E[{A_{2}}]$. For the second term $A_{1}$ in (3.11), using the Hölder and Young inequalities, we have

$$\begin{aligned} E[{A_{1}}] &\le {2^{p - 1}}\kappa _{1}^{p}{\theta ^{p}}T + {2^{p - 1}} \kappa _{1}^{p}{ \biggl\vert { \int _{0}^{t} {{V_{1}}(s)\, \mathrm{d}s} } \biggr\vert ^{p}} \\ &\le {2^{p - 1}}\kappa _{1}^{p}{\theta ^{p}}T + {2^{p - 1}} \kappa _{1}^{p}{T^{p - 1}} \int _{0}^{t} {E\bigl[ \bigl\vert {V_{1}}(s) \bigr\vert ^{p}\bigr]\,\mathrm{d}s}. \end{aligned}$$

(3.12)

Noting that $M_{t}^{H} = \lambda B(t) + {B^{H}}(t)$ and applying the inequality ${(a + b)^{n}} \le {2^{n - 1}}({a^{n}} + {b^{n}})$ to ${A_{2}}$, we have

$$ {A_{2}} \le {2^{p - 1}}\sigma _{1}^{p}{ \lambda ^{p}} {A_{3}} + {2^{p - 1}} {\lambda ^{p}}\sigma _{1}^{p}{A_{4}}, $$

(3.13)

where ${A_{3}} = { \vert {\int _{0}^{t} {\sqrt{|{V_{1}}(s)|} \,\mathrm{ {d}}B(s)} } \vert ^{p}}$ and ${A_{4}} = { \vert {\int _{0}^{t} {\sqrt{|{V_{1}}(s)|} \,\mathrm{d}B^{H}(s)} } \vert ^{p}}$. Applying the B-D-G inequality [13, 15] to $E[{A_{3}}]$ and using the inequality $x \le 1 + {x^{2}}$, we have

$$ E[{A_{3}}] \le { \biggl\vert { \int _{0}^{t} {E\bigl[ \bigl\vert {V_{1}}(s) \bigr\vert \bigr]\,{\mathrm{{d}}}s} } \biggr\vert ^{{p / 2}}} \le { \biggl\vert { \int _{0}^{t} {E\bigl[ \bigl\vert {V _{1}}(s) \bigr\vert \bigr]\,{\mathrm{{d}}}s} } \biggr\vert ^{p}} + 1. $$

Using the Hölder inequality, we obtain

$$ E[{A_{3}}] \le \int _{0}^{t} {E\bigl[ \bigl\vert {V_{1}}(s) \bigr\vert ^{p}\bigr]\,{\mathrm{{d}}}s} + 1. $$

(3.14)

Substituting (3.14) and Lemma 3.2 into (3.13), we have

$$ E[{A_{2}}] \le {c_{6}}(\lambda,p,\sigma,T,H) \int _{0}^{t} {E\bigl[ \bigl\vert {V_{1}}(s) \bigr\vert ^{p}\bigr]\,\mathrm{d}s} + {c_{7}}(\lambda,p,{\sigma _{1}},H,T), $$

(3.15)

where

$$\begin{aligned} &{c_{6}}(\lambda,p,\sigma,T,H) = {2^{p - 1}} {\lambda ^{p}}\sigma _{1} ^{p} + {2^{p - 1}} {\lambda ^{p}}\sigma _{1}^{p}{H^{p}} {c_{2}}(p,H), \\ &{c_{7}}(\lambda,p,{\sigma _{1}},H,T) = {2^{p - 1}}\sigma _{1}^{p}{\lambda ^{p}} {+} {2^{p - 1}} {\lambda ^{p}}\sigma _{1}^{p}{c_{3}}(p,H,T). \end{aligned}$$

Substituting (3.12) and (3.15) into (3.11) and letting

$$\begin{aligned} &{c_{8}} = {3^{p - 1}} \vert {v_{1}} \vert ^{p} + {6^{p - 1}}\kappa _{1}^{p}{ \theta ^{p}}T + {3^{p - 1}} {c_{7}}(\lambda,p,{ \sigma _{1}},H,T), \\ &{c_{9}} = {6^{p - 1}}\kappa _{1}^{p}{T^{p - 1}} + {3^{p - 1}} {c_{6}}( \lambda,p,{\sigma _{1}},T,H), \end{aligned}$$

we obtain

$$ E\bigl[{ \bigl\vert {{V_{1}}(t)} \bigr\vert ^{p}} \bigr] \le {c_{8}} + {c_{9}} \int _{0} ^{t} {E\bigl[ \bigl\vert {V_{1}}(s) \bigr\vert ^{p})\bigr]\,\mathrm{d}s}. $$

(3.16)

Hence the theorem follows from the Gronwall inequality. □

Lemma 3.3

The claim of Theorem 3.1 still holds if $p \in (0,2)$.

Proof

If $1 \le p < 2$, then applying the Cauchy inequality to ${V_{1}}(t )$ in Theorem 3.1, we have

$$ E\bigl[{ \bigl\vert {{V_{1}}(t )} \bigr\vert ^{p}} \bigr] \le E{\bigl[{ \bigl\vert {{V_{1}}(t )} \bigr\vert ^{2p}}\bigr]^{\frac{1}{2}}} \le { \Bigl[ {\mathop{\sup } _{t \in [0,T]} E\bigl[{{ \bigl\vert {{V_{1}}(t )} \bigr\vert }^{2p}}\bigr]} \Bigr] ^{\frac{1}{2}}}. $$

Noting that $2p \ge 2$ and using (3.9), we obtain

$$ E\bigl[{ \bigl\vert {{V_{1}}(t )} \bigr\vert ^{p}} \bigr] \le \sqrt{{C_{4}}(\lambda,p, \sigma _{1},{\theta _{1}},{\kappa _{1}},H,{v_{1}},T)}. $$

Because $t \in [0,T]$ is arbitrary, (3.9) is proved for $1 \le p < 2$.

For $0 < p < 1$, note that

$$\begin{aligned} { \bigl\vert {{V_{1}}(t )} \bigr\vert ^{p}} &= { \bigl\vert {{V_{1}}(t )} \bigr\vert ^{p}} {I_{\{ \vert {{V_{1}}(t )} \vert \ge 1\} }} + { \bigl\vert {{v_{1}}(t )} \bigr\vert ^{p}} {I_{\{ \vert {{V_{1}}(t )} \vert < 1 \} }} \\ &\le { \bigl\vert {{V_{1}}(t )} \bigr\vert ^{p + 1}} {I_{\{ \vert {{V_{1}}(t )} \vert \ge 1\} }} + { \bigl\vert {{V_{1}}(t )} \bigr\vert ^{p}} {I_{\{ \vert {{V_{1}}(t )} \vert < 1\} }}. \end{aligned}$$

Further we have

$$ { \bigl\vert {{V_{1}}(t )} \bigr\vert ^{p}} \le { \bigl\vert {{V_{1}}(t )} \bigr\vert ^{p + 1}} {I_{\{ \vert {{V_{1}}(t )} \vert \ge 1\} }} + 1 \le { \bigl\vert {{V_{1}}(t)} \bigr\vert ^{p + 1}} + 1. $$

Hence it follows that, in the case $1 < p < 2$,

$$ \mathop{\sup } _{t \in [0,T]} E\bigl[{ \bigl\vert {{V_{1}}(t )} \bigr\vert ^{p}}\bigr] \le \sqrt{{c_{4}}(\lambda,p, \sigma _{1},{\theta _{1}},{\kappa _{1}},H,{v_{1}},T)} + 1. $$

Thus the proof of the lemma is completed. □

Lemma 3.4

The stock price equation of the CEV model has a unique solution. For any positive constant p, we have

$$ \mathop{\sup } _{t \in [0,T]} E\bigl[{ \bigl\vert {{S_{i}}(t)} \bigr\vert ^{p}}\bigr] \le {c_{10}}(r,\lambda,p,\sigma _{i},H,{\theta _{i}},{\kappa _{i}},{v_{i}},{s_{i}},T), \quad i = 1,2. $$

(3.17)

Proof

A similar proof of the existence and uniqueness of stock price equation can be found in [14]; (3.17) can be obtained by following the proof of Lemma 3.1. □

4 Continuous dependence

In this section, we discuss the continuity of the stock price equation of the CEV model.

Theorem 4.1

The stock price process of the CEV model $\{ {S_{i}}(t),t \ge 0\}$ is continuous in t, $i=1,2$.

Proof

We only prove the case $i = 1$. Note that, for any $0 \le s < t \le T$,

$$ {S_{1}}(t) - {S_{1}}(s) = \int _{s}^{t} {r{S_{{ {1}}}}(\tau )\, \mathrm{d}\tau } + \int _{s}^{t} {\sqrt{ \bigl\vert {v_{1}}( \tau ) \bigr\vert } {S_{1}} {{(\tau )}^{{\alpha _{1}}}}} \,\mathrm{d}M _{1,1}^{H}(\tau ). $$

Using the inequality ${(a + b)^{p}} \le {2^{p - 1}}({a^{p}} + {b^{p}})$, we obtain

$$ { \bigl\vert {S(t) - S(s)} \bigr\vert ^{p}} \le {2^{p - 1}} {A_{5}} + {2^{p - 1}} {A_{6}}, $$

(4.1)

where ${A_{5}} = { \vert {\int _{s}^{t} {r{S_{1}}(\tau )\,\mathrm{d} \tau } } \vert ^{p}}$, ${A_{6}} = { \vert {\int _{s}^{t} {\sqrt{| {v_{1}}(\tau )|} {S_{1}}{{(\tau )}^{{\alpha _{1}}}}} \,\mathrm{d}M _{1,1}^{H}(\tau )} \vert ^{p}}$. Let $p > 0$, $q > 0$, $\frac{1}{p} + \frac{1}{q} = 1$. Using the Hölder inequality, since $\frac{p}{q} = p - 1$, we have

$$ { \biggl\vert { \int _{s}^{t} {{S_{1}}(\tau )\, \mathrm{d}\tau } } \biggr\vert ^{p}} \le {(t - s)^{\frac{p}{q}}} \int _{s}^{t} {{{ \bigl\vert {{S_{1}}( \tau )} \bigr\vert }^{p}}\,\mathrm{d}\tau } \le {(t - s)^{p - 1}} \int _{s}^{t} {{{ \bigl\vert {{S_{1}}(\tau )} \bigr\vert }^{p}}\,\mathrm{d} \tau }. $$

(4.2)

Inequalities (3.17) and (4.2) imply that

$$ E[{A_{5}}] \le {r^{p}} {c_{10}}(r, \lambda,p,\sigma _{1},H,{\theta _{1}}, {\kappa _{1}},{v_{1}},{s_{1}},T) \cdot { \vert {t - s} \vert ^{p}}. $$

(4.3)

Now we pay attention to $E[{A_{6}}]$. By the inequality ${(a + b)^{p}} \le {2^{p - 1}}({a^{p}} + {b^{p}})$ we have

$$\begin{aligned} {A_{6}} \le{}& {2^{p - 1}} { \biggl\vert { \int _{s}^{t} {\sqrt{ \bigl\vert {v_{1}}( \tau ) \bigr\vert } {S_{1}} {{(\tau )}^{{\alpha _{1}}}}} \,\mathrm{d} {B_{1,1}}( \tau )} \biggr\vert ^{p}} \\ &{}+ {2^{p - 1}} { \biggl\vert { \int _{s}^{t} {\sqrt{ \bigl\vert {v_{1}}( \tau ) \bigr\vert } {S_{1}} {{(\tau )}^{{\alpha _{1}}}}} \,\mathrm{d}B_{1,1}^{H}( \tau )} \biggr\vert ^{p}}. \end{aligned}$$

(4.4)

Using the B-D-G inequality [12] and the Hölder inequality and choosing $\frac{2}{p} + \frac{1}{q} = 1$, $p > 0$, $q > 0$, we have

$$\begin{aligned} &E\biggl[{ \biggl\vert { \int _{s}^{t} {\sqrt{ \bigl\vert {v_{1}}(\tau ) \bigr\vert } {S _{1}} {{(\tau )}^{{\alpha _{1}}}}} \,\mathrm{d} {B_{1,1}}(\tau )} \biggr\vert ^{p}}\biggr] \\ &\quad \le { \biggl\vert { \int _{s}^{t} {E\bigl[ \bigl\vert {v_{1}}(s) \bigr\vert \cdot \bigl\vert S(\tau ) \bigr\vert ^{2{\alpha _{1}}}\bigr]} \,\mathrm{d}\tau } \biggr\vert ^{{p / 2}}} \le { \biggl( { \int _{s}^{t} {E\bigl[ \bigl\vert {v_{1}}(\tau ) \bigr\vert ^{2q}\bigr]} \,\mathrm{d} \tau } \biggr)^{\frac{1}{2}p - 1}} \int _{s}^{t} {E\bigl[ \bigl\vert S(\tau ) \bigr\vert ^{{\alpha _{1}}p}\bigr]} \,\mathrm{d} \tau. \end{aligned}$$

Combining Theorem 3.1 and (3.17), we obtain

$$\begin{aligned} & E\biggl[{ \biggl\vert { \int _{s}^{t} {\sqrt{ \bigl\vert {v_{1}}(\tau ) \bigr\vert } {S _{1}} {{(\tau )}^{{\alpha _{1}}}}} \,\mathrm{d} {B_{1,1}}(\tau )} \biggr\vert ^{p}}\biggr] \\ &\quad \le {c_{11}}(r,\lambda,p,\sigma _{1},H,{\theta _{1}},{\kappa _{1}}, {v_{1}},{s_{1}},T) \cdot { \vert {t - s} \vert ^{\frac{1}{2}p}}. \end{aligned}$$

(4.5)

Following the similar proof of Lemma 3.1 and using the Hölder inequality, we have

$$\begin{aligned} &E\biggl[{ \biggl\vert { \int _{s}^{t} {\sqrt{ \bigl\vert {v_{1}}(\tau ) \bigr\vert } {S _{1}} {{(\tau )}^{{\alpha _{1}}}}} \,\mathrm{d}B_{1,1}^{H}(\tau )} \biggr\vert ^{p}}\biggr] \\ &\quad \le \frac{1}{{{2^{p}}}}{c_{1}}(p){H^{p}} {2^{p - 1}} \int _{s}^{t} {E\bigl[ \bigl\vert {V_{1}}(t ) \bigr\vert ^{{p / 2}} \bigl\vert {S_{1}}(\tau ) \bigr\vert ^{{\alpha _{1}}p}\bigr] \,\mathrm{d}t} + {c_{3}}(p,H) \bigl({t^{2H - 1}} - {s^{2H - 1}}\bigr) \\ &\quad \le \frac{1}{{{2^{p}}}}{c_{1}}(p){H^{p}} {2^{p - 1}} \int _{s}^{t} {\sqrt{E\bigl[ \bigl\vert {V_{1}}(t ) \bigr\vert ^{p}\bigr]E\bigl[ \bigl\vert {S_{1}}(\tau ) \bigr\vert ^{2{\alpha _{1}}p}\bigr]} \,{\mathrm{ {d}}}t} \\ &\qquad{}+ {c_{3}}(p,H) \bigl({t^{2H - 1}} - {s^{2H - 1}} \bigr). \end{aligned}$$

We use (3.10) and (3.17) to obtain

$$\begin{aligned} & E\biggl[{ \biggl\vert { \int _{s}^{t} {\sqrt{ \bigl\vert {v_{1}}(\tau ) \bigr\vert } {S _{1}} {{(\tau )}^{{\alpha _{1}}}}} \,\mathrm{d}B_{1,1}^{H}(\tau )} \biggr\vert ^{p}}\biggr] \\ &\quad \le {c_{12}}(p,H) (t - s) + {c_{13}}(p,H) \bigl({t^{2H - 1}} - {s^{2H - 1}}\bigr). \end{aligned}$$

(4.6)

Substituting (4.5) and (4.6) into (4.4) and combing (4.1), (4.3), and (4.4), we get

$$\begin{aligned} & E\bigl[{ \bigl\vert {S(t) - S(s)} \bigr\vert ^{4}} \bigr] \\ &\quad \le {c_{12}}(p,H) (t - s) + {c_{13}}(p,H) \bigl({t^{2H - 1}} - {s^{2H - 1}}\bigr) \\ &\qquad{}+ {c_{11}}(r,\lambda,p,\sigma _{1},H,{\theta _{1}},{\kappa _{1}},{v_{1}},{s_{1}},T) \cdot { \vert {t - s} \vert ^{\frac{1}{2}p}} \\ &\qquad{}+ {c_{10}}(r,\lambda,p,\sigma _{1},H,{\theta _{1}},{\kappa _{1}},{v_{1}},{s_{1}},T) \cdot { \vert {t - s} \vert ^{p}}. \end{aligned}$$

(4.7)

Therefore the theorem is proved. □

Let $T_{0}$ be a constant belonging to $(0, T)$. Let ${S_{i}}(t,{s _{i}})$ be the solution of ${S_{i}}(t)$ in (1.2) with ${S_{i}}({T_{0}}) = {s_{i}}$, $i = 1,2$. Now we consider the continuity of ${S_{i}}(t, {s_{i}})$ with respect to ${s_{i}}$, $i = 1,2$.

Lemma 4.1

For any fixed $t \in [{T_{0}},T]$, we have

$$ E\Bigl[\mathop{\sup } _{0 \le t \le T} \bigl\vert {S_{i}}(t,{s_{1}}) - {S_{i}}(t, {s_{2}}) \bigr\vert ^{2} \Bigr] \le {c_{13}} \vert {s_{1}} - {s_{2}} \vert ^{2}, $$

(4.8)

where ${c_{13}}$ is a constant depending on T and $T_{0}$, $i=1,2$.

Proof

We only prove the case $i= 1$. Let ${s_{2}} = {s_{1}} + \Delta s$ and $0 \le t \le T$. Then we have

$$\begin{aligned} {S_{1}}(t,{s_{1}}) - {S_{1}}(t,{s_{2}}) ={}& \Delta s + r \int _{0}^{t} {{S_{1}}(s,{s_{1}}) - {S_{1}}(t,{s_{2}})} \,\mathrm{d}s \\ &{}+ \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \bigl[{S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}})\bigr]} \,\mathrm{d}M_{1,1}^{(H)}(s). \end{aligned}$$

Thus it follows that

$$\begin{aligned} &\bigl\vert {S_{1}}(t,{s_{1}}) - {S_{1}}(t,{s_{2}}) \bigr\vert ^{2} \\ &\quad \le 3 \vert \Delta s \vert ^{2} + 3{r^{2}} \biggl\vert \int _{0}^{t} {{S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}})} \,\mathrm{d}s \biggr\vert ^{2} \\ &\qquad{}+ 3 \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \bigl[{S_{1}}(s,{s_{1}}) - {S_{1}}(s, {s_{2}})\bigr]} \,\mathrm{d}M_{1,1}^{(H)}(s) \biggr\vert ^{2}. \end{aligned}$$

(4.9)

Using the inequality ${(a + b)^{2}} \le 2({a^{2}} + {b^{2}})$, we have

$$ \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \bigl[{S_{1}}(s,{s_{1}}) - {S_{1}}(s, {s_{2}})\bigr]} \,\mathrm{d}M_{1,1}^{(H)}(s) \biggr\vert ^{2} \le 2{A_{7}} + 2 {\lambda ^{2}} {A_{8}}, $$

(4.10)

where

$$\begin{aligned} &{A_{7}} = \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \bigl[{S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}})\bigr]} \,\mathrm{d}B_{1,1}(s) \biggr\vert ^{2}, \\ &{A_{8}} = \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \bigl[{S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}})\bigr]} \,\mathrm{d}M_{1,1}^{(H)}(s) \biggr\vert ^{2}. \end{aligned}$$

The Burkholder–Davis–Gundy and Hölder inequalities lead to

$$\begin{aligned} E[{A_{7}}] &= \biggl\vert \int _{0}^{t} {\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \bigl[{S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}})\bigr]} \,\mathrm{d}B_{1}(s) \biggr\vert ^{2} \\ &\le \int _{0}^{t} E\bigl[\sqrt{ \bigl\vert {V_{1}}(s) \bigr\vert } \bigl({S_{1}}(s, {s_{1}}) - {S_{1}}(s,{s_{2}})\bigr)\bigr] ^{\mathrm{{2}}}\,{\mathrm{{d}}}s \\ &\le \int _{0}^{t} E\bigl[ \bigl\vert {V_{1}}(s) \bigr\vert \bigr] ^{\mathrm{{2}}}E\bigl[ \bigl\vert {S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}}) \bigr\vert ^{2}\bigr]\,{\mathrm{ {d}}}s. \end{aligned}$$

We use Theorem 3.1 to obtain

$$ E[{A_{7}}] \le {c_{14}}(\lambda,\sigma,{\kappa _{i}},H,{v_{i}},T) \int _{0}^{t} {E\bigl[ \bigl\vert {S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}}) \bigr\vert ^{2}\bigr]} \,\mathrm{d}s. $$

(4.11)

Similarly to the proof of (3.9), we have that

$$\begin{aligned} E[{A_{8}}] &\le {c_{1}} \int _{{T_{0}}}^{t} {\sqrt{E\bigl[ \bigl\vert {V_{1}}(s) \bigr\vert \cdot \bigl\vert {S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}}) \bigr\vert ^{2} \bigr]} } \,{\mathrm{ {d}}} {s^{H}} \\ &\le {c_{1}} \int _{{T_{0}}}^{t} {{s^{H - 1}}\sqrt{E\bigl[ \bigl\vert {V_{1}}(s) \bigr\vert \cdot \bigl\vert {S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}}) \bigr\vert ^{2}\bigr]} } \,\mathrm{d}s \\ &\le {c_{1}}T_{0}^{H - 1} \int _{{T_{0}}}^{t} {\sqrt{E\bigl[ \bigl\vert {V_{1}}(s) \bigr\vert \cdot \bigl\vert {S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}}) \bigr\vert ^{2} \bigr]} } \,\mathrm{d}s. \end{aligned}$$

Using Theorem 3.1, we have

$$ E[{A_{8}}] \le {c_{1}}T_{0}^{H - 1}{c_{14}} \int _{{T_{0}}}^{t} {\sqrt{E\bigl[ \bigl\vert {V_{1}}(s) \bigr\vert \cdot \bigl\vert {S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}}) \bigr\vert ^{2} \bigr]} } \,\mathrm{d}s. $$

(4.12)

Now we pay attention to $E[{A_{8}}]$. The Hölder inequality implies that

$$ E\biggl[ \biggl\vert \int _{0}^{t} {{S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}})} \,{\mathrm{ {d}}}s \biggr\vert ^{2}\biggr] \le \int _{0}^{t} {E\bigl[ \bigl\vert {S_{1}}(s,{s_{1}}) - {S_{1}}(s, {s_{2}}) \bigr\vert ^{2}\bigr]} \,\mathrm{d}s. $$

(4.13)

Therefore it follows from (4.9)–(4.13) that

$$\begin{aligned} &\bigl\vert {S_{1}}(t,{s_{1}}) - {S_{1}}(t,{s_{2}}) \bigr\vert ^{2} \\ &\quad \le 3 \vert \Delta s \vert ^{2} + \bigl(3{r^{2}} + 3{c_{14}} + 3{c_{1}}T_{0}^{H - 1} {c_{14}}\bigr) \int _{0}^{t} {E\bigl[ \bigl\vert {S_{1}}(s,{s_{1}}) - {S_{1}}(s,{s_{2}}) \bigr\vert ^{2}\bigr]} \,\mathrm{d}s. \end{aligned}$$

Then Gronwall’s inequality implies that

$$\begin{aligned} &E\Bigl[\mathop{\sup } _{0 \le t \le {T_{1}}} \bigl\vert {S_{1}}(t, {s_{1}}) - {S_{1}}(t,{s_{2}}) \bigr\vert ^{2}\Bigr] \\ &\quad \le 3 \vert \Delta s \vert ^{2}\exp \bigl\{ {{c_{15}}(t - {T_{0}})} \bigr\} \le 3 \vert \Delta s \vert ^{2} \exp \{ {{c_{15}}T} \}. \end{aligned}$$

This inequality is true for any $t \in [{T_{0}},T]$. Hence we have

$$ E\Bigl[\mathop{\sup } _{0 \le t \le T} \bigl\vert {S_{1}}(t,{s_{1}}) - {S_{1}}(t, {s_{2}}) \bigr\vert ^{2} \Bigr] \le 3 \vert \Delta s \vert ^{2}\exp \{ {{c_{15}}T} \} = {c_{16}} \vert {s_{1}} - {s_{2}} \vert ^{2}. $$

 □

5 Vulnerable option pricing

In this section, we investigate the European vulnerable options under the stochastic volatility model (1.2)–(1.4). Let T denote the expiration time of a vulnerable call option with payoff given by

$$ F\bigl({S_{1}}(T),{S_{2}}(T)\bigr) = \max \bigl\{ {S_{1}}(T) - K,0\bigr\} \biggl({I_{{S_{2}}(T) > {D^{*}}}} + \frac{{1 - \alpha }}{D}{I_{{S_{2}}(T) \le {D^{*}}}}\biggr). $$

(5.1)

Here, K is the strike price of the option. ${S_{2}}(T)$ is less than the amount ${D^{*}}$, which corresponds to the amount of claims D outstanding at execution time T. Once default events occur at execution time T, the recovery is $\frac{{(1 - \alpha )}}{D}{S_{2}}(T)$, where α represents the deadweight costs related to the bankruptcy or reorganization.

Under the risk neutral measure Q, the value of the vulnerable call option at current time t is defined by

$$ c\bigl(t,{S_{1}}(t),{S_{2}}(t)\bigr) = \exp \bigl\{ - r(T - t)\bigr\} {E_{t}}\bigl[F\bigl({S_{1}}(T), {S_{2}}(T)\bigr)\bigr]. $$

(5.2)

Now we are going to describe the time discretization of the SDE (1.2)–(1.3) over the time interval $[0,T]$, which is divided into N time steps, with

$$ \Delta t = {{(T - t)} / N} \quad\mathrm{and}\quad {t_{n}} = n\Delta t,\quad n = 0,1,2, \ldots,N. $$

(5.3)

Let $\{ S_{n}^{(1)}\}$, $\{ S_{n}^{(2)}\}$, $\{ v_{n}^{(1)}\}$, and $\{ v_{n}^{(2)}\}$ be approximations of $\{ {S_{1}}(t)\}$, $\{ {S_{2}}(t)\}$, $\{ {v_{1}}(t)\}$, and $\{ {v_{2}}(t)\}$ at time level $t_{n}$, respectively. The volatility processes $\{ {v_{1}}(t) \}$ and $\{ {v_{2}}(t)\}$ in (1.3) are written in the integral form as

$$ v_{t + \Delta t}^{(i)} = v_{t}^{(i)} + \int _{t}^{t + \Delta t} {{\kappa _{i}}\bigl( {\theta _{i}} - {v_{i}}(s)\bigr)\,\mathrm{d}s} + { \sigma _{i}} \int _{t}^{t + \Delta t} {\sqrt{{v_{i}}(t)}\, \mathrm{d}M_{2,i}^{H}(t)},\quad i =1,2. $$

(5.4)

Using the left-point rule of the Euler discretization, the integrals can be approximated as follows;

$$\begin{aligned} &\int _{t}^{t + \Delta t} {{\kappa _{i}}\bigl({ \theta _{i}} - {v_{i}}(s)\bigr)\,\mathrm{ {d}}s} \approx {\kappa _{i}}\bigl({\theta _{i}} - v_{t}^{(i)} \bigr)\Delta t, \end{aligned}$$

(5.5)

$$\begin{aligned} &\int _{t}^{t + \Delta t} {\sqrt{{v_{i}}(t)}\, \mathrm{d}M_{2,1}^{H}(t)} \approx {\sqrt{v _{t}^{(i)}}}\bigl(M_{2,i}^{H}(t + \Delta t) - M_{2,i}^{H}(t)\bigr). \end{aligned}$$

(5.6)

Substituting (5.5) and (5.6) into (5.4), the discretization of (1.3)–(1.4) produces

$$ v_{t + \Delta t}^{(i)} = v_{t}^{(i)} + { \kappa _{i}}\bigl({\theta _{i}} - v _{t}^{(i)} \bigr)\Delta t + {\sigma _{i}} {\sqrt{v_{t}^{(i)}}} \bigl(M_{2,i}^{H}(t + \Delta t) - M_{2,i}^{H}(t) \bigr), $$

(5.7)

$v_{0}^{(i)} = {v_{i}}$, $i = 1,2$. Following the similar proof of (5.7), the Euler discretization of the stock price ${S_{i}}(t)$ is

$$ S_{t + \Delta t}^{(i)} = S_{t}^{(i)} + \mathit{rS}_{t}^{(i)}\Delta t + \sqrt{v _{t}^{(i)}} {\bigl(S_{t}^{(i)} \bigr)^{{\alpha _{1}}}}\bigl(M_{1,1}^{H}(t + \Delta t) - M_{1,1}^{H}(t)\bigr), $$

(5.8)

$S_{0}^{(i)} = {S_{i}}$, $i=1,2$. The call price of a vulnerable option from this simulated asset price path is then computed using the formula of discounted payoff

$$ \exp \bigl\{ - r(T - t)\bigr\} F\bigl(S_{N}^{(1),k},S_{N}^{(2),k} \bigr), $$

(5.9)

where $\{ S_{j}^{(1),k},j = 1,2, \ldots,N\}$ and $\{ S_{j}^{(2),k},j = 1,2, \ldots,N\}$ are the kth simulations of $\{ {S_{1}}(\tau ), \tau \in [t,T]\}$ and $\{ {S_{2}}(\tau ), \tau \in [t,T]\}$, respectively. This completes a one-sample iteration of Monte Carlo simulation for vulnerable call option. After running the simulation (5.7)–(5.9) sufficiently many times, the expected value is obtained by computing the sample mean of estimates to (5.2). Let M denote the total number of simulation runs. The call value of vulnerable option is computed by

$$ {\hat{c}_{M,N}}\bigl(t,{S_{1}}(t),{S_{{{2}}}}(t) \bigr) = \exp \bigl\{ - r(T - t)\bigr\} \frac{1}{M}\sum _{k = 1}^{M} {F\bigl(S_{N}^{(1),k},S _{N}^{(2),k}\bigr)}. $$

(5.10)

In the following section, we present some simulation results to examine how the parameters of the mixed fractional CEV model affect the valuation of the vulnerable call option. All our numerical results have been performed with the parameters in Table 1.

Table 1 Parameters used for simulation

Example 1

If ${\kappa _{1}} = {\kappa _{2}} = 0$, ${\sigma _{1}} = {\sigma _{2}} = 0$, ${v_{2}}(0) = 0$, and $H = 0.5$, then we have ${v_{1}}(t) = 0.05$ and ${v_{2}}(t) = 0$. The value of the vulnerable call at current time t has the closed form

$$\begin{aligned} &c(t,{s_{1}},{s_{2}}) \\ &\quad= {s_{1}} {N_{2}}\bigl({d_{+} }(T - t,{{{s_{1}}}/ K}) + \sqrt{{v_{1}}(T - t)},{d_{-} }(T - t,{{{s_{2}}} / D}) + {\rho } \sqrt{{v_{1}}(T - t)}, {\rho }\bigr) \\ &\qquad{}- K \exp \bigl\{ - r(T - t)\bigr\} {N_{2}}\bigl({d_{+} }(T - t,{{{s_{1}}} / K}),{d_{-} }(T - t,{{{s_{2}}} / D}),{\rho _{1}}\bigr) \\ &\qquad{}+ \frac{ {(1 - \alpha )}}{D}{s_{2}}\exp \bigl\{ (r + {\rho } \sqrt{{v_{1}} {v_{2}}} ) (T - t)\bigr\} {N_{2}}({d_{1}},{d_{2}},{\rho }) \\ &\qquad{}+ \frac{ {(1 - \alpha ){s_{2}}K}}{D}{N_{2}}({d_{{{3}}}}, - {d_{{ {4}}}}, {\rho }), \end{aligned}$$

(5.11)

where $N_{2}$ is the bivariate normal cumulative distribution function, and

$$\begin{aligned} &{d_{+} }(t,{s_{1}}) = \frac{{\ln {s_{1}} + (r + 0.5{v_{1}})t}}{{\sqrt{ {v_{1}}t} }},\qquad {d_{-} }(t,{s_{2}}) = \frac{{\ln {s_{2}} + (r + 0.5 {v_{2}})t}}{{\sqrt{{v_{2}}t} }}, \\ &{d_{1}} = {d_{+} }(T - t,{{{s_{1}}} / K}) + \sqrt{{v_{1}}(T - t)} + {\rho }\sqrt{ {v_{2}}(T - t)}, \\ &{d_{2}} = {d_{-} }(T - t,{{{s_{2}}} / D}) - {\rho }\sqrt{{v_{1}}(T - t)} - \sqrt{ {v_{2}}(T - t)}, \\ &{d_{{{3}}}} = {d_{+} }(T - t,{{{s_{1}}} / K}) + {\rho }\sqrt{{v_{2}}(T - t)},\qquad {d_{{{4}}}} = {d_{-} }(T - t,{{{s_{2}}} / D})+\sqrt{{v_{2}}(T - t)}. \end{aligned}$$

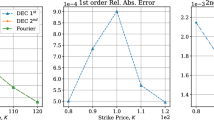
Here we compare the value of the vulnerable call using the scheme (5.7)–(5.10) with the explicit one obtained by (5.11). Figure 1 shows the price of the vulnerable call option with various values of M and N. In the figure, ${\hat{c}_{M,N}}(t,{S_{1}}(t),{S_{{ {2}}}}(t))$ converges to $c(t,{s_{1}},{s_{2}})$ as $(M,N) \to (\infty ,\infty )$. We also show the properties of option prices in Fig. 2, which shows accurate approximations for large numbers M (i.e., $M=20\text{,}000$) and how the prices of vulnerable call change with respect to the asset price $s_{1}$ and strike price K.

Figure 1

Vulnerable call option of different values of M and N

Figure 2

Vulnerable call option of different values of K and $s_{1}$

The next example shows the effect of the volatility equation on the vulnerable call.

Example 2

In this example, we consider the valuation of the vulnerable call option under the mixed fractional CEV model (1.2)–(1.3). Let $M = 2\text{,}000\text{,}000$ and $N = 20\text{,}000$. Figure 3 shows the valuation of the vulnerable call option for five amounts of claims $D = 10$, $D = 50$, $D = 90$, and $D = 130$ with different $s_{2}$. In Fig. 3, we observe that the option price has a decreasing trend of the D and an increasing trend of the $s_{2}$. Figure 4 shows the valuation of the vulnerable call option with respect to correlation ${\rho _{1}}$ and $s_{2}$.

Figure 3

Vulnerable call option for different values of D and $s_{2}$

Figure 4

Vulnerable call option for different values of ${\rho _{1}}$ and $s_{2}$