Abstract
We prove that uniformly small short-range perturbations do not close the bulk gap above the ground state of frustration-free quantum spin systems that satisfy a standard local topological quantum order condition. In contrast with earlier results, we do not require a positive lower bound for finite-system spectral gaps uniform in the system size. To obtain this result, we extend the Bravyi–Hastings–Michalakis strategy so it can be applied to perturbations of the GNS Hamiltonian of the infinite-system ground state.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the characteristic properties of gapped topologically ordered ground state phases of quantum many-body systems is the stability of the spectral gap above the ground state with respect to small perturbations of the Hamiltonian. Stability results for the ground state gap have a long history. The first result, due to Yarotsky [64], included the stability of the gap of the AKLT chain, named after Affleck, Kennedy, Lieb, and Tasaki [1]. The approach we follow in this paper has a much broader range of applicability; it was introduced by Bravyi, Hastings, and Michalakis [12] and further developed in [13, 26, 41, 48]. Other approaches have been introduced in recent years [17, 20,21,22]. These new approaches can also treat some cases of models with unbounded on-site Hamiltonians, see [48, Section 1] for a more detailed discussion. The Bravyi–Hastings–Michalakis strategy, however, is the only approach that handles general cases with non-trivial topological order.
One obstacle to proving spectral gaps for topological insulators is the common occurrence of gapless edge states. Spectral analysis for interacting many-body systems is usually carried out for finite systems for which edge states typically imply that there is no spectral gap uniform in the system size. Nevertheless, there may be a bulk gap, meaning excitations away from the boundary of the system have energy bounded below uniformly in the system size. The goal of this work is to prove stability for the bulk gap in a way that does not require the assumption of a uniform positive lower bound in the spectrum of finite systems. Previously, it was shown how certain cases can be handled by considering sequences of finite systems with suitable boundary conditions. For example, such an approach may work if the edge states are absent in the model considered with periodic boundary conditions [41, 48]. In general, however, there may not be a suitable boundary condition that ‘gaps out’ the boundary modes or we may not know whether such a boundary condition exists. Systems defined on a quasicrystal structure, for example, may be an instance where no simple way of removing gapless edge modes is available [39]. In our approach here, we only assume that the infinite system described in the Gelfand-Naimark-Segal (GNS) representation of the ground state has a gap. Under natural assumptions consistent with the previous works cited above, we prove that sufficiently small but extensive perturbations do not close the gap.
We adapt the strategy of Bravyi et al. [12] and Refs. [13, 41], and use the techniques we developed in [47, 48] to handle the infinite system setting. From a certain perspective, and apart from the technical aspects to deal with unbounded Hamiltonians, the infinite system setting allows for a simplification in the statement of conditions and the main result. In particular, the local topological quantum order (LTQO) condition is simpler to state directly for the infinite system. The LTQO property is well know to hold for one-dimensional systems with matrix product state (MPS) ground states [48, Appendix B]. It is also well-established for Kitaev’s quantum double models [16, 34] and the Levin-Wen string-net model [37, 57]. LTQO was recently also shown to hold for the AKLT model on a decorated hexagonal lattice [40].
For concreteness, we work in the quantum spin system setting but, using the arguments of [46], our approach is applicable to frustration-free lattice fermion systems too. We will provide a detailed account of this in a forthcoming paper, thus providing an alternative and generalization of the gap stability results for quasi-free lattice fermions in the literature [17, 26, 35].
The assumption that the bulk Hamiltonian has a gap in the spectrum above the ground state appears in several important recent works. For example, the construction of an index for the classification of symmetry-protected topological phases in the works of Ogata and co-authors makes use of this assumption [43, 49,50,51]. Other examples are in the recent work on adiabatic theorems for infinite many-body systems [3, 4, 29]. All of these works use the same general setting as described in Sect. 2.
In addition to the main stability result, we also prove Theorem A.1, which shows that a differentiability assumption introduced in [43] and also used in later work [49, 51, 52, 56] is always satisfied. A similar result appeared in the PhD dissertation of Moon [42, Appendix]. As a consequence, we establish a stability theorem for the bulk gap in the exact setting of the series of works of Ogata and others on the classification of Symmetry Protected Topological (SPT) phases cited above. This was the main motivation for this work.
Before closing this introduction, we comment on two specific applications of the stability theorem for infinite systems proved in this paper, and briefly elaborate on the relevance of the spectral analysis for infinite systems.
The first concerns spin liquids, specifically the ongoing search for two-dimensional spin models with topologically non-trivial spin liquid ground states characterized by a bulk gap and gapless edge modes. A plausible example of a rich phase diagram showing such a phase is found based on various numerical approaches for an SU(3)-invariant antiferromagnetic in [63]. As the discussion in that work illustrates, the existence of such phases and the precise nature of the edge modes is a topic of ongoing intense study. Assuming one has established the existence of such a phase, even if the expected properties of the local gaps and LTQO can be demonstrated, the question of the nature of the edge states may remain a challenge. What we can say based on our work is that the putative chiral spin liquid phases, if predictions based on numerical results are confirmed, are stable gapped phases in the usual sense. Granted, if the relevant models can be shown to be uniformly gapped on finite volumes with a torus geometry, there would be no need work in the GNS representation to prove stability of the gap. Next, we discuss an application where periodic boundary conditions are not an option and a general strategy to exclude edge modes in finite volume is not known.
The second application is the case of models defined on quasi-crystal lattices we mentioned before. Gapless edge modes are also expected to be relevant there. So far, they have been studied only in the single-particle setting with the goal to numerically distinguish the behavior of edge modes from bulk spectrum [39] or to prove the existence of a bulk gap in the presence of gapless edge modes [28]. These approaches have yet to be generalized to the many-body setting. Our approach here assumes only a general regularity property of the lattice, which is easily satisfied by quasi-crystals.
As a final remark, we wish to emphasize that significant progress has been made over the years studying both infinite systems as well as properties of finite systems and studying their asymptotics. Valid points in favor of either approach have been made in the literature. For example, in [15, Section 2.5], the authors argue that the mathematics of the infinite system setting could be a distraction for the audience they have in mind. In [62], the authors are motivated by the common observation that ‘many features of physical systems, both qualitative and quantitative, become sharply defined or tractable only in some limiting situation’, and introduce a general approach to formulate the dynamics of such limiting systems. The infinite system setting has recently seen increased interest and continues to serve as the setting of new interesting results, for example in [31, 53]. In our view, both approaches are fruitful in their particular contexts, and so proving stability directly in the infinite volume setting is interesting in its own right. Other works have similarly obtained infinite-system results for automorphic equivalence [43], the Lieb-Schultz-Mattis Theorem [54, 55], invertible states [5], and adiabatic theory [29].
In a previous paper on the topic, we discussed in some detail the literature on spectral gap stability, including historically important works and alternative methods [48]. Here, we just like to add to that discussion by mentioning two recent works based on adaptions of the iterative Lie Schwinger block-diagonalization method introduced by Fröhlich and Pizzo [22]. The new work aims at a more detailed analysis of two well-known quantum spin chains, the XXZ chain [19] and the AKLT model [18], supplementing the basic spectral gap stability obtained in previous works, including [41, 48, 61, 64].
The content of this paper is structured as follows. Section 2 provides the setup for interactions with stretched exponential decay we use, and includes the statement of the main results. This decay class can be regarded as a minor variation of the notions of almost-local observables used in [5, 30] and the Banach spaces of g-local observables in [43]. The main technical advance in this work is the incorporation of the (unbounded) GNS Hamiltonian in the development of the Bravyi–Hastings–Michalakis (BHM) strategy for proving gap stability. Properties such as the definition of the transformed Hamiltonian and its decomposition require a new look. Some properties that are obvious in the finite-system setting become non-trivial because they involve super operators formally acting on densely defined unbounded operators on a domain for which an explicit description is not available. We lay the ground work for dealing with these issues in Sect. 3, and carry out the BHM strategy in Sect. 4. Section 5 contains the proof of the form bound for the transformed Hamiltonian, which is a mild adaptation of a result of Michalakis and Zwolak [41] to the GNS setting. The final arguments needed to prove the main results are also contained in this section. In two appendices we prove two result that may be of independent interest. The first is that the LTQO property implies the kernel of the GNS Hamiltonian is one dimensional (something we use and that is often introduced as a separate assumption in other works). The second is about the differentiability of the quasi-adiabatic dynamics and is a variant of a result that first appeared in the PhD dissertation of Moon [42].
2 Setup and statement of the main results
2.1 Setup and notation
The models considered in this work are defined on a \(\nu \)-regular discrete metric space \((\Gamma ,d)\), for some \(\nu >0\). This means that there exists \(\kappa >0\) so that for all \(x\in \Gamma , n\ge 1\), \(|b_x(n)| \le \kappa n^\nu \), where \(b_x(n)= \{y\in \Gamma \mid d(x,y)\le n\}\). For \(\Lambda \in \mathcal {P}_0(\Gamma )\), the finite subsets of \(\Gamma \), and \(n\ge 0\), we also define the sets \(\Lambda (n)\) by
The algebra of local observables of the system is the usual \(\mathcal {A}^\textrm{loc} = \bigcup _{\Lambda \in \mathcal {P}_0(\Gamma )} \mathcal {A}_\Lambda \). Here, \(\mathcal {A}_\Lambda \) is the matrix algebra \(\bigotimes _{x\in \Lambda } M_{d_x}\) with \(d_x\) the dimension of the spin at x. The \(C^*\)-algebra of quasi-local observables \(\mathcal {A}\) is the completion of \(\mathcal {A}^\textrm{loc}\) with respect to the operator norm. For \(A\in \mathcal {A}^\textrm{loc}\), the support of A, denoted by \({\text {supp}}A\), is the smallest \(X\subset \Gamma \) such that \(A\in \mathcal {A}_X\). For any \(X\subset \Gamma \), \(\Pi _X: \mathcal {A}\rightarrow \mathcal {A}_X\) is the conditional expectation with respect to the tracial state \(\rho \) on \(\mathcal {A}\):
In particular, for local A, \(\Pi _X(A)\) is a normalized partial trace.
We are specifically interested in systems defined on infinite \(\Gamma \) and often want to consider approximations \(A_n\in \mathcal {A}_{\Lambda _n}\) of \(A\in \mathcal {A}\), where \(\Lambda _n\in \mathcal {P}_0(\Gamma )\) is an increasing sequence of finite volumes such that \(\bigcup _n \Lambda _n =\Gamma \). We call such a sequence \((\Lambda _n)\) an increasing and absorbing sequence (IAS). It will often be important to have an estimate for the speed of convergence of \(A_n\rightarrow A\), in terms of a non-increasing function \(g:[0,\infty )\rightarrow (0,\infty )\) that vanishes at infinity, which we call a decay function. In this paper we will only use decay functions that satisfy a moment condition of the form
In particular, we will often work with decay functions of the form
For \(a>0\) and \(\theta \in (0,1)\), such functions g are said to have stretched exponential decay. One checks that these functions satisfy
for some constant C.
Consider an IAS \((\Lambda _n)\) in \((\Gamma ,d)\), and a decay function g. Define a norm \(\Vert \cdot \Vert _{(\Lambda _n),g}\) on \(\mathcal {A}^\textrm{loc}\) and a Banach space \(\mathcal {A}^{(\Lambda _n),g}\) by
For a proof that \(\mathcal {A}^{(\Lambda _n),g}\) is the Banach space of all \(A\in \mathcal {A}\) for which \(\Vert A\Vert _{(\Lambda _n),g}<\infty \), see [43]. In fact, \(\mathcal {A}^{(\Lambda _n),g}\) is a Banach \(*\)-algebra.
For each \(x\in \Gamma \), \(\Lambda _n: =b_x(n)\) defines a IAS. In this case we set \(\Vert \cdot \Vert _{(b_x(n)),g} = \Vert \cdot \Vert _{x,g}\). Define the set
For any decay function g satisfying (2.5), any two norms from \(\{\Vert \cdot \Vert _{x,g}\mid x\in \Gamma \}\) are equivalent. Hence, for all \(x\in \Gamma \)
In this case, \(\mathcal {A}^g\) is a Banach \(*\)-algebra. Elements \(A\in \mathcal {A}^g\) are called g-local.
We will often also assume that a decay function g is uniformly summable over \(\Gamma \), i.e.,
and additionally, that there is a constant \(C>0\) such that
Any decay function g satisfying (2.9) and (2.10) will be called an F-function. For any \(\nu \)-regular \(\Gamma \), the following are F-functions appearing in this work:
In the case \(\Gamma ={\mathbb Z}^\nu \), which is \(\nu \)-regular, (2.11) defines an F-function for all \(\xi >\nu \). For a discussion of these examples and some basic inequalities, see [47, Appendix].
Assumption 2.1
(Initial Interaction) We assume the initial model is defined by a finite-range, uniformly bounded, frustration-free interaction h given in terms of a family \(h=\{ h_x \}_{x \in \Gamma }\) which satisfies:
-
1.
There is a number \(R \ge 0\), called the interaction radius, for which \(h_x^* = h_x \in \mathcal {A}_{b_x(R)}\) for all \(x \in \Gamma \).
-
2.
These terms are uniformly bounded in the sense that
$$\begin{aligned} \Vert h \Vert _{\infty } = \sup _{x \in \Gamma } \Vert h_x \Vert < \infty \, . \end{aligned}$$(2.12) -
3.
The interaction is frustration-free, meaning that \(h_x \ge 0\) for all \(x \in \Gamma \) and for any \(\Lambda \in \mathcal {P}_0( \Gamma )\),
$$\begin{aligned} \mathrm{min \, spec}(H_{\Lambda }) = 0 \quad \text{ where } \quad H_{\Lambda } = \sum _{{\mathop { \textrm{supp}(h_x) \subset \Lambda }\limits ^{x \in \Lambda :}}} h_x \, . \end{aligned}$$(2.13)
The frustration-free condition implies that the ground state space is \(\textrm{ker}(H_{\Lambda })\) for any finite volume \(\Lambda \). Moreover, \(\psi \in \textrm{ker}(H_{\Lambda })\) if and only if \(\psi \in \textrm{ker}(h_x)\) for each \(x \in \Lambda \) with \(\textrm{supp}(h_x) \subset \Lambda \). Thus, denoting by \(P_{\Lambda }\) the orthogonal projection onto \(\textrm{ker}(H_{\Lambda })\), for any \(\Lambda _0 \subset \Lambda \), one has
For such a model, the derivation \(\delta _0\) determining the infinite system dynamics is given by
It is a standard result that there is a closed derivation extending \(\delta _0\), which we also denote by \(\delta _0\), with domain \(\textrm{dom}(\delta _0)\) for which \(\mathcal {A}^\textrm{loc}\) is a core [11, Theorem 6.2.4] (note that the factor i is absorbed in the definition of the derivation in this reference). The system dynamics is then the strongly continuous one-parameter group of \(C^*\)-automorphisms \(\{\tau ^{(0)}_t \mid t\in {\mathbb R}\}\) satisfying
In fact, this differential equation holds for all \( A\in \textrm{dom}(\delta _0)\). Two other general properties are:
-
1.
\(\tau _t^{(0)}(\textrm{dom}(\delta _0))\subset \textrm{dom}(\delta _0)\) for all \(t \in \mathbb {R}\);
-
2.
\(\tau _t^{(0)}(\delta _0(A)) =\delta _0(\tau _t^{(0)}(A))\) for all \(A\in \textrm{dom}(\delta _0)\) and \(t \in \mathbb {R}\).
More generally, quantum spin models can be defined by an interaction on \(\Gamma \) which, by definition, is a map \(\Phi :\mathcal {P}_0(\Gamma )\rightarrow \mathcal {A}^\textrm{loc}\), with the property that \(\Phi (X)^* = \Phi (X) \in \mathcal {A}_X\) for all \(X\in \mathcal {P}_0(\Gamma )\). For any decay function g, an interaction norm is defined by
When the above quantity is finite for some interaction \(\Phi \), the function g is said to measure the decay of \(\Phi \). If g is an F-function, the norm \(\Vert \cdot \Vert _g\) is called an F-norm. If g is summable, in the sense of (2.9), and \(\Vert \Phi \Vert _g < \infty \), then a closable derivation on \(\mathcal {A}^\textrm{loc}\) can be defined by setting
One can prove conditions that guarantee that the derivation \(\delta \) defined on \(\mathcal {A}^\textrm{loc}\) is a generator of a strongly continuous dynamics given by automorphisms of \(\mathcal {A}\) [10, 11]. In practice, however, one usually directly proves the existence of the thermodynamic limit of the Heisenberg dynamics \(\{\tau _t\mid t\in {\mathbb R}\}\). Standard results along these lines prove the existence of the dynamics for \(\Phi \) in a suitable Banach space of interactions [11, 59, 60] starting from a convergent series for small |t|. An alternative approach, based on Lieb-Robinson bounds [38], was introduced by Robinson [58]. Lieb-Robinson bounds can be derived for any interaction \(\Phi \) with a finite F-norm [44], and this allows one to extend the results for existence of the dynamics beyond the Banach spaces of interactions \(\mathcal {B}_\lambda \) introduced by Ruelle [59]. These ideas are important for the construction of the spectral flow automorphisms [7]. This and some other generalizations relevant for the present work are discussed in detail in [47].
Recall that infinite-volume ground states associated to \(\delta \) are those states \(\omega \) on \(\mathcal {A}\) that satisfy
In the case of a frustration-free model as in (2.13), a state \(\omega \) is called a zero-energy ground state, or a frustration free ground state, if \(\omega (h_x)=0\) for all \(x\in \Gamma \). It is easy to see that a zero-energy ground state satisfies (2.19).
Let \((\mathcal {H},\pi ,\Omega )\) be the GNS triple of \(\omega \). This means that \(\pi :\mathcal {A}\rightarrow \mathcal {B}(\mathcal {H})\) is a representation of the \(C^*\)-algebra \(\mathcal {A}\) on a Hilbert space \(\mathcal {H}\) for which \(\{\pi (A) \Omega | A \in \mathcal {A}^\textrm{loc}\}\) is dense in \(\mathcal {H}\). Moreover, the normalized vector \(\Omega \in \mathcal {H}\) is such that \(\omega (A) = \langle \Omega , \pi (A) \Omega \rangle \) for all \(A\in \mathcal {A}\). For the GNS representation of a ground state, as in (2.19), there exists a unique, non-negative self-adjoint operator H on \(\mathcal {H}\), with dense domain \(\textrm{dom}H\), satisfying \(H \Omega =0\) and
The full domain of H is seldom described explicitly. However, for all systems we consider in this paper, \(\pi (\mathcal {A}^\textrm{loc})\Omega \) is a core for H.
The (GNS) gap of the model in the state \(\omega \) is defined as
If the set on the RHS is empty, one defines \(\textrm{gap}(H)=0\). We say that a ground state \(\omega \) is gapped if \(\textrm{gap}(H)>0\).
The equivalence of the following two conditions is easy to verify:
-
1.
For some \(\gamma >0\), \(\omega \) satisfies
$$\begin{aligned} \omega (A^* \delta (A)) \ge \gamma \omega (A^*A) \quad \text{ for } \text{ all } A \in \mathcal {A}^\textrm{loc} \text{ with } \omega (A) = 0; \end{aligned}$$(2.22) -
2.
The ground state of the GNS Hamiltonian H is unique and \(\textrm{gap}(H) \ge \gamma \).
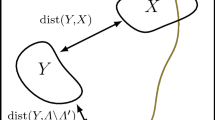
A case of special interest is when \(\Gamma \) is infinite and describes the bulk of a physical model while the same system on a subset of \(\Gamma \) with a boundary would describe an edge. In the first situation we will refer to the GNS gap as the bulk gap of the system. A model with the same interaction restricted to a subspace of \(\Gamma \) describing an edge, may have a vanishing gap while the bulk gap is positive. This is precisely the situation of interest here.
In this setting, the GNS representation \(\pi \) is an isometry. This follows from the fact that \(\mathcal {A}\) is simple [23, Theorem 5.1], which implies that \(\ker \pi =\{0\}\). We find it convenient to use this fact, see e.g. the proof of Lemma 4.5, however in many arguments the contraction property of \(\pi \) suffices.
2.2 Main results
We now state the assumptions for the main results.
Assumption 2.2
(Bulk gap) We assume \(\gamma _0:=\textrm{gap}(H_0)>0\), where \(H_0\) is the GNS Hamiltonian of an infinite-volume, zero-energy ground state \(\omega _0\) of a finite-range, uniformly bounded, frustration free interaction \(\{h_x\}\) as in Assumption 2.1.
We also need to impose a condition that the local gaps do not close too fast. There generally is some freedom in choosing the family of finite volumes on which to impose this condition. We will assume that there is a family
with \(b_x(n)\subset \Lambda (x,n)\) for all x and n, and an associated family of partitions of \(\Gamma \) which separates \(\mathcal {S}\) and has at most polynomial growth. Concretely, this means there is a family of sets \(\mathcal {T}=\{\mathcal {T}_n \mid n \ge 0\}\) and positive numbers c and \(\zeta \), such that for each \(n\ge 0\), \(\mathcal {T}_n = \{\mathcal {T}_n^i: i\in \mathcal {I}_n \}\) is a partition of \(\Gamma \) satisfying \(|\mathcal {I}_n|\le c n^\zeta \) and
In such cases, we say that \(\mathcal {T}\) is of \((c,\zeta )\)-polynomial growth.
As an example, in the case of \(\Gamma = {\mathbb Z}^\nu \), we may take for \(\Lambda (x,n)\) the \(\ell ^\infty \)-ball of radius n centered at x, define \(\mathcal {I}_n = \Lambda (0,n)\) and, for each \(i\in \mathcal {I}_n\), set
Assumption 2.3
(Local gaps) For an interaction \(\{h_x\}\) of range R, we assume there exist families \(\mathcal {S}\) and \(\mathcal {T}\), such that \(\mathcal {T}\) separates \(\mathcal {S}\) and is of \(\zeta \)-polynomial growth, and an exponent \(\alpha \ge 0\) and constant \(\gamma _1>0\), such that the finite-volume Hamiltonians satisfy:
It is important here that the local gaps are allowed to vanish in the limit of infinite system size. For example, certain types of topologically ordered two-dimensional systems are expected to have chiral edge modes with an energy of order \(L^{-1}\) on a finite volume of diameter L. Whether or not such edge modes occur in frustration-free systems, however, is not clear. For the class of systems studied in [36], the authors find that finite-volume gaps of a system with gapless edge modes in the thermodynamic limit would have to decay at least as fast as \(L^{-3/2}\). Other results of this type are in [2, 24, 32]. This is consistent with the gapless boundary modes found in a class of toy models called Product Vacua with Boundary States which are of order \(L^{-2}\) [6, 8]. In any case, regardless of the possible values of the exponent \(\alpha \), we will prove stability of the bulk gap.
The next assumption was introduced in the form we use here in [41] where it is called Local Topological Quantum Order (LTQO).
Assumption 2.4
(LTQO) There is a decay function \(G_0:[0,\infty )\rightarrow [0,\infty )\), with
and such that for all \(m\ge k\ge 0, x\in \Gamma \), and \(A \in \mathcal {A}_{b_x(k)}\), the ground state projections satisfy
As explained in detail in [48, Section 8], if both the initial Hamiltonian and the perturbation (see below) have a local gauge symmetry, only observables A that commute with this symmetry need to satisfy (2.27). Other discrete symmetries can be treated similarly (see [48, Section 8]). Therefore, the stability results proved here (Theorems 2.7 and 2.8) will also hold for symmetry-protected topological phases.
An interesting observation is that the GNS Hamiltonians associated to frustration free models which satisfy Assumption 2.4 automatically have a unique ground state. Since we also use this fact, see e.g. Sect. 3.2.3, we include a short proof in Appendix A.
Next, we turn to the perturbations of the Hamiltonian \(H_0\). We consider \(\Phi (x,n)^* = \Phi (x,n) \in \mathcal {A}_{b_x(n)}\) for all \(x \in \Gamma \) and \(n \ge 0\). These define what we call an anchored interaction \(\Phi \). By regrouping, we need only consider those terms with \(n \ge R\).
Assumption 2.5
(Short-range perturbation) There is a constant \(\Vert \Phi \Vert \ge 0\), \(a >0\), and \(\theta \in (0,1]\) such that for all \(x\in \Gamma \)
Remark 2.6
For a particular perturbation \(\Phi \), Assumption 2.5 is typically straight forward to check. Moreover, any such \(\Phi \) also has a finite F-norm for some F as in (2.11). This implies the general locality results found, e.g., in [47] necessarily hold. In fact, let \(\Phi \) satisfy Assumption 2.5. For any \(0<a' <a\) and \(\xi > \nu \), the function \(F:[0, \infty ) \rightarrow (0, \infty )\) given by
is an F-function on \(\Gamma \). Let \(\delta = a-a'>0\) and note that for any \(x,y \in \Gamma \) with \(d(x,y) \ge R\), we have
with \(C:= \kappa \Vert \Phi \Vert \sum _{n \ge 0} (1+ n)^{\nu + \xi } e^{- \delta n^{\theta }} < \infty \). Thus, \(\Vert \Phi \Vert _F \le C\), with F as in (2.29).
The focus of this work is to analyze the stability of the bulk gap under the presence of perturbations given by an anchored interaction \(\Phi \) satisfying Assumption 2.5. We will prove two different stability results. The first, Theorem 2.7 below, establishes that finite-volume perturbations of the GNS Hamiltonian \(H_0\) (defined in (2.31, 2.32) below) have a stable spectral gap uniform in the support of the perturbation. In this case, the initial GNS Hamiltonian and the perturbed Hamiltonians are all defined on the same GNS Hilbert space.
To describe the second result, Theorem 2.8 below, let \(\delta _\Phi \) denote the derivation defined by \(\Phi \) as in (2.18). This result shows that, for sufficiently small s, there exists a ground state \(\omega _s\) of the perturbed derivation \(\delta _0 + s \delta _\Phi \), whose GNS Hamiltonian has a positive gap. Although the GNS representations of \(\omega _s\) are, in general, inequivalent for different values of s, Theorem 2.8 will follow from Theorem 2.7 by a simple argument given in Sect. 5.2.
We consider perturbed Hamiltonians of the form
where, for any finite volume \(\Lambda \in \mathcal {P}_0(\Gamma )\),
Clearly, \(V_\Lambda \in \mathcal {A}_{\Lambda }\) is bounded and self-adjoint, and so \(H(\Lambda ,s)\) defines for all \(s\in {\mathbb R}\) a self-adjoint Hamiltonian on \(\mathcal {H}\) with the same dense domain as \(H_0\).
In the next several sections we will prove the following theorem, which establishes that the spectral gap of \(H(\Lambda ,s)\) remains open for small |s| uniformly in the finite volume \(\Lambda \).
Theorem 2.7
(Stability of the gap uniformly in the perturbation region) Suppose that \(\{h_x\}\) and \(\omega _0\) satisfy Assumptions 2.2 – 2.4, and \(\Phi \) is an anchored interaction satisfying Assumption 2.5. Then, for all \(\gamma \in (0,\gamma _0)\), there exists \(s_0(\gamma )>0\), such that for all real s, \(|s| < s_0(\gamma )\), and \(\Lambda \in \mathcal {P}_0(\Gamma )\), we have
with \(H(\Lambda , s)\) as in (2.31) and
We remark that the quantity \(s_0(\gamma )\) only depends on the values of \(\kappa \) and \(\nu \) of the lattice, \(\Vert h \Vert \), the gap \(\gamma _0\), the parameters in Assumption 2.3, the decay function in Assumption 2.4, and a suitable F-norm of the perturbation \(\Phi \). In particular, \(s_0(\gamma )\) is independent of the finite volume \(\Lambda \). From the arguments in this paper, one can derive an explicit lower bound for \(s_0(\gamma )\) in terms of these quantities, see Sect. 5.2.
We also investigate the situation where the perturbation region \(\Lambda \) tends to all of \(\Gamma \). Consider any IAS \((\Lambda _n)\). We will denote by \(\tau _t^{(\Lambda _n,s)}\) the dynamics on \(\mathcal {A}\) generated by the derivation
As discussed in [47, Definition 3.7], the sequence of interactions \(h + s \Phi \restriction _{\Lambda _n}\) converges locally in F-norm to the interaction \(h + s \Phi \). Using [47, Theorem 3.8], we conclude local convergence in the sense that
as well as
with \(\tau _t^{(s)}\) (respectively, \(\delta _s\)) being the a priori well-defined strongly continuous dynamics on \(\mathcal {A}\) (respectively, the closure of the derivation restricted to \(\mathcal {A}^\textrm{loc}\)) generated by the interaction \(h + s \Phi \). Neither of these limits depend on the choice of IAS sequence \(\Lambda _n\).
Our second result is then concerned with the ground state and its gap for a family of extensive perturbations. In particular, the uniformity of the stability result in Theorem 2.7 allows one to prove, almost as a corollary, that for all \(|s|\le s_0(\gamma )\) there is a gapped ground state \(\omega _s\) of \(\delta _s\) in the sense of (2.22). To make this precise, we introduce the limiting spectral flow. For any \(\gamma >0\) and IAS \((\Lambda _n)\), take
where the spectral flows \(\alpha _s^{\Lambda _n}\) will be introduced in more detail in the next section, see (3.23). For now, it suffices to observe that this limit exists and is independent of the choice of IAS. In fact, the interactions defining the spectral flows \(\alpha _s^{\Lambda _n}\) converge locally in F-norm by arguments as in [47, Section VI.E.2]. This limiting spectral flow \(\alpha _s\) defines a strongly continuous co-cycle of automorphisms of \(\mathcal {A}\), and moreover, under the assumptions we have made, for \(A\in \mathcal {A}^\textrm{loc}\), \(s \mapsto \alpha _s(A)\) is differentiable to all orders. We prove bounded differentiability for \(A\in \mathcal {A}^g\), for suitable g in Theorem A.1.
Theorem 2.8
(Stability of the bulk gap) Under the assumptions of Theorem 2.7, let \(\gamma \in (0,\gamma _0)\) and take s with \(|s| < s_0(\gamma )\). The state \(\omega _s=\omega _0\circ \alpha _s\) is a gapped ground state of the perturbed infinite dynamics \(\delta _s\), i.e.
In particular, the GNS Hamiltonian \(H_s\) of \(\omega _s\) has a one-dimensional kernel and \(\textrm{spec}H_s\) has a gap above its ground state bounded below by \(\gamma \).
3 Quasi-locality, domains and local decompositions
The strategy used here for proving spectral gap stability of infinite systems relies in an essential way on quasi-locality properties of the observables, the dynamics, and several transformations defined in terms of the dynamics. To this end, we first review these locality properties of the algebra and then, importantly, record how this local structure is mapped into the GNS space. Quasi-locality of observables is the topic of Sect. 3.1. In Sect. 3.1.1, we recall general methods for making strictly local approximations of both quasi-local observables and maps. The specific quasi-local maps and estimates used in the stability proof are discussed in Sects. 3.1.2–3.1.4. The stability results will follow from spectral perturbation theory applied in the GNS space. Section 3.2 succinctly makes clear the distinction between the relevant objects in the algebra and their counterparts in the GNS representation. Finally, in Sect. 3.3 we prove how the action of certain unbounded operators on a dense domain can be expressed as limits of sequences of bounded operators with finite support.
3.1 Quasi-Locality
We first recall some general features of quasi-locality estimates and then turn to some important examples relevant for this work.
3.1.1 Quasi-locality estimates
Let \(A \in \mathcal {A}\), \(X \in \mathcal {P}_0( \Gamma )\), and \(\epsilon >0\). In [14, 45] it was shown that if
then
A linear map \(\mathcal {K}:\mathcal {A}\rightarrow \mathcal {A}\) is said to be quasi-local with constant \(C\ge 0\), power \(p\ge 0\), and decay function G if for all \(X,Y\in \mathcal {P}_{0}(\Gamma )\)
Using (3.2), for such a map \(\mathcal {K}\) and \(A\in \mathcal {A}_{b_x(k)}\), we have
When the corresponding decay function G is summable, this estimate guarantees the absolute convergence of telescopic sums, i.e. for any \(n_0 \ge 0\),
since the terms satisfy
A common choice is \(n_0=0\) and we adopt the notation
We now review a few examples of quasi-local maps and indicate some of their important properties which will be used to prove stability of the gap. For more details of these maps see [47]. Throughout Sects. 3.1.2–3.2 we work under the assumptions of Theorem 2.7.
3.1.2 Dynamics
It is well-known that the unperturbed dynamics \(\tau _t^{(0)}\) defined as in (2.16) satisfies an exponential Lieb-Robinson bound [38]. Namely, for every \(\mu >0\) there exists \(C_{\mu } >0\) and \(v_{\mu }>0\) such that the bound
holds for any \(X,Y \in \mathcal {P}_0(\Gamma )\), all \(A \in \mathcal {A}_X\), \(B \in \mathcal {A}_Y\), and \(t \in \mathbb {R}\).
It is easy to check that the perturbed interaction \(h + s \Phi {\restriction _\Lambda }\) has a finite F-norm for the same F as \(\Phi \), and that this F-norm is uniformly bounded in \(|s|\le 1\) and \(\Lambda \). As a consequence, there are \(C_F>0\) and \(v_F>0\), independent of s and \(\Lambda \), such that for any choice of \(X,Y \in \mathcal {P}_0(\Gamma )\),
for all \(A \in \mathcal {A}_X\), \(B \in \mathcal {A}_Y\), and \(t \in \mathbb {R}\).
Since each \(sV_{\Lambda }\) is bounded and self-adjoint, [11, Proposition 5.4.1] implies that
where \(\{ K_t^{(\Lambda , s)} \, | \, t \in \mathbb {R} \}\) is a one-parameter family of unitaries on \(\mathcal {A}\) which are uniquely defined as the \(\mathcal {A}\)-valued solution of
These unitaries are quasi-local as, for any \(A \in \mathcal {A}^\textrm{loc}\) and \(t>0\),
An application of (3.8) then shows that for any \(\mu >0\) and \(A \in \mathcal {A}_X\) with \(X \in \mathcal {P}_0( \Gamma {\setminus } \Lambda )\),
for any \(s,t \in \mathbb {R}\). Thus, \(K_t^{(\Lambda , s)} \in \mathcal {A}^g\) for any exponential g, by (3.2).
3.1.3 Weighted integral operators
Fix \(\gamma >0\). For each \(\Lambda \in \mathcal {P}_0( \Gamma )\) and \(s\in {\mathbb R}\), we define two weighted integral operators \(\mathcal {F}_s^{\Lambda }: \mathcal {A}\rightarrow \mathcal {A}\) and \(\mathcal {G}_s^{\Lambda }: \mathcal {A}\rightarrow \mathcal {A}\) by
where the real-valued functions \(w_{\gamma }, W_{\gamma }\in L^1(\mathbb {R})\), are defined in [47, Section VI.B]. In particular, they decay faster than any stretched exponential. Both of these maps depend on the choice of \(\gamma \) through their weight functions, \(w_\gamma \) and \(W_\gamma \) respectively, but we suppress this in the notation. Arguing as in [47, Section VI.E.1], see also [48, Section 4.3.2], we find that for all \(A \in \mathcal {A}\)
where we have used that, by our choice of normalization, \(\Vert w_\gamma \Vert _1=1\). As a result, these maps are bounded uniformly with respect to \(s \in \mathbb {R}\) and \(\Lambda \in \mathcal {P}_0( \Gamma )\). Moreover, they are uniformly quasi-local in the sense that for each \(\mathcal {K}\in \{ \mathcal {F}, \mathcal {G}\}\) there is a decay function \(G_{\mathcal {K}}\) such that: for any choice of \(X,Y \in \mathcal {P}_0(\Gamma )\), we have
for all \(A \in \mathcal {A}_X\) and \(B \in \mathcal {A}_Y\). As shown in [47, Lemma 6.10–6.11], the decay functions \(G_{\mathcal {K}}\) can be made explicit. For our purposes here, we need only stress that they can be taken independent of \(\Lambda \in \mathcal {P}_0( \Gamma )\) and \(s \in [-1,1]\), and with decay faster than any power. Thus, for any \(\mu \ge 0\),
3.1.4 The spectral flow
Fix \(\gamma >0\). For each \(\Lambda \in \mathcal {P}_0( \Gamma )\) and \(s\in {\mathbb R}\), denote by
with \(\mathcal {G}^{\Lambda }_s\) as defined in (3.14). Clearly, \(D(\Lambda , s)\) is self-adjoint and \(s \mapsto D(\Lambda , s)\) is uniformly bounded by (3.15).
For \(t \in \mathbb {R}\) fixed, the strong derivative of \(s \mapsto \tau _t^{(\Lambda , s)}\) is given by the Duhamel formula [47, Proposition 2.7]:
Using (3.19), one obtains the norm continuity of \(s \mapsto D(\Lambda , s)\) from the following estimate:
Given these properties of \(D(\Lambda , s)\), there is a unique solution of
which is given by unitaries in \(\mathcal {A}\). Using similar arguments as in (3.13) with (3.16) and (3.18), one can show that for \(s>0\)
for any \(A \in \mathcal {A}_X\) with \(X \in \mathcal {P}_0( \Gamma {\setminus } \Lambda )\). Thus, \(U(\Lambda ,s) \in \mathcal {A}^g\) for some g with finite moments of all orders by (3.17).
The spectral flow is then the family of inner automorphisms on \(\mathcal {A}\) induced by \(U(\Lambda ,s)\):
This is Hastings’ quasi-adiabatic evolution [25, 27]. Quasi-locality of this map is then a consequnece of a Lieb-Robinson bound. To this end, first rewrite the generator as
using (2.32). Applying the conditional expectations and telescopic sum from (3.7), we further write
Arguing as in [48, Appendix A], there is a decay function \(G_{\Psi }\) and a positive number \(\Vert \Psi \Vert _{G_{\Psi }}\) such that for all \(\Lambda \in \mathcal {P}_0( \Gamma )\), \(s \in [-1,1]\), \(x \in \Lambda \) and \(k \ge R\),
One can be explicit about estimates for \(G_{\Psi }\), see [48, Corollary A.3], but for our purposes, we only need that is has finite moments of all orders. Given (3.25) and (3.26), well-known Lieb-Robinson bounds imply the existence of a decay function \(G_{\alpha }\) so that for all \(X,Y \in \mathcal {P}_0(\Gamma )\),
for all \(A \in \mathcal {A}_X\), \(B \in \mathcal {A}_Y\), and \(s \in \mathbb {R}\). \(G_{\alpha }\) is independent of \(\Lambda \in \mathcal {P}_0(\Gamma )\) and has finite moments of all orders.
3.2 In the GNS space
The spectral perturbation arguments are carried out in the GNS representation of the reference state \(\omega _0\). Recall that \((\mathcal {H}, \pi _0, \Omega )\) is our notation for the corresponding GNS triple. In this subsection, the quasi-local maps discussed previously are lifted to the GNS space. Here, and in what follows, we will use the notation \(\tilde{A} = \pi _0(A) \in \mathcal {B}( \mathcal {H})\) to describe the GNS representative of an observable \(A \in \mathcal {A}\). We now present the necessary properties we will need in this setting.
3.2.1 Dynamics
As discussed in Sect. 2.1, the unperturbed dynamics \(\tau _t^{(0)}\) is implemented in the GNS representation of \(\omega _0\) by the GNS Hamiltonian \(H_0\), as in (2.20). We further show that the perturbed dynamics \(\tau _t^{(\Lambda ,s)}\) is implemented in the GNS representation of \(\omega _0\) by the Hamiltonian
from (2.31). Specifically,
Applying the GNS representation to the interaction picture representation (3.10) gives
Then, (3.29) follows by observing that
as by (3.11) \(\tilde{K}_t^{(\Lambda , s)}:= \pi _0(K_t^{(\Lambda , s)})\) is the unique, unitary solution of
3.2.2 Weighted integral operators
For any \(\gamma >0\), \(\Lambda \in \mathcal {P}_0( \Gamma )\), and \(s \in \mathbb {R}\) we map the weighted integral operators of (3.14) to the GNS space by defining \(\tilde{\mathcal {F}}_s^{\Lambda }\) and \(\tilde{\mathcal {G}}_s^{\Lambda }\) by
for all \(A \in \mathcal {B}(\mathcal {H})\). Using (3.29), it is clear that
3.2.3 The spectral flow
For fixed \(\Lambda \in \mathcal {P}_0(\Gamma )\), following [47, Section VI.A] we define a norm-continuous family of unitaries \(\tilde{U}(\Lambda ,s)\in \mathcal {B}(\mathcal {H})\) as the unique solution of
where
The spectral flow associated with \(H(\Lambda ,s)\) is the family of automorphisms of \(\mathcal {B}(\mathcal {H})\) defined by
By (3.34) it is clear that \(\tilde{D}(\Lambda , s)=\pi _0(D(\Lambda , s))\) with \(D(\Lambda ,s)\) as in (3.18) and, hence, by the uniqueness of the unitary solution of (3.35), \(\tilde{U}(\Lambda ,s) = \pi _0(U(\Lambda ,s))\), where \(U(\Lambda ,s)\) is as in (3.21). Therefore, \(\pi _0\) lifts the spectral flow in \(\mathcal {A}\) to the GNS space:
Recall that \(E(\Lambda ,s)\) denotes the ground state energy of \(H(\Lambda ,s)\). Under our assumptions the ground state space of \(H(\Lambda ,0)=H_0\) is one-dimensional by Proposition A.1, and \(\gamma _0:=\textrm{gap}(H_0)\) is strictly positive. By standard results, see e.g [33], for |s| sufficiently small the kernel of \(H(\Lambda , s) - E(\Lambda , s) {\mathchoice{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.5pt}l}}{\mathrm {1\hspace{-2.77771pt}l}}}\) is one-dimensional and the ground state gap does not immediately close. More precisely, for any \(\gamma \in (0,\gamma _0)\), there is \(s_0^{\Lambda }(\gamma ) >0\) so that
for all \(|s| \le s_0^\Lambda (\gamma )\). Although the existence of \(s_0^{\Lambda }(\gamma )>0\) is trivial, the main objective for proving stability is to establish the existence of a \(\Lambda \)-independent \(s_0(\gamma )\), e.g. as in the statement of Theorem 2.7. Given this, an application of [47, Theorem 6.3] shows that
where by \(P^{\Lambda }(s)\) we denote the orthogonal projection onto the ground state space of \(H(\Lambda , s)\).
For any \(\Lambda \in \mathcal {P}_0( \Gamma )\) and \(s \in \mathbb {R}\), the state \(\omega _s^{\Lambda }\) given by
is a vector state in the GNS space:
where \(\Omega (\Lambda , s) = \tilde{U}(\Lambda ,s) \Omega \in \mathcal {H}\). By our assumptions, \(P^{\Lambda }(0) = \vert \Omega \rangle \langle \Omega \vert \). An application of (3.40) then shows that
and thus \(\Omega (\Lambda ,s)\) is the ground state of \(H(\Lambda , s)\).
Finally, we recall that with the parameters \(\gamma \) and s as above that the weighted integral operator \(\tilde{\mathcal {F}}_s^{\Lambda }\) from (3.33) satisfies the relation
See, e.g. [47, Lemma 6.8], for a proof of this property.
3.3 On domains
Recall that \((\Gamma , d)\) is a \(\nu \)-regular metric space. Let F be an F-function on \((\Gamma , d)\), and \(\Phi \) an interaction with \(\Vert \Phi \Vert _F<\infty \). As in Sect. 2, let \(\delta ^{\Phi }\) be the closed derivation with dense domain \(\textrm{dom}( \delta ^{\Phi }) \subset \mathcal {A}\), and which satisfies
Although the sum on the right-hand-side above may be infinite, it is absolutely convergent when \(\Phi \) has a finite F-norm. In fact, \(\delta ^{\Phi }\) is locally bounded:
see Example 4.7 of [47, Section IV.B.1]. We have the following lemma.
Lemma 3.1
Let \((\Gamma , d)\) be \(\nu \)-regular, F an F-function on \((\Gamma , d)\), and g a decay function with a finite \(\nu \)-moment, i.e.,
For any interaction \(\Phi \) on \(\Gamma \) with \(\Vert \Phi \Vert _F< \infty \), we have that \(\mathcal {A}^g\subset \textrm{dom}(\delta ^\Phi )\).
Proof
For \(n\ge 1\), and \(A\in \mathcal {A}^g\), for some \(x\in \Gamma \), and observables \(A_n \in \mathcal {A}_{b_x(n)}\) satisfying \(\Vert A - A_n\Vert \le \Vert A \Vert _{x, g} g(n)\). In this case, the bound \(\Vert A_{n+1} - A_n\Vert \le 2 \Vert A \Vert _{x, g} g(n)\) is clear. Using (3.46) and \(\nu \)-regularity of \(\Gamma \), we conclude
Thus, for all \(m<n\),
Since we assumed that g has a finite \(\nu \)-moment, this implies that \(\delta ^{\Phi }(A_n) \) is a Cauchy sequence. Since \(A_n\rightarrow A\) and \(\mathcal {A}^\textrm{loc}\) is a core for \(\delta ^\Phi \), it follows that \(A \in \textrm{dom}(\delta ^\Phi )\).
Given the assumptions of Theorem 2.7, Lemma 3.1 clearly applies to the derivation \(\delta _0\). Using that \(H_0 \Omega = 0\), one readily checks the relation
from which the inclusion \(\pi _0(\textrm{dom}(\delta _0))\Omega \subset \textrm{dom}(H_0)\) is clear. As a result, if g is a decay function with a finite \(\nu \)-moment, then \(\pi _0 (\mathcal {A}^g) \Omega \subset \textrm{dom}(H_0) = \textrm{dom}(H(\Lambda , s))\) for any \(\Lambda \in \mathcal {P}_0( \Gamma )\) and \(s \in \mathbb {R}\). Since \(U(\Lambda ,s)\in \mathcal {A}^g\) for some g with finite moments of all of orders by (3.22), it follows that \(\pi _0(A U(\Lambda ,s)) \Omega \in \textrm{dom}(H(\Lambda ,s))\), for any \(A\in \mathcal {A}^\textrm{loc}\), \(s\in {\mathbb R}\).
A consequence of this is a gap inequality for the perturbed ground state \(\omega _s^{\Lambda }\) from (3.41). Namely, we show that for \(\gamma \in (0,\gamma _0), \Lambda \in \mathcal {P}_0(\Gamma )\), and \(|s| \le s_0^{\Lambda }(\gamma )\):
To see this, fix \(|s| \le s_0^{\Lambda }(\gamma )\). Since \(\Omega (\Lambda ,s)\) is the unique ground state of \(H(\Lambda ,s)\),
for all \(\psi \in \textrm{dom}(H_0)\) with \(\langle \Omega (\Lambda , s), \psi \rangle =0\). In particular, if \(\omega ^\Lambda _s(A)=0\) for some \(A\in \mathcal {A}^\textrm{loc}\), then (3.52) holds for \(\psi = \pi _0(A) \Omega (\Lambda , s)=\pi _0(A U(\Lambda ,s)) \Omega \) since
Then (3.51) follows from rewriting (3.52).
It will be important that on an appropriate dense domain, the action of the unbounded Hamiltonians can be expressed as a limit of finite-volume quantities. This is the content of the next lemma.
Lemma 3.2
Let \((\mathcal {H},\pi _0,\Omega )\) be the GNS representation of \(\omega _0\), an infinite-volume, zero energy, ground state of a frustration free model as in Assumption 2.1. For any decay function g with a finite \(\nu \)-moment and any IAS \((\Lambda _n)\),
where \(H_{\Lambda _n} \in \mathcal {A}_{\Lambda _n}\) is as in (2.13) and \(H_0\) is the GNS Hamiltonian.
Proof
Note that (3.53) is trivially satisfied for \(\psi =\pi _0(A)\Omega \), for \(A\in \mathcal {A}^\textrm{loc}\) since
For the first equality we used \(\pi _0(H_{\Lambda _n})\Omega =0\), which is a consequence of the frustration-free property. Then, by the finite-range condition on the unperturbed model, \([H_{\Lambda _n},A]\) becomes constant for n sufficiently large.
Take \(\psi = \pi _0(A) \Omega \) for any \(A \in \mathcal {A}^g\). By the definition of \(\mathcal {A}^g\), there exists \(x \in \Gamma \) and observables \(A_m \in \mathcal {A}_{b_x(m)}\) so that \(\Vert A - A_m\Vert \le \Vert A \Vert _{x, g} g(m)\) for all \(m \ge 1\), and so the vectors \(\psi _m:= \pi _0(A_m) \Omega \) satisfy
Moreover, since the interaction h is uniformly bounded with range R, it follows from (3.45) and \(\nu \)-regularity that for any \(k\ge 1\),
where we use the bound \(|b_{x}(n+m)|\le |b_x(n)||b_x(m)|\). Then, by the last equality of (3.54), one finds that \((H_0\psi _m)_{m\in {\mathbb N}}\) is Cauchy as
where we set \(D = 4 \kappa ^2 R^{\nu } \Vert h \Vert _{\infty } \Vert A \Vert _{x, g}\). Since \(H_0\) is closed, and \(\psi \in \textrm{dom}(H_0)\) by Lemma 3.1 and the subsequent discussion, the bound
follows immediately from (3.55)–(3.56).
In the case of a local Hamiltonian, using again the first equality in (3.54), a similar argument shows that for all \(n \ge 1\),
Putting all of this together, one finds that for any \(n \ge 1\) and each \(k \ge 1\),
For \(k \ge 1\) sufficiently large, (3.57) and (3.58) guarantee that the first and last term above can be made arbitrarily small. Given such a k, the middle term vanishes for n sufficiently large, see the comment following (3.54). This completes the proof.
Lemma 3.2 also trivially applies to the perturbed system in the GNS space. In fact, for \(\Lambda \in \mathcal {P}_0(\Gamma )\) and \(s \in \mathbb {R}\), under assumptions as above, a direct application of Lemma 3.2 shows that we also have
Remark 3.3
An analogue of Lemma 3.2 holds more generally. In fact, if F is an F-function with a finite \(\nu \)-moment, then for any frustration free interaction \(\Phi \) with \(\Vert \Phi \Vert _F< \infty \), the GNS Hamiltonian again satisfies (3.53). The argument is identical to the above except that one uses the more general estimate in Lemma 3.1 and bounds the middle term in (3.59) by
For fixed k, the above is the sum of finitely many ‘tails’ of the uniformly summable function F.
We now investigate how the weighted integral operator \(\tilde{\mathcal {F}}_s^{\Lambda }\) from (3.33) can be applied to the unbounded Hamiltonian \(H(\Lambda , s)\). To begin, we prove an analogue of the desired statement for the unperturbed dynamics; this is Lemma 3.4 below. To this end, assume \(w\in L^1(\mathbb {R})\) satisfies
and define a weighted integral operator \(\tilde{\mathcal {F}}: \mathcal {B}( \mathcal {H}) \rightarrow \mathcal {B}(\mathcal {H})\) by setting
To simplify notation, let us also write
Our first result is as follows.
Lemma 3.4
Let \((\Gamma ,d)\) be \(\nu \)-regular, g be a decay function with a finite \(2 \nu \)-moment, and \(w \in L^1( \mathbb {R})\) satisfies (3.62). For each choice of IAS \((\Lambda _n)\), the weighted integral operator \(\tilde{\mathcal {F}}\) from (3.63) satisfies
where \(H_{\Lambda _n} \in \mathcal {A}_{\Lambda _n}\) is as in (2.13).
Proof
Fix an IAS \((\Lambda _n)\) and take \(\psi = \pi _0(A) \Omega \) for some \(A \in \mathcal {A}^g\). We can rewrite the convergence claimed in (3.65) as the convergence of integrals of a sequence of functions \(f_n: \mathbb {R} \rightarrow \mathcal {H}\) given by
Since \(H_0\Omega =0\), the above can be re-written as
using (2.20). We claim that there is a decay function \(g_{\tau }\) with a finite \(\nu \)-moment such that \(\tau _{-u}^{(0)}(A) \in \mathcal {A}^{g_{\tau }}\) for all \(u \in \mathbb {R}\). Given this, Lemma 3.2 applies and we find that
By (3.62), the integral of this limit coincides with the right-hand-side of (3.65). Therefore, to complete the proof we only need to justify an application of dominated convergence.
Let us first prove the existence of a decay function \(g_{\tau }\) as claimed. Fix \(A \in \mathcal {A}^g\). In this case, there is \(x \in \Gamma \), \(C \ge 0\), and observables \(A_m \in \mathcal {A}_{b_x(m)}\) for which \(\Vert A - A_m \Vert \le C g(m)\) for all \(m \in \mathbb {N}\). Let \(u \in \mathbb {R}\) and for any \(n \in \mathbb {N}\), set
where, to ease notation, we have written \(\Pi _n = \Pi _{b_x(n)}\), for the conditional expectation from Sect. 3.1.1. A straightforward estimate shows that for any \(\mu >0\),
where we used (3.8) and (3.4) for the final bound. The existence of the decay function \(g_{\tau }\) follows from the moment condition on g and the decay of the exponential term..
We now turn to finding a dominating function for \(f_n\). Recall that for any \(m_0 \in \mathbb {N}\), A can be written as an absolutely convergent, telescopic sum:
Inserting this decomposition of A into (3.67), we find that for any \(n \in \mathbb {N}\) and each \(u \in \mathbb {R}\):
Now, by the zero-energy property of the ground state we find the bound
which we stress is uniform in n. This suggests a mechanism for bounding the first term in (3.72). Let \(\ell _0 \ge m_0\) and write
where we have used the short-hand \(\Delta _m^{\ell }\) for \(\Delta _{b_x(m)}^{\ell }\) as in (3.7). For \(\ell = \ell _0\), the bound
follows from (3.73). For \(\ell \ge \ell _0\), the estimate
follows from another application of (3.73) and the quasi-locality estimate for the unperturbed dynamics in combination with (3.6). We conclude that
If we now take \(\ell _0 = \lceil v_{\mu }|u| + m_0 \rceil \), then we have found that there is \(K \ge 0\) for which
and here \(K = K(\kappa , \mu , \nu , R)\).
The terms \(B_k\) in (3.72) can be estimated similarly. Regarding k as \(m_0\) and arguing as in (3.74)–(3.77) with some \(\ell _0 \ge k\), a bound analogous to (3.78) can be found. Of course, here one replaces \(\Vert A_{m_0} \Vert \) with \(\Vert B_k \Vert \). Since \(\Vert B_k \Vert \le 2 C g(k-1)\) and g has a finite \(2 \nu \)-moment, we have obtained a bound on the right-hand-side of (3.72) of the form:
By the assumption on w, i.e. (3.62), the above is a dominating function for the sequence \(f_n\). This justifies dominated convergence and completes the proof.
We will also need a version of Lemma 3.4 for the perturbed system. Recall that for any \(\gamma >0\), \(s \in \mathbb {R}\), and \(\Lambda \in \mathcal {P}_0(\Gamma )\), the weighted integral operator \(\tilde{\mathcal {F}}_s^{\Lambda }: \mathcal {B}(\mathcal {H}) \rightarrow \mathcal {B}(\mathcal {H})\) are defined by
We note that \(w_\gamma \) from [47, Section VI.B] satisfies (3.62). It is clear that
since the dynamics leaves this bounded operator invariant and \(w_\gamma \) integrates to 1. Lemma 3.5 provides a differential version of this fact.
Lemma 3.5
Let \((\Gamma ,d)\) be \(\nu \)-regular, g be a decay function with a finite \(2 \nu \)-moment. Let \(\Lambda \in \mathcal {P}_0( \Gamma )\) and take \(s \in \mathbb {R}\). For each choice of IAS \((\Lambda _n)\), consider the weighted integral operator \(\tilde{\mathcal {F}}_s^{\Lambda }\), as in (3.80), with arbitrary \(w \in L^1(\mathbb {R})\) satisfying (3.62). Then
with \(H_{\Lambda _n} \in \mathcal {A}_{\Lambda _n}\) as in (2.13) and \(V_{\Lambda }\) as in (2.32).
Proof
Fix an IAS \((\Lambda _n)\) where we assume for convenience that \(\Lambda \subset \Lambda _1\). As in the proof of Lemma 3.4, take \(\psi = \pi _0(A) \Omega \) with \(A \in \mathcal {A}^g\), and for each \(n \in \mathbb {N}\), consider \(f_n: \mathbb {R} \rightarrow \mathcal {H}\) given by
where, in analogy to (3.64), we have set
Using (3.29), (3.10), and (2.20), we may write
for all \(u \in \mathbb {R}\). In this case, we find that
Following a similar argument and using (3.13), one shows that there is a decay function \(g'\) with a finite \(\nu \)-moment such that \(\tau ^{(0)}_{-u}( K_u^{(\Lambda ,s)} A) \in \mathcal {A}^{g'}\). As a result, the point-wise limit
is clear from properties of the interaction picture dynamics, see the discussion following (3.10).
The argument demonstrating that we can apply the dominated convergence theorem also proceeds as in the proof of Lemma 3.4. Since the differences stemming from the presence of the u-dependence in the operators \(A_{m_0}\) and \(B_k\) are minor, we leave the details to the reader.
4 Construction of a unitarily equivalent perturbed system
The crux of the stability strategy, as introduced in [12], is to use the spectral flow (aka quasi-adiabatic evolution) to construct a unitarily equivalent perturbed system for which one can prove a relative form bound using quasi-locality estimates and LTQO. In the infinite-system setting, this begins by justifying that the unbounded Hamiltonian \(H(\Lambda ,s)\) from (2.31) can be transformed by the spectral flow defined in the GNS space, see (3.37). To this end, note that in Sect. 3.1.4 we proved that \(U(\Lambda , s) \in \mathcal {A}^g\) for some g with finite moments of all orders, and thus, an application of Lemma 3.2 shows that \(\tilde{U}(\Lambda ,s)\pi _0(A)\Omega \in \textrm{dom}H(\Lambda ,s)\) for \(A\in \mathcal {A}^\textrm{loc}\). As a consequence, one may write
where \(E(\Lambda ,s)\) the ground state energy of \(H(\Lambda , s)\) from (2.34), and \(W(\Lambda , s)\) is well-defined since all other quantities in (4.1) are well-defined. Our goal now is to show that this defines \(W(\Lambda ,s)\) as a bounded operator with an explicit, \(\Lambda \)-independent form-bound with respect to \(H_0\).
In fact, the proof of Theorem 2.7 follows as a consequence of two results. The first, Theorem 4.1, establishes that \(W(\Lambda ,s)\) is indeed bounded and can be decomposed in a way that is suitable for deriving a relative form bound. The second, Theorem 5.1 in Sect. 5, is the relative form bound itself.
Theorem 4.1
Suppose Assumptions 2.1–2.2 and 2.4–2.5 hold, and fix \(\Lambda \in \mathcal {P}_0(\Gamma )\). Then, for any \(\gamma \in (0,\gamma _0)\) and \(|s|\le s_0^\Lambda (\gamma )\), there is a family of self-adjoint observables \(\Phi ^{(2)}(x,m,s)\in \mathcal {A}_{b_x(m)}\), for each \(x\in \Gamma \) and \(m\ge R\), with the following properties:
-
(i)
\(\Phi ^{(2)}(x,m,s)P_{b_x(m)} = P_{b_x(m)}\Phi ^{(2)}(x,m,s)=0\);
-
(ii)
\(\Vert \Phi ^{(2)}(x,m,s)\Vert \le 2sG^{(2)}_\Lambda (x,m)\) with
$$\begin{aligned} G^{(2)}_\Lambda (x,m) = G_\Lambda (x,m/2)+2G_\Lambda ^{(1)}(x,\lceil m/2\rceil )+2G_\Lambda ^{(1)}(x,R)\sqrt{\lceil m/2\rceil ^{\nu }G_0(m/2)} \end{aligned}$$(4.2)where \(P_{b_x(m)}\) is the ground state projection associated to \(H_{b_x(m)}\), \(G_\Lambda (x,m)\) is as in Theorem 4.2, \(G_\Lambda ^{(1)}(x,m) = \sum _{n\ge m}G_\Lambda (x,n)\), and \(G_0\) is from Assumption 2.4. Furthermore, \(W(\Lambda ,s)\) is given by the absolutely convergent sum
$$\begin{aligned} W(\Lambda ,s) = \sum _{x\in \Gamma }\sum _{m\ge R}\pi _0(\Phi ^{(2)}(x,m,s)). \end{aligned}$$(4.3)
Note that the operator \(W(\Lambda ,s)\) is a priori defined in the GNS representation. A posteriori, however, (4.3) implies that \(W(\Lambda ,s)\) is the image of a quasi-local observable in \(\mathcal {A}\).
The decomposition from Theorem 4.1 is proved in two steps. The first uses quasi-locality and conditional expectations to prove that for all \(|s|\le s_0^\Lambda (\gamma )\), the action of the spectral flow on the GNS Hamiltonian \(H(\Lambda ,s)\) can be again realized as a perturbation of \(H_0\). Namely, we show that for all \(\psi \in \pi _0(\mathcal {A}_\textrm{loc})\Omega \)
where the perturbation terms \(\tilde{\Phi }^{(1)}(x,m,s)\in \pi _0(\mathcal {A}_{b_x(m)})\) are self-adjoint, satisfy a norm bound that is linear in s, and are absolutely summable over \(x\in \Gamma \) and \(m\ge R\). This is accomplished in Theorem 4.2 of Sect. 4.1 below.
In the second step, carried out in Sect. 4.2, the final form of (4.3) from Theorem 4.1 is proved using the frustration-free and LTQO ground state properties to produce a refined decomposition of the perturbation terms from (4.4).
4.1 Quasilocal decomposition of the transformed perturbation
We now turn to establishing the first decomposition (4.4), which is the content of the following theorem.
Theorem 4.2
Under the conditions of Theorem 4.1, there exists a function \(G_\Lambda :\Gamma \times [0,\infty ) \rightarrow [0,\infty )\) for which
and a self-adjoint operator \(\tilde{\Phi }^{(1)}(x,m,s)^* = \tilde{\Phi }^{(1)}(x,m,s)\in \pi _0(\mathcal {A}_{b_x(m)})\) for each \(x\in \Gamma \) and \(m \ge R\), such that \(\Vert \tilde{\Phi }^{(1)}(x,m,s)\Vert \le s G_\Lambda (x,m)\) and
Moreover, for each \(x\in \Gamma \), the operator \(\tilde{\Phi }^{(1)}(x,s):= \sum _{m\ge R} \tilde{\Phi }^{(1)}(x,m,s) \) belongs to \(\pi _0(\mathcal {A})\) and commutes with the ground state projection \(\vert \Omega \rangle \langle \Omega \vert \).
The global term \(\tilde{\Phi }^{(1)}(x,s)\) above will result from applying quasi-local maps \(\mathcal {K}_s^{i,\Lambda }\), \(i=1,2\), to the interaction and perturbation terms associated to the site x. These maps are defined in terms of the examples introduced in Sect. 3.1, and emerge from fixing any IAS \((\Lambda _n)\) and then applying Lemmas 3.4, 3.5 to rewrite
where we choose \(\tilde{\mathcal {F}}=\tilde{\mathcal {F}}_0^\Lambda \). As the argument in the above limit is a finite sum of bounded operators, the various relationships (3.34)–(3.38) between the quasi-local maps in the GNS representation to those on the \(C^*\)-algebra implies that for each n:
Given this, for \(i=1,2\) the map \(\mathcal {K}^{i, \Lambda }_s: \mathcal {A}\rightarrow \mathcal {A}\) are defined by
It was proved, e.g. in [48, Lemma 4.4], that both of these maps satisfy a local bound and quasi-local estimate that is independent of the finite volume \(\Lambda \). Specifically, for each \(i=1,2\) there are non-negative numbers \(p_i\), \(q_i\) and \(C_i\), and a decay function \(G_{\mathcal {K}^i}\) (all independent of \(\Lambda \)) such that
hold for any \(X,Y \in \mathcal {P}_0( \Gamma )\), \(A \in \mathcal {A}_X\), \(B \in \mathcal {A}_Y\), and \(s \in \mathbb {R}\). In fact, one can take \(p_1=q_1=2\), \(p_2=0\) and \(q_2=1\) and make explicit estimates on the decay function, see e.g. [48, Remark 4.7]. However, it suffices to note that each \(G_{\mathcal {K}^i}\) have finite moments of all orders in the sense of (3.17).
However, as \(\Lambda _n\uparrow \Gamma \) when \(n\rightarrow \infty \), to prove that the decomposition in (4.6) is absolutely summable, we will need refinements of (4.10)–(4.11) for \(\mathcal {K}_s^{1,\Lambda }\) that also decay in the distance \(d(X,\Lambda )\). Both of these bounds will be a consequence of the perturbation \(V_\Lambda \) being locally supported, which implies that the spectral flow \(\alpha _s^{\Lambda }\) is approximately the identity far from \(\Lambda \). The necessary bounds are the content of Lemmas 4.3 and 4.4 below.
Lemma 4.3
(Distance Locality Bound for \(\mathcal {K}_s^1\)) There exists a decay function \(F_{\mathcal {K}^1}\), with finite moments of all orders for which, given any \(X,\Lambda \in \mathcal {P}_0( \Gamma )\) with \(d(X, \Lambda ) >0\), \(A\in \mathcal {A}_{X}\), and any \(s\in {\mathbb R}\), the following local bound holds:
It is easy to check that for fixed \(\epsilon \in (0,1)\) and any decay function F with finite \(\nu \)-moment, the function \(M_F^\epsilon :[0,\infty )\rightarrow [0,\infty )\) defined by
is also a decay function. The proof of Lemma 4.3 shows that one may take
where \(G_{\mathcal {F}}\) and \(G_{\Psi }\) are the decay functions previously discussed in (3.16) and (3.26). Since \(G_{\mathcal {F}}\) and \(G_{\Psi }\) both have finite moments of all orders, the same is true for \(F_{\mathcal {K}^1}\).
The proof of Lemma 4.3 will also make use of the following bound, which holds for any F and \(\epsilon \) as in (4.13), and \(\Lambda , X \in \mathcal {P}_0( \Gamma )\) such that \(d(X, \Lambda )>0\):
This follows from the following simple calculation
where the last inequality uses that \(|X(n)|\le \kappa n^\nu |X|\) for any \(n\ge 1\) by \(\nu \)-regularity, see (2.1).
Proof of Lemma 4.3
Fix \(X,\Lambda \in \mathcal {P}_0(\Gamma )\) such that \(X \cap \Lambda = \emptyset \), and let \(A \in \mathcal {A}_X\) be arbitrary. Recall that \(\mathcal {K}_s^{1, \Lambda }\) is as defined in (4.9), and that \(D(\Lambda , s)\) from (3.18) is the generator of the spectral flow. Then, since \(\alpha _0 = \textrm{id}\) and \(\mathcal {F}=\mathcal {F}_0^{\Lambda }\), it follows that
where one uses (3.19) and [47, Equation (6.37)] to obtain
Here, the final two equalities follow from integration by parts, and the fact that the supports of \(V_\Lambda \) and A are disjoint.
Returning to (4.17), we expand the generator as in (3.25) to write
Fix \(\epsilon \in (0,1)\), and for each \(z \in \Lambda \), set \(k_z(\epsilon ) = \epsilon d(z, X)\). For each term in (4.19), we approximate \( \mathcal {F}_r^{\Lambda }(A)\) with a strictly local approximation:
where one uses conditional expectation associated with the inflated set \(X(k_z(\epsilon ))\), see (2.1), (2.2). For the second term, one can apply the quasi-local bound for \(\mathcal {F}_r^{\Lambda }\) from (3.16) coupled with (3.4) to produce
Then, summing over \(z\in \Lambda \) and \(n\ge R\), and applying (3.26) and (4.15) gives the final estimate
To estimate the remaining terms in (4.20), note that for each \(z \in \Lambda \), \(b_z(n) \cap X(k_z(\epsilon )) \ne \emptyset \) only when \(n \ge k_z(1- \epsilon )\). As a result, arguments similar to the prior estimate produce the bound
Recalling the specific decay function from (4.14), the bound claimed in (4.12) now follows by inserting (4.19) into (4.17) and using the estimates found in (4.22) and (4.23) above.
By combining the estimate in Lemma 4.3 and the original quasi-locality bound from (4.11), one arrives that the following quasi-locality bound for \(\Vert [\mathcal {K}_s^{1, \Lambda }(A), B] \Vert \), which decays in both the distance between \(X={\text {supp}}(A)\) and \(Y={\text {supp}}(B)\) as well as the distance between \(\Lambda \) and X. This is the content of the next lemma.
Lemma 4.4
(Distance Quasi-Locality for \(\mathcal {K}_1\)) There exists a function \(G:[0,\infty )\times [0,\infty ) \rightarrow [0,\infty )\), non-increasing in both variables, such that given any \(\Lambda , X,Y \in \mathcal {P}_0(\Gamma )\) with \(d(X, \Lambda )>0\), the bound
holds for all \(A \in \mathcal {A}_X\), \(B \in \mathcal {A}_Y\), and \(s \in \mathbb {R}\). More precisely, for any \(\delta \in (0,1)\), one may choose
where \(F_{\mathcal {K}^1}\) and \(G_{\mathcal {K}^1}\) are the decay functions from Lemma 4.3 and (4.11), and \(G^\delta (m):=(G(m))^\delta .\)
In applications, it can be convenient to bound G(n, m) by a function that separates over the two arguments. In this case, taking \(\delta \) as in (4.25),
Proof
Fix \(0<\delta <1\). In the case that \(d(X,\Lambda ) \le d(X,Y)\), the quasi-locality estimate (4.11) shows that
where we have used that \(G_{\mathcal {K}^1}\) is non-increasing.
Alternatively, if \(d(X,\Lambda )>d(X,Y)\), the local bound from Lemma 4.3 implies
Since \(F_{\mathcal {K}^1}\) is also non-increasing, the bound \(F_{\mathcal {K}^1}(d(X, \Lambda )) \le F_{\mathcal {K}^1}^{\delta }\left( d(X,\Lambda )\right) F_{\mathcal {K}^1}^{1-\delta }\left( d(X,Y)\right) \) follows. The bound (4.24) is then a consequence of (4.27) and (4.28).
We conclude this section by proving Theorem 4.2, which will proceed as follows. We first define the global terms \(\tilde{\Phi }^{(1)}(x,s)\in \pi _0(\mathcal {A})\) and show that they commute with the ground state projection \(\vert \Omega \rangle \langle \Omega \vert \). Then, we use the localizing operators from (3.7) to define the local terms \(\Phi ^{(1)}(x,m,s)\) for \(m\ge R\) and show that they formally satisfy (4.6). The third and final step of the proof uses Lemmas 4.3, 4.4 to show that these new local interaction terms satisfy the desired norm bound for a function \(G_\Lambda (x,m)\) satisfying (4.5). This justifies the above-mentioned formal equality, and will be a consequence of considering the cases \(x\in \Lambda (R)\) and \(x\in \Gamma \setminus \Lambda (R)\) separately.
Proof of Theorem 4.2
Fix \(\gamma \in (0, \gamma _0)\), \(\Lambda \in \mathcal {P}_0( \Gamma )\), and take any IAS \((\Lambda _n)\) such that \(\Lambda \subseteq \Lambda _n\) for all n. Define the spectral flow \(\alpha _s^{\Lambda }\) and the weighted integral operators \(\mathcal {F}_s^{\Lambda }\), \(\mathcal {F}=\mathcal {F}_0^\Lambda \) with respect to the choices of \(\gamma \) and \(\Lambda \) as in (3.23) and (3.14), and then take \(\mathcal {K}_s^{i,\Lambda }\), \(i=1,2\), as defined (4.9).
For the first step, let \(\chi _{\Lambda }\) be the characteristic function of \(\Lambda \subset \Gamma \). Then, for each \(x \in \Gamma \) and \(s\in {\mathbb R}\) such that \(|s| \le s_0^{\Lambda }(\gamma )\), the self-adjoint operator \(\tilde{\Phi }^{(1)}(x,s) = \pi _0(\Phi ^{(1)}(x,s))\in \mathcal {B}(\mathcal {H})\) is defined by
To show that each \(\tilde{\Phi }^{(1)}(x,s)\) commutes with the ground state projection \(\vert \Omega \rangle \langle \Omega \vert \), recall that the ground state of the perturbed system is \(\Omega (\Lambda , s) = \tilde{U}(\Lambda ,s) \Omega \) if \(|s|\le s_\gamma ^\Lambda \). Then, recalling the relations (3.34)–(3.38), a simple calculation shows that for all \(A \in \mathcal {A}\)
where the final equality uses that (3.44) holds since \(|s| \le s_0^{\Lambda }(\gamma )\). Since (4.30) trivially holds for \(s=0\), considering (4.9), the above implies that
Hence, \([ \tilde{\Phi }^{(1)}(x,s), \vert \Omega \rangle \langle \Omega \vert ]=0\) for all \(x \in \Gamma \) and \(|s| \le s_0^{\Lambda }(\gamma )\) as claimed.
We now turn to the second step of the proof. To establish (4.6), use the conditional expectations from (3.7) to decompose each \(\tilde{\Phi }^{(1)}(x,s)\) as
where \(\tilde{\Phi }^{(1)}(x,m,s) = \pi _0(\Phi ^{(1)}(x,m,s) )\in \pi _0(\mathcal {A}_{b_x(m)})\) is defined for each \(m \ge R\) by
With respect to this notation, (4.7), (4.8) and (4.29) show that for all \(\psi \in \pi _0(\mathcal {A}^\textrm{loc})\Omega \),
Since this \(\pi _0(\mathcal {A}^\textrm{loc})\Omega \subseteq \mathcal {H}\) is dense, the equality in (4.6) follows from establishing absolute summability of the terms \(\tilde{\Phi }^{(1)}(x,m,s)\). This is achieved by defining a function
which bounds the norms of these terms and satisfies (4.5). Here, we note that \(\Lambda (R)\) is as in (2.1), and the functions \(G_1:[0,\infty )\rightarrow [0,\infty )\) and \( G_2:[0,\infty )\times [0,\infty )\rightarrow [0,\infty )\) will be independent of \(\Lambda \).
We now proceed to the final step of the proof. First, suppose \(x \in \Gamma \setminus \Lambda (R)\). As \(R \ge 0\) is the finite range of the unperturbed interaction, (4.33) simplifies to
Then, applying Lemmas 4.3 and 4.4 with the local approximation bound (3.6) one finds
where for any fixed \(\delta \in (0, 1)\), the function \(G_2\) can be taken to be
Here, \(C = \kappa ^2 R^{2 \nu } \Vert h \Vert _{\infty }\), \(F_{\mathcal {K}^1}\) is the function from Lemma 4.3, and
More specifically, the bound in (4.37) for \(m=R\) is a direct application of Lemma 4.3 while the bound for \(m \ge R+1\) follows from the quasi-local estimate in Lemma 4.4 and the subsequent bound (4.26) coupled with (3.3)-(3.6).
Given (4.35), the summability of \(G_\Lambda \) over the sites \(x\in \Gamma \setminus \Lambda (R)\) follows from observing that
as both \(F_{\mathcal {K}^1}\) and \(G_{\mathcal {K}^1}\) (and, thus, \(F_\delta \)) have finite moments of all orders. In particular, for any decay function \(F:[0,\infty )\rightarrow [0,\infty )\) with a finite \(\nu \)-moment,
We now turn to the sites \(x \in \Lambda (R)\), for which we demonstrate that
where \(G_1\) is a summable function. First consider (4.33) when \(m=R\). Combining the local bounds (4.10), the uniform bound (2.12), and the interaction bound in Assumption 2.5, one produces the x-independent bound
Alternatively, for \(m\ge R+1\), (4.33) can be estimated as
where one uses the quasi-local estimates from (4.11) and the local approximation bound in (3.6). Given Assumption 2.5, the final sum above can be further estimated as
To simplify notation, let \( M_{\Phi }(r):= \sum _{k \ge r} k^{\nu } e^{- a k^{\theta }} \) denote the \(\nu \)-th moment of the decay function associated with the perturbation \(\Phi \) from Assumption 2.5. Then, in summary, one has that for \(x\in \Lambda (R)\), (4.41) holds for the decay function \(G_1\) defined by
and for \(m \ge R+1\),
Since each of the decay functions in (4.46) has finite moments of all orders, it is clear that \(\sum _{m\ge R}G_1(m) <\infty \). As a consequence, \(G_\Lambda \) as in (4.35) satisfies
This demonstrates absolute summability of the terms in (4.6), and hence, completes the proof of Theorem 4.2.
4.2 The final decomposition of the transformed perturbation via LTQO
We now turn our attention to proving Theorem 4.1, which is a consequence of one last decomposition of the transformed perturbation from Theorem 4.2, i.e.
The key component for proving the desired norm bounds for this final decomposition is Lemma 4.5 below, and it is in the proof of this result where one needs the LTQO property from Assumption 2.4. To this end, we first shift the transformed perturbation terms by their expectation in the ground state \(\Omega \), as this will put us in the appropriate setting to apply LTQO.
Throughout this section, we assume \(\gamma \in (0,\gamma _0)\) is fixed and that \(s\in {\mathbb R}\) is such that \(|s|\le s_0^\Lambda (\gamma )\). As such, \(\Omega (\Lambda ,s) = \tilde{U}(\Lambda ,s)\Omega \) is the ground state of \(H(\Lambda ,s)\), and one finds that \( W(\Lambda , s) \Omega =0\) from considering (4.1) in the case \(\psi =\Omega \). Thus, Theorem 4.2 implies that for any \(\psi \in \pi _0( \mathcal {A}^\textrm{loc}) \Omega \)
where the (self-adjoint) observables \(\tilde{\Phi }^{(1)}_\omega (x,m,s) \in \pi _0(\mathcal {A}_{b_{x}(m)})\) are defined by
and normalized to have zero ground state expectation: \(\langle \Omega , \tilde{\Phi }^{(1)}_\omega (x,m,s) \Omega \rangle = 0\). For the proofs of Lemma 4.5 and Theorem 4.1, it is also convenient to set
which belongs to \(\pi _0(\mathcal {A})\) by Theorem 4.2.
Lemma 4.5
Let \(\tilde{P}_{b_x(n)}= \pi _0(P_{b_x(n)})\in \mathcal {B}(\mathcal {H})\) denote the representation of the ground state projection \(P_{b_x(n)}\) in the GNS space. Then, under the assumptions of Theorem 4.1, the bound
holds where \(G_0\) is the decay function from Assumption 2.4, and \(G_\Lambda ^{(1)}(x,m) = \sum _{k\ge m}G_\Lambda (x,k)\) with \(G_\Lambda \) as in Theorem 4.2.
Proof
To begin, one uses the LTQO property (2.27) to show that
where \(P_\Omega = \vert \Omega \rangle \langle \Omega \vert \) and \(\tilde{A} = \pi _0(A)\). To see this, first note that the inequality \(|a-b|^2 \le |a^2-b^2|\) for any \(a,b\ge 0,\) implies that
Recalling that \((\mathcal {H},\pi _0, \Omega )\) is the GNS representation of the unperturbed ground state \(\omega _0\), the second term on the right-hand-side above is simply
Here we find it convenient to use that \(\pi _0\) is norm-preserving. From this, it follows that
Given these observations, Assumption 2.4 then implies that
which establishes (4.51).
Now using (4.51) with \(\tilde{A} = \sum _{k=R}^m \tilde{\Phi }_\omega ^{(1)}(x,k,s) \in \pi _0(\mathcal {A}_{b_x(m)})\), one finds that for any \(n\ge m\),
where the last inequality follows from Theorem 4.2 as \(\Vert \tilde{\Phi }_\omega ^{(1)}(x,k,s)\Vert \le 2\Vert \tilde{\Phi }^{(1)}(x,k,s)\Vert \le 2\,s G_\Lambda (x,k)\).
The remaining operator norm from (4.53) can then be trivially bounded in terms of \(\tilde{\Phi }_\omega ^{(1)}(x,s)\) from (4.49) as follows:
Once again applying Theorem 4.2 then shows that
and, moreover, \([\tilde{\Phi }_{\omega }^{(1)}(x,s), P_{\Omega }]= [\tilde{\Phi }^{(1)}(x,s), P_{\Omega }]=0\). As a result, \( \left\| \tilde{\Phi }_{\omega }^{(1)}(x,s) P_{\Omega }\right\| =0\) since
where the last equality follows from (4.48), (4.49). Thus, inserting (4.55) into (4.53) proves (4.50).
We now prove Theorem 4.1, which uses both Lemma 4.5 and the frustration-free property.
Proof of Theorem 4.1
Fix \(x\in \Gamma \) and recall that \(P_\Omega = \vert \Omega \rangle \langle \Omega \vert \). Since \([\tilde{\Phi }_{\omega }^{(1)}(x,s), P_\Omega ]=0\), one can write
where the last equality uses (4.56). The terms \(\tilde{\Phi }^{(2)}(x,m,s)\) are defined by decomposing \({\mathchoice{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.5pt}l}}{\mathrm {1\hspace{-2.77771pt}l}}}-P_\Omega \) in terms of the finite volume ground state projections \(\tilde{P}_{n}:=\tilde{P}_{b_x(n)}\in \pi _0(\mathcal {A}_{b_x(n)})\).
First, note that \(\tilde{P}_{n}\) converges strongly to \(P_\Omega \) for all \(\psi \in \mathcal {H}\) by the frustration-free and LTQO properties. As a consequence, the collection of operators
forms a family of orthogonal projections that are mutually orthogonal and sum to \({\mathchoice{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.5pt}l}}{\mathrm {1\hspace{-2.77771pt}l}}}- P_\Omega \). That is,
where the second equality holds since the frustration-free property implies \(\tilde{P}_n\tilde{P}_m = \tilde{P}_m\) for \(m\ge n\). Moreover, it trivially holds that
Using (4.49), the above properties imply that for all \(\psi ,\phi \in \mathcal {H}\),
We note that the triple sum of operators actually converges absolutely in norm, and so the operator equality holds in the norm sense.
Each term \(\Phi ^{(2)}(x,m,s) \in \mathcal {A}_{b_x(m)}\) will be defined as a sum of two self-adjoint terms
each of which is annihilated by the ground state projection \(\tilde{P}_m\). Fix \(k\ge R\), and use the properties in (4.58), (4.59) to write
where \(\tilde{\Phi }_{k,m}=\tilde{\Phi }_{k,m}^*\) is defined by
Self-adjointness follows from noting that \({\mathchoice{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.5pt}l}}{\mathrm {1\hspace{-2.77771pt}l}}}-\tilde{P}_m = {\mathchoice{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.5pt}l}}{\mathrm {1\hspace{-2.77771pt}l}}}-\tilde{P}_{m-1} + \tilde{E}_m\).
For each \(m\ge R\), define \(\Theta _1(x,m,s) \in \pi _0(\mathcal {A}_{b_x(m)}),\) by
These operators are self-adjoint, satisfy \(\Theta _1(x,m,s)\tilde{P}_{m}=0\), and Theorem 4.2 implies that their norm is bounded from above by \(2sG_\Lambda (x,m/2)\) as for m even:
For the \(\Theta _2\) terms, one sums the remaining terms \(\sum _{m>2k}\tilde{\Phi }_{k,m}\) over k, and then uses the indicator function \(\chi _{m>2k}\) to exchange the summations as follows:
where, for \(m>2R\) one recalls (4.62) and defines
This definition is extended by setting \(\Theta _2(x,m,s)=0\) for \(R\le m \le 2R\). One sees that \(\Theta _2(x,m,s)\tilde{P}_m=0\) by applying \(\tilde{P}_m\tilde{P}_{m-1}=\tilde{P}_m\) to verify
Finally, applying Lemma 4.5,
where \(G_\Lambda ^{(1)}(x,m) = \sum _{n\ge m} G_\Lambda (x,n)\).
Therefore, setting \(\tilde{\Phi }^{(2)}(x,m,s) = \Theta _1(x,m,s)+\Theta _2(x,m,s)\) for all m, we have constructed self-adjoint operators such that
Moreover, these operators satisfy that for all \(m\ge R\) and \(x\in \Gamma \),
and, combining (4.64) and (4.66), their norms can be bounded above by
where
The absolute summability of the series in (4.67) is a direct consequence of \(G_0\) being summable as well as that both \(G_{\Lambda }\) and \(G_{\Lambda }^{(1)}\) satisfy (4.5). For \(G_\Lambda ^{(1)}\) this can easily be seen from the fact that \(G_\Lambda \) is a combination of functions with finite moments of all orders, see specifically (4.35), (4.38) and (4.46).
5 Proving Theorems 2.7 and 2.8 via a form bound for the GNS Hamiltonian
In this section, we generalize [48, Theorem 3.8], which was itself based off [41, Proposition 2], so that it is applicable to the setting of infinite systems in their GNS representation. Afterwards, we apply the form bound in conjunction with Theorem 4.1 to prove Theorem 2.7. We then conclude with the proof of Theorem 2.8, which follows as a consequence of Theorem 2.7.
5.1 The Michalakis–Zwolak relative form bound
The form bound result is stated in the setting described in Sect. 2 and, in particular, under Assumption 2.3. Thus, there is a family of sets
accompanied with a family \(\mathcal {T} = \{ \mathcal {T}_n: n \ge 0\}\) of separating partitions of \((c, \zeta )\)-polynomial growth, for which the associated finite volume Hamiltonians satisfy
Moreover, the local gaps are further assumed to satisfy \(\gamma (n) \ge \gamma _1/n^\alpha \) for some \(\gamma _1>0\) and \(\alpha \ge 0\).
Theorem 5.1
(Michalakis-Zwolak [41]) Let \(H_0\) be the GNS Hamiltonian associated with a zero-energy ground state of an initial system satisfying Assumptions 2.1 and 2.3, and let \(V\in \mathcal {A}\) be a perturbation associated with an absolutely-summable, anchored interaction on \((\Gamma , d)\). That is, there exist \(\Phi (x,n)^* = \Phi (x,n) \in \mathcal {A}_{b_x(n)} \) for all \(x\in \Gamma \) and \(n\ge R\) such that
In addition, assume that terms of V annihilate the finite-volume ground state projections of the initial system, i.e.
and that there is a decay function G with finite \((\zeta +\alpha )\)-moment such that \( \sup _{x \in \Gamma } \Vert \Phi (x,n) \Vert \le G(n) \,.\) Then, for all \(\psi \in \textrm{dom}{H_0}\),
In keeping with the notation from the previous sections, denote by \(\tilde{A} = \pi _0(A)\) the image of any observable \(A\in \mathcal {A}\) under the GNS representation \((\mathcal {H},\pi _0,\Omega )\) of the zero-energy ground state \(\omega _0\). The proof of Theorem 5.1 follows closely the argument proving [48, Theorem 3.8], with the proviso that one must check that the infinite operator sums replacing the finite operator sums from [48] are well-defined.
To this end, let \(n \ge R\), and consider the n-th separating partition \(\mathcal {T}_n = \{ \mathcal {T}_n^i: i \in \mathcal {I}_n \}\). For each \(i \in \mathcal {I}_n\) and any choice of \(x,y \in \mathcal {T}_n^i\), one has that
This follows since the corresponding algebra elements \(H_{\Lambda (x,n)},H_{\Lambda (y,n)}\in \mathcal {A}\) are supported on disjoint sets (and similarly for the ground state projections), which carries over to the GNS space by the homomorphism property.
With \(n \ge R\) and \(i \in \mathcal {I}_n\) fixed, denote by \(C_n^i\) the collection of all configurations associated to \(\mathcal {T}_n^i\). More precisely,
For each \( \sigma \in C_n^i \), we define \(|\sigma |\) by
Recall that \(\pi _{0}(\mathcal {A}^\textrm{loc}) \Omega \) is a dense subspace of \(\mathcal {H}\). Let \(\psi = \tilde{A} \Omega \) for some \(A \in \mathcal {A}_X\), and set \(\tilde{Q}_{\Lambda (x,n)}= {\mathchoice{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.5pt}l}}{\mathrm {1\hspace{-2.77771pt}l}}}-\tilde{P}_{\Lambda (x,n)}\). In this case, one has that
whenever \(\Lambda (x,n)\) satisfies \(\Lambda (x,n) \cap X = \emptyset \). It is also clear that for any \(X \in \mathcal {P}_0( \Gamma )\), the set of sites \(\{x \in \mathcal {T}_n^i: \Lambda (x,n) \cap X \ne \emptyset \}\) is finite. Thus, for any \(\psi \in \pi _{0}(\mathcal {A}^\textrm{loc}) \Omega \), define the operator \(S(\sigma )\) by
Note that, if \(|\sigma | < \infty \), then at most finitely many of these factors act non-trivially, and moreover, by (5.5), all factors above commute. Since \(\pi _{0}(\mathcal {A}^\textrm{loc}) \Omega \) is dense, there is a unique extension of \(S(\sigma )\) to an element of \(\mathcal {B}( \mathcal {H}_{\omega })\) for each \(\sigma \in C_n^i\). One checks that these operators satisfy:
Since \(\tilde{Q}_{\Lambda (x,n)}={\mathchoice{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.5pt}l}}{\mathrm {1\hspace{-2.77771pt}l}}}-\tilde{P}_{\Lambda (x,n)}\), by (5.5) one clearly has that
and as a result, also
For \(\sigma \in C_n^i\) with \(|\sigma | < \infty \), (5.11) implies \(0 = [ \tilde{Q}_{\Lambda (x,n)}, S(\sigma )] \psi \) for all \(\psi \in \pi _{0}(\mathcal {A}^\textrm{loc}) \Omega \) and, hence, for all \(\psi \in \mathcal {H}\). If \(|\sigma |=\infty \), then the commutator is zero by definition. Combining (5.10) and (5.12), we find that
for all \(\sigma , \sigma ' \in C_n^i\) and each \(x \in \mathcal {T}_n^i\).
We use these families of orthogonal projections in the following proof.
Proof of Theorem 5.1
In the GNS representation, the terms of \(\tilde{V}\) can be rearranged using the family of separating partitions from Assumption 2.3 as
since V is absolutely summable. As a result, for any \(\psi \in \mathcal {H}\), one has the bound
Now, since \(b_x(n) \subset \Lambda (x,n)\) for all \(\Lambda (x,n) \in \mathcal {S}\), the frustration free property implies
and so by (5.3) it follows that that for each \(x\in \mathcal {T}_n^i\), the term \(\tilde{\Phi }(x,n)\) satisfies
Arguing as in (5.12)-(5.13) above, one then finds that for all \(x \in \mathcal {T}_n^i\) and \(\sigma ,\sigma ' \in C_n^i\)
and, moreover,
As a consequence, one can use (5.10) and (5.19) to bound
Summing these orthogonal projections again, one obtains
where, the final bound follows since the representation preserves positivity and the operator inequality \(\gamma (n) Q_{\Lambda (x,n)} \le H_{\Lambda (x,n)}\) holds in the algebra.
Given the above, one concludes that for any \(\psi \in \textrm{dom}(H_0)\),
where the last inequality uses that \(\Lambda (x,n) \cap \Lambda (y,n) = \emptyset \) for distinct \(x, y \in \mathcal {T}_n^i\). Returning to (5.15), since these partitions satisfy the \((c,\zeta )\)-polynomial growth bound it is clear that
with \(\beta \) as in (5.4). This completes the proof.
5.2 Proofs of Theorems 2.7 and 2.8
Theorem 4.1 showed that for every finite \(\Lambda \subset \Gamma \), the Hamiltonian
transforms under the spectral flow unitary as follows
where \(E(\Lambda ,s)\) is the ground state energy of \(H(\Lambda ,s)\), and \(\Phi _\Lambda ^{(2)}(x,m,s)\) is a balled interaction satisfying the conditions of Theorem 5.1 with norm bounds that are linear in |s| and given in terms of a \(\Lambda \)-dependent decay function. However, we will show below that the constant \(\beta \) from Theorem 5.1 can be taken independent of \(\Lambda \). Theorem 2.7 will then follow from applying [48, Corollary 3.3]. In our context, the latter result states the following. Suppose that \(H_0\) is a self-adjoint, positive operator on a Hilbert space \(\mathcal {H}\) with \(\min \textrm{spec}H_0 = 0\) and \((0,\gamma _0)\cap \textrm{spec}(H_0) = \emptyset \). Then, for any \(V=V^*\in \mathcal {B}(\mathcal {H})\) such that there exists \(0\le \beta <1\) for which
one has that
Proof of Theorem 2.7
Fix \(\gamma \in (0,\gamma _0)\) where \(\gamma _0\) is as in Assumption 2.2, and let \(\Lambda \in \mathcal {P}_0\) be arbitrary. Given Theorem 4.1, it is clear that Theorem 5.1 applies and produces a non-trivial form bound (see (5.4)) so long as
has a finite \((\zeta +\alpha )\)-moment where, as stated in Assumption 2.3, \(\zeta \) is the polynomial growth of the separating partitions and \(\gamma (n) \ge \gamma _1 n^{-\alpha }\) is the lower bound on the local gaps. Moreover, to show that
see (3.39), we wish to show this form bound is uniform in \(\Lambda \).
To this end, recall that \(G_\Lambda \) from (4.35) is defined in terms of two functions \(G_1\), \(G_2\) that are independent of \(\Lambda \) and decay faster than any polynomial. It is then clear that for all \(\Lambda \in \mathcal {P}_0\), \(x\in \Gamma \) and \(m\ge R\),
and similarly, \(G_\Lambda ^{(1)}(x,m)\le G^{(1)}(m)\) where \(G^{(1)}(m) = \sum _{m\ge R}G(m)\). It follows immediately that
and that \(G^{(2)}\) has a finite \((\zeta +\alpha )\)-moment as long as \(G_0\) satisfies (2.26).
Given the norm bound from Theorem 4.1, it follows from Theorem 5.1 that for all \(\psi \in \textrm{dom}(H_0)\)
Thus, \(\textrm{gap}(H(\Lambda ,s)) \ge \gamma _0 -s\beta \gamma _0\) by (5.24) and, in particular, (5.25) holds since this implies
We conclude with using the uniform estimate from Theorem 2.7 to establish the claimed lower bound estimate on the gap of the extensively perturbed system from Theorem 2.8.
Proof of Theorem 2.8
Let \(0<\gamma < \gamma _0\) and consider \(|s|\le s_0(\gamma )\). Recall that for any IAS \((\Lambda _n)\), the following limits hold in \(\mathcal {A}\) as \(n\rightarrow \infty \):
see (2.37) and (2.38). As a consequence, \(\omega _s^{\Lambda _n}(A) = \omega _0\circ \alpha _s^{\Lambda _n}(A) \rightarrow \omega _s(A)\) for all \(A\in \mathcal {A}\) and, moreover, \(\omega _s\) is a ground state of \(\delta _s\).
Now consider \(A \in \mathcal {A}^\textrm{loc}\) for which \(\omega _s(A) =0\). Given Theorem 2.7, the GNS Hamiltonian \(H(\Lambda _n, s)\) along any IAS \((\Lambda _n)\) has a gap above its unique ground state lower bounded by \(\gamma \) for all \(|s|\le s_0(\gamma )\). Therefore, \(\omega _s^{\Lambda _n}\) satisfies (2.22) and, in particular, the inequality
holds for the observable \(B_n = A - \omega _s^{\Lambda _n}(A) {\mathchoice{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.22214pt}l}}{\mathrm {1\hspace{-2.5pt}l}}{\mathrm {1\hspace{-2.77771pt}l}}}\in \mathcal {A}^\textrm{loc}\).
Combining (5.27) and the local uniform convergence of \(\alpha _s^{\Lambda _n}\), the limit \(n \rightarrow \infty \) can be taken on both sides of (5.28) to obtain (2.39). The remaining claims follow as in (2.22).
Data availability
No data were collected or generated as part of the research reported in this paper.
References
Affleck, I., Kennedy, T., Lieb, E.H., Tasaki, H.: Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 59, 799 (1987)
Anshu, A.: Improved local spectral gap thresholds for lattices of finite size. Phys. Rev. B 101, 165104 (2020)
Bachmann, S., Bols, A., De Roeck, W., Fraas, M.: Quantization of conductance in gapped interacting systems. Ann. Henri Poincaré 19, 695–708 (2018)
Bachmann, S., Bols, A., De Roeck, W., Fraas, M.: Rational indices for quantum ground state sectors. J. Math. Phys. 62, 011901 (2021). arXiv:2001.06458
Bachmann, S., De Roeck, W., Donvil, B., Fraas, M.: Stability of invertible, frustration-free ground states against large perturbations. Quantum 2022, 06–11 (2022)
Bachmann, S., Hamza, E., Nachtergaele, B., Young, A.: Product Vacua and Boundary State models in \(d\) dimensions. J. Stat. Phys. 160, 636–658 (2015)
Bachmann, S., Michalakis, S., Nachtergaele, B., Sims, R.: Automorphic equivalence within gapped phases of quantum lattice systems. Comm. Math. Phys. 309, 835–871 (2012)
Bishop, M., Nachtergaele, B., Young, A.: Spectral gap and edge excitations of \(d\)-dimensional PVBS models on half-spaces. J. Stat. Phys. 162, 1485–1521 (2016)
Bourne, C., Ogata, Y.: The classification of symmetry protected topological phases of one-dimensional fermion systems. Forum Math. Sigma 9, E25 (2021)
Bratteli, O., Robinson, D.W.: Operator Algebras and Quantum Statistical Mechanics, vol. 1, 2nd edn. Springer Verlag, Berlin-Heidelberg-New York (1987)
Bratteli, O., Robinson, D.W.: Operator Algebras and Quantum Statistical Mechanics, vol. 2, 2nd edn. Springer Verlag, Berlin (1997)
Bravyi, S., Hastings, M., Michalakis, S.: Topological quantum order: stability under local perturbations. J. Math. Phys. 51, 093512 (2010)
Bravyi, S., Hastings, M.B.: A short proof of stability of topological order under local perturbations. Commun. Math. Phys. 307, 609 (2011)
Bravyi, S., Hastings, M.B., Verstraete, F.: Lieb-Robinson bounds and the generation of correlations and topological quantum order. Phys. Rev. Lett. 97, 050401 (2006)
Chen, C.-F., Lucas, A., Yin, C.: Speed limits and locality in many-body quantum dynamics. Rep. Prog. Phys. 86, 116011 (2023)
Cui, S.X., Dawei, D., Han, X., Penington, G., Ranard, D., Rayhaun, B.C., Shangnan, Z.: Kitaev’s quantum double model as an error correcting code. Quantum 4, 331 (2020). arXiv:1908.02829
De Roeck, W., Salmhofer, M.: Persistence of exponential decay and spectral gaps for interacting fermions. Commun. Math. Phys. 365, 773–796 (2019)
Del Vecchio, S., Fröhlich, J., Pizzo, A., Ranallo, A.: Boundary effects and the stability of the low energy spectrum of the AKLT model, arXiv:2308.02811, (2023)
Del Vecchio, S., Fröhlich, J., Pizzo, A., Ranallo, A.: Low energy spectrum of the XXZ model coupled to a magnetic field, arXiv:2306.02772, (2023)
Del Vecchio, S., Fröhlich, J., Pizzo, A., Rossi, S.: Lie-Schwinger block-diagonalization and gapped quantum chains with unbounded interactions. Commun. Math. Phys. 381, 1115–1152 (2021). arXiv:1908.07450
Del Vecchio, S., Fröhlich, J., Pizzo, A., Rossi, S.: Local interative block-diagonalization of gapped Hamiltonians: a new tool in singular perturbation theory. J. Math. Phys. 63, 073503 (2022). arXiv:2007.07667
Fröhlich, J., Pizzo, A.: Lie-Schwinger block-diagonalization and gapped quantum chains. Commun. Math. Phys. 375, 2039–2069 (2020). arXiv:1812.02457
Glimm, J.G.: On a certain class of operator algebras. Trans. Amer. Math. Soc. 95, 318–340 (1960)
Gosset, David, Mozgunov, Evgeny: Local gap threshold for frustration-free spin systems. J. Math. Phys. 57, 091901 (2016)
Hastings, M.B.: Lieb–Schultz–Mattis in higher dimensions. Phys. Rev. B 69, 104431 (2004)
Hastings, M.B.: The stability of free Fermi Hamiltonians. J. Math. Phys. 60, 042201 (2019). arXiv:1706.02270
Hastings, M.B., Wen, X.G.: Quasi-adiabatic continuation of quantum states: the stability of topological ground-state degeneracy and emergent gauge invariance. Phys. Rev. B 72, 045141 (2005)
Hege, P., Moscolari, M., Teufel, S.: Finding spectral gaps in quasicrystals. Phys. Rev. B 106, 155140 (2022)
Henheik, J., Teufel, S.: Adiabatic theorem in the thermodynamic limit. Part II: Systems with a gap in the bulk. Forum Math. Sigma 10(e4), 1–35 (2022). arXiv:2012.15239
Kapustin, A., Sopenko, N.: Hall conductance and the statistics of flux insertions in gapped interacting lattice systems. J. Math. Phys. 61, 101901 (2020). arXiv:2006.14151
Kapustin, A., Sopenko, N.: Local Noether theorem for quantum lattice systems and topological invariants of gapped states. J. Math. Phys. 63, 091903 (2022). arXiv:2201.01327
Kastoryano, M.J., Lucia, A.: Divide and conquer method for proving gaps of frustration free Hamiltonians. J. Stat. Mech. Theor. Exp. 2018, 033105 (2018)
Kato, T.: Perturbation Theory for Linear Operators. Springer-Verlag, Berlin (1995)
Kitaev, A.: Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006)
Koma, T.: Stability of the spectral gap for lattice fermions, arXiv:2005.04548, (2020)
Lemm, M., Mozgunov, E.: Spectral gaps of frustration-free spin systems with boundary. J. Math. Phys. 60, 051901 (2019). arXiv:1801.08915
Levin, M.A., Wen, X.-G.: String-net condensation: a physical mechanism for topological phases. Phys. Rev. B 71, 045110 (2005)
Lieb, E.H., Robinson, D.W.: The finite group velocity of quantum spin systems. Commun. Math. Phys. 28, 251–257 (1972)
Loring, T.: Bulk spectrum and K-theory for infinite-area topological quasicrystals. J. Math. Phys. 60, 081903 (2019)
Lucia, A., Moon, A., Young, A.: Stability of the spectral gap and ground state indistinguishability for a decorated AKLT model. Ann. Henri. Poincaré, (2023). https://doi.org/10.1007/s00023-023-01398-8
Michalakis, S., Zwolak, J.P.: Stability of frustration-free Hamiltonians. Commun. Math. Phys. 322, 277–302 (2013)
Moon, A.: Stable properties of gapped ground state phases in quantum spin chains, Ph.D. thesis, University of California, Davis, (2020)
Moon, A., Ogata, Y.: Automorphic equivalence within gapped phases in the bulk. J. Funct. Analysis 278, 108422 (2020). arXiv:1906.05479
Nachtergaele, B., Ogata, Y., Sims, R.: Propagation of correlations in quantum lattice systems. J. Stat. Phys. 124, 1–13 (2006)
Nachtergaele, B., Scholz, V., Werner, R. F.: Local approximation of observables and commutator bounds. In: Operator Methods in Mathematical Physics (J. Janas, P. Kurasov, A. Laptev, and S. Naboko, eds.), Operator Theory: Advances and Applications, vol. 227, Birkäuser Verlag, (2013), pp. 143–149
Nachtergaele, B., Sims, R., Young, A.: Lieb-Robinson bounds, the spectral flow, and stability for lattice fermion systems, Mathematical Results in Quantum Physics (F. Bonetto, D. Borthwick, E. Harrell, and M. Loss, eds.), Contemporary Mathematics, vol. 717, Amer. Math. Soc., (2018), pp. 93–115
Nachtergaele, B., Sims, R., Young, A.: Quasi-locality bounds for quantum lattice systems. I. Lieb–Robinson bounds, quasi-local maps, and spectral flow automorphisms. J. Math. Phys. 60, 061101 (2019)
Nachtergaele, B., Sims, R., Young, A.: Quasi-locality bounds for quantum lattice systems and perturbations of gapped ground states II. Perturbations of frustration-free spin models with gapped ground states. Ann. H. Poincaré 23, 393–511 (2022)
Ogata, Y.: A \(\mathbb{Z} _2\)-index of symmetry protected topological phases with time reversal symmetry for quantum spin chains. Commun. Math. Phys. 374, 705–734 (2020)
Ogata, Y.: A derivation of braided \(C^*\)-tensor categories from gapped ground states satisfying the approximate Haag duality. J. Math. Phys. 63, 011902 (2022)
Ogata, Y.: A \({H^3(G, T)}\)-valued index of symmetry protected topological phases with on-site finite group symmetry for two-dimensional quantum spin systems. Forum Math. Pi 9, e13 (2021). arXiv:2101.00426
Ogata, Y.: A \(\mathbb{Z} _2\)-index of symmetry protected topological phases with reflection symmetry for quantum spin chains. Commun. Math. Phys. 385, 1245–1272 (2021). arXiv:1904.01669
Ogata, Y.: Boundary states of a bulk gapped ground state in 2-d quantum spin systems, arXiv:2308.08087, (2023)
Ogata, Y., Tachikawa, Y., Tasaki, H.: General Lieb–Schultz–Mattis type theorems for quantum spin chains. Commun. Math. Phys. 385, 79–9 (2021). arXiv:2004.06458
Ogata, Y., Tasaki, H.: Lieb–Schultz–Mattis type theorems for quantum spin chains without continuous symmetry. Commun. Math. Phys. 372, 951–962 (2019)
Ogata, Y., Tasaki, H.: Lieb–Schultz–Mattis type theorems for quantum spin chains without continuous symmetry, Commun. Math. Phys. (2019), online, arXiv:1808.08740, published online, 5 Feb 2019
Qiu, Y., Wang, Z.: Ground subspaces of topological phases of matter as error correcting codes. Ann. Phys. 422, 168318 (2020)
Robinson, D.W.: Properties of propagation of quantum spin systems. J. Australian Math. Soc. 19, 387–399 (1976)
Ruelle, D.: Statistical Mechanics: Rigorous Results. Benjamin, New York (1969)
Simon, B.: The Statistical Mechanics of Lattice Gases, vol. 1. Princeton University Press, Princeton (1993)
Szehr, O., Wolf, M.M.: Perturbation theory for parent Hamiltonians of matrix product states. J. Stat. Phys. 159, 752–771 (2015). arXiv:1402.4175
van Luijk, L., Stottmeister, A., Werner, R. F.: Convergence of dynamics on inductive systems of Banach spaces, arXiv:2306.16063, (2023)
Xu, Y., Capponi, S., Chen, J.-Y., Vanderstraeten, L., Hasik, J., Nevidomskyy, A. H., Mambrini, M., Penc, K., Poilblanc, D.: Phase diagram of the chiral su(3) antiferromagnet on the kagome lattice, arXiv:2306.16192, (2023)
Yarotsky, D.A.: Ground states in relatively bounded quantum perturbations of classical lattice systems. Commun. Math. Phys. 261, 799–819 (2006)
Acknowledgements
Based upon work supported by the National Science Foundation under grants DMS-1813149 and DMS-21083901 (BN), and the DFG under EXC-2111–390814868 and TRR 352 (Grant: Number: 470903074): Mathematik der Vielteilchen-Quantensysteme und ihrer kollektiven Phänomene (AY). BN and AY acknowledge support of the Erwin Schrödinger International Institute for Mathematics and Physics (ESI), where part of this work was carried out during the “Tensor Networks: Mathematical Structures and Novel Algorithms” workshop. BN also gratefully acknowledges kind hospitality at the Technical University Munich during the final stages of this work and the Alexander von Humboldt Foundation for support provided through a Carl Friedrich von Siemens Research Award.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
LTQO implies uniqueness of the ground state
In this section, we prove a simple, yet general, uniqueness result within the framework of Sect. 2. To this end, let \(\mathcal {A}\) be a \(C^*\)-algebra of quasi-local observables associated to a quantum spin system defined over a \(\nu \)-regular, discrete metric space \((\Gamma , d)\). Let \(\Phi \) be a non-negative, frustration-free interaction on \((\Gamma , d)\) for which the corresponding derivation \(\delta \), defined initially on the local observable algebra as in (2.18), is a generator of a strongly continuous dynamics, denoted by \(\{ \tau _t \, | \, t \in \mathbb {R} \}\). Let \(\omega \) be an infinite-volume, zero-energy ground state associated to \(\delta \), i.e. \(\omega \) satisfies (2.19) and \(\omega (\Phi (X)) = 0\) for all finite \(X \subset \Gamma \). Denote by \((\mathcal {H}, \pi , \Omega )\) the GNS triple associate to \(\omega \). To simplify notation, let us set \(\tilde{A}:=\pi (A)\) the representative of \(A \in \mathcal {A}\) in the GNS space. We say that \(\omega \) satisfies LTQO if there is a function \(G: [0, \infty ) \rightarrow [0, \infty )\) with \(\lim _{m \rightarrow \infty } G(m) = 0\) for which: given any choices \(m \ge k \ge 0\), \(x \in \Gamma \), and \(A \in \mathcal {A}_{b_x(k)}\),
Note that the above is simply the reformulation of (2.27) in \(\mathcal {B}( \mathcal {H})\). The following result holds.
Proposition A.1
Let \(\omega \) be an infinite-volume, zero-energy ground state of a frustration-free model. If \(\omega \) satisfies LTQO, then the kernel of the GNS Hamiltonian H is one-dimensional.
Proof
By way of contradiction, assume there is a unit vector \(\psi \in \textrm{ker}(H)\) with \(\langle \psi , \Omega \rangle =0\). First, since \(\pi ( \mathcal {A}^\textrm{loc}) \Omega \) is dense in \(\mathcal {H}\), there is \(x \in \Gamma \) and operators \(A_n \in \mathcal {A}_{b_x(n)}\) for which \(\psi _n = \tilde{A}_n \Omega \rightarrow \psi \). In this case,
Thus, there is \(n_1 \in \mathbb {N}\) so that \(| \langle \Omega , \tilde{A}_n \Omega \rangle | \le 1/3\) for all \(n \ge n_1\).
Next, since \(\textrm{ker}(H) \subset \textrm{ker}( \tilde{H}_{b_x(m)})\) for all \(m \ge 0\) and \(x \in \Gamma \), we have
for all \(m \ge 0\). Since \(1 = \lim _{n \rightarrow \infty } \langle \psi , \psi _n \rangle \), there is some \(n_2 \in \mathbb {N}\) for which \(| \langle \psi , \psi _n \rangle | \ge 2/3\) for all \(n \ge n_2\). Combining this with (A.3), we find that for any \(m\ge n \ge n_2\),
It follows that for \(n\ge \max \{n_1,n_2\}\),
where we have applied (A.1). This is a contradiction as the decay function G satisfies \(G(m-n) \rightarrow 0\) as \(m \rightarrow \infty \).
Proof of bounded differentiability of the spectral flow
In this section, we demonstrate that the derivative of the spectral flow is a well-defined bounded operator when restricted to appropriate collections of quantifiably local observables \(\mathcal {A}^{(\Lambda _n),g}\). A related result also appears in [42, Appendix].
To state this result, we consider models of quantum spin systems defined over a \(\nu \)-regular, discrete metric space \((\Gamma , d)\). More specifically, we investigate differentiable curves of interactions \([0,1]\ni s \mapsto \Phi (s)\), i.e. for each finite \(X \subset \Gamma \) and \(0 \le s \le 1\), \(\Phi (X,s)^* = \Phi (X, s) \in \mathcal {A}_X\) and \(\Phi (X,\cdot ): [0,1] \rightarrow \mathcal {A}_X\) is differentiable. We assume that these curves have a finite norm of the following form:
where F is an F-function on \((\Gamma , d)\) of stretched exponential decay, i.e. as in (2.11). In this case, it was shown in [47, Section VI.E.2] that for any differentiable curves of interactions \(\Phi \) with finite norm \(\Vert \Phi \Vert ^1_F\), there is an F-function \(\tilde{F}\) and an s-dependent interaction \(\Psi (s)\) with
for which \(\Psi (s)\) is a generator of the infinite volume spectral flow automorphisms \(\alpha _s\). We further know by [47, Theorem 3.9], that this infinite volume spectral flow is differentiable on \(\mathcal {A}_{\Gamma }^\textrm{loc}\) with
Our aim is the show that
is a bounded map when defined on a suitable Banach algebra of g-local obervables, in the sense discussed in Sect. 2.1.
Theorem A.1
(Bounded Differentiability) Let \(g:[0, \infty ) \rightarrow [0, \infty )\) be non-increasing and satisfy \(\lim _{n \rightarrow \infty }g(n) =0\). Let \((\Lambda _n)\) be any increasing and absorbing sequence of finite subsets of \(\Gamma \) satisfying
Then, the derivative \(\alpha '_s\) of the spectral flow \(\alpha _s\) is a well-defined bounded linear map \(\mathcal {A}^{(\Lambda _n),g} \rightarrow \mathcal {A}\), satisfying
with \( \Vert \tilde{F} \Vert _1 \) as defined in (2.9).
Proof
We start by noting that for any local observable \(A \in \mathcal {A}_Y\) with \(Y \subset \Gamma \) finite, we have the following estimate:
Let \(A \in \mathcal {A}^{(\Lambda _n),g}\). By (2.6),
which implies that the sequence \(\{ \Pi _n(A) \}_{n=1}^{\infty }\) converges to A (in norm) at a rate governed by g. Define a map \(\alpha '_s: \mathcal {A}^{(\Lambda _n),g} \rightarrow \mathcal {A}\) by setting
Note that for any strictly local observable A, \(\Pi _n(A) = A\) if n is sufficiently large, and thus this definition agrees with the standard definition of the derivative of \(\alpha _s(A)\) for \(A\in \mathcal {A}^\textrm{loc}\).
Now, consider integers \(1 \le M< N < \infty \). For any observable A,
and for \(A \in \mathcal {A}^{(\Lambda _n),g} \), we also have that for any \(n \ge 1\),
where we have used (B.6) and the fact that g is non-increasing. We conclude that
Here, for the second inequality above we used (B.5), and the final bound comes from (B.9). We conclude that whenever g satisfies (B.3), the sequence \(\{ \alpha '_s( \Pi _n(A)) \}_{n=1}^{\infty }\) is norm Cauchy; hence, norm convergent. This shows that \(\alpha '_s\) as given in (B.7) is well-defined and equals the derivative of \(\alpha _s(A)\), for \(A\in \mathcal {A}^{(\Lambda _n),g} \). Moreover, for any \(N \ge 1\),
and therefore,
as claimed.
As an application of this result we can establish a relation between spectral gap stability, automorphic equivalence, and differentiability of the ground state. In particular, we find that Assumption 1.2 (vii) in [43], i.e. uniform differentiability of the ground state, follows from automorphic equivalence. Therefore, for perturbation that leave the gap stable, the differentiability assumption is always satisfied under the other items in [43, Assumption 1.2] (see also [9, 51]). Given [43, Theorem 1.3], one can also regard Assumption 1.2 (vii) as equivalent to automorphic equivalence. To clarify the relation between differentiability of the ground state and automorphic equivalence, we first define a notion of stable perturbations.
As before in this appendix, consider differentiable curves of interactions \(\Phi \). Let \(\omega _0\) be a ground state of the derivation defined by \(\Phi (\cdot ,0)\) as in (2.18)-(2.19), and let \(H_0\) denote the GNS Hamiltonian of \(\omega _0\). In this discussion we assume that all interactions have stretched exponential decay.
Definition A.2
We say that \(\Phi \) is stable with respect to \(\omega _0\) if there exists an IAS \((\Lambda _n)\) and a sequence of differentiable interactions \(\Phi _n\) converging locally in F-norm to \(\Phi \) (see [47, Definition 3.7]), such that sequence of perturbed Hamiltonians of the form
has a positive spectral gap above the ground state uniformly in n and \(s\in [0,s_0]\), for some \(s_0>0\). In this situation we refer to \([0,s_0]\) as the stability range.
The main result of this work establishes conditions under which an interaction \(\Phi (\cdot ,s)\) is stable for sufficiently small values of s, meaning there exists \(s_0>0\) such that \(\Phi (\cdot ,s)\) is stable with respect to \(\omega _0\) with stability range \([0,s_0]\).
To make the connection with the results in [43], assume that \(\Phi (\cdot ,s)\) has a unique ground state \(\omega _s\) for \(s\in [0,s_0]\) and that \(\Phi \) is stable with respect to \(\omega _0\) with stability range \([0, s_0]\). By automorphic equivalence ([7, Theorem 5.5], applied to the GNS representation), the spectral flows \(\alpha _s^{(\Lambda _n)}\) associated with the perturbations \(V_{\Lambda _n}(s)\) satisfy the following properties:
-
(i)
they converge strongly to a co-cycle of automorphisms in the thermodynamic limit:
$$\begin{aligned} \alpha _s = \lim _{n\rightarrow \infty } \alpha _s^{(\Lambda _n)}, s\in [0,s_0]; \end{aligned}$$ -
(ii)
\(\omega _s = \lim _{n\rightarrow \infty } \omega _0 \circ \alpha _s^{(\Lambda _n)}= \omega _s \circ \alpha _s, s\in [0,s_0]\);
-
(iii)
Theorem A.1 applies to \(\alpha _s, s\in [0,s_0]\).
Therefore, differentiability of the ground state follows from the differentiability of \(\alpha _s\) provided by Theorem A.1. As a result, [43, Assumption 1.2 (vii)] holds in the stability range.
We note that in the same way one obtains the extension of the invariants constructed by Ogata in [49, 51, 52] from models with finite-range interactions to the setting with interactions of stretched exponential decay.
Using methods as in [47], a similar result is seen to hold for more general quantum lattice models. In fact, equipped with these methods, see specifically [47, Section VI], minor modifications of the above proof demonstrate boundedness of the derivative of the spectral flow for models with unbounded on-sites perturbed by smooth bounded interactions.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nachtergaele, B., Sims, R. & Young, A. Stability of the bulk gap for frustration-free topologically ordered quantum lattice systems. Lett Math Phys 114, 24 (2024). https://doi.org/10.1007/s11005-023-01767-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11005-023-01767-8