A numerical study of two-point correlation functions of the two-periodic weighted Aztec diamond in mesoscopic limit

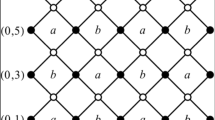
Abstract

In Bain (J Math Phys 64(2):023301, 2023. https://doi.org/10.1063/5.0097256), we found asymptotics of one-point correlation functions of the two-periodic weighted Aztec diamond in the mesoscopic limit, where the linear size of the ordered region is of the same order as the correlation length. In this paper, we follow up with a numerical study of two-point correlation functions of dimers separated by a mesoscopic distance.

Appendix A Definition of \({\mathcal {I}}^{j,k}_{{\varepsilon _1},{\varepsilon _2}} (a, x_1, x_2, y_1, y_2)\)

Let

$$\begin{aligned}c = \frac{1}{a + a^{-1}}.\end{aligned}$$

For $\omega \in {\mathbb {C}}\setminus i[-\sqrt{2c},\sqrt{2c}]$ we define

$$\begin{aligned} \sqrt{\omega ^2 + 2c} = i\sqrt{-i(\omega + i\sqrt{2c})}\sqrt{-i(\omega - i \sqrt{2c})} \end{aligned}$$

where the square roots on the right hand side are the principal branch of the square root. Define

$$\begin{aligned} G(\omega ) = \frac{1}{\sqrt{2c}}(\omega - \sqrt{\omega ^2 + 2c}). \end{aligned}$$

For even $x_1, x_2$ with $0< x_1,x_2 < 2n$ define

$$\begin{aligned} {\widetilde{H}}_{x_1,x_2}(\omega ) = \frac{\omega ^{2m}(-iG(\omega ))^{2m - x_1/2}}{(iG(\omega ^{-1}))^{2m-x_2/2}}. \end{aligned}$$

For $j,k,{\varepsilon _1},{\varepsilon _2} \in \{0,1\}$, define

$$\begin{aligned} V^{j,k}_{{\varepsilon _1}, {\varepsilon _2}} ({\omega _1}, {\omega _2}) = \frac{1}{2}\sum _{\gamma _1,\gamma _2=0}^1 (-1)^{\gamma _2 j + \gamma _1 k}(Q_{\gamma _1,\gamma _2}^{{\varepsilon _1},{\varepsilon _2}}(\omega _1,\omega _2) + (-1)^{{\varepsilon _2}+1}Q_{\gamma _1,\gamma _2}^{{\varepsilon _1},{\varepsilon _2}}(\omega _1,-\omega _2)) \end{aligned}$$

where the functions $Q_{\gamma _1,\gamma _2}^{{\varepsilon _1},{\varepsilon _2}}(\omega _1,\omega _2)$ are defined as follows. Let

$$\begin{aligned} f_{a,b}(u, v)= & {} (2a^2 uv + 2b^2 uv -ab(-1+u^2)(-1+v^2)) (2a^2 uv \nonumber \\{} & {} + 2b^2 uv +ab(-1+u^2)(-1+v^2)). \end{aligned}$$

Now we define the following rational functions. We temporarily consider weights a and b where b is not necessarily 1. Let

$$\begin{aligned} \begin{aligned} \textrm{y}_{0,0}^{0,0}(a,b,u,v)&= \frac{1}{4(a^2+b^2)^2 f_{a,b}(u, v)}(2a^7 u^2 v^2 - a^5 b^2(1 + u^4\\&\quad + u^2v^2 - u^4v^2 + v^4 - u^2v^4)\\&\quad - a^3 b^4(1+3u^2 + 3v^2 + 2u^2v^2 + u^4v^2 + u^2v^4 - u^4v^4) \\&\quad - a b^6(1+v^2+u^2+3u^2v^2)) \\ \textrm{y}_{0,1}^{0,0}(a,b,u,v)&= \frac{a}{4(a^2 + b^2)f_{a,b}(u, v)}(b^2 + a^2u^2)(2a^2v^2 + b^2(1 + v^2 - u^2 + u^2v^2)) \\ \textrm{y}_{1,0}^{0,0}(a,b,u,v)&= \frac{a}{4(a^2+b^2)f_{a,b}(u, v)}(b^2 + a^2v^2)(2a^2u^2 + b^2(1 - u^2 + v^2 + u^2v^2)) \\ \textrm{y}_{1,1}^{0,0}(a,b,u,v)&= \frac{a}{4f_{a,b}(u, v)}(2a^2u^2v^2 +b^2(- 1 + v^2 + u^2 + u^2v^2)). \end{aligned} \end{aligned}$$

For $\gamma _1,\gamma _2 \in \{0,1\}$ we define

$$\begin{aligned} \begin{aligned} \textrm{y}_{\gamma _1,\gamma _2}^{0,1}(a,b,u,v)&= \frac{\textrm{y}_{\gamma _1,\gamma _2}^{0,0}(b,a, u,v^{-1})}{v^2} \\ \textrm{y}_{\gamma _1,\gamma _2}^{1,0}(a,b,u,v)&= \frac{\textrm{y}_{\gamma _1,\gamma _2}^{0,0}(b,a,u^{-1},v)}{u^2} \\ \textrm{y}_{\gamma _1,\gamma _2}^{1,1}(a,b,u,v)&= \frac{\textrm{y}_{\gamma _1,\gamma _2}^{0,0}(a,b,u^{-1},v^{-1})}{v^2}. \end{aligned} \end{aligned}$$

When $b=1$, we write $\textrm{y}^{{\varepsilon _1},{\varepsilon _2}}_{\gamma _1,\gamma _2}(u,v) = \textrm{y}^{{\varepsilon _1},{\varepsilon _2}}_{\gamma _1,\gamma _2}(a,1,u,v)$. Then, define

$$\begin{aligned} \textrm{x}_{{\gamma _1}, {\gamma _2}}^{{\varepsilon _1}, {\varepsilon _2}}({\omega _1}, {\omega _2}) = \frac{G({\omega _1}) G({\omega _2})}{\prod _{i=1}^2 \sqrt{\omega _i^2 +2c} \sqrt{\omega _i^{-2} + 2c}} \text {y}_{{\gamma _1}, {\gamma _2}}^{{\varepsilon _1}, {\varepsilon _2}} (G({\omega _1}), G({\omega _2}))(1 - {\omega _1}^2{\omega _2}^2). \end{aligned}$$

and

$$\begin{aligned} Q_{{\gamma _1},{\gamma _2}}^{{\varepsilon _1},{\varepsilon _2}}({\omega _1},{\omega _2})&= (-1)^{{\varepsilon _1}+{\varepsilon _2}+{\varepsilon _1}{\varepsilon _2} + {\gamma _1}(1+{\varepsilon _2}) + {\gamma _2}(1+{\varepsilon _1})}\\&\quad \times t({\omega _1})^{{\gamma _1}}t({\omega _2}^{-1})^{{\gamma _2}} G({\omega _1})^{\varepsilon _1} G({\omega _2}^{-1})^{\varepsilon _2} \textrm{x}_{{\gamma _1}, {\gamma _2}}^{{\varepsilon _1}, {\varepsilon _2}}({\omega _1}, {\omega _2}^{-1}) \end{aligned}$$

where $t(\omega )$ is defined by

$$\begin{aligned} t(\omega ) = \omega \sqrt{\omega ^{-2} + 2c}. \end{aligned}$$

For $x = (x_1,x_2) \in \texttt{W}_{\varepsilon _1},$ and $y = (y_1,y_2) \in \texttt{B}_{\varepsilon _2}$ with ${\varepsilon _1},{\varepsilon _2}\in \{0,1\}$, define

$$\begin{aligned} \begin{aligned} h_{0,0}({\omega _1},{\omega _2})&= \frac{{\widetilde{H}}_{x_1 + 1, x_2}({\omega _1})}{{\widetilde{H}}_{y_1, y_2 + 1}({\omega _2})}\\ h_{1,0}({\omega _1},{\omega _2})&= \frac{{\widetilde{H}}_{x_1 + 1, x_2}({\omega _1})}{{\widetilde{H}}_{2n-y_1, y_2 + 1}({\omega _2})} \\ h_{0,1}({\omega _1},{\omega _2})&= \frac{{\widetilde{H}}_{x_1 + 1, 2n - x_2}({\omega _1})}{{\widetilde{H}}_{y_1, y_2 + 1}({\omega _2})} \\ h_{1,1}({\omega _1},{\omega _2})&= \frac{{\widetilde{H}}_{x_1 + 1, 2n - x_2}({\omega _1})}{{\widetilde{H}}_{2n-y_1, y_2 + 1}({\omega _2})} \end{aligned} \end{aligned}$$

Let $C_r$ denote a positively-oriented contour of radius r centered at the origin. For $a < 1$, $\sqrt{2c}< r < 1$ and $x = (x_1,x_2) \in \texttt{W}_{\varepsilon _1},\, y = (y_1,y_2) \in \texttt{B}_{\varepsilon _2}$ with ${\varepsilon _1},{\varepsilon _2}\in \{0,1\}$ define

$$\begin{aligned} {\mathcal {I}}^{j,k}_{{\varepsilon _1},{\varepsilon _2}} (a, x_1, x_2, y_1, y_2)&= \frac{i^{y_1-x_1}}{(2\pi i)^2} \int _{C_r} \frac{d{\omega _1}}{{\omega _1}} \int _{C_{1/r}}d{\omega _2} \frac{V_{{\varepsilon _1}, {\varepsilon _2}}^{j,k} ({\omega _1}, {\omega _2})}{{\omega _2} - {\omega _1}} h_{j,k}({\omega _1},{\omega _2}). \end{aligned}$$

(A1)