Abstract
The chain gravity properad introduced in Merkulov (Gravity prop and moduli spaces \({\mathcal {M}}_{g,n}\), 2021, http://arxiv.org/abs/2108.10644) acts on the cyclic Hochschild complex of any cyclic \(A_\infty \) algebra equipped with a scalar product of degree \(-d\). In particular, it acts on the cyclic Hochschild complex of any Poincare duality algebra of degree d, and that action factors through a quotient dg properad \({\mathcal{S}\mathcal{T}}_{3-d}\) of ribbon graphs which is in focus of this paper. We show that its cohomology properad \(H^\cdot ({\mathcal{S}\mathcal{T}}_{3-d})\) is highly non-trivial and that it acts canonically on the reduced equivariant homology \(\bar{H}_\cdot ^{S^1}(LM)\) of the loop space of any simply connected d-dimensional closed manifold M. By its very construction, the string topology properad \(H^\cdot ({\mathcal{S}\mathcal{T}}_{3-d})\) comes equipped with a morphism from the gravity properad \({\mathcal {G}} rav_{3-d}\) which is fully determined by the compactly supported cohomology of the moduli spaces \({\mathcal {M}}_{g,n}\) of stable algebraic curves of genus g with marked points. This result gives rise to new universal operations in string topology as well as reproduces in a unified way several known constructions: we show that (i) \(H^\cdot ({\mathcal{S}\mathcal{T}}_{3-d})\) is also a properad under the properad of involutive Lie bialgebras \({\mathcal {L}}{ ieb }^{\diamond }_{3-d}\) whose induced (via \(H^\cdot ({\mathcal{S}\mathcal{T}}_{3-d})\)) action on \(\bar{H}_\cdot ^{S^1}(LM)\) agrees precisely with the famous purely geometric construction of Chas and Sullivan (String topology, ; in: The legacy of Niels Henrik Abel, Springer, Berlin 2004), (ii) \(H^\cdot ({\mathcal{S}\mathcal{T}}_{3-d})\) is a properad under the properad of homotopy involutive Lie bialgebras \({\mathcal {H}}{ olieb }^{\diamond }_{2-d}\) which controls (via \(H^\cdot ({\mathcal{S}\mathcal{T}}_{3-d})\)) four universal string topology operations introduced in Merkulov (Propof ribbon hypergraphs and strongly homotopy involutive Lie bialgebras, 2020, http://arxiv.org/abs/1812.04913), (iii) E. Getzler’s gravity operad injects into \(H^\cdot ({\mathcal{S}\mathcal{T}}_{3-d})\) implying a purely algebraic counterpart of the geometric construction of Westerland (Math Ann 340:97–142, 2008) establishing an action of the gravity operad on \(\bar{H}_\cdot ^{S^1}(LM)\).
Similar content being viewed by others
Notes
For a nice introduction into the theory of props and properads, we refer to the paper [20] by B. Vallette.
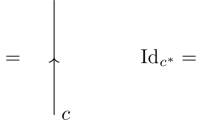
When representing elements of operads and props as decorated graphs, we tacitly assume that all edges and legs are directed along the flow going from the bottom of the graph to the top. The action of the element \(\sum _{k=1}^{3} (123)^k\in {\mathbb {K}}[{\mathbb {S}}_3]\) on any element a of an \({\mathbb {S}}_3\)-module is denoted by \(\oint _{123} a\).
For a ribbon graph \(\Gamma \), we denote by \(V(\Gamma )\) its set of vertices, \(B(\Gamma )\) its set of boundaries and by \(E(\Gamma )\) its set of edges. The genus of \(\Gamma \) is defined by \(g= 1+\frac{1}{2}\left( \# E(\Gamma ) - \# V(\Gamma )- \# B(\Gamma )\right) \).
We work in this section in the category of possibly infinite-dimensional vector spaces V which are direct limits, \(\displaystyle V=\lim _{\longrightarrow } V_p\), of finite-dimensional ones. Their dual vector spaces are defined as projective limits, \(\displaystyle V^*=\lim _{\longleftarrow } V^*_p\).
References
Chas, M., Sullivan, D.: String topology, arXiv:math/9911159
Chas, M., Sullivan, D.: Closed string operators in topology leading to Lie bialgebras and higher string algebra, in: The legacy of Niels Henrik Abel, pp. 771–784, Springer, Berlin, (2004)
Merkulov, S.A.: Prop of ribbon hypergraphs and strongly homotopy involutive Lie bialgebras, preprint arXiv:1812.04913 (2020)
Westerland, C.: Equivariant operads, string topology, and Tate cohomology. Math. Ann. 340(1), 97–142 (2008)
Willwacher, T.: M. Kontsevich’s graph complex and the Grothendieck-Teichmueller Lie algebra, Invent. Math. 200, 671-760 (2015)
Merkulov, S.A.: Gravity prop and moduli spaces \({\cal{M}}_{g,n}\), preprint arXiv:2108.10644 (2021)
Getzler, E.: Two-dimensional topological gravity and equivariant cohomology. Comm. Math. Phys. 163(3), 473–489 (1994)
Goldman, W.M.: Invariant functions on Lie groups and Hamiltonian flows of surface group representations. Invent. math. 85, 263–302 (1986)
Turaev, V. G.: Intersections of loops in two-dimensional manifolds, Mat. Sb. 106(148) (1978), 566-588. English translation: Math. USSR-Sb. 35, 229-250 (1979)
Alekseev, A., Kawazumi, N., Kuno, Y., Naef, F.: The Goldman-Turaev Lie bialgebra in genus zero and the Kashiwara-Vergne problem. Adv. Math. 326, 1–53 (2018)
Alekseev, A., Kawazumi, N., Kuno, Y., Naef, F.: Higher genus Kashiwara-Vergne problems and the Goldman-Turaev Lie bialgebra. C. R. Math. Acad. Sci. Paris 355(2), 123–127 (2017)
Alekseev, A., Naef, F.: Goldman-Turaev formality from the Knizhnik-Zamolodchikov connection. C. R. Math. Acad. Sci. Paris 355(11), 1138–1147 (2017)
Massuyeau, G.: Formal descriptions of Turaev’s loop operations. Quantum Topol. 9, 39–117 (2018)
Chen, X., Eshmatov, F., Gan, W.L.: Quantization of the Lie bialgebra of string topology. Comm. Math. Phys. 301(1), 37–53 (2011)
Naef, F., Willwacher, T.: String topology and configuration spaces of two points, preprint arXiv:1911.06202 (2019)
Campos, R., Willwacher, T.: A model for configuration spaces of points, arxiv:1604.02043 (2016)
Tradler, T., Zeinalian, M.: Algebraic string operations. K-Theory 38(1), 59–82 (2007)
Lambrechts, P., Stanley, D.: Poincaré duality and commutative differential graded algebras. Ann. Sci. Ec. Norm. Super. 41(4), 495–509 (2008)
Kontsevich, M.: Formality Conjecture, In: D. Sternheimer et al. (eds.), Deformation Theory and Symplectic Geometry, Kluwer, 139-156 (1997)
Vallette, B.: A Koszul duality for props. Trans. Amer. Math. Soc. 359, 4865–4943 (2007)
Dolgushev, V., Willwacher, T.: Operadic twisting – with an application to Deligne’s conjecture. Journal of Pure and Applied Algebra 219, 1349–1428 (2015)
Dotsenko, V., Shadrin, S., Vallette, B.: The twisting procedure, arXiv:1810.02941 (2018)
Merkulov, S.A., Willwacher, T.: Props of ribbon graphs, involutive Lie bialgebras and moduli spaces of curves, preprint arXiv:1511.07808 51pp (2015)
Drinfeld, V.: Hamiltonian structures on Lie groups, Lie bialgebras and the geometric meaning of the classical Yang-Baxter equations. Soviet Math. Dokl. 27, 68–71 (1983)
Campos, R., Merkulov, S., Willwacher, T.: The Frobenius properad is Koszul. Duke Math. J. 165(1), 2921–2989 (2016)
Costello, K.: The \(A_\infty \) operad and the moduli space of curves, arXiv: math.AG/0402015 (2004)
Costello, K.: A dual version of the ribbon graph decomposition of moduli space. Geometry & Topology 11, 1637–1652 (2007)
Chas, M.: Combinatorial Lie bialgebras of curves on surfaces. Topology 43(3), 543–568 (2004)
Cieliebak, K., Fukaya, K., Latschev, J.: Homological algebra related to surfaces with boundary. Quantum Topology 11(4), 691–837 (2020)
Ward, B.: Maurer-Cartan elements and cyclic operads. J. Noncommut. Geom. 10(4), 1403–1464 (2016)
Merkulov, S., Willwacher, T.: Deformation theory of Lie bialgebra properads, In: Geometry and Physics: A Festschrift in honour of Nigel Hitchin, Oxford University Press, pp (2018)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Merkulov, S.A. From gravity to string topology. Lett Math Phys 113, 62 (2023). https://doi.org/10.1007/s11005-023-01686-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11005-023-01686-8