Exact results for the six-vertex model with domain wall boundary conditions and a partially reflecting end

Abstract

The trigonometric six-vertex model with domain wall boundary conditions and one partially reflecting end on a lattice of size $2n\times m$, $m\le n$, is considered. The partition function is computed using the Izergin–Korepin method, generalizing the result of Foda and Zarembo from the rational to the trigonometric case. Thereafter, we specify the parameters in Kuperberg’s way to get a formula for the number of states as a determinant of Wilson polynomials. We relate this to a new type of alternating sign matrices, similar to how the six-vertex model with domain wall boundary conditions is related to normal alternating sign matrices. In an appendix, we compute the partition function again, showing that it is also possible to find it with the method of Foda and Wheeler.

1 Introduction

The first example of a six-vertex (6V) model was the ice-model, where all states have the same weight. This and some other special cases of the 6V model with periodic boundary conditions were solved in 1967 by Lieb [1]. The same year, Sutherland [2] solved the general case.

One of the first nontrivial examples of fixed boundaries were the domain wall boundary conditions (DWBC) [3]. In 1996, Zeilberger [4] proved the alternating sign matrix conjecture of Mills, Robbins and Rumsey [5], which gives a formula for the number of alternating sign matrices (ASMs). There is a bijection between the ASMs and the states of the 6V model with DWBC. Izergin [6, 7] showed that the partition function of the 6V model with DWBC can be expressed as a determinant, which Kuperberg [8] used to give another proof of the alternating sign matrix conjecture.

Tsuchiya [9] used the Izergin–Korepin method to obtain a determinant formula for the partition function of the 6V model with one diagonal reflecting end and DWBC on the three other sides on a lattice of size $2n\times n$. Kuperberg [10] used this to give a formula for the number of the corresponding UASMs. The UASMs are alternating sign matrices with U-turns on one side and generalize the vertically symmetric alternating sign matrices (VSASMs).

Foda and Wheeler [11] found a determinant formula for the partition function of the 6V model with partial DWBC on a lattice of size $m\times n$, which generalizes the determinant formula of Korepin and Izergin. Foda and Zarembo [12] found the corresponding generalization of Tsuchiya’s determinant formula in the rational case. They obtained a determinant formula for the rational 6V model on a lattice with $2n\times m$ sites, $m\le n$, with DWBC and where the reflecting end has a triangular K-matrix. These boundary conditions are called DWBC with a partially reflecting end. Pozsgay [13] used the homogeneous limit of Tsuchiya’s $2n\times n$ determinant to compute overlaps (i.e. inner products) between (off-shell) Bethe states and certain simple product states, such as the Néel states. In a similar way, Foda and Zarembo used their rational $2n\times m$ determinant formula to compute overlaps between Bethe states and more general objects which they call partial Néel states.

Foda and Wheeler commented that in the case of partial DWBC on a lattice of size $n\times m$, it is not obvious if and how one could count ASM-like objects with Kuperberg’s specialization, due to phases that vary between different states, coming from the trigonometric weights. However, in the present paper, we find that in the case of DWBC and partial reflection, it is possible to count the states, since similar phases do not appear in this case. The reason for this is the alternating orientations of the lines.

Counting ASMs can be generalized to x-enumerations. In an x-enumeration of ASMs, each state is counted with a weight $x^k$, where k is the number of $-1$’s in the ASM. A formula in the general case is not known, but in some special cases, $x=1, 2$ and 3, there are closed expressions [4, 5, 8]. Colomo and Pronko [14] obtained a simplified treatment of x-enumerations by rewriting the Hankel determinant representation of the partition function of the 6V model with DWBC in terms of orthogonal polynomials. The method can be used to find a formula for the x-enumerations for those x where the underlying orthogonal polynomials belong to the Askey scheme of hypergeometric orthogonal polynomials. This works for the 1-, 2- and 3-enumerations. In the original case of 1-enumerations, the orthogonal polynomials are continuous Hahn polynomials.

In this paper, we study the trigonometric 6V model with DWBC on three sides and one partially reflecting end, on a lattice with $2n\times m$ sites, $m\le n$. We first find a determinant formula for the partition function. Then we specialize the parameters in Kuperberg’s manner to finally find a formula that counts the number of states of the model.

At first, in Sect. 2, we introduce the model. In Sect. 3 we follow the Izergin–Korepin method to obtain a determinant formula for the partition function in Theorem 3.5, i.e. the trigonometric generalization of what Foda and Zarembo did in the rational case. The alternative method of Foda and Wheeler to find the determinant formula is presented in “Appendix A”.

In Sect. 4, we find a formula for the number of states in terms of the partition function. We connect this to the enumeration of a type of generalized UASMs. The objective of Sect. 5 is to specialize the parameters in the determinant formula in Kuperberg’s way. We rewrite the partition function following the ideas of Colomo and Pronko [14]. The determinant can be represented by a matrix consisting of a Hankel matrix part and a Vandermonde matrix part, and the underlying orthogonal polynomials are Wilson polynomials. Then in Theorem 5.1, we finally write down a determinant formula counting the number of states of the 6V model with DWBC and one partially reflecting end.

2 Preliminaries

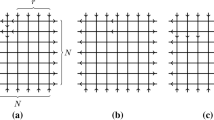
Consider a square lattice with $2n\times m$ lines, where the horizontal lines are connected pairwise at the left side, as in Fig. 1. Each such pair of horizontal lines can be thought of as one single line turning at a wall on the left side. We assign a spin $\pm 1$ to each edge. A lattice with a spin assigned to each edge is called a state.

Fig. 1

The 6V model with DWBC and one partially reflecting end. The parameters $\lambda _i$ and $\mu _j$ are the spectral parameters

In order to assign weights to the states, we give each line an orientation. We choose a positive direction, which goes upwards for the vertical lines, to the left for the lower part of the horizontal double line, and to the right for the upper part. The positive direction is indicated by an arrow at the end of a line. Graphically, spin $+1$ corresponds to an arrow pointing in the positive direction of the line, and spin $-1$ corresponds to an arrow pointing in the opposite direction. At each vertex, the so-called ice rule must hold, which demands that two arrows must be pointing inwards to the vertex and two arrows must be pointing outwards. Because of the ice rule, there are only six types of possible vertices, see Fig. 2.

To each vertical line, we assign a spectral parameter $\mu _j$, and to each horizontal double line, we assign a spectral parameter which is $-\lambda _i$ on the lower part of the double line and shifts to $\lambda _i$ on the upper part. In Fig. 1, we write these parameters at the lines. Also define a fixed boundary parameter $\zeta \in \mathbb {C}$, associated with the reflecting wall at the turns.

Fig. 2

The possible vertices and their vertex weights for the 6V model. The orientation of the lines through a vertex is indicated with an arrow in the end of each line. Given the orientation up and to the right, the spins are indicated by an arrow halfway the edge, where right and up are positive spins, and left and down are negative spins. The vertex weights also depend on the spectral parameters $\lambda$ and $\mu$. In a state of the 6V model with reflecting end, the oriented vertices are tilted 90 degrees counterclockwise on every second row

Fig. 3

The possible boundary configurations and boundary weights for the triangular reflecting end. The weights depend on the spectral parameter $\lambda$ as well as on a boundary parameter $\zeta$

Define $f(x)=2\sinh (x)$ and let $\gamma \notin 2\pi i\mathbb {Z}$ be a fixed parameter. Then define local weights

$$\begin{aligned}&a_\pm (\lambda )=1,\quad b_\pm (\lambda )=e^{\mp \gamma }\frac{f(\lambda )}{f(\lambda +\gamma )}, \quad c_\pm (\lambda )=e^{\pm \lambda }\frac{f(\gamma )}{f(\lambda +\gamma )}, \end{aligned}$$

(1)

$$\begin{aligned}&k_\pm (\lambda , \zeta )=e^{\zeta \mp \lambda } f(\zeta \pm \lambda ),\quad k_c(\lambda , \zeta )=\varphi f(2\lambda ), \end{aligned}$$

(2)

to each vertex and each turn as in Figs. 2 and 3. Here $\varphi$ is a fixed number. We call the turns $k_\pm$ a ‘positive’ and ‘negative’ turn, respectively, and $k_c$ can be seen as a turn with creation of arrows. These choices of weights satisfy the Yang–Baxter equation and the reflection equation with a triangular K-matrix where $k_c(\lambda , \zeta )$ is an off-diagonal element (see Sect. 2.1). Observe that $k_c$ does not depend on $\zeta$, and for $\varphi =0$, we have diagonal reflection. Sometimes, we will refer to a ‘w vertex’, where w is one of $a_\pm , b_\pm$ or $c_\pm$, meaning a vertex with spin configurations corresponding to weight $w(\lambda )$, for some $\lambda$. Similarly, a ‘$k_\pm$ turn’ or ‘$k_c$ turn’ will refer to a turn with weight $k_\pm (\lambda , \zeta )$ or $k_c(\lambda , \zeta )$, respectively. The terms ‘positive’ or ‘negative turn’ will sometimes also be used to refer to a $k_\pm$ turn, respectively.

The local weight at a vertex with the positive directions up and to the right depends on the spins of the surrounding edges, as well as on the difference between the spectral parameters on the incoming lines from the left and the bottom. Because of the reflecting ends, we need to differentiate between the vertices on the left-oriented and the right-oriented horizontal lines. The vertices in the right-oriented rows are depicted in Fig. 2, and the vertices in the left-oriented rows are the same, tilted 90 degrees counterclockwise, as in Fig. 4b. The (local) weight of the vertex in Fig. 4a is $w(\lambda _i-\mu _j)$, and for the vertex in Fig. 4b, the weight is $w(\mu _j-(-\lambda _i))=w(\lambda _i+\mu _j)$, where w is one of $a_\pm , b_\pm$ or $c_\pm$. The (local) boundary weight at each turn depends on the spin on the turning edge, but also on the spectral parameter $\lambda _i$ of the line going through the turn, and on the fixed boundary parameter $\zeta$, as in Fig. 3. The weight of a state is the product of all local weights of the vertices and the turns.

On the three sides without reflecting end, we impose the domain wall boundary conditions, with outgoing spin arrows to the right and ingoing arrows on the upper and lower boundaries. The ice rule implies that $n\ge m$ and that there are $n-m$ turns of type $k_c$.

The model described above is the six-vertex (6V) model of size $2n\times m$ with DWBC and one partially reflecting end. We want to find a determinant formula for the partition function

$$\begin{aligned} Z_{n,m}(\varvec{\lambda }, \varvec{\mu })=\sum _\text {state} \text {weight}(\text {state}) \end{aligned}$$

(3)

of this model, generalizing Tsuchiya’s [9] partition function for $m=n$. This also generalizes the results of Foda and Zarembo [12] from the rational to the trigonometric case.

Fig. 4

The different vertex weights depending on the direction of the row in the 6V model with reflecting end, with spectral parameters $\lambda _i$ and $\mu _j$

2.1 The Yang–Baxter equation and the reflection equation

Define V as a two-dimensional complex vector space. To each line of the lattice, we associate a copy of V. Given a parameter $\lambda \in \mathbb {C}$, define operators $R(\lambda )\in \text {End}(V\otimes V)$ by

$$\begin{aligned} R(\lambda )= \begin{pmatrix} a_+(\lambda ) &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad b_+(\lambda ) &{}\quad c_-(\lambda ) &{}\quad 0 \\ 0 &{}\quad c_+(\lambda ) &{}\quad b_-(\lambda ) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad a_-(\lambda ) \end{pmatrix}, \end{aligned}$$

with the weights parametrized as in (1). The operator is called the R-matrix and satisfies the Yang–Baxter equation (YBE) on $V_1\otimes V_2\otimes V_3$ (where $V_i$ are copies of V), i.e.

$$\begin{aligned} R_{12}(\lambda _1-\lambda _2)R_{13}(\lambda _1-\lambda _3)R_{23}(\lambda _2-\lambda _3)=R_{23}(\lambda _2-\lambda _3)R_{13}(\lambda _1-\lambda _3)R_{12}(\lambda _1-\lambda _2), \end{aligned}$$

where the indices indicate on which spaces the R-matrix acts, e.g.

$$\begin{aligned} R_{12}(\lambda _1-\lambda _2)=R(\lambda _1-\lambda _2)\otimes Id , \end{aligned}$$

and similarly for $R_{23}$ and $R_{13}$. The YBE is depicted in Fig. 5.

To describe the reflecting boundary, define a triangular operator $K(\lambda , \zeta )\in \text {End}(V)$, by

$$\begin{aligned} K(\lambda , \zeta )= \begin{pmatrix} k_+(\lambda , \zeta ) &{}\quad k_c(\lambda , \zeta ) \\ 0 &{}\quad k_-(\lambda , \zeta ) \\ \end{pmatrix}, \end{aligned}$$

with entries parametrized as in (2). The operator is called the K-matrix and satisfies the reflection equation for the above R-matrix on $V_0\otimes V_{0'}$ [15], i.e.

$$\begin{aligned}&R_{00'}(\lambda -\lambda ')K_0(\lambda , \zeta )R_{0'0}(\lambda +\lambda ')K_{0'}(\lambda ', \zeta )\\&\quad =K_{0'}(\lambda ', \zeta )R_{00'}(\lambda +\lambda ')K_0(\lambda , \zeta )R_{0'0}(\lambda -\lambda '), \end{aligned}$$

where $K_0(\lambda , \zeta )=K(\lambda , \zeta )\otimes Id$ and $K_{0'}(\lambda , \zeta )=Id \otimes K(\lambda , \zeta )$, see Fig. 6.

Fig. 5

The Yang–Baxter equation

Fig. 6

The reflection equation

Fig. 7

The partition function is symmetric in the $\mu _j$’s. Because of the DWBC, an extra vertex can be moved through the lattice by using the YBE

3 Izergin–Korepin method

Foda and Zarembo [12] used the Izergin–Korepin method [3, 6] to find the partition function (3) in the rational case, i.e. where $f(x)=x$, which in turn means that all weights are rational. We follow the Izergin–Korepin procedure to find the determinant formula for the partition function in the trigonometric case.

Lemma 3.1

$Z_{n,m}(\varvec{\lambda }, \varvec{\mu })$ is symmetric in $\lambda _i$ and $\mu _j$ separately.

To prove this, we will use the so-called train argument.

Proof

Consider two adjacent vertical lines with spectral parameters $\mu$ and $\mu '$. Insert an extra vertex below the lattice, as in Fig. 7. Since we have DWBC, this will be a vertex with weight $a_+(\mu -\mu ')$. By the YBE, the extra vertex can be moved through the whole lattice to end up on the top, where it can be removed. On the top, the extra vertex has the weight $a_-(\mu -\mu ')$. Since $a_+(\mu )=a_-(\mu )\ne 0$ for all $\mu$, these factors cancel. Hence, this procedure switches $\mu$ and $\mu '$.

To prove the symmetry in the $\lambda _i$’s, we add two extra vertices on the right, as in Fig. 8. The vertices can then be pulled through each other in a similar way as before, using the YBE and the reflection equation. Because of the boundary conditions and the ice rule, the extra vertices give rise to two extra factors on each side of the equation, see Fig. 8. Again since $a_+(\lambda )=a_-(\lambda )\ne 0$, the extra factors cancel. In this manner, we can pairwise switch spectral parameters on adjacent lines, which proves the lemma. $\square$

Fig. 8

The partition function is symmetric in the $\lambda _i$’s. Two adjacent double rows can switch places by adding extra vertices that can be moved through the lattice by using the YBE and the reflection equation. The triple arrows should be understood as n vertical arrows

Lemma 3.2

For any $1\le j\le m$, the function

$$\begin{aligned} e^{(2n-2)\mu _j}\prod _{i=1}^n\prod _{j=1}^m \left[ f(\lambda _i+\mu _j+\gamma )f(\lambda _i-\mu _j+\gamma )\right] Z_{n,m}(\varvec{\lambda }, \varvec{\mu }) \end{aligned}$$

is a polynomial of degree $2n-1$ in $e^{2\mu _j}$.

Proof

Multiply each vertex weight (1) by $f(\lambda +\gamma )$. This is the same as to multiply the partition function by

$$\begin{aligned} \prod _{i=1}^n\prod _{j=1}^m \left[ f(\lambda _i+\mu _j+\gamma )f(\lambda _i-\mu _j+\gamma )\right] . \end{aligned}$$

Then, the new weights are

$$\begin{aligned} \hat{a}_\pm (\lambda )=f(\lambda +\gamma ),\quad \hat{b}_\pm (\lambda )=e^{\mp \gamma }f(\lambda ), \quad \hat{c}_\pm (\lambda )=e^{\pm \lambda } f(\gamma ). \end{aligned}$$

For a given j, all vertices involving $\mu _j$ lie along the same vertical line. Along a vertical line, the spin must be changed at least once from up spin on the bottom of the lattice to down spin on the top. Each vertical line thus contains at least one $\hat{c}_+(\lambda +\mu )$ or one $\hat{c}_-(\lambda -\mu )$ vertex, since these are the only combinations changing the spin in this way, see Fig. 2. These weights each contain a factor $e^{\mu _j}$. Each additional $\hat{c}_\pm$ vertex yields a factor $e^{\pm \mu _j}$. Each $\hat{a}_\pm$ and $\hat{b}_\pm$ vertex gives rise to a factor $e^{\mu _j+x}-e^{-\mu _j-x}$, where x possibly contains $\lambda _i$ and $\gamma$. There can be a maximum of $2n-1$ vertices of type $\hat{a}_\pm$ and $\hat{b}_\pm$ involving $\mu _j$. We multiply $\prod _{i=1}^n\prod _{j=1}^m \left[ f(\lambda _i+\mu _j+\gamma )f(\lambda _i-\mu _j+\gamma )\right] Z_{n,m}(\varvec{\lambda }, \varvec{\mu })$ by $e^{(2n-2)\mu _j}$ to get a polynomial of degree $2n-1$ in $e^{2\mu _j}$. $\square$

Lemma 3.3

$Z_{n,m}(\varvec{\lambda }, \varvec{\mu })$ satisfies recurrence relations when setting $\mu _k=\pm \lambda _l$, namely,

$$\begin{aligned}&Z_{n,m}(\varvec{\lambda }, \varvec{\mu })\vert _{\mu _k=\pm \lambda _l}= e^{-n\gamma }e^{\zeta \pm \lambda _l} f(\zeta \mp \lambda _l) \prod _{i=1}^n \frac{f(\lambda _i+\lambda _l)}{f(\lambda _i+\lambda _l+\gamma )} Z_{n-1, m-1}(\varvec{\hat{\lambda }_l}, \varvec{\hat{\mu }_k}), \end{aligned}$$

where

$$\begin{aligned} \varvec{\hat{\lambda }_l}=(\lambda _1, \dots , \hat{\lambda }_l, \dots , \lambda _n), \qquad \varvec{\hat{\mu }_k}=(\mu _1, \dots , \hat{\mu }_k, \dots , \mu _m), \end{aligned}$$

and $\hat{\lambda }_l$ indicates that the variable $\lambda _l$ is omitted, and similarly $\hat{\mu }_k$ indicates that the variable $\mu _k$ is omitted.

Proof

The vertices marked with a dot in Fig. 9 can only be $b_+$ or $c_\pm$ vertices, because of the ice rule and the DWBC. Specialize $\mu _1=-\lambda _1$ as in the left lattice. Now if the vertex at the bottom right is of type $b_+$, it has zero weight and does not contribute to the partition function. Hence, the vertex must be a $c_+$ vertex. Then, the ice rule determines the spins on the two horizontal bottom lines and the rightmost vertical line, i.e. the vertices within the frozen region (the area marked with a dotted line) are determined uniquely. The part of the lattice outside the frozen region is then a lattice of size $2(n-1)\times (m-1)$ with DWBC. This yields a recursion relation for the partition function. Likewise, specializing $\mu _1=\lambda _n$, as in the right lattice, forces the vertex marked with a dot to be a $c_-$ vertex, and the ice rule determines the rest of the vertex weights within the frozen region. Lemma 3.1 yields that the recursion relations hold for $\mu _k=\pm \lambda _l$ for any $1\le l\le n$, $1\le k\le m$. $\square$

Fig. 9

Specializing $\mu _j=\pm \lambda _i$ determines the vertices inside the frozen region (the area marked with a dotted line). The part of the lattice outside the frozen region is then a lattice of size $2(n-1)\times (m-1)$ with DWBC. This yields a recursion relation for the partition function

Lemma 3.4

For $m=0$, the partition function is

$$\begin{aligned} Z_{n,0}(\varvec{\lambda }) =\varphi ^n \prod _{i=1}^n f(2\lambda _i). \end{aligned}$$

Proof

For $m=0$, there are no vertical lines. In this case, the partition function is just a product of n turns of type $k_c$. $\square$

Because of the ice rule, $n\ge m$, so $n=0$ is only possible if the system has no lines at all. It makes little sense to think of a system with no lines, but for the sake of the following induction argument, we define $Z_{0,0}=1$ as the empty product, which is in line with the above lemma.

Lemmas 3.2, 3.3 and 3.4 together determine $Z_{n,m}(\varvec{\lambda }, \varvec{\mu })$. A polynomial of degree $2n-1$ is uniquely determined by its values in 2n distinct points. Starting from the case $m=0$, we can hence establish $Z_{n,m}(\varvec{\lambda }, \varvec{\mu })$ as a function of $\mu _j$ by induction, using Lemma 3.3.

Theorem 3.5

For the 6V model with DWBC and a partially reflecting end on a lattice of size $2n\times m$, $m\le n$, the partition function is

$$\begin{aligned}&Z_{n,m}(\varvec{\lambda }, \varvec{\mu })=\varphi ^{n-m} e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm\right) \gamma } f(\gamma )^m\prod _{i=1}^m \left[ e^{\mu _i+\zeta } f(\mu _i-\zeta )\right] \prod _{i=1}^n f(2\lambda _i)\nonumber \\&\quad \times \frac{\prod _{i=1}^n\prod _{j=1}^m \left[ f(\mu _j+\lambda _i)f(\mu _j-\lambda _i)\right] }{\prod _{1\le i<j\le m}\left[ f(\mu _j+\mu _i)f(\mu _j-\mu _i)\right] \prod _{1\le i< j\le n}\left[ f(\lambda _i-\lambda _j)f(\lambda _i+\lambda _j+\gamma )\right] } \nonumber \\&\quad \times \det _{1\le i,j\le n} M, \end{aligned}$$

(4)

where M is an $n\times n$ matrix with

$$\begin{aligned} M_{ij}= {\left\{ \begin{array}{ll} F(\lambda _i, \mu _j), &{}\quad \text {if } i\le m,\\ h((n-i)(2\lambda _j+\gamma )), &{}\quad \text {if } m< i<n,\\ 1, &{}\quad \text {if } i=n \text { and } m\ne n, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} F(\lambda _i, \mu _j)=\frac{1}{f(\mu _j+\lambda _i)f(\mu _j-\lambda _i)f(\mu _j+(\lambda _i+\gamma ))f(\mu _j-(\lambda _i+\gamma ))}, \end{aligned}$$

$f(x)=2\sinh (x)$ and $h(x)=2\cosh (x)$.

To prove this, it is enough to check that the right-hand side of (4) satisfies the properties stated in Lemmas 3.1 through 3.4.

Proof

Let $\tilde{Z}_{n,m}(\varvec{\lambda }, \varvec{\mu })$ be the right-hand side of (4). The symmetry in the $\lambda _i$’s and $\mu _j$’s is obvious, so the condition in Lemma 3.1 holds for (4). Proving that the statements in Lemmas 3.3 and 3.4 hold for (4) is straightforward: put $\lambda _l=\mu _k$ into (4). Then all terms with $f(\mu _k-\lambda _l)=0$ vanish. The only terms left are the terms coming from the part of the determinant containing $f(\mu _k-\lambda _l)$, since the corresponding factor from the numerator cancels. The terms left are

$$\begin{aligned}&\tilde{Z}_{n,m}(\varvec{\lambda }, \varvec{\mu })\vert _{\mu _k=\lambda _l}\\&\quad =\frac{(-1)^{k+l}e^{-n\gamma }f(\gamma ) e^{\mu _k+\zeta }f(\mu _k-\zeta ) f(2\lambda _l)}{f(\mu _k+(\lambda _l+\gamma ))f(\mu _k-(\lambda _l+\gamma ))}\\&\qquad \times \prod _{\begin{array}{c} 1\le i \le n\\ i\ne l \end{array}}\left[ f(\mu _k+\lambda _i)f(\mu _k-\lambda _i)\right] \prod _{\begin{array}{c} 1\le j \le m\\ j\ne k \end{array}}\left[ f(\mu _j+\lambda _l)f(\mu _j-\lambda _l)\right] \\&\qquad \times \frac{1}{\prod _{1\le i< l}\left[ f(\lambda _i-\lambda _l)f(\lambda _i+\lambda _l+\gamma )\right] \prod _{l< i\le n}\left[ f(\lambda _l-\lambda _i)f(\lambda _l+\lambda _i+\gamma )\right] } \\&\qquad \times \frac{1}{\prod _{1\le i<k}\left[ f(\mu _k+\mu _i)f(\mu _k-\mu _i)\right] \prod _{k<i\le m}\left[ f(\mu _i+\mu _k)f(\mu _i-\mu _k)\right] }\\&\qquad \times \tilde{Z}_{n-1,m-1}(\varvec{\hat{\lambda }_l}, \varvec{\hat{\mu }_k}). \end{aligned}$$

Simplifying this, we can conclude that the recurrence relation in Lemma 3.3 holds. The proof is similar for $\tilde{Z}_{n,m}(\varvec{\lambda }, \varvec{\mu })\vert _{\mu _k=-\lambda _l}$.

For $m=0$, the right-hand side of (4) is

$$\begin{aligned}&\tilde{Z}_{n,0}(\varvec{\lambda })=\frac{\varphi ^n\prod _{i=1}^n f(2\lambda _i)}{\prod _{1\le i< j\le n}\left[ f(\lambda _i-\lambda _j)f(\lambda _i+\lambda _j+\gamma )\right] } \det _{1\le i,j\le n} M, \end{aligned}$$

where M is an $n\times n$ matrix with

$$\begin{aligned} M_{ij}= {\left\{ \begin{array}{ll} h((n-i)(2\lambda _j+\gamma )), &{}\quad \text {for } 1\le i\le n-1,\\ 1, &{}\quad \text {for } i=n. \end{array}\right. } \end{aligned}$$

Now let

$$\begin{aligned} D=\prod _{1\le i< j\le n}\left[ f(\lambda _i-\lambda _j)f(\lambda _i+\lambda _j+\gamma )\right] \end{aligned}$$

and put $y_i=h(2\lambda _i+\gamma )$. Then, we can write $D=\prod _{1\le i< j\le n} (y_i-y_j)$. By row operations, we can rewrite $\det M$ as a determinant of a Vandermonde matrix $\tilde{M}_{ij}=y_j^{n-i}.$ The determinant of a Vandermonde matrix is exactly D. Hence, the condition in Lemma 3.4 holds.

The only thing left is to prove the condition of Lemma 3.2. Observe that both the determinant and the denominator of (4) are 0 when $\mu _i=\pm \mu _j$. It is easy to see that $e^{2(m-1)\mu _i}$ times the denominator is a polynomial of order $2(m-1)$ in $e^{2\mu _i}$ and is hence determined by its value in $2(m-1)$ points (except for a constant factor). Since the determinant and the denominator share zeroes, the denominator is a factor in the determinant. This proves that $\tilde{Z}_{n,m}(\varvec{\lambda }, \varvec{\mu })$ is a Laurent polynomial in $e^{\mu _i}$. To determine the order, we check what happens with the determinant when $\mu _i\rightarrow \infty$. For this part of the proof, let $x_i=e^{-2\mu _i}$ and $y_j=h(2\lambda _j+\gamma )$. Let

$$\begin{aligned}&\hat{F}(x_i, y_j)=\frac{1}{f(\mu _i+\lambda _j)f(\mu _i-\lambda _j)f(\mu _i+(\lambda _j+\gamma ))f(\mu _i-(\lambda _j+\gamma ))}. \end{aligned}$$

Then, each entry of the determinant involving $\mu _i$ is

$$\begin{aligned} \hat{F}(x_i, y_j)=\frac{x_i^2}{(1-e^{-\gamma }x_i y_j+e^{-2\gamma }x_i^2)(1-e^{\gamma }x_i y_j+e^{2\gamma }x_i^2)}. \end{aligned}$$

We can see that $y_j$ always stands together with $x_i$, so in the Taylor series expansion, the power of $x_i$ is always bigger than the power of $y_j$. The Taylor series expansion around $x_i=0$ is

$$\begin{aligned} \hat{F}(x_i, y_j) =x_i^2 \left( \sum _{\begin{array}{c} l\le n-m-1\\ l \le k \end{array}} A_{k,l} x_i^k y_j^l+\sum _{\begin{array}{c} n-m\le l \\ l\le k \end{array}} A_{k,l} x_i^k y_j^l\right) , \end{aligned}$$

for some constants $A_{k,l}$. The sum on the left can be written in terms of the last $n-m$ rows of the matrix. Hence in the determinant, the left sum can be removed by row operations, and we can change the entries $\hat{F}(x_i, y_j)$ in the determinant to

$$\begin{aligned} x_i^2 \sum _{l=n-m}^k A_{k,l} x_i^k y_j^l. \end{aligned}$$

Letting $x_i\rightarrow 0$ (i.e. letting $\mu _i\rightarrow \infty$), $A_{n-m,n-m} x_i^{n-m+2} y_j^{n-m}$ is the leading term of the determinant, so the degree of the determinant in the variable $e^{2\mu _i}$ is $m-n-2$. The degree of $e^{(2n-2)\mu _i}\prod _{i=1}^n\prod _{j=1}^m \left[ f(\lambda _i+\mu _j+\gamma )f(\lambda _i-\mu _j+\gamma )\right] \tilde{Z}_{n,m}(\varvec{\lambda }, \varvec{\mu })$ in $e^{2\mu _i}$ is

$$\begin{aligned} 3n-m+1+\deg _{e^{2\mu _i}} (\det M) =2n-1 \end{aligned}$$

which proves the condition in Lemma 3.2. $\square$

For $m=n$, the determinant formula in Theorem 3.5 coincides with Tsuchiya’s determinant formula.

In [12], another way to find the partition function is suggested, by starting from Tsuchiya’s determinant for $2n\times n$ lattices and step by step removing the extra vertical lines by letting the corresponding variables $\mu _j\rightarrow \infty$, following Foda and Wheeler [11]. We prove Theorem 3.5 with this method in “Appendix A”.

4 Kuperberg’s specialization of the parameters

In this section, we specialize the parameters in the definition of the partition function (3). By doing this, we find a way to count the total number of states of the model in terms of the partition function.

First, we will state and prove the $2n\times m$ generalization of Lemma 3.1 in [16]. For any given state, let $\nu (w)$ denote the number of vertices of type w.

Lemma 4.1

For any given state of the 6V model with DWBC and one partially reflecting end on a $2n\times m$ lattice, we have

$$\begin{aligned} \nu (b_+)-\nu (b_-)=\left( {\begin{array}{c}n+1\\ 2\end{array}}\right) -\left( {\begin{array}{c}n-m+1\\ 2\end{array}}\right) \quad \text { and } \quad \nu (c_+)-\nu (c_-)=m-2\nu (k_-). \end{aligned}$$

Proof

We follow the same reasoning as in [16]. For the first result, we count the number of different spin arrows. To be able to keep track of the arrow flow through the system, in particular where the arrows go up and down, we think of a $k_+$ turn as one left, one up and one right arrow, and likewise we think of a $k_-$ turn as one right, one down and one left arrow. To get the number of up arrows, we count the number of the different vertices and turns with up arrows, and similarly for the down arrows. To not count the edges twice, we count the vertices on every second row and add the edges from the boundaries. Hence, we get two different equations, depending on which rows we choose to count. Denote by $w^N$ a vertex of type w on the upper part of a double line and similarly $w^S$ for a vertex of type w on the lower part (N for north, S for south). We get the equations

$$\begin{aligned}&\nu (\uparrow )=2\nu (a_+^S) + 2\nu (b_+^S) + \nu (c_+^S) + \nu (c_-^S) + \nu (k_+), \end{aligned}$$

(5)

$$\begin{aligned}&\nu (\uparrow )=2\nu (a_+^N) + 2\nu (b_-^N) + \nu (c_+^N) + \nu (c_-^N) + \nu (k_+) + m, \end{aligned}$$

(6)

$$\begin{aligned}&\nu (\downarrow )=2\nu (a_-^S) + 2\nu (b_-^S) + \nu (c_+^S) + \nu (c_-^S) + \nu (k_-)+m, \end{aligned}$$

(7)

and

$$\begin{aligned} \nu (\downarrow )=2\nu (a_-^N) + 2\nu (b_+^N) + \nu (c_+^N) + \nu (c_-^N) + \nu (k_-). \end{aligned}$$

(8)

To get the number of left arrows, we count the number of the different vertices with left arrows, plus the number of all $k_+$ and $k_-$ turns, then divide everything by two. The number of left arrows is

$$\begin{aligned} \nu (\leftarrow )=\nu (a_-^N) + \nu (b_-^N) + \nu (a_+^S) + \nu (b_-^S) + \frac{\nu (c_+) + \nu (c_-) +\nu (k_+)+\nu (k_-)}{2}. \end{aligned}$$

(9)

Similary, the number of right arrows is

$$\begin{aligned} \nu (\rightarrow )&=\nu (a_+^N) + \nu (b_+^N) + \nu (a_-^S) + \nu (b_+^S)+ \frac{\nu (c_+) + \nu (c_-)+\nu (k_+)+\nu (k_-)}{2}\nonumber \\&\quad +\nu (k_c)+n. \end{aligned}$$

(10)

Adding Eqs. (5), (8) and two times (10), and subtracting (7), (6) and two times (9) yields

$$\begin{aligned} 4[\nu (b_+)-\nu (b_-)]=2\nu (\rightarrow )-2\nu (\leftarrow )-2n+2m-2\nu (k_c). \end{aligned}$$

(11)

With the given boundary conditions, we have $\nu (k_c)=n-m$, and furthermore, we must have $\nu (\rightarrow )=2n(m+1)-\frac{m(m+1)}{2}$ and $\nu (\leftarrow )=\frac{m(m+1)}{2}$ to satisfy the ice rule. Insert this into (11). The first part of the lemma follows.

For the second part of the lemma, we observe that at a $k_+$ double row, the upper part of the double line starts and ends with a right arrow, and the lower part of the line starts with a left arrow and ends with a right arrow. The only vertex types that can change the arrows are the $c_\pm$ vertices. Hence at each $k_+$ double row,

$$\begin{aligned} \nu (c_+^S)=\nu (c_-^S)+1 \quad \text {and} \quad \nu (c_+^N)=\nu (c_-^N), \end{aligned}$$

and similarly at each $k_-$ double row,

$$\begin{aligned} \nu (c_+^S)=\nu (c_-^S) \quad \text {and} \quad \nu (c_+^N)=\nu (c_-^N)-1. \end{aligned}$$

At a $k_c$ double row, each row starts and ends with right arrows, so

$$\begin{aligned} \nu (c_+^S)=\nu (c_-^S) \quad \text {and} \quad \nu (c_+^N)=\nu (c_-^N). \end{aligned}$$

Since $\nu (c_+)=\nu (c_-)$ on the $k_c$ rows, we only need to consider the $k_+$ and $k_-$ rows. There are m rows of this type. Hence, we get the sum $\nu (c_+)=\nu (c_-)+m-2\nu (k_-)$, which is the second result of the lemma. $\square$

Furthermore, we can count the number of $a_\pm$ vertices.

Corollary 4.2

For any given state of the 6V model with DWBC and one partially reflecting end on a $2n\times m$ lattice, the number of vertices of type a (i.e. $a_+$ and $a_-$ together) is

$$\begin{aligned} \nu (a)=mn+\left( {\begin{array}{c}m\\ 2\end{array}}\right) -m+2[\nu (k_-)-\nu (b_-)-\nu (c_-)]. \end{aligned}$$

Proof

We have that $\nu (a)=2mn-\nu (b)-\nu (c)$. Use Lemma 4.1 to compute $\nu (b)$ in terms of $\nu (b_-)$, and $\nu (c)$ in terms of $\nu (c_-)$. $\square$

Now let $\gamma =4\pi \mathrm {i}/3$ so that $e^\gamma$ becomes a third root of 1. Then, let $\lambda _i\rightarrow \gamma$ and $\mu _j\rightarrow 0$ in the partition function $Z_{n,m}(\varvec{\lambda }, \varvec{\mu })$. In this limit, the weights (1) and (2) are

$$\begin{aligned}&a_\pm (\gamma )=1,&\&b_+(\gamma )=c_-(\gamma )=-e^{-\gamma },&\&b_-(\gamma )=c_+(\gamma )=-e^{\gamma }f(\gamma ),\\&k_+(\gamma )=e^{2\zeta }-e^{-2\gamma },&\&k_-(\gamma )=e^{2\zeta }-e^{2\gamma },&\&k_c(\gamma )=\varphi f(2\gamma ), \end{aligned}$$

and the partition function becomes

$$\begin{aligned} Z_{n,m}(\gamma , \dots , \gamma , 0, \dots , 0)&=\sum _{\text {states}} a_+(\gamma )^{\nu (a_+)}a_-(\gamma )^{\nu (a_-)}b_+(\gamma )^{\nu (b_+)} b_-(\gamma )^{\nu (b_-)} \\&\quad \times c_+(\gamma )^{\nu (c_+)}c_-(\gamma )^{\nu (c_-)} k_+(\gamma )^{\nu (k_+)}k_-(\gamma )^{\nu (k_-)}k_c(\gamma )^{\nu (k_c)}. \end{aligned}$$

Here we have used that for $\gamma =4\pi \mathrm {i}/3$, it holds that $f(2\gamma )=-f(\gamma )$. Inserting the expressions for the weights and using Lemma 4.1 and Corollary 4.2, the partition function can be computed to be:

$$\begin{aligned} Z_{n,m}(\gamma , \dots , \gamma , 0, \dots , 0)&= (-1)^{\left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm+n}\varphi ^{n-m} e^{\left( \left( {\begin{array}{c}m+1\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^{n-m}\\&\quad \times \sum _{k=0}^m N_k (e^{2\zeta }-e^{-2\gamma } )^{k}\left( \frac{e^{2\zeta }-e^{2\gamma }}{e^{2\gamma }} \right) ^{m-k}, \end{aligned}$$

where $N_k$ is the number of states with $\nu (k_+)=k$, i.e. where k is the number of $k_+$ turns. Let $Z_{n,m, k}(\varvec{\lambda }, \varvec{\mu })$ be the partition function for the same model where the number of $k_+$ turns is fixed to $\nu (k_+)=k$. Then,

$$\begin{aligned} N_k&=(-1)^{\left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm+n}\varphi ^{m-n} e^{\left( nm-\left( {\begin{array}{c}m+1\\ 2\end{array}}\right) \right) \gamma }f(\gamma )^{m-n}\nonumber \\&\quad \times \left( \frac{1}{e^{2\zeta }-e^{-2\gamma }}\right) ^k\left( \frac{e^{2\gamma }}{e^{2\zeta }-e^{2\gamma }} \right) ^{m-k} Z_{n,m,k}(\gamma , \dots , \gamma , 0,\dots , 0). \end{aligned}$$

(12)

Finally,

$$\begin{aligned} A(m,n):=\sum _{k=0}^m N_k \end{aligned}$$

(13)

counts the total number of states of the model.

4.1 Connection to alternating sign matrices

By specializing the parameters in the partition function for the 6V model with DWBC (without reflecting end), Kuperberg [8] was able to count the number of alternating sign matrices (ASMs). ASMs are matrices where the entries consist of 1, $-1$ and 0, such that the nonzero elements in each row and each column alternate in sign and such that the sum of the elements of any row or any column is 1. Hence, the first and last nonzero element of each row and each column is always 1.

In the case of DWBC and partially reflecting end, we also get a bijection to a type of ASM-like objects. Consider matrices of size $2n\times m$, $m\le n$, consisting of elements 0, $-1$ and 1. Vertically and horizontally the nonzero elements alternate in sign. The sum of the elements of each column is 1, as for ASMs. Horizontally connect the rows pairwise on the left edge to form a double row as in Fig. 10. A double row may consist of only zeroes. If a row has any nonzero elements, the rightmost of these must be 1. Furthermore, the sum of the entries in a double row must be 0 or 1. Equivalently, a double row can not consist of two rows both having 1 as their leftmost nonzero element.

Proposition 4.3

The expression A(m, n) yields the number of matrices of size $2n\times m$, $m\le n$, described above.

Proof

There is a bijection between the states of the 6V model and matrices consisting of 0, 1 and $-1$ [8] (see Fig. 11), where $a_\pm$ and $b_\pm$ correspond to 0 in the matrix, and in the case of reflecting end, a $c_-$ vertex in the upper part of a double row corresponds to 1, and $c_+$ corresponds to $-1$. On the lower part of a double row, $c_+$ corresponds to 1, and $c_-$ corresponds to $-1$. Due to the ice rule and the boundary conditions, the rest of the vertices are determined uniquely.

Fig. 10

The three matrices on the left are counted by A(m, n), whereas the rightmost matrix does not correspond to a state in the model considered in this paper

Fig. 11

The bijection between a UASM and a state of the 6V model with DWBC and a reflecting end

The fact that there are more rows than columns allows for rows without $c_\pm$ vertices, corresponding to rows with only zeroes in the matrix. If there are any $c_\pm$ vertices on the lower part of a double row, $k_-$ and $k_c$ turns on that double row force the leftmost $c_\pm$ vertex to be $c_-$, corresponding to $-1$ in the matrix, whereas a $k_+$ turn forces it to be $c_+$, corresponding to 1 in the matrix. Similarly, if there are any $c_\pm$ vertices on the upper part of the double row, $k_+$ and $k_c$ force the leftmost nonzero element in the matrix to be $-1$, and $k_-$ yields that the leftmost nonzero matrix element is 1. In this way, we can see that both rows cannot have 1 as their leftmost nonzero element. In a similar way, the DWBC impose that if a row has any nonzero element, then the rightmost of them must be 1.

$\square$

From the discussion above, it follows that $N_k$ (12) counts the number of matrices equivalent to states of the 6V model with exactly k positive turns. In the case $m=n$, the sum of the elements in each double row must be 1, and A(m, n) counts the number of UASMs [10]. The case where $m=n$ and $k=0$ corresponds to VSASMs.

5 Specialization in the determinant

In this section, we specialize the parameters in the determinant formula in the same way as in the previous section. We show that with this specialization of the variables, the partition function can be written as a determinant of Wilson polynomials, and finally we use this together with the results from the previous section to give a formula for the number of states of the model.

5.1 Moments and orthogonal polynomials

We start by rewriting the determinant formula of the partition function (4). Let $x_i=\lambda _i-\gamma$ and $y_j=\mu _j$. In the previous section, we let $\lambda _i\rightarrow \gamma$ and $\mu _i\rightarrow 0$, which corresponds to letting $x_i\rightarrow 0$ and $y_i\rightarrow 0$. For $1\le i \le n$, multiply column i of the determinant by $f(2x_i)$ and for $1\le j\le m$, multiply row j of the determinant by $f(2y_j)$. Then specify $\gamma =4\pi \mathrm {i}/3$. By row operations on the lower part of the determinant, we can then rewrite the partition function as

$$\begin{aligned}&Z_{n,m}(x_1 + \gamma , \dots , x_n + \gamma , y_1, \dots , y_m)\nonumber \\&\quad =\varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^m\dfrac{\prod _{i=1}^{m} \left[ e^{y_i+\zeta } f(y_i-\zeta )\right] \prod _{i=1}^n f(2x_i+2\gamma )}{\prod _{i=1}^n f(2x_i)\prod _{j=1}^m f(2y_j)}\nonumber \\&\qquad \times \frac{\prod _{i=1}^n\prod _{j=1}^{m} \left[ f(y_j+(x_i+\gamma ))f(y_j-(x_i+\gamma ))\right] }{\prod _{1\le i<j\le m}\left[ f(y_j+ y_i)f(y_j- y_i)\right] \prod _{1\le i<j\le n}\left[ f(x_i+ x_j)f(x_i- x_j)\right] }\nonumber \\&\qquad \times \det _{1\le i,j\le n} \tilde{M}, \end{aligned}$$

(14)

where

$$\begin{aligned} \tilde{M}_{ij}= {\left\{ \begin{array}{ll} g(x_j, y_i), &{}\quad \text { for } 1\le i \le m,\\ f(2(n-i+1) x_j), &{}\quad \text { for } m+1\le i\le n, \end{array}\right. } \end{aligned}$$

with

$$\begin{aligned} g(x,y)=\frac{f(2x)f(2y)}{f(y+ (x+\gamma ))f(y- (x+\gamma ))f(y+(x+2\gamma ))f(y-(x+2\gamma ))}. \end{aligned}$$

It is apparent that $f(x)=\sinh x$ and g(x, y) are odd functions. Furthermore, $x=0$ is a zero of f(x), and $x=0$ and $y=0$ are zeroes of g(x, y). Hence, we can write the functions as $f(x)=x \hat{f}(x^2)$ and $g(x,y)=xy \hat{g}(x^2,y^2)$, where $\hat{f}$ and $\hat{g}$ are analytic at $x=y=0$. The partition function (14) can thus be written:

$$\begin{aligned}&Z_{n,m}(x_1 + \gamma , \dots , x_n + \gamma , y_1, \dots , y_m)\\&\quad =2^{n-m}(n-m)!\ \varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^m \\&\qquad \times \frac{\prod _{i=1}^{m} \left[ e^{y_i+\zeta } f(y_i-\zeta )\right] \prod _{i=1}^n f(2x_i+2\gamma )}{\prod _{i=1}^n f(2x_i)\prod _{j=1}^m f(2y_j)} \\&\qquad \times \frac{\prod _{i=1}^n\prod _{j=1}^{m} \left[ f(y_j+(x_i+\gamma ))f(y_j-(x_i+\gamma ))\right] \prod _{j=1}^n x_j \prod _{k=1}^m y_k}{\prod _{1\le i<j\le m}\left[ f(y_j+ y_i)f(y_j- y_i)\right] \prod _{1\le i<j\le n}\left[ f(x_i+ x_j)f(x_i- x_j)\right] }\\&\qquad \times \det _{1\le i, j\le n}\hat{M}, \end{aligned}$$

where

$$\begin{aligned} \hat{M}_{ij}= {\left\{ \begin{array}{ll} \hat{g}(x_j^2, y_i^2), &{}\quad \text { for } 1\le i \le m,\\ \hat{f}((2(n-i+1) x_j)^2), &{}\quad \text { for } m+1\le i\le n. \end{array}\right. } \end{aligned}$$

Now regard $x_i^2$ and $y_j^2$ as our variables. Then in the limit where all $x_i,y_j \rightarrow 0$, the determinant can be written in terms of partial derivatives. Subtract the first column from the second and divide by $x^2_2-x^2_1$; then in the limit $x_i\rightarrow 0$, this equals the first partial derivative. Similarly for the kth column, subtract the $(k-1)$th-order Taylor series expansion of each entry around $x_k^2=0$, which in the limit is a sum of the first $k-1$ columns. Then divide by $\prod _{i=1}^{k-1} (x_k^2-x_i^2)/k!$. By l’Hôpital’s rule, this limit equals the $(k-1)$th partial derivative. A similar argument for the first m rows lets us write the entries as partial derivatives in $y_i^2$ as well. The method is described in detail in [7]. Hence in the limit, the partition function equals

$$\begin{aligned}&Z_{n,m}(\gamma , \dots , \gamma , 0, \dots , 0)\\&\quad =\lim _{x_i, y_j \rightarrow 0} 2^{n-m}(n-m)!\ \varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^m \\&\qquad \times \frac{\prod _{i=1}^{m} \left[ e^{y_i+\zeta } f(y_i-\zeta )\right] \prod _{i=1}^n f(2x_i+2\gamma )}{\prod _{i=1}^n f(2x_i)\prod _{j=1}^m f(2y_j)}\\&\qquad \times \frac{\prod _{i=1}^n\prod _{j=1}^{m} \left[ f(y_j+(x_i+\gamma ))f(y_j-(x_i+\gamma ))\right] \prod _{j=1}^n x_j \prod _{i=1}^m y_i}{\prod _{1\le i<j\le m}\left[ f(y_j+ y_i)f(y_j- y_i)\right] \prod _{1\le i<j\le n}\left[ f(x_i+ x_j)f(x_i- x_j)\right] }\\&\qquad \times \dfrac{\prod _{1\le i< j\le n} (x_j^2-x_i^2)\prod _{1\le i < j\le m} (y_j^2-y_i^2)}{\prod _{i=1}^n (i-1)!\prod _{j=1}^m (j-1)!}\\&\qquad \times \det \begin{pmatrix} \hat{g}(x_1^2, y_1^2) &{}\quad \frac{\partial }{\partial x_2^2}\hat{g}(x_2^2, y_1^2) &{}\quad \cdots &{}\quad \frac{\partial ^{n-1}}{\partial x_n^{2(n-1)}}\hat{g}(x_n^2, y_1^2)\\ \frac{\partial }{\partial y_2^2}\hat{g}(x_1^2, y_2^2) &{}\quad \frac{\partial ^2}{\partial x_2^2 y_2^2}\hat{g}(x_2^2, y_2^2) &{}\quad \cdots &{}\quad \frac{\partial ^n}{\partial x_n^{2(n-1)}y_2^2}\hat{g}(x_n^2, y_2^2)\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \frac{\partial ^{m-1}}{\partial y_m^{2(m-1)}} \hat{g}(x_1^2, y_m^2) &{}\quad \frac{\partial ^m}{\partial x_2^2 y_m^{2(m-1)}}\hat{g}(x_2^2, y_m^2) &{}\quad \cdots &{}\quad \frac{\partial ^{n+m-2}}{\partial x_n^{2(n-1)}y_m^{2(m-1)}}\hat{g}(x_n^2, y_m^2)\\ \hat{f}((2(n-m)x_1)^2) &{}\quad \frac{\partial }{\partial x_2^2}\hat{f}((2(n-m)x_2)^2) &{}\quad \cdots &{}\quad \frac{\partial ^{n-1}}{\partial x_n^{2(n-1)}}\hat{f}((2(n-m)x_n)^2)\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \hat{f}((2 x_1)^2) &{}\quad \frac{\partial }{\partial x_2^2}\hat{f}((2 x_2)^2) &{}\quad \cdots &{}\quad \frac{\partial ^{n-1}}{\partial x_n^{2(n-1)}}\hat{f}((2 x_n)^2) \end{pmatrix}. \end{aligned}$$

To cancel the zeroes in the denominators, the prefactors can be simplified by

$$\begin{aligned}&\lim _{x_i,y_j\rightarrow 0}\left( \frac{\prod _{i=1}^n x_i \prod _{j=1}^m y_j }{\prod _{i=1}^n f(2x_i)\prod _{j=1}^m f(2y_j)}\right. \\&\qquad \times \left. \frac{\prod _{1\le i< j\le n} (x_j^2-x_i^2)\prod _{1\le i< j\le m} (y_j^2-y_i^2)}{\prod _{1\le i<j\le n}\left[ f(x_i+ x_j)f(x_i- x_j)\right] \prod _{1\le i<j\le m}\left[ f(y_j+ y_i)f(y_j- y_i)\right] }\right) \\&\quad =\frac{(-1)^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) }}{2^{n^2+n+m^2+m}}. \end{aligned}$$

Moreover,

$$\begin{aligned} f(2l x) =4lx\left( 1+\frac{(2 lx)^2}{3!}+\frac{(2 lx)^4}{5!}+\cdots \right) , \end{aligned}$$

so

$$\begin{aligned} \hat{f}(x)=2\left( 1+\frac{x}{3!}+\frac{x^2}{5!}+\cdots \right) , \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^k}{\partial x^{2k}}\hat{f}((2 lx)^2)\vert _{x=0} = \frac{2(2 l)^{2k}k!}{(2k+1)!}. \end{aligned}$$

For $\gamma =4\pi \mathrm {i}/3$,

$$\begin{aligned} g(x,y) =\frac{f(x-y)}{f(3x-3y)}-\frac{f(x+y)}{f(3x+3y)}. \end{aligned}$$

Following [14], we use Fourier transforms to see that

$$\begin{aligned} \frac{f(x)}{f(3x)}=\frac{1}{2\sqrt{3}}\int _{-\infty }^{\infty } e^{-\mathrm {i}xt}\frac{\sinh (\pi t/6)}{\sinh (\pi t /2)}\mathrm{d}t. \end{aligned}$$

From this, it follows that

$$\begin{aligned} \frac{f(x-y)}{f(3x-3y)}-\frac{f(x+y)}{f(3x+3y)}= \frac{2}{\sqrt{3}}\int _0^\infty \sin (xt) \sin (yt)\frac{\sinh (\pi t/6)}{\sinh (\pi t /2)}\mathrm{d}t. \end{aligned}$$

By Taylor expansion and Lebesgue’s dominated convergence theorem, we get

$$\begin{aligned} g(x,y) =xy\frac{2}{\sqrt{3}}\sum _{k,l=0}^\infty \left( \frac{(-1)^{k+l}x^{2k}y^{2l}}{(2k+1)!(2l+1)!}\int _0^\infty t^{2k+2l+2}\frac{\sinh (\pi t/6)}{\sinh (\pi t /2)}\mathrm{d}t\right) , \end{aligned}$$

for $\vert x\vert ,\vert y\vert <\pi /3$, so

$$\begin{aligned} \hat{g}(x^2,y^2) =\frac{2}{\sqrt{3}} \sum _{k,l=0}^\infty \left( \frac{(-1)^{k+l}x^{2k}y^{2l}}{(2k+1)!(2l+1)!}\int _0^\infty t^{2k+2l+2}\frac{\sinh (\pi t/6)}{\sinh (\pi t /2)}\mathrm{d}t\right) . \end{aligned}$$

Hence,

$$\begin{aligned}&\frac{\partial ^{k+l}}{\partial x^{2k}y^{2l}} \hat{g}(x^2, y^2)\bigg \vert _{x=y=0}\\&\quad =\frac{2(-1)^{k+l}k!l!}{\sqrt{3} (2k+1)!(2l+1)!}\int _0^\infty t^{2k+2l+2}\frac{\sinh (\pi t/6)}{\sinh (\pi t /2)}\mathrm{d}t. \end{aligned}$$

Let $c_k$ denote the moment

$$\begin{aligned} c_k=\int t^k \mathrm{d}\mu (t), \end{aligned}$$

where

$$\begin{aligned} \int f(t) \mathrm{d}\mu (t)=\int _0^\infty f(t^2) t^2 \frac{\sinh (\pi t/6)}{\sinh (\pi t /2)}\mathrm{d}t. \end{aligned}$$

The corresponding inner product is

$$\begin{aligned} \left\langle p(t), q(t)\right\rangle =\int _0^\infty p(t^2) q(t^2) t^2 \frac{\sinh (\pi t/6)}{\sinh (\pi t /2)}\mathrm{d}t, \end{aligned}$$

for polynomials p and q.

In the limit $x_i, y_j\rightarrow 0$, the partition function thus equals

$$\begin{aligned}&Z_{n,m}(\gamma , \dots , \gamma , 0, \dots , 0) = (-1)^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) +mn}\prod _{i=1}^n \frac{1}{(2i-1)!}\prod _{j=1}^m \frac{1}{(2j-1)!}\\&\quad \times \frac{2^{n-2m-m^2-n^2}}{3^{m/2}}(n-m)!\ \varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -mn\right) \gamma }f(\gamma )^{m+2mn}f(2\gamma )^n(1-e^{2\zeta })^m \\&\quad \times \det \begin{pmatrix} c_0 &{}\quad -c_1 &{} \quad \cdots &{}\quad (-1)^{n+1} c_{n-1}\\ -c_1 &{}\quad c_2 &{}\quad \cdots &{}\quad (-1)^{n+2} c_n\\ \vdots &{} \quad \vdots &{}\quad \ddots &{}\quad \vdots \\ (-1)^{m+1} c_{m-1} &{}\quad (-1)^{m+2}c_m &{}\quad \cdots &{} (-1)^{n+m} c_{n+m-2}\\ 1 &{}\quad (2(n-m))^2 &{}\quad \cdots &{}\quad (2(n-m))^{2(n-1)}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{} \quad \vdots \\ 1 &{}\quad 2^2 &{}\quad \cdots &{}\quad 2^{2(n-1)} \end{pmatrix}. \end{aligned}$$

We can write the entries $c_k$ in terms of inner products. Since

$$\begin{aligned} (-1)^{\frac{n(n-1)}{2}+\left\lfloor \frac{n}{2}\right\rfloor }=1 \end{aligned}$$

for all n, the partition function above becomes

$$\begin{aligned}&Z_{n,m}(\gamma , \dots , \gamma , 0, \dots , 0)=(-1)^{mn-m(m-1)/2}\prod _{i=1}^n \frac{1}{(2i-1)!}\prod _{j=1}^m \frac{1}{(2j-1)!}\\&\quad \times \frac{2^{n-2m-m^2-n^2}}{3^{m/2}} (n-m)!\ \varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^{2mn+m}f(2\gamma )^n(1-e^{2\zeta })^m\\&\quad \times \det \begin{pmatrix} \left\langle 1,1\right\rangle &{} \left\langle t,1\right\rangle &{} \cdots &{} \left\langle t^{n-1},1\right\rangle \\ \left\langle 1,t\right\rangle &{} \left\langle t,t\right\rangle &{} \cdots &{} \left\langle t^{n-1},t\right\rangle \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \left\langle 1, t^{m-1}\right\rangle &{} \left\langle t, t^{m-1}\right\rangle &{} \cdots &{} \left\langle t^{n-1}, t^{m-1}\right\rangle \\ 1 &{} -(2(n-m))^2 &{} \cdots &{} (-1)^{n-1}(2(n-m))^{2(n-1)}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} -2^2 &{} \cdots &{} (-1)^{n-1}2^{2(n-1)} \end{pmatrix}. \end{aligned}$$

Similar determinants show up, for example, in [14]. By row and column operations, the determinant can be rewritten, and the partition function is

$$\begin{aligned}&Z_{n,m}(\gamma , \dots , \gamma , 0, \dots , 0) =(-1)^{mn-m(m-1)/2}\prod _{j=1}^n \frac{1}{(2j-1)!}\prod _{j=1}^m \frac{1}{(2j-1)!}\\&\quad \times \frac{2^{n-2m-m^2-n^2}}{3^{m/2}} (n-m)!\ \varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^{2mn+m}f(2\gamma )^n(1-e^{2\zeta })^m\\&\quad \times \det \begin{pmatrix} \left\langle p_0(t), q_0(t)\right\rangle &{}\quad \left\langle p_1(t), q_0(t)\right\rangle &{}\quad \cdots &{}\quad \left\langle p_{n-1}(t),q_0(t)\right\rangle \\ \left\langle p_0(t), q_1(t)\right\rangle &{}\quad \left\langle p_1(t), q_1(t)\right\rangle &{}\quad \cdots &{}\quad \left\langle p_{n-1}(t),q_1(t)\right\rangle \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \left\langle p_0(t), q_{m-1}(t)\right\rangle &{}\quad \left\langle p_1(t), q_{m-1}(t)\right\rangle &{}\quad \cdots &{}\quad \left\langle p_{n-1}(t), q_{m-1}(t)\right\rangle \\ p_0(-(2(n-m))^2) &{}\quad p_1(-(2(n-m))^2) &{}\quad \cdots &{} p_{n-1}(-(2(n-m))^2)\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ p_0(-4^2) &{}\quad p_1(-4^2) &{}\quad \cdots &{}\quad p_{n-1}(-4^2)\\ p_0(-2^2) &{}\quad p_1(-2^2) &{}\quad \cdots &{}\quad p_{n-1}(-2^2) \end{pmatrix}, \end{aligned}$$

where $p_k(t)$ and $q_k(t)$ are arbitrary monic polynomials of degree k. We can choose $\{p_i=q_i\}_{i=1}^n$ orthogonal, i.e.

$$\begin{aligned} \left\langle p_k(t), p_l(t)\right\rangle =\int p_k(t) p_l(t) \mathrm{d}\mu (t)=h_k \delta _{kl}, \end{aligned}$$

(15)

for some $h_k$. Then, most entries in the upper part of the matrix become 0, and we can simplify the expression further. We also rearrange the rows. Then, the partition function is

$$\begin{aligned}&Z_{n,m}(\gamma , \dots , \gamma , 0, \dots , 0)\nonumber \\&\quad =\frac{2^{n-2m-m^2-n^2}}{3^{m/2}} (n-m)!\ \varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^{2mn+m}f(2\gamma )^n(1-e^{2\zeta })^m\nonumber \\&\qquad \times (-1)^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) +m}\prod _{j=1}^n \frac{1}{(2j-1)!}\prod _{j=1}^m \frac{1}{(2j-1)!} \prod _{i=0}^{m-1} \left\langle p_i(t), p_i(t)\right\rangle \nonumber \\&\qquad \times \det \begin{pmatrix} p_m(-2^2) &{}\quad p_{m+1}(-2^2) &{}\quad \cdots &{}\quad p_{n-1}(-2^2)\\ p_m(-4^2) &{}\quad p_{m+1}(-4^2) &{}\quad \cdots &{}\quad p_{n-1}(-4^2)\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ p_m(-(2(n-m))^2) &{}\quad p_{m+1}(-(2(n-m))^2) &{}\quad \cdots &{}\quad p_{n-1}(-(2(n-m))^2) \end{pmatrix}. \end{aligned}$$

(16)

5.2 Wilson polynomials

Colomo and Pronko [14] found a way to write the determinant formula of the partition function of the 6V model with DWBC in terms of orthogonal polynomials. In this section, we show that we can rewrite the determinant formula (4) in terms of orthogonal polynomials as well.

We can rewrite the weight $\mu (t)$ in terms of the gamma function, defined as the analytic continuation of the integral

$$\begin{aligned} \Gamma (z)=\int _0^\infty x^{z-1} e^{-x} \mathrm{d}x, \end{aligned}$$

which is defined only for $Re (z)>0$. It can be shown that the gamma function satisfies the following identities:

$$\begin{aligned} \vert \Gamma (1+\mathrm {i}x)\vert ^2=\frac{\pi x}{\sinh (\pi x)} \end{aligned}$$

and

$$\begin{aligned} \prod _{k=0}^{l-1}\Gamma \left( x+\frac{k}{l}\right) =(2\pi )^{\frac{l-1}{2}} l^{\frac{1}{2}-lx}\Gamma (lx). \end{aligned}$$

(17)

Hence, we have

$$\begin{aligned} \mu (t)&= t^2 \frac{\sinh (\pi t/6)}{\sinh (\pi t /2)}\nonumber \\&=\frac{3^2}{2^2\pi ^3}\left| \frac{\Gamma (\mathrm {i}t/6+1/3)\Gamma (\mathrm {i}t/6+1/2)\Gamma (\mathrm {i}t/6+2/3)\Gamma (\mathrm {i}t/6+1)}{\Gamma (\mathrm {i}t/3)}\right| ^2. \end{aligned}$$

(18)

This is the orthogonality weight for a known family of polynomials, namely the Wilson polynomials. These are defined in terms of generalized hypergeometric series as (see, e.g. [17])

$$\begin{aligned} \frac{W_k(x^2; a, b,c,d)}{(a+b)_k (a+c)_k (a+d)_k}= {}_4 F_3 \left( \begin{matrix} -k, k+a+b+c+d-1, a+\mathrm {i}x, a-\mathrm {i}x\\ a+b, a+c, a+d \end{matrix} \bigg \vert 1 \right) , \end{aligned}$$

where the orthogonality condition reads

$$\begin{aligned}&\frac{1}{2\pi } \int _0^\infty W_k(x^2; a, b,c,d) W_l(x^2; a, b,c,d)\nonumber \\&\qquad \times \left| \frac{\Gamma (\mathrm {i}x+a)\Gamma (\mathrm {i}x+b)\Gamma (\mathrm {i}x+c)\Gamma (\mathrm {i}x+d)}{\Gamma (2\mathrm {i}x)} \right| ^2 \mathrm{d}x\nonumber \\&\quad =\frac{\Gamma (k+a+b)\Gamma (k+a+c)\Gamma (k+a+d)\Gamma (k+b+c)\Gamma (k+b+d)\Gamma (k+c+d)}{\Gamma (2k+a+b+c+d)}\nonumber \\&\qquad \times (k+a+b+c+d-1)_k k! \delta _{kl}, \end{aligned}$$

(19)

and where $(a)_k=a(a+1)\cdots (a+k-1)$, for $k\ge 1$, and $(a)_0=1$ is the rising factorial. Comparing this to (15) and (18), we choose the parameters $a=1/3$, $b=1/2$, $c=2/3$, $d=1$ and $x=t/6$. Then, the Wilson polynomials are:

$$\begin{aligned}&W_k\left( \left( \frac{t}{6}\right) ^2; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right) \nonumber \\&\quad = (5/6)_k (4/3)_k k! \sum _{j=0}^k \frac{(-k)_j (3/2+k)_j(1/3+\mathrm {i}t/6)_j(1/3-\mathrm {i}t/6)_j}{(5/6)_j (4/3)_j (j!)^2}. \end{aligned}$$

(20)

These are polynomials in $t^2$ of degree k, with leading coefficient

$$\begin{aligned} \kappa _k = \frac{(-1)^k (3/2+k)_k }{6^{2k}}. \end{aligned}$$

(21)

The polynomials can hence be written

$$\begin{aligned} W_k\left( \left( \frac{t}{6}\right) ^2; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right) =\kappa _k p_k(t^2), \end{aligned}$$

where $p_k(t)$ is a monic polynomial of degree k in t. The right-hand side of (19) with the above choices of parameters is

$$\begin{aligned}&\frac{\Gamma (k+5/6)\Gamma (k+1)\Gamma (k+4/3)\Gamma (k+7/6)\Gamma (k+3/2)\Gamma (k+5/3)}{\Gamma (2k+5/2)}\nonumber \\&\quad \times (k+3/2)_k k!\delta _{kl} = \frac{\pi ^2 (k+3/2)_k k! (6k+4)!(2k+1)!}{2^{2k-1}3^{6k+9/2}(4k+3)!}\delta _{kl}, \end{aligned}$$

(22)

where we have used (17) and the fact that $\Gamma (j+1)=j!$ if j is a nonnegative integer.

We insert (19)–(22) into (15) and get

$$\begin{aligned}&\left\langle p_k(t), p_l(t) \right\rangle =\frac{2^{2k+1} k! (6k+4)!(2k+1)!}{3^{2k+3/2} (3/2+k)_k(4k+3)!}\delta _{kl}. \end{aligned}$$

Hence,

$$\begin{aligned} \prod _{j=0}^{m-1} \left\langle p_j(t), p_j(t)\right\rangle&=\frac{2^{2m^2-m}}{3^{m^2+m/2} }\prod _{j=1}^{m} \frac{(6j-2)!((2j-1)!)^2(2j-2)!}{ (4j-3)! (4j-1)!}, \end{aligned}$$

where we used that

$$\begin{aligned} (x)_k=\frac{\Gamma (x+k)}{\Gamma (x)}. \end{aligned}$$

(23)

Insert $p_k(t^2)=W_k\left( \left( \frac{t}{6}\right) ^2; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right) /\kappa _k$ into the partition function (16), which then reads

$$\begin{aligned}&Z_{n,m}(\gamma , \dots , \gamma , 0, \dots , 0)\\&\quad = \frac{2^{n-n^2-3m+m^2}}{3^{m^2+m} } (n-m)!\ \varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^{2mn+m}f(2\gamma )^n(1-e^{2\zeta })^m\nonumber \\&\qquad \times (-1)^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) +m}\prod _{i=m+1}^n \frac{1}{(2i-1)!}\prod _{j=1}^m \frac{(6j-2)!(2j-2)!}{(4j-3)! (4j-1)!}\nonumber \\&\qquad \times \det _{1\le l,j\le n-m}\left( W_{m+j-1}\left( -\frac{l^2}{9}; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right) \bigg /\kappa _{m+j-1}\right) . \end{aligned}$$

We factor out $\kappa _{m+j-1}$ from each column of the determinant and use (23) and get

$$\begin{aligned}&Z_{n,m}(\gamma , \dots , \gamma , 0, \dots , 0)\nonumber \\&\quad = \frac{2^{n^2-n-m^2-m}}{3^{2m^2-n^2+n} } (n-m)!\ \varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^{2mn+m}f(2\gamma )^n(1-e^{2\zeta })^m\nonumber \\&\qquad \times (-1)^{\left( {\begin{array}{c}m+1\\ 2\end{array}}\right) }\prod _{j=1}^n \frac{(2j-2)!}{(4j-3)!} \prod _{j=1}^m \frac{(6j-2)!}{ (4j-1)!}\prod _{j=m+1}^n \frac{1}{(j-1)!}\nonumber \\&\qquad \times \det _{1\le l,j\le n-m}\left( W_{m+j-1}\left( -\frac{l^2}{9}; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right) \right) . \end{aligned}$$

(24)

5.3 A formula for the number of states

Next, we rewrite the partition function as a sum over the number of positive turns, k, to be able to identify the terms with the terms in the formulas from Sect. 4. We write

$$\begin{aligned} 1-e^{2\zeta }=-\frac{e^{\gamma }f(\gamma )}{f(2\gamma )}\left( (e^{2\zeta }-e^{-2\gamma })+\frac{e^{2\zeta }-e^{2\gamma }}{e^{2\gamma }}\right) , \end{aligned}$$

and by using the binomial theorem we get

$$\begin{aligned} (1-e^{2\zeta })^m =\left( -\frac{e^\gamma f(\gamma )}{f(2\gamma )}\right) ^m\sum _{k=0}^m \left( \left( {\begin{array}{c}m\\ k\end{array}}\right) (e^{2\zeta }-e^{-2\gamma })^k\left( \frac{e^{2\zeta }-e^{2\gamma }}{e^{2\gamma }}\right) ^{m-k}\right) . \end{aligned}$$

For $\gamma =4\pi \mathrm {i}/3$, we have $f(2\gamma )=-f(\gamma )$ and $f(\gamma )^2=-3$. The partition function (24) thus becomes

$$\begin{aligned}&Z_{n,m}(\gamma , \dots , \gamma , 0, \dots , 0)=\sum _{k=0}^m \left( \left( {\begin{array}{c}m\\ k\end{array}}\right) (e^{2\zeta }-e^{-2\gamma })^k\left( \frac{e^{2\zeta }-e^{2\gamma }}{e^{2\gamma }}\right) ^{m-k}\right) \\&\quad \times (-1)^{\left( {\begin{array}{c}m+1\\ 2\end{array}}\right) +mn+n}\frac{2^{n^2-n-m^2-m}}{3^{2m^2-n^2+n-mn}} (n-m)!\ \varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m+1\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^{m+n}\\&\quad \times \prod _{j=1}^n \frac{(2j-2)!}{(4j-3)!} \prod _{j=1}^m \frac{(6j-2)!}{ (4j-1)!}\prod _{j=m+1}^n \frac{1}{(j-1)!}\\&\quad \times \det _{1\le l,j\le n-m}\left( W_{m+j-1}\left( -\frac{l^2}{9}; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right) \right) . \end{aligned}$$

The terms $(e^{2\zeta }-e^{-2\gamma })^k\left( \frac{e^{2\zeta }-e^{2\gamma }}{e^{2\gamma }}\right) ^{m-k}$ are linearly independent for different k’s as functions of $\zeta$, since the kth term has a zero of degree $m-k$ in $\zeta =\gamma$. Therefore, we can fix a k as in the previous section, and we get

$$\begin{aligned}&Z_{n,m,k}(\gamma , \dots , \gamma , 0,\dots , 0)=\left( {\begin{array}{c}m\\ k\end{array}}\right) (e^{2\zeta }-e^{-2\gamma })^k\left( \frac{e^{2\zeta }-e^{2\gamma }}{e^{2\gamma }}\right) ^{m-k}\nonumber \\&\quad \times (-1)^{\left( {\begin{array}{c}m+1\\ 2\end{array}}\right) +mn+n}\frac{2^{n^2-n-m^2-m}}{3^{2m^2-n^2+n-mn}} (n-m)!\ \varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m+1\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^{m+n}\nonumber \\&\quad \times \prod _{j=1}^n \frac{(2j-2)!}{(4j-3)!} \prod _{j=1}^m \frac{(6j-2)!}{ (4j-1)!}\prod _{j=m+1}^n \frac{1}{(j-1)!}\nonumber \\&\quad \times \det _{1\le l,j\le n-m}\left( W_{m+j-1}\left( -\frac{l^2}{9}; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right) \right) . \end{aligned}$$

(25)

Now we can go back to $N_k$ (12), the number of states where k is the number of $k_+$ turns. We insert (25) and get the following theorem.

Theorem 5.1

For the 6V model with DWBC and a partially reflecting end, the number of states with exactly k turns of type $k_+$ is

$$\begin{aligned} N_k&=\left( {\begin{array}{c}m\\ k\end{array}}\right) \frac{2^{n^2-n-m^2-m}(n-m)!}{3^{2m^2-m-n^2+n-mn}} \prod _{j=1}^n \frac{(2j-2)!}{(4j-3)!} \prod _{j=1}^m \frac{(6j-2)!}{ (4j-1)!}\prod _{j=m+1}^n \frac{1}{(j-1)!}\nonumber \\&\quad \times \det _{1\le l,j\le n-m}\left( W_{m+j-1}\left( -\frac{l^2}{9}; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right) \right) . \end{aligned}$$

(26)

As a corollary, we get that the total number of states (13) of the model is

$$\begin{aligned} A(m,n)&=\frac{2^{n^2-n-m^2}(n-m)!}{3^{2m^2-m-n^2+n-mn}} \prod _{j=1}^n \frac{(2j-2)!}{(4j-3)!} \prod _{j=1}^m \frac{(6j-2)!}{ (4j-1)!}\prod _{j=m+1}^n \frac{1}{(j-1)!}\\&\quad \times \det _{1\le l,j\le n-m}\left( W_{m+j-1}\left( -\frac{l^2}{9}; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right) \right) . \end{aligned}$$

From Proposition 4.3, it thus follows that the number of matrices described in Sect. 4.1 is also given by this expression.

5.4 An alternative expression for the number of states

In this section, we derive another way to present the expression (26). We can insert the formula (20) for $W_{m+j-1}\left( -\frac{k^2}{9}; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right)$ into the determinant

$$\begin{aligned} D=\det _{1\le k,j\le n-m}\left( W_{m+j-1}\left( -\frac{k^2}{9}; \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1\right) \right) . \end{aligned}$$

Factor out $(5/6)_{m+j-1} (4/3)_{m+j-1} (m+j-1)!$ from each column j. We can rewrite the sum in each determinant entry

$$\begin{aligned} \sum _{l=0}^{m+j-1} \frac{(1-m-j)_l (1/2+m+j)_l(1/3-k/3)_l(1/3+k/3)_l}{(5/6)_l(4/3)_l (l!)^2} \end{aligned}$$

of row k and column j to go from 0 to $n-1$, since the terms disappear when $l> m+j-1$. We then get

$$\begin{aligned} D&=\prod _{j=m}^{n-1}(5/6)_j (4/3)_j j! \\&\quad \times \det _{1\le k,j\le n-m}\left( \sum _{l=0}^{n-1} \frac{(1-m-j)_l (1/2+m+j)_l(1/3+k/3)_l(1/3-k/3)_l}{(5/6)_l (4/3)_l (l!)^2}\right) . \end{aligned}$$

We use linearity of the rows and write the determinant as a sum of determinants. The above becomes

$$\begin{aligned} D&=\prod _{j=m}^{n-1}(5/6)_j (4/3)_j j!\sum _{l_1, l_2, \dots , l_{n-m}=0}^{n-1}\left( \prod _{i=1}^{n-m} \frac{((1-i)/3)_{l_i}((1+i)/3)_{l_i}}{(5/6)_{l_i} (4/3)_{l_i} (l_i!)^2}\right. \\&\quad \left. \times \det _{1\le k,j\le n-m}\left( (1-m-j)_{l_k} (1/2+m+j)_{l_k}\right) \right) . \end{aligned}$$

Since $(x)_j/(x)_i=(x+i)_{j-i}$, for $j\ge i$, we can write

$$\begin{aligned}&(1-m-j)_{l_k} (1/2+m+j)_{l_k}\\&\quad =\frac{(1-n)_{l_k}(m+3/2)_{l_k}}{(1-n)_{n-m-j}(m+3/2)_{j-1}}(1-n+l_k)_{n-m-j}(m+3/2+l_k)_{j-1}, \end{aligned}$$

and we can factor out all factors that depend either only on row k or only on column j. The determinant D now becomes

$$\begin{aligned} D&= \prod _{j=m}^{n-1}(5/6)_j (4/3)_j j! \\&\quad \times \sum _{l_1, l_2, \dots , l_{n-m}=0}^{n-1}\left( \prod _{i=1}^{n-m} \frac{((1-i)/3)_{l_i}((1+i)/3)_{l_i}(1-n)_{l_i}(m+3/2)_{l_i}}{(5/6)_{l_i} (4/3)_{l_i} (l_i!)^2 (1-n)_{i-1}(m+3/2)_{i-1}}\right. \\&\quad \times \left. \det _{1\le k,j,\le n-m}\left( (1-n+l_k)_{n-m-j}(m+3/2+l_k)_{j-1}\right) \right) . \end{aligned}$$

Each element of the alternant matrix

$$\begin{aligned} \hat{D}=\det _{1\le k,j,\le n-m}\left( (1-n+l_k)_{n-m-j}(m+3/2+l_k)_{j-1}\right) \end{aligned}$$

is a polynomial in $l_k$ of degree $n-m-1$. This is a special case of a bigger family of determinants, see further [18,  Lemma 3]. The determinant is

$$\begin{aligned} \hat{D}=C \prod _{1\le i < j \le n-m} (l_i-l_j) \end{aligned}$$

for some C not depending on the $l_k$’s. To find C, we put $l_k=-k-m-1/2$ which makes the matrix triangular. Then,

$$\begin{aligned}&\prod _{j=0}^{n-m-1}(-1)^j j!(-1/2-n-m-j)_{n-m-1-j} =C \prod _{1\le i < j \le n-m} (j-i), \end{aligned}$$

so

$$\begin{aligned} C =\prod _{j=1}^{n-m}(5/2+2n-2j)_{j-1}. \end{aligned}$$

Hence, the determinant D becomes

$$\begin{aligned} D&=\prod _{j=m}^{n-1}(5/6)_j (4/3)_j j!\prod _{j=1}^{n-m} \frac{(5/2+2n-2j)_{j-1}}{(1-n)_{j-1}(m+3/2)_{j-1}}\\&\quad \times \sum _{l_1, l_2, \dots , l_{n-m}=0}^{n-1}\left( \prod _{i=1}^{n-m} \frac{((1-i)/3)_{l_i}((1+i)/3)_{l_i}(1-n)_{l_i}(m+3/2)_{l_i}}{(5/6)_{l_i} (4/3)_{l_i} (l_i!)^2}\right. \\&\quad \left. \times \prod _{1\le i < j \le n-m} (l_i-l_j)\right) . \end{aligned}$$

Series of similar type appear, for example, in [19, 20].

Inserting the above into (26) of the last section, we get an expression for the number of states with exactly k turns of type $k_+$ as an $(n-m)$-fold hypergeometric sum,

$$\begin{aligned} N_k&=\left( {\begin{array}{c}m\\ k\end{array}}\right) \frac{2^{n^2-n-m^2-m}(n-m)!}{3^{2m^2-m-n^2+n-mn}} \prod _{j=1}^n \frac{(2j-2)!}{(4j-3)!}\prod _{j=1}^m \frac{(6j-2)!}{(4j-1)!} \\&\quad \times \prod _{j=m+1}^n (5/6)_{j-1} (4/3)_{j-1}\prod _{j=1}^{n-m} \frac{(5/2+2n-2j)_{j-1}}{(1-n)_{j-1}(m+3/2)_{j-1}}\\&\quad \times \sum _{l_1, l_2, \dots , l_{n-m}=0}^{n-1}\left( \prod _{i=1}^{n-m} \frac{((1-i)/3)_{l_i}((1+i)/3)_{l_i}(1-n)_{l_i}(m+3/2)_{l_i}}{(5/6)_{l_i} (4/3)_{l_i} (l_i!)^2}\right. \\&\quad \times \left. \prod _{1\le i < j \le n-m} (l_i-l_j)\right) . \end{aligned}$$

Appendix A: Foda–Wheeler method

Another way to find the partition function is suggested in [12], by starting from Tsuchiya’s determinant for the partition function on a $2n\times n$ lattice and step by step removing the extra vertical lines by letting the corresponding variables $\mu _j\rightarrow \infty$, following Foda and Wheeler [11].

To do this, we need to choose weights that behave well in the limit. The weights that we have chosen in Sect. 2 will do the job. In the lattice, the local weights are either $w(\lambda -\mu )$ for vertices on the upper part of a double line, or $w(\mu +\lambda )$ for vertices on the lower part, where w is one of $a_\pm$, $b_\pm$ and $c_\pm$. When letting $\mu _i\rightarrow \infty$, the local weights become

$$\begin{aligned}&\lim _{\mu \rightarrow \infty } a_\pm (\lambda -\mu )=\lim _{\mu \rightarrow \infty } a_\pm (\lambda +\mu )=1,&\ \\&\lim _{\mu \rightarrow \infty } b_-(\lambda -\mu )=e^{2\gamma },&\ \\&\lim _{\mu \rightarrow \infty } b_+(\lambda -\mu )=1,\\&\lim _{\mu \rightarrow \infty } b_-(\lambda +\mu )=1,&\\&\lim _{\mu \rightarrow \infty } b_+(\lambda +\mu )=e^{-2\gamma },\\&\lim _{\mu \rightarrow \infty } c_-(\lambda -\mu )=-e^\gamma (e^\gamma -e^{-\gamma }),&\\&\lim _{\mu \rightarrow \infty } c_+(\lambda -\mu )=-\lim _{\mu \rightarrow \infty } e^\gamma (e^\gamma -e^{-\gamma }) \frac{1}{e^{2\mu -2\lambda }},\\&\lim _{\mu \rightarrow \infty } c_+(\lambda +\mu )=\frac{e^\gamma -e^{-\gamma }}{e^\gamma },&\\&\lim _{\mu \rightarrow \infty } c_-(\lambda +\mu )=\lim _{\mu \rightarrow \infty } \left( \frac{e^\gamma -e^{-\gamma }}{e^\gamma }\right) \frac{1}{e^{2\mu +2\lambda }}. \end{aligned}$$

We start from Tsuchiya’s determinant for $2n\times n$ lattices,

$$\begin{aligned}&Z_n(\varvec{\lambda }, \varvec{\mu })= e^{-\left( {\begin{array}{c}n+1\\ 2\end{array}}\right) \gamma } f(\gamma )^n\prod _{i=1}^n\left[ e^{\mu _i+\zeta } f(\mu _i-\zeta )f(2\lambda _i)\right] \nonumber \\&\quad \times \frac{\prod _{i=1}^n\prod _{j=1}^n \left[ f(\mu _j+\lambda _i)f(\mu _j-\lambda _i)\right] }{\prod _{1\le i<j\le n}\left[ f(\mu _j+\mu _i)f(\mu _j-\mu _i)f(\lambda _i-\lambda _j)f(\lambda _i+\lambda _j+\gamma )\right] } \det _{1\le i,j\le n} M, \end{aligned}$$

(A1)

where M is an $n\times n$ matrix with

$$\begin{aligned} M_{ij}= \frac{1}{f(\mu _i+\lambda _j)f(\mu _i-\lambda _j)f(\mu _i+(\lambda _j+\gamma ))f(\mu _i-(\lambda _j+\gamma ))}. \end{aligned}$$

Tsuchiya considered a diagonal K-matrix, but we have a triangular K-matrix. This does not affect the determinant formula in the $2n\times n$ case, since the ice rule implies that there cannot be any $k_c$ turns, coming from the off-diagonal entry in the K-matrix.

We first consider the $2\times 1$ lattice with reflecting end, since the observations that can be made for this case are important in the general case. This partition function consists of two terms (see Fig. 12),

$$\begin{aligned} c_+(\lambda +\mu )k_+(\lambda )b_+(\lambda -\mu )+b_+(\lambda +\mu )k_-(\lambda )c_-(\lambda -\mu ), \end{aligned}$$

which in the limit is $\frac{e^\gamma -e^{-\gamma }}{e^\gamma }(k_+(\lambda )-k_-(\lambda ))$. It is easy to check that $k_+(\lambda )-k_-(\lambda )=\frac{k_c(\lambda )}{\varphi }$. Hence, letting $\mu \rightarrow \infty$ yields that the partition function becomes $\frac{e^\gamma -e^{-\gamma }}{\varphi e^\gamma } k_c(\lambda )$. This makes sense in the picture as well, where removing the vertical line means that both the $k_+$ and the $k_-$ turn in the $2\times 1$ lattice become a $k_c$ turn in the $2\times 0$ lattice. Conversely, the $k_c$ turn in the smaller lattice can come from removing the vertical line from a state with a $k_+$ turn, as well as from a state with a $k_-$ turn.

Fig. 12

A $k_c$ turn comes from the sum of a $k_+$ and $k_-$ turn, when removing the vertical line from the one size bigger lattice

Fig. 13

The $k_c$ turns in a lattice of size $2n\times m$ come from either one of these configurations in the lattice of size $2n\times (m+1)$, when letting $\mu _{m+1}\rightarrow \infty$

Lemma A.1

Taking the limits $\mu _j\rightarrow \infty$, for $m+1\le j\le n$, in Tsuchiya’s determinant formula $Z_n(\varvec{\lambda }, \varvec{\mu })$, one after each other, starting with $\mu _n\rightarrow \infty$, we obtain

$$\begin{aligned}&Z_{n,m}(\varvec{\lambda }, \mu _1, \dots , \mu _m)\nonumber \\&\quad =\frac{\varphi ^{n-m}}{(1-e^{-2(n-m)\gamma })\cdots (1-e^{-4\gamma })(1-e^{-2\gamma })} \lim _{\mu _n, \mu _{n-1}, \dots , \mu _{m+1} \rightarrow \infty } Z_n(\varvec{\lambda }, \varvec{\mu }). \end{aligned}$$

(A2)

Proof

Consider a lattice of general size. In each state, the leftmost vertical line has an odd number of $c_\pm$ vertices, because of the DWBC and the ice rule. The $c_\pm$ vertices appear as products $c_+(\lambda _i+\mu _m)c_+(\lambda _j-\mu _m)$ or $c_-(\lambda _i+\mu _m)c_-(\lambda _j-\mu _m)$, where both $i=j$ or $i\ne j$ are possible, except for one single $c_+(\lambda _k+\mu _m)$ or $c_-(\lambda _k-\mu _m)$ vertex which is not paired up. In the limit $\mu _m\rightarrow \infty$, the nonzero contribution to $Z_{n,m}(\varvec{\lambda }, \mu _1, \dots , \mu _m)$ comes from the states with exactly one $c_\pm$ vertex in the mth column, so we only need to consider these states. In this case, each state contains exactly one of the configurations in Fig. 13a or 13b.

Each state has $n-m$ turns of type $k_c$. For $m<n$, each state of size $2n \times m$ comes from letting $\mu _{m+1}\rightarrow \infty$ in states of size $2n\times (m+1)$. In the smaller lattice, all turns are the same as in the bigger lattice, except for at one double row k, where the $k_c$ turn corresponds to either a $k_+$ turn or a $k_-$ turn in a bigger lattice configuration, just as in the case $n=1$. Each $k_+$ or $k_-$ turn in the smaller lattice comes from one of the configurations in Fig. 14 in the bigger lattice. In the limit, each state in Fig. 14, although consisting of two vertices and one turn, also has total weights $k_+(\lambda _i)$ or $k_-(\lambda _i)$, respectively. We are interested in how the partition function for the smaller lattice differs from the bigger lattice, and therefore, we only need to consider the $k_c$ turns in the $2n\times m$ lattice, see Fig. 15. All turns of type $k_c$ below row k come from turns of the type in Fig. 13c. All turns of type $k_c$ above row k come from turns of the type in Fig. 13d. Each turn of type Fig. 13c has weight $e^{-2\gamma }k_c(\lambda _i)$, and each turn of type Fig. 13d has weight $k_c(\lambda _i)$ in the limit.

Fig. 14

The turns that are not $k_c$ turns in a lattice of size $2n\times m$ come from either one of these configurations in the lattice of size $2n\times (m+1)$, when letting $\mu _{m+1}\rightarrow \infty$

Fig. 15

The $k_c$ turns of a state of size $2n\times m$ come from letting $\mu _{m+1}\rightarrow \infty$, i.e. removing the leftmost vertical line, in all states of size $2n\times (m+1)$ where all turns are the same as in the smaller lattice, except at some row k, where the $k_c$ turn in the smaller lattice corresponds to a $k_+$ or a $k_-$ turn at row k in the bigger lattice. In the bigger lattice, all $k_c$ double rows below row k are forced to be of the type in Fig. 13c and all $k_c$ double rows above are of the type in Fig. 13d

The row k can be chosen in $n-m$ different ways, so we need to sum over all these possibilities. Putting all of the above together, we conclude that

$$\begin{aligned}&Z_{n,m+1}(\varvec{\lambda }, \mu _1, \dots , \mu _{m+1}) \rightarrow \frac{e^\gamma -e^{-\gamma }}{\varphi e^\gamma }\left( 1+\frac{1}{e^{2\gamma }}+\cdots +\frac{1}{e^{2(n-m-1)\gamma }}\right) \nonumber \\&\quad \times Z_{n,m}(\varvec{\lambda }, \mu _1, \dots , \mu _m), \end{aligned}$$

(A3)

as $\mu _{m+1}\rightarrow \infty$. By iteration, the lemma follows. $\square$

We now prove the determinant formula by induction.

Proposition A.2

For the 6V model with DWBC and a partially reflecting end on a lattice of size $2n\times m$, $m\le n$, the partition function is

$$\begin{aligned}&Z_{n,m}(\varvec{\lambda }, \mu _1, \dots , \mu _m)=\frac{\varphi ^{n-m}e^{-\left( {\begin{array}{c}n+1\\ 2\end{array}}\right) \gamma } f(\gamma )^n}{(1-e^{-2(n-m)\gamma })\cdots (1-e^{-4\gamma })(1-e^{-2\gamma })}\nonumber \\&\quad \times \frac{\prod _{i=1}^{m} \left[ e^{\mu _i+\zeta } f(\mu _i-\zeta )\right] \prod _{i=1}^n f(2\lambda _i)\prod _{i=1}^n\prod _{j=1}^{m} \left[ f(\mu _j+\lambda _i)f(\mu _j-\lambda _i)\right] }{\prod _{1\le i<j\le m}\left[ f(\mu _j+\mu _i)f(\mu _j-\mu _i)\right] \prod _{1\le i<j\le n}\left[ f(\lambda _i-\lambda _j)f(\lambda _i+\lambda _j+\gamma )\right] }\nonumber \\&\quad \times \det \begin{pmatrix} F(\lambda _1, \mu _1) &{}\quad \cdots &{}\quad F(\lambda _n, \mu _1)\\ \vdots &{}\quad \ddots &{}\quad \vdots \\ F(\lambda _1, \mu _m) &{}\quad \cdots &{}\quad F(\lambda _n, \mu _m)\\ C_{n-m-1}(\lambda _1) &{}\quad \cdots &{}\quad C_{n-m-1}(\lambda _n)\\ \vdots &{}\quad \ddots &{}\quad \vdots \\ C_0(\lambda _1) &{} \quad \cdots &{}\quad C_0(\lambda _n) \end{pmatrix}, \end{aligned}$$

(A4)

where

$$\begin{aligned} F(\lambda _i, \mu _j)=\frac{1}{f(\mu _j+\lambda _i)f(\mu _j-\lambda _i)f(\mu _j+(\lambda _i+\gamma ))f(\mu _j-(\lambda _i+\gamma ))}, \end{aligned}$$

and

$$\begin{aligned} C_k(\lambda _i)=\quad \mathop \sum \limits _{{\begin{array}{c} k_1, k_2, k_3, k_4\ge 0 \\ k_1+k_2+k_3+k_4=k \end{array}}} e^{(k_1+k_2-k_3-k_4)v_i+(k_1-k_2+k_3-k_4)\gamma } \end{aligned}$$

(A5)

for $v_i=2\lambda _i+\gamma$.

Proof

We start from Tsuchiya’s determinant formula (A1). Let $P_{n-m}$ be the claim that (A4) holds. We know that $P_0$ is true, since this is Tsuchiya’s determinant. Assume $P_{n-m}$. We will prove that $P_{n-m+1}$ also holds. From (A3), we have

$$\begin{aligned} Z_{n,m-1}(\varvec{\lambda }, \mu _1, \dots , \mu _{m-1})=\frac{\varphi }{1-e^{-2(n-m+1)\gamma }}\lim _{\mu _m\rightarrow \infty }Z_{n,m}(\varvec{\lambda }, \mu _1, \dots , \mu _{m}) \end{aligned}$$

Insert (A4). Absorb factors that have to do with $\mu _m$ into the mth row of the matrix,

$$\begin{aligned}&Z_{n,m-1}(\varvec{\lambda }, \mu _1, \dots , \mu _{m-1}) = \frac{\varphi ^{n-m+1}e^{-\left( {\begin{array}{c}n+1\\ 2\end{array}}\right) \gamma } f(\gamma )^n}{(1-e^{-2(n-m+1)\gamma })\cdots (1-e^{-4\gamma })(1-e^{-2\gamma })}\\&\quad \times \frac{\prod _{i=1}^{m-1} \left[ e^{\mu _i+\zeta } f(\mu _i-\zeta )\right] \prod _{i=1}^n f(2\lambda _i)\prod _{i=1}^n\prod _{j=1}^{m-1} \left[ f(\mu _j+\lambda _i)f(\mu _j-\lambda _i)\right] }{\prod _{1\le i<j\le m-1}\left[ f(\mu _j+\mu _i)f(\mu _j-\mu _i)\right] \prod _{1\le i<j\le n}\left[ f(\lambda _i-\lambda _j)f(\lambda _i+\lambda _j+\gamma )\right] }\\&\quad \times \lim _{\mu _m\rightarrow \infty }\det \begin{pmatrix} F(\lambda _1, \mu _1) &{}\quad \cdots &{}\quad F(\lambda _n, \mu _1)\\ \vdots &{}\quad \ddots &{}\quad \vdots \\ F(\lambda _1, \mu _{m-1}) &{}\quad \cdots &{}\quad F(\lambda _n, \mu _{m-1})\\ d_1^{m}(\epsilon _m) &{}\quad \cdots &{}\quad d_n^{m}(\epsilon _m)\\ C_{n-m-1}(\lambda _1) &{}\quad \cdots &{}\quad C_{n-m-1}(\lambda _n)\\ \vdots &{}\quad \ddots &{}\quad \vdots \\ C_0(\lambda _1) &{}\quad \cdots &{}\quad C_0(\lambda _n) \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} d_j^k=\frac{e^{\mu _k+\zeta } f(\mu _k-\zeta )\prod _{i=1}^n \left[ f(\mu _k+\lambda _i)f(\mu _k-\lambda _i)\right] }{\prod _{i=1}^{k-1}\left[ f(\mu _k+\mu _i)f(\mu _k-\mu _i)\right] } F(\lambda _j, \mu _k). \end{aligned}$$

Write $v_i=2\lambda _i+\gamma$. Then

$$\begin{aligned} F(\lambda _i, \mu _j){=}\frac{e^{-4\pi }}{(1-e^{-2\mu _j+v_i{+}\gamma })(1-e^{{-}2\mu _j+v_i-\gamma })(1{-}e^{-2\mu _j-v_i+\gamma })(1-e^{-2\mu _j-v_i-\gamma })}. \end{aligned}$$

By Taylor expansion,

$$\begin{aligned} F(\lambda _i, \mu _j)=\sum _{k=0}^\infty C_k(\lambda _i) e^{-2(k+2)\mu _j}, \end{aligned}$$

with $C_k(\lambda _i)$ as defined in (A5).

Consider

$$\begin{aligned} d_j^m=\frac{e^{\mu _m+\zeta } f(\mu _m-\zeta )\prod _{i=1}^n \left[ f(\mu _m+\lambda _i)f(\mu _m-\lambda _i)\right] }{\prod _{i=1}^{m-1}\left[ f(\mu _m+\mu _i)f(\mu _m-\mu _i)\right] } \sum _{l=0}^\infty C_l(\lambda _j) e^{-2(l+2)\mu _m}. \end{aligned}$$

By row reduction in the determinant, all terms with $C_l(\lambda _j)$, for $0\le l \le n-m-1$, can be removed from the sum. The elements of row m become

$$\begin{aligned} \hat{d}_j^m=\frac{e^{\mu _m+\zeta } f(\mu _m-\zeta )\prod _{i=1}^n \left[ f(\mu _m+\lambda _i)f(\mu _m-\lambda _i)\right] }{\prod _{i=1}^{m-1}\left[ f(\mu _m+\mu _i)f(\mu _m-\mu _i)\right] } \sum _{l=n-m}^\infty C_l(\lambda _j) e^{-2(l+2)\mu _m}. \end{aligned}$$

Now we take the limit,

$$\begin{aligned} \lim _{\mu _m\rightarrow \infty }\hat{d}_j^m&=\lim _{\mu _m\rightarrow \infty } \frac{(1-e^{2\zeta -2\mu _m})\prod _{i=1}^n \left[ (1-e^{-2\mu _m-2\lambda _i})(1-e^{-2\mu _m+2\lambda _i})\right] }{\prod _{i=1}^{m-1}\left[ (1-e^{-2\mu _m-2\mu _i})(1-e^{-2\mu _m+2\mu _i})\right] } \nonumber \\&\quad \times e^{2(n-m+2)\mu _m}\sum _{l=n-m}^\infty C_l(\lambda _j) e^{-2(l+2)\mu _m}\nonumber \\&=C_{n-m}(\lambda _j), \end{aligned}$$

so $P_{n-m+1}$ is true. $\square$

The last thing left to do is to simplify the last $n-m$ rows of the determinant.

Theorem A.3

(Theorem 3.5) For the 6V model with DWBC and a partially reflecting end on a lattice of size $2n\times m$, $m\le n$, the partition function is

$$\begin{aligned}&Z_{n,m}(\varvec{\lambda }, \mu _1, \dots , \mu _m)=\varphi ^{n-m}e^{\left( \left( {\begin{array}{c}m\\ 2\end{array}}\right) -nm\right) \gamma }f(\gamma )^m\nonumber \\&\quad \times \frac{\prod _{i=1}^{m} \left[ e^{\mu _i+\zeta } f(\mu _i-\zeta )\right] \prod _{i=1}^n f(2\lambda _i)\prod _{i=1}^n\prod _{j=1}^{m} \left[ f(\mu _j+\lambda _i)f(\mu _j-\lambda _i)\right] }{\prod _{1\le i<j\le m}\left[ f(\mu _j+\mu _i)f(\mu _j-\mu _i)\right] \prod _{1\le i<j\le n}\left[ f(\lambda _i-\lambda _j)f(\lambda _i+\lambda _j+\gamma )\right] }\nonumber \\&\quad \times \det \begin{pmatrix} F(\lambda _1, \mu _1) &{}\quad \cdots &{}\quad F(\lambda _n, \mu _1)\\ \vdots &{}\quad \ddots &{}\quad \vdots \\ F(\lambda _1, \mu _m)&{}\quad \cdots &{}\quad F(\lambda _n, \mu _m)\\ h(2(n-m-1)(\lambda _1+\gamma /2)) &{}\quad \cdots &{}\quad h(2(n-m-1)(\lambda _n+\gamma /2))\\ \vdots &{}\quad \ddots &{}\quad \vdots \\ h(2(\lambda _1+\gamma /2)) &{}\quad \cdots &{}\quad h(2(\lambda _n+\gamma /2))\\ 1 &{}\quad \cdots &{}\quad 1 \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} F(\lambda _i, \mu _j)=\frac{1}{f(\mu _j+\lambda _i)f(\mu _j-\lambda _i)f(\mu _j+(\lambda _i+\gamma ))f(\mu _j-(\lambda _i+\gamma ))}, \end{aligned}$$

and where $f(x)=2\sinh x$ and $h(x)=2\cosh x$.

Remark A.1

In Theorem  3.5, the determinant is expressed in a more compact form.

Proof

We start from the determinant (A4) from the last proposition. Focus on the entries of the lower part of the determinant, defined in (A5) as

$$\begin{aligned} C_k(\lambda _j)=\quad \mathop \sum \limits _{{\begin{array}{c} k_1, k_2, k_3, k_4\ge 0 \\ k_1+k_2+k_3+k_4=k \end{array}}} e^{(k_1+k_2-k_3-k_4)v_j+(k_1-k_2+k_3-k_4)\gamma }. \end{aligned}$$

These are clearly Laurent polynomials of degree k in $e^{v_j}$, and they are even in $v_j$. We have already seen that $C_0(\lambda _j)=1$. For $k>0$, the leading coefficient is

$$\begin{aligned} \mathop \sum \limits _{{\begin{array}{c} k_1, k_2\ge 0 \\ k_1+k_2=k \end{array}}} e^{(k_1+k_2)v_j+(k_1-k_2)\gamma } =\frac{f((k+1)\gamma )}{f(\gamma )}. \end{aligned}$$

Thus by row reduction in the determinant, we can replace $C_k(\lambda _j)$ by

$$\begin{aligned} \frac{f((k+1)\gamma )}{f(\gamma )}(e^{k v_j}+e^{-k v_j}) \end{aligned}$$

for $k>0$. Switching back to the variables $\lambda _j$ and factoring out $\frac{f((k+1)\gamma )}{f(\gamma )}$ from each row of the lower part of the determinant yields the desired result. $\square$