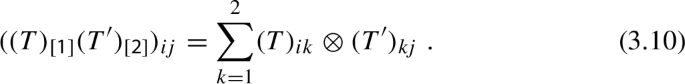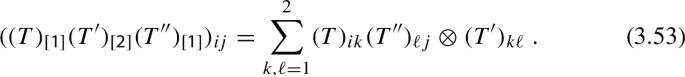Abstract
The equitable presentation of the quantum algebra \(U_q(\widehat{sl_2})\) is considered. This presentation was originally introduced by Ito and Terwilliger. In this paper, following Terwilliger’s recent works the (nonstandard) positive part of \(U_q(\widehat{sl_2})\) of equitable type \(U_q^{IT,+}\) and its second realization (current algebra) \(U_q^{T,+}\) are introduced and studied. A presentation for \(U_q^{T,+}\) is given in terms of a K-operator satisfying a Freidel–Maillet-type equation and a condition on its quantum determinant. Realizations of the K-operator in terms of Ding–Frenkel L-operators are considered, from which an explicit injective homomorphism from \(U_q^{T,+}\) to a subalgebra of Drinfeld’s second realization (current algebra) of \(U_q(\widehat{sl_2})\) is derived, and the comodule algebra structure of \(U_q^{T,+}\) is characterized. The central extension of \(U_q^{T,+}\) and its relation with Drinfeld’s second realization of \(U_q(\widehat{gl_2})\) is also described using the framework of Freidel–Maillet algebras.
Similar content being viewed by others
Notes
As usual, ‘\(\mathrm tr_{12}\)’ stands for the trace over \(\mathcal V_1 \otimes \mathcal V_2\). Also, we denote \(P^{-}_{12}=(1-P)/2\).
The index [j] characterizes the ‘quantum space’ \(V_{[j]}\) on which the entries of \(L^\pm (z)\) act. With respect to the ordering \(V_{[1]}\otimes V_{[2]}\), one has:
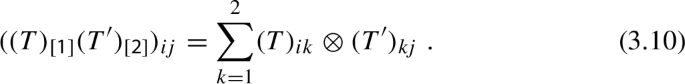
With respect to the ordering \(V_{[1]}\otimes V_{[2]}\):
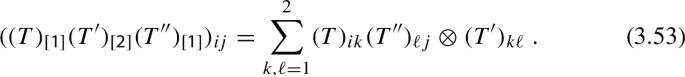
References
Baseilhac, P.: The alternating presentation of \(U_q(\widehat{gl_2})\) from Freidel-Maillet algebras. Nucl. Phys. B 967, 115400 (2021). arXiv:2011.01572
Baseilhac, P.: Freidel-Maillet type presentations of \(U_q(sl_2)\), arXiv:2106.11715
Baxter, R.: Exactly Solvable Models in Statistical Mechanics. Academic Press, New York (1982)
Beck, J.: Braid group action and quantum affine algebras. Commun. Math. Phys. 165, 555–568 (1994)
Beck, J., Chari, V., Pressley, A.: An algebraic characterization of the affine canonical basis Duke Math. J. 99(3), 455–487 (1999). arXiv:math/9808060
Chari, V., Pressley, A.: Quantum affine algebras. Commun. Math. Phys. 142, 261–283 (1991)
Chari, V., Pressley, A.: A Guide to Quantum Groups. Cambridge University Press, Cambridge (1994)
Cherednik, I.V.: Factorizing particles on the half-line and root systems. Theor. Math. Fiz. 61, 35–44 (1984)
Ding, J., Frenkel, I.: Isomorphism of two realizations of quantum affine algebra \(U_q(\widehat{sl(n)})\). Commun. Math. Phys. 156, 277–300 (1993)
Drinfeld, V.G.: Quantum groups. Proc. ICM Berkeley 1, 789–820 (1986)
Drinfeld, V.G.: A new realization of yangians and quantum affine algebras. Sov. Mat. Dokl. 36, 212–216 (1988)
Faddeev, L.D., Reshetikhin, N.Y., Takhtajan, L.A.: Quantization of Lie groups and Lie algebras. Algebra Anal. 1(1), 118–206 (1989). (Russian)
Faddeev, L.D., Reshetikhin, N.Y., Takhtajan, L.A.: Quantization of Lie Groups and Lie Algebras, Yang-baxter Equation in Integrable Systems, Advanced Series in Mathematical Physics, vol. 10, pp. 299–309. World Scientific, Singapore (1989)
Freidel, L., Maillet, J.M.: Quadratic algebras and integrable systems. Phys. Lett. B 262, 278 (1991)
Frenkel, E., Mukhin, E.: The Hopf algebra \(RepU_q\widehat{gl}_\infty \). Sel. Math. 8, 537–635 (2002). arXiv:math/0103126v2
Gao, Y., Jing, N.: \(U_q(\widehat{gl_N})\) action on \(\widehat{gl_N}\)-modules and quantum toroidal algebras. J. Algebra 273, 320–343 (2004). arXiv:math/0202292
Ito, T., Terwilliger, P.: Tridiagonal pairs and the quantum affine algebra \(U_q(\widehat{sl_2})\). Ramanujan J. 13, 39–62 (2007). arXiv:math/0310042
Jimbo, M.: A q-difference analog of \(U(\widehat{g})\) and the Yang-Baxter equation. Lett. Math. Phys. 10, 63–69 (1985)
Jing, N., Liu, M., Molev, A.: Isomorphism between the R-matrix and Drinfeld presentations of quantum affine algebra: type C. J. Math. Phys. 61, 031701 (2020). arXiv:1903.00204
Jing, N., Liu, M., Molev, A.: Isomorphism between the R-Matrix and Drinfeld presentations of quantum affine algebra: Types B and D. SIGMA 16, 043 (2020). arXiv:1911.03496
Liashyk, A., Pakuliak, S.Z.: On the R-matrix realization of quantum loop algebras. arXiv:2106.10666
Reshetikhin, N.Y., Semenov Tian-Shansky, M.: Central extensions of quantum current roups. Lett. Math. Phys. 19, 133–142 (1990)
Sklyanin, E.K.: Boundary conditions for integrable quantum systems. J. Phys. A 21, 2375–2389 (1988)
Terwilliger, P.: Using Catalan words and a q-shuffle algebra to describe a PBW basis for the positive part of \(U_q(\widehat{sl_2})\). J. Algebra 525 359–373 (2019). arXiv:1806.11228
Terwilliger, P.: The alternating PBW basis for the positive part of \(U_q(\widehat{sl_2})\). J. Math. Phys. 60, 071704 (2019). arXiv:1902.00721
Terwilliger, P.: The alternating central extension for the positive part of \(U_q(\widehat{sl_2})\). Nucl. Phys. B 947, 114729 (2019). arXiv:1907.09872
Terwilliger, P.: The algebra \(U_q^+\) and its alternating central extension \({\cal{U}}_q^+\), preprint (2021)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Drinfeld–Jimbo and Drinfeld (second realization) presentation of \(U_q(\widehat{sl_2})\)
Appendix A. Drinfeld–Jimbo and Drinfeld (second realization) presentation of \(U_q(\widehat{sl_2})\)
For the quantum affine Kac–Moody algebra \(U_q(\widehat{sl_2})\), two standard presentations are recalled. The Drinfeld–Jimbo presentation \(U_q^{DJ}\) and the Drinfeld (second) presentation \(U_q^{Dr}\), see, e.g., [7, p.392].
1.1 A.1. Drinfeld–Jimbo presentation \(U_q^{DJ}\)
Define the extended Cartan matrix \(\{a_{ij}\}\) (\(a_{ii}=2\), \(a_{ij}=-2\) for \(i\ne j\)). The quantum affine algebra \(U_{q}(\widehat{sl_2})\) over \({{\mathbb {C}}}(q)\) is generated by \(\{E_j,F_j,K_j^{\pm 1}\}\), \(j\in \{0,1\}\) which satisfy the defining relations
together with the \(q-\)Serre relations (\(i\ne j\))
The product \(C=K_0K_1\) is the central element of the algebra.
The Hopf algebra structure is ensured by the existence of a comultiplication \(\Delta \) , antipode \(\mathcal{S}\) and a counit \(\mathcal{E}\) with
and
1.2 A.2. Drinfeld’s second realization \(U_q^{Dr}\)
A second presentation for the quantum affine algebra \(U_q(\widehat{sl_2})\), known as the Drinfeld’s second realization, is now recalled. In [11], it is shown that \(U_q(\widehat{sl_2})\) is isomorphic to the associative algebra over \({{\mathbb {C}}}(q)\) with generators \(\{{{\textsf {x}}}_k^{\pm }, {\textsf {h}}_{\ell }, {\textsf {K}}^{\pm 1} |k\in {{\mathbb {Z}}},\ell \in {{\mathbb {Z}}}\backslash \{0\} \}\), central elements \(C^{\pm 1/2}\) and the following relations (see, e.g., [7, Theorem 12.2.1]):
where the \(\psi _{k}\) and \(\phi _{k}\) are defined by the following equalities of formal power series in the indeterminate z:
Note that there exists an automorphism such that:
An isomorphism \(U_q^{DJ}\rightarrow U_q^{Dr}\) is given by (see, e.g., [7, p. 393]:
Note that it is still an open problem to find the complete Hopf algebra isomorphism between \(U_q^{DJ}\) and \(U_q^{Dr}\). Only partial information is known, see, e.g., [6, Section 4.4].
Rights and permissions
About this article
Cite this article
Baseilhac, P. On the second realization for the positive part of \(U_q(\widehat{sl_2})\) of equitable type. Lett Math Phys 112, 2 (2022). https://doi.org/10.1007/s11005-021-01502-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11005-021-01502-1