1 Introduction

Density functional theory (DFT) [33] has probably become the most popular work-horse for quantum mechanical calculations among chemists and physicists with a wide application on molecular and solid-state systems [4, 7]. On one side, nowadays density functional theory is understood to be Kohn–Sham DFT (KS-DFT) [36], a variant of DFT where some amount of the electron–electron interaction is approximated by the so-called exchange-correlation functional, while the kinetic energy is obtained from the eigenfunctions of a fictitious system of N non-interacting particles having the same electron density like the system of interest. Consequently, the KS method requires solving a system of N coupled differential equations similar to the wavefunction-based Hartree-Fock method [50]. On the other side, the Hohenberg-Kohn theorems [33] provide the theoretical foundation for a purely density-based quantum mechanical treatment of matter, circumventing the need of solving for the KS eigenfunctions. Instead, in an orbital-free density functional formalism, a single equation, the so-called Euler equation [43], yields the minimizing electron density via functional differentiation of the total energy under the constraint that the density stays normalized to the number of electrons N.

This method, however, requires the knowledge of the electronic kinetic energy as a functional of the electron density or at least some reasonable approximation to it. Unlike the exchange-correlation energy, being roughly 10% of the total energy, the kinetic energy is of the order of magnitude as the total energy itself. Thus, reliable approximations for the kinetic energy are the crucial point in orbital-free density functional theory (OF-DFT). The most well-known kinetic energy functional is probably the Thomas–Fermi approximation, derived independently by Thomas [51] and Fermi [12] in 1927 and 1928, respectively. However, conventional density-gradient expansions do not form a convergent series [11]. Therefore, empirical convergence studies, known under the term generalized-gradient expansion (GGA), emerged as a rapidly evolving research field among theoretical physicists and chemists. While successful in case of approximations for the electron–electron interaction, a straightforward application in case of the kinetic energy seems to be more difficult. An elusive study about the compatibility of various constraints in the design of GGA-type kinetic energy approximations can be found here [34]. Other types of functional approximations have been developed and tested, among them functional approximations that are based on information theoretical aspects [29, 30] or expansions in terms of density moments [3]. While special model cases, like for example one-dimensional systems [8, 47], allow for analytic expressions for the electronic kinetic energy, a general analytic treatment for three-dimensional Coulomb systems is still out of reach. Note that, applications within the field of chemistry and material science require correct treatment of atomic, molecular and solid-state systems, which all fall under the latter category. The lack of sufficiently accurate functional approximations for the kinetic energy has been the major drawback within the last fifty years, preventing realistic applications in the field of OF-DFT [34]. The problem here is not to properly model the kinetic energy for a given system of interest (what can always be achieved numerically by inversion of the KS equations or by a convenient choice of suitable parameters), but to properly model kinetic energy differences, e.g., for a molecule with varying nuclear coordinates or different molecular/solid-state systems. However, providing sufficiently accurate bond distances is a mandatory prerequisite in quantum chemical modeling.

Lately, it has been shown that the recently introduced bifunctional formalism together with the subsequently applied atomic fragment approximation yields sufficiently accurate kinetic energies (and energy differences) able to properly model chemical bonding [20, 21, 24]. Note that the bifunctional formalism employed, here, has to be distinguished from the bifunctional construction of Lieb [44]. The bifunctional formalism employed, in the present work, is an exact reformulation of the respective density functional formalism and allows to extract the functional value with the help of its respective functional derivative, the potential. While this part of the formalism is, in principle, exact, realistic applications in chemistry require sufficiently accurate potential approximations. It has been shown lately that based on chemical reasoning numerically accurate approximations can be generated in order to model chemical bonding in molecules [20, 21, 24]. Further development of kinetic energy functionals is an active research topic for theoretical chemists and physicists in the field of OF-DFT for either puristic reasons and ongoing interest in the original variant of DFT or for the promising computational benefit in large-scale applications. Besides that, a reliably working OF-DFT scheme provides considerable conceptual benefit as it allows to treat solid-state calculations within a pure real-space approach and, thus, permits to treat real crystals by omitting the requirement of fully obeying translational symmetry, and therefore, without the concept of bandstructures. The recently introduced bifunctional approach would certainly benefit from further mathematical investigations and hopefully attracts interest from mathematically inclined researchers as there remain a number of open questions due to the nature of the introduced bifunctional expression while still being close to the conventional density functional formalism.

The paper is organized as follows: Sects. 2 and 3 briefly review the KS and the OF-DFT method, respectively. In Sect. 3.1 a few problems of conventional gradient expansion techniques are addressed. A less conventional splitting of the non-interacting kinetic energy into a bosonic and a fermionic term is, therefore, presented in Sect. 3.2. The method allows to split the kinetic energy into a known density functional, the von Weizsäcker kinetic energy, and a remainder, the so-called Pauli term, that—in general—needs further approximations. After a detailed introduction of the bifunctional formalism in Sect. 4, the method is applied to the von Weizsäcker term and the Pauli kinetic energy in Sects. 4.1 and 4.2, respectively. Since the Weizsäcker term is known analytically in terms of the electron density, while the Pauli kinetic energy is not, Sect. 4.1 is meant to demonstrate the numerical equivalence of the Weizsäcker kinetic energy in the density functional formalism and the bifunctional formalism. It is shown that the ambiguity of the kinetic energy density, see Sect. 2, is transferred to the bifunctional kernel. The functional derivative, however, is up to a constant [41] uniquely defined, and thus, the bifunctional approach allows for a direct comparison of approximate and KS-based potentials. This advantage is especially helpful when addressing the Pauli kinetic energy, see Sect. 4.2. Approximate numerical Pauli potentials for atoms, molecules, and extended systems are given in Sects. 4.2.1, 4.2.2, and 4.2.3, respectively. Finally, a discussion section compiling the advantages of the approach and the remaining open questions are given in Sects. 5.1 and 5.2, respectively, before the concluding remarks concerning the bifunctional formalism are shortly summarized in Sect. 6.

2 Kohn–Sham density functional theory

The currently used form of density functional theory for molecular and solid-state applications is Kohn–Sham density functional theory (KS-DFT) [36]. In KS-DFT the electron density of the real system \(\rho (\mathbf {r})\) (a scalar function representing the distribution of electrons in position space \(\mathbf {r}\)) is represented by a set of N quasiparticles, the so-called non-interacting electrons, given in terms of KS orbitals \(\lbrace \phi _i \rbrace \), such that the corresponding Slater determinant:

$$\begin{aligned} {|{\varPsi }\rangle } = \frac{1}{\sqrt{N!}} \mathrm{det}\lbrace \phi _1 \ldots \phi _N \rbrace \end{aligned}$$
(1)

yields the exact energy E from:

$$\begin{aligned} {\hat{H}}_{\text {eff}} {|{\varPsi }\rangle } = E {|{\varPsi }\rangle } \end{aligned}$$
(2)

with the effective Hamiltonian (given in atomic units):

$$\begin{aligned} {\hat{H}}_{\text {eff}} = \sum _i^N \frac{\hat{p_i}^2}{2} + h_{\text {eff}}(\mathbf {r}) \end{aligned}$$
(3)

which accounts for the kinetic energy of the non-interacting electrons \(T_s\) through the impulsoperator \(\hat{p_i} = \mathbf {\nabla }_i / i\) and all Coulomb interactions between the particles through the help of a local effective Hamiltonian \(h_{\text {eff}}(\mathbf {r})\) given in position space \(\mathbf {r}\) that acts as multiplicative operator.

The KS orbitals are obtained as eigenfunctions from:

$$\begin{aligned} -\frac{1}{2} \mathbf {\nabla }^2 \phi _i(\mathbf {r}) + h_{\text {eff}}(\mathbf {r})\phi _i(\mathbf {r}) = \epsilon _i \phi _i(\mathbf {r}) \end{aligned}$$
(4)

and \(\epsilon _i\) are the corresponding eigenvalues. In the KS formalism the non-interacting kinetic energy is directly evaluated from the orbitals of the KS Slater determinant:

$$\begin{aligned} T_s = {\langle {\varPsi }|} \sum _i^N \frac{\hat{p_i}^2}{2} {|{\varPsi }\rangle }. \end{aligned}$$
(5)

There are two natural choices for the kinetic energy density, namely the so-called Schrödinger form \(t_s(\mathbf {r})\):

$$\begin{aligned} t_s(\mathbf {r}) = -\frac{1}{2} \sum _i^N \phi _i(\mathbf {r}) \mathbf {\nabla }^2 \phi _i(\mathbf {r}) \; \; \end{aligned}$$
(6)

and the positive kinetic energy \(\tau (\mathbf {r})\):

$$\begin{aligned} \tau (\mathbf {r}) = \frac{1}{2} \sum _i^N |\mathbf {\nabla }\phi _i(\mathbf {r})|^2 \; \; , \end{aligned}$$
(7)

depending on the fact whether the impulsoperator acts twice on the right-hand side or once on the right-hand side and its complex conjugate on the left-hand side. Notably, the non-interacting kinetic energy is the same in both cases. The kinetic energy densities differ by a fraction of the density Laplacian:

$$\begin{aligned} t_s(\mathbf {r}) = \tau (\mathbf {r}) - \frac{1}{4} \mathbf {\nabla }^2 \rho (\mathbf {r}) \; \; , \end{aligned}$$
(8)

which itself integrates to zero:

$$\begin{aligned} \int \mathbf {\nabla }^2 \rho (\mathbf {r}) \, \mathrm {d}\mathbf {r}= 0 \; \; . \end{aligned}$$
(9)

and thus, the integral over \(t_s(\mathbf {r})\) and \(\tau (\mathbf {r})\) yields the same expectation value for the kinetic energy. This aspect is known as ambiguity of the kinetic energy density, and it additionally complicates the procedure of finding approximations (approximate functionals are labeled with tilde) for the non-interacting kinetic energy \({\tilde{T}}_s\) in form of:

$$\begin{aligned} {\tilde{T}}_s[\rho (\mathbf {r})] = \int {\tilde{t}}([\rho (\mathbf {r})]; \mathbf {r}) \, \mathrm {d}\mathbf {r}\; \; . \end{aligned}$$
(10)

Due to the ambiguity of \({\tilde{t}}(\mathbf {r})\) a pointwise comparison between KS data and proposed approximations is somewhat awkward (although it might be of some use in practice). As will shown later, the bifunctional formalism resolves this problem.

Since the KS wavefunction is actually eigenfunction to the effective Hamiltonian \({\hat{H}}_{\text {eff}}\) and \(h_{\text {eff}}\) is a multiplicative operator, the non-interacting kinetic energy obeys:

$$\begin{aligned} T_s[\rho _{\uplambda }(\mathbf {r})] = \uplambda ^2 T_s[\rho (\mathbf {r})] \end{aligned}$$
(11)

for the homogeneously scaled electron density \(\rho _{\uplambda }(\mathbf {r}) = \uplambda ^3 \rho (\uplambda \mathbf {r})\), where \(\uplambda \) is a parameter [42]. This scaling property applies to the non-interacting kinetic energy \(T_s\) of Kohn–Sham theory, but not to the exact kinetic energy T. Their difference \(T_c\):

$$\begin{aligned} T_c = T - T_s \end{aligned}$$
(12)

is always non-negative [11] and has shown to be of marginal magnitude [32]. In practice the correlation part of the kinetic energy \(T_c\) is always merged with the functional approximations of the local effective Hamiltonian.

3 Orbital-free density functional theory

Orbital-free density functional theory aims to circumvent the need of solving for the KS eigenfunctions, cf. Eq. 4. According to the Hohenberg-Kohn (HK) theorems [33], the total electronic energy \(E[\rho (\mathbf {r})]\) of a system can be expressed as a functional of the electron density \(\rho (\mathbf {r})\):

$$\begin{aligned} E[\rho (\mathbf {r})] = T_s[\rho (\mathbf {r})] + E_{\text {H}}[\rho (\mathbf {r})] + E_{XC}[\rho (\mathbf {r})] + E_Z[\rho (\mathbf {r})] . \end{aligned}$$
(13)

For a condensed writing the explicit position dependence is omitted from now on. As given in Eq. 13, the total electronic energy is usually divided into four components, where \(T_s[\rho ]\) is the non-interacting kinetic energy, \(E_{\text {H}}[\rho ]\) is the classical part of the electron–electron repulsion, the so-called Hartree term, \(E_{XC}[\rho ]\) is the non-classical part of the electron–electron repulsion, called exchange-correlation energy, and \(E_Z[\rho ]\) is the electron-nuclear attraction. In the above equation the energy terms \(E_{\text {H}}[\rho ]\) and \(E_Z[\rho ]\) are known exactly in terms of the electron density, while for \(T_s[\rho ]\) and \(E_{XC}[\rho ]\) sufficiently accurate approximations have to be found.

Once those approximations are chosen, minimizing the energy under the constraint that the electron density integrates to N electrons yields:

$$\begin{aligned} 0 = \frac{\delta \left( E[\rho ] - \mu \left( N - \int \rho (\mathbf {r}) \, \mathrm {d}\mathbf {r}\right) \right) }{\delta \rho } \end{aligned}$$
(14)

the Euler equation [43], written explicitly:

$$\begin{aligned} 0 = v_{\text {T}}([\rho ]; \mathbf {r}) + v_{\text {H}}([\rho ]; \mathbf {r}) + v_{XC}([\rho ]; \mathbf {r}) + v_Z([\rho ]; \mathbf {r}) - \mu , \end{aligned}$$
(15)

where \(v_{\text {T}}([\rho ]; \mathbf {r})\), \(v_{\text {H}}([\rho ]; \mathbf {r})\), \(v_{XC}([\rho ]; \mathbf {r})\), and \(v_Z([\rho ]; \mathbf {r})\) are the kinetic energy potential, the Hartree potential, the exchange-correlation potential, and the nuclear-attraction potential, respectively, and \(\mu \) is the Lagrange multiplier originating from the constraint of a normalized density.

For functional expressions given analytically in terms of \(\rho \) solving the Euler equation, cf. Eq. 15, or minimizing the total energy, cf. Eq. 13, finally, yields the same results.

In contrast to KS theory, where a system of N coupled differential equations must be solved, a single equation, the so-called Euler equation, cf. Eq. 15, allows to access the minimizing electron density within OF-DFT. However, this procedure requires knowing the kinetic energy as a functional of the electron density in order to obtain the kinetic energy potential \(v_{\text {T}}([\rho ]; \mathbf {r})\), cf. Eq. 15, as functional derivative:

$$\begin{aligned} v_{\text {T}}([\rho ]; \mathbf {r}) = \frac{\delta T_s[\rho ]}{\delta \rho } \end{aligned}$$
(16)

of the respective energy \(T_s\).

The availability of exact or sufficiently accurate approximations of the kinetic energy crucially depend on the nature of the particles and the system under consideration. As will be shown later, the kinetic energy for a bosonic groundstate can be expressed analytically and, thus, is known for any density. However, since electrons are fermions, it is necessary to find approximations that account for the fermionic nature of the wavefunction in order to compute the full kinetic energy. Special cases allow for an analytical treatment of the electronic kinetic energy, like for example for a uniform electron density distribution [12, 51] or in case of one-dimensional systems [8, 47].

3.1 Gradient expansions of the kinetic energy

Since the kinetic energy for a uniform electron density distribution is known exactly, systematic density-gradient expansion series were among the first studied functional approximations [11]:

$$\begin{aligned} T_s[\rho ] \approx T_0[\rho ] + T_2[\rho ] + T_4[\rho ] + \cdots . \end{aligned}$$
(17)

The first terms are [11]:

$$\begin{aligned} T_0[\rho ]= & {} T_{\text {TF}}[\rho ] = \int \frac{3}{10}\left( 3\pi ^2\right) ^{\frac{2}{3}} \rho ^{\frac{5}{3}}(\mathbf {r}) \, \mathrm {d}\mathbf {r}, \end{aligned}$$
(18)
$$\begin{aligned} T_2[\rho ]= & {} \int \frac{1}{72} \frac{\left( \mathbf {\nabla }\rho (\mathbf {r}) \right) ^2}{\rho (\mathbf {r})} \, \mathrm {d}\mathbf {r}, \end{aligned}$$
(19)

and:

$$\begin{aligned} T_4[\rho ]= & {} \frac{1}{540 \left( 3 \pi ^2\right) ^{\frac{2}{3}}} \nonumber \\&\quad \int \rho ^{\frac{1}{3}}(\mathbf {r}) \left[ \left( \frac{\mathbf {\nabla }^2\rho (\mathbf {r})}{\rho (\mathbf {r})} \right) ^2 \!-\!\frac{9}{8}\left( \frac{\mathbf {\nabla }^2\rho (\mathbf {r})}{\rho (\mathbf {r})}\right) \left( \frac{\mathbf {\nabla }\rho (\mathbf {r})}{\rho (\mathbf {r})}\right) ^2 \!+\!\frac{1}{3} \left( \frac{\mathbf {\nabla }\rho (\mathbf {r})}{\rho (\mathbf {r})}\right) ^4 \right] \, \mathrm {d}\mathbf {r}\nonumber \\ \end{aligned}$$
(20)

The first term \(T_0\) is identical to the Thomas–Fermi approximation \(T_{\text {TF}}\) [12, 51], and the second term \(T_2\) equals up to a factor the functional approximation first introduced by von Weizsäcker [52]:

$$\begin{aligned} T_{\text {W}}[\rho ] = \int \frac{1}{8} \frac{\left( \mathbf {\nabla }\rho (\mathbf {r}) \right) ^2}{\rho (\mathbf {r})} \, \mathrm {d}\mathbf {r}. \end{aligned}$$
(21)

Series involving the fourth-order term \(T_4\) are called Laplacian-level functional approximations. Higher-order terms diverge when exponentially decaying electron densities are inserted [11]. Therefore, gradient expansion series including higher-order terms are not suitable for applications on molecular and solid-state systems. While truncated series up to fourth order provide kinetic energies close to \(T_s\) when the corresponding KS electron densities are inserted in the functional approximation, those series do not yield reasonable electron densities from the variational procedure, as those densities do not exhibit proper atomic shell structure [11].

Interestingly, the modulating function \(f_1(\mathbf {r})\) that locally corrects the Thomas–Fermi contribution to the full von Weizsäcker term, such that the exact positive kinetic energy density is represented by this ansatz:

$$\begin{aligned} \tau [\rho ] = f_1(\mathbf {r}) t_{\text {TF}}[\rho ] + t_{\text {W}}[\rho ] \end{aligned}$$
(22)

displays the proper atomic shell structure throughout the whole periodic table. The modulating function \(f_1(\mathbf {r})\) displayed in the above equation is actually the kernel of the electron localization function (ELF) [5, 48]. Moreover, any ansatz for \(\tau (\mathbf {r})\) in terms of the Thomas–Fermi energy density and the von Weizsäcker contribution times a local correction

$$\begin{aligned} \tau [\rho ]= & {} t_{\text {TF}}[\rho ] + f_2(\mathbf {r})t_{\text {W}}[\rho ] \end{aligned}$$
(23)
$$\begin{aligned} \tau [\rho ]= & {} f_3(\mathbf {r}) \left( t_{\text {TF}}[\rho ] + t_{\text {W}}[\rho ] \right) \end{aligned}$$
(24)
$$\begin{aligned} \tau [\rho ]= & {} f_4(\mathbf {r}) t_{\text {TF}}[\rho ] \end{aligned}$$
(25)
$$\begin{aligned} \tau [\rho ]= & {} f_5(\mathbf {r}) t_{\text {W}}[\rho ] \end{aligned}$$
(26)

provides modulating functions \(f_i(\mathbf {r})\), which display proper atomic shell structure [15]. Note that, the shell structure of an atom is a rather specific function. For example it can be shown that for any set of orthonormal 1s and 2s functions being eigenfunctions of the bare Coulomb Hamiltonian, the function \(\tau (\mathbf {r}) / \rho (\mathbf {r})\), which is close to \(f_4(\mathbf {r})\), exhibits one single shell-separator no matter of the eigenfunctions and eigenvalues that enter \(\tau (\mathbf {r})\) and \(\rho (\mathbf {r})\). Therefore, the atomic shell structure can solely be attributed to the Pauli exclusion principle [17]. Given this, modeling the local kinetic energy \(\tau (\mathbf {r})\) via a purely density-based ansatz for ELF or its kernel, cf. Eq. 22, seemed to be a promising ansatz. Indeed, such density-based indicators displaying the atomic shell structure in close relation to ELF exist [28, 53]. The so-called charge sampling functionals \(C_p\) sample the amount of electronic charge within a region of given electron density inhomogeneity \(I_p(\varOmega _i)\):

$$\begin{aligned} I_p(\varOmega _i) = \int _{\varOmega _i} \root p \of {|\rho (\mathbf {r}) - {\bar{\rho }}_i|^p} \, \mathrm {d}\mathbf {r}\end{aligned}$$
(27)

with the averaged electron density within that region:

$$\begin{aligned} {\bar{\rho }}_i = 1/V_i \int _{\varOmega _i} \rho (\mathbf {r}) \, \mathrm {d}\mathbf {r}. \end{aligned}$$
(28)

The inhomogeneity \(I_p\) clearly depends on the decay of the electron density and the region \(\varOmega _i\). Now, imagine such a space-filling, mutually exclusive, compact division of space into so-called microcells [37, 38], that each microcell is described by the same amount of inhomogeneity \(\omega _{I_p}\), and integrate the electron density within those regions. This procedure yields the number of electrons in regions of same electron density inhomogeneity. Those charges, of course, depend on the chosen amount of inhomogeneity \(\omega _{I_p}\). The limes after rescaling (dividing by the proper amount of restriction value \(\omega _{I_p}\)) finally yields a quasi-continuous function revealing the dependence between the number of electrons and the inhomogeneity of the electron density within certain region. The final result are the charge sampling functionals:

$$\begin{aligned} C_p(\mathbf {r}) = \rho (\mathbf {r}) \left[ \frac{2\left( p+1 \right) ^{\frac{1}{p}}}{|\mathbf {\nabla }\rho (\mathbf {r})|}\right] ^{\frac{3p}{\left( 3+p\right) }}, \end{aligned}$$
(29)

which display atomic shell structure [28, 53]. Of course, the inhomogeneity \(I_p\) depends on the measure of p applied to the so-called \(\omega \)-restricted space partitioning (\(\omega \)-RSP). One is free to choose an appropriate measure p that is convenient for a given purpose. Thus, one could search for an optimal p-value such that the charge sampling functional mimics the electron localization function (ELF), which involves the local kinetic energy \(\tau (\mathbf {r})\). Indeed, such an optimal choice is possible for all atomic species within the periodic table [14]. The resulting indicator \(C_p\) with \(p = 0.6\) is the closest density-based representation of ELF within this ansatz. Consequently, \(C_{0.6}\) can be used in order to design a density-based approximation to \(\tau \). While this is possible and provides good agreement of total kinetic energies as well as good agreement between local kinetic energy densities [16], the presented approach fails to provide reasonable electron densities from variational procedure, and thus, confronts with the same issues as the conventional gradient expansion series. It is, thus, desirable to search for procedures that provide control over the functional derivative rather than the functional itself. One such possibility of designing functionals with specific functional derivatives is given here [25]. However, the functional construction of the ansatz reported in this work [25] is still approximate. The bifunctional formalism circumvents this problem and provides a direct path to the functional value by exploiting the scaling behavior of the (otherwise unknown) functional. Before introducing the bifunctional formalism itself, it is useful to be familiar with another approach how to divide the kinetic energy.

3.2 Kinetic energy in terms of bosonic and fermionic contributions

The density-gradient expansion for the non-interacting kinetic energy given in Eq. 17 is not free of mathematical problems concerning the justification of central arguments leading to the general Kirzhnits formalism [35] and, thus, does not provide a convergent series [11].

No matter whether a given object can be expressed as a convergent series or not, it can—for sure—be divided into separate pieces. In the previous section a division:

$$\begin{aligned} T_s[\rho ] = T_{\text {Model}}[\rho ] + T_{\text {Rest}}[\rho ] \end{aligned}$$
(30)

was presented. In case of the gradient expansion series:

$$\begin{aligned} T_{\text {Model}}[\rho ] = T_0[\rho ] + T_2[\rho ] + T_4[\rho ] \end{aligned}$$
(31)

and

$$\begin{aligned} T_{\text {Rest}}[\rho ] = T_s[\rho ] - \left( T_0[\rho ] + T_2[\rho ] + T_4[\rho ] \right) . \end{aligned}$$
(32)

The question remains how to model the remainder \(T_{\text {Rest}}[\rho ]\) of such a decomposition. Any decomposition into some model and a rest is equally valid. In the following a separation with appealing interpretation in terms of a bosonic and fermionic contribution is presented.

Following the idea of March [45], it is possible to divide the total non-interacting kinetic energy \(T_s[\rho ]\) into a bosonic term, the von Weizsäcker part \(T_{\text {W}}[\rho ]\) (with known density functional dependence) [52] and a fermionic part \(T_{\text {P}}[\rho ]\), the so-called Pauli kinetic energy [45]:

$$\begin{aligned} T_s[\rho ] = T_{\text {W}}[\rho ] + T_{\text {P}}[\rho ]. \end{aligned}$$
(33)

Since the Pauli kinetic energy is actually defined as the remainder:

$$\begin{aligned} T_{\text {P}}[\rho ] = T_s[\rho ] - T_{\text {W}}[\rho ], \end{aligned}$$
(34)

it captures—by definition—all necessary contributions in order to provide the full non-interacting kinetic energy. Thus, the Pauli kinetic energy is not of empirical origin, but results from the choice of decomposition for the non-interacting kinetic energy. However, in most cases functional approximations for \(T_{\text {P}}[\rho ]\) are of empirical nature, as there is no formal expansion series for this splitting.

The von Weizsäcker kinetic energy may be regarded as the kinetic energy of a bosonic system in its groundstate having the same density as the actual fermionic system. In a bosonic groundstate all particles occupy the same orbital \(\phi _B(\mathbf {r})\) being proportional to the square root of the density

$$\begin{aligned} \phi _B(\mathbf {r}) = \frac{1}{\sqrt{N}} \sqrt{\rho (\mathbf {r})}. \end{aligned}$$
(35)

Inserting Eq. 35 into Eq. 7 immediately yields:

$$\begin{aligned} \tau (\mathbf {r})= & {} \frac{1}{2} \sum _i^N |\mathbf {\nabla }\frac{1}{\sqrt{N}} \sqrt{\rho (\mathbf {r})}|^2 \nonumber \\= & {} \frac{1}{8} \frac{\left( \mathbf {\nabla }\rho (\mathbf {r})\right) ^2}{\rho (\mathbf {r})} = t_{\text {W}}([\rho ]; \mathbf {r}) \; \; \end{aligned}$$
(36)

the von Weizsäcker kinetic energy. The formal connection between the gradient correction and the kinetic energy of a bosonic groundstate has already been noticed by von Weizsäcker in his original work [52].

Dividing the non-interacting energy into the von Weizsäcker term and the Pauli kinetic energy, cf. Eq. 33 is—by definition—an exact ansatz. Moreover, both terms can be access analytically, \(T_{\text {W}}\) in terms of \(\rho \) and \(T_{\text {P}}\) in terms of KS orbitals, cf. Eq. 34. This allows a direct comparison between an approximate model for the Pauli kinetic energy and the Pauli kinetic energy from the respective KS calculation. As stated before the local kinetic energy is not uniquely defined, which renders a direct comparison between the KS data and the approximate model somewhat arbitrary. Thus, it would be of great advantage to have access to the functional value from a procedure that allows a one-to-one comparison between the approximate ansatz and the respective KS calculation. Such a procedure is presented in the next section.

4 The bifunctional formalism

For a density functional \(F[\rho ]\) which obeys homogeneous scaling behavior:

$$\begin{aligned} F[\rho _{\uplambda }] = \uplambda ^{k} F[\rho ] \end{aligned}$$
(37)

with the homogeneously scaled electron density \(\rho _{\uplambda }(\mathbf {r}) = \uplambda ^3 \rho (\uplambda \mathbf {r})\), where \(\uplambda \) is a parameter, k is the respective scaling constant, and \(\mathbf {r}\) are the three-dimensional coordinates, the functional value can equally be obtained from [42]:

$$\begin{aligned} F[\rho ] = - \frac{1}{k} \int \rho (\mathbf {r}) \, \mathbf {r}\cdot \mathbf {\nabla }v([\rho ]; \mathbf {r}) \, \mathrm {d}\mathbf {r}\end{aligned}$$
(38)

where \(v([\rho ]; \mathbf {r})\) is the functional derivative of F:

$$\begin{aligned} v([\rho ]; \mathbf {r})=\frac{\delta F[\rho ]}{\delta \rho }. \end{aligned}$$
(39)

Note the explicit functional dependence of the functional derivative on the density. Therefore, \(F[\rho ]\) from Eq. (38) is considered to be a density functional. In contrast, \(F[\rho , v]\) is a bifunctional:

$$\begin{aligned} F[\rho , v] = - \frac{1}{k} \int \rho (\mathbf {r}) \, \mathbf {r}\cdot \mathbf {\nabla }v(\mathbf {r}) \, \mathrm {d}\mathbf {r}\end{aligned}$$
(40)

since the density dependence of the potential \(v(\mathbf {r})\) is suppressed, therefore, being a formal functional derivative in this context. While the bifunctional yields the same value as the density functional, for a pointwise correspondence of the functional derivative \(v([\rho ]; \mathbf {r})\) and the formal functional derivative \(v(\mathbf {r})\):

$$\begin{aligned} v([\rho ]; \mathbf {r}) = v(\mathbf {r}) \;\;\; \;\;\; \forall \mathbf {r}, \end{aligned}$$
(41)

the corresponding parent functional \(F[\rho ]\) can only be obtained from Eq. (38). Thus, the bifunctional \(F[\rho , v]\) given by Eq. (40) provides the functional value, but not the functional dependence in terms of the density \(\rho \).

This subtle difference is actually the key issue in the bifunctional formalism. Since the density dependence of the formal functional derivative is suppressed (or simply unknown), the potential can be approximated by models having any density dependence (or no density dependence at all), which seems profitable to model certain physical tasks. For a density functional, there is no such freedom, as the density functional must obey various mathematical constraints like for example proper homogeneous scaling law [41, 42]. This renders the bifunctional approach an exact and flexible formalism able to match results from KS-DFT but from formal functional derivatives.

Note that only the interpretation of the formulas in terms of the bifunctional approach, cf. Eq. 40, is a recent development, while the formulas themselves derived for the corresponding density functionals go back to the prominent work of Mel Levy in 1982 and his application of the Feynman theorem [13] in density functional theory [39]. Explicit expressions can also be found in the work of Levy and Perdew [42], Levy and Ou-Yang [41] as well as in the work of Levy and Ayers [40]. A detailed derivation of Eq. 38 can also be found in the work of Ghosh and Parr [31].

4.1 The von Weizsäcker kinetic energy as a bifunctional

The bifunctional formalism described in the previous section can be applied to any functional that obeys homogeneous density scaling, e.g., the exchange energy as applied here [27]. However, the most prominent applications of the bifunctional formalism lie in the field of orbital-free density functional theory, where the burden is to find reliably working approximate kinetic energy functionals [20, 21, 24]. In case of the von Weizsäcker kinetic energy the bifunctional as well as the corresponding density functional are known exactly, and thus, both formalisms can be compared directly. Additionally, an alternative bifunctional expression yielding the same functional value but from another kernel is presented.

For one and closed-shell two-electron systems the Pauli kinetic energy is zero; consequently, the total kinetic energy is given by the von Weizsäcker term \(T_{\text {W}}\) alone. The von Weizsäcker term can be seen as the kinetic energy of a bosonic groundstate having the same density as the actual fermionic system. In a bosonic groundstate all particles occupy the lowest orbital, which is proportional to the square root of the density. Thus, an analytical formula for the von Weizsäcker kinetic energy can easily be derived, cf. Eq. 36 [45, 52]. Consequently, the corresponding functional derivative is also known analytically in terms of the electron density:

$$\begin{aligned} v_{\text {W}}([\rho ]; \mathbf {r})=\frac{\delta T_{\text {W}}[\rho ]}{\delta \rho } = \frac{1}{8} \frac{\left( \mathbf {\nabla }\rho (\mathbf {r}) \right) ^2}{\rho (\mathbf {r})^2} - \frac{1}{4} \frac{\mathbf {\nabla }^2 \rho (\mathbf {r}) }{\rho (\mathbf {r})}\; \; . \end{aligned}$$
(42)

In the bifunctional formalism, introduced in Sect. 4, the von Weizsäcker kinetic energy is obtained from:

$$\begin{aligned} T_{\text {W}}[\rho , v_{\text {W}}] = - \frac{1}{2} \int \rho (\mathbf {r}) \, \mathbf {r}\cdot \mathbf {\nabla }v_{\text {W}}(\mathbf {r}) \, \mathrm {d}\mathbf {r}\end{aligned}$$
(43)

since the non-interacting kinetic energy (as well as its components) scale with a factor of two for homogeneous density scaling [42].

Another, but equivalent bifunctional expression can be obtained by combining Eqs. (7) and (8) from reference [40], where the non-interacting kinetic energy is expressed with the help of the Kohn–Sham potential \(v_s(\mathbf {r})\) (defined by Eq. (2) in reference [40]):

$$\begin{aligned} T_{s}[\rho , v_s] = - \frac{1}{2} \int v_s(\mathbf {r}) \,\left[ 3 \rho (\mathbf {r}) + \mathbf {r}\cdot \mathbf {\nabla }\rho (\mathbf {r}) \right] \, \mathrm {d}\mathbf {r}. \end{aligned}$$
(44)

Depending on the nature of \(v_s\) the above equation can be considered a bifunctional (in case of unknown density dependence of \(v_s\)) or a density functional expression (for \(v_s\) with analytically known density dependence). Observe that for one and closed-shell two electron systems:

$$\begin{aligned} v_s = - v_{\text {W}}([\rho ]; \mathbf {r}) + \epsilon \; \; , \end{aligned}$$
(45)

where \(\epsilon \) is the eigenvalue of the occupied eigenfunction. This, finally, yields another bifunctional expression for the von Weizsäcker kinetic energy:

$$\begin{aligned} T_{\text {W}}[\rho , v_{\text {W}}] = \frac{1}{2} \int \left[ v_{\text {W}}([\rho ]; \mathbf {r}) - \epsilon \right] \,\left[ 3 \rho (\mathbf {r}) + \mathbf {r}\cdot \mathbf {\nabla }\rho (\mathbf {r}) \right] \, \mathrm {d}\mathbf {r}. \end{aligned}$$
(46)

Although both expressions for the von Weizsäcker kinetic energy, cf. Eqs. (43) and (46), look quite different, they must represent an identity, since both were derived from the virial theorem [39, 40, 42] and the von Weizsäcker potential \(v_{\text {W}}([\rho ]; \mathbf {r})\) is known analytically in terms of the electron density. The integral kernels of those bifunctional expressions may, of course, differ from one another, as any function that integrates to zero may be added to a given integral kernel without changing the integral itself. In the community of theoretical chemists and physicists, this aspect is especially known in connection with the ambiguity of the kinetic energy (although it applies to other energy densities as well). While all kinetic energy densities yield the same expectation value from the wavefunction \(\varPsi \) when integrated over all space, their local representations (when integrated over all particle coordinates but one) differ and there is no a priori choice for a particular expression for a joint distribution of position and momentum and hence, for a specific local kinetic energy [9, 10].

In case of the kinetic energy, a given kinetic energy density corresponds to a specific choice of operators (or joint distribution of position and momentum), see references [9, 10] for more details. How does this aspect relate to the bifunctional formalism—especially to the two expressions given in Eqs. (43) and (46), in which case the integral kernels also just differ by a fraction of the density Laplacian?

While a general proof is not part of this work, the issue can be illustrated by a simple example. Consider the hydrogen atom with nuclear charge \(Z = 1\), having a only a single electron, in which case the Schrödinger equation [50] can be solved exactly:

$$\begin{aligned} {\hat{H}} \phi _H(r) = \epsilon \phi _H(r) \end{aligned}$$
(47)

with the Hamilton operator \({\hat{H}}\) (in atomic units) [50]:

$$\begin{aligned} {\hat{H}} = -\frac{1}{2} \mathbf {\nabla }^2 - \frac{Z}{r} \end{aligned}$$
(48)

The lowest hydrogen eigenvalue \(\epsilon \) and eigenfunction \(\phi _H(r)\) are:

$$\begin{aligned} \epsilon= & {} -\frac{1}{2} \alpha ^2, \end{aligned}$$
(49)
$$\begin{aligned} \phi _H(r)= & {} N_0 e^{- \alpha r}, \end{aligned}$$
(50)

where \(\alpha \) is a parameter (that equals the nuclear charge \(Z = 1\) for the minimizing eigenfunction, but will be kept as a general parameter here) and \(N_0\) is a normalization constant such that the spherically electron density \(\rho _H(r)\):

$$\begin{aligned} \rho _H(r)= & {} \phi _H(r)^2 = N_0^2 e^{- 2\alpha r}, \end{aligned}$$
(51)
$$\begin{aligned} 1= & {} \int \rho _H(r) \, \mathrm {d}\mathbf {r}, \end{aligned}$$
(52)

integrates to the number of particles (being one here).

The density gradient in the direction of r is:

$$\begin{aligned} \mathbf {\nabla }_r\rho _H(r) = -2\alpha \rho _H(r), \end{aligned}$$
(53)

the density Laplacian is given by:

$$\begin{aligned} \mathbf {\nabla }^2 \rho _H(r) = \left[ 4\alpha ^2 -\frac{4\alpha }{r} \right] \rho _H(r), \end{aligned}$$
(54)

and the von Weizsäcker potential reduces to:

$$\begin{aligned} v_{\text {W}}([\rho _H]; r) = -\frac{1}{2} \alpha ^2 + \frac{\alpha }{r}\; \; . \end{aligned}$$
(55)

For the hydrogen atom the von Weizsäcker kinetic energy as given by the density functional expression from Eq. (21), is:

$$\begin{aligned} T_{\text {W}}[\rho ] = \int \frac{1}{8} \frac{\left[ -2\alpha \rho _H(r)\right] ^2}{\rho _H(r)} \, \mathrm {d}\mathbf {r}= \frac{1}{2} \alpha ^2 \int \rho _H(r) \, \mathrm {d}\mathbf {r}= \frac{1}{2} \alpha ^2 \; \; . \end{aligned}$$
(56)

In case of the density functional expression the integral kernel \(t_{\text {W}}^{df}(r)\):

$$\begin{aligned} t_{\text {W}}^{df}(r) = \frac{1}{2} \alpha ^2 \rho _H(r) \; \; \end{aligned}$$
(57)

is positive everywhere and can be associated with the positive kinetic energy density \(\tau \), as given in Eq.( 7).

The bifunctional expression as given by Eq. 43 yields the same integral:

$$\begin{aligned} T_{\text {W}}[\rho , v_{\text {W}}]= & {} - \frac{1}{2} \int \rho _H(r) \left[ -\frac{\alpha }{r} \right] \, \mathrm {d}\mathbf {r}= \frac{1}{2} \alpha ^2 \nonumber \\= & {} \int \frac{\alpha }{2 r} \rho _H(r) \, \mathrm {d}\mathbf {r}+ \frac{1}{8} \int \mathbf {\nabla }^2 \rho _H(r) \, \mathrm {d}\mathbf {r}, \end{aligned}$$
(58)

what is easily noticed by adding a fraction of the density Laplacian to the integral kernel. The integral kernel of the bifunctional, given in Eq. (43) \(t_{\text {W}}^{bi1}(r)\):

$$\begin{aligned} t_{\text {W}}^{bi1}(r) = \frac{\alpha }{2r} \rho _H(r) \end{aligned}$$
(59)

is positive in case that the nucleus is located at the origin of the coordinate system. However, the integral kernel does not directly correspond to the positive kinetic energy density and does, of course, depend on the choice of the coordinate system, while the integral itself does not.

Equally, the bifunctional expression for the von Weizsäcker kinetic energy as given by Eq. 46:

$$\begin{aligned} T_{\text {W}}[\rho , v_{\text {W}}]= & {} \frac{1}{2} \int \left[ - \frac{1}{2} \alpha ^2 + \frac{\alpha }{r} + \frac{1}{2} \alpha ^2 \right] \left[ 3\rho _H(r) -2\alpha r \rho _H(r)\right] \, \mathrm {d}\mathbf {r}= \frac{1}{2} \alpha ^2 \nonumber \\= & {} \int \left[ \frac{3 \alpha }{2r} - 2 \alpha ^2 \right] \rho _H(r) \, \mathrm {d}\mathbf {r}+ \frac{3}{8} \int \mathbf {\nabla }^2 \rho _H(r) \, \mathrm {d}\mathbf {r}\end{aligned}$$
(60)

yields the same integral value \( T_{\text {W}} = 1/2 \alpha ^2\), but from another kernel:

$$\begin{aligned} t_{\text {W}}^{bi2}(r) = \left[ \frac{3 \alpha }{2r} - 2 \alpha ^2 \right] \rho _H(r). \end{aligned}$$
(61)

In the present example, both bifunctional expressions are evaluated from integral kernels that differ only by a given amount of the density Laplacian. Since the density Laplacian integrates to zero, both kernels provide the same integral value. Here, those observations are based on a simple model, and a general proof for \(T_{\text {W}}\) (and possibly \(T_s\)) is desirable. Another question relates to the choice of origin. As easily noticed by the reader, integral kernels of the proposed bifunctional expressions are origin dependent. However, the integrals themselves are not. Thus, the ambiguity of the kinetic energy density is transferred to the integral kernel of the bifunctional formalism, while the formal functional derivative allows for a one-to-one-comparison between analytical expression and approximate models. While for the von Weizsäcker kinetic energy no such approximations are necessary (since the functional is known analytically in terms of the electron density), this procedure is of great importance when designing approximations for the Pauli kinetic energy.

4.2 The Pauli kinetic energy as a bifunctional

The Pauli kinetic energy, cf. Eq. 34, remains the only unknown part of the non-interacting kinetic energy, from which a large part, the kinetic energy of a bosonic system in its groundstate with the density of the actual fermionic system, namely the von Weizsäcker kinetic energy, has been subtracted. Consequently, the Pauli kinetic energy captures all many-body effects of the kinetic energy that are due to the fermionic nature of the electrons. The Pauli kinetic energy is known exactly in terms of the KS orbitals, cf. Eq. 34, and so is its formal functional derivative, the Pauli potential [26, 41]:

$$\begin{aligned} v_{\text {P}}(\mathbf {r}) = \frac{\delta T_{\text {P}}}{\delta \rho } = \frac{t_{\text {P}}(\mathbf {r})}{\rho (\mathbf {r})} + \sum _i \left( \epsilon _M - \epsilon _i \right) \frac{|\phi _i(\mathbf {r})|^2}{\rho (\mathbf {r})} \end{aligned}$$
(62)

with \(\epsilon _M\) being the highest occupied eigenvalue and \(t_{\text {P}}\) being the Pauli kinetic energy density:

$$\begin{aligned} t_{\text {P}}(\mathbf {r}) = \frac{1}{2} \sum _i |\nabla \phi _i(\mathbf {r})|^2 - t_{\text {W}}(\mathbf {r}). \end{aligned}$$
(63)

In the spirit of the local effective Hamiltonian from the KS procedure, the Pauli potential may be seen as a local effective multiplicative potential that acts on the fictitious bosonic system in order to enforce the minimizing density to be the same as for the real fermionic system and, thus, providing an eigenvalue equation for the square root of the electron density [43, 45] (being proportional to the minimizing orbital of the bosonic system):

$$\begin{aligned} -\frac{1}{2} \mathbf {\nabla }^2 \sqrt{\rho (\mathbf {r})} + \left[ v_{\text {P}}(\mathbf {r}) + h_{\text {eff}}(\mathbf {r})\right] \sqrt{\rho (\mathbf {r})} = \epsilon _M \sqrt{\rho (\mathbf {r})}. \end{aligned}$$
(64)

As such the Pauli potential is a rigorously defined quantity (for an auxiliary system of bosonic quasiparticles), that can be expressed analytically via the KS eigenfunctions and eigenvalues, cf. Eq. 62. In contrast to the kinetic energy density, the Pauli potential is (up to a constant [41]) uniquely defined and, thus, can be compared pointwise in space. While for some model cases the Pauli potential can be expressed analytically [45], in general \(v_{\text {P}}(\mathbf {r})\) is unknown in terms of the electron density alone. Therefore, sufficiently accurate approximations have to be found.

Once a sufficiently accurate approximate Pauli potential \({\tilde{v}}_{\text {P}}(\mathbf {r})\) is generated, the approximative Pauli kinetic energy \({\tilde{T}}_{\text {P}}\) is evaluated via the bifunctional formalism:

$$\begin{aligned} {\tilde{T}}_{\text {P}}[\rho , {\tilde{v}}_{\text {P}}] = - \frac{1}{2} \int \rho (\mathbf {r}) \, \mathbf {r}\cdot \mathbf {\nabla }{\tilde{v}}_{\text {P}}(\mathbf {r}) \, \mathrm {d}\mathbf {r}. \end{aligned}$$
(65)

Individual physical tasks demand for individual specific properties of the Pauli potential. In principle, it is always possible to reach the exact KS limit by inserting appropriate functions into Eq. 62. This, however, would result in some sort of complicated KS procedure, since the Euler equation is nonlinear with respect to linear expansion of orbitals in terms of basis functions (like this is usually done in the conventional KS procedure). Still an extension toward the KS system is possible within this ansatz as \(v_{\text {P}}(\mathbf {r})\) is known analytically in terms of the KS eigenfunctions. In practice, however, one would like to avoid the necessity of calculating KS orbitals. Therefore, sufficiently accurate approximation to \(v_{\text {P}}(\mathbf {r})\) is needed that still capture the relevant physical aspects of the problem. In the following approximate Pauli potentials for three different physical tasks are presented.

4.2.1 Atomic systems: preserving the atomic shell structure

While \(v_{\text {P}}(\mathbf {r})\) obtained from a previous KS calculation via Eq. 62 clearly yields the KS density from Eq. 64 and the corresponding Pauli kinetic energy from Eq. 65, it is desirable to reveal the connection between the atomic shell structure and the Pauli potential from an orbital-free ansatz. It is indeed possible to design approximate Pauli potentials—in form of formal functional derivatives \({\tilde{v}}_{\text {P}}(\mathbf {r})\) as well as in the form of \({\tilde{v}}_{\text {P}}([\rho (\mathbf {r})]; \mathbf {r})\)—that provide properly structured electron densities from variational procedure via Eq. 64 [18]. In both cases \({\tilde{T}}_{\text {P}}\) has to be accessed via the bifunctional formalism, cf. Eq. 65, because those approximative Pauli potentials violate certain scaling rules and, thus, cannot be regarded as true functional derivatives [18]. The latter approximations of the Pauli potential require careful parameterization and previous knowledge of the atomic shell structure. Note that, the atomic shell structure and respective radii can indeed be approximatively expressed analytically in terms of the nuclear charge Z [19] and thus, such a parameterization is possible for all atoms in the periodic table. While the above-mentioned approach is empiric, it shows that a purely density-based method within density functional theory preserving the atomic shell structure is possible.

Lately, another—less empiric—orbital-free approach preserving the atomic shell structure was presented [22]. It attempts to approximate the KS eigenfunctions and eigenvalues via node-less Slater functions and the one-electron model (which is exact for the H atom), respectively. Node-less Slater functions \(\chi _i\) are given by: [49, 54]

$$\begin{aligned} \chi _i(\mathbf {r}) = N_0 r^{a_i} e^{-\alpha _i r}\; \; \end{aligned}$$
(66)

with:

$$\begin{aligned} N_0 = \sqrt{ \frac{(2\alpha _i)^{2a_i+3}}{4\pi (2a_i+2)! } } , \end{aligned}$$
(67)

\( a_i =n^* -1 \) and \( \alpha _i = {Z - s} / {n^*}\), whereby Z is the nuclear charge, \(n^*\) is an effective quantum number, and s is the so-called shielding constant [49]. Furthermore the KS eigenvalues are approximated by \(\eta _i\):

$$\begin{aligned} \eta _i = -\frac{1}{2} \alpha _i^2 . \end{aligned}$$
(68)

Replacing \(\epsilon _i\) by \(\eta _i\) and \(\phi _i\) by \(\chi _i\) in Eq. 62, respectively, yields the desired approximation for the Pauli potential. The Pauli kinetic energy is evaluated from the bifunctional formalism, cf. Eq. 65, and the electron density is given by:

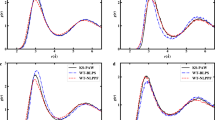
$$\begin{aligned} \rho (\mathbf {r}) = \sum _i n_i \chi _i^2(\mathbf {r}) . \end{aligned}$$
(69)

with \(n_i\) being the occupation numbers for the respective atomic shells. The above approach allows for a minimization of the total energy with respect to the exponents \(\alpha _i\). Those approximate functions and related energy states allow to construct a model for the Pauli potential that is able to respond to the actual density changes—like this is true for the KS Pauli potential. This model is still considered to be an orbital-free method, since no eigenvalue equation, cf. Eq. 4, is ever solved. The model works fine for light atoms (from hydrogen till carbon) and allows to access a bosonic-like as well as a fermionic-like energy minimum separately from variational procedure [22]. Exemplarily, results are shown for the carbon atom. Figure 1b depicts the energy landscape as a functional of the two exponents for the core \(\alpha _{\text {1s}}\) and valence region \(\alpha _{\text {2s}}\). As can be seen from the data, the energy landscape exhibits two separate minima, one deep energy minimum with similar exponents (\(\alpha _{\text {1s}} \approx \alpha _{\text {2s}}\)), this minimum is called bosonic-like energy minimum, and a second shallow energy minimum in the region where the core exponent is much higher than the valence exponent (\(\alpha _{\text {1s}} > \alpha _{\text {2s}}\)), which is considered to be a fermion-like energy minimum. The respective radial densities are depicted in Fig. 1a, c, respectively. The radial electron density from the fermionic minimum displays proper atomic shell structure, whereas one maximum is found for the bosonic-like solution.

Fig. 1
figure 1

Radial electron densities and energy landscape for the carbon atom. a Minimizing radial density for the fermionic-like minimum. Core and valence electron densities, shown in blue and green, respectively, are clearly separated. Electronic states are well separated and ordered (\(\alpha _{\text {1s}} > \alpha _{\text {2s}}\)). b Total energy as a function of the two exponents of the first (\(\alpha _{\text {1s}}\)) and second atomic shell (\(\alpha _{\text {2s}}\)). Ten equally spaced isolines are drawn from -35 hartree to -34 hartree in order to reveal the minimum in the fermionic-like region. c Minimizing radial density for the bosonic-like minimum. Both functionals occupy the same region. Electronic states are of similar magnitude (\(\alpha _{\text {1s}} \approx \alpha _{\text {2s}}\))

Full size image

4.2.2 Molecular systems: accurate modeling of chemical bonding

Obtaining properly structured electron densities from an OF-DFT ansatz is an important issue in the field of physics, e.g., for the simulation of processes where electrons change their state with time. For most of the chemical processes, however, like for example molecular bonding, changes of the inner atomic shell structure are not expected. For this reason, the concept of core-valence-separation is employed successfully for questions that handle problems of molecular bonding processes. The core-valence-separation does not alter due to different chemical environments and, thus, can be attributed to the atom itself. Consequently, a simple superposition of atomic Pauli potentials may serve as a first approximation for the molecular Pauli potential. Indeed this simple ansatz, the so-called atomic fragment approach, yields a qualitatively correct description of chemical bonding [20]. Later it was found that equilibrium bond lengths depend on the electronic state of the employed atomic fragments. Within the molecular environment the atomic fragment resembles more an artificial closed-shell atom that its atomic groundstate. Consequently, molecular Pauli potentials build from the superposition of artificial closed-shell atomic fragments perform better with respect to the equilibrium bond length compared to the initial approach using groundstate atoms [21].

The reason why the atomic fragment approach works so well for molecular systems lies in the form of the Pauli potential. Within an atom, the Pauli potential exhibits its highest values close to the nucleus. At each shell boundary the Pauli potential displays a sharp peak, which is responsible for the change of sign of the curvature of the radial electron density [18]. After the last boundary (the core-valence-separation) the Pauli potential falls off rapidly with \(r^{-2}\). Thus, in the valence region itself the Pauli potential is marginal. During the process of molecular bonding atomic fragments tend to overlap only with their valence regions. For this reason the atomic superposition provides a good approximation to the molecular Pauli potential in most cases.

However, in cases where the number of shared electrons exceeds a certain amount, antibonding orbitals are populated. In a certain sense, this can be seen as build-up of a new shell since the penultimate shell is already full. The most prominent case of such an example is the Neon dimer. The Neon atom has already a fully filled valence shell. It electronic configuration is Ne:1s\(^2\)2s\(^8\) with two electrons in the core and eight electrons in the valence region. Adding further electrons would demand for the creation of the third atomic shell. Thus, when two Ne atoms approach, this process must be visible in the pattern of the molecular Pauli potential. Indeed, the build-up of such a shell border in between the atoms is observed for the Neon dimer. The molecular Pauli potential evaluated from KS orbitals for the Ne dimer at equilibrium distance is depicted in Fig. 2a. The prominent regions of high values, shown in white, are circled around the nuclei and correspond to the core-valence-separation. Those signatures are well captured by the atomic fragment ansatz depicted in Fig. 2b. In contrast, the shallow maximum in between the atoms, indicating the shell boundary due to the filling of antibonding states, is not captured by the simple superposition.

It has been shown, lately, that even those signatures, that arise during the molecular formation, can approximately be modeled by purely density-based ansatzes, see Fig. 2c. In the present case this is achieved by adding a deformation potential that accounts for the constructive and destructive electron sharing in the valence region via a sort of electronic two-level system build from the constructive (plus sign) or the destructive (minus sign) combination of the individual atomic density contributions:

$$\begin{aligned} \varPhi _{\pm }(\mathbf {r}) = \frac{1}{\sqrt{2(1 \pm S)}} \left( \varPhi _A(\mathbf {r}) \pm \varPhi _B(\mathbf {r}) \right) \end{aligned}$$
(70)

with the help of their respective atomic shape functions [2]:

$$\begin{aligned} \varPhi _A(\mathbf {r}) = \sqrt{\frac{\rho _A(\mathbf {r})}{N_A}}, \end{aligned}$$
(71)

whereby \(N_A\) and \(\rho _A(\mathbf {r})\) are the number of electrons and the electron density of atom A, respectively. This procedure is similar to the construction of molecular orbitals. However, no eigenvalue equation is ever solved and thus, the model is considered to be an OF-DFT approach. Here, as in the case of the atomic approach that preserves the shell structure, the aim is to incorporate those aspects of the orbital picture that are necessary for handling the actual physical problem, not to reproduce the orbitals themselves, although this is in principle possible and thus, allows for a systematic interpolation between the simplest fragment ansatz and the KS data.

Fig. 2
figure 2

Pauli potentials for the Neon dimer. a obtained from KS orbitals (computed with ADF [1] using LDA Xonly and the QZ4P basis set), b atomic fragment ansatz (fragments computed with ADF [1] using LDA Xonly and the QZ4P basis set), c: atomic fragment ansatz plus the deformation potential (for details see references [24])

Full size image

4.2.3 Extended systems: the pathway beyond translational symmetry

Besides molecules, extended systems are in the focus of chemists, physicists, and material engineers. Nowadays, solid-state systems are usually described by bandstructure calculations and related concepts. The concept of bandstructures allows to describe the whole extended material via a small region, the so-called unit cell, that is the smallest unit obeying translational symmetry in space. The so-called Bloch theorem allows to significantly reduce the computational effort by a multiplicative ansatz of the one-particle eigenfunctions into a part that accounts for the symmetry in space and a part that describes the respective eigenfunction within the unit cell. This leads to a set of symmetry-dependent (usually labeled with k) eigenvalue equations, and their solution is the well-known bandstructure. This procedure allows to handle the whole extended system by the help of its unit cell—if and only if the extended system obeys translational symmetry. Therefore, defects or amorphous systems cannot be described by this ansatz.

In principle the extended system can be treated like a molecule. It, just, has an incredible huge number of one-electron eigenfunctions to be computed within the KS approach. Within an orbital-free approach, however, the whole procedure scales with the physical system size, the volume—and not with the number of electrons. Moreover, a purely density-based formulation of quantum mechanics would allow for a purely local treatment, which could be handled in real space only. There would be no requirement for the Bloch theorem—since no one-particle eigenfunctions have to be computed. Consequently, there is no requirement for obeying translational symmetry. Therefore, all condensed matter (amorphous and crystalline) could be handled by the same ansatz. The key point for such a development is actually a correct treatment of the Pauli potential within the bifunctional formalism. The key issue is, thus, to develop sufficiently accurate models for the Pauli potentials for extended systems.

Exemplarily, such an ansatz is presented for aluminum. Aluminum is a prototype of a metal, its structure is periodic, and it crystallizes in face-centered cubic (fcc) structure-type. The orbital-based KS Pauli potential (computed using FHI-aims [6], the PBE functional [46], and a tight basis set) in the xy plane of an 8*2*1 supercell for conventional fcc-Al is depicted in Fig. 3a. As can be seen from the data, the Pauli potential of extended aluminum exhibits sharp peaks at the atomic nuclei, indicating the core region, and falls off rapidly in a sort of step-like structure. Note that, as in the case of molecules the Pauli potential is marginal in the region in between the atoms. Thus, the atomic fragment approach may serve as a reasonable approximation to the Pauli potential of the extended system. The Pauli potential evaluated as simple superposition of artificial closed-shell Al atoms (computed using the ADF program [1], using LDA-Xonly [36] and the QZ4P basis set) is depicted in Fig. 3b. Indeed, by comparing the orbital-based KS Pauli potential and the fragment model, the proposed ansatz seems to provide a reasonable model.

Fig. 3
figure 3

Pauli potentials for an 8*2*1 supercell of conventional fcc aluminum (\(a~=~7.6534\) bohr) in the xy plane (z = 0 bohr). a Obtained from KS orbitals, b atomic fragment ansatz

Full size image

5 Discussion

5.1 Advantages of the formalism

While the general aim of this work is to promote the field of orbital-free density functional theory, it specifically addresses two separate topics. The first issue is the bifunctional formalism itself, which allows to access the value of a functional while keeping its functional dependence unrevealed. The bifunctional formalism is an exact reformulation of the density functional formalism and can be applied to any functional that obeys homogeneous scaling. This formalism is the key concept that allows to address the problem of functional design from a completely different viewpoint. In the bifunctional formalism the potential being the formal functional derivative is regarded as being independent from the electron density (and thus being a formal functional derivative). This is in contrast to other approaches in functional design, which—based on the one-to-one correspondence [33]—usually expressed the functional derivative in terms of the electron density. Note that, the bifunctional formalism does not conflict with the one-to-one correspondence. It simply resigns on the possibility of an analytical expression (in terms of a sufficiently simple formula). The approach allows to address the problem of functional design via their respective formal functional derivatives, the potentials. Unlike, kinetic energy densities, those potentials are (up to a constant [41]) uniquely defined. This aspect substantially facilitates functional design, as orbital-based potentials and their respective approximate models can be compared pointwise in space. This, actually, is the major advantage of the bifunctional formalism compared to traditional functional approximations within the field of OF-DFT. However, the new formalism is not free of additional mathematical subtleties. A list of open questions is, therefore, compiled in the next section.

The second part of this work deals with the practical approximation of the Pauli potential. While the numerically good results of those approximations, hopefully, stimulate further development in this direction, those approximations must be distinguished from the formalism itself. The bifunctional formalism is an exact reformulation for density functionals obeying homogeneous scaling law [42]. The concept of dividing the non-interacting kinetic energy into a bosonic and a fermionic contribution is—by definition—also exact, since the Pauli kinetic energy is defined as the remainder. Up to here, the procedure can be applied to any quantum mechanical task and for some model cases even analytical expressions can be found for the Pauli potential [45]. However, quantum mechanical calculations that treat problems within chemistry and material science require approximations for the Pauli potential for three dimensional Coulomb systems in order to handle atoms, molecules, and solid-state materials. At present there is still no systematic analytical approach to the Pauli potential of such systems. However, sufficiently accurate models (based on empirical reasoning) have been proposed, that are able to preserve the atomic shell structure, correctly predict chemical bonding, and provide numerically reasonable models for the Pauli potentials in extended systems.

5.2 Open questions

The bifunctional formalism, introduced in Sect. 4, allows to obtain the functional value (for a homogeneously scaling functional) with the help of the minimizing electron density and the formal functional derivative, the potential, while keeping the functional dependence of the parent functional unrevealed since the functional dependence of the potential is suppressed (or simply unknown). This formalism allows to address the problem of functional design via their respective formal functional derivatives, instead of the functionals themselves, an aspect that has been shown to be quite useful for physical applications as it provides the possibility of directly approximating those potentials, and thus, a better control of the latter. Additionally, in contrast to the functionals themselves where any function integrating to zero may be added to the integral kernel, potentials are (up to a constant [41]) unambiguously defined and thus, may be compared pointwise. The latter point is of extreme importance for practical functional design. The advantage, here, is that the approximate potentials may be directly compared and adjusted to their KS counterparts.

As illustrated in the previous section, bifunctionals are equivalent to density functionals when the functional dependence is known analytically. Moreover, since the bifunctional expression holds for any trial density and its functional derivative [42] (not just the groundstate density), direct minimization of the bifunctional expression is possible. Consequently, a direct minimization of the total energy including some energy terms originating from the bifunctional expression leads to the same results as when solving the Euler equation directly (as it is for density functionals). However, does this remain true for bifunctionals involving approximate potentials? At this stage it has to be distinguished between different scenarios.

  1. 1.

    The potential corresponds pointwise to the true functional derivative at the solution point (the minimizing KS density), cf. Eq. 41. This for example would be the case when the formal functional derivative is obtained numerically by inversion of the KS equations. In this case solving the Euler equation directly will for sure yield the same minimizing density as it would be obtained from the KS procedure, since the potentials numerically correspond to each other. However, in case that this numerical potential is kept fixed and inserted into the bifunctional expression with subsequent minimization of the total energy, is it guaranteed that the optimization procedure will yield the same minimizing density? The question, here, arises because the numerical potential for sure corresponds to the functional derivative of the final minimizing electron density. However, this numerical potential certainly does not correspond to the functional derivative of any prior trial density. Thus, is it guaranteed that the minimizing point will be reached via direct optimization of the bifunctional?

  2. 2.

    The potential is a reasonably accurate approximation to the true functional derivative at the solution point. This will be the most prominent case, where a suitable model for the potential is proposed and its performance tested. Since the potential is approximate, it will not yield the same minimizing density as a comparable KS procedure. To what extend do the final electron densities differ from each other when determined via the Euler equation? This is equivalent to the question to what extent a given functional derivative influences the minimizing electron density. However, the final solution may also be obtained by minimization of the total energy, which involves the bifunctional expression. The approximate potential does not correspond to the minimizing KS density, but to the electron density obtained by directly solving the Euler equation (with that approximate potential). In this case, is it guaranteed that a direct optimization of the total energy involving the bifunctional expression will yield the same density?

  3. 3.

    Regardless of whether the potential corresponds to the true KS functional derivative or to some approximation to it, the basis set representation or equally the density representation on grid will certainly influence the results. In other words to what extent does a finite basis set representation influence the final electron densities obtained from the Euler equation or by minimizing the total energy?

Recent applications show that meaningful results can be obtained via both routes: either by direct minimization of the total energy or by solving the Euler equation directly. Both approaches yield bound molecular systems when reasonably accurate potential approximations are employed [21, 23, 24].

6 Conclusion

The bifunctional approach introduced in this work presents an alternative to the conventional density functional formalism. In contrast to density functional theory, where (due to the one-to-one correspondence proved by Hohenberg and Kohn) the energy is regarded as density functional and, thus, depends on one single variable, namely the electron density, the bifunctional approach formally deals with two separate variables, which are the electron density and the potential, in this context being a formal functional derivative. As in density functional theory, the functional value of a homogeneously scaling functional can be obtained as a spatial integral over a kernel function that involves the electron density and the functional derivative (multiplied with a factor that depends on the actual scaling of the functional). As such the functional value is determined as a spatial integral with the help of the functional derivative. In case that the functional dependence of the derivative in terms of the electron density is known analytically, the respective expression is treated as a density functional and belongs to its analytically given parent functional (from which equally the functional value can be obtained). However, in case of a formal functional derivative the functional value can only be obtained from the integral kernel originating from the scaling law. The parent functional remains unrevealed as the functional dependence of the formal functional derivative is suppressed (or simply unknown). This offers the pathway to design functional approximations based on their formal derivatives. Unlike the functionals constructed from the respective energy densities, where any function integrating to zero may be added to the initial kernel, potentials are up to a constant uniquely defined, as they determine the minimizing electron density via the Euler equation and, thus, may be compared pointwise. The bifunctional approach thus offers a more flexible route in functional design, while still being able to exactly match the results from density functional theory for a pointwise correspondence of the formal and true functional derivatives.

In case of analytically known density functionals, minimizing the total energy or solving the Euler equation yields the same results, and so does the energy optimization involving the bifunctional. In case of approximate potentials, however, this issue is still unresolved and may be worth further mathematical investigations.