1 Introduction

Metric graphs or quantum graphs are metric spaces constituted of intervals which are glued together at their endpoints according to the structure a combinatorial graph. They can be understood as one possible generalization of intervals, and one can see them as objects between one- and higher-dimensional domains. One can define a self-adjoint Laplace operator (or Laplacian), which operates edgewise as the second derivative on those square summable functions that satisfy prescribed vertex conditions. In this note, we focus on standard, Dirichlet and \(\delta \)-coupling conditions. The Laplacian can have some surprising features such as eigenfunctions vanishing on some edges – a violation of the unique continuation principle and a metric-graph specific phenomenon which never happens in connected domains in any dimension, see also [21] for more insights into this phenomenon such as a classification of the minimal supports of these eigenfunctions.

One motivation for this article arises from the question whether the \(\limsup \nu _n/n\), where \(\nu _n\) denotes the number of so-called nodal domains of the n-th eigenfunction, always behaves as in the one-dimensional case, that is \(\limsup \nu _n/n = 1\). In other words, we ask whether the topological complexity of metric graphs alone is indeed unable to warp the nodal domain asymptotics in such a way that they differ from the one-dimensional case and exhibit higher dimensional features. This has been proved only under technical assumptions so far. Our first result, Theorem 1 proves that this is indeed universally true on tree graphs with standard conditions at all vertices, thus partly settling a conjecture asked in [14]. Theorem 2 generalizes this to all connected graphs with at least one Dirichlet vertex. Theorems 3 and 4 show that these results are robust when standard conditions are replaced by \(\delta \)-coupling conditions and when an edgewise constant potential is added to the Laplacian. Indeed, Theorems 1 to 4 prove something stronger, namely the existence of an infinite sequence of so-called generic eigenvalues. These are simple eigenvalues such that the corresponding normalized eigenfunctions are nonzero on all non-Dirichlet vertices. The term generic arises from the fact that for any given combinatorial graph the set of edge lengths that lead to an infinite sequence of generic eigenvalues of the corresponding metric graph is a residual set – with the notable exception of the cycle graph [12], see also Example 6 below. Therefore, in the class of metric graphs we consider in this note, we show that generic eigenvalues are even a universal phenomenon. There are no exceptions.

Our technical novelty is a new expression for a secular function, that is an analytic function the positive zeros of which are in one-to-one correspondence with the spectrum of the Laplacian. Our secular function differs from usual expressions which are constructed as \(\det ({\text {Id}} - U(\omega ))\) for a unitary matrix U. The latter function boasts the advantage that one can incorporate all possible self-adjoint boundary conditions in the theory and that it is known that the order of its (positive) zeros coincides with the multiplicity of the eigenvalue. Our secular function has the advantage that it is a priori real-valued and that we can explicitly understand the effects of some graph operations on it. Some topological properties of the graph are also directly observable from the formalism, see Proposition 9.

We introduce notation and main results in Sect. 2. The secular function is introduced in Sect. 3 where also Theorem 1 is proved. Sections 4, 5.1, and 5.2 contain the proofs of Theorems 2, 3, and 4.

2 Preliminaries and main results

Let \({\mathcal {G}}\) be a compact and connected metric graph, that is a finite, connected combinatorial graph \({\mathsf {G}}\) with edge set \({\mathsf {E}}={\mathsf {E}}_{\mathcal {G}}\) and vertex set \({\mathsf {V}}={\mathsf {V}}_{\mathcal {G}}\) where each edge \({\mathsf {e}}\) is identified with an interval \([0,\ell _{\mathsf {e}}]\) of finite length \(\ell _{\mathsf {e}}\in (0,\infty )\). For a rigorous definition of metric graphs as metric measure spaces see also [17]. We write \({\mathcal {G}}=({\mathsf {G}},\ell )\) where \(\ell = (\ell _{\mathsf {e}})_{{\mathsf {e}}\in {\mathsf {E}}}\in {\mathbb {R}}^{|{\mathsf {E}}|}\) denotes the vector of edge lengths. The initial and terminal vertex of \({\mathsf {e}}\) is the vertex \({\mathsf {v}}\in {\mathsf {V}}\) incident to \({\mathsf {e}}\) which is identified with 0 or \(\ell _{\mathsf {e}}\), respectively. This suggests the notation \({\mathsf {e}}={\mathsf {v}}{\mathsf {w}}\) for an edge \({\mathsf {e}}\) connecting the initial vertex \({\mathsf {v}}\) with the terminal vertex \({\mathsf {w}}\) which we will use when appropriate. The degree of a vertex \({\mathsf {v}}\) is the number of edges \({\mathsf {v}}\) belongs to.

We are interested in spectral properties of the Laplacian \(-\Delta =-\Delta _{\mathcal {G}}\) on \({\mathcal {G}}\) that acts edgewise as the negative second derivative \(-\frac{\mathrm {d}^2}{\mathrm {d} x_{\mathsf {e}}^2}\) and whose domain is the space of functions f that are edgewise in the Sobolev space \(H^2(0,\ell _{\mathsf {e}})\) and satisfy for each vertex \({\mathsf {v}}\in {\mathsf {V}}\) one of the following vertex conditions:

  • Standard or Kirchhoff-Neumann conditions: f is continuous in \({\mathsf {v}}\) and satisfies the Kirchhoff condition

    $$\begin{aligned} \sum _{{\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}} \partial _{{\mathsf {e}}}f({\mathsf {v}})=0 \end{aligned}$$
    (1)

    where \({\mathsf {E}}_{\mathsf {v}}\) denotes the set of edges incident to \({\mathsf {v}}\) and \(\partial _{{\mathsf {e}}}f({\mathsf {v}})\) is the outward derivative of f on \({\mathsf {e}}\) at \({\mathsf {v}}\);

  • Dirichlet conditions: f takes the value 0 in \({\mathsf {v}}\).

We denote by \({\mathsf {V}}_N\) the set of vertices in \({\mathsf {V}}\) with standard conditions and by \({\mathsf {V}}_D={\mathsf {V}}\setminus {\mathsf {V}}_N\) the set of vertices with Dirichlet vertex conditions. It is well-known that \(-\Delta \) is a non-negative self-adjoint operator with purely discrete spectrum. In Theorem 3 we will also consider

  • \(\delta \)-coupling conditions: f is continuous in \({\mathsf {v}}\) and satisfies the relation

    $$\begin{aligned} \sum _{{\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}} \partial _{\mathsf {e}}\psi ({\mathsf {v}}) = \alpha _{\mathsf {v}}\psi ({\mathsf {v}}) \end{aligned}$$
    (2)

    for real coupling constants \(( \alpha _{\mathsf {v}})_{{\mathsf {v}}\in {\mathsf {V}}}\).

Since adding a dummy vertex with standard conditions on an edge does not change the spectral properties of the operators considered in this article, we assume that the underlying combinatorial graph \({\mathsf {G}}\) does not contain any loops, meaning that the initial and terminal vertex of any edge in \({\mathsf {E}}_{\mathcal {G}}\) do not coincide. Indeed, this can be achieved by adding such a vertex on every such loop. Furthermore, we assume that all vertices with Dirichlet conditions are of degree one. Indeed, if a Dirichlet vertex was of higher degree \(k > 1\), then we could replace it by k distinct Dirichlet vertices of degree one without affecting the spectrum of the Laplacian. We also emphasize that the assumed connectedness of \(\mathcal {G}\) refers to connectedness after all Dirichlet vertices have been split and turned into vertices of degree one as just described.

Our starting point is Conjecture 4.3 in [14] which states that for every compact connected metric graph there exists an orthonormal base \((\psi _n)_{n \in \mathbb {N}}\) of Laplace-eigenfunctions with monotonous eigenvalues such that such that for a subsequence \((n_k)_{k \in \mathbb {N}}\), all \(\psi _{k_n}\) have full support, i.e. none of these eigenfunctions vanishes identically on any edge of \(\mathcal {G}\). Together with Proposition 3.4 in [14], this would imply for this choice of eigenfunctions

$$\begin{aligned} \limsup _{n \rightarrow \infty } \frac{\nu _n}{n} = 1 \end{aligned}$$
(3)

where \(\nu _n\) denotes the number of nodal domains of \(\psi _n\), that is the number of connected components in which \(\psi _n\) is nonzero.

For domains, one already knows the bound \({\nu _n} \le n\)  [10] and the identity (3) holds on bounded intervals since Sturm’s Oscillation Theorem [20] yields \(\nu _n = n\) in this case. The validity of the conjecture (3) would thus show that Pleijel’s Theorem is a truly higher-dimensional effect and cannot be reproduced on metric graphs which, despite having a topologically more complex structure than intervals, are locally still one-dimensional metric spaces.

Analouges of Sturm’s Oscilation Theorem are known for metric graphs: it was shown in [2, 19] that \(\nu _n=n\) holds if and only if \({\mathcal {G}}\) is a tree, i.e. a graph without cycles. For metric graphs with higher Betti number \(\beta \) – the number of independent cycles in \({\mathcal {G}}\) –, it was shown in [13] (upper bound) and [5] (lower bound) that \(n-\beta \le \nu _n\le n\) holds for so-called generic eigenfunctions \(\psi _n\), namely eigenfunctions that correspond to eigenvalues of multiplicity one and are nonzero in every vertex of \({\mathcal {G}}\). In particular, they must have full support. We also refer to [3] for further reading on the topic of nodal counts on metric graphs. It is known that for a graph \({\mathsf {G}}\) (without loops), the set of vectors of side lengths \(( \ell _{\mathsf {e}})_{{\mathsf {e}}\in {\mathsf {E}}}\) which lead to the genericity of all eigenfunctions is of the second Baire category [7], i.e. “generic eigenfunctions are generic", and (3) is generically true.

It is however not known if (3) holds for any metric graph. In fact, there is a remarkable dichotomy of special cases in which the conjecture is known to be true: on the one hand, these are graphs with pairwise rationally dependent side lengths, cf. [14, Theorem 4.2]. The crucial idea is to use their resonance and to construct a fully supported eigenfunction by putting cosine waves on all edges. This allows for an easy construction of fully supported eigenfunctions, but in general (when the graph has loops, i.e. if it is not a tree), these eigenfunctions will be degenerate, since eigenfunctions to the same eigenvalue can also be constructed by arranging sine waves on loops. As we shall see, this degeneracity of eigenvalues prevents the application of certain techniques. Furthermore, this construction strongly relies on the rational dependence which will break down under arbitrarily small perturbations.

On the other hand, empirically, rationally independent side lengths will generate chaos and favour the emergence of generic eigenfunctions: for graphs with rationally independent edge lengths, it is was shown in [1, Proposition A.1] that there exists an infinite sequence of generic eigenfunctions and, thus, the conjecture also holds in that case.

This dichotomy of methods—resonance in the case of rationally dependent and chaos for rationally independent side lengths—does not seem amenable to a unification.

Our first result surmounts this at least on trees and shows that every metric tree graph has a sequence of generic eigenfunctions.

Theorem 1

Let \({\mathcal {G}}\) be a connected and compact metric tree with standard conditions at all vertices of \(\mathcal G\). Then there exist an infinite sequence of generic eigenvalues, that is a strictly increasing sequence of eigenvalues \((\lambda _k)_{k\in {\mathbb {N}}}\) of multiplicity one and a sequence of corresponding eigenfunctions \((\psi _k)_{k\in {\mathbb {N}}}\) of \(-\Delta \), so that each \(\psi _k\) does not vanish at the vertices of \({\mathcal {G}}\).

The proof of Theorem 1 relies on the secular function approach given in Sect. 3. A close look at the proof indicates the modifications necessary to also treat metric graphs (not only trees!) with at least one Dirichlet vertex and leads to our next result. We comment in Remark 10 on the challenges to generalize Theorem 1 to general graphs without Dirichlet vertices.

Theorem 2

Let \({\mathcal {G}}\) be a connected and compact metric graph with at least one Dirichlet vertex. Then there exist an increasing sequence of generic eigenvalues, that is a strictly increasing sequence \((\lambda _k)_{k\in {\mathbb {N}}}\) of multiplicity one and a sequence of corresponding eigenfunctions \((\psi _k)_{k\in {\mathbb {N}}}\) of \(-\Delta \), so that each \(\psi _k\) is nonzero in all vertices of \({\mathcal {G}}\) except in the Dirichlet vertices.

The proof of Theorem 2 is given in Sect. 4. Using a perturbation argument, we can obtain some more consequences and generalizations. The first one are \(\delta \)-coupling conditions:

Theorem 3

The statements of Theorems 1 and 2 remain valid if any number of standard conditions are replaced by \(\delta \)-coupling conditions as in (2).

Then, we can also modify the operator by adding a piecewise constant potential, that is we choose real parameters \((q_{\mathsf {e}})_{{\mathsf {e}}\in {\mathsf {E}}}\) and consider the operator H that acts edgewise as negative second derivative plus potential \(- \frac{\mathrm {d}^2}{\mathrm {d} x_{\mathsf {e}}^2} \psi + q_{\mathsf {e}}\psi \).

Theorem 4

The statements of Theorems 1, 2, and 3 remain valid if we add any real-valued, edgewise constant potential to the Laplacian.

Note that step-function potentials that take distinct values on a finite number of connected components of the metric graph are incorporated within Theorem 4 after adding additional standard vertices at all points where the potential switches values. The proof of Theorem 3 is in Sect. 5.1 and the proof of Theorem 4 in Sect. 5.2.

3 A secular function for pedestrians and its application to trees

In this section, we reformulate the eigenvalue problem for \(- \Delta \) in terms of a frequency-dependent finite dimensional matrix \(A_\omega \) which has non-trivial kernel if and only if \(\omega ^2\) is an eigenvalue of \(-\Delta \). The function \(\omega \mapsto \det A_\omega \) is a secular function, that is a holomorphic function the non-negative zeros of which are in one-to-one correspondence with \(\sigma (-\Delta )\).

Secular functions are a common tool in the spectral theory of metric graphs. They are usually constructed as a determinant of a matrix on a complex \(2 |{\mathsf {E}}|\)-dimensional vector space using a scattering approach at the vertices [15]. This leads to an a priori complex-valued secular function, even though it can be made real-valued by a multiplication with a phase, see [6, Remark 2.10], and allows to incorporate all possible choices of self-adjoint vertex conditions in one theory [4].

Our approach seems to be a bit more hands-on. We assume continuity at the vertices, which is not required for all self-adjoint vertex conditions, but which is certainly the case for standard, Dirichlet and \(\delta \)-coupling conditions. Our matrices are purely real-valued which would a priori require a real \(4 |{\mathsf {E}}|\)-dimensional vector space (recall that this is the real dimension of a complex \(2 |{\mathsf {E}}|\)-dimensional vector space), but thanks to continuity of the eigenfunctions, this reduces to \(|{\mathsf {V}}|+ 2 |{\mathsf {E}}|\) dimensions.

More precisely, to define the secular function, we use the following reductions: At fixed eigenvalue \(\lambda = \omega ^2\), \(\omega \ge 0\), an eigenfunction \(\psi \) is uniquely determined by

  • its \(|{\mathsf {V}}|\) many values at vertices \(\{ \psi ({\mathsf {v}}) \}_{{\mathsf {v}}\in {\mathsf {V}}}\),

  • its \(2 |{\mathsf {E}}|\) many outward derivatives at the end points of edges \(\{ \partial _{\mathsf {e}}\psi ({\mathsf {v}}) \}_{{\mathsf {v}}\in {\mathsf {V}}, {\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}}\).

On any edge \({\mathsf {e}}= {\mathsf {v}}{\mathsf {w}}\), an eigenfunction is a linear combination of \(\sin \) and \(\cos \) waves with frequency \(\omega \). This implies for \(\omega > 0\) the following consistency condition between function values and derivatives at the endpoints

$$\begin{aligned} \begin{pmatrix} \psi ({\mathsf {w}})\\ \partial _{\mathsf {e}}\psi ({\mathsf {w}})\\ \end{pmatrix} = \begin{pmatrix} \cos (\ell _{\mathsf {e}}\omega ) &{} -\frac{\sin (\ell _{\mathsf {e}}\omega )}{\omega }\\ - \omega \sin (\ell _{\mathsf {e}}\omega ) &{} -\cos (\ell _{\mathsf {e}}\omega )\\ \end{pmatrix} \begin{pmatrix} \psi ({\mathsf {v}})\\ \partial _{\mathsf {e}}\psi ({\mathsf {v}})\\ \end{pmatrix} \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \begin{pmatrix} \psi ({\mathsf {w}})\\ \frac{\partial _{\mathsf {e}}\psi ({\mathsf {w}})}{\omega }\\ \end{pmatrix} = \begin{pmatrix} \cos (\ell _{\mathsf {e}}\omega ) &{} -\sin (\ell _{\mathsf {e}}\omega )\\ - \sin (\ell _{\mathsf {e}}\omega ) &{} -\cos (\ell _{\mathsf {e}}\omega )\\ \end{pmatrix} \begin{pmatrix} \psi ({\mathsf {v}})\\ \frac{\partial _{\mathsf {e}}\psi ({\mathsf {v}})}{\omega }\\ \end{pmatrix}, \end{aligned}$$
(4)

or equivalently

$$\begin{aligned} \begin{pmatrix} 1 &{} -\cos (\ell _{\mathsf {e}}\omega ) &{} \sin (\ell _{\mathsf {e}}\omega ) &{} 0\\ 0 &{} \sin (\ell _{\mathsf {e}}\omega ) &{} \cos (\ell _{\mathsf {e}}\omega ) &{} 1\\ \end{pmatrix} \begin{pmatrix} \psi ({\mathsf {w}})\\ \psi ({\mathsf {v}})\\ \frac{\partial _{\mathsf {e}}\psi ({\mathsf {v}})}{\omega }\\ \frac{\partial _{\mathsf {e}}\psi ({\mathsf {w}})}{\omega } \end{pmatrix} =0. \end{aligned}$$
(5)

Identity (5) holds on every edge \({\mathsf {e}}\in {\mathsf {E}}\) which leads to \(2 |{\mathsf {E}}|\) equations with \((|{\mathsf {V}}|+2|{\mathsf {E}}|)\) variables. We combine them with the \(|{\mathsf {V}}|\) many vertex conditions (as of now we focus on standard or Dirchlet conditions and discuss \(\delta \)-coupling conditions in Sect. 5.1) into a \(\omega \)-dependent \( (|{\mathsf {V}}|+2|{\mathsf {E}}|) \times ( |{\mathsf {V}}|+2|{\mathsf {E}}|) \)-square matrix

(6)

The top \(|{\mathsf {V}}|\) rows of the matrix represent the vertex conditions, the bottom \(2 |{\mathsf {E}}|\) rows the consistency conditions (5) across edges. When appropriate, we omit the dependence on the graph \({\mathcal {G}}\) and the Dirichlet vertex set \({\mathsf {V}}_D\) and simply write \(A_\omega \). We will also write \(A_\omega ({\mathcal {G}})\) if \({\mathsf {V}}_D=\emptyset \) is empty, and \(A_\omega (\mathcal G,{\mathsf {v}})=A_\omega ({\mathcal {G}},{\mathsf {V}}_D)\) if \({\mathsf {V}}_D=\{{\mathsf {v}}\}\) is a one-element set.

Now, to every eigenfunction \(\psi \) of \(-\Delta \) with eigenvalue \(\lambda = \omega ^2 > 0\), corresponds a uniquely determined vector \(x = x(\psi ) \in \ker A_\omega \subset \mathbb {R}^{|{\mathsf {V}}|+ 2 |{\mathsf {E}}|}\) given by

$$\begin{aligned} x = \begin{pmatrix} \{ x({\mathsf {v}}) \}_{{\mathsf {v}}\in {\mathsf {V}}} \\ \{ x({\mathsf {v}},{\mathsf {e}})\}_{{\mathsf {v}}\in {\mathsf {V}}, {\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}} \end{pmatrix} = \begin{pmatrix} \{ \psi (v) \}_{{\mathsf {v}}\in {\mathsf {V}}} \\ \{ \frac{\partial _{\mathsf {e}}\psi ({\mathsf {v}})}{\omega } \}_{{\mathsf {v}}\in {\mathsf {V}}, {\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}} \end{pmatrix}. \end{aligned}$$
(7)

Conversely, every nonzero vector \(x\in \ker A_\omega \) uniquely determines linear combinations of \(\sin \) and \(\cos \) waves with frequency \(\omega \) on every edge \({\mathsf {e}}\) which satisfy boundary conditions at all vertices. Therefore, x uniquely determines an eigenfunction \(\psi \) of \(- \Delta \) to the eigenvalue \(\omega ^2\). In other words, we have proved:

Lemma 5

For \(\omega > 0\) and \(\lambda =\omega ^2\) the mapping

$$\begin{aligned}\mathrm {Eig}(-\Delta ,\lambda )\rightarrow \ker (A_\omega ), \quad \psi \mapsto x(\psi )\end{aligned}$$

is a well-defined isomorphism of vector spaces. In particular, \(\lambda \) is an eigenvalue of \(-\Delta \) if and only if \(\det A_\omega = 0\).

Fig. 1
figure 1

The cycle graph

Full size image

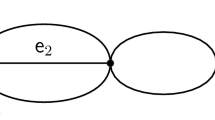
Example 6

We illustrate our construction of \(A_\omega \) and the corresponding secular function \(\det A_\omega \) via a simple example; the cycle graph \({\mathcal {G}}\) parametrised via two edges \({\mathsf {e}},{\mathsf {f}}\) of respective lengths \(\ell _{\mathsf {e}}\) and \(\ell _{\mathsf {f}}\) that connect two vertices \({\mathsf {v}}, {\mathsf {w}}\) (see Fig. 1).

Then the matrix \(A_\omega \) is given by

(8)

Its determinant is \(\det A_\omega =-4 \sin (\frac{L}{2}\omega )^2\)  where \(L=\ell _{\mathsf {e}}+\ell _{\mathsf {f}}\) is the total length of \({\mathcal {G}}\). We observe that the positive zeroes of \(\det A_\omega \) are \(\omega =\frac{2\pi k}{L}\) for \(k\in {\mathbb {N}}\), and their squares are the non-trivial eigenvalues of the negative Laplacian on \(\mathcal {G}\).

Also note that in this case, every non-trivial eigenvalue has multiplicity two. This illustrates why the statement on generic eigenvalues in Theorem 1 cannot be generalized to arbitrary metric graphs without Dirichlet vertices. However, the article [12] also suggests that the cycle is the only generically adversial example.

The next lemma shows that this secular function \(\omega \mapsto \det A_\omega \) is well-defined:

Lemma 7

The above defined secular function \(\omega \mapsto \det A_\omega \) does not change when

  1. (a)

    the orientation of an edge is inverted,

  2. (b)

    an edge is subdivided into two edges by a vertex of degree 2 with standard conditions on the new vertex.

Proof

For simplicity, we only consider vertices with standard conditions since Dirichlet conditions lead to very similar calculations. We frequently use the fact that simultaneous permutations of lines and columns as well as adding multiples of a row or column to another one will not affect the determinant. Denoting the edge by \({\mathsf {e}}= {\mathsf {v}}{\mathsf {w}}\), (a) is shown by demonstrating that the following two determinants are equal:

$$\begin{aligned} \det \end{aligned}$$
(9)

and

$$\begin{aligned} \det \end{aligned}$$
(10)

Since the matrix in (9) results from the one in (10) by multiplication from the left with the matrix

$$\begin{aligned} \begin{pmatrix} 1 &{} &{} &{} &{} \\ &{} 1 &{} &{} &{} \\ &{} &{} \begin{matrix} \sin (\ell _{\mathsf {e}}\omega ) &{} - \cos (\ell _{\mathsf {e}}\omega )\\ \cos (\ell _{\mathsf {e}}\omega ) &{} \sin (\ell _{\mathsf {e}}\omega )\\ \end{matrix} &{} &{}\\ &{} &{} &{} \dots &{} \\ &{} &{} &{} &{} 1\\ \end{pmatrix}, \end{aligned}$$

which itself has determinant 1, (a) follows.

For (b), let us denote the original edge \(\tilde{\mathsf {e}}= {\mathsf {u}} {\mathsf {w}}\) which is subdivided in two edges \({\mathsf {e}}= {\mathsf {u}} {\mathsf {v}}\) and \({\mathsf {f}}= {\mathsf {v}}{\mathsf {w}}\) by inserting a new vertex \({\mathsf {v}}\) on \(\tilde{\mathsf {e}}\). We describe a sequence of steps which reduce the secular function of the extended graph to the one of the original one. After simultaneous permutations of lines and columns, the matrix corresponding to the graph with extra vertex will be

(11)

We now perform the following sequence of manipulations, all of which leave the determinant of (11) invariant:

  • subtract the \(\partial _{\mathsf {f}}{\mathsf {v}}/ \omega \) column from the \(\partial _{\mathsf {e}}{\mathsf {v}}/ \omega \) column,

  • develop along the \({\mathsf {v}}\) row (which now has only one nonzero entry),

  • in the resulting minor subtract \(\sin (\ell _{\mathsf {f}}\omega )\) times the \(\partial _{\mathsf {e}}{\mathsf {v}}/ \omega \) row from the \(\partial _{\mathsf {f}}{\mathsf {v}}/ \omega \) row and add it \(\cos (\ell _{\mathsf {f}}\omega )\) times to the \(\partial _{\mathsf {f}}{\mathsf {w}}/ \omega \) row,

  • develop along the \({\mathsf {v}}\) column (which has only one nonzero entry),

  • in the resulting minor add \(\cos (\ell _{\mathsf {e}}\omega )\) times the \(\partial _{\mathsf {e}}{\mathsf u} / \omega \) row to the \(\partial _{\mathsf {f}}{\mathsf {v}}/ \omega \) row and \(\sin (\ell _{\mathsf {e}}\omega )\) times \(\partial _{\mathsf {e}}{{\mathsf {u}}} / \omega \) to the \(\partial _{\mathsf {e}}{{\mathsf {u}}} / \omega \) row,

  • develop along the \(\partial _{\mathsf {e}}{\mathsf {v}}/ \omega \) column (which has only one nonzero entry and yields a prefactor \(-1\)),

  • swap the \(\partial _{\mathsf {e}}{\mathsf {u}} / \omega \) column and the \(\partial _{\mathsf {f}}{\mathsf {w}}/\omega \) column (compensating the prefactor \(-1\)).

This simplifies the determinant of (11) to

where we used that due to \(\ell _{\tilde{\mathsf {e}}} = \ell _{\mathsf {e}}+ \ell _{\mathsf {f}}\) we have

$$\begin{aligned} \cos (\ell _{\tilde{\mathsf {e}}} \omega )&= \cos (\ell _{\mathsf {e}}\omega )\cos (\ell _{\mathsf {f}}\omega )- \sin (\ell _{\mathsf {e}}\omega )\sin (\ell _{\mathsf {f}}\omega ), \quad \text {and} \\ \sin (\ell _{\tilde{\mathsf {e}}} \omega )&= \sin (\ell _{\mathsf {e}}\omega )\cos (\ell _{\mathsf {f}}\omega )+ \cos (\ell _{\mathsf {e}}\omega )\sin (\ell _{\mathsf {f}}\omega ). \end{aligned}$$

After relabeling, this determinant corresponds to the structure of the original graph. \(\square \)

Nevertheless, there is a common problem with secular matrices: the isomorphism between \(\mathrm {Eig}(-\Delta ,\lambda )\) and \(\ker (A_\omega )\) in Lemma 5 does not persist at \(\omega = 0\), i.e. for the matrix

Indeed, bearing in mind that \(\lim _{\omega \rightarrow 0} \sin (\ell _{\mathsf {e}}\omega ) / \omega = \ell _{\mathsf {e}}\), the eigenspace corresponding to the eigenvalue \(\lambda = 0\) would correspond to the kernel of the different matrix

(12)

The matrix in (12) describes edgewise linear, that is harmonic functions on the graph and has one-dimensional kernel whereas the kernel of \(A_0\) will in general have higher dimension, see Proposition 9 below. Fortunately, if the graph is a tree, the matrix \(A_0\) retains useful properties which are reminiscent of the ground state of the Laplacian:

Lemma 8

If \({\mathcal {G}}\) is a metric tree with standard conditions at all vertices (i.e \({\mathsf {V}}_D=\emptyset \)), then the matrix \(A_0\) has one-dimensional kernel and

$$\begin{aligned} \ker A_0 = {\text {Span}} \{ x_0 \}, \quad \text {where} \quad x_0 := \frac{1}{\sqrt{|{\mathsf {V}}|}} \begin{pmatrix} 1\\ \dots \\ 1\\ 0\\ \dots \\ 0\\ \end{pmatrix} . \end{aligned}$$

Proof

Clearly \(x_0 \in \ker A_0\). Furthermore, it follows from the structure of \(A_0\) that any solution to \(A_0 x = 0\) has the same entry in all of its \(|{\mathsf {V}}|\) first coordinates. It remains to see that all elements in the \({\text {Ker}} A_0\) vanish on the last \(2 |{\mathsf {E}}|\) entries. This is due to the tree structure: The lower left submatrix of \(A_0\) implies that entries corresponding to derivatives at both end points of an edge must be identical while the standard conditions, encoded in the top right submatrix of \(A_0\), imply that all entries corresponding to outgoing derivatives at all leaves must vanish. Inductively, one can now remove leaves from the graph and eventually find that all of the last \(2 |{\mathsf {E}}|\) entries of \(x \in \ker A_0\) vanish. \(\square \)

More generally, the matrix \(A_0\) contains information on the topological structure of the underlying graph:

Proposition 9

We have on connected graphs

$$\begin{aligned}\dim \ker A_0=\beta ({\mathcal {G}})+1\end{aligned}$$

if \({\mathsf {V}}_D=\emptyset \) and

$$\begin{aligned}\dim \ker A_0=\# {\mathsf {V}}_D +\beta ({\mathcal {G}})-1\end{aligned}$$

if \(\#{\mathsf {V}}_D\ge 1\) where \(\beta ({\mathcal {G}}) = \# {\mathsf {E}}- \# {\mathsf {V}}+ 1 \ge 0\) is the first Betti number of the graph.

Proof

We only prove the first statement, since the second one can be shown using similar arguments. We first observe that \(\ker A_0(\mathcal G)\) may be decomposed as

$$\begin{aligned}\ker A_0({\mathcal {G}})=V({\mathcal {G}})\oplus W({\mathcal {G}})\end{aligned}$$

where

$$\begin{aligned}V({\mathcal {G}})=\mathrm {Span} \begin{pmatrix} 1\\ \dots \\ 1 \end{pmatrix}\subset {\mathbb {R}}^{|V|}\end{aligned}$$

and \(W({\mathcal {G}})\subset {\mathbb {R}}^{2|{\mathsf {E}}|}\) is the space of vectors \(\{x({\mathsf {v}},{\mathsf {e}})\}_{{\mathsf {v}}\in {\mathsf {V}}, {\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}}\) satisfying

$$\begin{aligned}x({\mathsf {v}},{\mathsf {e}})= -x({\mathsf {w}},{\mathsf {e}})\end{aligned}$$

for all edges \({\mathsf {e}}\in {\mathsf {E}}\) connecting two vertices \({\mathsf {v}}\) and \({\mathsf {w}}\) and

$$\begin{aligned}\sum _{{\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}} x({\mathsf {v}},{\mathsf {e}})=0\end{aligned}$$

for all vertices \({\mathsf {v}}\in {\mathsf {V}}\). We thus have to show that \(\dim W({\mathcal {G}})=\beta ({\mathcal {G}})\). To do so we proceed by induction over \(\beta \). For \(\beta =0\) the statement follows from Lemma 8. For \(\beta >0\), we may cut \({\mathcal {G}}\) through some appropriately chosen vertex \({\mathsf {v}}\) in \({\mathcal {G}}\), so that \({\mathsf {v}}\) is split into two vertices \({\mathsf {v}}_1\) and \({\mathsf {v}}_2\) resulting in a new connected graph \(\tilde{{\mathcal {G}}}\) with first Betti number \(\beta (\tilde{{\mathcal {G}}})=\beta (\mathcal G)-1\), or equivalently

$$\begin{aligned} \beta ({\mathcal {G}})=\beta (\tilde{{\mathcal {G}}})+1. \end{aligned}$$
(13)

Moreover, by definition of \(W({\mathcal {G}})\), we have

$$\begin{aligned}W(\tilde{{\mathcal {G}}})=\left\{ \{x({\mathsf {v}},{\mathsf {e}})\}_{{\mathsf {v}}\in {\mathsf {V}}, {\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}}\in W({\mathcal {G}})~\big |~\sum _{{\mathsf {e}}\in {\mathsf {E}}_{{\mathsf {v}}_1}}x({\mathsf {e}},{\mathsf {v}})=0\right\} ,\end{aligned}$$

from which we infer that \(W(\tilde{{\mathcal {G}}})\) has codimension 1 in \(W({\mathcal {G}})\).

$$\begin{aligned} \dim W({\mathcal {G}})=\dim W(\tilde{{\mathcal {G}}})+1. \end{aligned}$$
(14)

Thus, the stated equality \(\dim W({\mathcal {G}})=\beta ({\mathcal {G}})\) follows by induction over \(\beta ({\mathcal {G}})\) using (13) and (14). \(\square \)

Remark 10

Proposition 9 can be seen as an illustration for the reason why we cannot go beyond trees if there are standard conditions at all vertices. Below, we will strongly rely on the fact that on trees, \(\det A_\omega \) has a zero of first order at \(\omega = 0\). If \(\mathcal {G}\) is not a tree, then it has nonzero Betti number, whence \(A_0\) will have a higher dimensional kernel and \(\omega \mapsto \det A_\omega \) will have a zero of higher order at \(\omega = 0\). Therefore, the case of non-tree graphs with only standard conditions remains open.

Now comes a subtle point: In general, if \(A_\omega \) has k-dimensional kernel, then the secular function \(\omega \mapsto \det A_\omega \) must have a zero of at least k-th order at \(\omega \). We have not been able to prove that the order of the zero is equal to the dimension of the kernel, even though this seems very plausible. This is actually one disadvantage of our approach compared to more classical forms of the secular function where it is known that the order of positive zeros coincide with the dimension of the eigenspace [4]. On metric trees, the matrix \(A_0\) does have one-dimensional kernel, but we would like to use that \(\det A_\omega \) has a zero of order one at \(\omega = 0\). This is why we need the following proposition:

Proposition 11

If \({\mathcal {G}}\) is a metric tree

$$\begin{aligned} \frac{\partial }{\partial \omega }_{\mid \omega = 0} \big [\det A_\omega ({\mathcal {G}})\big ] = - \sum _{{\mathsf {e}}\in {\mathsf {E}}} \ell _{\mathsf {e}}. \end{aligned}$$

In particular, the map \(\omega \mapsto \det A_\omega ({\mathcal {G}})\) has a zero of order one at \(\omega = 0\).

The proof of Proposition 11 relies on the following two lemmas. We believe that Lemma 12 is interesting in its own right and a strength of our secular function since it establishes a connection between a secular function and certain graph surgeries. Recall that \(A_\omega (\mathcal {G}, {\mathsf {v}})\) denotes the secular function of the metric graph \(\mathcal {G}\) with a Dirichlet condition at the vertex \({\mathsf {v}}\) and standard conditions elsewhere.

Lemma 12

Let \({\mathcal {G}}\) be a compact metric graph and \({\mathcal {G}}^+\) be the graph obtained by attaching a new edge \({\mathsf {e}}= {\mathsf {v}}{\mathsf {w}}\) between a vertex \({\mathsf {v}}\) of \({\mathcal {G}}\) with standard conditions and a new vertex \({\mathsf {w}}\).

  1. (i)

    If we impose standard conditions at \({\mathsf {w}}\), then

    $$\begin{aligned} \det A_\omega ({\mathcal {G}}^+,{\mathsf {V}}_D) = - \sin (\ell _{\mathsf {e}}\omega ) \det A_\omega ({\mathcal {G}} , {\mathsf {V}}_D\cup \{{\mathsf {v}}\}) + \cos (\ell _{\mathsf {e}}\omega ) \det A_\omega ({\mathcal {G}},{\mathsf {V}}_D) . \end{aligned}$$
    (15)
  2. (ii)

    If we impose Dirichlet conditions at \({\mathsf {w}}\), then

    $$\begin{aligned} \det A_\omega ({\mathcal {G}}^+ , {\mathsf {V}}_D\cup \{{\mathsf {w}}\}) = \sin (\ell _{\mathsf {e}}\omega ) \det A_\omega (\mathcal G,{\mathsf {V}}_D) + \cos (\ell _{\mathsf {e}}\omega ) \det A_\omega ({\mathcal {G}} , {\mathsf {V}}_D\cup \{{\mathsf {v}}\}).\nonumber \\ \end{aligned}$$
    (16)
  3. (iii)

    If we impose Dirichlet vertex conditions at \({\mathsf {v}}\) and \({\mathcal {G}}\setminus \{ {\mathsf {v}}\}\) is disconnected

    $$\begin{aligned} \det A_\omega ({\mathcal {G}} , {\mathsf {v}})=\prod _{i=1}^n \det A_\omega ({\mathcal {G}}_i, {\mathsf {v}}) \end{aligned}$$
    (17)

    where \({\mathcal {G}}_1,\ldots ,{\mathcal {G}}_n\) denote the components of \({\mathcal {G}}\setminus \{ {\mathsf {v}}\}\) with a copy of the vertex \({\mathsf {v}}\) added again to each component.

Proof

Simultaneous permutations of rows and columns do not change the determinant, so we may assume that the first four rows and columns of the matrix correspond to \( ({\mathsf {w}},{\mathsf {v}},\partial _{\mathsf {e}}{\mathsf {v}}/\omega , \partial _{\mathsf {e}}{\mathsf {w}}/\omega )\). We calculate

$$\begin{aligned} \det A_\omega ({\mathcal {G}}^+, {\mathsf {V}}_D)&= \det \end{aligned}$$
$$\begin{aligned}&= \det \end{aligned}$$
$$\begin{aligned}&= - \sin (\ell _{\mathsf {e}}\omega ) \det \underbrace{\begin{pmatrix} 1 &{} *\\ 0 &{} *\\ \end{pmatrix} }_{= \det A_\omega ({\mathcal {G}}, {\mathsf {V}}\cup \{ {\mathsf {v}}\} )} + \cos (\ell _{\mathsf {e}}\omega ) \det A_\omega ({\mathcal {G}}, {\mathsf {V}}_D) \end{aligned}$$

where we developed the determinant along the \({\mathsf {w}}\) row in the first step and along the \(\partial _{\mathsf {e}}{\mathsf {w}}/ \omega \) row in the second step. This shows (15). For (16), we calculate

$$\begin{aligned} \det A_\omega ({\mathcal {G}}^+, {\mathsf {V}}\cup \{ {\mathsf {w}}\} )&= \det \end{aligned}$$
$$\begin{aligned}&= \det \end{aligned}$$
$$\begin{aligned}&= \cos (\ell _{\mathsf {e}}\omega ) \underbrace{ \det \begin{pmatrix} 1 &{} *\\ 0 &{} *\\ \end{pmatrix} }_{= \det A_\omega ({\mathcal {G}} , {\mathsf {V}}\cup \{ {\mathsf {v}}\})} + \sin (\ell _{\mathsf {e}}\omega ) \det A_\omega ({\mathcal {G}}, {\mathsf {V}}_D). \end{aligned}$$

Finally, (17) follows by similar manipulations using again that simultaneous permutations of rows and columns do not affect the determinant

$$\begin{aligned} \det \end{aligned}$$
$$\begin{aligned}&= \det \end{aligned}$$
$$\begin{aligned} = \det \end{aligned}$$

\(\square \)

Lemma 13

Let \({\mathcal {G}}\) be a tree with Dirichlet boundary conditions at exactly one leaf \({\mathsf {v}}\) (that is a vertex of degree one) and standard conditions elsewhere. Then

$$\begin{aligned} \det A_0 ({\mathcal {G}}, {\mathsf {v}}) = 1 . \end{aligned}$$
(18)

Proof

We proceed by induction over \(|{\mathsf {E}}|\).

If \(|{\mathsf {E}}|= 1\), then there are exactly two leaves and

$$\begin{aligned} \det A_\omega = \det \begin{pmatrix} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0\\ 1 &{} - \cos (\omega \ell _{\mathsf {e}}) &{} \sin (\omega \ell _{\mathsf {e}}) &{} 0 \\ 0 &{} \sin (\omega \ell _{\mathsf {e}}) &{} \cos (\omega \ell _{\mathsf {e}}) &{} 1 \\ \end{pmatrix} = \cos (\omega \ell _{\mathsf {e}}) . \end{aligned}$$

For the induction step, let us add to a tree \(\mathcal {G}\) a new edge \({\mathsf {v}}{\mathsf {w}}\) with Dirichlet boundary conditions at the leaf \({\mathsf {v}}\) and call the new tree \(\mathcal {G}^+\). Then, by (16)

$$\begin{aligned} \det A_0 ({\mathcal {G}}^+, {\mathsf {v}})&= \sin (0) \det A_0({\mathcal {G}}) + \cos (0) \underbrace{\prod _i \det A_0({\mathcal {G}}_i, {\mathsf {w}})}_{= 1} = 1. \end{aligned}$$

\(\square \)

We are now ready for the proof of Proposition 11.

Proof of Proposition 11

We proceed by induction over \(|{\mathsf {E}}|\).

If \(|{\mathsf {E}}|= 1\), then

$$\begin{aligned} \det A_\omega = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} 1 &{} 0\\ 1 &{} - \cos (\omega \ell _{\mathsf {e}}) &{} \sin (\omega \ell _{\mathsf {e}}) &{} 0 \\ 0 &{} \sin (\omega \ell _{\mathsf {e}}) &{} \cos (\omega \ell _{\mathsf {e}}) &{} 1 \\ \end{pmatrix} = -\sin ( \omega \ell _{\mathsf {e}}) \end{aligned}$$

which has derivative

$$\begin{aligned} \frac{\partial }{\partial \omega } \det A_\omega \mid _{\omega = 0} = -\ell _{\mathsf {e}}\cos ( \omega \ell _{\mathsf {e}}) \mid _{\omega = 0} = - \ell _{\mathsf {e}}. \end{aligned}$$

For the induction step, we call \({\mathcal {G}}^+\) the tree obtained by adding another edge \(\tilde{\mathsf {e}}= {\mathsf {v}}{\mathsf {w}}\) with standard conditions at \({\mathsf {v}}\) and \({\mathsf {w}}\) to the graph \({\mathcal {G}}\) and find by (15) and (18)

$$\begin{aligned} \frac{\partial }{\partial _\omega } \left[ \det A_\omega ({\mathcal {G}}^+) \right] _{\omega = 0}&= \frac{\partial }{\partial _\omega } \left[ - \sin (\ell _{\tilde{\mathsf {e}}} \omega ) \det A_\omega ({\mathcal {G}} , {\mathsf {v}}) + \cos (\ell _{\tilde{\mathsf {e}}} \omega ) \det A_\omega ({\mathcal {G}}) \right] _{\omega = 0} \\&= - \ell _{\tilde{\mathsf {e}}} \underbrace{\det A_0 ({\mathcal {G}}, {\mathsf {v}})}_{=1} + \frac{\partial }{\partial \omega } \left[ \det A_\omega ({\mathcal {G}}) \right] _{\omega = 0} \\&= -\ell _{\tilde{\mathsf {e}}} - \sum _{{\mathsf {e}}\in {\mathsf {E}}_{\mathcal {G}}} \ell _{\mathsf {e}}= -\sum _{{\mathsf {e}}\in {\mathsf {E}}_{{\mathcal {G}}^+}} \ell _{\mathsf {e}}. \end{aligned}$$

\(\square \)

From now on, the tree \({\mathcal {G}}\) is fixed and we use the analytical properties of the secular function to prove Theorem 1. Denote by \(\Vert \cdot \Vert _{\mathrm {F}}\) the Frobenius norm on \(\mathbb {R}^{|{\mathsf {V}}|+ 2 |E |\times |{\mathsf {V}}|+ 2 |E |}\), that is

$$\begin{aligned} \Vert M \Vert _{\mathrm {F}}^2 = \sum _{i,j} |M_{i,j} |^2, \end{aligned}$$

and let \(|\cdot |\) denote the Euclidean norm on \(\mathbb {R}^{|{\mathsf {V}}|+ 2 |{\mathsf {E}}|}\). Note that on finite dimensional spaces, all norms are equivalent whence convergence in Frobenius norm is equivalent to convergence in any other norm on \(\mathbb {R}^{|{\mathsf {V}}|+ 2 |E |\times |{\mathsf {V}}|+ 2 |E |}\). The main tool in the proof of Theorem 1 is the following

Lemma 14

There exists a sequence \((\omega _n)_{n \in \mathbb {N}}\) with \(\det A_{\omega _n} = 0\) for all \(n\in \mathbb {N}\), such that \(\omega _n \rightarrow \infty \) and \(A_{\omega _n} \rightarrow A_0\) as \(n\rightarrow \infty \).

Proof

It suffices to show that for all \(C>0\) and all \(0<\varepsilon <1\) there exists some \(\hat{\omega }\ge C\), so that \(\det A_{\hat{\omega }}=0\) and \(\Vert A_{\hat{\omega }}-A_{0}\Vert _F\le M \varepsilon \), where \(M>0\) is some constant that does not depend on \(\varepsilon \) or C. From this the desired sequence may be constructed recursively.

We consider the functions \(F,h:{\mathbb {R}}\rightarrow {\mathbb {R}}\), \(F(\omega ):=\det A_\omega \) and

$$\begin{aligned} h(\omega ) := F(\omega )^2 + (F'(\omega ) - F'(0))^2 + \Vert A_\omega -A_0\Vert _F^2 \end{aligned}$$

for \(\omega \in {\mathbb {R}}\). They are clearly analytic and by Lemma 18, there exists \(\delta > 0\) such that, if

$$\begin{aligned} \max \left\{ |F(\omega ) |, |F'(\omega ) - F'(0) |\right\} \le \delta , \end{aligned}$$
(19)

then F must have a zero in an \(\varepsilon \)-neighbourhood of \(\omega \). Moreover, the function h is a nonnegative trigonometric polynomial and thus almost periodic with \(h(0) = 0\), see for instance [8] for a reference. Thus, there exist some \(\omega _0\ge C+\varepsilon \) with

$$\begin{aligned} h(\omega _0) \le \min \left\{ \delta ^2, \epsilon ^2 \right\} . \end{aligned}$$
(20)

In particular, \(\omega _0\) satisfies (19), which in turn yields that there is some \(\hat{\omega }\in [\omega _0-\varepsilon ,\omega _0+\varepsilon ]\) with \(F(\hat{\omega }) = \det A_{\hat{\omega }} = 0\). Using \(|\hat{\omega }-\omega _0|\le \varepsilon \) and (20) we estimate

$$\begin{aligned} \Vert A_{\hat{\omega }}-A_0\Vert _F^2&\le 2(\Vert A_{\hat{\omega }}-A_{\omega _0}\Vert _F^2 +\Vert A_{\omega _0}-A_0\Vert _F^2) \\&= 2 \left( \sum _{i,j} \Big |\int _{\hat{\omega }}^{\omega _0} \frac{\partial }{\partial t} a_{ij}(t) \mathrm {d} t \Big |^2 + \epsilon ^2 \right) \\&\le 2 \left( (|{\mathsf {E}}|+ 2 |{\mathsf {V}}|)^2 \max _{i,j} \sup _{\omega \in \mathbb {R}} \Big |\frac{\partial }{\partial \omega } a_{ij}(\omega ) \Big |^2 + 1\right) \varepsilon ^2 =: M^2 \epsilon ^2 .\square \end{aligned}$$

Proof of Theorem 1

Take the sequence \((\omega _n)_{n \in \mathbb {N}}\) from Lemma 14. Since \(\det A_{\omega _n}=0\) holds for all \(n\in {\mathbb {N}}\), there exists a sequence \((x_n)_{n\in \mathbb N}\) with \(x_n \in \ker A_{\omega _n}\) and \(|x_n|=1\) for all \(n\in {\mathbb {N}}\). By compactness, we may assume—after passing to a subsequence—that \((x_n)_{n\in {\mathbb {N}}}\) converges to some \(x_\infty \) with \(|x_\infty |=1\). Note that, by choice of \((\omega _n)_{n\in {\mathbb {N}}}\), the sequence \((A_{\omega _n})_{n\in {\mathbb {N}}}\) converges to \(A_0\). We obtain

$$\begin{aligned}A_0x_\infty =\lim _{n\rightarrow \infty }A_{\omega _n}x_n=0.\end{aligned}$$

Thus, \(x_\infty \) is a normalized element of the (one-dimensional) kernel of \(A_0\), and Lemma 8 yields

$$\begin{aligned}x_\infty =\pm \frac{1}{\sqrt{|V |}} \begin{pmatrix} 1\\ \dots \\ 1\\ 0\\ \dots \\ 0\\ \end{pmatrix} . \end{aligned}$$

Therefore, for sufficiently large \(n\in {\mathbb {N}}\), the first \(| {\mathsf {V}}|\) entries of \(x_n\) must differ from 0. This, in turn, means that for sufficiently large n the eigenfunction \(\psi _n\) of \(\Delta \) that corresponds to \(x_n\) in the sense of Lemma 5 does not vanish in any of the vertices of \({\mathcal {G}}\) and is thus supported on the whole graph \(\mathcal G\). This completes the proof. \(\square \)

4 Metric graphs with at least one Dirichlet vertex

In this section, we prove Theorem 2 for graphs with at least one Dirichlet vertex. The proof relies on the fact that the eigenfunction corresponding to the lowest eigenvalue \(\omega _0^2 > 0\) of \(- \Delta _\mathcal {G}\) does not vanish on \({\mathcal {G}} \setminus {\mathsf {V}}_D\) if \({\mathcal {G}}\setminus {\mathsf {V}}_D\) is connected (see [16]). Moreover it uses the following

Proposition 15

If \({\mathsf {V}}_D\) is nonempty and \({\mathcal {G}}\setminus {\mathsf {V}}_D\) is connected, then

$$\begin{aligned} \frac{\partial }{\partial \omega } \det A_\omega (\mathcal {G}, {\mathsf {V}}_D) \mid _{\omega = \omega _0} \ne 0. \end{aligned}$$

In particular, the map \(\omega \mapsto \det A_\omega (\mathcal {G}, {\mathsf {v}}_D)\) has a zero of order one at \(\omega = \omega _0\).

Proof

Let \({\mathsf {v}}\) be a Dirichlet vertex, of degree one and connected to a vertex \({\mathsf {w}}\) with standard conditions via an edge \({\mathsf {e}}\). In this proof, we consider the dependence of the ground state eigenvalue on the length of the edge \({\mathsf {e}}\). For this purpose let \(\mathcal G_{s}\) denote the metric graph with the same combinatorial structure as \({\mathcal {G}}\) but where the edge \({\mathsf {e}}\) has been modified to have length \(s>0\). With this notation \({\mathcal {G}}_{\ell _{\mathsf {e}}}={\mathcal {G}}\).

It is well-known that locally around \(\ell _{\mathsf {e}}\) there is a differentiable map \(s\mapsto \omega (s)\) with \(\omega (\ell _{\mathsf {e}}) = \omega _0\), and \(\det A_\omega ({\mathcal {G}}_s,{\mathsf {V}}_D) = 0\) if and only if \(\omega = \omega (s)\). Moreover, it follows from a Hadamard-type formula that said map is strictly decreasing in s, see for instance [6, Sect. 3.1.] or [11] for reference, that is \(\frac{\partial }{\partial s} \omega (s) > 0\) in a neighbourhod of \(s = \ell _{\mathsf {e}}\).

Now, let \(F(\omega ,s) := \det A_\omega ({\mathcal {G}}_s,{\mathsf {V}}_D)\). Locally around \(s = \ell _{\mathsf {e}}\), we calculate

$$\begin{aligned} 0 = \frac{\mathrm {d}}{\mathrm {d} s} \left( F (\omega (s), s) \right) = \frac{\partial }{\partial s} \omega (s) \left( \frac{\partial }{\partial \omega } F \right) (\omega (s),s) + \left( \frac{\partial }{\partial s} F \right) (\omega (s),s) \end{aligned}$$

whence in particular

$$\begin{aligned} \frac{\partial }{\partial \omega } \det A_\omega (\mathcal {G}, {\mathsf {V}}_D) \mid _{\omega = \omega _0} = - \frac{ \frac{\partial }{\partial s} \det A_{\omega _0}(\mathcal {G}_s, V_D) }{ \frac{\partial }{\partial s} \omega (s) \mid _{s = \ell _{\mathsf {e}}} }. \end{aligned}$$

Thus it sufficices to see that the partial derivative of \(\det A_{\omega _0}({\mathcal {G}}_s, V_D)\) in the s-direction is non-vanishing. Lemma 12 (ii) yields

$$\begin{aligned} \det A_\omega (\mathcal {G}_s,{\mathsf {V}}_D)&= \cos (s \omega ) \det A_\omega (\mathcal {G}^-, ({\mathsf {V}}_D\setminus \{{\mathsf {v}}\})\cup {\mathsf {w}})\\&\quad + \sin (s \omega ) \det A_\omega (\mathcal {G}^-,{\mathsf {V}}_D\setminus \{{\mathsf {v}}\})\\&= \cos (s \omega ) X(\omega ) + \sin (s \omega ) Y(\omega ) \end{aligned}$$

where \(\mathcal {G}^-\) stands for the graph with the edge \({\mathsf {e}}\) removed. This expression is 0 at \(\omega _0\) by assumption, but we know that \(X(\omega _0) \ne 0\), since the ground state (the first positive zero) of the smaller graph \(\mathcal {G}^-\) must be strictly above the ground state of the larger graph \(\mathcal {G}\). Now,

$$\begin{aligned} \frac{\partial }{\partial {s}} \det A_\omega (\mathcal {G}_s,{\mathsf {V}}_D) = \omega \left[ - \sin (s \omega ) X(\omega ) + \cos (s \omega ) Y(\omega ). \right] \end{aligned}$$

So, if this derivative were zero at \(s=\ell _{\mathsf {e}}\) and \(\omega = \omega _0\), we would obtain

$$\begin{aligned} \begin{pmatrix} X(\omega _0) \\ Y(\omega _0) \end{pmatrix} \in \ker \begin{pmatrix} \cos (\ell _{\mathsf {e}}\omega ) &{} \sin (\ell _{\mathsf {e}}\omega ) \\ -\sin (\ell _{\mathsf {e}}\omega ) &{} \cos (\ell _{\mathsf {e}}\omega ) \\ \end{pmatrix} = \left\{ \begin{pmatrix} 0 \\ 0 \end{pmatrix} \right\} \end{aligned}$$

contrary to \(X(\omega _0) \ne 0\). \(\square \)

The rest of the proof of Theorem 2 is analogous to the proof of Theorem 1 with the differences that Proposition 15 replaces Proposition 11, and that the eigenfunction corresponding to \(\omega _0^2\) is merely nonzero on all standard vertices. But since every edge contains at least one standard vertex, non-vanishing on all standard vertices implies that the corresponding eigenfunction must have full support.

5 Metric graphs with \(\delta \)-couplings and edgewise constant potentials

In this section we prove Theorems 3 and 4. Throughout this section we assume that \({\mathcal {G}}\) is a tree or that \({\mathcal {G}}\) has at least one Dirichlet vertex. If \({\mathcal {G}}\) is a tree, we put \(\omega _0:=0\), if there is at least one Dirichlet vertex, let \(\omega _0>0\) be the frequency corresponding to the ground state of \(-\Delta _{\mathcal {G}}\). As in the previous sections let \(A_\omega \) for \(\omega \in {\mathbb {R}}\) denote the matrix defined in (6). The main tool in the proofs of Theorems 3 and 4 is the following perturbation lemma that generalizes Lemma 14.

Proposition 16

Let \(a>0\) and, for each \(\omega \ge a\), let \(P_\omega \in \mathbb R^{|{\mathsf {V}}|+2|{\mathsf {E}}|\times |{\mathsf {V}}|+2|{\mathsf {E}}|}\) be a matrix such that the map \(\omega \mapsto P_\omega \) is bounded and infinitely differentiable on \([a,\infty )\) in every entry such that all of its derivatives are bounded on \([a,\infty )\). Then, for the perturbed matrices

$$\begin{aligned}B_\omega := A_\omega +\omega ^{-1} P_\omega ,\quad \omega \ge a,\end{aligned}$$

there exists an increasing sequence \((\omega _n)_{n\in {\mathbb {N}}}\) in \([a,\infty )\) with \(\omega _n\rightarrow \infty \), so that \(\det B_{\omega _n}=0\) for all \(n\in {\mathbb {N}}\) and \(B_{\omega _n}\rightarrow A_{\omega _0}\) as \(n\rightarrow \infty \).

Proof

It suffices to show that for all \(C>0\) and all \(0<\varepsilon <1\) there exists \(\hat{\omega }\ge C\) with \(\det B_{\hat{\omega }}=0\) and \(\Vert B_{\hat{\omega }}-A_{\omega _0}\Vert _F\le M \varepsilon \), where \(M>0\) does not depend on \(\varepsilon \) or C.

Consider the functions \(F(\omega )=\det A_\omega \), and \(G(\omega )=\det B_\omega \). By Proposition 11 or 15, respectively, we have \(F(\omega _0) = 0\) and \(F'(\omega _0) \ne 0\). By assumption there exists a bounded and smooth function \(R:[C,\infty )\rightarrow {\mathbb {R}}\) with uniformly bounded derivatives, so that

$$\begin{aligned} G(\omega )=F(\omega )+\omega ^{-1}R(\omega ), \quad \omega \ge C. \end{aligned}$$

In particular, \(\max _{x \in [1, \infty )} |G'' |< \infty \). By boundedness of R and \(R'\), we may assume that \(C>0\) is large enough so that

$$\begin{aligned} |G^{(j)}(\omega )-F^{(j)}(\omega )|\le \frac{\delta }{2} \quad \text {for }j \in \{0,1\} \hbox { and for all } \omega \ge C, \end{aligned}$$
(21)

and, by boundedness of \(P_\omega \)

$$\begin{aligned} \Vert B_\omega -A_\omega \Vert _F\le \varepsilon , \quad \omega \ge C. \end{aligned}$$
(22)

Now, let \(h:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be given by

$$\begin{aligned}h(\omega ):= F(\omega ) + (F'(\omega )-F'(\omega _0))^2+\Vert A_\omega -A_0\Vert _F^2\end{aligned}$$

for \(\omega \in {\mathbb {R}}\). This is a nonnegative trigonometric polynomial (thus almost periodic) with \(h(\omega _0) = 0\), where \(\delta > 0\) is the \(\varepsilon -\) and G-dependent parameter from Lemma 18. Therefore, there exists \(\omega _1 \in [C + \varepsilon , \infty )\) with

$$\begin{aligned} h(\omega _1)\le \max \left( \frac{\delta ^2}{4},{\varepsilon ^2}\right) . \end{aligned}$$
(23)

Using (21) and (23) we obtain \(|G(\omega _1) |\le \delta \), and \(|G'(\omega _1) - F'(\omega _0) |\le \delta \).

Lemma 18 then yields the existence of \(\hat{\omega }\in [\omega _1-\varepsilon ,\omega _1+\varepsilon ] \subset [C, \infty ) \) with \( G(\hat{\omega }) = \det B_{\hat{\omega }} = 0\). Moreover, using (22), (23) and \(|\omega _1-\hat{\omega }|\le \varepsilon \) we obtain

$$\begin{aligned} \Vert B_{\hat{\omega }}-A_{\omega _0}\Vert _F^2&\le 3(\Vert B_{\hat{\omega }}-B_{\omega _1}\Vert _F^2+\Vert B_{\omega _1}-A_{\omega _1}\Vert _F^2+\Vert A_{\omega _1}-A_{\omega _0}\Vert _F^2)\\&\le 3 \left( (|{\mathsf {E}}|+ 2 |{\mathsf {V}}|)^2 \max _{i,j} \sup _{\omega \in [1, \infty )} \Big |\frac{\partial }{\partial \omega } b_{ij}(\omega ) \Big |^2 +2 \right) \varepsilon ^2 =: M^2 \varepsilon ^2. \end{aligned}$$

\(\square \)

5.1 Metric graphs with \(\delta \)-couplings

In this section, we indicate the modifications necessary to prove Theorem 3. Using the notation in (7), the \(\delta \)-coupling condition (2) at \({\mathsf {v}}\in {\mathsf {V}}\) is equivalent to

$$\begin{aligned} - \alpha _{\mathsf {v}}\frac{x({\mathsf {v}})}{\omega } + \sum _{{\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}} x({\mathsf {v}},{\mathsf {e}}) = 0, \end{aligned}$$

leading to the perturbed matrix

for \(\omega >0\) where \(A_\omega \) corresponds to Laplacian where all \(\delta \)-couplings have been replaced by standard conditions and P is an \(\omega \)-independent matrix. Thus, Lemma 16 may be applied to the matrix \(B_\omega \). From here Theorem 3 can be proved following the arguments of the proof of Theorem 1, or Theorem 2, respectively.

5.2 Edgewise constant potential

We now indicate the modifications needed when an edgewise constant potential \(q=(q_{\mathsf {e}})_{{\mathsf {e}}\in {\mathsf {E}}}\in {\mathbb {R}}^{|{\mathsf {E}}|}\) is added to the Laplacian, that is if one has the equation

$$\begin{aligned} - \psi '' + q_{\mathsf {e}} \psi = \lambda \psi \quad \text {on every edge~} \mathsf {e} \in \mathsf {E}. \end{aligned}$$
(24)

As we are primarily interested in the construction of a sequence of non-vanishing eigenfunctions, it is sufficient to consider large eigenvalues. More precisely, we consider positive eigenvalues \(\lambda \) with

$$\begin{aligned}\lambda >\max \{q_{\mathsf {e}}~|~{\mathsf {e}}\in {\mathsf {E}}\}\end{aligned}$$

with corresponding eigenfrequency \(\omega = \sqrt{\lambda }\). Eigenfunctions will be a linear combination of \(\sin \) and \(\cos \) waves with local frequency \(\omega _{\mathsf {e}}= \sqrt{\lambda - q_{\mathsf {e}}} = \sqrt{\omega ^2 - q_{\mathsf {e}}}\) on every edge \({\mathsf {e}}\). Thus, the only change to the construction of the secular function in Sect. 3 is that \(\sin (\ell _{\mathsf {e}}\omega )\) and \(\cos (\ell _{\mathsf {e}}\omega )\) need to be replaced by \(\sin (\ell _{\mathsf {e}}\sqrt{\omega ^2 - q_{\mathsf {e}}})\) and \(\cos (\ell _{\mathsf {e}}\sqrt{\omega ^2 - q_{\mathsf {e}}})\), respectively. We obtain the new matrix

operating on

$$\begin{aligned} x = \begin{pmatrix} \{ x({\mathsf {v}}) \}_{{\mathsf {v}}\in {\mathsf {V}}} \\ \{ x({\mathsf {v}},{\mathsf {e}})\}_{{\mathsf {v}}\in {\mathsf {V}}, {\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}} \end{pmatrix} = \begin{pmatrix} \{ \psi (v) \}_{{\mathsf {v}}\in {\mathsf {V}}} \\ \big \{ \frac{\partial _{\mathsf {e}}\psi ({\mathsf {v}})}{\sqrt{\omega ^2-q_{\mathsf {e}}}} \big \}_{{\mathsf {v}}\in {\mathsf {V}}, {\mathsf {e}}\in {\mathsf {E}}_{\mathsf {v}}} \end{pmatrix}. \end{aligned}$$
(25)

Lemma 17

For all \(j \in \{0,1,\dots \}\) there are \(a_j, C_j > 0\) such that for all \(\omega \in [a_j, \infty )\), we have

$$\begin{aligned} \left|\frac{\partial ^j}{\partial \omega ^j} \left( \sin (\ell _{\mathsf {e}}\sqrt{\omega ^2 - q_{\mathsf {e}}}) - \sin (\ell _{\mathsf {e}}\omega ) \right) \right|&\le \frac{C_j}{\omega }, \quad \text {and}\\ \left|\frac{\partial ^j}{\partial \omega ^j} \left( \cos (\ell _{\mathsf {e}}\sqrt{\omega ^2 - q_{\mathsf {e}}}) - \cos (\ell _{\mathsf {e}}\omega ) \right) \right|&\le \frac{C_j}{\omega }. \end{aligned}$$

Proof

We only show the first identity for \(j = 0\). The proof of the identity with cosine terms is completely analogous and the cases of higher derivatives follow inductively from similar calculations. Setting \(a_0 := \max \sqrt{ |q_{\mathsf {e}}|}\) and \(C_0 := \max \frac{|q_{\mathsf {e}}|}{\ell _{\mathsf {e}}}\), we estimate for \(\omega \ge a_0\)

$$\begin{aligned} |\sin (\ell _{\mathsf {e}}\sqrt{\omega ^2 - q_{\mathsf {e}}}) - \sin (\ell _{\mathsf {e}}\omega )|&= \frac{1}{\ell _{\mathsf {e}}} \left| \int _\omega ^{\sqrt{\omega ^2 - q_{\mathsf {e}}}} \cos (\ell _{\mathsf {e}}x) \mathrm {d} x\right| \le \frac{1}{\ell _{\mathsf {e}}} |\sqrt{\omega ^2 - q_{\mathsf {e}}} - \omega |\\&= \frac{|q_{\mathsf {e}}|}{\ell _{\mathsf {e}}(\sqrt{\omega ^2 - q_{\mathsf {e}}} + \omega )} \le |q_{\mathsf {e}}|(\ell _{\mathsf {e}}\omega )^{-1} \le \frac{C_0}{\omega } . \square \end{aligned}$$

This allows again to express the matrix \(B_\omega \) corresponding to the operator with potential in a form

$$\begin{aligned} B_\omega = A_\omega + \omega ^{-1} P_\omega \end{aligned}$$

for sufficiently large \(\omega \) where again \(A_\omega \) is the matrix corresponding to the free Laplacian and with all \(\delta \)-couplings replaced by standard conditions. Lemma 17 shows that the perturbation \(P_\omega \) indeed satisfies the conditions of Lemma 16 and we can repeat the arguments used in the proof of Theorems 1 or 2 to prove Theorem 4.