n-Extended Lorentzian Kac–Moody algebras

Abstract

We investigate a class of Kac–Moody algebras previously not considered. We refer to them as n-extended Lorentzian Kac–Moody algebras defined by their Dynkin diagrams through the connection of an $A_n$ Dynkin diagram to the node corresponding to the affine root. The cases $n=1$ and $n=2$ correspond to the well-studied over- and very-extended Kac–Moody algebras, respectively, of which the particular examples of $E_{10}$ and $E_{11}$ play a prominent role in string and M-theory. We construct closed generic expressions for their associated roots, fundamental weights and Weyl vectors. We use these quantities to calculate specific constants from which the nodes can be determined that when deleted decompose the n-extended Lorentzian Kac–Moody algebras into simple Lie algebras and Lorentzian Kac–Moody algebra. The signature of these constants also serves to establish whether the algebras possess SO(1, 2) and/or SO(3)-principal subalgebras.

1 Introduction

The symmetry algebras relevant in the formulation of fundamental theories in particle physics have become increasingly complex over the years. While finite dimensional Lie algebras are sufficient for the characterisation of local gauge symmetries describing three of the four known fundamental forces in nature, it was noticed well over thirty years ago that infinite dimensional Kac–Moody algebras [1] are needed for an adequate description in the context of some string and conformal field theories [2,3,4]. For some string theories, type II superstring theories or M-theory [5], a particular type of Lorentzian Kac–Moody algebras has turned out to be especially relevant [6,7,8,9,10,11], providing an alternative approach to treating M-theories as gauged supergravities in dimensions $D\ge 4$ by means of the embedding tensor as carried out, for instance, in [12,13,14,15].

In general, from a mathematical point of view the understanding of Kac–Moody algebras is still partially incomplete [1]. However, based on their Dynkin diagrams, that encode the structure of their corresponding Cartan matrices, see, e.g. [16], many subclasses have been fully classified. The best-known and studied subclasses are semisimple Lie algebras of finite or affine type characterised by finite connected Dynkin diagrams. Their Cartan matrices are positive definite in the former and positive semi-definite in the latter case. In addition, hyperbolic Kac–Moody algebras have also been fully classified [17]. In terms of their connected Dynkin diagrams they are defined by the property that the deletion of any one node leaves a possibly disconnected set of connected Dynkin diagrams each of which is of finite type, except for at most one affine type. Their Cartan matrices are nonsingular with exactly one negative eigenvalue, i.e. they are Lorentzian.

While $E_{10}$ is a hyperbolic Kac–Moody algebra [18], $E_{11}$ is not [19], which, partially motivated by string theory, led to the study of a larger class of Kac–Moody algebras that are also Lorentzian [20, 21]. In [21], these algebras were characterised in terms of their connected Dynkin diagrams such that the deletion of at least one node leaves a possibly disconnected set of connected Dynkin diagrams each of which is of finite type, except for at most one affine type. This definition is obviously more general than the one for hyperbolic Kac–Moody algebras, including them as subcases.

Of these algebras, a particular type is very distinct. Referring to Dynkin diagrams of the affine algebras as extended, the over-extended Dynkin diagrams consist of connecting a node to the affine root and the very-extended ones of connecting another new node to this new root. Here, we study root lattices resulting from Dynkin diagrams for which these extensions are continued by adding successively nodes to the previous ones and refer to them as n-extended Dynkin diagrams. Our notation is such that $n=0$ corresponds to the extended system, $n=1$ to the over-extended system, $n=2$ to the very-extended system and $n>2$ to new systems previously not studied. As we shall see below, these algebras occur naturally in the decomposition of the over- and very-extended systems, for instance the decomposition of the over-extended algebra $D_{17}$ contains a 5-extended $E_{8}$-algebra.

When decomposing the n-extended algebras, we encounter reduced Dynkin diagrams which consist of an $A_{r}$-Dynkin diagram with an $A_{n}$-Dynkin diagram attached to the mth node. We denote the corresponding algebras by ${\hat{A}}_{r}^{(n,m)}$. We study the corresponding weight lattices in more detail with a special focus on the case in which an $A_{n}$-Dynkin is attached to the middle node of $A_{r}$ referring to it as ${\hat{A}}_{r}^{(n)}$.

Our manuscript is organised as follows: In Sect. 2, we recall some known facts about the extended, over-extended and very-extended root lattices to establish our notations and conventions. In Sect. 3, we define the new n-extended Lorentzian algebras and construct their roots, fundamental weights and Weyl vectors. In Sect. 4, we discuss the necessary criteria for the occurrence of SO(1, 2) and SO(3) principal subalgebras. In Sect. 5, we compute a special set of constants obtained from the inner product of the Weyl vector and a fundamental weight, whose overall signs provide necessary and sufficient conditions for the occurrence of SO(1, 2) and SO(3) principal subalgebras and the decomposition of the n-extended Lorentzian algebras, which are then studied in detail in Sect. 6. Section 7 contains a similar analysis to the one in Sects. 5 and 6 for the ${\hat{A}} _{r}^{(n,m)}$-algebras. Our conclusions are stated in Sect. 8.

2 Preliminaries, extended, over-extended and very-extended root lattices

Before we present our extended version of the Lorentzian Kac–Moody algebra, we recall some of the known results on the extended, over-extended and very-extended root lattices to establish our conventions and notations. There exist various types of choices to define the corresponding root spaces, especially with regard to the selection of the inner product in the corresponding vector space [22, 23]. Here, we adopt most of the conventions used and introduced in [2, 21, 24].

The root lattice $\Lambda$ for a Lorentzian Kac–Moody algebra ${\mathbf {g}}$ consists of two parts. The first, $\Lambda _{{\mathbf {g}}}$, is spanned by the simple roots $\alpha _{i}$, $i=1,\ldots ,r$, of the semisimple Lie algebra ${\mathbf {g}}$ with rank r. The second is the self-dual Lorentzian lattice $\Pi ^{1,1}$ equipped with the inner product

$$\begin{aligned} z\cdot w=-z^{+}w^{-}-z^{-}w^{+} \end{aligned}$$

(2.1)

for $z,w\in \Pi ^{1,1}$ of the form $z=(z^{+},z^{-})$, $w=(w^{+},w^{-})$. There are two primitive null vectors in $\Pi ^{1,1}$, that will be important below, $k=(1,0)$, ${\bar{k}}=(0,-1)$, with $k\cdot k={\bar{k}}\cdot {\bar{k}}=0$, $k\cdot {\bar{k}}=1$ and two vectors $\pm \left( k+{\bar{k}}\right)$ of length 2. An extended, or affine, root lattice is obtained by adding to the set of simple roots the negative of the highest root $\theta :=\sum \nolimits _{i=1}^{r}n_{i}\alpha _{i}$, with Kac labels$n_{i}\in {\mathbb {N}}$. Here, we add the modified negative highest root $\alpha _{0}=k-\theta$ to obtain a differently extended root lattice $\Lambda _{ {\mathbf {g}}_{0}}=\Lambda _{{\mathbf {g}}}\oplus \Pi ^{1,1}$. Adding to this set of roots the root $\alpha _{-1}=-\left( k+{\bar{k}}\right)$, we obtain the over-extended root lattice $\Lambda _{{\mathbf {g}}_{-1}}=\Lambda _{ {\mathbf {g}}_{0}}\oplus \Pi ^{1,1}$ and adding the root $\alpha _{-2}=k-\left( \ell +{\bar{\ell }}\right)$ produces the very-extended root lattice $\Lambda _{{\mathbf {g}}_{-2}}=\Lambda _{{\mathbf {g}}_{-1}}\oplus \Pi ^{1,1}$. Here $\ell$, ${\bar{\ell }}$ are two primitive null vectors in the second self-dual Lorentzian lattice.

We summarise these properties in the following Table 1.

Table 1 Extended, over-extended and very-extended Lie algebras, root lattices, extensions and partial Dynkin diagrams

To study the decomposition of the algebras, we require the explicit forms and some properties of the fundamental weights. First, we report them for the extended, over-extended and very-extended Lie algebras. Denoting the fundamental weight vectors of the semisimple Lie algebra ${\mathbf {g}}$ as $\lambda _{i}^{f}$, $i=1,\ldots ,r$, the authors of [21] constructed the fundamental weights for the over-extended and very-extended algebras as

$$\begin{aligned} \lambda _{i}^{o}= & {} \lambda _{i}^{f}+n_{i}\lambda _{0}^{o},\ \lambda _{0}^{o}={\bar{k}}-k,\quad \lambda _{-1}^{o}=-k, \end{aligned}$$

(2.2)

$$\begin{aligned} \lambda _{i}^{v}= & {} \lambda _{i}^{f}+n_{i}\lambda _{0}^{v}, \lambda _{0}^{v}={\bar{k}}-k+\frac{\ell +{\bar{\ell }}}{2},\quad \lambda _{-1}^{v}=-k,\quad \lambda _{-2}^{v}=-\frac{\ell +{\bar{\ell }}}{2}, \end{aligned}$$

(2.3)

respectively, with $i=1,\ldots ,r$. Using an inner product of Lorentzian type as defined in (2.1), these weights satisfy the orthogonality relations

$$\begin{aligned} \lambda _{i}^{o}\cdot \alpha _{j}= & {} \delta _{ij},\quad i,j=-1,0,1,\ldots ,r, \end{aligned}$$

(2.4)

$$\begin{aligned} \lambda _{i}^{v}\cdot \alpha _{j}= & {} \delta _{ij},\quad i,j=-2,-1,0,1,\ldots ,r, \end{aligned}$$

(2.5)

with $\alpha _{i}$ being simple roots of the appropriate root spaces. The corresponding Weyl vectors$\rho$, defined as the sum over all fundamental roots, are then obtained as [2]

$$\begin{aligned} \rho ^{o}= & {} \sum _{j=-1}^{r}\lambda _{j}=\rho ^{f}+h{\bar{k}}-(1+h)k, \end{aligned}$$

(2.6)

$$\begin{aligned} \rho ^{v}= & {} \sum _{j=-2}^{r}\lambda _{j}=\rho ^{f}+h{\bar{k}}-(1+h)k-(1-h) \frac{\ell +{\bar{\ell }}}{2}, \end{aligned}$$

(2.7)

respectively, with h denoting the Coxeter number and $\rho ^{f}$ the Weyl vector of the finite dimensional semisimple Lie algebra.

3 n-Extended root lattices, weight lattices and Weyl vectors

Let us now enlarge these systems further and define the extended algebras ${\mathbf {g}}_{-n}$ with root lattices comprised of the root lattice $\Lambda _{ {\mathbf {g}}_{0}}$ of the rank r semisimple Lie algebra ${\mathbf {g}}$ extended by n copies of the self-dual Lorentzian lattice $\Pi ^{1,1}$

$$\begin{aligned} \Lambda _{{\mathbf {g}}_{-n}}=\Lambda _{{\mathbf {g}}}\oplus \Pi _{1}^{1,1}\oplus \cdots \oplus \Pi _{n}^{1,1}. \end{aligned}$$

(3.1)

Each of the root spaces $\Pi _{i}^{1,1}$, $i=1,\ldots ,n$ is equipped with two null vectors $k_{i}$ and ${\bar{k}}_{i}$ with $k_{i}\cdot k_{i}={\bar{k}} _{i}\cdot {\bar{k}}_{i}=0$, $k_{i}\cdot {\bar{k}}_{i}=1$ and two vectors $\pm \left( k_{i}+{\bar{k}}_{i}\right)$ of length 2. The simple root systems then consist of the r simple roots $\alpha _{i}~$of the semisimple Lie algebra ${\mathbf {g}}$, the modified affine root $\alpha _{0}$ and n-extended roots $\alpha _{-i}$, $i=1,\ldots ,n$

$$\begin{aligned} \alpha ^{(n)}:= & {} \left\{ \alpha _{1},\ldots ,\alpha _{r},\alpha _{0}=k_{1}-\theta ,\alpha _{-1}=-\left( k_{1}+{\bar{k}}_{1}\right) ,\ldots ,\alpha _{-j}\nonumber \right. \\= & {} \left. k_{j-1}-\left( k_{j}+{\bar{k}}_{j}\right) \right\} , \end{aligned}$$

(3.2)

for $j=2,\ldots ,n$. Using the orthogonality relation

$$\begin{aligned} \lambda _{i}^{(n)}\cdot \alpha _{j}^{(n)}=\delta _{ij},\quad i,j=-n,0,1,\ldots ,r, \end{aligned}$$

(3.3)

together with $\lambda _{i}^{(n)}=\sum _{j=-n}^{r}K_{ij}^{-1}\alpha _{j}^{(n)}$, $K_{ij}^{-1}=\lambda _{i}^{(n)}\cdot \lambda _{j}^{(n)}$, we construct the $n+r+1$ fundamental weights $\lambda _{i}^{(n)}$ of the n-extended weight lattice $\Lambda _{{\mathbf {g}}_{-n}}$ as

$$\begin{aligned} \lambda _{i}^{(n)}= & {} \lambda _{i}^{f}+n_{i}\lambda _{0}^{(n)},~~\ \ i=1,\ldots ,r, \end{aligned}$$

(3.4)

$$\begin{aligned} \lambda _{0}^{(n)}= & {} {\bar{k}}_{1}-k_{1}+\frac{1}{n}\sum \limits _{i=2}^{n} \left[ k_{i}+(n+1-i){\bar{k}}_{i}\right] , \end{aligned}$$

(3.5)

$$\begin{aligned} \lambda _{-1}^{(n)}= & {} -k_{1}, \end{aligned}$$

(3.6)

$$\begin{aligned} \lambda _{-2}^{(n)}= & {} -\frac{1}{n}\sum \limits _{i=2}^{n}\left[ k_{i}+(n+1-i) {\bar{k}}_{i}\right] , \end{aligned}$$

(3.7)

$$\begin{aligned} \lambda _{-3}^{(n)}= & {} \frac{1}{n}(n-2)(k_{2}-{\bar{k}}_{2})-\frac{2}{n} \sum \limits _{i=3}^{n}\left[ k_{i}+(n+1-i){\bar{k}}_{i}\right] , \end{aligned}$$

(3.8)

$$\begin{aligned} \lambda _{-4}^{(n)}= & {} \frac{1}{n}(n-3)(k_{2}-{\bar{k}}_{2}+k_{3}-2{\bar{k}} _{3})-\frac{3}{n}\sum \limits _{i=4}^{n}\left[ k_{i}+(n+1-i){\bar{k}}_{i}\right] , \end{aligned}$$

(3.9)

$$\begin{aligned}&\vdots \nonumber \\ \lambda _{-\ell }^{(n)}= & {} \frac{1}{n}(n+1-\ell )\sum \limits _{i=2}^{\ell -1} \left[ k_{i}+(1-i){\bar{k}}_{i}\right] \nonumber \\&+\frac{(1-\ell )}{n}\sum \limits _{i=\ell }^{n}\left[ k_{i}+(n+1-i){\bar{k}}_{i}\right] , \end{aligned}$$

(3.10)

$$\begin{aligned}= & {} \frac{(1-\ell )}{n}\sum \limits _{i=2}^{n}\left[ k_{i}+(1-i){\bar{k}}_{i} \right] +\sum \limits _{i=2}^{\ell -1}\left[ k_{i}+(1-i){\bar{k}}_{i}\right] \nonumber \\&+(1-\ell )\sum \limits _{i=\ell }^{n}{\bar{k}}_{i}, \end{aligned}$$

(3.11)

Summing up these weights, we derive the Weyl vector for the n-extended system

$$\begin{aligned} \rho ^{(n)}= & {} \sum _{j=-n}^{r}\lambda _{j} \nonumber \\= & {} \rho ^{f}+h{\bar{k}}_{1}-(1+h)k_{1}+\sum \limits _{i=2}^{n}\left[ \left( \frac{h}{n}+\frac{n+1-2i}{2}\right) k_{i}\nonumber \right. \\&\left. +\frac{(n+1-i)(2h+n(1-i))}{2n}\bar{k }_{i}\right] . \end{aligned}$$

(3.12)

For $n=1$ and $n=2$, the expressions reduce to the previously known formulae in (2.6) and (2.7), respectively.

Having found a generic expression for the Weyl vector $\rho ^{(n)}$, we can now determine the generalisation of the Freudenthal–de Vries strange formula by computing its square. For a semisimple Lie algebra ${\mathbf {g}}$ with rank r, it is well known to be, see, e.g. [16, 25] and references therein,

$$\begin{aligned} \left( \rho ^{f}\right) ^{2}=\frac{h}{12}\text {dim}\mathbf {g=}\frac{h(h+1)r}{ 12}. \end{aligned}$$

(3.13)

A direct calculation using expression (3.12) yields the generalisation for the n-extended algebras

$$\begin{aligned} \rho ^{(n)}\cdot \rho ^{(n)}=\frac{h(h+1)r+n(n^{2}-1)}{12}-\frac{h(h+n)(1+n) }{n}, \end{aligned}$$

(3.14)

for $n\ge 1$. For $n=1$ this corresponds to the expression found in [21] for the over-extended case.

4 SO(1, 2) and SO(3) principal subalgebras

As the class of Lorentzian Kac–Moody algebras is very large, several attempts have been made in seeking for further properties that distinguish between different subclasses. One such property that has turned out to be very powerful when analysing integrable systems based on finite or affine Kac–Moody algebras [26, 27], as well as the structure of Kac–Moody algebras themselves, is the feature of possessing a principal SO(3)-subalgebra [28]. In terms of the generators in the Chevalley basis $H_{j}$, $E_{i}$, $F_{i}$, obeying the standard commutation relations $[H_{i},H_{j}]$$=0$, $[E_{i},F_{j}]$$=\delta _{ij}H_{i}$, $[H_{i},E_{j}]$$=K_{ij}E_{j}$, $[H_{i},F_{j}]$$=-K_{ij}F_{j}$ with K denoting the Cartan matrix, the principal SO(3)-generators

$$\begin{aligned} J_{3}=\sum _{i=1}^{r}D_{i}H_{i},\quad J_{+}=\sum _{i=1}^{r}n_{i}E_{i},\quad J_{-}=\sum _{i=1}^{r}n_{i}F_{i},\quad D_{i}:=\sum _{j=1}^{r}K_{ji}^{-1}, \end{aligned}$$

(4.1)

satisfy $\left[ J_{+},J_{-}\right] =J_{3}$, $\left[ J_{3},J_{\pm }\right] =\pm J_{\pm }$. The Hermiticity properties $E_{i}^{\dagger }=F_{i}$, $H_{i}^{\dagger }=H_{i}$ are inherited by the generators $J_{+}$ and $J_{-}$ as $J_{+}^{\dagger }=J_{-}$ when $n_{i}\in {\mathbb {R}}$. The SO(3)-commutation relation $\left[ J_{+},J_{-}\right] =J_{3}$ is satisfied when $n_{i}=\sqrt{D_{i}}$.

In the case of the Lorentzian Kac–Moody algebras, the analogue of the SO(3)-principal subalgebra is a SO(1, 2)-principal subalgebra [21, 24] with generators

$$\begin{aligned} {\hat{J}}_{3}=-\sum _{i=1}^{r}{\hat{D}}_{i}H_{i},\quad {\hat{J}}_{+}= \sum _{i=1}^{r}p_{i}E_{i},\quad {\hat{J}}_{-}=\sum _{i=1}^{r}q_{i}F_{i},\quad {\hat{D}}_{i}:=\sum _{j=1}^{r}K_{ji}^{-1}, \end{aligned}$$

(4.2)

satisfying $\left[ {\hat{J}}_{+},{\hat{J}}_{-}\right] =-{\hat{J}}_{3}$, $\left[ {\hat{J}}_{3},{\hat{J}}_{\pm }\right] =\pm {\hat{J}}_{\pm }$ and being Hermitian when $p_{i}q_{i}=\left| p_{i}\right| ^{2}=-{\hat{D}}_{i}$. Thus, a necessary and sufficient condition for the existence of a SO(3)-principal subalgebra or a SO(1, 2)-principal subalgebra is $D_{i}>0$ or ${\hat{D}}_{i}<0$ for all i, respectively.

We argue further that a necessary condition for an extended algebra $\mathbf { g}_{-n}$ to possess a SO(3)-principal subalgebra and a SO(1, 2)-principal subalgebra is that there exists a $k\in S=\{-n,\ldots ,0,1,\ldots ,r\}$ such that $D_{k}=\sum _{j=-n}^{r}K_{jk}^{-1}=0$. We may then decompose the index set S as ${\tilde{S}}=S\backslash \{k\}=S_{1}\cup S_{2}$, such that $K_{ij}=0$ for all $i\in S_{1}$, $j\in S_{2}$ and $K_{i^{\prime }k}\ne 0$, $K_{j^{\prime }k}\ne 0$ for two specific $i^{\prime }\in S_{1}$ and $j^{\prime }\in S_{2}$. Thus, removing the node k from the connected Dynkin diagram ${\mathbf {g}}_{-n}$ will decompose it into two connected diagrams such that two generators indexed by $i\in S_{1}$ and $j\in S_{2}$ will commute. Thus, when $D_{i}>0$ for $i\in S_{1}$ and $D_{j}<0$ for $j\in S_{2}$ we can formulate two commuting principal subalgebras with generators $\{J_{3},J_{\pm }\}$ and $\{{\hat{J}}_{3},{\hat{J}}_{\pm }\}$. For instance, we have

$$\begin{aligned} \left[ J_{3},{\hat{J}}_{+}\right]= & {} \sum \nolimits _{i\in S_{1},j\in S_{2}}D_{i} \sqrt{-{\hat{D}}_{j}}\left[ H_{i},E_{j}\right] \nonumber \\= & {} \sum \nolimits _{i\in S_{1},j\in S_{2}}D_{i}\sqrt{-{\hat{D}}_{j}}K_{ij}E_{j}=0, \end{aligned}$$

(4.3)

and similarly for the other generators. This commuting structure extends to the SO(3) and SO(1, 2) Casimir operators

$$\begin{aligned} C=J_{3}J_{3}-J_{+}J_{-}-J_{-}J_{+},\quad \text {and}\quad {\hat{C}}={\hat{J}}_{3} {\hat{J}}_{3}-{\hat{J}}_{+}{\hat{J}}_{-}-{\hat{J}}_{-}{\hat{J}}_{+}, \end{aligned}$$

(4.4)

respectively. So that we have $\hbox {SO}(3)\oplus \hbox {SO}(1, 2)$ with $[C,{\hat{C}}]=0$.

Computing the inner products of the generators in the adjoint representation, as carried out, for instance, in [24], yields

$$\begin{aligned} (J_{3},J_{3})= & {} \rho ^{(n)}\cdot \rho ^{(n)}>0,\quad \text {and}\quad (J_{\pm },J_{\pm })=\rho ^{(n)}\cdot \rho ^{(n)}>0, \end{aligned}$$

(4.5)

$$\begin{aligned} ({\hat{J}}_{3},{\hat{J}}_{3})= & {} \rho ^{(n)}\cdot \rho ^{(n)}<0,\qquad \text { and }({\hat{J}}_{\pm },{\hat{J}}_{\pm })=-\rho ^{(n)}\cdot \rho ^{(n)}>0. \end{aligned}$$

(4.6)

Thus, identifying the signatures of $\rho ^{(n)}\cdot \rho ^{(n)}$ serves as a necessary condition for the existence of the respective principal subalgebras. Using the generalised Freudenthal–de Vries strange formula (3.14) for a given semisimple Lie algebra ${\mathbf {g}}$ with rank r, the maximal value of $n_{\text {max}}$ for ${\mathbf {g}}_{-n}$ to possess a SO(1, 2)-principal subalgebras is easily determined from the inequalities in (4.6). Using relation (3.14) with a given rank, we compute for the exceptional semisimple Lie algebras

$$\begin{aligned} E_{6}:\,n_{\text {max}}=23,\quad E_{7}:\,n_{\text {max}}=17,\quad E_{8}:\,n_{\text {max}}=14. \end{aligned}$$

(4.7)

For the $A_{r}$ and $D_{r}$ algebras we present the results in Fig. 1 for different values of r.

Fig. 1

Maximum values of n for ${\mathbf {g}}_{-n}$ with rank r to possess a SO(1, 2)-principal subalgebra from the necessary condition $\rho ^{2}<0$ versus the necessary and sufficient condition $D_{i}<0, \forall i$

We observe from Fig. 1 that for $A_{r}$ and $D_{r}$ with $r\ge 24$, no n-extended algebra exists that possesses a SO(1, 2)-principal subalgebras. This agrees with the findings in [3] for $n=1$. For $r<24$, such a possibility exists, but $\rho ^{2}<0$ implies it does not exist when $n>12$ and $n>16$, for $A_{r}$ and $D_{r}$, respectively.¹ As the criterion (4.6) is only necessary, but not sufficient, let us compute the values for $D_{i}^{(n)}$ to obtain the more restrictive necessary and sufficient information.

5 Expansion coefficients of the diagonal principal subalgebra generator

Having constructed the expressions for all fundamental weights and the Weyl vector, we can evaluate the expansion coefficients $D_{i}$ directly from the definition (4.1). Focussing here on the case for which the finite semisimple part is simply laced, so that all roots have length 2, the inverse Cartan matrix is symmetric and acquires a simple form in terms of the fundamental weights $\lambda _{i}^{(n)}$ as $K_{ji}^{-1}=$$\lambda _{j}^{(n)}\cdot \lambda _{i}^{(n)}$. Therefore, the constants

$$\begin{aligned} D_{k}^{(n)}=\sum _{j=-n}^{r}K_{kj}^{-1}=\rho ^{(n)}\cdot \lambda _{k}^{(n)},\quad k=-n,\ldots ,-1,0,1,\ldots ,r, \end{aligned}$$

(5.1)

can be computed either by using the generic expressions for the weight vectors (3.4)–(3.11) and Weyl vectors (3.12) or by directly inverting the Cartan matrix as in (5.1). From the generic expressions, we derive general formulae for the expansion coefficients

$$\begin{aligned} D_{i}^{(n)}= & {} D_{i}^{f}+n_{i}D_{0}^{(n)},\quad and \nonumber \\ D_{-j}^{(n)}= & {} (n-j+1)\left( \frac{j-1}{2}-\frac{h}{n}\right) ,\quad i=1,\ldots ,r;j=0,\ldots ,n, \end{aligned}$$

(5.2)

for the semisimple Lie algebraic and extended part, respectively. We abbreviated $D_{i}^{f}:=\rho ^{f}\cdot \lambda _{i}^{f}$. For the over-extended and very-extended algebras, the expressions in (5.2) become, for instance,

$$\begin{aligned} D_{-1}^{o}= & {} -h,\quad D_{0}^{o}=-(2h+1),\quad D_{i}^{o}=D_{i}^{f}+n_{i}D_{0}^{o},\end{aligned}$$

(5.3)

$$\begin{aligned} D_{-2}^{v}= & {} \frac{1}{2}(1-h),\quad D_{-1}^{v}=-h,\nonumber \\ D_{0}^{v}= & {} - \frac{3}{2}(h+1),\quad D_{i}^{v}=D_{i}^{f}+n_{i}D_{0}^{v}. \end{aligned}$$

(5.4)

The fundamental Weyl vectors $\rho ^{f}$, Coxeter numbers h and Kac labels $n_{i}$ are algebra specific and well known, see, e.g. [29]. We list them here for convenience in Table 2.

Table 2 Kac labels, exponents and Coxeter number for the simply laced Lie algebras

Also the Weyl vectors are known in these cases in terms of the simple roots

$$\begin{aligned} A_{r} :~\rho ^{f}= & {} \sum \limits _{i=1}^{r}\frac{i}{2}(r-i+1)\alpha _{i}, \end{aligned}$$

(5.5)

$$\begin{aligned} D_{r} :~\rho ^{f}= & {} \sum \limits _{i=1}^{r-2}\left[ ir-\frac{i(i+1)}{2}\right] \alpha _{i}+\frac{r(r-1)}{4}(\alpha _{r-1}+\alpha _{r}), \end{aligned}$$

(5.6)

$$\begin{aligned} E_{6} :\rho ^{f}= & {} 8\alpha _{1}+11\alpha _{2}+15\alpha _{3}+21\alpha _{4}+15\alpha _{5}+8\alpha _{6}, \end{aligned}$$

(5.7)

$$\begin{aligned} E_{7} :\rho ^{f}= & {} \frac{1}{2}(34\alpha _{1}+49\alpha _{2}+66\alpha _{3}+96\alpha _{4}\nonumber \\&+75\alpha _{5}+52\alpha _{6}+27\alpha _{7}), \end{aligned}$$

(5.8)

$$\begin{aligned} E_{8} :\rho ^{f}= & {} 46\alpha _{1}+68\alpha _{2}+91\alpha _{3}+135\alpha _{4}+110\alpha _{5}\nonumber \\&+84\alpha _{6}+57\alpha _{7}+29\alpha _{8}. \end{aligned}$$

(5.9)

Hence, we compute the terms $D_{i}^{f}$ in the general expressions for the expansion coefficients (5.2) as

$$\begin{aligned} A_{r} :D_{i}^{f}= & {} \frac{i}{2}(r-i+1),\quad i=1,\ldots ,r\nonumber \\ D_{r} :D_{r-1}^{f}= & {} D_{r}^{f}=\frac{r(r-1)}{4},\quad D_{j}^{f}=jr-\frac{j(j+1) }{2},\quad j=1,\ldots ,r-2 \nonumber \\ E_{6} :D_{1}^{f}= & {} 8,\; D_{2}^{f}=11,\; D_{3}^{f}=15,\; D_{4}^{f}=21,\; D_{5}^{f}=15,\; D_{6}^{f}=8, \nonumber \\ E_{7} :D_{1}^{f}= & {} 17,\; D_{2}^{f}=\frac{49}{2} ,\; D_{3}^{f}=33,\; D_{4}^{f}=48,\nonumber \\ D_{5}^{f}= & {} \frac{75}{2} ,\; D_{6}^{f}=26,\; D_{7}^{f}=\frac{27}{2}, \nonumber \\ E_{8} : D_{1}^{f}= & {} 46,\; D_{2}^{f}=68,\; D_{3}^{f}=91,\; D_{4}^{f}=135,\; D_{5}^{f}=110,\nonumber \\ D_{6}^{f}= & {} 84,\; D_{7}^{f}=57,\; D_{8}^{f}=29. \end{aligned}$$

(5.10)

Evidently, all constants $D_{i}^{f}$ for all semisimple Lie algebras are positive. For the over-extended algebras, we obtain therefore

$$\begin{aligned} A_{r}^{(1)} : D_{-1}^{o}= & {} -(r+1),\quad D_{0}^{o}=-(2r+3),\nonumber \\ D_{i}^{o}= & {} \frac{i }{2}(r-i+1)-(2r+3) \end{aligned}$$

(5.11)

$$\begin{aligned} D_{r}^{(1)} :D_{-1}^{o}= & {} 2-2r,\; D_{0}^{o}=3-4r,\; D_{1}^{o}=2-3r,\nonumber \\ D_{j}^{o}= & {} (j-8)r-\frac{ j(j+1)}{2}+6, \end{aligned}$$

(5.12)

$$\begin{aligned} D_{r-1}^{o}= & {} D_{r}^{o}=\frac{r(r+1)}{4}+3-4r, \nonumber \\ E_{6}^{(1)} :D_{-1}^{o}= & {} -12,\; D_{0}^{o}=-25,\; D_{1}^{o}=-17,\; D_{2}^{o}=-89,\nonumber \\ D_{3}^{o}= & {} -110,\; D_{4}^{o}=-154, \end{aligned}$$

(5.13)

$$\begin{aligned} D_{5}^{o}= & {} -185,\; D_{6}^{o}=-267, \nonumber \\ E_{7}^{(1)} :D_{-1}^{o}= & {} -18,\; D_{0}^{o}=-37,\; D_{1}^{o}=-57,\nonumber \\ D_{2}^{o}= & {} - \frac{99}{2},\; D_{3}^{o}=-78,\; D_{4}^{o}=-100, \end{aligned}$$

(5.14)

$$\begin{aligned} D_{5}^{o}= & {} -\frac{147}{2},\; D_{6}^{o}=-48,\; D_{7}^{o}=-\frac{47}{2}, \nonumber \\ E_{8}^{(1)} :D_{-1}^{o}= & {} -30,\; D_{0}^{o}=-61,\; D_{1}^{o}=-15,\nonumber \\ D_{2}^{o}= & {} -359,\; D_{3}^{o}=-580,\; D_{4}^{o}=-658,\nonumber \\ D_{5}^{o}= & {} -927,\; D_{6}^{o}=-1075,\; D_{7}^{o}=-1346,\; D_{8}^{o}=-1740, \end{aligned}$$

(5.15)

with $i=1,\ldots ,n$, $j=2,\ldots ,n-2$ and for the very-extended algebras we compute

$$\begin{aligned} A_{r}^{(2)} :D_{-2}^{v}= & {} -\frac{r}{2},\; D_{-1}^{v}=-(r+1),\; D_{0}^{v}=-\frac{3 }{2}(r+2),\nonumber \\ D_{i}^{v}= & {} \frac{r}{2}(i-3)+\frac{i}{2}(1-i)-3, \end{aligned}$$

(5.16)

$$\begin{aligned} D_{r}^{(2)} :D_{-2}^{v}= & {} \frac{3}{2}-r,\; D_{-1}^{v}=2-2r,\nonumber \\ D_{0}^{v}= & {} \frac{3}{ 2}-3r,\; D_{1}^{v}=\frac{1}{2}-2r,\nonumber \\ D_{j}^{v}= & {} (j-6)r-\frac{j(j+1)}{2}+3,\nonumber \\ D_{r-1}= & {} D_{r}=\frac{r(r+1)}{4}+\frac{3 }{2}-3r, \end{aligned}$$

(5.17)

$$\begin{aligned} E_{6}^{(2)} :D_{-2}^{v}= & {} -\frac{11}{2},\; D_{-1}^{v}=-12,\; D_{0}^{v}=-\frac{39 }{2},\nonumber \\ D_{1}^{v}= & {} D_{6}^{v}=-\frac{23}{2},\; D_{2}^{v}=-28,\nonumber \\ D_{3}^{v}= & {} D_{5}^{v}=-24,\; D_{4}^{v}=-\frac{75}{2}, \end{aligned}$$

(5.18)

$$\begin{aligned} E_{7}^{(2)} :D_{-2}^{v}= & {} -\frac{17}{2},\; D_{-1}^{v}=-18,\; D_{0}^{v}=-\frac{57 }{2},\; D_{1}^{v}=-40,\nonumber \\ D_{2}^{v}= & {} -\frac{65}{2},\; D_{3}^{v}=-\frac{105}{2},\nonumber \\ D_{4}^{v}= & {} -66,\; D_{5}^{v}=-48,\; D_{6}^{v}=-31,\; D_{7}^{v}=-15, \end{aligned}$$

(5.19)

$$\begin{aligned} E_{8}^{(2)} :D_{-2}^{v}= & {} -\frac{29}{2},\; D_{-1}^{v}=-30,\; D_{0}^{v}=-\frac{93 }{2},\nonumber \\ D_{1}^{v}= & {} -47,\; D_{2}^{v}=-\frac{143}{2},\; D_{3}^{v}=-95, \nonumber \\ D_{4}^{v}= & {} -144,\; D_{5}^{v}=-\frac{245}{2}x,\; D_{6}^{v}=-102, \nonumber \\ D_{7}^{v}= & {} - \frac{165}{2},D_{8}^{v}=-64. \end{aligned}$$

(5.20)

with $i=1,\ldots ,n$, $j=2,\ldots ,n-2$.

From these expressions, we find directly the maximal value of n for $\mathbf { g}_{-n}$ with rank r to possess a SO(1, 2)-principal subalgebra from the necessary and sufficient condition $D_{i}<0$, $\forall i$. For the exceptional Lie algebras, we obtain

$$\begin{aligned} E_{6}:\,n_{\text {max}}=5,\quad E_{7}:\,n_{ \text {max}}=6,\quad E_{8}:\,n_{\text {max}}=7. \end{aligned}$$

(5.21)

For $A_{r}$ and $D_{r}$, the results are reported in Fig. 1. Comparing these exact values to those resulting from the analysis of the necessary condition $\rho ^{2}<0$ shows consistency, but also that the latter values are much more restrictive.

6 Direct decomposition of n-extended Lorentzian Kac–Moody algebras

As argued above, when a constant $D_{k}^{(n)}$ vanishes we can potentially, simultaneously find a SO(1, 2)-principal subalgebras and a SO(3)-principal subalgebra. This requires, however, that the $D_{i}^{(n)}$ for i belonging to the two separate index sets $S_{1}$ and $S_{2}$ are of definite sign. If that is not the case, the algebra can be decomposed further. To identify when either of these scenarios occurs, we can set our solutions in (5.2) to zero and solve for n, i, j, with the only meaningful solutions being those for which $n,i\in {\mathbb {N}}$ and $i\le n$, $j\le n$.

For the extended parts of the Dynkin diagrams, we easily find from (5.2 )

$$\begin{aligned} D_{-j}^{(n)}=0,\quad \text {for}\;\; j=1+\frac{2h}{n}. \end{aligned}$$

(6.1)

For a given value of n, there can only be a finite number of solutions due to the restriction $j\le n$. Using the Coxeter numbers from Table 2, we find the solutions

$$\begin{aligned} A_{r}^{(n)} :D_{i}^{(n)}= & {} 0\quad \text {for }\nonumber \\ (n,r,j)= & {} (3,2,3),(4,1,2),(4,3,2),(4,5,4),(5,4,3),\ldots \end{aligned}$$

(6.2)

$$\begin{aligned} D_{r}^{(n)} :D_{i}^{(n)}= & {} 0\quad \text {for }\nonumber \\ (n,r,j)= & {} (4,4,4),(5,6,5),(6,4,3),(6,7,5),(7,8,5),\ldots \end{aligned}$$

(6.3)

and for the exceptional Lie algebras the only possible solutions are

$$\begin{aligned} E_{6}^{(n)}= & {} E_{6}^{(j-1)}\diamond L\diamond A_{n-j}\quad \text {for }\;\; (n,j)=(6,5),(8,4),(12,3),(24,2), \end{aligned}$$

(6.4)

$$\begin{aligned} E_{7}^{(n)}= & {} E_{7}^{(j-1)}\diamond L\diamond A_{n-j}\quad \text {for }\;\; (n,j)=(9,5),(12,4),(18,3),(36,2), \end{aligned}$$

(6.5)

$$\begin{aligned} E_{8}^{(n)}= & {} E_{8}^{(j-1)}\diamond L\diamond A_{n-j}~~\text {for }\nonumber \\ (n,j)= & {} (10,7),(12,6),(15,5),(20,4),(30,3),(60,2).~~~~ \end{aligned}$$

(6.6)

We denote the Lorentzian root corresponding to the node that needs to be deleted by L.

For the parts of the Dynkin diagrams corresponding to semisimple Lie algebras also the expressions for $\rho ^{f}$ need to be treated case-by-case. We find

$$\begin{aligned} A_{r}^{(n)} :D_{i}^{(n)}= & {} 0~~~~\ \text {for }i=\frac{r+1}{2}\pm \frac{1}{2} \sqrt{r^{2}-6r-4n-11-\frac{8(1+r)}{n}}, \end{aligned}$$

(6.7)

$$\begin{aligned} D_{r}^{(n)} :D_{i}^{(n)}= & {} 0~~~~\ \text {for }i=\frac{r-1}{2}\pm \sqrt{ r^{2}-9r-2n+\frac{25}{4}+\frac{8(1-r)}{n}}. \end{aligned}$$

(6.8)

For the over- and very-extended algebras, the only solutions are

$$\begin{aligned}&A_{r}^{(1)} : r=16,i=7,10; ~r=18,i=6,13 ; r=26,j=5,22 \text {,} \end{aligned}$$

(6.9)

$$\begin{aligned}&A_{r}^{(2)} :~r=12,i=6,7; ~r=13,i=5,9; ~r=18,j=4,15 \text {,} \nonumber \\&D_{r}^{(1)} :~r=17,j=13; ~r=18,j=12; ~r=20,j=11\text { ; }r=39,j=9\text {,} \nonumber \\&D_{r}^{(2)} :~r=13,j=10; ~r=14,j=9; ~r=25,j=7\text {.} \end{aligned}$$

(6.10)

Table 3 Decomposition of the n-extended algebras $A_{r}^{(n)}$

Table 4 Decomposition of the n-extended algebras $D_{r}^{(n)}$

There are no solutions for the E-series on this part of the Dynkin diagram. The complete list of solution with corresponding decomposition is presented in Tables 3 and 4. We observe that in the reduced part, we also obtain some algebras that are not of the n-extended form as described above. To refer to them, we introduce the notation ${\hat{A}}_{r}^{(n,m)}$ labelling an $A_{r}$-Dynkin diagram with n roots successively attached to the mth node in form of an $A_{n}$-algebra. The special case of the n-extended symmetric Dynkin diagram with n roots attached to the middle node of $A_{r}$ we denote by ${\hat{A}}_{r}^{(n)}$. Some of the ${\hat{A}} _{r}^{(n,m)}$-algebras are equivalent to the n-extended versions of the E-series. We have ${\hat{A}}_{5}^{(n+2,3)}\equiv E_{6}^{(n-2)}$, ${\hat{A}} _{n}^{(1,4)}\equiv E_{7}^{(n-7)}$ and ${\hat{A}}_{n}^{(1,3)}\equiv E_{8}^{(n-8)}$. We also have the symmetries ${\hat{A}}_{r}^{(n,m)}={\hat{A}} _{r}^{(n,r+1-m)}={\hat{A}}_{n+m}^{(r+1-m,m)}={\hat{A}}_{r+n+1-m}^{(m-1,m)}$. In the resulting decomposition, we also encounter algebras that decompose further by possessing Lorentzian roots on their extended legs of the corresponding Dynkin diagrams. We mark them in bold in Tables 3 and 4. The precise way in which they decompose is reported below in Tables 6 and 7.

6.1 Reduced system versus n-extended versions

We shall now discuss how to express quantities, such as roots, weights, Weyl vectors and determinants of the Cartan matrix, related to the full n-extended lattices in terms of those obtained from the reduced versions and vice versa. We follow here largely the reasoning presented in [21], however, with the key difference that the node to be removed from the full n-extended Dynkin diagram is not identified as the one that decomposes the system into finite and affine diagrams, but rather the node $\ell$ for which $D_{\ell }^{(n)}=0$. The former node might in fact not even exist for the cases considered here. Moreover, these two types of nodes are always different. Our construction applies to all n-extended lattices.

We denote roots and weights related to the n-extended lattice as the above by $\alpha _{i},\lambda _{i}$ for $i\in S=\{-n,\ldots ,0,1,\ldots ,r\}$ and weights and roots related to the reduced system as ${\tilde{\alpha }}_{i}, {\tilde{\lambda }}_{i}$ for $i\in {\tilde{S}}=S\backslash \{\ell \}=S_{1}\cup$$S_{2}$. The root related to the node $\ell$ can then be expressed as

$$\begin{aligned} \alpha _{\ell }=x-\nu ,\quad \text {with }\;\nu :=-\sum \nolimits _{i\in \tilde{S }}K_{\ell i}{\tilde{\lambda }}_{i}, \end{aligned}$$

(6.11)

where the vector x is defined by the orthogonality properties $x\cdot {\tilde{\alpha }}_{i}=x\cdot \nu =0$. Consequently, we have $K_{\ell \ell }=\alpha _{\ell }^{2}=2=\nu ^{2}+x^{2}$ and the fundamental weights can be expressed as

$$\begin{aligned} \lambda _{\ell }=\frac{x}{x^{2}},\quad \lambda _{i}=\ {\tilde{\lambda }} _{i}+\left( \nu \cdot {\tilde{\lambda }}_{i}\right) \lambda _{\ell }. \end{aligned}$$

(6.12)

Summing up the fundamental weights to construct the Weyl vector then yields a relation between the Weyl vectors in the two respective systems

$$\begin{aligned} \rho =\sum \limits _{i\in S}\ \lambda _{i}=\lambda _{\ell }+\sum \limits _{i\in {\tilde{S}}}\ \lambda _{i}={\tilde{\rho }}+\left( 1+\nu \cdot {\tilde{\rho }}\right) \lambda _{\ell }. \end{aligned}$$

(6.13)

Next, we relate the determinants of the Cartan matrices for the two systems. Employing Cauchy’s expansion theorem for bordered matrices, see, e.g. [30], we have

$$\begin{aligned} \det K=K_{\ell \ell }\det {\tilde{K}}-\sum \limits _{i,j\in {\tilde{S}}}K_{\ell i}(\text{ adj }{\tilde{K}})_{ij}K_{j\ell }, \end{aligned}$$

(6.14)

where $\text{ adj }{\tilde{K}}$ denotes the adjugate matrix of ${\tilde{K}}$, i.e. the transpose of its cofactor matrix. Recalling that $(\text{ adj } {\tilde{K}})_{ij}={\tilde{K}}_{ij}^{-1}\det {\tilde{K}}$, ${\tilde{K}} _{ij}^{-1}=\lambda _{i}\cdot \lambda _{j}$ and $K_{\ell \ell }=2$, relation (6.14) can be re-expressed as

$$\begin{aligned} \det K=\left( 2-\nu ^{2}\right) \det {\tilde{K}}. \end{aligned}$$

(6.15)

To illustrate the working of this formula and at the same time to check our expressions from above for consistency, we present explicitly two examples from Tables 3 and 4.

Example$D_{17}^{(1)}=E_{8}^{(5)}\diamond L\diamond D_{4}:$ With $\nu =\lambda _{1}^{D_{4}}+\lambda _{-5}^{E_{8}^{(5)}}$, $\left( \lambda _{1}^{D_{4}}\right) ^{2}=1$, $\left( \lambda _{-5}^{E_{8}^{(5)}}\right) ^{2}=4/5$, we compute $\nu ^{2}=9/5$. Furthermore, we calculate the determinants $\det K_{D_{17}^{(1)}}=-4$, $\det K_{E_{8}^{(5)}}=-5$, $\det K_{D_{4}}=4$ and hence confirm formula (6.15).

Example$D_{25}^{(2)}=E_{7}^{(1)}\diamond L\diamond D_{18}:$ With $\nu =\lambda _{1}^{D_{8}}+\lambda _{-1}^{E_{7}^{(1)}}$, $\left( \lambda _{1}^{D_{8}}\right) ^{2}=1$, $\left( \lambda _{-1}^{E_{7}^{(1)}}\right) ^{2}=0$, we compute $\nu ^{2}=1$. We also calculate the determinants $\det K_{D_{25}^{(2)}}=-8$, $\det K_{E_{7}^{(1)}}=-2$, $\det K_{D_{18}}=4$ and hence confirming once more formula (6.15).

6.2 Decomposition of the very-extended $D_{25}$-algebra aka $k_{28}$

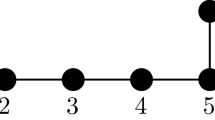
Let us now elaborate further on the last example. As is clear from the above, the construction of extended Dynkin diagrams, or equivalently the corresponding Cartan matrices, of Lorentzian Kac–Moody algebras can be carried out in many alternative ways. As a detailed example, we present now the case of the very-extended $D_{25}$-diagram, that is the $D_{25}^{(2)}$-algebra in our notation. It has the following Dynkin diagram:

The algebra belongs to the special class of hyperbolic Kac–Moody algebras singled out by Gaberdiel et al. [21], which posses at least one node that when removed leaves a set of disconnected Dynkin diagrams of finite type with at most one being of affine type. Indeed, when removing the node corresponding to the root labelled by $\alpha _{6}$, we are left with a disconnected diagram of which one corresponds to the finite dimensional $D_{19}$-algebra and the other to the affine $E_{7}^{(0)}$-algebra. The corresponding root space is constructed as indicated in (3.2).

Here, we are especially interested in the construction of the reduced Dynkin diagram corresponding to $E_{7}^{(2)}\diamond D_{18}$. Instead of representation (3.2), we may also represent the roots as

$$\begin{aligned} \beta _{1}:= & {} \alpha _{8}+\ell , \beta _{i}:=\alpha _{i+7},\quad i=2,\ldots ,18, \end{aligned}$$

(6.16)

$$\begin{aligned} \gamma _{i}:= & {} \alpha _{i},\quad i=1,\ldots ,4,\;\gamma _{5}:=\alpha _{0},\;\gamma _{6}:=\alpha _{-1},\;\gamma _{7}:=\alpha _{-2},\; \gamma _{0}:=\alpha _{5}-{\bar{k}}, \end{aligned}$$

(6.17)

$$\begin{aligned} \gamma _{-1}:= & {} -(k+{\bar{k}})-\ell \text {, }\gamma _{-2}:=-(\ell +{\bar{\ell }} ). \end{aligned}$$

(6.18)

Using the standard rules for the construction of Dynkin diagrams, we obtain the same diagram as above:

The construction differs form the previous one in the sense that we have not used the standard representation for the over-extended and very-extended root, but have now linked the very-extended root $\gamma _{-2}$ of $E_{7}^{(2)}$ with a simple root $\beta _{1}$ of the semisimple Lie algebra $D_{18}$. Deleting now ${\bar{\ell }}$ has the effect that the two links connecting $\gamma _{-2}$ are severed so that this algebra decomposes into $E_{7}^{(1)}\oplus \Pi ^{1,1}\oplus D_{18}$. Thus, $\gamma _{-2}=-\ell$ has become a separate disconnected root of zero length $\gamma _{-2}\cdot \gamma _{-2}=\ell ^{2}=0$. In addition, we obtain two separate disconnected Dynkin diagrams for the over-extended algebra $E_{7}^{(1)}$ and the semisimple Lie algebra $D_{18}$:

We also notice that the root $\alpha _{\ell }=\alpha _{7}$ for which $D_{\ell }=0$ is different from the root $\alpha _{6}$ that need to be chosen for the very-extended root lattice to reduce to an affine and a finite Kac Moody algebra.

6.3 Examples for double and triple decompositions

As indicated in Tables 3 and 4 above, there exist also n-extended algebras for which there are two or even three nodes, say $\ell ,\ell ^{\prime }$ and $\ell ^{\prime \prime }$ , for which $D_{\ell }=D_{\ell ^{\prime }}=D_{\ell ^{\prime \prime }}=0$. We present here two examples of Dynkin diagrams that decompose on the semisimple part as well as on the extended part. For instance, we have a triple decomposition for

for which the final disconnected Dynkin diagram is:

Similarly, $D_{36}^{(14)}$ doubly decomposes as

Further examples can be obtained from Tables 3 and 4 for the cases with bold entries.

7 Roots, weights, Weyl vectors and decomposition of the ${\hat{A}}_{r}^{(n,m)}$-algebras

Since the ${\hat{A}}_{r}^{(n,m)}$-algebras occur naturally in the decomposition of the n-extended Lorentzian Kac–Moody algebras, we shall now discuss them in further detail, with particular emphasis on their decomposition. The corresponding Dynkin diagrams are equivalent to those arising in the description of the so-called $T_{p,q,r}$-singularities [31], with the identification ${\hat{A}}_{p+q+1}^{(r,p+1)}\equiv T_{p,q,r}$. We represent the simple ${\hat{A}}_{r}^{(n,m)}$-roots in terms of the r simple roots $\alpha _{i}~$of the semisimple Lie algebra ${\mathbf {g}}$ and the Lorentzian roots, with the $m^{\text {th}}$ root modified similarly as the affine root for the n-extended algebras $\alpha _{m}\rightarrow \alpha _{m}+k_{1}$. Thus, the $r+n$ simple ${\hat{A}}_{r}^{(n,m)}$-roots are represented as

$$\begin{aligned} {\hat{\alpha }}= & {} \left\{ \alpha _{1},\ldots ,\alpha _{m-1},\alpha _{m}+k_{1},\alpha _{m+1},\ldots ,\alpha _{r},\alpha _{-1}\nonumber \right. \\= & {} \left. -k_{1}-{\bar{k}} _{1},\ldots ,\alpha _{-j}=k_{j-1}-k_{j}-{\bar{k}}_{j}\right\} , \end{aligned}$$

(7.1)

with $~j=2,\ldots ,n$. Using the orthogonality relation

$$\begin{aligned} \lambda _{i}^{(n,m)}\cdot {\hat{\alpha }}_{j}=\delta _{ij},\qquad i,j=-n,\ldots ,-1,1,\ldots ,r, \end{aligned}$$

(7.2)

together with $\lambda _{i}^{(n,m)}=\sum _{j=1}^{n+r}{\hat{K}}_{ij}^{-1}\hat{ \alpha }_{j}$, ${\hat{K}}_{ij}^{-1}=\lambda _{i}^{(n,m)}\cdot \lambda _{i}^{(n,m)}$, we can construct the $n+r$ fundamental weights. We shall focus here on the case for which the extension is attached onto the middle node ${\hat{A}}_{r=2\ell +1}^{(n,\ell +1)}$, so that $m=h/2$, and refer to them as ${\hat{A}}_{r}^{(n)}$. We find in this case the fundamental weights

$$\begin{aligned} {\hat{\lambda }}_{i}^{(n)}= & {} \lambda _{i}^{f}+\frac{2n}{nh-4(n+1)}\min (i,h-i)\left( \lambda _{0}^{(n)}-\lambda _{h/2}^{f}\right) ,\quad i=1,\ldots ,r, \end{aligned}$$

(7.3)

$$\begin{aligned} {\hat{\lambda }}_{-j}^{(n)}= & {} \lambda _{-j}^{(n)}+\frac{4(n-j+1)}{nh-4(n+1)} \left( \lambda _{0}^{(n)}-\lambda _{h/2}^{f}\right) ,\quad j=1,\ldots ,n, \end{aligned}$$

(7.4)

where $\lambda _{i}^{f}~$ are the fundamental weights of $A_{r}$ and $\lambda _{0}^{(n)}$, $\lambda _{-j}^{(n)}$ are fundamental weights for the n-extended Lorentzian Kac–Moody algebras as determined above in equations ( 3.5), (3.11). The Weyl vector results therefore to

$$\begin{aligned} {\hat{\rho }}^{(n)}=\sum _{j=-n,j\ne 0}^{r}{\hat{\lambda }}_{i}^{(n)}=\rho ^{(n)}-h\lambda _{0}^{(n)}+\frac{n(h^{2}+4n+4)}{2n(h-4)-8}\left( \lambda _{0}^{(n)}-\lambda _{m}^{f}\right) . \end{aligned}$$

(7.5)

Next, we compute the constants

$$\begin{aligned} {\hat{D}}_{i}^{(n)}= & {} {\hat{\rho }}^{(n)}\cdot {\hat{\lambda }}_{i}^{(n)}=\frac{ n(4+4n+h^{2})}{16+4n(4-h)}\min (i,h-i)+\frac{i}{2}(h-i), \nonumber \\&i=1,\ldots ,r, \end{aligned}$$

(7.6)

$$\begin{aligned} {\hat{D}}_{-j}^{(n)}= & {} {\hat{\rho }}^{(n)}\cdot {\hat{\lambda }}_{-j}^{(n)}=\frac{ (j-n-1)[h^{2}+4j(1+n)+nh(1-j)]}{2n(h-4)-8}, \nonumber \\&j=1,\ldots ,n. \end{aligned}$$

(7.7)

The algebras decompose, for the same reasons as previously argued for the n-extended algebras ,when the constants ${\hat{D}}^{(n)}$ vanish. We determine

$$\begin{aligned} {\hat{D}}_{i}^{(n)}= & {} 0,\quad \text {for}\;\;i=\frac{n(4n+4+h^{2})}{2n(h-4)-8},h- \frac{n(4n+4+h^{2})}{2n(h-4)-8}, \end{aligned}$$

(7.8)

$$\begin{aligned} {\hat{D}}_{-j}^{(n)}= & {} 0,\quad \text {for}\;\;j=\frac{h(h+n)}{n(h-4)-4}, \end{aligned}$$

(7.9)

Thus, the only meaningful solutions, i.e. those for which $i,\in {\mathbb {N}}$, $i\le r$, to (7.8) give rise to the decompositions on the leg of the Dynkin diagram corresponding to the $A_{r}$-diagram as listed in Table 5.

Table 5 Decomposition of the algebras $A_{r}^{(n)}$ on the $A_{r}$-leg of the Dynkin diagram

On the extended leg of the Dynkin diagram, we find with $j\in {\mathbb {N}}$, $j\le n$, the solutions to (7.8) as reported in Table 6.

Table 6 Decomposition of the algebras $A_{r}^{(n)}$ on the extended leg of the Dynkin diagram

Table 7 Decomposition of the algebras ${\hat{A}}_{r}^{(n,m)}$ that occur in Table 4

Finally, we consider the ${\hat{A}}_{r}^{(n,m)}$-algebras in general. We will not present here a full discussion of the weight lattices, the Weyl vectors and the constants ${\hat{D}}_{i}^{(n,m)}$ as for the special ${\hat{A}} _{r}^{(n)}$-case, but only list the decompositions of those cases that appear in Table 4. Our results are reported in Table 7.

${\hat{A}}_{r}^{(n,m)}$-algebras that appear in Table 4 and are not reported in Table 7 do not decompose. Thus, similarly as discussed in Sect. 6.3, we also obtain double decompositions involving these type of algebras. For instance, we have

as seen from Tables 4, 7 and (6.3).

8 Conclusions

We defined and investigated a new class of Kac–Moody algebras, referred to as n-extended Lorentzian Kac–Moody algebras ${\mathbf {g}}_{-n}$. For the corresponding Dynkin diagrams, we constructed the associated root and weight lattices with generic expressions for all simple roots $\alpha _{i}^{(n)}$ and fundamental weights $\lambda _{i}^{(n)}$. The latter were used to derive closed expressions for the Weyl vectors $\rho ^{(n)}$ for any value of n. The signatures of the product $\rho ^{(n)}\cdot \rho ^{(n)}$, that is the generalisation of the Freudenthal–de Vries strange formula, led to a necessary condition for the n-extended Lorentzian Kac–Moody algebras to possess a SO(1, 2)-principal subalgebra. From the inner products of the Weyl vector $\rho ^{(n)}$ and the fundamental weights $\lambda _{i}^{(n)}$, we compute the expansion coefficients $D_{i}^{(n)}$ for the $J_{3}$-generator of the principal SO(1, 2) or SO(3) subalgebra. When these constants vanish, the decomposition the corresponding Dynkin diagram can be reduced. For the reduced diagrams, we analyse in detail whether $D_{i}>0$ or ${\hat{D}}_{i}<0$ for all i, which constitutes a necessary and sufficient condition for the existence of a SO(3)-principal subalgebra or a SO(1, 2)-principal subalgebra, respectively. We derive explicit formulae augmented by examples that allow to express quantities related to the n-extended systems in terms of the reduced counterparts and vice versa. We provide complete lists for all decompositions of the n-extended Lorentzian Kac–Moody algebras ${\mathbf {g}}_{-n}$. A similarly detailed analysis is presented for the $A_{r}^{(n)}$-algebras, but for ${\hat{A}}_{r}^{(n,m)}\ne A_{r}^{(n)}$ we only report the decomposition for the cases appearing in the decomposition of ${\mathbf {g}}_{-n}$.

Besides the aforementioned applications in string theory, one may also apply the constructions here in the context of classical and quantum integrable systems that are formulated in terms of roots, weights or even directly in terms of principle subalgebras, such as Toda theories [26] and Calogero–Moser–Sutherland systems. Even though it was found that for some of the Toda theories based on Lorentzian root systems do not pass the Painlevé test [32], and are therefore not integrable, the constructions presented here suggest that they contain some integrable components and hence are candidates for a systematic study of nonintegrable quantum field theories [33].