1 Introduction

Growing interest has emerged in recent years for data-driven techniques supported by pattern recognition (PR) and statistical/machine learning (ML) approaches applied to slope stability and landslide prediction (Achour and Pourghasemi 2020; Ma et al. 2021), due to their ability to deal with different uncertainty sources commonly found in geotechnical and natural hazard engineering (Phoon 2020). Probabilistic analysis of slopes using surrogate models (Li et al. 2016), reliability-based design optimization (Pandit and Babu 2018), location of the critical slip in soil slopes (Li et al. 2020), statistical dependence of critical factors on debris flow (Tang et al. 2018), landslide susceptibility (Korup and Stolle 2014), and data-driven safety analysis of slopes (Samui 2013) are among the problems for which solutions have been proposed using PR/ML approaches. However, the uncertainty due to scarcity of available geotechnical data is still a challenge when a data-driven approach using real-world information is adopted (Phoon et al. 2021). Such is the case with slope stability prediction and landslide susceptibility, which have limited data and features per site/experiment, typically cohesion (c), friction angle (\(\varphi \)), unit weight (\(\gamma \)), and geometric properties in the first case or geological/topographic factors (land coverage, hydrology conditions, among others) for the latter.

In this direction, many computational learning methods have been proposed for data-driven slope/landslide classification using real-world datasets. Advanced classifiers for slope stability based on gradient boosting machines (Zhou et al. 2019), ensemble machine learning (Qi and Tang 2018), and extreme learning (Hoang and Bui 2017) have been reported in the literature. Similarly, in landslide susceptibility, logistic regression (Lee et al. 2015), random forest, and adaptive boosting (AdaBoost) methods for feature engineering (Micheletti et al. 2014), support vector classifiers (Huang and Zhao 2018), comparison/ensemble between ML methods (Chen et al. 2017b, a), and deep learning algorithms (Huang et al. 2020), among other methods (Reichenbach et al. 2018), have been applied. Nevertheless, any engineering application of PR/ML should ideally have as few parameters as possible (Mohri et al. 2018, p. 23), that is, the lower the number of parameters to tune, the less complex and more effective explanatory models that can be obtained for real-world problems under adaptive environments (Murdoch et al. 2019). In this regard, Fernández-Delgado et al. (2014, p. 3134) noted that “A researcher may not be able to use classifiers arising from areas in which he/she is not an expert (e.g., to develop [a proper] parameter tuning)...” These issues have also been highlighted in geotechnical and natural hazard engineering by Pourghasemi and Rahmati (2018) and Ospina-Dávila and Orozco-Alzate (2020), who suggested an incremental analysis of parsimony for PR systems applied to slope stability problems.

In a practical context, nonparametric classification rules such as the nearest neighbor rule (Cover and Hart 1967) could be simple enough to support this parameter-free or parameterless ML approach (Keogh et al. 2004; Bicego and Orozco-Alzate 2021). Furthermore, this nearest neighbor approach can provide the basis for more advanced methods which can address complex pattern classification problems while maintaining a simple decision scheme without a complicated (hyper)parameter tuning process. Such is the case with the nearest feature line (NFL) classifier (Li and Lu 1999) and its segmented and rectified version, the rectified nearest feature line segment (RNFLS) (Du and Chen 2007), as well as with adaptive (non)metric distance learning strategies, such as the hypersphere classifier (HC) (Lopes and Ribeiro 2015) or the adaptive nearest neighbor (ANN) classifier (Wang et al. 2007), which are powerful methods that enhance the representational capacity for small datasets and improve the classification performance in overlapping situations, without having to rely on tricky (hyper)parameter tuning tasks, which in some situations are large and very often impose inappropriate assumptions (Keogh et al. 2007).

Therefore, this paper empirically shows the appropriateness of this kind of method for slope/landslide data classification when uncertainty plays a key role due to data scarcity, keeping as few parameters as possible in striving for parsimony and interpretability, when a PR viewpoint is adopted. In addition, this experimental setup and results are established under a very reproducible framework (Keogh 2007; Vandewalle et al. 2009). For this purpose, three publicly available datasets—namely Taiwan (Cheng and Hoang 2015), Multinational (Hoang and Pham 2016), and Yongxin (Fang et al. 2020)—are utilized; the first two relate to slope stability and the last to landslide susceptibility. The computational procedures using source code snippets in Python language are also presented.

The rest of the paper is organized as follows. Section 3 introduces the methods from PR/ML that motivate the present work. In Sects. 4 and 5, the experimental setup and the results, discussed under the premise of letting the data themselves speak to us in a data-driven slope/landslide prediction approach, are described in detail. Finally, Sect. 6 presents a discussion regarding the importance of a parameterless and reproducible research perspective in this particular problem.

2 Description of Available Data

The main properties of the three datasets used for the experiments are summarized in Table 1. The positive class in Taiwan and Multinational corresponds to examples of collapsing slopes and, similarly, the positive class in Yongxin refers to landslide cases.

Table 1 Main properties of the datasets used for the experiments
Full size table

The first two belong to the slope stability problem and are available as tables in the corresponding papers of Cheng and Hoang (2015, Table 2) and Hoang and Pham (2016, Appendix). Tables 2 and 3 summarize the main properties of each dataset. A graphical representation of this kind of problems is given in Fig. 1.

Fig. 1
figure 1

Representation of geotechnical/geometric properties in the slope stability problem

Full size image

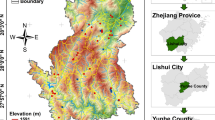
The Yongxin dataset is released on a companion repository [see the URL in Ref. Fang et al. (2020)] related to a landslide susceptibility problem located at the western part of Jiangxi Province, China (see Fig. 2). This dataset includes 16 factors, whose graphical distribution over the Yongxin area can be seen in Figs. 3 and 4, among which are the normalized difference vegetation index (NDVI), sediment transport index (STI), stream power index (SPI), and topographic wetness index (TWI); for further explanation and details, see (Fang et al. 2020).

Fig. 2
figure 2

Yongxin area: location of landslides. Source (Fang et al. 2020) (permission granted by Elsevier Ltd. by order number 5333851293554)

Full size image
Table 2 Main properties of the Taiwan dataset. Source (Cheng and Hoang 2015)
Full size table

3 Methods

One of the most representative classification rules is the nearest neighbor (1-NN) classifier (Cover and Hart 1967), which is nonparametric and is known for its clear geometric interpretation. Moreover, the 1-NN classifier in Euclidean space has at most twice the Bayes error rate,Footnote 1 in an asymptotic sense (Pȩkalska and Duin 2008). However, its performance is strongly dependent on (1) the representational capacity of the dataset, that is, a potential loss in its performance when the training set is small (Pȩkalska and Duin 2002), and (2) the choice of a proper dissimilarity measure, especially when facing complex PR problems (Duin et al. 2014). To counteract these disadvantages, which are also present in data-driven geotechnical and natural hazard engineering problems (see Sect. 1), three simple but powerful variants of the 1-NN classifier are considered in the present study, namely the RNFLS classifier, which enriches the feature space via a linear interpolation between two prototype feature pointsFootnote 2 (Du and Chen 2007), and two methods—ANN (Wang et al. 2007) and HC (Lopes and Ribeiro 2015)—that use a (non)metric distance learning strategy based on the concept of territorial hyperspheres. In fact, the RNFLS classifier also defines territorial hyperspheres as sample territories in its learning scheme. A formal description of these three classifiers, as well as their key concepts, will be introduced in the following subsections.

Fig. 3
figure 3

Yongxin area: landslide factors. Source (Fang et al. 2020) (permission granted by Elsevier Ltd. by order number 5333851293554)

Full size image
Table 3 Main properties of the multinational dataset. Source (Hoang and Pham 2016)
Full size table

3.1 Territorial Hyperspheres

The three enriched/enhanced nearest feature classifiers compared in this paper for slope/landslide data classification are supported by the common idea of a region of influence, which is based on the concept of so-called territorial hyperspheres.

Let \({\varvec{x}} \in {\mathbb {R}}^{d}\) be a query point and \({\varvec{x}}_{i}^{c} \in {\mathbb {R}}^{d}\) be the ith prototype feature point with an associated class label \(c \in \{ 1, \ldots , C\}\). The territorial hypersphere of the prototype \({\varvec{x}}_{i}^{c}\) is centered at it and has a radius defined by

$$\begin{aligned} \rho _{{\varvec{x}}_{i}^{c}} = \underset{1\leqslant c,r \le C, \,\, c\ne r}{\min }\ \left\| {\varvec{x}}_{i}^{c} - {\varvec{x}}_{j}^{r} \right\| \quad \forall j=1, \ldots , n, \end{aligned}$$
(1)

where n is the number of prototype feature points in the class r, \(\left\| \cdot \right\| \) is assumed to be the Euclidean norm, and the radius is computed as the minimum distance from the prototype \({\varvec{x}}_{i}^{c}\) to the nearest prototype belonging to a different class, \({\varvec{x}}_{j}^{r}\), that is, with \(c\ne r\).

Fig. 4
figure 4

Yongxin area: landslide factors (continuation). Source (Fang et al. 2020) (permission granted by Elsevier Ltd. by order number 5333851293554)

Full size image

For the case of RNFLS, the hypersphere associated with \({\varvec{x}}_{i}^{c}\) is called the sample territory, which determines the class territory for all the prototype feature points belonging to the same class. The class territory is used to eliminate the interpolation inaccuracy of the original NFL classifier. On the other hand, for HC and ANN rules, these hyperspheres constitute an important part of the so-called adaptive procedure: HC subtracts \(\rho _{{\varvec{x}}_i^c}\) from \(\left\| {\varvec{x}} - {\varvec{x}}_{i}^{c} \right\| \) and ANN divides \(\left\| {\varvec{x}} - {\varvec{x}}_{i}^{c} \right\| \) by \(\rho _{{\varvec{x}}_i^c}\) such that for both cases, the query point \({\varvec{x}}\) is no longer classified according to its nearest prototype feature point, \({\varvec{x}}_{i}^{c}\)—in the conventional sense—but to the class of the \({\varvec{x}}_{i}^{c}\) that becomes the closest after scaling the distance by the radius of its nearest region of influence.

The first procedure for the three classifiers under comparison is computing the territorial hyperspheres; see Listing 1, which shows the code that returns the radii of the training vectors. Here, a vector saves the information provided by a prototype feature point; similarly, a collection of these vectors are saved as arrays or matrices. All vectors and matrices are stored as NumPy arrays (Harris et al. 2020). The radius for each training vector is equal to the distance to its closest neighbor belonging to a different class. Note that the diagonal of this matrix is initialized with Inf values instead of zeros; this is for convenience when characterizing a vector according to the classes of its closest neighbors, in particular to avoid the case in which a point is considered the closest neighbor to itself when sorting the distances. Note also that only the upper triangular part of the distance matrix is explicitly computed, and it is then copied to the lower part, taking advantage of the symmetric property of the matrix in order to avoid unnecessary computations.

figure a

3.2 Feature Lines

A feature line is a linear interpolation (and also extrapolation) between two prototype feature points of the same class. The so-called NFL classifier (Li and Lu 1999) is a nearest feature method which uses the additional information provided by these feature lines in order to enrich and generalize the representativeness of the original set of prototype feature points. Its effectiveness has been tested on several problems with small datasets, for instance in machine perception (Li and Lu 2013).

The NFL classifier generalizes each pair of prototype feature points, \(\left\{ {\varvec{x}}_{i}^{c}, {\varvec{x}}_{j}^{c} \right\} \), in the same class by a feature line subspace, \(L_{ij}^c\) (see Fig. 5). A query point \({\varvec{x}}\) is then projected onto \(L_{ij}^c\) as follows

$$\begin{aligned} \tilde{{\varvec{x}}}_{ij}^c = {\varvec{x}}_{i}^{c} + \mu ( {\varvec{x}}_{j}^{c} - {\varvec{x}}_{i}^{c}), \end{aligned}$$
(2)

where \(\mu \) is the position parameter given by \(\mu = ( {\varvec{x}} - {\varvec{x}}_{i}^{c} )\cdot ( {\varvec{x}}_{j}^{c} - {\varvec{x}}_{i}^{c} ) / \Vert {\varvec{x}}_{j}^{c} - {\varvec{x}}_{i}^{c} \Vert \in {\mathbb {R}}\).

Fig. 5
figure 5

Three query points, \({\varvec{x}}, {\varvec{x}}_1, {\varvec{x}}_2\), and their distances \(d(\cdot ,L_{ij}^{c})\) to the feature line \(L_{ij}^{c}\)

Full size image

The classification of \({\varvec{x}}\) is performed by assigning the class label \({\hat{c}}\) to it, according to the nearest feature line

$$\begin{aligned} d({\varvec{x}},L_{{\hat{i}}{\hat{j}}}^{{\hat{c}}})&= \underset{1\leqslant c \le C, \, 1\le i, j\le n_{c}\,\, i\ne j}{\min } d({\varvec{x}},L_{ij}^{c}), \end{aligned}$$
(3)

where

$$\begin{aligned} d({\varvec{x}},L_{ij}^{c}) = \Vert {\varvec{x}}-\tilde{{\varvec{x}}}_{ij}^{c} \Vert . \end{aligned}$$
(4)

Figure 5 shows three query points to classify, denoted by \({\varvec{x}}, {\varvec{x}}_1\), and \({\varvec{x}}_2\). The projected point for the first one lies in the interpolating part, and the projections of the last two lie in the extrapolating part of \(L_{ij}^{c}\). In all cases, the distance \(d(\cdot ,L_{ij}^{c})\) is computed by means of the projected point.

figure b

3.3 The Rectified Nearest Feature Line Segment Classifier

In the NFL classifier, the interpolating and/or extrapolating part of some feature lines could involve two trespass errors: the extrapolation inaccuracy pointed out by Zheng et al. (2004) and the interpolation inaccuracy considered by Du and Chen (2007). Several refined NFL approaches for handling these issues have been reported in the literature. One rule that addresses both types of trespassing issues of NFL is the RNFLS classifier (Du and Chen 2007), which overcomes them in a two-stage procedure, building at the end an RNFLS subspace.

Fig. 6
figure 6

The two-stage procedure of the RNFLS classifier

Full size image

First, and in contrast to the NFL classifier, when the projection of the query lies in the extrapolation part, only a segment (denoted by \(\widetilde{L_{ij}^{c}}\)) of the feature line subspace is used, where \(d({\varvec{x}},\widetilde{L_{ij}^{c}})\) is assumed as the distance from the query, \({\varvec{x}}\), to the closest point of the feature line segment, \({\varvec{z}} \in \widetilde{L_{ij}^{c}}\). In Fig. 6a, \({\varvec{z}}\) might correspond to any point along the line but between \({\varvec{x}}_{i}^c\) and \({\varvec{x}}_{j}^c\). Thus, this distance is obtained by reformulating Eqs. (3) and (4) in terms of \(\widetilde{L_{ij}^{c}}\), such that Eq. (4) becomes

$$\begin{aligned} d({\varvec{x}},\widetilde{L_{ij}^{c}}) = \underset{ {\varvec{z}} \in \widetilde{L_{ij}^{c}}}{\min } \Vert {\varvec{x}}- {\varvec{z}} \Vert . \end{aligned}$$
(5)

Note that in this case, the distance obtained in Eq. (5)—called distance2line in Listing 2—depends on whether the position parameter takes a value less than zero or greater than 1 when computing the closest point. This position parameter, \(\mu \), is computed and saved in the variable mu; the extremes of the feature line segment subspace, \({\varvec{x}}_{i}^c\) or \({\varvec{x}}_{j}^c\), are also defined by the variables pointLeft and pointRight. Then the closest point, called p, is assigned.

Subsequently, if the projection of the query lies on the interpolation part, hyperspheres are used to examine the territories of each class and determine whether the feature line segment trespasses a territory which belongs to another class; if so, that feature line segment would be removed. Here, the sample territory, \(T_{{\varvec{x}}_{i}^{c}} \subseteq {\mathbb {R}}^{n}\), is expressed as

$$\begin{aligned} T_{{\varvec{x}}_{i}^{c}} = \left\{ {\varvec{h}} \in {\mathbb {R}}^{n}: \left\| {\varvec{h}}-{\varvec{x}}_{i}^{c} \right\| \le \rho _{{\varvec{x}}_{i}^{c}} \right\} , \end{aligned}$$
(6)

where \(\rho _{{\varvec{x}}_{i}^{c}}\) is defined by Eq. (1), and the union of the sample territories belonging to the same class leads to the class territory \({\mathcal {T}}_{c} = \underset{c}{\bigcup }\ T_{{\varvec{x}}_{i}^{c}}\). When a feature line segment from a different class r trespasses the c-class territory, then it is rejected, or vice versa. In this case, \(\mu \) takes a value between zero and 1 such that the projected point, \(\tilde{{\varvec{x}}}_{ij}^c\), is computed in the variable p which corresponds to Eq. (2). The distance to the projected point is then computed in the distance2line variable.

Figure 6b shows an example of a feature line segment from \({\varvec{x}}_{1}^{c}\) to \({\varvec{x}}_{3}^{c}\), belonging to c-class, that is rejected because it trespasses the r-class territory, composed of three circles. The implementation of this trespass verification is shown in Listing 3 for a given query point and two prototype feature points from the same class, which in turn is derived from Listing 4 in order to compute all accepted/rectified feature line segments for each class.

figure c
figure d

3.4 Hypersphere-Based Scaling

As mentioned above, the HC and ANN classifiers make use of the territorial hypersphere concept in order to obtain a (non)metric learning version of the 1-NN method where these methods essentially attempt to weigh distances to prototype feature points which are well inside their class (Orozco-Alzate et al. 2019), meaning that the larger the hypersphere, the more influential its center for the assignment of the class labels.

HC (Lopes and Ribeiro 2015) defines the region of influence of a given prototype feature point \({\varvec{x}}_{i}^{c} \in {\mathbb {R}}^{d}\) as \(\eta _i = \rho _i \mathbin {/} 2\), where \(\rho _i\) is its radius computed by Eq. (1). Thus, the distance from \({\varvec{x}}\) to \({\varvec{x}}_{i}^{c}\) for HC is given by

$$\begin{aligned} d_{HC}\left( {\varvec{x}}, {\varvec{x}}_{i}^{c} \right) = \left\| {\varvec{x}} - {\varvec{x}}_{i}^{c} \right\| - g\eta _i, \end{aligned}$$
(7)

where g is the parameter that controls the overlapping between hyperspheres from different classes. The original version of the HC method proposes a value of \(g=2\), resulting in

$$\begin{aligned} d_{HC}\left( {\varvec{x}}, {\varvec{x}}_{i}^{c} \right) = \left\| {\varvec{x}} - {\varvec{x}}_{i}^{c} \right\| - \rho _i. \end{aligned}$$
(8)

On the other hand, according to the ANN classifier (Wang et al. 2007), the distance is scaled as

$$\begin{aligned} d_{ANN}\left( {\varvec{x}}, {\varvec{x}}_{i}^{c} \right) = \frac{\left\| {\varvec{x}} - {\varvec{x}}_{i}^{c} \right\| }{\rho _i}. \end{aligned}$$
(9)

This hypersphere-based scaling was recently applied with successful results in a problem of seismic-volcanic signal classification by Bicego et al. (2022).

4 Experimental Setup

First, even though the Yongxin dataset was originally provided in separate parts for training and test, it was decided to fuse them into a single one (the so-called design set) which was then conveniently split into training and test according to the k-fold cross-validation protocol.

Commonly in PR tasks, a normalization preprocessing of data is required when the values are very different, especially when the Euclidean distance is used in a distance-based classifier such as 1-NN or support vector machine (SVM) classifiers; Listing 5 shows this procedure when the training and test sets have been defined beforehand.

figure e

As suggested by Bramer (2016, p. 185), a common means of finding the best classifier for a particular problem is using the receiver operating characteristic (ROC) graph and measuring the distances from the point (FP rate, TP rate) of each classifier to the (0,1) point, which corresponds to a perfect classification. The ROC graph is a plot which shows the trade-off between costs (FP rate) and benefits (TP rate) (Fawcett 2006), where FP is the false positive rate of a classifier and is estimated by

$$\begin{aligned} FP\approx \frac{\text {Negatives incorrectly classified}}{\text {Total negatives}}, \end{aligned}$$
(10)

and where TP is the true positive rate, which is estimated by

$$\begin{aligned} TP\approx \frac{\text {Positives correctly classified}}{\text {Total positives}}. \end{aligned}$$
(11)

This approach was adopted in order to find the best classifier for each dataset. The performance estimation is shown in Listing 6, where a counter of FP, TP, and “successes” (hits) of the results of a given classifier are saved.

figure f

Note that the Multinational and Yongxin datasets have a balanced number of positive and negative examples; in contrast, for the Taiwan dataset, the number of negative examples is more than 2.5 times the number of positive ones. The imbalance is an important factor to take into account when analyzing the reported classification accuracy.

Part of the Multinational dataset originally comes from Zhou and Chen (2009). In that part, the label of a specific sample from the Multinational dataset does not match the originally assigned label. After checking the Multinational dataset, rows 43 and 60 were found to have the same feature values but different labels, so it was assumed that the correct label was the one given originally in Zhou and Chen (2009), namely label 1.

In order to obtain reliable but computationally feasible performance estimations, the approach suggested in Japkowicz and Shah (2011, p. 203) is adopted, namely the leave-one-out estimate for small datasets and the k-fold cross-validation for moderate-sized ones. Accordingly, leave-one-out was used for experiments with the Taiwan and Multinational datasets, and fivefold cross-validation for the Yongxin dataset. Recall that leave-one-out is a particular case of k-fold cross-validation, where k is equal to the number of instances in the dataset (Bramer 2016, p. 83); moreover, since there is no randomness involved in leave-one-out, the same performance figures are obtained when the experiment is repeated. This cross-validation procedure, based on the Scikit-learn Python package, is coded in Listing 7.

figure g

5 Results and Discussion

For the three datasets used in this paper, a comparative evaluation is performed considering the test phase scheme proposed in Listing 8 for the 1-NN, ANN, and HC methods, and in Listing 9 for the RNFLS method, according to the description given in Sect. 4.

figure h
figure i

The performance rates were computed as shown in Listing 10, whose results for classification accuracy are presented in Table 4. First, note that very sound accuracy was obtained with 1-NN—the baseline method in the present paper—for the slope stability (Taiwan and Multinational) datasets; moreover, this also applies to the RNFLS classifier, which shows the highest accuracy highlighted in boldface. Note that the RNFLS classifier boosts the discriminant capacity of the 1-NN classifier, suitably addressing the imbalance condition of the Taiwan dataset. Apart from that, the ANN and HC methods show very similar performance for all three datasets.

Competitive results for classification accuracy were also obtained for the landslide Yongxin dataset, in particular with the RNFLS classifier. This would suggest that if a landslide dataset had a greater number of prototypes, that is, an enriched feature space, higher classification accuracy could be achieved. On the other hand, enhanced descriptions of key features, such as rainfall infiltration analysis (Tang et al. 2018), could be an important factor when designing a PR classifier.

In addition, it should be highlighted that for all datasets, the performance of the RNFLS classifier is consistently the best. This is also consistent with the ROC graphs, which are shown in Fig. 7, and the corresponding distances to the best classifier which are reported in Table 5. It suggests that “non-exotic” shapes dominate the data distribution in the feature space; thus, a linear subspace of synthetic prototype feature point generation may be a potential choice for classifying slope/landslide condition as stable or at risk of collapse. With that in mind, geometric classifiers could be evaluated, all based on simple but powerful geometric rules whose main advantage is supported by the enrichment of the feature space, such as affine/convex hulls (Cheema et al. 2015). Table 5 shows, highlighted in boldface, the results for the RNFLS classifier.

figure j
Table 4 Classification accuracy. Estimations for Taiwan and Multinational were made with leave-one-out; fivefold cross-validation was used for Yongxin
Full size table
Fig. 7
figure 7

ROC graphs for Taiwan, Multinational, and Yongxin datasets considering 1-NN, ANN, HC, and RNFLS

Full size image

6 Conclusion

Because of the frequent scarcity of available data on slope stability and landslide susceptibility when dealing with real-world information, the use of simple but powerful enrichment/enhancement of existing PR techniques was evaluated in this paper. These techniques derive from the fields of machine perception and computer vision, and until now have been unexplored for this type of geotechnical and natural hazard problem.

The experimental comparison offers sound results under a well-established step-by-step design cycle of a PR system, and provides meaningful insights when a data-driven focus is used. A parameter-free or parameterless classification framework based on the RNFLS, ANN, and hypersphere classifiers supports this inference, where the cornerstone is the powerful concept of territorial hyperspheres. Furthermore, the RNFLS classifier showed the best performance, thus indicating that it is more important to enrich the representational capacity of the prototype feature set for data-driven slope/landslide prediction problems. Also, the experimental comparison enables reproducible results, as (1) only publicly available datasets were used, (2) the entire actual code was presented using source snippets in a free general-purpose programming language such as Python, and (3) the classifiers employed in this paper do not require any previous knowledge in order to tune a (hyper)parameter set.

Table 5 Distances to the perfect classifier: (0,1) corner of the ROC graph
Full size table

Finally, an interesting direction in which this paper may be extended is the use or ensemble of advanced geometric classifiers, mentioned in the final part of Sect. 4. In particular, a geometric extension of the NFL, the so-called nearest feature plane (NFP), may be suitable for data-driven slope/landslide prediction.