Abstract
Understanding geographical characteristics of distribution patterns and spatial association is essential for spatial statistical inference such as factor exploration and spatial prediction. The geographical similarity principle was recently developed to explain the association between geographical variables. It describes the comprehensive degree of approximation of a geographical structure instead of explicit relationships between variables. However, there are still challenges for geographical similarity-based methods. For instance, all samples are used for prediction, leading to increased calculation burden and reduced prediction accuracy due to the noise and unrelated data in large spatial data sets. This study develops a geographically optimal similarity (GOS) model for accurate and reliable spatial prediction based on the geographical similarity principle. In GOS, the geographical configurations are first characterized, and similarities between unknown and known observation locations are assessed. Next, an optimal threshold is determined to select a small number of observations with optimal similarities for the prediction at each unknown location. Finally, a reliable uncertainty assessment approach is developed to assess and map uncertainties of GOS predictions. A new R package “geosimilarity” is developed to conduct GOS models. In this study, GOS is implemented in predicting spatial distributions of trace elements in a mining region in Australia. Results show that GOS can use a small number of observations to derive more accurate and reliable spatial predictions than linear regression and basic configuration similarity models. In addition, pattern characteristics of predictions can be improved by GOS by eliminating the phenomenon wherein predictions are clustered near mean values and contain striped textures. Therefore, GOS demonstrates greater potential for implementing the geographical similarity principle in spatial predictions by bringing information from samples with relatively high similarities at any location across space for more accurate and effective predictions in broader fields and practice.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Spatial statistical inference is the basis of spatial analysis such as factor exploration and spatial prediction (Jacquez 1999; Møller 2013; Song and Wu 2021). Understanding distribution patterns and spatial association of geographical attributes is an essential approach for spatial statistical inference in geographical information science and mathematical geosciences (Hackeloeer et al. 2014). Current methods based on geographical characteristics for spatial statistical inference can be classified into five categories.
The first category involves assessing the spatial overlap relationships of geographical variables. Spatial overlap analysis is essential for understanding geographical characteristics, patterns, and associations (Zanni et al. 2021; Guo et al. 2010). It can be used to identify the location-based relations of multiple geographical variables to assess the structure of overlap maps and evaluate the overlay error propagation process (Shi et al. 2004).
The second category describes spatial dependence characteristics of variables for modeling spatial patterns and association. The spatial dependence principle assumes that values of attributes at near locations are more closely related than those at distant locations (Tobler 1970). The spatial dependence is usually quantified as spatial neighbor relations, lagged effects, or space-weighted matrix (Song and Wu 2021). The commonly used measures include spatial autocorrelation models (Moran 1950; Anselin 1995), spatial Bayesian hierarchical models (Haining and Haining 2003), geographically weighted regression and improved models (Brunsdon et al. 1996; Fotheringham et al. 2003), and singularity and anomaly models (Cheng 2007; Zuo et al. 2009; Chen and Cheng 2016). For instance, the widely used geographically weighted regression model explores the spatial non-stationarity of geographical attributes through the locally varied association between response and explanatory variables (Brunsdon et al. 1996).
The third category of methods aims at investigating the inherent unequal characteristics of geographical phenomena (i.e., spatial heterogeneity) (Hartshorne 1939). Geostatistical models (i.e., kriging family models) are commonly used methods in this category (Krige 1951; Goovaerts 1997). In kriging family models, hybrid models have been developed by integrating multiple types of geographical characteristics. The typical hybrid kriging models include regression kriging (Hengl et al. 2004), universal kriging (Zimmerman et al. 1999), machine learning-based kriging (Hengl et al. 2018), and geo-additive models (Kammann and Wand 2003). Another essential method is the spatial stratified heterogeneity models (Wang et al. 2010). For instance, the geographical detector model describes spatial stratified heterogeneity by comparing variance within strata and that of the whole study area (Wang et al. 2010, 2016). Meanwhile, advanced models have been developed for spatial statistical inference based on the spatial stratified heterogeneity theory, including optimal parameters-based geographical detectors (OPGD) (Song et al. 2020), interactive detector for spatial associations (IDSA) (Song and Wu 2021), spatial association detector (SPADE) (Cang and Luo 2018), geographically optimal zones-based heterogeneity (GOZH) (Luo et al. 2022), and robust geographical detector (RGD) (Zhang et al. 2022) models.
The fourth category of methods is the second-dimension spatial association (SDA), which explores spatial association using geospatial data outside sampling locations that contain essential geographically local characteristics (Song 2022). SDA models implement more information from spatial data than the first-dimension spatial association (FDA) models that quantify spatial association only using data at sampling locations, such as statistical, machine learning, and most geospatial models. Studies demonstrate that SDA models provide more smooth, effective, and low-uncertainty spatial predictions than FDA models (Song 2022).
The last category is methods of the geographical similarity principle (i.e., the Third Law of Geography), which assumes that similar values of a geographical attribute at different locations are associated with their similar geographical configurations (Zhu et al. 2018; Zhu and Turner 2022). The geographical similarity principle includes three basic concepts. First, a specific target variable’s geographical configuration reveals the target variable’s geographical structure around study locations. The geographical configuration is defined by a set of geographical explanatory variables to the target variable. Second, the similarity of geographical configurations is used to describe the comprehensive degree of approximation of the geographical structure at a location compared with the geographical structure at all other locations. Thus, the geographical similarity of a target variable at an unknown location is determined by explanatory variables at all locations across the study area. Finally, the similarity of geographical configurations is a comparative relationship of a target variable at study locations instead of an explicit relationship between the target variable and explanatory variables commonly used in regression models. Under the geographical similarity principle, geographical attributes can be predicted regarding the geographical configurations of samples and unknown locations (Zhu et al. 2018; Zhu and Turner 2022).
However, there are still challenges for geographical similarity-based models in improving modeling accuracy and effectiveness by describing various geographical characteristics (Zhu and Turner 2022). For instance, the basic configuration similarity (BCS) model, which is the individual sample-based predictive soil mapping method (iPSM), is an innovative method based on the geographical similarity principle (Zhu et al. 2015). In the BCS model, all observations will be used for the prediction at each unknown location since the numbers of observations are relatively small in most of the BCS-based case studies. For a large data set, the computation time will be critically increased, and noise and unrelated data will be included with increased observations in BCS. Therefore, observations should be selected and reduced to improve the prediction accuracy and efficiency.
This study proposed a geographically optimal similarity (GOS) model for accurate and reliable spatial prediction based on the geographical similarity principle. The primary processes of GOS include characterizing geographical configurations using explanatory variables, assessing similarities between unknown and known observation locations, estimating the optimal percentage threshold parameter for selecting observations with the optimal similarities for each unknown location, predicting spatial distributions, and assessing prediction uncertainty. In this study, GOS is implemented in predicting spatial distributions of trace elements, including Cu, Zn, and Pb, in a mining region in Australia.
The remainder of this article is structured as follows. Section 2 describes the steps for calculating the GOS model. Section 3 presents the case study of implementing GOS in trace element prediction, which includes a study area, data, and experiment design. Section 4 shows the results of the GOS-based case study, including outcomes of GOS steps, model validation, spatial prediction and evaluation, and a discussion of the contributions of this study and future recommendations for relevant research. Finally, the study is concluded in Sect. 5.
2 Geographically Optimal Similarity
2.1 Concepts
The geographical similarity assumes that similar values of a geographical attribute at different locations are associated with their similar geographical configurations (Zhu et al. 2018; Zhu and Turner 2022). Based on this principle, the proposed GOS model employs the similarity information at sampling locations with relatively higher similarities with an unknown location than that at other sample locations, which is the optimal similarity, instead of using the similarity information at all sample locations in the BCS model, for more effectively using the geographical similarity and more accurate and reliable spatial prediction. The details of the GOS model stages are presented in the following section.
2.2 Method
A schematic overview of the GOS model is shown in Fig. 1. The GOS model contains the following stages for spatial prediction: characterizing geographical configurations using explanatory variables, assessing similarities between unknown and observation locations, selecting samples with optimal similarities, and analyzing prediction uncertainty. The stages of the GOS model are explained as follows. A new R package “geosimilarity” is developed to conduct GOS models (https://cran.r-project.org/web/packages/geosimilarity/index.html).
2.2.1 Characterizing Geographical Configurations
In the first stage, the geographical configurations are characterized using explanatory variables (i.e., covariates). Geographical configurations reveal the geographical structure and variation of a targeted variable (Zhu and Turner 2022). They are characterized by geographical explanatory variables closely related to the spatial variation of the targeted variable at both sample and unknown locations (Zhu et al. 2015). Thus, selecting effective explanatory variables for characterizing geographical configurations is essential. The primary criteria for selecting explanatory variables are the availability of data and the ability of variables to describe spatial variations of the response variable Z.
In GOS, the variable selection consists of the following steps. First, correlation analysis is used to select potential explanatory variables. Variables significantly correlated with the response variable are used in the subsequent steps. In the second step, the multicollinearity among explanatory variables is examined using a variance inflation factor (VIF). In general, a VIF higher than 10 or 4 will be considered as high multicollinearity, where 4 is a conservative threshold (Song et al. 2021a, b). The determination of the VIF threshold is related to the data size and aim of variable selection. Thus, in this study, 4 is used as the VIF threshold, and variables with VIF values higher than 4 will be removed until the VIF values of all the selected explanatory variables are lower than 4. Finally, the selected variables are used to characterize geographical configurations. The geographical configuration at a given location is presented as a vector of explanatory variables
where \(e_i\) (\(i = 1,...,p\)) is the value of the explanatory variable \(X_i\) (\(i = 1,...,p\)) at a given location.
2.2.2 Assessing Similarity
The second stage is the assessment of similarities between unknown and observation locations based on geographical configurations. Consider the problem of predicting values of a response variable Z at unknown locations \({\textbf{v}}\) using observations at locations \({\textbf{u}}\). The similarity between an unknown location \(\mathbf {v_\beta }\) (\(\beta =1,...,n\)) and an observation location \(\mathbf {u_\alpha }\) (\(\alpha =1,...,m\)) is computed as
where \(S(\mathbf {u_\alpha },\mathbf {v_\beta })\) is the similarity, \(E_i\) is the function for computing the similarity between locations \(\mathbf {u_\alpha }\) and \(\mathbf {v_\beta }\) based on the ith covariate, and P is the function for determining the similarity between \(\mathbf {u_\alpha }\) and \(\mathbf {v_\beta }\) by comparing the covariate-scale similarities of all covariates. In GOS, the minimum operator is used as the P function, as it was found to be effective in determining similarity in previous studies (Zhu et al. 1997, 2015). For the continuous variable \(X_i\), the function \(E_i\) is defined as
where \(\sigma \) is the standard deviation of explanatory variable \(X_i\), including all unknown and observation locations, and \(\delta ({\textbf{u}},{\textbf{v}})\) is the square root of the mean deviation of \(X_i\) at all unknown locations \(\mathbf {v_\beta }\) from that at the observation location \(\mathbf {u_\alpha }\)
Further, the similarity between an unknown location \(\mathbf {v_\beta }\) and all observation locations \({\textbf{u}}\) is presented as a vector of similarities between \(\mathbf {u_\alpha }\) and \(\mathbf {v_\beta }\)
Thus, the value of the response variable at an unknown location can be predicted as a similarity-weighted mean value
where \({\hat{Z}}(\mathbf {v_\beta })\) is equivalent to the BCS-based prediction at the unknown location \(\mathbf {v_\beta }\).
2.2.3 Determining Optimal Similarity
The third stage is the selection of observation locations with optimal similarities with an unknown location by identifying a threshold for determining the optimal similarity. Identifying the optimal similarity threshold is performed using a cross-validation-based prediction error assessment approach. This process includes the following steps.
First, the observation data are randomly divided into training and testing data sets. For instance, 50% of the data are training data, and 50% of the data are testing data. Next, similarities between training and testing locations are computed, and values of the response variable at testing locations are predicted using Eq. 6. The training and testing process is repeated multiple times, for example 10 times, for the more reliable threshold parameter identification. Third, a series of optional percentage threshold \(\kappa \) (\(\kappa \in (0,1]\)) values are used to select observation locations with relatively high similarities with unknown locations
where \(\tau \) is the probability of the quantiles of similarity values. The quantile approach is effective for identifying optimal parameters in models for indicating geographical characteristics and spatial association (Song et al. 2020; Song and Wu 2021; Luo et al. 2021; Song 2022). If \(\kappa =1\) (i.e., \(\tau =0\)), all observations are used to predict values at each unknown location. Fourth, prediction accuracy is assessed using the cross-validation root-mean-square error (RMSE) under each optional percentage threshold \(\kappa \)
where \({\hat{Z}}_j\) and \(Z_j\) are the prediction and observation values at the jth testing location, respectively. Finally, the process of the above steps is repeated N times, and a relationship can be found between \(\hbox {RMSE}\) values and corresponding \(\kappa \) values; the optimal threshold is the percentage threshold that enables the minimum cross-validation \(\hbox {RMSE}\)
where \(\lambda \) is the selected threshold that enables the optimal observation locations for computing similarity. The corresponding similarity threshold is \(S_\lambda \), and \(\hbox {RMSE}(\kappa )\) is the \(\hbox {RMSE}\) value under the percentage threshold \(\kappa \).
Thus, the similarity vector at the unknown location \(\mathbf {v_\beta }\) shown in Eq. 5 is converted as
2.2.4 Spatial Prediction and Uncertainty Analysis
The GOS-based spatial prediction is calculated with the optimal similarity threshold and similarity vectors derived from the above stage using the following equation
where \({\hat{Z}}(\mathbf {v_\beta })\) is the prediction at the unknown location \(\mathbf {v_\beta }\), and \(Z_\lambda (\mathbf {u_\alpha })\) is the observation at location \(\mathbf {u_\alpha }\) with the optimal similarity.
In GOS, the prediction uncertainty is inversely associated with the similarities between unknown and observation locations (Zhu and Turner 2022). The GOS uncertainty is calculated as
where \(\Delta (\mathbf {v_\beta })\) is the uncertainty at the unknown location \(\mathbf {v_\beta }\), Q is the quantile operator, and \(\zeta \) is a probability value which is used to identify the similarity values that have a critical impact on prediction results. In GOS, the recommended \(\zeta \) values are 0.9, 0.95, 0.99, 0.995, 0.999, and 1, where \(\zeta =1\) means that Eq. 12 is equivalent to \(\Delta (\mathbf {v_\beta }) =1-\max (\mathbf {S_\lambda }({\textbf{u}},\mathbf {v_\beta }))\).
3 Application: Geographically Optimal Similarity Models for the Spatial Prediction of Trace Elements
3.1 Study Area and Trace Element Data
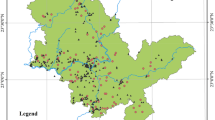
In this study, the GOS model is implemented in the spatial prediction of trace elements in the northwestern Shire of Leonora, a local government area (LGA) and a primarily mining region in Western Australia. The study area is 11,582.6 km\(^2\). Figure 2 shows the location of the study area in Australia, the geological (a) and geographical environments (b), and sampling locations of trace elements in the study area. The geological information includes the locations of faults and spatial distributions of lithology, including regolith, sedimentary siliciclastic, high-grade metamorphic rock, igneous felsic intrusive, igneous mafic intrusive, igneous mafic volcanic, igneous volcanic, and meta-igneous mafic/ultramafic volcanic. The spatial data for faults and lithology are sourced from the Surface Geology of Australia 1:1 million scale data set 2012 edition (Raymond et al. 2012). The geographical information consists of multiple types of natural and social environments, such as locations of mining sites, state and local roads, rivers, and lakes.
The trace element samples are sourced from the Geological Survey of Western Australia (GSWA) Geochemistry data set, which contains geochemical element samples across Western Australia and is stored in the Western Australian Geochemistry or WACHEM database (Department of Mines, Industry Regulation and Safety, Government of Western Australia 2022). The samples of geochemical elements in the WACHEM database were collected from rocks, regoliths, and drill cores (Department of Mines, Industry Regulation and Safety, Government of Western Australia 2022). The GSWA Geochemistry data set has been implemented in a series of geological and mining analyses in Western Australia, including regional-scale regolith geochemistry (Morris et al. 1998), proterozoic mineralization identification (Morris et al. 2003), and mineral footprint assessment (Wells et al. 2016). However, studies have indicated that the GSWA Geochemistry data are “significantly underutilized” (Morin-Ka et al. 2019). Thus, in this study, the GSWA Geochemistry data are used to predict spatial distributions of trace elements in a mining region in Western Australia. In addition, Table 1 shows a statistical summary of trace element observations of Cu, Zn, and Pb samples. In the study area, observations with duplicate locations are calculated as mean values. The resulting numbers of Cu, Zn, and Pb samples are 947, 966, and 953, respectively, and the mean values are 44.04 ppm, 43.52 ppm, and 15.76 ppm, respectively.
3.2 Experiment Design
The GOS-based spatial prediction of trace elements in the study area is designed as shown in Fig. 3. The case study predicts spatial distributions of trace elements at 1-km resolution. The case study process consists of five steps: preprocessing of trace element data, processing and selection of geological explanatory variables data, collection and processing of geographical explanatory variables data, GOS modeling and model validation, and spatial prediction and evaluation. The details of the steps are explained as follows.
The first step is the preprocessing of trace element data. The trace element data were transformed using a logarithm function to avoid impacts on data distributions since trace element data are skewed distributed as shown in Table 1. The potential outliers of trace element data will not be removed if they exist in the logarithm-transformed data, as the high values may indicate the clusters of mineral deposits, which are essential for mining analysis (Cheng et al. 1994; Chen and Cheng 2018).
The second step is the processing and selection of faults and lithology types associated with trace elements. Faults and lithology are essential variables demonstrating geological conditions that are primary determinants of mineral deposits and linked with the spatial distributions of trace elements (Yuce et al. 2009; Song et al. 2012). Thus, this study employs the faults and lithology data sourced from the Surface Geology of Australia 1:1 million scale data set 2012 edition (Raymond et al. 2012) for describing geological conditions. The study area contains 202 parts of faults and eight types of lithology, as shown in Fig. 2. Methods for selecting trace element-related faults and lithology types and deriving faults and lithology-related variables are as follows. First, the mean value (\(\mu _m(F_h,d)\)) of a trace element m at samples within a given distance d from a fault \(F_h\) is compared with the mean value (\(\mu _m\)) of this trace element across the study area. If \(\mu _m(F_h,d)>\mu _m\), the fault \(F_h\) is selected as a trace element m-related fault. When all the trace element-related faults are selected, the distance to the selected faults is calculated as the faults-related variable for the spatial prediction. In this process, the preliminary analysis is required with consideration of the deposit process of trace elements and the spatial distributions of trace elements, faults, and lithology data. According to the preliminary statistical analysis, the parameter d is set as 10 km, as the trace element values within 10 km from faults are closely associated with the distance to faults. In addition, the mean value (\(\mu _m(L_k)\)) of a trace element m in a certain type of lithology \(L_k\) is compared with the mean value (\(\mu _m\)) of trace element m in the whole study area. If \(\mu _m(L_k)>\mu _m\), this type is selected as a trace element m-related lithology. When all the trace element-related lithologies are selected, the distance to the selected lithologies is calculated as the lithology-related variable for spatial prediction.
The third step is the collection and processing of data on potential geographical explanatory variables related to natural and social environments. Although variables of natural and social environments may not link with the causes of trace elements, they are still closely associated with trace element distributions and can be used for the prediction. In the study, nine geographical variables were collected, including elevation, slope, and aspect of terrain; distance to water, including rivers and lakes; vegetation coverage represented using the normalized difference vegetation index (NDVI); soil organic carbon and pH; distance to roads, including state and local roads; and distance to mining sites. The elevation, slope, and aspect of terrain were computed using the Australian Smoothed Digital Elevation Model with a spatial resolution of 30.93 m (Geosciences Australia 2015) and processed using Google Earth Engine (GEE) (Gorelick et al. 2017). The river and lake data were sourced from the GEODATA TOPO 250K Series 3 provided by Geosciences Australia (Geoscience Australia 2006). The annual mean NDVI in 2010 was collected from the Moderate Resolution Imaging Spectroradiometer (MODIS) Terra Vegetation Indices product (MOD13Q1.006) with a 16-day global observation and 250-m spatial resolution processed on GEE (Didan 2015). The soil organic carbon and pH data were sourced from the Soil and Landscape Grid of Australia product with a 92.77 m resolution on GEE (Viscarra Rossel et al. 2014). State and local road network data were sourced from the Road Network data provided by Main Roads Western Australia (Main Roads Western Australia 2020). Locations of mining sites were derived from the GEODATA TOPO 250K Series 3 provided by Geosciences Australia (Geoscience Australia 2006).
The explanatory variable data were computed at both observation sample locations and the 1-km grids for prediction to characterize the geographical configurations. For the grid data, the raster data of elevation, slope, aspect, NDVI, organic carbon, and pH were then converted to grid data with a spatial resolution of 1 km. Distances between 1-km grids and water, roads, and mining sites were calculated using the collected spatial data for rivers and lakes, state and local roads, and mining sites.
The fourth step is GOS modeling and model validation. The prediction accuracy of GOS was evaluated by comparing it with a few commonly used spatial prediction models and previous geographical similarity-based models. The models used for comparing modeling accuracy with GOS include ordinary kriging (OK), multivariate linear regression (MLR), regression kriging (RK), and basic configuration similarity (BCS) models. In the cross-validation, observation data were randomly divided into two parts, where 50% of the data were training data, and 50% of the data were testing data. This process was performed 50 times, and the mean cross-validation indicators were used to evaluate model accuracy. The cross-validation indicators included RMSE as shown in Eq. 8 and mean absolute error (MAE) computed as
The last step is the GOS-based spatial prediction of trace elements and prediction evaluation. The GOS-based spatial prediction and corresponding uncertainty estimation were performed according to the descriptions of the GOS model explained in Sect. 2. The spatial predictions derived from the above five models and prediction uncertainty derived from GOS and BCS were compared to evaluate modeling accuracy. The prediction uncertainty is evaluated using Eq. 12. In addition, this study compares the relationships between similarity and distance of the selected observations used for prediction to demonstrate that the observations with high similarity can be near or remote samples, which is one of the advantages of GOS. Finally, anomalies are identified from the GOS-based spatial predictions of trace elements to examine the probability of mineral deposits using a window-based local singularity analysis (Cheng 1999, 2007; Chen and Cheng 2016; Zuo et al. 2009). First, a series of windows is set with variable sizes at any locations in the study area, where the window sizes are recorded as r. In this study, the window sizes are set as 1 km, 2 km, 3 km, ..., and 10 km. Next, the mean values are calculated for a trace element within different window sizes at any location. The mean values are recorded as b(r). Finally, the relationship between b(r) and r is estimated using Eq. 14
where A is the singularity index, and c is a constant coefficient. The estimation of A at all locations in the study area can generate a map of local singularity. On the singularity map, \(A \ne 2\) indicates the potential anomalies (i.e., extreme values from normal and lognormal distributions) (Cheng 2007).
4 Results and Discussion
4.1 Preprocessed Trace Element Data
Figure 4 shows the statistical summary of the logarithm-transformed trace element data for Cu, Zn, and Pb, respectively. As shown in the summary of the original sample data in Table 1, the trace element data have skewed distributions. The logarithm-transformed data of the three trace elements Cu, Zn, and Pb are close to normal distributions. The data of logarithm-transformed Cu contain three outliers with relatively high values, which are retained in the data set as they may be related to the essential information of mineral deposits.
4.2 Characterization of Geographical Configurations
4.2.1 Selection of Geological Variables
The geological conditions are closely associated with trace element distributions. Figure 5 shows the processes and results of selecting geological variables, including faults and lithology-related variables. Figure 5a shows the selected lithology types closely associated with trace elements. The mean values of trace elements in the areas of selected lithologies are higher than the overall mean values. Figure 5b shows the selected trace element-related faults and the comparisons of spatial distributions of trace element observations and the selected faults and lithology types. Results demonstrate that the relatively high values of trace elements are generally located surrounding the selected faults and lithologies. Figure 5c shows the relationships between trace elements and the geological variables for spatial prediction, including the distance to the selected faults and distance to the selected lithologies. The results show negative correlations between trace elements and distance to trace element-related faults or lithologies.
The processes (a) and results (b) of selecting geological variables, including faults and lithology-related variables, and their relationships with trace element observations (c). Lithology types include regolith (RE), sedimentary siliciclastic (SS), high-grade metamorphic rock (HM), igneous felsic intrusive (IFI), igneous mafic intrusive (IMI), igneous mafic volcanic (IMC), igneous volcanic (IV), and meta-igneous mafic/ultramafic volcanic (MM)
4.2.2 Spatial Distributions of Explanatory Variables
Figure 6 shows the maps of potential explanatory variables used in the study to characterize geographical configurations and predict trace elements. The explanatory variables demonstrate the geological, natural, and social environments across space. The explanatory variables will be selected in GOS.
4.3 Optimal Similarity of Geographical Configurations
Table 2 shows the selected variables for trace elements Cu, Zn, and Pb. The selected variables are significantly correlated with the logarithm-transformed trace element data. The variables with the highest correlation coefficients with Cu, Zn, and Pb are the distance to Cu-related lithology (\(R=-0.432\)), the distance to Zn-related lithology (\(R=-0.428\)), and pH (\(R=0.281\)), respectively. The multicollinearity indicator VIF values are all lower than 4, where the maximum VIF values for modeling Cu, Zn, and Pb are 3.25, 2.97, and 1.95, respectively.
Figure 7 shows the processes and results of determining the optimal percentage thresholds \(\lambda \) used to identify observations with optimal similarities with unknown locations based on geographical configurations. Results show that the cross-validation RMSE tends to be decreased at the beginning and increase after a certain point with the growth of \(\kappa \), the percentage of data used for prediction. This means that if we use fewer observations, the predictions are not reliable. Suppose we use more observations to calculate similarities and perform predictions. In that case, the prediction error will be increased because observations with low similarities with the unknown locations will bring errors, noise, and unrelated information to the prediction process. Thus, the phenomenon also confirms that selecting a reasonable number of observations is essential to assess the similarity of geographical configurations. Results show that the optimal percentage thresholds \(\lambda \) values for the predictions of Cu, Zn, and Pb are 0.05, 0.04, and 0.05, respectively. The \(\lambda \) values indicate that only about 4 to 5% of observation data are required for the spatial predictions at each unknown location.
4.4 Model Validation
Figure 8 shows a summary of cross-validation MAE, and RMSE values of spatial predictions performed using OK, MLR, RK, BCS, and GOS for Cu, Zn, and Pb. Table 3 shows the summary of mean values, cross-validation MAE and RMSE, and error reductions by GOS compared with other models. Results show that compared with kriging and linear regression models, spatial prediction errors can be critically reduced by the geographical similarity-based models, including BCS and GOS. Further, compared with BCS, GOS can effectively reduce prediction errors by using the optimal similarity. Compared with OK, the MAE and RMSE values can be reduced by 8.6 to 14.4% and 4.3 to 10.6% by GOS models for Cu, Zn, and Pb predictions, respectively. Compared with BCS, the MAE and RMSE values can be further reduced by 2.3 to 3.4% and 0.9 to 2.4% by GOS models for predicting different types of trace elements, respectively. The reductions by GOS compared with MLR and RK are between the reductions compared with OK and BCS.
4.5 Spatial Prediction and Evaluation
4.5.1 Spatial Prediction
Figure 9 shows the spatial predictions of trace elements across the study area using GOS, OK, MLR, RK, and BCS models. The distributions of predictions can indicate the following findings. First, compared with geographical similarity-based models, (i.e., BCS and GOS), OK underestimates the relatively high and low values, and MLR overestimates and underestimates regions with relatively high and low values, respectively. For instance, in the MLR-based Cu predictions, map values in the northwestern and southwestern regions were much lower than in maps of BCS- and GOS-based predictions. This means that the predictions in these regions may be underestimated. In the MLR-based Zn and Pb prediction maps, Zn in the central and northern regions and Pb in the central and southwestern areas are much higher than that predicted by BCS and GOS-based predictions and may be overestimated by MLR.
In addition, BCS-based predictions contain more values close to the mean values of trace elements in the study area than that predicted by other models, and predictions have striped texture. The phenomenon is also demonstrated by the statistical density distributions (Allegre and Lewin 1995) of trace element predictions shown in Fig. 10. This phenomenon also existed in the BCS-based spatial predictions in previous studies, such as BCS-based elevation prediction and reconstruction (Zhu et al. 1997), soil moisture prediction maps (Zhu et al. 2015), flea index of transmitting plague (Du et al. 2020). Thus, the GOS models can effectively address the issue. From a geochemical perspective, GOS contributes to more accurate, reasonable, and locally detailed predictions. Thus, GOS brings more potential to implement the geographical similarity principle in spatial predictions in broader fields and address practical issues.
4.5.2 Uncertainty Analysis
Figure 11 shows statistics and spatial distributions of uncertainties of predictions derived from BCS and GOS models. Results of the three types of trace elements have similar patterns, and the modeling of Cu is used as an example to show the analysis of prediction uncertainty. Table 4 shows a summary of prediction uncertainties under different probability values (i.e., \(\zeta =0.9, 0.95, 0.99, 0.995, 0.999, 1\)), in quantiles for estimating uncertainties of predicting Cu, Zn, and Pb. The results of prediction uncertainties can be explained from the following aspects. First, the uncertainties of GOS-based predictions are generally lower than that of BCS-based predictions when \(\zeta \ne 1\). When \(\zeta \ne 1\), the mean uncertainties of the three trace elements derived from GOS range from 0.031 to 0.083, but that derived from BCS range from 0.043 to 0.283. The mean uncertainty can be reduced by 28.5 to 74.1% by GOS compared with BCS models when the \(\zeta \) value ranges from 0.9 to 0.999. This means that the prediction uncertainty can be reduced compared to previous geographical similarity-based models. In addition, when \(\zeta =1\), BCS and GOS models will generate identical uncertainties across the study area, although their predictions are critically different. In this scenario, the uncertainty is only related to the maximum similarity at unknown locations. However, similarity values and observation samples used for the prediction at any unknown locations are different in BCS and GOS models. Therefore, it is recommended to consider uncertainty scenarios under different probability (\(\zeta \)) values to ensure the reliable assessment of geographical similarity-based spatial predictions.
4.5.3 Relationship between Similarity and Distance
Figure 12 shows an analysis of the relationship between similarity and distance to sample observations with optimal similarities at any unknown locations across space. The analysis of Cu predictions is used as an example to demonstrate the relationships, and the results of Zn and Pb are similar to that of Cu predictions. In the Cu predictions, 5% of data (i.e., 47 samples), are used for the prediction at an unknown location. Figure 12a and b show the mean (\(\mu \)) and standard deviation (\(\sigma \)) of the distances between the unknown location and the locations of the 5% of sample data used for predicting the trace element value at this unknown location. The maps indicate that data with high similarities can be samples at near, long-distance, and even remote locations. In Fig. 12c and d show four types of distances between unknown locations and their similar samples: \(H_\mu -H_\sigma \) (red), \(H_\mu -L_\sigma \) (orange), \(L_\mu -H_\sigma \) (purple), and \(L_\mu -L_\sigma \) (green), where H and L mean high and low, respectively. This means that in the central regions (green), most of the samples used for prediction are located at short distances, and the variations of the distances are limited, but it does not work in the other three types of regions. For instance, in the eastern region (red), most of the samples used for prediction are located in long-distance areas, and the distances are critically varied. Therefore, the analysis demonstrates that GOS can effectively implement data with high similarities and at critically varied distances to unknown locations for spatial prediction.
Relationships between similarity and distance: spatial distribution of the mean (a) and standard deviation (b) of distances to the observations of Cu samples with optimal similarities; Relationships between mean and standard deviation of distances (c), where the horizontal and vertical lines are mean values, and the spatial distribution of the four types of distances to their similar sample observations
4.5.4 Identification of Anomalies
Figure 13 shows the maps of local singularities of Cu, Zn, and Pb and their statistical a plots. Both the maps and density plots demonstrate that the singularities in most of the areas are close to 2, where the mean values of singularities of Cu, Zn, and Pb are 2.023, 2.017, and 2.006, respectively. This means that the anomalies or extreme values exist in relatively small areas (i.e., the red and blue regions on maps). The locations of the identified anomalies are helpful for the analysis of potential mineral deposits.
4.6 Contributions and Future Recommendations
In summary, the case study of the GOS-based spatial prediction of trace elements demonstrates the following advantages of GOS in spatial modeling based on geographical similarity. First, in GOS, a small number of observations with the optimal similarities for each unknown location (e.g., 4 to 5% of observations) are identified for prediction instead of using all observations in previous geographical similarity-based models. This means that the prediction at an unknown location is only associated with a small number of more similar observations than others instead of all observations. Secondly, by using fewer observations for the prediction, GOS can provide more accurate predictions regarding the cross-validation of prediction accuracy and the comparison with OK, MLR, RK, and BCS models. The RMSE can be reduced by 4.3 to 10.6% by GOS compared with OK and reduced by 0.9 to 2.4% by GOS compared with BCS. Third, the analysis of prediction distributions indicates that GOS can effectively address the issue that many prediction values are close to the mean value and have striped texture in previous geographical similarity-based models. GOS can bring more potential to implement the geographical similarity principle in spatial predictions in broader fields and practice. Finally, GOS includes a new and reliable uncertainty assessment approach (Eq. 12) for geographical similarity-based spatial prediction. The prediction uncertainty assessment indicates that the mean uncertainty in the study area can be reduced by 28.5 to 74.1% by GOS compared with BCS.
Future studies can be developed from the following aspects based on the GOS approach. First, GOS can be integrated with spatial models developed based on spatial dependence and heterogeneity theories for spatial prediction. Each type of spatial prediction method has its advantages, and previous massive studies indicate that integrating different methods can significantly improve prediction accuracy. For instance, GOS can replace the regression part in the regression kriging model to integrate GOS with kriging for prediction. Thus, the GOS-kriging model can reveal the geographical similarity and heterogeneity characteristics in geographical attributes. In this aspect, models that have the potentials to be integrated with GOS include kriging models, geographically weighted regression, geographical detectors, and machine learning algorithms. In addition, it would be helpful to evaluate the model performance of GOS and compare it with other models (e.g., kriging models, geographically weighted regression, and second-dimension spatial association (Song 2022)) under various scenarios, such as different sample sizes and spatial scales. Finally, more applications of GOS in broader fields are recommended to evaluate the effectiveness of the geographical similarity principle in spatial statistical inference. In addition to the definition in this study, the spatial similarity may also be defined by the local and surrounding geographical conditions, structures, and texture at the sample and unknown locations.
5 Conclusion
This study proposed a GOS model for the geographical similarity principle-based spatial prediction. The detailed steps of GOS and the implementation of GOS in practice were provided in the study. Compared with previous geographical similarity-based approaches, GOS contains the following two new components for modeling. First, an optimal percentage threshold determination approach was developed to select a small number of observations with optimal similarities for the prediction at each unknown location. In addition, a reliable uncertainty assessment approach was developed for assessing and mapping uncertainties of GOS predictions. In this study, GOS was implemented in predicting spatial distributions of trace elements, including Cu, Zn, and Pb, in a mining region in Australia. Results show that GOS can effectively explain geographical configuration information of trace elements and can use a small number of observations to derive more accurate and reliable spatial predictions than linear regression and basic configuration similarity models. In addition, pattern characteristics of predictions can be improved by GOS compared with previous geographical similarity-based models by eliminating the phenomenon that predictions are clustered near mean values and containing striped textures. Therefore, GOS can bring more potential to implement the geographical similarity principle in spatial predictions in broader fields and practice.
References
Allegre CJ, Lewin E (1995) Scaling laws and geochemical distributions. Earth Planet Sci Lett 132(1–4):1–13
Anselin L (1995) Local indicators of spatial association-lisa. Geogr Anal 27(2):93–115
Brunsdon C, Fotheringham AS, Charlton ME (1996) Geographically weighted regression: a method for exploring spatial nonstationarity. Geogr Anal 28(4):281–298
Cang X, Luo W (2018) Spatial association detector (spade). Int J Geogr Inf Sci 32(10):2055–2075
Chen G, Cheng Q (2016) Singularity analysis based on wavelet transform of fractal measures for identifying geochemical anomaly in mineral exploration. Comput Geosci 87:56–66
Chen G, Cheng Q (2018) Fractal-based wavelet filter for separating geophysical or geochemical anomalies from background. Comput Geosci 50(3):249–272
Cheng Q (1999) Multifractality and spatial statistics. Comput Geosci 25(9):949–961
Cheng Q (2007) Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in gejiu, yunnan province, china. Ore Geol Rev 32(1–2):314–324
Cheng Q, Agterberg F, Ballantyne S (1994) The separation of geochemical anomalies from background by fractal methods. J Geochem Explor 51(2):109–130
Department of Mines, Industry Regulation and Safety, Government of Western Australia (2022) Gswa geochemistry. https://www.dmp.wa.gov.au/GeoChem-Extract-Geochemistry-1559.aspx. Accessed 1 Mar 2022
Didan K (2015) Mod13q1 modis/terra vegetation indices 16-day l3 global 250m sin grid v006 [data set]. nasa eosdis land processes daac. https://developers.google.com/earth-engine/datasets/catalog/MODIS_006_MOD13Q1
Du H, Zhu AX, Wang Y (2020) Spatial prediction of flea index of transmitting plague based on environmental similarity. Ann GIS 26(3):227–236
Fotheringham AS, Brunsdon C, Charlton M (2003) Geographically weighted regression: the analysis of spatially varying relationships. Wiley, New York
Geoscience Australia (2006) Geodata topo 250k series 3. https://ecat.ga.gov.au/geonetwork/srv/eng/catalog.search#/metadata/63999
Australia G (2015) Digital elevation model (DEM) of Australia derived from lidar 5 metre grid. Canberra, Commonwealth of Australia and Geoscience Australia
Goovaerts P (1997) Geostatistics for natural resources evaluation. Oxford University Press on Demand
Gorelick N, Hancher M, Dixon M, Ilyushchenko S, Thau D, Moore R (2017) Google earth engine: planetary-scale geospatial analysis for everyone. Remote Sens Environ 202:18–27
Guo Y, Pan M, Wang Z, Qu H, Lan X (2010) A spatial overlay analysis method for three-dimensional vector polyhedrons. In: 2010 18th international conference on geoinformatics. IEEE, pp 1–5
Hackeloeer A, Klasing K, Krisp JM, Meng L (2014) Georeferencing: a review of methods and applications. Ann GIS 20(1):61–69
Haining RP, Haining R (2003) Spatial data analysis: theory and practice. Cambridge University Press, Cambridge
Hartshorne R (1939) The nature of geography: a critical survey of current thought in the light of the past. Ann Assoc Am Geogr 29(3):173–412
Hengl T, Heuvelink GB, Stein A (2004) A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 120(1–2):75–93
Hengl T, Nussbaum M, Wright MN, Heuvelink GB, Gräler B (2018) Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 6:e5518
Jacquez GM (1999) Spatial statistics when locations are uncertain. Geograph Inf Sci 5(2):77–87
Kammann E, Wand MP (2003) Geoadditive models. J Roy Stat Soc Ser C (Appl Stat) 52(1):1–18
Krige DG (1951) A statistical approach to some basic mine valuation problems on the witwatersrand. J S Afr Inst Min Metall 52(6):119–139
Luo P, Song Y, Wu P (2021) Spatial disparities in trade-offs: economic and environmental impacts of road infrastructure on continental level. GIScience Remote Sens 58(5):756–775
Luo P, Song Y, Huang X, Ma H, Liu J, Yao Y, Meng L (2022) Identifying determinants of spatio-temporal disparities in soil moisture of the northern hemisphere using a geographically optimal zones-based heterogeneity model. ISPRS J Photogramm Remote Sens 185:111–128
Main Roads Western Australia (2020) Road network in western Australia. https://catalogue.data.wa.gov.au/sv/dataset/mrwa-road-network
Møller J (2013) Spatial statistics and computational methods, vol 173. Springer, New York
Moran PA (1950) Notes on continuous stochastic phenomena. Biometrika 37(1/2):17–23
Morin-Ka S, Beardsmore TJ, Duuring P, Guilliamse J, Burley L (2019) The mineral systems atlas-delivering greater value from precompetitive geoscience data. ASEG Ext Abstr 1:1–3
Morris PA, Sanders AJ, Pirajno F, Faulkner JA, Coker J (1998) Regional-scale regolith geochemistry: identification of metalloid anomalies and the extent of bedrock in the archaean and proterozoic of western Australia. In: Taylor G, Pain C (eds) Regolith 98:101–108
Morris PA, Pirajno F, Shevchenko S (2003) Proterozoic mineralization identified by integrated regional regolith geochemistry, geophysics and bedrock mapping in western Australia. Geochem Explor Environ Anal 3(1):13–28
Raymond OL, Liu S, Gallagher R, Zhang W, Highet LM (2012) Surface geology of Australia 1:1 million scale dataset 2012 edition. http://pid.geoscience.gov.au/dataset/ga/74619
Shi W, Cheung CK, Tong X (2004) Modelling error propagation in vector-based overlay analysis. ISPRS J Photogramm Remote Sens 59(1–2):47–59
Song XY, Danyushevsky LV, Keays RR, Chen LM, Wang YS, Tian YL, Xiao JF (2012) Structural, lithological, and geochemical constraints on the dynamic magma plumbing system of the jinchuan ni-cu sulfide deposit, nw china. Miner Deposita 47(3):277–297
Song Y (2022) The second dimension of spatial association. Int J Appl Earth Obs Geoinf 111(102):834
Song Y, Wu P (2021) An interactive detector for spatial associations. Int J Geogr Inf Sci 35(8):1676–1701
Song Y, Wang J, Ge Y, Xu C (2020) An optimal parameters-based geographical detector model enhances geographic characteristics of explanatory variables for spatial heterogeneity analysis: Cases with different types of spatial data. GIScience Remote Sens 57(5):593–610
Song Y, Shen Z, Wu P, Viscarra Rossel RA (2021a) Wavelet geographically weighted regression for spectroscopic modelling of soil properties. Sci Rep 11(1):1–11
Song Y, Wu P, Li Q, Liu Y, Karunaratne L (2021b) Hybrid nonlinear and machine learning methods for analyzing factors influencing the performance of large-scale transport infrastructure. IEEE Trans Intell Transp Syst 23:12287–12300
Tobler WR (1970) A computer movie simulating urban growth in the detroit region. Econ Geogr 46(sup1):234–240
Viscarra Rossel RA, Chen C, Grundy M, Searle R, Clifford D, Odgers N, Holmes K, Griffin T, Liddicoat C, Kidd D (2014) Soil and landscape grid national soil attribute maps—soil attribute release 1. v2. https://doi.org/10.1071/SR14366, https://developers.google.com/earth-engine/datasets/catalog/CSIRO_SLGA
Wang JF, Li XH, Liao Christakos G, Liao YL, Zhang T, Gu X, Zheng XY (2010) Geographical detectors-based health risk assessment and its application in the neural tube defects study of the heshun region, china. Int J Geogr Inf Sci 24(1):107–127
Wang JF, Zhang TL, Fu BJ (2016) A measure of spatial stratified heterogeneity. Ecol Ind 67:250–256
Wells M, Laukamp C, Hancock E (2016) Integrated spectral mapping of precious and base metal-related mineral footprints, nanjilgardy fault, western Australia. GSWA 2016 EXTENDED ABSTRACTS Promoting the prospectivity of Western Australia p 26
Yuce G, Ugurluoglu D, Dilaver AT, Eser T, Sayin M, Donmez M, Ozcelik S, Aydin F (2009) The effects of lithology on water pollution: natural radioactivity and trace elements in water resources of eskisehir region (turkey). Water Air Soil Pollut 202(1):69–89
Zanni M, Brivio F, Grignolio S, Apollonio M (2021) Estimation of spatial and temporal overlap in three ungulate species in a mediterranean environment. Mammal Res 66(1):149–162
Zhang Z, Song Y, Wu P (2022) Robust geographical detector. Int J Appl Earth Obs Geoinf 109(102):782
Zhu AX, Liu J, Zhang DuF, SJ, Qin CZ, Burt J, Behrens T, Scholten T (2015) Predictive soil mapping with limited sample data. Eur J Soil Sci 66(3):535–547
Zhu AX, Turner M (2022) How is the third law of geography different? Ann GIS 28(1):57–67
Zhu AX, Band L, Vertessy R, Dutton B (1997) Derivation of soil properties using a soil land inference model (solim). Soil Sci Soc Am J 61(2):523–533
Zhu AX, Lu G, Liu J, Qin CZ, Zhou C (2018) Spatial prediction based on third law of geography. Ann GIS 24(4):225–240
Zimmerman D, Pavlik C, Ruggles A, Armstrong MP (1999) An experimental comparison of ordinary and universal kriging and inverse distance weighting. Math Geol 31(4):375–390
Zuo R, Cheng Q, Agterberg FP, Xia Q (2009) Application of singularity mapping technique to identify local anomalies using stream sediment geochemical data, a case study from gangdese, tibet, western china. J Geochem Explor 101(3):225–235
Acknowledgements
The author would like to thank Dr. Guoxiong Chen and two anonymous reviewers for their constructive suggestions and valuable feedback on earlier versions of this paper.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that there are no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Song, Y. Geographically Optimal Similarity. Math Geosci 55, 295–320 (2023). https://doi.org/10.1007/s11004-022-10036-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11004-022-10036-8