Porosity Dynamics through Carbonate-Reaction Kinetics in High-Temperature Aquifer Storage Applications

Abstract

While near-surface geothermal energy applications for the heating and cooling of buildings have been in use for decades, their practical adoption is limited by the energy transport rates through soils. Aquifers provide a means to use convective heat transport to improve heat transfer between the building and the aquifer. However, the solid matrix in the aquifer is carbonaceous in nature, and calcification prevention techniques in the heat exchangers for the building also lead to dissolution of the aquifer matrix. Due to the Arrhenius nature of the reaction, dissolution rates may decrease with increasing temperature. An effective medium model is derived for the energy, calcium species, and fluid transport through a dynamic calcite porous medium which undergoes a reaction between the matrix and fluid. To better discern how these competing phenomena affect thermal transport in the aquifer, a two-dimensional Cartesian system is considered, where the vertical axis is parallel to the borehole axis, and flow is in the horizontal direction. An effective medium model is derived for the energy, calcium species, and fluid transport through a dynamic calcite porous medium which undergoes a reaction between the matrix and fluid. Since the fluid velocity decays algebraically with radial distance from the borehole axis, two flow regimes are considered. In one regime, far from the borehole where flow rates are small, conductive thermal transport acts faster than the species transport, leading to a case where precipitation dominates and regions of the smallest porosity contract to limit energy recovery. In regions with larger porosity, moderate advection of the species is sufficient to prevent significant pore closures over the time scale of exploration. The second regime, closer to the borehole, larger flow rates reduce species concentrations sufficiently to dissolve the solid phase between pores. In this second regime, Taylor dispersion effects in both energy and species transport compete, but thermal conduction acts more slowly than advection, promoting dissolution. The critical limitation in modeling the long-term evolution of the aquifer structure is the in situ dissolution rate.

1 Introduction

Thermal regulation of buildings is a sizable portion of the energy budget worldwide, with residential and commercial sectors accounting for nearly 40% of the total U.S. energy consumption in 2018 according to the U.S. Energy Information Administration. (https://www.eia.gov/tools/faqs/faq.php?id=86&t=1). Finding an economically competitive technology that has a minimum carbon impact is crucial to reducing CO$_2$ concentrations in the atmosphere. One option is geothermal energy, and while large-scale harnessing of energy near geologically active sites is a more familiar approach to capturing thermal energy from the earth, a lower-power alternative captures excess ambient heat in the summer and stores this in the earth, to be retrieved in the winter for heating. Small residential systems have been installed nationwide for nearly 40 years, and recently the start-up Dandelion Energy, started from Alphabet’s X division, has begun to install these systems in the US (see https://x.company/projects/dandelion/). However, these systems are limited by the rate that energy can be delivered from the earth to the residence, so that if geologically the only means of energy transfer is conduction, a larger and more expensive piping network is required to retrieve or deposit the energy.

Aquifers provide a natural and promising solution to this thermal bottleneck. The thermal mass of the matrix allows for comparable energy storage as would be found for these conduction-dominated systems, with the benefit that the fluid connectivity throughout the aquifer provides a means to use the fluid as a coolant, greatly improving the heat transfer rates. One such system is in the Upper Malm formation within the Bavarian Molasse Basin in Germany. The formation is a carbonate-karstified groundwater aquifer which attains a vertical thickness up to 600 m (Prestel et al. 1991). While the Pullach site takes advantage of the higher-fluid temperatures at the deepest parts of the aquifer for geothermal energy production (Baumann et al. 2017), our work here centers on a carbonaceous aquifer in the northeastern part of the Bavarian Molasse Basin. Here, ambient temperatures are 22$^{\circ }$C, and have tight caprock formations above and below the aquifer (Dorsch and Pletl 2012; Fritzer et al. 2014). Karstification in this region allows better flow transport compared to the porosity of the calcite material found in the solid fraction. The goal for this site would be for the energy to be stored in the water fraction (Lee 2013).

At this site a research borehole was drilled, and a push-pull heat storage test was conducted as described in Ueckert and Baumann (2019). The heat storage test was performed at a flow rate of $15\,$L/s and with injection/production cycles ranging over $2.5\,$ days (Ueckert and Baumann 2019). Nearly 48% of the injected energy was recovered. During the injection phase of the cycle, $\hbox {CO}_{2}$ was added to the injected fluid during heating of the water, before the heat exchangers. This injected solution was slightly supersaturated with respect to calcite at this elevated temperature, but was undersaturated at the ambient temperature of the aquifer. This led to significant dissolution of carbonates from the aquifer.

During the initial stage of this test, the time scales over which the temperature and species concentrations equilibrated were much slower than the advective transport near the borehole. The full reaction problem near the fluid/matrix interface is likely far from equilibrium in this case. Most experimental models of this reaction depend on the local species concentrations of the reactants and products, the coefficients of which depend nonlinearly on temperature which is spatially uniform Plummer et al. (1978), and under the assumption of weak gradients in species concentrations and temperature. Further, these dissolution rate models change in form radically over pH, while a consistent behavior of these models is that the dissolution rate decreases with increasing temperature and increasing calcium concentrations. In our model that follows, we assume that the net effects of the nonequilibrium effects over the time-scales of temperature equilibration are negligible compared to the much longer time scale of the heat storage and retrieval test and application.

In particular, data related to the composition and flow properties of the Malm aquifer site centered on core samples from the drilling of the research borehole, and hydraulic testing once the borehole was established. Core samples consisted primarily of calcite and dolomite, and the pore scales of these samples were nearly impermeable to water. However, there was a 100 m section of the Malm aquifer for which no data were collected, and it is surmised that this section may consist of karst topography through which the matrix may be quite permeable. The hydraulic tests later confirmed this hypothesis, leading to a net transmissivity of $0.1\,$m$^2/$s (Ueckert and Baumann 2019). The maximum local hydraulic conductivity of $6\times 10^{-3}\,$m/s, with a porosity of nearly 20% suggests a pore radius of nearly $1\,$mm.

Given that a high-temperature aquifer storage system is expected to last decades due to its high installation cost, a mathematical or computational model is needed to better understand the long-term impact of dissolution on the system performance. Any modeling description needs to represent the impact over meters of the dominant physics on the pore scale of $1\,$mm. The time scales of these processes range from minutes to days, and the goal would be to understand the net behavior over years. These disparate length and time scales show that direct computational approaches are simply not feasible to achieve all of these requirements. Further, given that the flow rate in the aquifer is inversely proportional to the radial distance from the borehole, this modeling approach needs to be applicable for a wide range of flow rates. The central scientific question of this work is How does calcite kinetics with fluid flow affect the thermal performance and structural integrity of the aquifer?

In this work, a mathematical description is derived on the meter-length scale (macroscale), which captures the average effects of hydrochemistry, hydrology and thermal transport over the fine-scale (microscale). To facilitate the modeling, a simple geometric structure to the solid phase of the aquifer is assumed, which allows for convenient analytical solutions of the unknowns in terms of variations over the macroscale. Closure of the macroscale dependence of the unknowns is determined through a modification of the asymptotic technique of homogenization (see Mei and Vernescu 2010 for an overview). By choosing an initially simple geometry for the solid phase, the permeability tensor components can be determined analytically based on the local pore size, which dynamically evolve over long time scales. While limited to the simple geometries, our approach allows for a quantitative understanding of the coupling of different physical processes and their impact on the energy storage performance of the aquifer. These reduced models are then solved computationally. Since the computational models are resolved on the macroscale, run times are significantly reduced, allowing for the exploration over a range of parameters. This research approach provides insight into the hierarchy of dominant mechanisms contributing to heat and mass transport within the system.

Several reactive transport modeling approaches have been tried in the past decade. Classical homogenization techniques have centered on the reactant transport through a reactive media whose structure does not evolve during the process (for example, Allaire et al. 2010). These models require that the flow profile within the pore be laminar, or more precisely, that inertial terms in the momentum equations be much smaller than viscous effects in the flow. As the Péclet number of the system increases, however, secondary advection effects become pertinent in species or thermal transport. Two approaches in this limit are the extension of Taylor dispersion to porous media flows (see Salles et al. 1993), and hybrid homogenization approaches, such as the review from Scheibe et al. (2015), or more specifically for reacting flows, the hybrid model by Battiato et al. (2011). In this latter model, nonuniform reaction rates are determined over a mesoscale between the pore scale and the continuum scale. The relations between pore scale, CO$_2$ concentration, pore evolution in calcite and flow have been explored by Agrawal et al. (2020) for a single isothermal pore, experimentally and computationally. They find that not capturing the pore evolution on the 100$\,\mu$m scale properly leads to underpredicting flow conductivities up to 80%, if their results are incorporated into a pore network model. While recent computational advances to multiscale reactive transport phenomena in porous media have been significant (e.g. see Molins and Knaber (2019) and Molins et al. (2020) for reviews of several approaches), these techniques are computationally intensive and not amenable to large parametric explorations. In all of these applications, energy transport is not included, and how effects on fluid flow during the reaction (e.g. dissolution and precipitation) mitigate energy transport is critical to the evaluation of the aquifer’s potential for use in energy storage.

The remainder of this paper is organized as follows. In Sect. 2 the derivation of the effective medium model in two regions is presented: far from the borehole (species diffusion-limited) and near the borehole (species transport is advection limited). In Sect. 3 the results for both of these cases are presented, focusing on the dynamics during an initial injection phase, along with behavior of the system to periodic cycles of injection and productions. Conclusions are given in Sect. 4.

2 Problem Formulation

Our research methodology here is to formulate a canonical two-dimensional model of a meter-scale section of the aquifer that captures the dominant behavior of species transport and energy transport. Once this model problem has been formulated, the asymptotic techniques of homogenization and a regular asymptotic analysis are used to derive a reduced system of equations that describe species mass conservation, energy conservation, momentum conservation, and the effects of dissolution and precipitation on the porous structure. This reduced model is then solved computationally over the macroscale, and by assuming no significant variations in the solutions in the vertical direction, quantitative results can be achieved over a range of relevant porosities and flow rates.

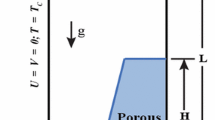
Consider a series of channels within solid calcite, as shown in Fig. 1. Within each channel is a solution of water and ion species, whose composition depends on the local solution temperature and species concentrations that evolve depending on the dominant aqueous carbonaceous reactions. Further, along each solid-liquid interface, surface reactions occur which correspond to the carbon-based kinetics of dissolution of calcite. These reaction rates depend on the aqueous chemistry within each channel, the amount of $\hbox {CO}_{2}$ dissolved in solution, the local pH of the solution, and the local temperature. The goal of this modeling formulation is to incorporate the dominant aqueous and surface chemistry and energy conservation in order to understand the laminate dynamics within high-temperature aquifer storage applications. Reaction rates are necessarily temperature dependent, and knowing how each channel evolves over many storage cycles can aid in determining the energy storage capabilities of an aquifer.

Fig. 1

Schematic of a research borehole near an anisotropic aquifer formation. Heated water, with added $\hbox {CO}_{2}$ to prevent calcification in the heat exchangers, flows through the borehole into the calcite lamellar formation for heat storage. For energy retrieval the solution is pumped from the aquifer, through the borehole to the surface. The model considered in this work centers on a section of the aquifer; a microscale portion is denoted by the red rectangle, and shown in more detail in the upper portion of the Figure

A cell problem is defined as one fluid channel and one calcite laminate. The lower boundary of a characteristic channel is denoted $y^* = -H\,h_{1}(x^*,t^*)$, the upper boundary of this characteristic channel as $y^* = H\,h_2(x^*,t^*)$, and the upper boundary of the calcite laminate as $y^* = H\,h_3(x^*,t^*)$, where H is the characteristic thickness of the cell problem. Let $h_\ell = h_2 + h_1$ be the nondimensional channel thickness, or the liquid fraction of the cell, and $h_s = h_3-h_2$ be the solid fraction of the cell. For all of these functions, variations in $x^*$ are assumed to occur over a longer characteristic scale than the cell length ($L \gg H$); this assumption is intrinsic to the modeling approach for the effective problem derived below. In terms of the structure of the media, a volumetric constraint between liquid and solid fractions of the medium is assumed

$$\begin{aligned} h_\ell + h_s = H\,\lambda \left( \frac{x^*}{L},\frac{y^*}{L}\right) \ , \end{aligned}$$

(1)

where $\lambda$ is the modulation of the period between solid laminates and fluid-filled channels.

Within each channel, dissolved reactants and products are denoted $c_i^{(1)}$, the molar concentration of species i, and they are governed by advection, diffusion, reaction equations

$$\begin{aligned} \frac{\partial c_i^{(1)}}{\partial t} + \mathbf {u}\cdot \nabla c_i^{(1)} = \nabla \cdot \left\{ D_i(T^{(1)})\nabla c_i^{(1)}\right\} + \mathcal {R}_i^{*}(T^{(1)},c_1^{(1)},\ldots ,c_n^{(1)}), \end{aligned}$$

(2)

where $\mathbf {u}$ is the fluid velocity, $D_i(T^{(1)}) = (\rho _1 k_B T)/(6 \pi \mu R)$, is the Stokes-Einstein relation for mass diffusion, with $k_B$ as Boltzmann’s constant, and R is a characteristic radius of the ionic pair, $T^{(1)}$ is temperature of the solution, $\mathcal {R}_i^{*}$ is the reaction rate for the $i^\mathrm{th}$ reaction per unit volume, which can depend on the other species concentrations and temperature. For simplicity, species diffusivity is assumed to be independent of temperature in the following.

From the reduced chemistry model Plummer et al. (1978), the following aqueous reactions take place in each channel

$$\begin{aligned} {\hbox {CO}_{2\mathrm{(g)}} + \hbox {H}_{2}\hbox {O} \rightleftharpoons {\hbox {H}_{2}\hbox {CO}_{3}}^{*}}&,&{\hbox {H}_{2}\hbox {CO}_{3}}^{*} \rightleftharpoons \hbox {H}^{+} + {\hbox {HCO}_{3}}^{-} \ , \ \end{aligned}$$

(3)

$$\begin{aligned} {{\hbox {HCO}_{3}}^{-} \rightleftharpoons \hbox {H}^{+} + \hbox {CO}_{3}^{2-}}&,&{\hbox {H}_{2}\hbox {O} \rightleftharpoons \hbox {H}^{+} + \hbox {OH}^{-}}, \ \end{aligned}$$

(4)

using the the notation

$$\begin{aligned} {{\hbox {H}_{2}\hbox {CO}_3}^{*}} = {\hbox {CO}_{2\mathrm{(aq)}}} + {[\hbox {H}_{2}\hbox {CO}_{3}]} . \end{aligned}$$

(5)

Along each channel wall, dissolution of the solid matrix takes place based on the local temperature and local solid composition of the matrix. The aquifers of interest consist of a mixture of calcite and dolomite, and in this model, our focus is on the evolution of the calcite reactions. The forward reaction is modeled from Plummer et al. (1978), which is pH-dependent

$$\begin{aligned} \hbox {CO}_{2\mathrm{(g)}} + \hbox {H}_{2}\hbox {O} + \hbox {CaCO}_{3} \leftrightarrow \hbox {Ca}^{2+} + {2\hbox {HCO}_{3}}^{-} . \end{aligned}$$

(6)

Note that the reaction times of (3)-(4) are on the order of seconds, compared to the reaction time of the surface reaction (6), which is on the diffusion time scale on the order of hours. Hence, the aqueous reactions are assumed to be quasi-steady, which results in the following equilibrium relations for the molar concentrations (Plummer et al. 1978)

$$\begin{aligned} K_1(T^{(1)}) = \frac{{[{\hbox {H}_{2}\hbox {CO}_3}^{*}]}}{{[\hbox {CO}_{2\mathrm{(g)}}]}}&,&K_2(T^{(1)}) = \frac{{[\hbox {H}^{+}]}\,{[{\hbox {HCO}_{3}}^{-}]}}{{[{{\hbox {H}_{2}\hbox {CO}_{3}}^{*}}]}} , \ \end{aligned}$$

(7)

$$\begin{aligned} K_3(T^{(1)}) = \frac{{[\hbox {CO}_{3}^{2-}]}\,{[\hbox {H}^{+}]}}{{[{\hbox {HCO}_{3}}^{-}]}}&,&K_4(T^{(1)}) = {[\hbox {H}^+]}\,{[\hbox {OH}^{-}]} , \ \end{aligned}$$

(8)

where $K_{i}$ is the equilibrium ‘constant’ of reaction i, where $i = 1,2,3,4$. Each of these $K_i$ depends on solvent temperature $T^{(1)}$ in the form

$$\begin{aligned} K_{i}(T^{(1)}) = K_{oi}\,e^{-A_{i}\left( \frac{1}{T^{(1)}}-\frac{1}{T_o}\right) }\, T_o = 298\,\mathrm{K}. \end{aligned}$$

(9)

In solution within each channel, ${[\hbox {Ca}^{2+}]}$ does not undergo reaction, so the concentration is governed by advection and diffusion

$$\begin{aligned} \frac{\partial c_1^{(1)}}{\partial t} + \mathbf {u}\cdot \nabla c_1^{(1)} = \nabla \cdot \left\{ D\,\nabla c_i^{(1)}\right\} . \end{aligned}$$

(10)

The solution in the channels is electrically neutral, and the number of positive and negative ion species balance uniformly. Since the charge density for each species is the species concentration times the charge per ion, balancing positive and negative charge gives the relation

$$\begin{aligned} 2\,{[\hbox {Ca}^{2+}]} + {[\hbox {H}^+]}= & {} {[{\hbox {HCO}_{3}}^{-}]} + 2\,{[\hbox {CO}_3^{2-}]} +{[\hbox {OH}^{-}]}, \end{aligned}$$

(11)

which, when combined with (8) gives an expression in terms of ${[\hbox {H}^+]}$, ${[{\hbox {HCO}_{3}}^{-}]}$ and ${[\hbox {Ca}^{2+}]}$.

For notational convenience, let $c_1^{(1)} = {[\hbox {Ca}^{2+}]}$, $c_2^{(1)} = {[{\hbox {HCO}_{3}}^{-}]}$, $c_3^{(1)} = {[\hbox {CO}_{2\mathrm{(g)}}]}$, and $c_4^{(1)} = {[\hbox {H}^{+}]}$, and where the other species can be found from these quantities through (7).

The fluid mixture is convected in the positive $x^*$-direction by the application of a time-dependent pressure drop of amplitude $\varDelta P$. The fluid temperature at the medium inlet is elevated compared to the ambient temperature $T_o$ by a temperature magnitude of $T_i - T_o$. Of interest is to capture the evolution of the channel walls due to the reaction kinetics between the solid matrix and the solution, while incorporating the temperature and flow dynamics over time on macroscopic length scales. These processes change the pore geometries, whose characteristic length scale across each channel, H, is much smaller than the macroscopic characteristic length scale along the channel, L.

For simplicity, the fluid mixture within the channel can be described mechanically by an incompressible viscous fluid (water),

$$\begin{aligned} \nabla \cdot \mathbf {u} = 0&,&\rho _1 \left\{ \frac{\partial \mathbf {u}}{\partial t} + \mathbf {u}\cdot \nabla \mathbf {u}\right\} = -\nabla p + \mu \nabla ^2\mathbf {u}, \end{aligned}$$

(12)

where $\mathbf {u} = u \mathbf {i} + v \mathbf {j}$ is the fluid velocity, $\rho _1$ is the fluid density, p is the fluid pressure, and $\mu$ is the fluid dynamic viscosity. Energy transport within the channel is dominated by convection and diffusion

$$\begin{aligned} \rho _1 c_{p1} \left\{ \frac{\partial T^{(1)}}{\partial t} + \mathbf {u}\cdot \nabla {T^{(1)}}\right\} = k_1 \nabla ^2 T^{(1)}\ , \end{aligned}$$

(13)

where $c_{p1}$ is the heat capacity of the fluid, and $k_1$ is the thermal conductivity of the fluid. The fluid properties are assumed to be unaffected by the chemistry and the energy transport within the pore.

In the solid phase, energy transport is governed by conduction

$$\begin{aligned} \rho _2 c_{p2} \left\{ \frac{\partial T^{(2)}}{\partial t}\right\}= & {} k_2\,\nabla ^2 T^{(2)}, \end{aligned}$$

(14)

where $\rho _2, c_{p2}$, and $k_2$ are the density, specific heat, and thermal conductivity of the calcite, respectively.

Let $c_1^{(2)} = \left[ \mathrm {CaCO}_3\right]$ as the molar volume fraction of calcite in the matrix. For mass conservation, per unit axial length in each channel

$$\begin{aligned} \frac{\partial \left\{ h_s\,\rho _2\right\} }{\partial t}= & {} -M_1^{(2)}\,c_1^{(2)}\, \left\{ \left. \sqrt{1+h_{2,x^{*}}^{*2}}\,\mathcal {R}^*\right| _{y^* = h_2^{*}} + \left. \sqrt{1+h_{3,x^{*}}^{*2}}\,\mathcal {R}^*\right| _{y^* = h_3^{*}}\right\} ,\qquad \end{aligned}$$

(15)

where $M_1^{(2)}$ is the molecular weight of calcite, and $\mathcal {R}^{*} = k^* \left\{ K_{eq,s}\,c_1^{(1)}/(K_{eq,s}\,c_1^{(1)} + 1)\right\}$ corresponds to the surface reaction of dissolution of calcite, with $k^*$ being the reaction rate, Plummer et al. (1978).

$$\begin{aligned} k^* = \bar{k}\left\{ a_{1}{[\hbox {H}^{+}]} + a_2{[\hbox {H}_{2}\hbox {CO}_{3}]} + a_3 {[\hbox {H}_{2}\hbox {O}]} - a_4 {[\hbox {Ca}^{2+}]} {[{\hbox {HCO}_{3}}^{-}]}\right\} , \end{aligned}$$

(16)

with

$$\begin{aligned} a_1 = \exp {\left\{ 0.198-444/T^{(2)}\right\} }&,&a_2 = \exp {\left\{ 2.84-2711/T^{(2)}\right\} } \ ,\ \\ a_3 = \exp {\left\{ -5.86-317/T^{(2)}\right\} }&,&a_4 = \exp {\left\{ -1.1-1737/T^{(2)}\right\} } . \end{aligned}$$

$\bar{k}$ carries the units of the reaction. The functional dependence of $c_1^{(1)}$ follows that for Langmuir-isotherm models in surface-based reactions, with $K_{eq,s}$ as a surface equilibrium constant, in units of cm$^3$/mole.

Finally, each channel wall is dynamic due to the reaction (15), which gives the kinematic boundary condition for the dynamics of the channel thickness

$$\begin{aligned} \frac{\partial h_\ell }{\partial t} = \frac{M_1^{(2)}\,c_1^{(2)}}{\rho _2} \left\{ \left. \sqrt{1+h_{2,x^{*}}^{*2}}\,\mathcal {R}^*\right| _{y^* = h_2^{*}} + \left. \sqrt{1+h_{1,x^{*}}^{*2}}\,\mathcal {R}^*\right| _{y^* = h_1^{*}}\right\} , \end{aligned}$$

(17)

requiring that the reaction rate at the lower boundary of the fluid channel be the same for each $x^*$ as the reaction rate at the upper boundary of the laminate.

At each channel wall, the no-slip boundary condition, continuity of temperature, the balance of normal heat flux, and the mass balance of calcium for the reaction are applied (6),

$$\begin{aligned} \mathbf {u}\cdot \mathbf {t}= & {} 0, \ \end{aligned}$$

(18)

$$\begin{aligned} T^{(1)}= & {} T^{(2)}, \ \end{aligned}$$

(19)

$$\begin{aligned} k_1 \nabla T^{(1)}\cdot \mathbf {n}= & {} k_2\nabla T^{(2)}\cdot \mathbf {n}, \end{aligned}$$

(20)

$$\begin{aligned} \left\{ \mathbf {q}_1^{(1)} + 2\,\mathbf {q}_2^{(1)}-\mathbf {q}_3^{(1)}\right\} \cdot \mathbf {n}= & {} \,\mathcal {R}^*, \end{aligned}$$

(21)

where $\mathbf {q}_j^{(1)} = -D\nabla c_j^{(1)} + \mathbf {u} c_j^{(1)}$ is the flux (diffusion and convection) of species j in the fluid. The vectors $\mathbf {t}$ and $\mathbf {n}$ denote the unit tangent and normal vectors along the pore wall

$$\begin{aligned} \mathbf {t} = \frac{\mathbf {i} + (\partial h_\ell /\partial x^*)\mathbf {j}}{\sqrt{1+h_{\ell ,x^{*2}}}} \, \ \mathbf {n} = \frac{\mathbf {j} - (\partial h_\ell /\partial x^*)\,\mathbf {i}}{\sqrt{1+h_{\ell ,x^{*2}}}}. \end{aligned}$$

Table 1 List of characteristic dimensional values of parameters.

Finally, the boundary conditions in the streamwise direction of cell problem, which depend on the flow conditions of the application, are given by

$\underline{\mathrm{{Injection}\mathrm{:}}}$:

Heated fluid from the well enters the channel and displaces fluid

$$\begin{aligned}&\underline{x^* = 0}: p = \rho _1 c_{p1}T^{(1)}_{x^*} = \rho _1\,c_{1} u (T^{(1)} - T_i) \ , \ D\,c^{(1)}_{1x^*} = u (c^{(1)}_1 - C_i), \nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned}&\underline{x^* = L}: p = P_o\ , \ k_1\,T^{(1)}_{x^*} = 0 \ , \ D\,c^{(1)}_{1x^*} = 0, \end{aligned}$$

(23)

$\underline{\mathrm{{Production}\mathrm{:}}}$:

   Fluid is pulled from the system

$$\begin{aligned}&\underline{x^* = 0}: p = P_p - P_o\ , \ k_1\,T^{(1)}_{x^*} = 0 \ , \ D\,c^{(1)}_{1x^*} = 0, \end{aligned}$$

(24)

$$\begin{aligned}&\underline{x^* = L}: k_1\,T^{(1)}_{x^*} = -\rho _1\,c_{p1} u (T^{(1)} - T_o) \ , \ D\,c^{(1)}_{1x^*} = -u (c^{(1)}_1 - C_o). \qquad \end{aligned}$$

(25)

In these conditions, $P_i$ is the applied pressure at the inlet during injection, $P_o < P_i$ is the ambient pressure of the system (assumed to be applied at $x^* = L$), and $T_i$ is the injection temperature of the fluid, while $C_i$ is the injection concentration of the calcium ion species. During production, $P_p < P_o$ is the production pressure to remove the fluid from the system, and $T_o, C_o$ are the values of the equilibrium temperature and calcium activity in the channel. Note that these conditions may not be representative of the actual conditions of the system during these processes, but do represent a reasonable first approach in order to understand the dynamics of the pore shape during injection and production.

Table 2 List of characteristic nondimensional parameters. Based on the values of Table 1

An asymptotic approach is used to reduce this problem to one that is computationally feasible on the time and length scales of interest. The derivation can be found in the Supplemental Materials document on the Journal’s website. The resulting equations depend on the distance the domain of interest is from the borehole, since the characteristic velocity of the region is inversely proportional to the distance from the borehole based on mass conservation. Thus, far from the borehole, $Pe_c$ is small, and here is defined as $Pe_c = \epsilon \overline{Pe}_c$, where $\overline{Pe}_c= O(1)$. The momentum balance in the fluid, species mass conservation, energy conservation, and channel wall dynamics are described by, to leading order

$$\begin{aligned} \frac{\partial }{\partial x_1}\left\{ \frac{h_\ell ^3}{12}\frac{\partial p_o}{\partial x_1} \right\}= & {} \frac{v_{12}\,Da}{\overline{Pe}_c}\, \mathcal {R}, \end{aligned}$$

(26)

$$\begin{aligned} h_{\ell }\,\frac{\partial c_1^{(1)}}{\partial t}-\overline{Pe}_c\, \frac{h_\ell ^3}{12}\,\frac{\partial p_o}{\partial x_1}\,\frac{\partial c_1^{(1)}}{\partial x_1}= & {} \frac{\partial }{\partial x_1} \left\{ h_\ell \,\frac{\partial c_1^{(1)}}{\partial x_1}\right\} + \frac{Da}{5}\,\mathcal {R}, \end{aligned}$$

(27)

$$\begin{aligned} \bar{c}_p\,\frac{\partial \theta _o}{\partial t} - \overline{Pe}_c\,\frac{h_\ell ^3}{12}\,\frac{\partial p_o}{\partial x_1}\,\frac{\partial \theta _o}{\partial x_1}= & {} \nabla \cdot \left\{ \left( \begin{array}{cc} \bar{\alpha } &{} 0 \\ 0 &{} \hat{\alpha } \end{array} \right) \nabla \theta _o \right\} \end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial h_{\ell }}{\partial t}= & {} v_{12}\,Da \mathcal {R}, \end{aligned}$$

(29)

where Da is the Damköhler number, $\bar{\alpha }$ is the effective thermal conductivity of the medium in the $x_1-$direction, $\hat{\alpha }$ is the effective thermal conductivity of the medium in the $x_2-$direction, and $v_{12}$ is the calcium density ratio of the solution to the solid matrix. Our interest is in how the dynamics of the medium depends on different stages of energy storage and retrieval. These stages can be described in terms of energy injection: fluid at an elevated temperature and prescribed flux molar fraction of calcium ions entering the pore at $x_1= 0$ at a prescribed velocity; energy production: fluid removed at a particular velocity with the temperature of the entering fluid $x_1\gg 1$ determined by the local matrix temperature. Note that these boundary conditions need to be averaged in the $x_2$-direction. Mathematically this gives us the following set of boundary conditions in $x_1$ for $p_o, \theta _o$ and $c_{1}^{(1)}$

$\underline{\mathrm{{Injection}\mathrm{:}}}$:

Heated fluid from the well enters the aquifer and displaces fluid

$$\begin{aligned} \underline{x_1= 0}:&p = 1\ , \ \theta _{x_1} = \left\{ -\frac{\overline{Pe}_c\,h_\ell ^3}{12\,\lambda } \frac{\partial p}{\partial x_1} + \frac{(\lambda -h_{\ell })}{k\,Le\,\lambda }\right\} (\theta - \varDelta T) \ , \ \nonumber \\&c^{(1)}_{1x_1} = -\frac{\overline{Pe}_c\,h_\ell ^3}{12\lambda } \frac{\partial p}{\partial x_1}(c^{(1)}_1 - \varDelta C) \ , \end{aligned}$$

(30)

$$\begin{aligned} \underline{x_1= L}:&p = 0\ , \ \theta _{x_1} = -\frac{(\lambda -h_{\ell })}{k\,Le\,\lambda }\,\theta \ , \ c^{(1)}_{1x_1} = 0, \end{aligned}$$

(31)

$\underline{\mathrm{{Production}\mathrm{:}}}$:

Fluid is pulled from the aquifer and enters the borehole

$$\begin{aligned} \underline{x_1= 0}:&p = -1\ , \ \theta _{x_1} = \frac{(\lambda -h_{\ell })}{k\,Le\,\lambda }(\theta - \varDelta T) \ , \ c^{(1)}_{1x_1} = 0 , \end{aligned}$$

(32)

$$\begin{aligned} \underline{x_1= L}:&p = 0 \ , \ \theta _{x_1} = -\frac{(\lambda -h_{\ell })}{k\,Le\,\lambda }\,\theta \ , \ c^{(1)}_{1x_1} = 0. \end{aligned}$$

(33)

For the dynamics closer to the borehole, the model (26) - (29) is not relevant, since the values of the Péclet number are larger than $O(\epsilon )$. In this situation, interactions between the solutal or thermal gradients and the flow through the pores result in an additional streamwise diffusive effect in the mean which is commonly called Taylor dispersion (Taylor 1953). Extensions to porous media were initially done by Brenner (1980), but we follow Salles et al. (1993) in the following formulation, along with using the notation in Ortan et al. (2009).

When convection effects are promoted compared to the previous model, time needs to be rescaled in order to capture the effects of convection,

$$\begin{aligned} t \rightarrow \frac{t}{\epsilon } . \end{aligned}$$

(34)

In other words, when $Pe_c = O(\epsilon )$, one dimensionless time unit of t corresponded to 23 days in the physical application. In the regime where convection effects are promoted, $Pe_c = O(1)$, the new scale shown in (34) results in a nondimensional time unit of approximately 33 minutes, for $\epsilon = 10^{-3}$. Following Salles et al. (1993), with $h_{\ell }$ quasi-steady in the species and energy equations, the resulting new set of (26)– (29) results in

$$\begin{aligned} \frac{\partial }{\partial x_1}\left\{ \frac{h_\ell ^3}{12}\frac{\partial p_o}{\partial x_1} \right\}= & {} \frac{\epsilon \,v_{12}\,Da}{Pe_c}\, \mathcal {R}, \end{aligned}$$

(35)

$$\begin{aligned} h_{\ell }\,\frac{\partial c_1^{(1)}}{\partial t}-Pe_c\, \frac{h_\ell ^3}{12}\,\frac{\partial p_o}{\partial x_1}\,\frac{\partial c_1^{(1)}}{\partial x_1}= & {} \epsilon \,\frac{\partial }{\partial x_1} \left\{ \left( h_\ell + \frac{h_{\ell }^2\,Pe_c^2}{210}\right) \,\frac{\partial c_1^{(1)}}{\partial x_1}\right\} + \frac{\epsilon \,v_{1}^{(2)}\,Da}{5}\,\mathcal {R}, \nonumber \\ \end{aligned}$$

(36)

$$\begin{aligned} \bar{c}_p\,\frac{\partial \theta _o}{\partial t} - Pe_c\,\frac{h_\ell ^3}{12}\,\frac{\partial p_o}{\partial x_1}\,\frac{\partial \theta _o}{\partial x_1}= & {} \epsilon \nabla \cdot \left\{ \left( \begin{array}{cc} \bar{\alpha }\left[ 1 + \frac{h_{\ell }^2\,Pe_c^2}{210}\right] &{} 0 \\ 0 &{} \hat{\alpha } \end{array} \right) \nabla \theta _o \right\} \end{aligned}$$

(37)

$$\begin{aligned} \frac{\partial h_{\ell }}{\partial t}= & {} \epsilon \,v_{12}\,Da \mathcal {R} . \end{aligned}$$

(38)

For the boundary conditions, the new time scale yields the following conditions during injection and production cases:

$\underline{\mathrm{{Injection}\mathrm{:}}}$:

   Heated fluid from the well enters the aquifer and displaces fluid

$$\begin{aligned} \underline{x_1= 0}:&p = 1\ , \ \theta _{x_1} = \left\{ -\frac{Pe_c\,h_\ell ^3}{12\,\lambda } \frac{\partial p}{\partial x_1} + \frac{\epsilon \,h_s}{k\,Le\,\lambda }\right\} (\theta - \varDelta T), \nonumber \\&\ c^{(1)}_{1x_1} = -\frac{Pe_c\,h_\ell ^3}{12\lambda } \frac{\partial p}{\partial x_1}(c^{(1)}_1 - \varDelta C), \end{aligned}$$

(39)

$$\begin{aligned} \underline{x_1= L}:&p = 0\ , \ \theta _{x_1} = -\frac{\epsilon \,h_s}{k\,Le\,\lambda }\,\theta \ , \ c^{(1)}_{1x_1} = 0, \end{aligned}$$

(40)

$\underline{\mathrm{{Production}\mathrm{:}}}$:

Fluid is pulled from the aquifer and enters the borehole

$$\begin{aligned} \underline{x_1= 0}:&p = -1\ , \ \theta _{x_1} = \frac{\epsilon \,h_s}{k\,Le\,\lambda }(\theta - \varDelta T) \ , \ c^{(1)}_{1x_1} = 0, \end{aligned}$$

(41)

$$\begin{aligned} \underline{x_1= L}:&p = 0 \ , \ \theta _{x_1} = -\frac{\epsilon \,h_s}{k\,Le\,\lambda }\,\theta \ , \ c^{(1)}_{1x_1} = 0 . \end{aligned}$$

(42)

3 Results

Porosity changes in the aquifer are determined by the dissolution rate, which depends on the temperature and species concentration. The dissolution rate $\mathcal {R}$ depends on the concentration $c_1^{(1)}$ and the temperature $\theta$. The number of nondimensional parameters in the dissolution rate (see Supplemental Materials, (5)) is large, so these parameters are kept fixed throughout this study. In Fig. 2, a contour plot about the ambient temperature $\theta = 0$ is shown. For $\mathcal {R} = 0$, the equilibrium concentration of the calcium ions decreases with increasing temperature. Thus, if excess calcium is found in the entering solution, then precipitation within the porous medium is expected. Inlet conditions considered here are in the dissolution region of Fig. 2, which is consistent with scaling prevention within the borehole.

Fig. 2

Contour plot of the dissolution rate $\mathcal {R}$ over the range of $\theta$ and values of the calcium ion concentration $c_1^{(1)}$. Note that positive values correspond to states where dissolution takes place

Our choice of $\varDelta C$ is based on the applied temperature difference $\varDelta T$. In the application, the inlet species concentration of the fluid is held below equilibrium conditions in order to prevent scaling. $\varDelta C$ is chosen so that if the temperature of the borehole fluid is elevated, the species concentration is below the equilibrium value at that elevated temperature. The relevant input concentration depends, critically, on the difference between the equilibrium concentration and $\varDelta C$. However, this equilibrium concentration depends on temperature, which changes based on the temperature difference $\varDelta T$ of the incoming fluid and the ambient aquifer temperature. Because of this, the units for $\varDelta C$ are either the fraction of the borehole equilibrium concentration at the borehole fluid temperature $\varDelta T$, or the fraction of the species concentration in the aquifer at ambient temperature.

3.1 Computational Approach and Assumptions

The model (26)–(29) is investigated subject to boundary conditions (30)–(31) or (32)–(33) using finite difference methods. To better understand the different physical mechanisms at work during injection and production, the simpler case when all of the unknown quantities $h_{\ell }, p, \theta , c_{1}^{(1)}$ are independent of $x_2$ is considered. Physically, this corresponds to a uniform distribution as a function of depth. The parameter values of the simulation are shown in Table 2, noting that the Péclet number ranges over three decades. These fixed parameters in the dissolution rate $\mathcal {R}$, as defined in (5) in the Supplemental Materials document, result in a dissolution rate shown in Fig. 2. Note that near the equilibrium contour, dissolution increases with decreasing species concentration and temperature. This figure serves as a guide to see if a system at a particular location and time is in dissolution or precipitation.

Spatially, two grids are introduced on $x_1$, each with spacing $\varDelta x_1$. One grid $\left\{ \varDelta x_1,\ 2\varDelta x_1,\ \ldots ,\ N\,\varDelta x_1\right\}$ where $\varDelta x_1= 1/(N+1)$ is called the Dirichlet grid, and our finite-difference representation of the pressure p is defined on this grid. Our second grid, called the Neumann grid, includes the endpoints of the domain $x_1\in \left[ 0,1\right]$, with grid spacing $\varDelta x_1$, and on this grid our finite-difference representations of the remaining dependent variables $h,\ \theta ,\ c_1^{(1)}$ are defined. These different grids are chosen since the equation for pressure (26) is elliptic, while the equations for $h,\ \theta ,$ and $c_1^{(1)}$ are parabolic, and based on their respective boundary conditions.

The evolution of the system is discretized in time using a fully implicit Crank-Nicolson scheme on (27)–(29) with adaptive time-stepping. The algebraic system is linearized about the current time step, keeping all terms that are linear in terms of the delta formulation for a given time step $\varDelta t$, which gives a truncation error of $O(\varDelta t^2)$. Then, the same problem is solved for two time steps each of duration$(\varDelta t)/2$ each. This latter calculation is used for the starting value of the next time step, and this value along with coarser estimate of the unknowns at the larger time step is used to determine the next time step in order for the solution to be within a given tolerance.

For simplicity in this study, a common set of initial conditions is used. The pressure p and temperature $\theta$ are initially set to zero, $h_{\ell } = 1$, while the initial data for the $c_1^{(1)}$ is picked to be the following form

$$\begin{aligned} c_1^{(1)}(x_1,0) = c_{1,eq} + (\varDelta C - c_{1,eq})e^{-10\,x_1} \, \end{aligned}$$

(43)

where $c_{1,eq}$ is the equilibrium species concentration at the ambient temperature $\theta = 0$ (far-field equilibrium within the aquifer), and $\varDelta C$ is the inlet value of the species concentration. This choice of initial conditions for $c_1^{(1)}$ and of $\varDelta C$ in (43) allows for a smooth, short, transient time over which these initial conditions relax to a relevant local quasi-equilibrium without inducing numerical instabilities.

Another aspect of this problem for which potential numerical instabilities need to be addressed is the transition between injection and production. To prevent instabilities, the following function of time is used as a “switch”:

$$\begin{aligned} f(t) = \frac{1}{2}\left\{ 1 + \tanh {\left[ \sigma (t-t_o)\right] }\right\} . \end{aligned}$$

This function has a transition region $-\log {(10)}/\sigma< t-t_o < \log {(10)}/\sigma$ over which f(t) undergoes a transition between 0.01 and 0.99. The choice of $\sigma$ is flexible, but this value is chosen so that the transition between stages is short, but long enough in order for the simulation to be temporally well-resolved. This transition from injection to production, for example, is regulated by changing the inlet pressure from 1 to $-1$ over the transition period, and then the boundary conditions for $\theta$ and $c_{1}^{(1)}$ are then modulated based on the volumetric flow rate at that given time. One can extend this technique in the determination of $\varDelta T$, for example, when looking at an example similar to the heat storage test described in Ueckert and Baumann 2019 (see Sect. 3.3.2).

The code is designed to run over a fixed time interval, but there are limits to which the current model is physically pertinent. The system (26)–(29) is valid only when $0< h_{\ell } < \lambda$, or if the alternating vertical structure of fluid galley/calcite laminate is maintained. Hence, conditions are introduced at which the script terminates if $h_{\ell } < h_{min} = 0.001$ or $h_{s} < h_{min}$. In the results shown below, this ending time of the simulation is a good metric for determining the dominant physical processes under certain operating conditions.

Lastly, Our results are presented in terms of the porosity $\phi$ and permeability K of the medium over time. To find these properties in terms of the variables of the current model, the extension to the capillary pore model are used (e.g. see Bear 1988; Costa 2016)

$$\begin{aligned} \phi = \frac{h_\ell }{\lambda }&,&K = \frac{h_{\ell }^3}{12\,\lambda }. \end{aligned}$$

(44)

3.2 $Pe_c = O(\epsilon )$

Small values of the Péclet number correspond to low flow rates through the porous medium. These low flow rates, based on the anticipated flow conditions of the energy storage system, correspond to the response of the reacting matrix far from the borehole (hundreds of meters from the borehole). Although this location may not, at first, seem relevant to the short-term behavior of the system, over decades this section of the aquifer will change and these changes may affect the overall ability to transfer energy to and from the aquifer. Further, this limit provides a convenient framework for describing how the interacting processes of energy transfer, species transfer, and reaction interact, providing a conceptual framework for the description of the $Pe_c = O(1)$ results. Recall that the reduced Péclet number $\overline{Pe}_c$ is defined as $Pe_c = \epsilon \,\overline{Pe}_c$, $\overline{Pe}_c= O(1)$, and our results are presented in terms of $\overline{Pe}_c$.

3.2.1 Injection

For the results in this subsection, an injection case is simulated, with the time of the simulation set to $0< t < 8$, which corresponds to a dimensional running time of 6 months. Our focus is to investigate some characteristic behaviors of the media dynamics and transport properties over this time for different $\overline{Pe}_c$ and initial porosities $\phi _o$. After identifying the different physical mechanisms taking place in these examples, variations in porosity and minimum permeability over the $(\phi _o,\overline{Pe}_c)$ parameter space are explored.

Firstly, consider the case for small flow rates through regions on small porosity. In Figs. 3 and 4, the case where $\phi _o$ = 0.01, $\overline{Pe}_c= 10$, $\varDelta T = 0.3$, and $\varDelta C$ = 99% of the ambient temperature equilibrium concentration is shown. Fig. 3 presents the porosity dynamics for this case when $0< t < 6$. In Fig. 3a, the spatial mean of the porosity shows a transient which increases slightly for small times but evolves to a steady decrease reflecting that precipitation dominates in the medium. Figure 3b shows the evolution of the spatial variation in porosity relative to its mean value. For short times, dissolution appears to be faster at the inlet of the flow compare to the outlet, but over longer times, the porosity at the inlet appears to finer compared to the outlet.

Fig. 3

Porosity evolution over time for $\overline{Pe}_c= 10$, $\phi _o = 0.01$, $\varDelta T = 0.3$, and $\varDelta C = 99$%. a Spatial average of porosity over $0< t < 6$. Note that initial transient evolves to steady reduction in porosity due to precipitation. b Spatial porosity profiles relative to the spatial mean

The mechanisms related to this change are due to the different rates of energy and solutal transport during the simulation. In Fig. 4a, the pressure relative to a prescribed linear pressure profile based on the boundary conditions at $x_1 = 0$ and $x_1 = 1$ is shown. Notice that for $t = 6$ the pressure deviation is sufficiently large so that there is no net flow beyond $x_1= 0.5$. This suggests that a circulatory flow has developed in the region $x_1 < 0.5$, resulting in a reduction of solutal and thermal transport by advection. While the convective portion of thermal transport is reduced, conductive thermal transport persists. Further, the circulatory flow limits solutal transport through the medium, resulting in locally larger concentrations near the inlet. This local increase in concentration promotes precipitation near the inlet. As a confirmation of these different rates of thermal and solutal transport, in Fig. 4b, the evolution of the spatial average of the temperature scaled on $\varDelta T$ (solid curve) and the spatial average of the species concentration relative to the far-field equilibrium concentration are shown. Note that the elevated temperature compared to equilibrium is significantly larger compared to the drop in species concentration, suggesting that precipitation would on average dominate over the medium. Hence, the lack of solutal transport compared to thermal transport results in precipitation.

Fig. 4

a Pressure deviation from a linear pressure profile for $t = 2$, $t = 4$ and $t = 6$. Note that at $t = 6$ a stagnation point in the flow develops near $x_1 = 0.5$, preventing advective transport of energy and reduced species. b Transient of the scaled, spatially averaged temperature (solid blue curve) and the scaled averaged calcium concentration (red dashed curve). The values of $\overline{Pe}_c, \phi _o, \varDelta T,$ and $\varDelta C$ are the same as in Fig. 3

Secondly, consider the case where advection plays a more significant role. Consider the case $\overline{Pe}_c= 40$, $\phi _o = 1/3$ and operating conditions $\varDelta T = 0.3$ and $\varDelta C = 99\%$ of the equilibrium value. Figure 5a shows the evolution of the spatially averaged porosity over $0< t < 6$. In this case, porosity increases over this simulation, and note in Fig. 5b that the porosity of the medium is larger at the inlet compared to the outlet. Figure 6a shows the pressure deviation over this range, and note that the magnitude of this disturbance pressure is only 6% of the peak pressure, so flow through the medium is unimpeded. This higher permeability allows for faster solutal and thermal transport, which is seen in Fig. 6b. Note that the spatially averaged temperature equilibrates faster than the solutal average. This solutal average shows the net species balance between dissolution and advective transport. The combination of the elevated temperature and the reduced species concentration results in dissolution throughout the entire medium, which results in the eventual removal of the solid matrix at a finite time.

Fig. 5

a Spatial average of the porosity over time for $\overline{Pe}_c= 40$, $\phi _o = 1/3$, $\varDelta T = 0.3$, and $\varDelta C = 99\%$ of its equilibrium value. b Spatial profile of the porosity relative to the average porosity shown in (a)

Fig. 6

Intermediate time evolution of the system for $\overline{Pe}_c= 40$, $\phi _o = 1/3$, $\varDelta T = 0.3$ and the value of $\varDelta C$ at 99$\,\%$ of the value of equilibrium at the inlet

From these examples, the rates of solutal and thermal transport dictate the behavior of the porosity over time. In order to understand how these effects vary over different $\overline{Pe}_c$ and initial porosity $\phi _o$, consider a variety of values for these parameters, while keeping $\varDelta T$ and $\varDelta C$ fixed. Simulations are performed for $\overline{Pe}_c= 10, 20, \ldots , 100$ and $\phi _o = 1/100, 1/50, 1/25, 1/20, 1/10, 1/8, 3/20, 1/5, 1/4, 1/3$. This gives us 100 parameter value pairs, and all of these simulations are run with the same initial conditions described above for $0< t < 8$. After collecting these data, level curves of the mean porosity $\bar{\phi }$ and the ratio of the minimum value of permeability compared to its initial value $K_{min}/K_o$ are interpolated over the $(\phi _o, \overline{Pe}_c)$ parameter space at $t = 8$

$$\begin{aligned} \bar{\phi } = \int _0^1\, \phi (x_1,8)\,dx_1\ \ , \ \ \left. \frac{K_{min}}{K_o}\right| _{t = 8} = \min _{0<x_1<1} h_{\ell }(x_1,8)^3 \ . \end{aligned}$$

Figure 7 shows these parameter plots for the average porosity (a) and the scaled minimum permeability (b) for $\varDelta T = 0.3$ and $\varDelta C$ at 99% of the inlet equilibrium value. Note that after $t = 8$, the value of the average porosity is slightly reduced for the porosity with $\overline{Pe}_c= 100$, but that minimum permeability decreases for $\phi _o < 0.1$. For values of $\overline{Pe}_c< 70$, the minimum scaled permeability is reduced for all values of $\phi _o$ considered. This observation is consistent with the final porosity profile in Fig. 5a, since the minimum porosity at the outlet is about 0.25, which is significantly less than $\phi _o = 1/3$. In terms of flow and dissolution, this constriction leads to a lower pressure gradient for values of $0< x_1< 0.8$, and then a steeper gradient for $0.8< x_1< 1$. This lower gradient suggests a recirculation flow in the background of the applied pressure drop in the pores.

Fig. 7

Parameter plot of final average porosity (a) and minimum permeability relative to the initial permeability (b) for $10< \overline{Pe}_c< 100$ and $1/100< \phi _o < 1/3$, for $\varDelta T = 0.3$ and $\varDelta C$ kept at 99$\,\%$ of the equilibrium value at the inlet

Fig. 8

Parameter plot of final average porosity (a) and minimum permeability relative to the initial permeability (b) for $10< \overline{Pe}_c< 100$ and $1/100< \phi _o < 1/3$, for $\varDelta T = 0.2$ and $\varDelta C$ kept at 99$\,\%$ of the equilibrium value at the inlet

In Figs. 8 and 9, consider the simulations at the same $\overline{Pe}_c$ and $\phi _o$, but now with $\varDelta T = 0.2$ and $\varDelta T = 0.1$, respectively. From Fig. 2, the dynamics are expected to promote dissolution compared to precipitation, and these plots reinforce this expectation. Note especially the middle figures that denote the scaled minimum permeability, where the regions for which $K_{min}/K_{o}$ are greater than unity now drop below $\overline{Pe}_c= 30$ for $\phi _o = 1/3$. The figures on the right, denoting the average dissolution rate, also show that precipitation is confined for the smallest Péclet numbers and the smallest initial porosities. These curves suggest that poor solutal transport in the porous system relative to thermal transport is the driving mechanism for precipitation.

3.2.2 Long-Term Behavior

The benefit of our modeling choice is that long time scales pertinent to the field application are computationally feasible. Of particular interest is how the inlet temperature varies over time. During injection, a value near that of $\varDelta T$ is expected, and during production, this value should decrease as fluid at an ambient equilibrium temperature enters the computational domain from the outlet. Poor advective transport could also result in less energy being produced, and this would be seen in our model as an inlet temperature which does reach the values of $\varDelta T$.

Consider several cases of $\varDelta T$ and $\varDelta C$ for times over $0< t < 80$, which corresponds to a time range of 5 years. Injection and production periods are assumed to be the same 6-month duration. The data of interest centers on the behavior of the porosity, temperature, pressure and species concentration varies over time at the inlet. The same operating parameters for $\overline{Pe}_c$ and $\phi _o$ are considered as described in the previous section, and we use the same metrics to determine how permeability and average porosity varies over this time frame.

Figure 10 shows (a) the inlet pressure value; (b) the spatial average relative to $\varDelta T$ or $c_{1,eq}$ for the temperature and species, respectively; (c) the transient of the spatial mean of the porosity; and (d) the spatial profile of the porosity relative to its spatial mean over time for $\overline{Pe}_c= 10, \phi _o = 0.01$, $\varDelta T = 0.1$ and $\varDelta C = 99\,\%$ of its equilibrium value. The pressure plot shows the seasonal variation for injection ($p(0,t) > 0$) and production ($p(0,t) < 0$). What is interesting to note here is that the porosity, temperature, and species concentration have nearly the same value at the inlet and the outlet, suggesting that the spatial variations of these quantities are minimal after transients evolve. Note that equilibrium values for the spatial mean are attained after approximately 1 year, while the porosity value continues to be reduced over nearly three years. Physically, the poor advective transport results in the energy being balanced by conduction, and the evolution of the species concentration and the porosity is governed by the reaction rate. Hence, poor permeability in the matrix results in a reduced retrieval of energy from the medium over time.

Fig. 9

Parameter plot of final average porosity (a) and minimum permeability relative to the initial permeability (b) for $10< \overline{Pe}_c< 100$ and $1/100< \phi _o < 1/3$, for $\varDelta T = 0.1$ and $\varDelta C$ kept at 99$\,\%$ of the equilibrium value at the inlet

Fig. 10

a Inlet pressure denoting injection (positive) and production (negative) stages; b Evolution of spatial mean of temperature relative to $\varDelta T$ (solid blue curve) and the spatial mean of the species concentration relative to the far-field equilibrium value (dashed red curve); c Evolution of spatial mean of the porosity over time; d spatial profiles of the porosity relative to its spatial mean. The parameter values here are $\overline{Pe}_c= 10, \phi _o = 1/100, \varDelta T = 0.1, \varDelta C = 0.99$

In contrast, Fig. 11 shows the case when $\overline{Pe}_c= 40$, $\phi _o = 1/3$, $\varDelta T = 0.1$, and $\varDelta C = 0.99$ of the equilibrium value at the inlet for (a) the evolution of the spatial mean of the porosity; (b) the spatial variation of the porosity with respect to the mean; (c) the evolution of the relative spatial mean of the temperature and species concentration over time. Notice that over the simulation the porosity is steadily increasing to above 80%, and the temperatures reach nearly the value of $\varDelta T$ during the injection cycles. Further, the species concentration remains in the dissolution regime for values of $\theta$ shown. Hence for larger initial porosities and for sufficiently large reduced Péclet numbers, solutal transport in the void regions are sufficient to maintain a dissolution reaction until locally a solid layer is breached.

Fig. 11

a Evolution of the spatial mean of the porosity over time; b Spatial profiles of the porosity relative to the spatial mean value; c Evolution of the spatial mean of the temperature relative to $\varDelta T$ (solid blue curve) and the spatial mean of the species concentration relative to $c_{1,eq}$ (dashed red curve). Parameter values are $\overline{Pe}_c= 40, \phi _o = 1/3, \varDelta T = 0.1, \varDelta C = 0.99$

A summary of these results can be seen in Fig. 12, where (a) shows the mean porosity at $t = 80$ over a parameter range of $10< \overline{Pe}_c< 100$ and $1/100< \phi _o < 1/3$. Notice that for the $\overline{Pe}_c= 10$ that the mean porosity is reduced for values of $\phi _o < 0.15$, approximately. For $\overline{Pe}_c> 10$, dissolution appears to be the dominant behavior in this system, and the scaled minimum permeability in these cases results in much larger values of permeability. One anticipates from these figures that over much longer time scales, the dissolution would continue for the larger reduced Péclet numbers; this suggests that a porosity coarsening of the aquifer would occur as a result at these values of $\varDelta T, \varDelta C$. Regions with smaller initial porosity result in smaller values, since the solutal transport in these regions are limited. In regions where the porosity is larger and where convective transport of the species is sufficient, dissolution takes place unchecked by any contrary physical process.

In the case of $\varDelta T = 0.1$, as shown in Fig. 12, the cases are simulated for the full duration of the time interval $0< t < 80$. For larger values of $\varDelta T$, however, this is not the case, and the simulation for some $\overline{Pe}_c$ and $\phi _o$ terminate early. In Figs. 13 and 14 shows the mean porosity (a), and the scaled minimum permeability (b) when the simulation terminates. The time at which the simulation terminates is shown in the right-hand figure in both Figs. 13 and 14. Notice that for regions in the lower left-hand side of the domain (small $\overline{Pe}_c$ and small $\phi _o$), the termination of the program is due to precipitation within the pores, while in the upper right-hand side of the domain, dissolution is dominant. These regions, however, do depend significantly on $\varDelta T$. Comparing the regions where the solution ends before $t = 80$ for $\varDelta T = 0.2$ (Fig. 13) and for $\varDelta T = 0.3$ (Fig. 14), these regions of dissolution and precipitation both increase.

Fig. 12

Parameter plot of final average porosity (a) and minimum permeability relative to the initial permeability (b) for $10< \overline{Pe}_c< 100$ and $1/100< \phi _o < 1/3$, for $\varDelta T = 0.1$ and $\varDelta C$ kept at 99$\,\%$ of the equilibrium value at the inlet over $0< t < 80$

Fig. 13

Parameter plot of final average porosity (a) and minimum permeability relative to the initial permeability (b) for $10< \overline{Pe}_c< 100$ and $1/100< \phi _o < 1/3$, for $\varDelta T = 0.2$ and $\varDelta C$ kept at 99$\,\%$ of the equilibrium value at the inlet over $0< t < 80$

Fig. 14

Parameter plot of final average porosity (a) and minimum permeability relative to the initial permeability (b) for $10< \overline{Pe}_c< 100$ and $1/100< \phi _o < 1/3$, for $\varDelta T = 0.3$ and $\varDelta C$ kept at 99$\,\%$ of the equilibrium value at the inlet over $0< t < 80$

3.3 $Pe_c = O(1)$

While the same computational techniques described in Sect. 3.1 can be implemented to solve (35)–(38), the disparate balance between the advection and conduction terms in the energy equation (37) requires a longer domain in $x_1$ to determine the behavior. Further, the scales between the reaction time scale and the advection time scale differ by $O(1/\epsilon )$, making this system stiff. Using the implicit scheme in time then results in taking small time steps in order to ensure stability of the solutions. The sampling of data in parameter space $Pe_c = O(1)$ require significantly more time and computational resources. Hence, the results presented here are more limited, but they reinforce the behavior seen in the previous section. Please note, for this section, the time variable t has been rescaled by $1/\epsilon$, so a single time unit corresponds to around 33 minutes, compared to the time unit of 23 days in Sect. 3.2.

3.3.1 Injection

In this section, consider the integration of the system (35)–(38) subject to the boundary conditions (39)–(40) over the domain $0< t < 5000$. The initial conditions are the same as used in Sect. 3.2. The goal is to determine the evolution of the mean porosity and the minimum permeability, scaled on its initial value, after this evolution.

Figure 15 shows an example of the evolution of species and energy transport for $Pe_c = 10$, $\phi _o = 1/100$, $\varDelta T = 0.3$ and $\varDelta C = 99$ % of its inlet equilibrium value. In Fig. 15a, the evolution of the scaled temperature at $t = 10$ (solid blue curve) and $t = 20$ (dashed blue curve) are shown, superimposed with the scaled species concentration at the same times. Note that profile of the scaled species curve translates nearly uniformly over this time interval, during which the temperature profile shows the slower migration of energy into the medium. These disparate transport rates are better displayed by looking at the spatial average values shown in Fig. 15b over $0< t < 1000$. The averaged species concentration decays nearly linearly from $t = 0$ to about $t = 40$, at which point a steady concentration profile takes shape. However, the scaled average temperature evolves on a much longer time scale, since for $\phi _o = 1/100$, energy transport is conduction limited.

Fig. 15

a Short-time evolution of scaled temperature profile at times $t = 10$ (solid blue curve) and $t = 20$ (dashed blue curve) and of the scaled species concentration at $t = 10$ (solid red curve) and at $t = 20$ (dashed red curve). Note that the transport of species occurs much more quickly than that of energy. a Longer-time response for the scaled spatial mean of temperature (solid blue curve) and species (dashed red curve) for $0< t < 1000$. Here $Pe_c = 10$, $\varDelta T = 0.3$ and $\varDelta C = 0.99$

As noted in Sect. 3.2, larger initial porosities allow for more effective removal of the species due to better advection, which would lead to potentially better conditions for dissolution. However, this argument rests on rates of energy transport being larger than rates of species transport. With $Pe_c = O(1)$, however, larger initial porosities allow for better energy transport, so that larger Péclet numbers result in an initial transient for temperature and species to a nearly uniform profile, after which the porosity dynamics is governed primarily by the dissolution rate. With this argument, dissolution effects are expected to be more pronounced for smaller Péclet numbers and where porosity is small: regions in parameter space where energy transport is limited, as shown in Fig. 16. The trends for the final mean porosity (left figure) all point toward dissolution, but the changes with respect to $Pe_c$ are not significant. Changes in the scaled minimum permeability (Fig. 16b) are largest for the smallest values of initial porosity and the smaller values of $Pe_c$.

Fig. 16

Parameter plot of final average porosity (a) and minimum permeability relative to the initial permeability (b) for $10< Pe_c < 100$ and $1/100< \phi _o < 1/3$, for $\varDelta T = 0.3$ and $\varDelta C$ kept at 99$\,\%$ of the equilibrium value at the inlet over $0< t < 5000$

3.3.2 Heat Storage Test

Lastly, consider a situation similar to that found in Ueckert and Baumann (2019) for the heat storage test. In this case, the system was run at a flow rate of $15\,$L/s over an exposed aquifer depth of nearly 300 m. Table 3 shows the nondimensional versions of the different stages of their heat storage test: the start and stop times, and the scaled temperature difference applied to the entering fluid. Note that the ambient temperature of the fluid in the aquifer is $10^{\circ }\,$C, and so $\varDelta T$ chosen here may vary compared to the values at the site.

Table 3 Nondimensional parameters for the simulation of the heat storage test from Ueckert and Baumann (2019). $\varDelta C$ is varied in the results below

In order to interpret the results, consider two characteristic values. The first represents $\varDelta T$ which, as shown in Table 3, varies depending on the injection stage. In order to compare the injection and production temperatures for cases with different initial porosity, a characteristic value of $\varDelta T = 0.3$ is used for displaying the data only, so on a scaled temperature plot, stages 0 & 1 cannot achieve a relative temperature rise of 1, and for stages 2 & 3 it is possible to achieve a relative temperature rise above 1. This characteristic temperature scale then dictates the characteristic calcium concentration scale, since this is the equilibrium value of the species for temperature $\varDelta T = 0.3$. This characteristic concentration is denoted $c_{0,eq}$.

Only two different values of $\varDelta C$ are considered in this section, the basis of which depends on the dissolution rate $\mathcal {R}$. The first value, $\varDelta C = 99$ % of the equilibrium value, is chosen where $\partial \mathcal {R}/\partial \theta < 0$, that is, higher temperature result in lower dissolution rates. This is the behavior expected based on the Arrhenius form of the reaction rate. The second value, $\varDelta C = 50$ % of the equilibrium value, corresponds to increasing dissolution rates for increasing temperatures, or $\partial \mathcal {R}/\partial \theta > 0$. While a full parameter exploration would be ideal, the computational cost of such a study is still prohibitive, even with this reduced model.

Our computational domain and approach here includes a domain on the field scale. The domain $0< x_1 < 100$ is chosen, which corresponds to a domain on the order of 10  m. Our resolution for the domain is coarser than our computations above, with a mesh size of $\varDelta x_1 = 0.2$, and the time step determined adaptively to maintain second-order truncation errors. Further, we modify the initial conditions for the species concentration so that a transition region between the inlet concentration and the far-field concentration is well delineated

$$\begin{aligned} c_1^{(1)}(x_1,0) = \frac{1}{2}\left\{ \varDelta C + c_{1,eq} + (c_{1,eq}-\varDelta C)\,\tanh {\left( x_1 - 10\right) }\right\} . \end{aligned}$$

This profile, and the resulting species profile at the beginning of each stage, are shown in Fig. 17a for the case when $\varDelta C = 99$ % of the equilibrium value, $\phi _o = 0.02$. Note that the species values change minimally outside of the transition region, due to the better advection transport. The corresponding temperature profile $\theta$ at each of these times is shown in Fig. 17b. Note that the thermal boundary layer near the inlet is gradually increasing at each stage, however, the domain over which the temperature varies significantly is much smaller than the domain over which the species concentration varies. This discrepancy impacts the reaction rate over this test, as we describe below.

Fig. 17

a Species concentration $c_1^{(1)}$ as a function of $x_1$ at the start of each stage, as denoted in Table 3. $\varDelta C = 99$ % of the equilibrium value at the inlet, and $\phi _o = 0.02$. b Corresponding temperature profiles $\theta$ at the same times and conditions as (a)

The case when $\varDelta C$ is 99% of its equilibrium value for $\varDelta T = 0.3$ is considered in Fig. 18, where other conditions are prescribed in Table 3, for initial porosity values of $\phi _o = 0.02$, $\phi = 0.05$, $\phi = 0.12$, $\phi = 0.2$, and $\phi = 0.33$. Figure 18a shows the relative change of the average porosity over time for these cases, and overall these changes are minimal. An explanation of this result can be seen in Fig. 18b, where we show the final distribution of the porosity profile. These profiles are nearly identical except near the inlet, where the majority of the variation between the final profiles can be seen. Effectively, the species transport controls the dissolution rate away from the inlet, since the temperature has not deviated significantly from equilibrium. Near the inlet, however, the temperature variation is is significant. In Fig. 18c, we show the inlet temperature value over time for the duration of the heat storage test for each of the initial porosity cases. We note that the more porous cases result better energy transport, which leads to larger deviations of the pore structure near the inlet for those cases. Finally, for this case we note that at equilibrium $\partial \mathcal {R}/\partial \theta < 0$, and larger temperatures result in lower rates of dissolution, and this is reflected in Fig. 18d. While the dissolution rate is nearly uniform for the case $\phi _o = 0.2$, the cases corresponding to the largest values of $\phi _o$ evolve to a lower relative inlet porosity compared to the smaller $\phi _o$ values. The reason for this is that at later stages of the heat storage test, the dissolution rate becomes negative near the inlet region, corresponding to precipitation, and then the porosity is reduced near that region.

Fig. 18

Heat storage test simulation for $Pe_c = 4$ and $\phi _o = 0.02$ (blue dashed curve), $\phi = 0.05$ (red dashed-dot curve), $\phi = 0.12$ (magenta dotted curve), $\phi = 0.2$ (green solid curve), and $\phi = 0.33$ (black dashed curve) with the simulation pattern shown in Table 3. Here, $\varDelta C = 99$ % of the equilibrium value of the solutal concentration $c_{0,eq}$ at $\varDelta T = 0.3$. a Evolution of the relative inlet porosity growth; b Scaled final porosity profile; c Evolution of the relative inlet temperature; d Evolution of the inlet dissolution rate

These changes in the porosity provide a window into the energy production capabilities which are shown in Fig. 18c. Note that for the smallest porosities that the increase in productivity is slowly increasing over each injection/production cycle. Injection stages are where the inlet temperature is increasing, and production cycles correspond to reductions in the inlet temperature. Only when initial porosities are above $\phi = 0.2$ do we see that the inlet temperature approaches the peak temperature for that stage. Hence, the capability of an aquifer to be used effectively for energy storage depends significantly on the local porosity.

In Fig. 19, the results of the heat storage test are presented in the case when $\varDelta C$ is 50 % of the equilibrium value of $c_{o,eq}$ when $\varDelta T = 0.3$. In this situation, the dissolution rate increases with increasing temperature ($\partial \mathcal {R}/\partial \theta$). There are two ways in which this difference in the dissolution rate behavior with temperature affects the pore dynamics. Firstly, there are no local conditions at which $\mathcal {R}<0$, so the matrix in the entire domain is dissolving over the heat storage test. This global variation with respect to the initial porosity is shown in Fig. 19a, since the thermal penetration depth at the inlet increases with increasing porosity, dissolution is then enhanced due to the locally higher temperatures, and hence larger porosity variations on average are observed. Secondly, as the thermal penetration depth increases from the inlet, higher dissolution rates in this local region are expected, and this effect is shown in Fig. 19b. Finally, the inlet evolution of the temperature, shown in Fig. 19c and the inlet dissolution rate, shown in Fig. 19d, are in phase, suggesting that the dissolution rate at the inlet is governed primarily with the changes in the local temperature.

Fig. 19

Heat storage test simulation for $Pe_c = 4$ and $\phi _o = 0.02$ (blue dashed curve), $\phi = 0.05$ (red dashed-dot curve), $\phi = 0.12$ (magenta dotted curve), $\phi = 0.2$ (green solid curve), and $\phi = 0.33$ (black dashed curve) with the simulation pattern shown in Table 3. Here, $\varDelta C = 50$ % of the equilibrium value of the solutal concentration $c_{0,eq}$ at $\varDelta T = 0.3$. a Evolution of the relative inlet porosity growth; b, Scaled final porosity profile; c Evolution of the relative inlet temperature; d Evolution of the inlet dissolution rate

4 Conclusions

In this work, an effective medium model is derived which describes the dominant flow, energy transport, species transport, and carbonaceous reaction kinetics on the meter-length scale of aquifer medium used under high temperature aquifer storage conditions. By averaging these physical effects over the microscale, a computational implementation of the model needs only to be resolved on the spatial macroscale, which is compared to a direct numerical simulation. This approach allows for a broad parameter exploration over flow rates and initial porosities. Hence, while the model is limited to the prescribed initially anisotropic media and to flow rates where Taylor dispersion effects are pertinent, a robust description of the competition between the dominant mechanisms is found.

A direct numerical simulation of the full problem is simply not feasible. From an order analysis, a direct simulation of the full problem would require $1/\epsilon$ more mesh points per spatial dimension compared to the effective model, even with neglecting Reynolds stress terms in the Navier-Stokes equation. The current computational scheme of the effective model does not lead to a banded matrix for the Crank-Nicolson solver, suggesting that the time step would have to be reduced by $\epsilon ^2$ in order to maintain the same accuracy as the effective model. Given that $\epsilon = 10^{-3}$, $10^6$ more steps per time unit would be required, and each time step would take between $10^3$ and $10^6$ times the computational operations of the effective model to solve. Since this problem is a transient problem, parallelization, either through multiple processors or the use of GPUs, would be of limited use to speed up the simulation.

The ability to use aquifers to store and recover thermal energy depends on the capability of harnessing the energy and the integrity of the overall carbonaceous structure. Both items depend on the interaction of energy, species and momentum balances taking place during operation of the geothermal energy site. The species balance depends on the rate of dissolution, and comparatively the rates of diffusion and advection of the species. The energy balance relies primarily from this modeling on convection and conduction through the medium, while the momentum balance in this study pits viscous stresses with normal velocities induced by the pore dynamics instigated by the dissolution kinetics. Hence, our focus in this work has been on the relative rates of species, energy and momentum transport compared to the rates of the pore dynamics and dissolution.

From this model, the relative rates of energy and species transport dictate the dynamics of the pore structure to first order in the injection stage. When energy transport is dominated by conduction and the species transport is limited, precipitation can take place, preventing further reductions in the local species concentration. Physically, this corresponds to small values of the Péclet number and small porosity. For larger values of porosity, number, species concentrations are balanced by dissolution, advection and diffusion, where the dissolution source can be limited as the temperature within the porous medium increases. The reduced calcium species concentration of the entering fluid plays a significant role in these dynamics according to this model. So, for small $Pe_c$, the smallest pores become smaller while the larger pores become larger, and potentially, change the representative length scale over which the porous medium derivation takes place. For significantly reduced inlet concentrations compared to its equilibrium value, the model’s predictions are limited due either to porosity reductions by three orders of magnitude, or to nearly complete removal of the solid phase.

For larger flow rates ($Pe_c = O(1)$), Taylor dispersion plays a role in increasing diffusive transport in both energy and species. This increased transport affects the species transport more quickly than energy transport, resulting in dissolution over shorter times until the temperature in the porous medium equilibrates. The effects on the pore dynamics on the fluid flow are reduced in this case as well. From our model, higher rates of advective species and conductive energy transport of energy and species result in a reduced impact of the evolution of the pore structure.

For this system to be pragmatic for a duration on the order of decades, the long-time evolution of the matrix structure is critical to the determination of energy recovery. In the case of smaller flow rates, viability depends on the degree to which the input species concentration is below its equilibrium value. For inlet species concentrations near its inlet equilibrium value, significantly large permeability changes are predicted over a 5-year cycle. Note that during the production phase of this simulation, the entering fluid is assumed to be at the equilibrium concentration of the initial natural ambient value. It is unclear how the species concentration of the entering fluid is closer to the equilibrium value at the elevated temperature would affect the pore dynamics over these time scales. For larger flow rates, the computational requirements of the current model are significantly higher, and the limit of a few months to one year is the practical limit of our study. Note that our simulation of conditions analogous to the heat storage test of Ueckert & Baumannn Ueckert and Baumann (2019) shows that the effects of the pore structure may be manageable, based on the dependence of the dissolution rate on species and temperature. Future work in this area centers on simulation of the effective model in two dimensions, to see the effect of thermal transport and borehole flow rate variation on the pore structure of the aquifer. Extensions of this model to cylindrical coordinates to capture the effects of the flow rate decaying radially from the borehole would be of interest.

In total, this study suggests that the most critical limitation is the understanding of the dissolution rate under field and operating conditions. The choice here was quite sensitive to the parameter values, and as shown in the heat storage test simulations, slight variations in the modeling choices can result in effects which may lead to significant changes in the porosity evolution. Efforts to a better dissolution rate estimate in this regard would help greatly in connecting how flow conditions can lead to behaviors in high temperature aquifer storage.