Abstract
An analytical solution is presented for the displacement, strain and stress of a three-dimensional poro-elastic model with three layers, where the three layers are an underburden, a reservoir with a given fluid pressure, and an overburden. The fluid pressure in the reservoir is assumed symmetrical around the z-axis and represented by a Fourier cosine series. The poro-elastic solution is expressed as a superposition of the solutions for each term in the Fourier series. It is shown that the bulk strain in the reservoir layer is proportional to the fluid pressure and that the bulk strain in the underburden and overburden is zero. Using these properties of the bulk strain, a solution is derived for the three-layer model where the fluid flow and mechanics are fully coupled. A particular aim of the model is to study the surface uplift from a given reservoir pressure. The expansion of the reservoir and the uplift of the surface are studied in terms of the wavelengths in the Fourier representation of the pressure. It is shown that the surface uplift can be written in a similar form to the 1D vertical expansion of the reservoir layer, but where the fluid pressure is based on the Fourier series. It is shown that the amplitudes with average wavelengths longer than \(2\pi \) times the thickness of the reservoir give expansion of the reservoir, but average wavelengths much shorter than this limit do not. Similarly, amplitudes with average wavelengths much longer than \(2\pi \) times the thickness of the overburden produce surface uplift, but wavelengths much shorter do not. The stress in the overburden, which is generated by the reservoir fluid pressure, is also analysed in terms of the wavelengths. A case is given where the analytical uplift is compared with the results of a numerical simulation and the agreement is excellent.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The global annual emissions of \(\text{ CO }_2\) were 32 Gt in 2016 (International Energy Agency 2016), and the concentration of \(\text{ CO }_2\) in the atmosphere has increased from around 280 ppm in 1900 to more than 400 ppm in 2017. \(\text{ CO }_2\) is a greenhouse gas and its increasing concentration in the atmosphere has been found to be the reason for global warming (Bryant 1997). The injection of large volumes of \(\text{ CO }_2\) into aquifers or depleted oil and gas reservoirs is considered a promising way to reduce \(\text{ CO }_2\) emissions and thereby reduce global warming (Bachu 2008; Benson and Cole 2008; Bickle 2009).
\(\text{ CO }_2\) injection leads to a pressure build-up and an expansion of the reservoir, and in turn to surface uplift. An example of subsurface \(\text{ CO }_2\) injection and surface uplift is the In Salah storage project, where 3.8 Mt has been injected since its start in 2004, and where a total uplift of roughly 15 mm has been measured around three injection wells (Rutqvist 2012). The uplift measured at In Salah has attracted a considerable amount of scientific interest, and a number of modelling studies have been published (Vasco et al. 2008; Rutqvist et al. 2010; Rutqvist 2012; Bissell et al. 2011; Verdon et al. 2011; Zhou et al. 2010; Shi et al. 2012; Rinaldi and Rutqvist 2013; Rucci et al. 2013; White et al. 2014; Vilarrasa et al. 2015, 2017; Rinaldi et al. 2017). Similarly, seabed uplift is expected over offshore \(\text{ CO }_2\) sites, although it is more difficult to measure than land uplift. Land-based water pumping from aquifers and land-based oil and gas production are known to produce surface subsidence as the fluid pressure is lowered.
Geertsma (1973) developed an early model to compute land subsidence, which was applied to the Groningen gas field. The model gives the poro-elastic subsidence above a horizontal disk-shaped reservoir with a constant thickness and a constant pressure. The reservoir is placed at a finite depth in the infinite half-space and has a stress-free surface. The model is based on the nucleus-of-strain concept in the half-space, which was introduced by Mindlin and Cheng (1950) and Sen (1950) as a method to solve thermo-elastic problems. A particular feature of the model of Geertsma (1973) is that a constant pressure reduction gives a maximum subsidence that is approximately 1.5 times larger than the one-dimensional (vertical) compaction of the reservoir layer. The model gives a maximum horizontal displacement (contraction) that is also approximately 1.5 times the one-dimensional compaction.
The classical model of Geertsma (1973) has recently been modified by Tempone et al. (2010): the infinite half-space was replaced by a rigid basement underneath the reservoir. Tempone et al. (2010) compare the displacement, stress and strain of their model with the classical Geertsma model (Geertsma 1973). The comparisons show that a rigid basement close to the reservoir gives more uplift than the classical model, because less of the reservoir compaction goes vertically downward into the layer underneath the reservoir.
Another approach is taken by Fokker and Orlic (2006). They model the poro-elastic subsidence by a semi-analytical approach, which allows for an arbitrary number of layers. They use a numerical method to fit a set of analytical solutions to approximate the boundary condition in an optimal manner.
Selvadurai (2009), Kim and Selvadurai (2015), Selvadurai and Kim (2016) and Niu et al. (2017) have developed analytical models for different configurations of a reservoir and a caprock. Selvadurai and Kim (2016) present analytical poro-elastic solutions for a storage aquifer with a caprock; the solutions are given by an integral representation. The model was used to study how the surface displacement is controlled by the radius and the depth of the injection region. Finally, Chang and Segall (2016) studied how fluid pressure variations from injection or production in reservoirs could induce poroelastic stress changes and fault slip in the basement.
In the present article, a different approach is taken, by first solving the poro-elastic equations for a three-dimensional model with three layers when the reservoir pressure is just one term in a Fourier series. The same approach was taken by Wangen et al. (2018) with a two-dimensional model of a reservoir with an overburden, but no underburden. The three layers in the present model are an overburden, a reservoir and an underburden, where the underburden is placed on a rigid basement. Each layer in the model is of infinite lateral extent and of constant thickness. A periodic pressure distribution can be represented by a Fourier series, and the displacement, strain and stress becomes the superposition of the effect of each term in the Fourier series. The model has a stress-free surface, except for the shear stress xz and yz components, which turn out to be negligible for normal configurations of the reservoir and the overburden. The displacement field and the stress, except for the xx and yy stress components, are continuous across the internal layer boundaries, which are the top and the base of the reservoir. A particular feature of this model is that it allows a decoupling of the equation for fluid flow from the equations of the displacement field. This decoupling simplifies considerably the derivation of analytical solutions of the fully coupled problem of fluid flow and mechanics. This model is well suited for a study of how the displacement, stress and uplift depend on the wavelengths of the reservoir pressure and the layer thicknesses. ‘Short’ and ‘long’ wavelengths in the pressure distribution produce different displacement fields and stresses, where ‘short’ and ‘long’ are with respect to layer thicknesses.
The present paper is organized as follows: The poro-elastic assumption and notation are introduced, and the expansion of the one-dimensional vertical poro-elastic layer is established. The geometry of the three-layer model is explained, and the boundary conditions are discussed. The solution for the displacement field is presented, and then the limit as the wavelength goes to infinity is investigated. How the fluid pressure can be decomposed in a double Fourier series is demonstrated before a Fourier solution for the fully coupled problem of fluid flow and mechanics is derived. The uplift is studied in terms of the wavelengths of the Fourier decomposition, and a special solution for the displacement for a reservoir on top of a rigid basement is presented. The analytical solution for the uplift is compared with a numerical finite element solution. An example of the analytical solution is given, which demonstrates the displacement field and the stress field. The stress in the caprock is investigated with respect to the wavelength of the Fourier components in the reservoir pressure.
2 Poro-elasticity
The stress state \(\sigma _{ij}\) in the model is given by the sum of the initial stress \(\sigma ^{(0)}_{ij}\) and the change \(\sigma ^{(1)}_{ij}\) in the poro-elastic stress caused by a change in the fluid pressure in the reservoir
where the indices i and j indicate the three spatial dimensions \(x=1\), \(y=2\) and \(z=3\). The stress state \(\sigma _{ij}\) fulfills the equilibrium equations
where \(\rho \) is the rock bulk density, g is the acceleration due to gravity, and \(\delta _{iz}\) is the Kronecker delta, that is, \(\delta _{iz}=1\) for \(i=z\) and \(\delta _{iz}=0\) for \(i\ne z\). Einstein’s summation convention is used in the equilibrium Eq. (2), where summation is understood for each pair of the same indices.
The initial stress state also fulfills the equilibrium Eq. (2), which implies that the stress produced by poro-elastic changes fulfills an equilibrium equation without body forces
The effective stress can also be decomposed into the initial effective stress and the effective stress produced by changes in the fluid pressure in the reservoir
The initial effective stress is given by
where \(p^{(0)}\) is the initial fluid pressure and \(\alpha \) is the Biot coefficient. Similarly, the difference in the poro-elastic effective stress is given by
where \(p^{(1)}\) is the change in the reservoir pressure. The change \(\tau ^{(1)}_{ij}\) in the effective stress produces poro-elastic deformations
where \(\varLambda \) is the Lamé parameter, G is the shear modulus, \(\varepsilon _{ij}=\frac{1}{2}(u_{i,j} + u_{j,i})\) is the strain tensor, and \(u_i\) is the displacement vector (\(i=x,y,z\)). An upper case \(\varLambda \) is used for the Lamé parameter, since the lower case \(\lambda \) will be used for the wavelength. Notice that normal effective stress is positive when the rock is tensile and negative when it is compressive. The elastic moduli are for drained conditions. The equations for the displacement field \(u_i\) are obtained by inserting the stress from Eq. (7) into the equilibrium Eq. (3), which yields
where \(\gamma =\varLambda /G\). For simplicity, the layers in the system are taken to have the same geomechanical parameters \(\varLambda \), G and \(\alpha \). The gradient of the pressure change appears as an internal load on the left-hand side of the equilibrium equations. Therefore, Eq. (8) gives the displacement field when the pressure is known. The displacement field has a feedback on the pressure. The equation for the fluid pressure that includes poro-elastic deformations is
where \(K_\mathrm{f}\) is the modulus of fluid compressibility, \(K_\mathrm{s}\) is the modulus of the solid constituting the rock matrix, \(\phi \) is the porosity, \(\kappa \) is the permeability, \(\mu \) is the pore fluid viscosity, \(\varepsilon =\partial {u_i}/\partial {x_i}\) is the bulk strain and t is the time. The notation is simplified by denoting the pressure change by \(p=p^{(0)}\). The notation for the displacement field is also simplified by writing \(u=u_x\), \(v=u_y\) and \(w=u_z\). For instance, the bulk strain can now be written \(\varepsilon =\partial {u_i}/\partial {x_i}=\partial {u}/\partial {x}+\partial {v}/\partial {y}+\partial {w}/\partial {z}\), where it is noted that summation is understood over pairs of equal indices. In the following, the fluid overpressure is assumed known and the displacement equations are solved with the given overpressure.
3 One-dimensional Vertical Uplift
The one-dimensional vertical poro-elastic expansion of a reservoir layer due to a constant increase \(p_0\) in the overpressure is an important reference model. The equations for the displacement field (8) become
for one-dimensional vertical displacements, when \(u=0\) and \(v=0\). The vertical displacement w(z) is obtained by integrating Eq. (10) twice
where it is assumed that the base of the reservoir layer at \(z=z_0\) is fixed (\(w=0\)). The surface of the reservoir layer has a maximum displacement given by
where h is the thickness of the reservoir layer. In case the reservoir layer has an overburden, the overburden is uplifted by w when the base is fixed. The one-dimensional reservoir expansion (12) turns out to be an important reference for the uplift.
4 The Three-Layer Model
The model consists of three layers of infinite extent, as shown in Fig. 1. The middle layer is the reservoir and it has an overburden and an underburden. To simplify the analytical solution for the displacement field, the three layers are assigned the same mechanical properties. Only the reservoir layer is considered permeable and has a change in the fluid pressure. The z-axis is positive upwards, and \(z=0\) is the base of the model (the underburden). The base of the reservoir layer is at \(z=z_1\), the top of the reservoir layer is at \(z=z_2\) and the top of the model (the surface) is at \(z=z_3\). The thicknesses of the underburden, the reservoir and the overburden are \(h_1\), \(h_2\) and \(h_3\), respectively, and the layer boundaries become \(z_1=h_1\), \(z_2=h_1+h_2\) and \(z_3=h_1+h_2+h_3\).
5 Boundary Conditions
The layers are of infinite extent, and the boundary conditions are at the base and at the top surface of the model. The base surface has zero vertical displacement, and the top surface has zero lateral displacement. These boundary conditions can be written as
The boundary condition \(w(z\,=\,0)=0\) implies that the underburden is resting on an absolutely rigid base. The top surface may move vertically, but it is prevented from lateral displacements, since it is assumed that \(u(z\,=\,z_3)=0\> \text{ and }\> v(z\,=\,z_3)=0\). It will be seen that this boundary condition leads to an approximately stress-free top surface when the overburden is much thicker than the reservoir. This approximation works fine for ‘long’ wavelengths in the reservoir pressure, because they give locally almost one-dimensional vertical surface deformations. Furthermore, it is seen that ‘short’ wavelengths in the reservoir pressure produce deformations that decrease to almost zero towards the surface.
6 The Solution for the Displacement Field
The displacement field is first found for a periodic reservoir fluid overpressure of the form
which is one term in a Fourier representation of a fluid pressure that is symmetrical around the z-axis. The overpressure (14) is independent of the depth inside the reservoir layer. The amplitude of the fluid pressure is \(p_0\), and the wavenumbers in the x- and y-directions are \(k_1\) and \(k_2\), respectively. These wavenumbers correspond to the wavelengths
respectively. The full solution for the displacement field of the three-layer model consists of three parts: one for each of the three layers comprising the underburden, the reservoir and the overburden. The solution gives a displacement field that is continuous across the layer boundaries. The derivation of the solution is presented in the “Appendix”. The underburden (\(0\le z \le z_1\)) has the following solution for the displacement field
where the average wavenumber is
and where
and
are two coefficients. The reservoir (\(z_1\le z \le z_2\)) has the displacement field
where
and
are two functions of z. Finally, the overburden (\(z_2\le z \le z_3\)) has the solution
where
is a coefficient. It is seen that all parts of the displacement field are proportional to the coefficient \(D_0\) and the pressure amplitude \(p_0\). Another observation is that the functions \(F_2(z)\) and \(F_3(z)\) have the following properties
These relations are useful in the expressions for the strain and for verifying that the stress fulfills the equilibrium equations.
The strain \(\varepsilon _{ij}=\frac{1}{2}(u_{i,j} + u_{j,i})\) is straightforward to compute from the displacement field, and the strain tensor for each layer is given in the “Appendix”. The effective stress follows from the strain by Eq. (7) and the effective stress tensor \(\tau ^{(1)}_{ij}\) for each layer is also given in the “Appendix”. The stress \(\sigma ^{(1)}_{ij}\) is equal to the effective stress in the overburden and the underburden where the fluid overpressure is zero. In the reservoir layer, the normal stress is obtained from the effective stress by subtracting the reservoir pressure multiplied by Biot’s coefficient; see Eq. (14). Finally, it is straightforward to verify that the stress \(\sigma ^{(1)}_{ij}\) fulfills the equilibrium Eq. (3).
It is also straightforward to verify that the displacement field (u, v, w) and the stress components \(\sigma ^{(1)}_{zz}\), \(\sigma ^{(1)}_{xz}\), \(\sigma ^{(1)}_{yz}\) and \(\sigma ^{(1)}_{xy}\) are continuous across the internal boundaries at the base and at the top of the reservoir. In the same way, it can be seen that the stress components \(\sigma ^{(1)}_{xx}\) and \(\sigma ^{(1)}_{yy}\) are discontinuous across the horizontal layer interfaces. The stress is \(\Delta \sigma ^{(1)}_{xx}=\Delta \sigma ^{(1)}_{yy}=\varLambda D_0 p_0\cos (k_1 x)\cos (k_2 y)\) larger in the reservoir than right above in the caprock or right below in the underburden. The following two relations are useful for showing the continuity of the stress field across the internal layers
where the first relation applies to the base of the reservoir and the second to the top of the reservoir.
7 The Limit as \(k_1\rightarrow 0\) and \(k_2\rightarrow 0\)
An important aspect of the solution (16)–(29) is what happens in the limit as both \(k_1\rightarrow 0\) and \(k_2\rightarrow 0\). This is the limit of infinite wavelengths in both the x- and y-directions, where the pressure (14) becomes laterally constant with an amplitude \(p_0\). Notice that the four functions \(F_1\) to \(F_4\) depend on the arguments \(cz_1\), \(cz_2\) and \(cz_3\), and that c also goes to zero when both \(k_1\) and \(k_2\) do so. The limit \(k_1\rightarrow 0\) and \(k_2\rightarrow 0\) can be studied by using \(k_1=k_2=k\) and \(c=\sqrt{2}k\), and letting the wavenumber \(k\rightarrow 0\). A fixed value of x gives that
and similarly for fixed values of y and z. This implies that the factor \(k/c^2\) disappears in all expressions for u(x, y, z) and v(x, y, z), which are Eqs. (16), (17), (22), (23), (27) and (28). Next, it is seen that
which implies that the lateral displacement field goes to zero in the limit \(k_1,k_2\rightarrow 0\). This is as expected for a constant pressure distribution, because it is a one-dimensional vertical model. The same argument as above implies that the vertical displacement field of the underburden goes to zero in the limit \(k_1,\,k_2\rightarrow 0\).
The vertical displacement field of the reservoir depends on the function \(F_3\) in the limit \(c\rightarrow 0\), and it can be seen that \(F_3\rightarrow (cz - cz_2)\). Therefore, the vertical displacement field of the reservoir (24) has the limit \(w\rightarrow D_0\,p_0\cdot (z- z_1\)) when \(k_1,\,k_2\rightarrow 0\), which is the solution for the one-dimensional vertical reservoir expansion.
In the overburden, the vertical displacement field depends on the function \(F_4\), which has the limit \((cz_2-cz_1)\) when \(c\rightarrow 0\). Therefore, the vertical displacement of the overburden has the limit \(w\rightarrow D_0\,p_0\cdot (z_2- z_1)\), which is, as expected, the maximum vertical expansion of the reservoir layer.
Furthermore, it follows that the strain and the effective stress tensors are zero in the limit \(k_1,\,k_2\rightarrow 0\) for all layers, with exceptions for the strain \(\varepsilon _{zz}=\alpha p_0/(\varLambda +2G)\) and effective stress \(\tau ^{(1)}_{zz}=\alpha p_0\) for the reservoir layer.
8 Fourier Representation of the Reservoir Pressure
The reservoir pressure can be represented as a double Fourier cosine series, assuming that the pressure is symmetrical around the z-axis
where the Fourier coefficients are given by
and where the wavenumbers for indices m and n are
respectively; see Kreyszig (2011). The domain sizes in the x- and y-directions are \(L_1\) and \(L_2\), respectively. A Fourier series gives an exact representation of any periodic and well-behaved function, with periods \(L_1\) and \(L_2\) in the x- and y-directions, respectively, in the limit \(N_1\rightarrow \infty \) and \(N_2\rightarrow \infty \). The domain size is assumed sufficiently large for the pressure to go to zero before the edges of the domain. A finite representation, where \(N_1\) and \(N_2\) are of order 100, normally gives an excellent approximation of the reservoir overpressure. It is convenient to write the series (40) compactly as
where the coefficients \(A'_{mn}\) are given by \(A'_{0,0}=\frac{1}{4}A_{0,0}\), \(A'_{m,0}=\frac{1}{2}A_{m,0}\), \(A'_{0,n}=\frac{1}{2}A_{0,n}\) and \(A'_{m,n}=A_{m,n}\) for \(m,n\ne 0\).
The displacement field is linear in the reservoir overpressure, which also implies that the strain and the stress are linear in the overpressure. Since the model is linear, the displacement, stress and strain from a pressure distribution written as a Fourier series become the superposition of the displacement, stress and strain from each term in the Fourier series. For instance, if S(x, y, z) is a property such as the displacement, the stress or the strain, it implies that
where \(S'(k_mx,k_ny,cz)\) is the contribution to the property from one Fourier component, and where \(p_0\) is replaced by the pressure \(A'_{m,n}\). The function \(S'(k_mx,k_ny,cz)\) is zero for \(m=0\) and \(n=0\), except for a displacement w in the vertical direction, the strain \(\varepsilon _{zz}\) and the effective stress \(\tau ^{(1)}_{zz}\), as already shown.
9 Solution of the Coupled Biot Equations
The strain tensor in the underburden, reservoir and the overburden is straightforward to compute from the displacement field; see the Appendix. It may be seen from the Appendix that the bulk strain is zero in the underburden and the overburden. On the other hand, the bulk strain in the reservoir layer is proportional to the pressure, \(\varepsilon =D_0 p\), when the pressure is represented by a Fourier series. This allows for a decoupling of the pressure Eq. (9) from the displacement Eq. (8). The pressure equation for the reservoir layer can now be written as
in terms of the effective modulus \({K}_{\mathrm {eff}}\). The pressure Eq. (45) has a time-dependent solution of the form
where
is the characteristic time associated with the average wave length \(\lambda =2\pi /(k_m^2+k_n^2)^{1/2}\). The Fourier coefficients in Eq. (46) give the initial condition, which decays to zero with time. The solution (46) provides a Fourier series that solves for the case of fully coupled fluid pressure and deformations.
10 Uplift as a Function of Wavelengths and Layer Thicknesses
A particular aim with this model is to study which wavelengths (wavenumbers) in a Fourier series of the reservoir pressure give surface uplift. Therefore, the vertical deformations are studied for one term in the Fourier series, as represented by the fluid pressure (14). The surface uplift is given by the vertical displacement (29) for \(z=z_3\), and it can be written as
and where
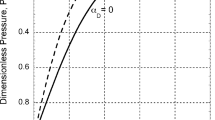
The first of the three factors in the uplift (48) is the one-dimensional reservoir expansion produced by a constant reservoir pressure \(p_0\). The second factor, \({f}_{\mathrm {surf}}\), is a dimensionless surface uplift: it turns out to be a number between 0 and 1. The dimensionless function depends on the three parameters \({ ch}_1\), \({ ch}_2\) and \({ ch}_3\), where
are the average wavenumber and the average wavelength, respectively. The dimensionless surface uplift \({f}_{\mathrm {surf}}\) describes how the uplift depends on the layer thicknesses and the average wavenumber, or, alternatively, the average wavelength. Figure 2 shows the dimensionless uplift as a function of \({ ch}_1\) and \({ ch}_2\) for the three different underburden thicknesses given as \({ ch}_1=0.1\), 1 and 10. For all three cases, the uplift is close to one for \({ ch}_2\ll 1\) and \({ ch}_3\ll 1\). Another way to state this condition is that the average wavelength must be larger than both the reservoir thickness and the overburden thickness multiplied by \(2\pi \), i.e. \(\lambda \gg 2\pi h_2\) and \(\lambda \gg 2\pi h_3\). This is a generalization of the condition for uplift found with the two-dimensional plain-strain model of Wangen et al. (2018), which has a reservoir layer and an overburden, but no underburden. The dimensionless uplift (49) gives exactly the same dimensionless uplift as in Wangen et al. (2018) under plain strain conditions (\(k_2=0\)) and with an underburden of zero thickness (\(h_1=0\)).
The dimensionless surface uplift (49) as a function of \({ ch}_1\), \({ ch}_2\) and \({ ch}_3\)
The surface uplift comes from the expansion of the reservoir. Vertical movements of the top and the base of the reservoir can be expressed in a similar way as the surface uplift. The vertical displacement of the top reservoir is given by either Eqs. (24) or (29) at \(z=z_2\), because the displacement field is continuous at the layer interfaces, and it can be written as
and where
Figure 3 shows the dimensionless uplift of the top reservoir, Eq. (52). It lies between 1 / 2 and 1 for \({ ch}_2\ll 1\), or alternatively \(\lambda \gg 2\pi h_2\). When \({ ch}_2\ll 1\) and \({ ch}_3\ll 1\), the dimensionless uplift is \(\approx 1\), and when \({ ch}_2\ll 1\) and \({ ch}_3\gg 1\), it is \(\approx 1/2\), unless the overburden is ‘thin’, \({ ch}_1\ll 1\), in which case it is \(\approx 1\). In the opposite regime, \({ ch}_2\gg 1\) (\(\lambda \ll 2\pi h_2\)), it is almost zero. Wavelengths much shorter than \(2\pi h_2\) do not produce an uplift of the top of the reservoir. The vertical movement of the base of the reservoir is given by Eqs. (18) and (24) for \(z=z_1\) and can be expressed as
where the dimensionless vertical displacement for the base of the reservoir is
The dimensionless displacement \({f}_{\mathrm {base}}\) is plotted in Fig. 4, which shows that the base of the reservoir has a negative displacement. This means that it is pressed down into the underburden. Figure 4a shows that the conditions \({ ch}_2\ll 1\) and \({ ch}_3\ll 1\) give small negative displacements of the base reservoir. Furthermore, it can be seen from Fig. 4 that the maximum downward displacement of the base of the reservoir takes place for \({ ch}_2\ll 1\) and \({ ch}_1,{ ch}_3\gg 1\). This condition can also be written as \(\lambda \gg 2\pi h_2\) and \(\lambda \ll 2\pi h_1,2\pi h_3\). The condition says that the average wavelength must be ‘long’ compared to the thickness of the reservoir and at the same time ‘short’ compared with the thickness of the underburden and the overburden.
Finally, the dimensionless expansion of the reservoir is given by the difference between the vertical displacements of its top and base
The dimensionless expansion is plotted in Fig. 5. It can be seen that the condition for expansion of the reservoir is that \({ ch}_2\ll 1\) or, alternatively, that \(\lambda \gg 2\pi h_2\), regardless of the overburden and the underburden. Comparing the dimensionless reservoir expansion of Fig. 5 with the dimensionless surface uplift of Fig. 2 shows that the expansion of the reservoir reaches the surface only when \({ ch}_3\ll 1\) or \(\lambda \gg 2\pi h_3\). Since the overburden is normally much thicker than the reservoir, \(h_3\gg h_2\), the condition for surface uplift becomes \(\lambda \gg 2\pi h_3\), in terms of the average wavelength.
11 Reservoir and Overburden Above a Rigid Basement
The model is simplified considerably if it is assumed that the reservoir rests on an absolutely rigid basement. Then, the underburden thickness can be set to zero (\(h_1=0\)). In this case, the displacement field for the reservoir layer (\(0\le z\le z_2\)) becomes
and for the overburden (\(z_2\le z\le z_3\))
The vertical displacement (58) gives the dimensionless uplift for this case:
which becomes the same as the dimensionless uplift reported for the two-layer plain-strain model by Wangen et al. (2018) by setting either \(k_1=0\) or \(k_2=0\). It should be noted that the dimensionless uplift is given by a different expression by Wangen et al. (2018), but it is easily rewritten to be as in Eq. (59).
a The overpressure plume at times 10, 100 and 1000 days. The solid line is the Theis solution, and the circular markers show the overpressure from a Fourier series. b The surface uplift pressure given by Eq. (62)
12 An Example of Surface Uplift from Reservoir Pressure
This section gives the uplift, at three different times, from a pressure plume that spreads out from an injection well. The pressure plume is expressed by Theis’ equation (Theis 1935),
where Q is the injection rate, \(h_2\) is, as before, the thickness of the aquifer, \(r=(x^2+y^2)^{1/2}\) is the radius from the injection well and t is the time. The example has a reservoir thickness \(h_2=50\) m, porosity \(\phi =0.1\), fluid compressibility \(1/K_\mathrm{f}={5}\times 10^{-8}\) \(\text{ Pa }^{-1}\), solid matrix compressibility \(1/K_\mathrm{s}=0\) \(\text{ Pa }^{-1}\), aquifer permeability \(\kappa ={1}\times 10^{-12}\) \(\text{ m }^{2}\) and injection rate \(Q=0.278\) \(\text{ m }^3\,\text{ s }^{-1}\). The overburden thickness is \(h_3=1000\) m, and the reservoir layer is placed on a rigid basement, which gives \(h_1=0\) m. Young’s modulus is \(E=15\) GPa, and the Poisson ratio is \(\nu =0.2\). Since \(E\gg K_\mathrm{f}\), the fluid compressibility dominates the compressibility of the rock, and the right-hand side of Eq. (9) can be ignored.
How the pressure plume spreads out from the origin is plotted in Fig. 6a by showing the pressure at 10, 100 and 1000 days. In Fig. 6a, the solid curve shows the Theis solution, and the markers show the pressure computed from the Fourier series. The uplift for one Fourier component is expressed by Eq. (48). Since the model is linear, the uplift becomes the superposition of uplift from each term in the Fourier series. Therefore, the uplift from the pressure plume can be expressed as
where \({p}_{\mathrm {up}}(x,y)\), the uplift pressure, is defined by
where
The surface uplift (61) has the same form as the one-dimensional reservoir expansion (12) when it is expressed using the uplift pressure (62). The uplift pressure is the Fourier representation of the reservoir pressure filtered with the factor \({f}_{\mathrm {surf}}\), which is a number between 0 and 1. Figure 6b shows the uplift pressure corresponding to the pressure plume in Fig. 6a. The uplift pressure is seen have roughly the same width as the corresponding pressure plume, but it has much less height. These observations are explained by the factor \({f}_{\mathrm {surf}}\), which reduces ‘short’ wavelengths in the Fourier series.
a The Fourier coefficients as functions of the wavenumber for the three overpressure plumes. b The average wavelength as a function of average wavenumber. c The dimensional uplift \({f}_{\mathrm {surf}}\), Eq. (49), as a function of the wavenumber
The Fourier coefficients as a function of the average Fourier number, \({n}_{\mathrm {av}}=(m^2+n^2)^{1/2}\), are plotted in Fig. 7a. Figure 7a shows that the first Fourier coefficients become larger as the plume spreads out. The first three Fourier coefficients for the pressure plume at 1000 days are considerably larger than the others.
Figure 7a shows that the largest Fourier coefficients are found for an average Fourier number less than 2. These Fourier numbers correspond to an average wavelength that is longer than 10 km, as seen from Fig. 7b. The pressure plumes at times 10 and 100 days are not wide enough to have noticeable Fourier coefficients for the lowest Fourier numbers.
The Fourier coefficients are multiplied with the \({f}_{\mathrm {surf}}\)-function, which lies in the range 0.8–1 for Fourier numbers up to 2. For Fourier numbers larger than 4, the \({f}_{\mathrm {surf}}\)-function is less than 0.5, as it converges towards 0. The large Fourier coefficients of large wavelengths, which dominate the pressure plume at time 1000 days, are not reduced very much by the \({f}_{\mathrm {surf}}\)-function, and therefore they contribute to the surface uplift.
The actual uplift at the three times is plotted in Fig. 8a–c. These curves show the uplift computed by expression (62) (the red circles) and the results of a finite element computation (the blue curve). The agreement between the analytical expression and the numerical FE computation is excellent. Figure 8a–c also show the one-dimensional reservoir expansion (12), when applied locally, as the green curve. The uplift from the pressure plume approaches the one-dimensional reservoir expansion as it gets wider and therefore has Fourier components with longer wavelengths. The one-dimensional reservoir expansion becomes a reasonable approximation for the surface uplift when the width of the plume exceeds \(2\pi h_3\approx 6000\) m.
Expressions similar to those for the surface uplift (61), where the uplift has the same form as the one-dimensional reservoir expansion, can be made for the displacement at the base of the reservoir and the top of the reservoir.
13 An Example of Displacement, Strain and Stress from Reservoir Pressure
Another version of the preceding example is shown in Fig. 9. The reservoir layer with the reservoir pressure and the overburden is the same, but a 2000 m underburden is added. Figure 9 shows a two-dimensional xz-cross section of the model through the z-axis. The fluid overpressure is limited to the reservoir layer, as seen from Fig. 9a, and Fig. 9b shows that the displacement field u is symmetric around the origin. The displacement field u is also restricted to the surroundings of the reservoir layer. Figure 9c shows the vertical displacement field w from the expansion of the reservoir layer, which produces negative vertical displacements in the underburden and positive displacements in the overburden. The positive vertical displacements reach the surface, where it produces an uplift.
Figure 10 shows the stress corresponding to the overpressure and the displacement field in Fig. 9. Recall that the stress is the effective stress minus the pore pressure, Eq. (6), and that it is the effective stress that is responsible for deformations, Eq. (7). A negative value of \(\sigma ^{(1)}_{xx}\) and \(\sigma ^{(1)}_{zz}\) indicates compression. A positive pore pressure acts to expand the rock, but there is a compressive stress that holds the expansion back. Otherwise, the rock would have been maximally expanded and stress-free. The deformations are much larger in the vertical direction than in the x-direction, which implies that there is less compressive stress in the z-direction than in the x-direction. The shear stress \(\sigma ^{(1)}_{xz}\) is located near the centre of the pressure plume in the underburden, the reservoir and the overburden. The absolute value of the shear stress is also two orders of magnitude less than the overpressure.
14 Stress in the Overburden
The surface of the model (\(z=z_3\)) is stress-free, except for the shear stress components \(\sigma ^{(1)}_{xz}\) and \(\sigma ^{(1)}_{yz}\), as seen from Eqs. (178)–(182). It turns out that the coefficient \(F_4\) can be used to obtain a condition for when these two shear stress components are close to zero. The shear stress \(\sigma ^{(1)}_{xz}\) at the surface (\(z=z_3\)) can be constrained in the following way,
since \(k_1/c\le 1\), \(\alpha \le 1\) and \(\gamma >0\). How \(F_4=F_4({ ch}_1, { ch}_2, { ch}_3)\) depends on \({ ch}_1\), \({ ch}_2\) and \({ ch}_3\) is shown in Fig. 11, where it can be seen that the shear stress \(\sigma ^{(1)}_{xz}\) at the surface is negligible if one of following two conditions is fulfilled. The first is that \({ ch}_3\gg 1\), and the second is that \({ ch}_2\ll 1\) and \({ ch}_3\gg { ch}_2\). If it is assumed that the overburden is much thicker than the reservoir layer, the second condition becomes just \({ ch}_2\ll 1\). These two inequalities can be rewritten in terms of the average wavelength as \(\lambda \ll 2\pi h_3\) and \(2\pi h_2 \ll \lambda \). Since the overburden is assumed thicker than the reservoir layer, these intervals overlap, and the condition for negligible shear stress at the surface is fulfilled for all wavelengths. Exactly the same argument shows that \(\sigma ^{(1)}_{yz}\) is close to zero at the surface.
The stress in the caprock, Eqs. (178)–(183), shows that all the components of the stress tensor are proportional to the coefficient \(F_4\). The components of the stress tensor depend on the z-position in the caprock by either the factor \(\cosh (cz_3-cz)\) or \(\sinh (cz_3-cz)\). This implies that the stress increases nearly exponentially, from the surface towards the base of the overburden, when \({ ch}_3\gg 1\), because \(0\le cz_3-cz\le { ch}_3\). In the other regime, where \({ ch}_3\ll 1\), these two factors can be approximated by \(\cosh (cz_3-cz)\approx 1\) and \(\sinh (cz_3-cz)\approx 0\). It can therefore be concluded that the short wavelengths in the fluid pressure, \({ ch}_3\gg 1\) or \(\lambda \ll 2\pi h_3\), produce stress in the caprock that is maximal towards its base. Long wavelengths, \({ ch}_3\ll 1\) or \(\lambda \gg 2\pi h_3\), produce a weak stress in the caprock for normal basin configurations where the overburden is much thicker than the reservoir (\(h_2\ll h_3\)).
15 Conclusions
An analytical solution is presented for the displacement, strain and stress of the poro-elastic equations for a three-dimensional model of three horizontal layers with the same rock properties. The three layers are an underburden on a rigid basement, a reservoir with a pore pressure change, and an overburden. The overburden and the underburden are assumed impermeable with no fluid pressure change. The boundary conditions are zero vertical displacement at the base of the underburden and zero horizontal displacement at the top surface. It has been shown that the top surface is stress-free, except for the shear stress components xz and yz, which are almost zero for common basin configurations where the overburden is much thicker than the reservoir.
The pressure distribution in the reservoir is assumed symmetrical around the z-axis, in which case the pressure can be represented by a double Fourier cosine series. The model provides a solution for the displacement, the strain and the stress as a superposition of contributions from each term in the Fourier series. It is shown that the bulk strain in the overburden and the underburden is zero, and that the bulk strain in the reservoir layer is proportional to the fluid overpressure. By means of this property of the bulk strain, a Fourier series solution is derived where the fluid flow and mechanics are fully coupled.
The contribution from each term in the Fourier series is proportional to the amplitude and a factor of proportionality that is a function of the average wavelength and the layer thicknesses. These factors provide insight into how the fluid pressure deforms the layers with respect to wavelengths and layer thicknesses. It is seen that only terms in the Fourier series with average wavelengths larger than \(2\pi \) times the thickness of the reservoir (\(\lambda \gg 2\pi h_2\)) produce an expansion of the reservoir. A second condition must be fulfilled for the expansion of the reservoir to produce a surface uplift, which is that the average wavelength must be larger than \(2\pi \) times the thickness of the overburden (\(\lambda \gg 2\pi h_3\)). When the second condition is not fulfilled, the expansion of the reservoir does not reach the surface. The expansion of the reservoir can also press down the underburden in this case.
The surface uplift can be written in the same form as the one-dimensional vertical reservoir expansion, where the fluid pressure is based on the Fourier series for the reservoir pressure. This expression shows that the surface uplift in this model can never be larger than the expansion of the reservoir. The analytical expressions for the surface uplift are compared with the numerically computed surface uplift for a case where the reservoir is resting on a rigid basement, and the match is excellent.
The model predicts a discontinuity in the xx and yy components of the stress tensor at the top and the base of the reservoir. Furthermore, ‘short’ wavelengths (\(\lambda \ll 2\pi h_3\)) in the Fourier series for the fluid pressure produce a stress at the base of the overburden with nearly the same strength as the amplitude in the Fourier series, but the stress does not extend far upwards into the overburden. Terms with ‘long’ average wavelengths (\(\lambda \gg 2\pi h_3\)) produce negligible stress in the overburden.
It remains to study how the model eventually can be extended to layers with different mechanical properties.
References
Bachu S (2008) CO\(_2\) storage in geological media: role, means, status and barriers to deployment. Prog Energy Combust Sci 34:254–273
Benson S, Cole RD (2008) CO\(_2\) sequestration in deep sedimentary formations. Elements 4:325–331
Bickle M (2009) Geological carbon storage. Nat Geosci 2:815–819
Bissell R, Vasco D, Atbi M, Hamdani M, Okwelegbe M, Goldwater M (2011) A full field simulation of the In Salah gas production and CO\(_2\) storage project using a coupled geo-mechanical and thermal fluid flow simulator. Energy Proc 4:3290–3297
Bryant E (1997) Climate process and change. Cambridge University Press, Cambridge, UK
Chang KW, Segall P (2016) Seismicity on basement faults induced by simultaneous fluid injection-extraction. Pure Appl Geophys 173:2621–2636
Fokker PA, Orlic B (2006) Semi-analytic modelling of subsidence. Math Geol 38(5):565–589, ISSN 1573-8868
Geertsma J (1973) Land subsidence above compacting oil and gas reservoirs. J Pet Technol 59(6):734–744
International Energy Agency (2016) Energy snapshot, Global energy-related carbon dioxide emissions 1980–2016, https://www.iea.org/newsroom/energysnapshots
Kim J, Selvadurai A (2015) Ground heave due to line injection sources. Geomech Energy Environ 2:1–14
Kreyszig E (2011) Advanced engineering mathematics. Wiley, Hoboken
Mindlin RD, Cheng DH (1950) Thermoelastic stress in the semi-infinite solid. J Appl Phys 21(9):931–933
Niu Z, Li Q, Wei X (2017) Estimation of the surface uplift due to fluid injection into a reservoir with a clayey interbed. Comput Geotech 87(Supplement C):198–211, ISSN 0266-352X
Rinaldi AP, Rutqvist J (2013) Modeling of deep fracture zone opening and transient ground surface uplift at KB-502 CO\(_2\) injection well, In Salah, Algeria. Int J Greenh Gas Control 12(Supplement C):155–167, ISSN 1750-5836
Rinaldi AP, Rutqvist J, Finsterle S, Liu HH (2017) Inverse modeling of ground surface uplift and pressure with iTOUGH-PEST and TOUGH-FLAC: the case of \({\rm CO}_{2}\) injection at In Salah, Algeria. Comput Geosci 108(Supplement C):98–109, ISSN 0098-3004
Rucci A, Vasco DW, Novali F (2013) Monitoring the geologic storage of carbon dioxide using multicomponent SAR interferometry. Geophys J Int 193(1):197–208
Rutqvist J (2012) The geomechanics of \({\rm CO}_{2}\) storage in deep sedimentary formations. Geotech Geol Eng 30:525–551
Rutqvist J, Vasco D, Myer L (2010) Coupled reservoir-geomechanical analysis of \({\rm CO}_{2}\) injection and ground deformations at In Salah, Algeria. Int J Greenh Gas Control 4:225–230
Selvadurai A (2009) Heave of a surficial rock layer due to pressures generated by injected fluids. Geophys Res Lett 36(14):L14302
Selvadurai A, Kim J (2016) Poromechanical behaviour of a surficial geological barrier during fluid injection into an underlying poroelastic storage formation. In: Proceedings of the Royal Society A, The Royal Society Publishing, pp 1–22
Sen B (1950) Note on the stress produced nuclei of thermoplastic strain in a semi-infinite elastic solid. Q Appl Math 8:635
Shi JQ, Sinayuc C, Durucan S, Korre A (2012) Assessment of carbon dioxide plume behaviour within the storage reservoir and the lower caprock around the KB-502 injection well at In Salah. Int J Greenh Gas Control 7(Supplement C):115–126, ISSN 1750-5836
Tempone P, Fjær E, Landrø M (2010) Improved solution of displacements due to a compacting reservoir over a rigid basement. Appl Math Modell 34(11):3352–3362, ISSN 0307-904X
Theis C (1935) The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage. EOS Trans Am Geophys Union 2:519–524
Vasco DW, Ferretti A, Novali F (2008) Reservoir monitoring and characterization using satellite geodetic data: Interferometric synthetic aperture radar observations from the Krechba field, Algeria. Geophysics 73(6):WA113–WA122
Verdon J, Kendall J, White D, Angus D (2011) Linking microseismic event observations with geomechanical models to minimize the risks of storing \({\rm CO}_{2}\) in geological formations. Earth Planet Sci Lett 305:143–152
Vilarrasa V, Rinaldi AP, Rutqvist J (2017) Long-term thermal effects on injectivity evolution during CO\(_2\) storage. Int J Greenh Gas Control 64(Supplement C):314–322, ISSN 1750-5836
Vilarrasa V, Rutqvist J, Rinaldi AP (2015) Thermal and capillary effects on the caprock mechanical stability at In Salah, Algeria. Greenh Gases Sci Technol 5(4):449–461, ISSN 2152-3878
Wangen M, Halvorsen G, Gasda S, Bjørnarå T (2018) An analytical plane-strain solution for surface uplift due to pressurized reservoirs. Geomech Energy Environ 13:25–34
White JA, Chiaramonte L, Ezzedine S, Foxall W, Hao Y, Ramirez A, McNab W (2014) Geomechanical behavior of the reservoir and caprock system at the In Salah \({\rm CO}_{2}\) storage project. Proc Natl Acad Sci 111(24):8747–8752
Zhou R, Huang L, Rutledge J (2010) Microseismic event location for monitoring \({\rm CO}_{2}\) injection using double-difference tomography. Lead Edge 29:201–214
Acknowledgements
This research was partially supported by the Research Council of Norway through the Project 280567, “Prediction of CO\(_{2}\) leakage from reservoirs during large scale storage”.
Author information
Authors and Affiliations
Corresponding author
Appendix: Derivation of the Solution
Appendix: Derivation of the Solution
For each of the three spatial directions, the equations for the displacement field (8) can be written as follows
where the source terms on the right-hand side are
for the fluid pressure (14).
1.1 Homogeneous Solution
Equations (65)–(67) are solved for one layer, and the one-layer solution is used to build a three-layer solution. The one-layer solution is the sum of a homogeneous solution (\(S_x=S_y=0\)) and a special solution with nonzero pressure terms. A homogeneous solution for the displacement field has the form
Inserting expressions (70–72) into equations (65–66) for the displacement field gives a linear system of equations
where \({\mathbf A}\) is
The system of linear Eq. (73) has a nonzero solution for the vector \([u_1, v_1, w_1]\) when \(\det ({\mathbf A})=0\). If the determinant of \({\mathbf A}\) is zero, then
and the linear Eq. (73) implies that the coefficients \(u_1\), \(v_1\) and \(w_1\) are related by
The same procedure can be applied for a homogeneous solution of the displacement field of the alternative form
where \(\det ({\mathbf A})=0\) once more implies \(c^2=k_1^2+k_2^2\), and where
now implies that
1.2 A Special Solution
A special solution of (65)–(67) is searched of the form
Inserting the displacements (81)–(83) into equations (65)–(66) gives the following equations for the unknowns A and B
which have the solution
1.3 The General Three-Layer Solution
The full solution for the displacement field is built from one solution for each of the three layers. The underburden (\(0\le z \le z_1\)) has the displacement field
The reservoir layer (\(z_1\le z \le z_2\)) with the fluid pressure (14) has the displacement field
where the coefficient
represents the change in fluid pressure (14). The overburden (\(z_2\le z \le z_3\)) has the solution
There are 18 unknown coefficients \(u_i\), \(v_i\) and \(w_i\) for \(i=1,\ldots , 6\) in the solution (88)–(97). These are found from the boundary conditions (13), the continuity in the displacement field across the layer boundaries, and algebraic constraints, such as Eqs. (75) and (80).
1.4 The Solution for the Coefficients in the Three-Layer Solution
The coefficients in the three-layer solution are related by (75) and (80), and all six relations for the three layers are
The boundary condition at the base, \(w(z\,=\,0)=0\), implies that \(w_1=-w_2\). The boundary conditions at the surface, \(u(z\,=\,z_3)=0\) and \(v(z\,=\,z_3)=0\), imply
These expressions for \(u_6\) and \(v_6\) are inserted into (103), and then, with the help of (102), it gives
The displacement field is continuous at the base and the top of the reservoir at the vertical positions \(z=z_1\) and \(z=z_2\), respectively. The continuity at the top of the reservoir layer gives
and similarly, for the base of the reservoir
where \(w_1\), \(w_2\), \(u_6\), \(v_6\) and \(w_6\) are removed from the system. In order to simplify the process of obtaining the unknown coefficients \(u_i\), \(v_i\) and \(w_i\) for \(i=1,\ldots , 6\), the following relations are conjectured
Inserting the conjectures (113)–(114) into the relations (98)–(101), respectively, gives that
and it gives that
The coefficients for the lateral displacements are now expressed by coefficients for the vertical displacement. The coefficients \(u_5\) and \(v_5\) follow from the interface relations (107) and (108), respectively.
Next, the interface relation (110) is multiplied by \(k_1\), and the interface relation (111) is multiplied by \(k_2\). These relations are then added together, and by using relations (100) and (101), it gives that
Similarly, the interface relations (107) and (108) are multiplied by \(k_1\) and \(k_2\), respectively, then added, and once more by the relations (100) and (101) give that
It gives four equations, the interface Eqs. (112) and (109), in addition to the two Eqs. (122) and (123), for the four unknowns \(w_0\), \(w_3\), \(w_4\) and \(w_5\). The pair of Eqs. (112) and (122) give that
and similarly, Eqs. (112) and (122) give that
These two pairs of expressions for \(w_3\) and \(w_4\) are useful in deriving these coefficients from either \(w_0\) or \(w_5\). Finally, these two alternative expressions give that
The coefficients \(w_0\) and \(w_5\) give \(w_3\) and \(w_4\) from the pair of equations (124)–(125) or (126)–(127). Then, the coefficients \(u_i\) and \(v_i\) for \(i=1,2,3,4\) are obtained from \(w_3\) and \(w_4\) using relations (118)–(121). The coefficients \(u_5\) and \(v_5\) are found from interface relations (107) and (107), respectively, and finally, \(u_6\), \(v_6\) and \(w_6\) are obtained from Eqs. (104)–(106), respectively.
1.5 Summary of the Coefficients
The 18 coefficients \(u_i\), \(v_i\) and \(w_i\) for \(i=1,\ldots ,6\) for the three-layer model are listed below.
It can be seen that some coefficients depend on the coefficients listed previously. All coefficients can be traced backward to either \(w_1\) or \(w_5\). They are therefore all proportional to the pressure perturbation, \(D_1\). The following form of the coefficients is compact and very well suited for programming. It is straightforward to obtain the solution in the form given in Sect. 10 using the coefficients (130)–(147).
1.6 Strain
The solution for the displacement field, Eqs. (16)–(29), gives the following expressions for the strain \(\varepsilon _{ij}=\frac{1}{2}(u_{i,j} + u_{j,i})\).
The strain in the underburden (\(0 \le z \le z_1\)) is
The strain in the reservoir layer (\(z_1 \le z \le z_2\)) with overpressure is
The strain in the overburden (\(z_2 \le z \le z_3\)) is
One observes that both the underburden and the overburden have zero bulk strain \(\varepsilon =\epsilon _{xx}+\varepsilon _{yy}+\epsilon _{zz}=0\), and that the reservoir has a bulk strain proportional to the pressure, \(\varepsilon =D_0 p_0\cos (k_1 x)\cos (k_2 y)\).
1.7 Effective Stress
The effective stress follows from the strain computed in the preceding subsection when inserted in the constitutive law (7). The fact that there is a zero bulk strain in the overburden and the underburden simplifies the expressions for the effective stress in these two layers.
The effective stress in the underburden (\(0 \le z \le z_1\)) is
The effective stress in the reservoir (\(z_1 \le z \le z_2\)) is
The effective stress in the overburden (\(z_2 \le z \le z_3\)) is
The stress is \(\sigma ^{(1)}_{ij}=\tau ^{(1)}_{ij}\) in the underburden and the overburden, because three is no change in the fluid pressure in these two layers. In the reservoir, the stress is obtained from the definition of the effective stress, Eq. (6), as \(\sigma ^{(1)}_{ij}=\tau ^{(1)}_{ij}-\alpha p^{(1)}\delta _{ij}\), where the reservoir overpressure is given by (14). It is straightforward to check that the stress \(\sigma ^{(1)}_{ij}\) in each layer fulfills the equilibrium Eq. (3).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wangen, M., Halvorsen, G. A Three-Dimensional Analytical Solution for Reservoir Expansion, Surface Uplift and Caprock Stress Due to Pressurized Reservoirs. Math Geosci 52, 253–284 (2020). https://doi.org/10.1007/s11004-019-09821-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11004-019-09821-9