Abstract
A pattern-based simulation technique using wavelet analysis is proposed for the simulation (wavesim) of categorical and continuous variables. Patterns are extracted by scanning a training image with a template and then storing them in a pattern database. The dimension reduction of patterns in the pattern database is performed by wavelet decomposition at certain scale and the approximate sub-band is used for pattern database classification. The pattern database classification is performed by the k-means clustering algorithm and classes are represented by a class prototype. For the simulation of categorical variables, the conditional cumulative density function (ccdf) for each class is generated based on the frequency of the individual categories at the central node of the template. During the simulation process, the similarity of the conditioning data event with the class prototypes is measured using the L 2-norm. When simulating categorical variables, the ccdf of the best matched class is used to draw a pattern from a class. When continuous variables are simulated, a random pattern is drawn from the best matched class. Several examples of conditional and unconditional simulation with two- and three- dimensional data sets show that the spatial continuity of geometric features and shapes is well reproduced. A comparative study with the filtersim algorithm shows that the wavesim performs better than filtersim in all examples. A full-field case study at the Olympic Dam base metals deposit, South Australia, simulates the lithological rock-type units as categorical variables. Results show that the proportions of various rock-type units in the hard data are well reproduced when similar to those in the training image; when rock-type proportions between the training image and hard data differ, the results show a compromise between the two.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Simulation at spatially correlated continuous and/or categorical variables such as the geological units and metal grades of mineral deposits, or sedimentary facies and pertinent attributes of petroleum reservoirs and water aquifers is a challenging task. The well-known variogram-based two-point statistical techniques (Goovaerts 1997; Deutsch and Journel 1998) are limited in its ability to adequately model spatial complexity (Journel and Alabert 1989). To address the limitations of two-point statistical models, new developments have introduced high-order spatial statistics in the form of the multi-point models (mp) (Guardiano and Srivastava 1993; Tjelmeland 1998; Journel 1997). In multi-point models, a pattern is defined as a set of values spatially distributed over a given template of spatial locations (Arpat and Caers 2007; Remy et al. 2009). During simulation, multi-point conditioning data in the form of a template is compared with patterns of the training image (a geological analogue of what is being modeled) and a pattern is selected from the training image. A pattern is selected either based on the most similar pattern (Arpat and Caers 2007) or a random pattern from the best matched class (Zhang et al. 2006; Wu et al. 2008). Different distance functions are used for similarity measures, including Manhattan distance (Zhang et al. 2006), L 2-norm (Chatterjee and Dimitrakopoulos 2011), and others.
The main goal of mp simulation methods is finding the best matching pattern from a pattern database with the conditioning data event. A pattern database is generated by scanning the training image using the given template. The snesim algorithm (Strebelle 2000, 2002) generates a search tree from the training image and modeled conditional cumulative distribution function (ccdf) of patterns. The main disadvantage of the snesim algorithm is that it is demanding in terms of computer random-access memory (RAM) particularly when very large training images are used. RAM requirements may limit snesim when large size simulation of several multiple categories is needed. The snesim algorithm searches for exact replicates of conditioning data event. Since exact replicates may not always be possible to obtain from the pattern database, some conditioning data points from the conditioning data event are deleted. Arpat and Caers (2007) proposed an mp simulation algorithm termed as simpat (simulation with patterns), which is not based on the exact match of the training patterns with the conditioning data event but rather it searches for the best possible match. A simpat algorithm considers the training image as a collection of patterns, same as snesim, from which a pattern can be selected to locally match as close as possible to the conditioning data event. The main advantage of this algorithm is that no conditioning data points from the conditioning data event are required to be deleted; however, the major limitation is that the entire pattern database will be searched to find the best match at each simulating node; therefore computational time will be extensively high.
The filtersim (simulation using filter scores) algorithm overcomes simpat’s computing limitation (Zhang et al. 2006; Wu et al. 2008). Like simpat, the main advantage of filtersim is that no conditioning data points need to be deleted from the conditioning data event for matching with the patterns from the pattern database. In filtersim, similarly to snesim and other mp simulation approaches, scanning of the entire training image is performed using a given template to obtain patterns. Different filters are applied on patterns to obtain values of filter scores. The patterns in the pattern database are then grouped, based on their filter score values, into different classes. The classes are represented by their prototype, which is the average value of all patterns in a class. During simulation, the conditioning data event is compared with the class prototypes to find the closest matched class. Unlike simpat, filtersim does not need to search the entire pattern database. The algorithm is looking for ‘best match’ rather than ‘exact match’; therefore, no elimination of conditioning data points from the data event is required. Honarkhah and Caers (2010) introduced a distance-based simulation algorithm for efficiently classifying pattern database. Their results show that the algorithm performs better than filtersim for pattern reproduction. However, in all-pattern-bases simulation, a pattern is drawn randomly from a class; no conditional cumulative distribution function (ccdf) is generated for each class like snesim for categorical variable simulation. Therefore, the success of the technique is dependent on how well the patterns in the pattern database are classified. Since no ccdf’s are generated, the pattern obtained from a ‘best match’ class is random; no statistics are involved in it.
In other approaches to mp simulation, researchers proposed a high-order spatial cumulants-based technique where ccdf was generated by Legendre polynomials (Dimitrakopoulos et al. 2010; Mustapha and Dimitrakopoulos 2010). In this framework, the coefficients of Legendre polynomials are calculated using cumulant maps generated from a training image. This high-order simulation technique is data driven instead of training image driven and therefore reproduces high-order spatial statistics of the data. The limit of this approach is that, at present, the framework is limited to simulating continuous variables. Gloaguen and Dimitrakopoulos (2009) present a different technique of conditional simulation using the inter-scale dependency at the wavelet domain. The advantage of this approach is that the direct conditioning is easy, but it is difficult to fitting the conditioning data in the wavelet domain.
As an alternative to other mp simulations, a pattern-based simulation algorithm using wavelet analysis is proposed in this paper termed as wavesim. The pattern database is generated in a manner similar to other mp simulation techniques. The pattern database is classified by using wavelet approximate sub-band coefficients of each pattern. The wavelet approximate sub-band can capture most of the pattern variability, and at the same time reduce the dimensionality of the pattern database. Pattern database classification is performed using the k-means clustering technique. For categorical data simulation, the ccdf of the individual prototype class for the central node category of the template is developed using the probability of each individual category within the class; however, for continuous data simulation, a random sample is selected from ‘best match’ class. For simulation, the similarity of the prototype classes with the conditioning data event is calculated. A random pattern is generated from the developed ccdf of the ‘best match’ class. Unlike filtersim, wavesim is not generating a random pattern from a class; rather, it generates a random pattern from a ccdf developed for a class. However, for continuous data, no ccdf is generated.
The present paper is organized as follows. Section 2 describes the wavesim method. A brief overview of pattern-based simulation is presented in Sect. 2.1, and the basic fundamentals of wavelet analysis and dimensional reduction techniques are presented in Sect. 2.2. The pattern database classification technique is presented in Sect. 2.3, while Sect. 2.4 describes the ccdf generation of a class. The similar measures of the class prototype with the conditional data event are presented in Sect. 2.5. Section 3.1 presents unconditional simulation using binary training image, three-categories training image and continuous training image for two-dimensional problem. The conditional simulations of two- and three-dimensional continuous data are presented in Sect. 3.2. The sensitivity of wavesim is presented in Sect. 4. An application for simulating categorical variable of three-dimensional data at the Olympic Dam base metal deposit in South Australia is presented in Sect. 5; and, conclusion and discussion follow.
2 Method
2.1 Generation of a Pattern Database
Pattern-based simulation is viewed as an image reconstruction problem (Arpat 2004; Zhang et al. 2006; Wu et al. 2008). Instead of directly reproducing the multiple-point statistics of a training image, the training image patterns are reproduced in a stochastic manner, and this ultimately respects the multi-point statistics of the training image (Arpat and Caers 2007). Pattern-based simulation algorithms consist of two steps. First, a pattern database is generated by scanning the training image using a given template. Then, a pattern that provides the best match to the conditioning data is searched from in the pattern database.
Define \(\operatorname{ti}(u)\) as a value of the training image ti where u∈G ti and G ti is the regular Cartesian grid discretizing the training image, \(\operatorname{ti}_{T}(u)\) indicates a specific multiple-point vector of \(\operatorname{ti}(u)\) within a template T centered at node u, that is
where the h α vectors are the vectors defining the geometry of the n T nodes of template T and α={1,2,…,n T }. The vector h 1=0 represents the central location u of template T. The pattern database is then obtained by scanning ti using template T and stored the multi-point \(\operatorname{ti}_{T}(u)\) vectors in the database. For a categorical training image with M categories, the training image is first transformed into M sets of binary values I m (u),m=1,…,M,u∈T,
Thus, a pattern of M-categories can be represented as M sets of binary patterns, where the mth binary pattern with indicator value 1 represents the presence of category m, and value 0 represents the absence of category m at a certain location in the template. Note that for continuous training images, no such transformation was made and patterns \(\operatorname{ti}_{T}(u)\) are saved as extracted from the training image. The pattern database generated from continuous training image or categorical training image with M-categories is now defined as patdbT.
2.2 Dimensional Reduction of a Pattern Database
After generating the patdbT irrespective of using a continuous or a categorical training image, the classification of the pattern database will be performed so that during simulation, instead of searching the entire pattern database (patdbT), only some representative members, i.e. prototypes of the classes, are compared with the conditioning data event. However, when the template dimension is large, the dimension of patdbT will also be large. Therefore, classification of this large dimensional pattern database patdbT is a computationally demanding task. In previous research, the patdbT classification was performed by reducing the dimensions of the pattern by using few filter scores (Zhang et al. 2006; Wu et al. 2008). Zhang et al. (2006) and Wu et al. (2008) used 6 and 9 filters for two- and three-dimensional training images, respectively. Any dimensional pattern in the patdbT is represented by 6×M filter scores (for a two-dimensional image) where M is the number of categories (M=1 for continuous image) present in the training image. A wavelet-based representation of patterns is introduced where the dimension of the pattern-for-pattern classification can be reduced by selecting the scale of wavelet decomposition.
Wavelets analysis can decompose a training image into different frequency components (Mallat 1998). The wavelet decomposition of an image provides one approximate sub-band image and three high frequency sub-band images after one scale decomposition of a two-dimensional training image. For further decomposition, the approximate image is decomposed to obtain the next scale sub-band images. The approximate sub-band provides average type information about the training image and preserves most of the data variability of the training image. If the high frequency sub-bands are added to the approximate sub-band, then the training image is perfectly reconstructed. It is noted that the amount of data in an approximate sub-band is 2j×d times less than the amount of data in the training image, where j is the scale number in wavelet decomposition, and d is the dimension of the original image. Figure 1 shows an example of an original image and the reconstructed image after keeping only the approximate sub-band image and zero padding to all wavelet sub-band coefficients after one scale decomposition. Figure 1 demonstrates that the image is well reconstructed after reducing 75% of the data of the original image.
Let \(\operatorname{ti}_{T}\) be a pattern from the pattern database patdbT with size p×p. If wavelet decomposition of the given pattern is performed, then it can be presented as
where D={LH,HL,HH}, \(N_{j} = \frac{N}{2^{j}}\), and J is the number of scales, L and H are low-pass and high-pass filters obtained from wavelet basis function, N=p when p is even, N=(p+1) when p is odd, ϕ j is scaling function and \(\psi^{B}_{j}\) are wavelet functions. The scaling and wavelet coefficients a j−1 and w j−1 at scale j−1 can be experimentally calculated by taking inner products

Each of these basis functions (ϕ j and \(\psi^{B}_{j}\)) is used to scan the M binary training image. At each pixel location, the template of neighborhood data values is convoluted by these basis functions to obtain the approximate and wavelet sub-band data for category m. The length of the vector of generated approximate sub-band for the M-categories image will be
where d is the number of dimensions of the image. It is noted that the original length of pattern vector is ((N)d×M). Therefore, depending on the value of j, the dimension of the original pattern vector can be significantly reduced. For example, a three-dimensional template with size 16×16×16 for 4 categories has a vector length of 16,384, and if 2-scale wavelet decomposition is performed, the length of the vector will be 256, which is significantly less than the original.
2.3 Pattern Database Classification
For classification of pattern database patdbT, the approximate sub-band of the patterns, which is reduced in dimension depending on the value of j, is used. The k-means clustering technique (MacQueen 1967; Hartigan and Wong 1979; Ding and He 2004) is applied to classify the pattern database patdbT. The main idea of k-means clustering is to divide the patdbT into a number of classes such that the sum of the inter-class distance is maximized.
The k-means clustering is a simple unsupervised learning algorithm (MacQueen 1967). In this algorithm, the pattern database is classified based on the selected priory cluster number (k). First, k patterns from the patdbT are randomly selected. These k patterns represent the initial class centroids. Since the patdbT classification is performed by using the approximate sub-band of patterns, randomly selected approximate sub-band of k patterns from patdbT will act as initial centroids. Then each pattern from the patdbT is assigned to a class which has the closest distance to the centroids. After assigning all patterns into any one of those classes, the centroids’ positions are recalculated. This is an iterative process and the algorithm stops when the centroids’ positions no longer change. The aim of the k-means clustering algorithm is to minimize the following objective function
where \(\| t_{i}^{(j)} - c_{j} \|^{2}\) is the squared Euclidean distance between a pattern \(t_{i}^{(j)}\) and the centroids of class c j , and is a measure of the distance of the n patterns from their respective cluster centers.
To provide an example of k-means clustering, Fig. 1(a) shows a two-categories training image. A template size of 15×15 is used to extract patterns from the training image. The approximate sub-band of two-scale decomposition is used for patdbT classification. If the number of classes is 300 for k-means clustering, Fig. 2 represents all patterns (36) falling in a particular class after classification of patdbT. It is observed from the figure that the patterns look very similar, and the algorithm can easily classify the patterns. Since the pattern classification was performed using the approximate sub-band after two-scale decomposition, the dimensionality of the patterns is reduced from 225 (15×15) to 16 (4×4, size of approximate sub-band). After classifying the patdbT by minimizing the objective function at (6), prototypes of classes are calculated. These prototypes are used during the simulation process, when the similarity between the conditional data event and prototype class is calculated. The prototype value is obtained by averaging all patterns falling into a particular class. Figure 3 presents the prototype of 36 patterns presented in Fig. 2.
Prototype of a class 36 patterns of Fig. 2
2.4 Similarity Measures Between Conditional Data and Class Prototypes
After classifying the patdbT prototype calculation, simulation was carried out. During simulation, the similarity between the conditioning data event and the prototypes of the classes are carried out. A sequential simulation algorithm (Goovaerts 1997) is used for pattern-based simulation in this paper. At each visited node, a conditioning data event is obtained by placing the same template used in the training image, centering at the node to be simulated. The similarity between the conditioning data and prototypes of classes are calculated by a distance function. A distance function is used to calculate the distance from the prototypes of classes to the conditioning data event. The distance function used in this paper is L 2-norm for its success in template matching (Goshtasby et al. 1984; Kuglin and Hines 1975; Chatterjee and Dimitrakopoulos 2011), and it is


where x is the conditioning data event, y is the prototype of class, n type is the number of data from a particular data type, w i is weight associated with data types. Three different data types are considered for distance calculation: hard conditioning data, previously simulated node data, and pattern pasting node data. Generally, hard conditioning data have higher weights than other data types.
If all the nodes within a template are known when simulating a node, the distance calculation with a large template can be computationally demanding. To reduce the computational time of a distance calculation, approximate sub-band coefficients after wavelet decomposition of the conditioning data event are used. The modified distance function can be presented as
where n approx is a number of approximate sub-band coefficients after the wavelet decomposition, x approx is an approximate sub-band coefficient of conditioning data event, and y approx is an approximate sub-band coefficient of prototype class. If within the conditioning data event any hard data are presented, (7) will be used for distance calculations even if all the nodes within a template are fully known.
2.5 Conditional Cumulative Distribution Function (ccdf) of a Class for Categorical Image
After measuring the similarities of the conditioning data event with the prototypes of classes, the best matching class is selected. In filtersim, a random pattern from the selected class is drawn and pasted in a simulated node. The probability of the central node categories within a class may be different, which has not been considered in filtersim. However in wavesim, a conditional cumulative distribution function (ccdf) is generated for each class. This is developed by calculating the probability of occurrence of a particular category in the central template node, divided by the total number of patterns in that class. For example in Fig. 2, out of 36 patterns, 7 times the central node category is lithology A, and 29 times it is lithology B. Therefore, the probability of occurrence of lithology A is 0.1944 (7/36) and probability of occurrence of lithology B is 0.8056 (29/36). The ccdf of that class can be presented as in Fig. 4.
During the simulation process, after finding the best matched class, a uniform random number is generated. From the developed ccdf, the category at the central node is obtained corresponding to the generated random number. Then, a random pattern is drawn from the matched class patterns which have the same central node category as the category obtained from the ccdf. After pasting the drawn pattern at a simulated node, the next node is visited in a random path. The same distance function and the patterns-drawing algorithm are performed until all nodes are simulated. The algorithm stops when no nodes are left unvisited. It is noted that, for continuous image, a random pattern is drawn from a class; no ccdf is generated for continuous case.
The main steps of the wavesim are as follows:
-
1.
Scan the training image ti using the given template T. Perform wavelet decomposition of the generated patterns using selected wavelet basis function and scale. Save the wavelet coefficient and approximate coefficients in the pattern database. If the training image is categorical image, generate M binary image from the M-categories training image before wavelet decomposition.
-
2.
Classify the patterns, based on only the approximate sub-band coefficients in previously defined cluster numbers and calculate the class prototype using the point-wise averaging of all patterns within a class.
-
3.
Define a random path visiting once and only once all unsampled nodes.
-
4.
Use the same template shape T at each unsampled location u. The distance from the class prototype is calculated from the conditioning data available within the template using either (7) or (9). Select the class which has minimum distance from the conditioning data. If no conditioning data are available, a random class is selected.
-
5.
Draw a random pattern from the prototype class and paste the pattern by centring at the simulated location u. If any hard data or central node value of any already simulated locations are present in any node within the template T at location u, they are frozen before simulated pattern pasting. For categorical data, the random sample is drawn based on ccdf generated for each class as described in Sect. 2.5.
-
6.
Add the simulated value at point u to a different file to use it during distance calculation.
-
7.
Repeat Steps 4 and 6 for the next points in the random path defined in Step 3.
-
8.
Repeat Steps 3 to 7 to generate different realizations using different random paths.
To demonstrate the strengths and improved performance of the ccdf-based model over the random-sampling-based method for simulating the categorical image, an example is demonstrated here. The patterns are extracted from Fig. 5(a) which represents a binary channel image using a 9×9 template. The unconditional simulations are performed using wavesim-ccdf approach and without ccdf approach considering the same random path. The numbers of clusters are same for both simulations. In Fig. 5, parts (b) and (c) present one realization generated using ccdf-based approach, and non-ccdf-based approach (random sampling), respectively. The results clearly demonstrated that ccdf-based approach can reproduced better the channels’ shapes in comparison with non-ccdf approach.
3 Application of the Proposed Method
The wavesim algorithm is validated by simulating known categorical and continuous two-dimensional and three-dimensional data sets. The exhaustive data sets are obtained from different sources. All runs are performed on a 3.2 GHz Intel(R) Xeon (TM) PC with 2 GB of RAM. For wavelet decomposition, the Haar basis functions are applied for all cases unless otherwise specified. The results of wavesim are compared with filtersim results to make a valid comparison. The filtersim results are generated by using SGeMS software (Remy et al. 2009). To assess the wavesim method, unconditional and conditional simulations are performed for categorical and continuous data sets which are then compared against results from filtersim.
3.1 Unconditional Simulation
To perform unconditional simulation, binary training image, three-categories training image, and continuous training image are considered and presented hereafter.
3.1.1 Two-categories Training Image
For unconditional simulation of categorical image, the wavelet decomposition is performed after generating the pattern database to reduce the dimensionality of the pattern database. The critical step of wavelet decomposition for dimensionality reduction is the selection of optimal scale. The main goal of dimensional reduction is to retain maximum data variability by fewer dimensions. The successfulness of the dimensional reduction is depends on how the lower dimensional space is preserving the energy (entropy) of the original data (Huber 1985). In wavelet analysis, the energy is distributed over the scales. Therefore, an optimal scale, in which the characteristics frequency is most dominated compared to the other, must be selected. The Shannon entropy (Schürmann 2004) is an efficient tool for calculating the entropy at different scales. To select optimal scale, we have calculated wavelet entropy value of each pattern \(\operatorname{ti}_{T}\) at scale j using the following equation
where
and
and j is the scale of decomposition; w j,i,l is wavelet coefficients in scale j at location (i,l).
The average of entropy for all patterns in the pattern database is calculated by
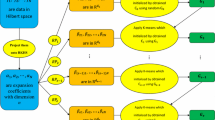
where s is number of patterns in pattern database. The value of (11) is compared by changing the scale j and optimal scale is selected where the value is the maximum. Figure 6 demonstrates the optimal scale selection algorithm applied in this paper. The entropy value is calculated starting from scale j=1 and stopped when the maximum scale is reached. The maximum scale is that when no more decomposition is possible, i.e. the scaling image has only one pixel (data).
To demonstrate our scale selection algorithm, we have used a binary training image (Honarkhah and Caers 2010; Strebelle 2000). The training image is presented in Fig. 5(a). This training image represents complex channels presented in a deposit. The template size is selected using the method proposed in Honarkhah and Caers (2010) and it is 9×9. The patterns are extracted from the training image and up to scale 4 wavelet decomposition was performed. The average entropy values are calculated for each scale using (11) and plotted in Fig. 7(a). Form Fig. 7(a) it is observed that the entropy value of the binary channel training image is first increased from scale 1 to scale 2 to and then starts decreasing. Thus, the optimal scale for the example is 2. To check the scale selection approach, we have unconditionally simulated the binary training image using the approximate sub-band of scale 1 to scale 4 and presented in Fig. 7(b)–(d). These figures show that the simulated realizations are almost same for scale 1 and scale 2; but the channel reproduction deteriorates when we move from scale 2 to scales 3 and 4. Therefore, the channel reproduction of the simulated realization also supports that the optimal scale for this example is 2.
After selecting the optimal scale, the unconditional simulation is performed using the same binary training image and compared to the results obtained from filtersim. The parameters used for the simulations from the wavesim and filtersim are the same. Note that the inner patch size is 5×5. The k-means clustering algorithm is used with number of classes at 100. Two different unconditionally generated realizations using wavesim and filtersim are presented in Fig. 8. It is observed from the figure that the wavesim can reproduce channels presented in the training image. On the other hand, filtersim fails to reproduce the continuity of the channels. The main difference between the wavesim and filtersim is the way of classifying the patterns in patterns’ database. The example shows that when classifying patterns, using only few filter scores is not always possible to capture the complexity present in the available patterns, resulting in discontinuities of the channels when unconditional simulations are performed.
3.1.2 Multi-Categories Training Image
To perform unconditional simulation with multiple categories, a three-categories training image is obtained from Osterholt (2006). The training image size is 50×200 pixels coding three different geological units (Fig. 6(a)). The template size used in this example is 11×11 and pasting is 7×7. The optimal scale of decomposition for this example is also 2. The number of wavelet coefficients used for classification after two-scale wavelet decomposition is 9. Different unconditionally simulated realizations of the wavesim and filtersim are presented in Fig. 9. It is observed from the figure that wavesim provides better reproduction of geological model as compared to filtersim.
3.1.3 Contentious Training Image
For unconditional simulation of continuous data, an exhaustive two-dimensional continuous horizontal slice is obtained from a three-dimensional fluvial reservoir. The exhaustive data sets used here are obtained from the Stanford V Reservoir Data Set (Mao and Journel 1999). The channel configurations and orientation is complex in nature form one slice to another in the vertical direction. The size of the domain to be simulated is 100×128. The number of clusters chosen for this analysis is 200. The sensitivity of the number of clusters is presented in Sect. 4.
The template size used in this study is large enough to capture high variability of patterns (15×15). Two-scale wavelet decomposition was performed after zero padding with template since wavelet needs even size template. After zero padding at last column and last row, template size is converted to 16×16. The pattern database is generated by scanning the entire training image and performing the wavelet decomposition of the pattern database. The approximate sub-band is utilized for pattern data classification. The optimal scale for this problem is 3. Therefore, the dimension of the data for pattern classification is reduced from 225 (template size 15×15) to 16 (approximate sub-band size 4×4). Two realizations are generated by wavesim and filtersim algorithm and presented in Fig. 10. It is observed from the figure that with wavesim channels are well reproduced; however, filtersim fails to reproduce channels. Moreover, from visual observation, it shows that the proportions of high, medium, and low values are well reproduced by wavesim which is not reproduced by the filtersim algorithm. This observation is also supported by the histograms of simulated realizations of wavesim and filtersim (Fig. 11) and their comparisons with the histogram of the training image.
3.2 Conditional Simulation
Two different examples are shown for conditional simulation with the wavesim and compared with the filtersim results. One two-dimensional and one three-dimensional continuous data examples are presented hereafter.
3.2.1 Two-Dimensional Conditional Simulation with Continuous Data
The same Stanford V Reservoir Data Set (Mao and Journel 1999) is used for conditional simulation example. One slice of the three-dimensional reservoir data is used as reference image where from conditioning data are sampled. Another slice is used as the training image. The size of the domain to be simulated is 100×128.
The reference image to be simulated is presented in Fig. 12(a). The simulation was performed using two different data sets. The first data set consists of 208 data on regular grid at equal spacing. The second data set consists of 100 data at irregular spacing scattered all over the domain. In Fig. 12, parts (b) and (c) represent first and second data sets, respectively. The training image used in this study is the same as used in last example (Fig. 10(a)). The template size and scale of wavelet decomposition are also the same as in last example (Sect. 3.1.3). The k-means clustering with cluster number 300 is used for training pattern classification. During simulation, the distance from the cluster centers to the conditional data are calculated either using (7) or (9) depending on whether the conditional data template is fully informed or not. The weights of hard data, previously simulated node point, and patch data are 0.5, 0.3, and 0.2, respectively for distance calculation. When the conditioning data set is fully informed, only approximate sub-band coefficients after wavelet decomposition are used. The conditionally simulated realizations generated by wavesim and filtersim using the first data set, are presented in Fig. 13. The realizations show that the high-valued channels are well reproduced. The comparison study with filtersim realizations shows that the channels continuity is well reproduced using wavesim as compared to filtersim. The histogram and variogram of the simulated realizations are compared with the data histogram and variogram and presented in Fig. 14. The results revealed that the first- and second-order statistics are well reproduced using wavesim. To show the multi-point reproduction of wavesim method, the 3-point cumulant maps of the training image and simulated realizations are generated. The 3-point template presented in Fig. 15(a) is used for cumulant calculation. Figure 15(b)–(d) demonstrates that wavesim can reproduce well the cumulant map of the training image.
In the second example, data set 2, shown in Fig. 12(c), is used as hard conditioning data. All other parameters are kept the same as in the previous example. Two conditional realizations using wavesim and filtersim algorithm are presented in Fig. 16. It is observed from the figure that the channels are not reproduced as good as in previous example using wavesim as well as filtersim, which is reasonable with less number of conditioning data. However, continuity of high-valued channels is much better as compared to filtersim algorithm. The histograms and variograms of realizations are well reproduced in the hard data histogram and variogram as presented in Fig. 17. Same as in previous example, we have generated cumulant maps of the simulated realizations and presented them in Fig. 18. The figure shows that 3-point cumulant maps are well reproduced in the training image cumulant maps.
3.2.2 Three-Dimensional Conditional Simulation with Continuous Data
To performed three-dimensional conditional simulation for continuous data, we have rescaled the Stanford V Reservoir Data Set (Mao and Journel 1999) to 100×100×28. One part of the three-dimensional reservoir data is used as training image and the other part is simulated using wavesim and filtersim algorithm. The size of the training image and reference image is 100×5×28 each.
The reference image to be simulated and the training image are presented in Fig. 19(a) and (b). The simulation was performed using 153 hard data from reference image. The template size used in this example is 11×11×7 and 7×7×5 pattern is pasted. The optimal scale of decomposition for this example is 2. Therefore, two-scale wavelet decomposition is performed and approximate sub-band of size 3×3×2 is used for pattern classification. Due to dimensional reduction technique using wavelet decomposition, the pattern dimension is reduced from 847 (11×11×7) to 18 (3×3×2). The dimensionality of the data is reduced more than 47 times. Since major computational time of the pattern-based simulation is utilized for pattern similarity search during simulation, therefore the computing time of the algorithm will be also reduced after dimension reduction. The number of clusters used in this example is 300. Figure 19(c) and (d), shows two different realizations generated using wavesim and filtersim algorithms. After comparing with reference image, it is observed that wavesim well reproduced the channels shapes; however, filtersim fails to reproduce the channels shapes.
A contributor to the success of a simulation algorithm, in terms of use for real world applications, is its computational efficiency. The proposed algorithm is implemented in the MATLAB environment, which makes it difficult to compare the CPU time taken in our various examples to filtersim or other algorithms which are implemented in the C++ environment. The main difference between our proposed algorithm and filtersim is the dimensionality reduction. Both the algorithms are using the same clustering algorithm and simulation steps are almost the same. The computing time depends on the number of reduced dimensions.
In Sect. 3.1.1 and for a binary training image, we have used the approximate sub-band of 2-scale wavelet decomposition of a 9×9 training image. Therefore, the number of variables used for classification in our algorithm is 9 in comparison to 6 of filtersim. Thus, the computing time of our proposed approach is slightly higher than that of filtersim for the simulation images in Fig. 8. However, in Fig. 7 we have presented different realizations of the same training image using 3-scale (4 variables) and 4-scale (1 variable) decomposition. It is observed in Fig. 7 that the simulation using 3-scale and 4-scale decomposition is also performing better than the filtersim results (Fig. 8(c), (d)). Since 3-scale and 4-scale are using less number of variables, 4 and 1 respectively, than filtersim, computing time will also be less for the proposed method compared to filtersim.
4 Sensitivity Analysis
It is now clear from presented examples that wavesim has performed better than the filtersim algorithm for continuous and categorical, two- and three-dimensional problems. However, the success of the proposed method, same as for filtersim, depends on some parameters. In this section, we will present the sensitivity of the proposed method to different parameters. The number of clusters for pattern database classification, type of basis functions used, weights assigned to the distance calculation, the number of wavelet coefficients used for distance calculation will be investigated in the simulated realization. In this section, the sensitivity of the method is tested using conditional simulation techniques with same data set presented in Sect. 3.2.1. The data set 1 is used as conditioning data for sensitivity analysis unless otherwise mentioned.
4.1 Sensitivity to the Cluster Number
The sensitivity of the wavesim algorithm is studied using the training image of Fig. 10(a). All parameters are kept the same as in the example of Sect. 3.2.1 except the number of clusters. It is noted that during simulation the distances are calculated from the conditioning data to the cluster centers. Therefore, when the number of clusters is large, several distance values have to be calculated and consequently the computational time becomes higher. On other hand, due to large number of clusters, the number of patterns within a cluster will be less. Therefore, when a random drawing is performed from a cluster, it is expected that the closely similar pattern of conditioning data event will be drawn from a cluster. In this example, four different cluster numbers 50, 100, 200, and 300 are chosen. Figure 20 presents simulated realization generated by changing the cluster numbers. The result revealed, as expected, that the channels are reproduced much better, same as in the other pattern base simulation, when number of clusters is bigger. However, computational time is also highest for cluster number 300.
4.2 Sensitivity to the Wavelet Basis
In this example, we have presented the effect of wavelet basis function in the proposed algorithm. Three different basis functions are used: Haar, Daubechies 3 (db3) and Daubechies 5 (db5) (Daubechies 1992). Higher-order Daubechies filter has higher vanishing moments thus the approximate sub-band of db5 can store more energy of the pattern than the db3 and Haar. Therefore, it is expected when the distance calculation will be performed based on only the approximate sub-band, db5 or higher Daubechies filter may provide better cluster match with conditioning data event. In this example, number of clusters is 200. The weight values are 0.5, 0.3, and 0.2 for hard data, previously simulated nodes, and patch nodes, respectively. Only the approximate sub-band is used for patterns database classification. Figure 21 presents the simulated realizations generated with three different basis functions. The channels are well reproduced with three different basis functions, as reproduced in previous examples. The results show that there are no such significant differences observed in simulated realizations when different basis functions are used.
It is always expected that when the higher order wavelet basis functions will be used, the results of the simulated map should be improved. However, we have not observed that improvement in this case. The possible reason may be that the approximate sub-band coefficients using Haar basis are sufficient to capture the complexity present in the patterns of the training image. It implies that even if we have not seen any such improvement in this case with increasing the order of wavelet basis, the improvement may be observed when the training image pattern is more complex.
4.3 Sensitivity to the Training Image
In this example, the sensitivity of the training image is performed. In this test, the training image of the previous examples is rotated to change the orientation of the channels. Figure 22(a) shows the rotated training image used in this example. Data set 1 and data set 2 are used as hard data for this exercise. The number of classes is 300 in this example. The weights and other parameters are the same as in example in Sect. 4.2. Figure 22 represents different realizations for data set 1 and data set 2 with the rotated training image. The result showed that the directions of the channels of the simulated realizations are the same as the reference image with data set 1; whereas the directions of channels are different with data set 2, as expected. The result revealed that changing the orientation of the training image does not affect the simulated image in terms of orientation of channels when sufficient number of hard data is available; however, the conflict between hard data and training image is observed, same as other pattern base simulation, when small number of hard data are available for simulation.
4.4 Sensitivity to the Number of Wavelet Coefficients
The examples presented so far were performed by calculating the distance from the conditioning data event to the cluster center using only approximate sub-band coefficients if the conditioning data event is fully informed (9). However, it is presented in different literature that by only keeping few wavelet coefficients with approximate sub-band coefficients can improve the quality of the reconstructed image significantly (Donoho et al. 1996; Vannucci and Corradi 1999). Therefore, in this example, the distance calculation was performed by using few wavelet coefficients along with approximate sub-band coefficients when the conditioning data event is fully informed. The dimension of the resultant data for distance calculation will be not increased much by adding few wavelet coefficients; however, adding few coefficients may increase the power of the algorithm. Four different runs were performed by changing the number of wavelet coefficients. In the first run, only approximate sub-band is used. In other three runs, numbers of wavelet coefficients incorporated for distance calculation are 40, 80, and 100.
Figure 23 presents the realizations generated by four different runs. The result showed that when 40 wavelet coefficients are incorporated for distance calculation, there is some improvement in the generated realization; however, when 80 and 100 wavelet coefficients are incorporated, very little improvement is observed for this example. It is noted that increasing the number of wavelet coefficients for distance calculation means the representative features of the template is tending towards exact template. When all the wavelet coefficients will be incorporated, it will represent the exact template and the computational time will be the same as the pixel-wise distance calculation. Therefore, a trade-off between the complexity and accuracy, as always, needs to be carried out. The result revealed from this example that with few wavelet coefficients (in this example, 40) along with approximate sub-band can reasonably calculate the distance from the cluster centers, thus improving the quality of the simulated maps. It is noted that the observation is a case in a specific example. One may need more number of wavelet coefficients when the image is more complex.
5 Case Study
The Olympic Dam base metal deposit, Southern Australia, is simulated in this section, using the hard data presented in Fig. 24 and the training image shown in Fig. 25. The training image ti is scanned with the three-dimensional template (T) to generate pattern database patdbT. The size of template is generally decided based on both the size and complexity of the training image. For large and complex training images, a large template is used; however, for small and less complex training images, a small sized template is sufficient for capturing the pattern variability. In this case study, the template size chosen is 7×7×3. The pattern database is classified using the k-mean clustering algorithm. The number of clusters used in this study is 300 to capture the complexity of patterns present in the study area. A total of 64,000 blocks are simulated with the proposed approach within the study area. Three-dimensional sections of five simulated realizations of the study area are presented in Fig. 26.
To assess the performance of the algorithm, histograms, indicator variograms, and indicator cross-variograms were calculated for the various rock codes. Histograms of hard data, the training image and five simulated realizations are presented in Fig. 27 and show that the proportion of rock code 0 is well reproduced; however there are some deviations for other rock codes. The reason is that the proportions of rock codes are not same in the training image and available hard data. All simulated realization proportions for these rock codes are in-between the hard data and the training image proportions. These results demonstrate that if the training image and hard data share the same proportion of rock codes, the proposed algorithm can reproduce the exact proportions.
The reproduction of the directional variability is tested by calculating directional indicator variograms. The directional indicator variograms hard data and simulated realizations are presented elsewhere (Chatterjee and Dimitrakopoulos 2010). The indicator variograms and cross-variograms show that the directional variability of hard data for these rock types is reproduced by the simulated realizations.
Similarly to other multi-point simulation techniques, since the patterns are obtained from the training image, the wavesim is also training image driven. Thus, when conditional simulation is performed, the simulated realization reproduces the statistics of the training image. When the amount of hard data is increased, the effect of hard data is introduced in the resultant simulated realizations, and a clear conflict between hard data and training image statistics will be observed in simulated realizations, similarly to other mp simulation algorithms. As a result, if the statistics of the hard data and the training image are distinctly different and the conditional simulation is performed using a considerable number of hard data, the simulated realizations will fail to reproduce the training image or hard data statistics.
6 Conclusions
A pattern-based conditional simulation algorithm, wavesim, is presented. The algorithm uses wavelet basis function for dimensional reduction of patterns. The technique is based on pattern classification and pattern matching; the dimensional reductions of the patterns were performed by wavelet decomposition. The pattern classification was performed by the k-means clustering algorithm. The algorithm is verified by two- and three-dimensional conditional and unconditional simulation using different data sets like binary and two-class categorical data, continuous complex channels data. The algorithm reproduced the continuity of the channels for two- and three-dimensional examples using conditional and unconditional simulation. The comparative study with the filtersim algorithm showed that the wavesim performed better than the filtersim for reproducing the continuity of the channels for all examples.
The sensitivity of the algorithm to different parameters was also explored. The study shows that the algorithm is sensitive to the number of clusters, like other pattern-based simulation methods, and the orientation of training image. Therefore, optimal selection of the cluster number may help to improve the performance of the wavesim algorithm. Moreover, the algorithm is not sensitive to two key parameters of the wavesim algorithm, that is, the wavelet basis functions and number of wavelet coefficients. However, this is the case specific observation. It is true that an extensive sensitivity study is required with different levels of complex training image to show the true effects of wavelet basis functions. That will be considered in our future study. The case study at Olympic Dam mine was presented for multi-class categorical conditional simulation. The results showed that the proportion of the rock codes is reasonably reproduced.
The major advantages of the wavesim algorithm are: (a) due to the nature of the approximate sub-band of the wavelet decomposition, which reduces the dimensionality of the pattern and captures most of the data variability, the pattern classification of the high dimensional pattern database can be performed successfully with less computational effort; and (b) since the ccdf is developed for each class for categorical simulation, the pattern drawing from a class is performed based on a probability law, rather than random drawing, which may help with the reproduction of channels better.
The limits of this technique are similar to other mp simulation methods: (a) the algorithm is training image driven, therefore when the statistics of the training image and hard data are different, the algorithm will reproduce statistics in-between the hard data and training image; and (b) when the number of categories in the categorical image increases, the dimension of the pattern database will increase considerably, thus the dimensional reduction technique using the approximate sub-band after wavelet decomposition of the pattern database may not be computationally efficient.
References
Arpat GB (2004) Sequential simulation with patterns. PhD thesis, Stanford University, Stanford, CA
Arpat G, Caers J (2007) Conditional simulation with patterns. Math Geol 39(2):177–203
Chatterjee S, Dimitrakopoulos R (2010) Wavelet-based indicator simulation using training images: an application at Olympic Dam Mine, South Australia. COSMO Res Rep 4(2):153–186
Chatterjee S, Dimitrakopoulos R (2011) Multi-scale stochastic simulation with a wavelet-based approach. Comput Geosci. doi:10.1016/j.cageo.2011.11.006
Daubechies I (1992) Ten lectures on wavelets. Philadelphia, SIAM
Deutsch CV, Journel AG (1998) GSLIB: geostatistical software library and user’s guide. Oxford University Press, New York
Dimitrakopoulos R, Mustapha H, Gloaguen E (2010) High-order statistics of spatial random fields: exploring spatial cumulants for modeling complex non-Gaussian and non-linear phenomena. Math Geosci 42(1):65–99
Ding C, He X (2004) K-means clustering via principal component analysis. In: Proc int’l conf machine learning (ICML 2004), pp 225–232
Donoho DL, Johnstone IM, Kerkyacharian G, Picard D (1996) Density estimation by wavelet thresholding. Ann Stat 24(2):508–539
Goovaerts P (1997) Geostatistics for natural resources evaluation. Oxford University Press, New York
Goshtasby A, Gage SH, Bartholic JF (1984) A two-stage cross-correlation approach to template matching. IEEE Trans Pattern Anal Mach Intell 6(3):374–378
Gloaguen E, Dimitrakopoulos R (2009) Two-dimensional conditional simulation based on the wavelet decomposition of training images. Math Geosci 41(7):679–701
Guardiano J, Srivastava RM (1993) Multivariate geostatistics: beyond bivariate moments. In: Soares A (ed) Geostatistics Tróia’92, vol 1. Kluwer Academic, Dordrecht, pp 133–144
Hartigan JA, Wong MA (1979) Algorithm AS 136: A K-means clustering algorithm. J R Stat Soc, Ser C, Appl Stat 28(1):100–108
Honarkhah M, Caers J (2010) Stochastic simulation of patterns using distance-based pattern modelling. Math Geosci 42:487–517
Huber PJ (1985) Projection pursuit. Ann Stat 13(2):435–475
Journel AG, Alabert F (1989) Non-Gaussian data expansion in the earth sciences. Terra Nova 1:123–134
Journel AG (1997) Deterministic geostatistics: a new visit. In: Baafy E, Shofield N (eds) Geostatistics Woolongong’96. Kluwer Academic, Dordrecht, pp 213–224
Kuglin C, Hines D (1975) The phase correlation image alignment method. In: Proc IEEE int conf on cybernetics and society, pp 163–165
MacQueen JB (1967) Some methods for classification and analysis of multivariate observations. In: Proc of 5th Berkeley symposium on mathematical statistics and probability, vol 1, pp 281–297
Mallat S (1998) A wavelet tour of signal processing. Academic Press, San Diego
Mao S, Journel AG (1999) Generation of a reference petrophysical and seismic three-dimensional data set: the Stanford V reservoir; Stanford Center for Reservoir Forecasting Annual Meeting. Available at: http://ekofisk.stanford.edu/SCRF.html
Mustapha H, Dimitrakopoulos R (2010) High-order stochastic simulations for complex non-Gaussian and non-linear geological patterns. Math Geosci 42(5):457–485
Osterholt V (2006) Simulation of ore deposit geology and an application at the Yandicoogina iron ore deposit, Western Australia. PhD thesis (Unpublished), University of Queensland, 144 p
Remy N, Boucher A, Wu J (2009) Applied geostatistics with SGeMS: a user’s guide. Cambridge University Press, Cambridge
Schürmann T (2004) Bias analysis in entropy estimation. J Phys A, Math Gen 37:L295–L301
Strebelle S (2000) Sequential simulation drawing structures from training images. PhD thesis, Stanford University, Stanford, CA
Strebelle S (2002) Conditional simulation of complex geological structures using multiplepoint statistics. Math Geol 34(1):1–21
Tjelmeland H (1998) Markov random fields with higher order interactions. Scand J Stat 25:415–433
Vannucci M, Corradi F (1999) Covariance structure of wavelet coefficients: Theory and models in a Bayesian perspective. J R Stat Soc B 61(4):971–986
Wu J, Zhang T, Journel A (2008) Fast filtersim simulation with score-based distance. Math Geosci 40(7):773–788
Zhang T, Switzer P, Journel A (2006) Filter-based classification of training image patterns for spatial simulation. Math Geol 38(1):63–80
Acknowledgements
The work in this paper was funded by NSERC Discovery Grant 239019 and the members of McGill’s COSMO Lab, AngloGold Ashanti, Barrick Gold, BHP Billiton, De Beers, Newmont Mining, and Vale. We would like to thank the management of Olympic Dam mine for giving permission to use their data. We would also like to thank our reviewers Mehrdad Honarkhah, Jef Caers, and Jianbing Wu for their valuable comments to improve our first version of the manuscript.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chatterjee, S., Dimitrakopoulos, R. & Mustapha, H. Dimensional Reduction of Pattern-Based Simulation Using Wavelet Analysis. Math Geosci 44, 343–374 (2012). https://doi.org/10.1007/s11004-012-9387-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11004-012-9387-4