The street music business: consumer responses to buskers performing on the street and on online video platforms

Abstract

The street music business dates back hundreds of years and exists in many cities of the world. Although anecdotal evidence suggests that the number of listeners who donate varies widely, academic research has not examined why listeners donate to buskers. An intensive field study covering 80,471 consumers assessed the relevance and magnitude of theoretically derived drivers. A second study investigated the degree to which offline success factors predict consumer responses to buskers performing on online video platforms. Estimation results reveal several drivers, many of which differ from musicians’ commonly held beliefs. This study contributes not only to the marketing of buskers but also to marketing of other businesses that engage in fundraising in public spaces.

Introduction

Buskers perform in the New York subway, at Shanghai’s Shibuya crossing, in London’s Covent Garden, in Cologne’s Dom Square, and in fact, in most cities of the world. By definition, street music is free of charge, and musicians’ motivations to play on the street vary. While some street musicians are trained professionals promoting CDs and social media channels, others play only as a hobby (Nowakowski, 2016). Some play because busking provides a social identity (Rebeiro Gruhl, 2017), whereas others perform for their only source of income. Street musicians’ incomes range from as little as $1000 to over $100,000 per year (Economic Research Institute, 2019). While anecdotal evidence suggests huge variation in consumers’ willingness to pay for busking performances, academic research has barely investigated why and how consumers donate to street musicians, which is the focus of our study.

This study contributes to several streams in the marketing literature. First, we contribute to the “pay-what-you-want” (PWYW) literature (e.g., Kim et al., 2009; Santana & Morwitz, 2021), as street music could be seen as a service for which consumers pay voluntarily. Second, we relate the topic to the donation literature (e.g., Fajardo et al., 2018; Shang et al., 2008; Wedekind, 1998; Winterich et al., 2013), as consumers often refer to and perceive their contributions as donations. Traditionally, street music has been free, often without an implicit or explicit expectation for everyone who listens to pay. Even though both literature streams identify critical drivers, which help build our conceptual model, they do not examine how environmental factors (e.g., weather) may influence altruistic behavior. In addition, both literature streams mainly involve laboratory experiments. While laboratory experiments are effective in establishing causality, observational data are necessary to demonstrate external validity. Our study—a field study conducted over 3 months—identifies which factors influence donations to buskers taking environment-specific factors into account.

A third literature stream in marketing focuses on entrepreneurship and small businesses (Davis et al., 1991; Reuber & Fischer, 2011; Rind, 1996). In a broad sense, buskers are entrepreneurs who run their own music business and market their music performance to consumers, who may be willing to pay for such services. Like entrepreneurs, buskers build their business on creativity, flexibility, risk-taking, and innovativeness (Davis et al., 1991). We extend this literature stream by identifying factors that generate success as a street music entrepreneur.

A fourth stream of studies—in musicology—focuses on qualitative research of the street music business. The topics include experience reports (Nowakowski, 2016), the role of street music in society (Breyley, 2016), the relationships of buskers with the law (McNamara & Quilter, 2016), and selected success factors of solo musicians (Anglada-Tort et al., 2019).

We add to all four literature streams by being the first to systematically investigate consumer responses to a wide range of buskers over time (study 1 and RQ 1). Further, as many buskers supplement their income by posting videos on online platforms such as YouTube and Facebook (Watt, 2016), we investigate whether a busker’s success on the street can be translated into success on online video platforms (study 2 and RQ 2). We address the following research questions:

• 1. What factors influence consumer responses to buskers on the street?

• 2. Can consumer responses on the street predict a busker’s success on online video platforms?

We investigated consumer responses by counting how many consumers out of 80,471 donated to 72 buskers in the city center of Cologne, Germany. We observed these 72 buskers up to five times over 3 months. To assess consumer responses to buskers in the online context, we investigated consumers’ willingness to watch buskers’ videos online. We relied on a controlled quasi-experiment with 50 participants, each watching 20 randomly selected videos of street musicians (= 1000 observations).

In addition to making theoretical contributions, we also describe implications for practitioners. First, the study results are relevant for marketers who are in charge of fundraising in public spaces and nonprofits that generate donations in public spaces (e.g., Fajardo et al., 2018), as practical guidance is very limited. Second, the study results offer street musicians guidance on how to better market themselves. As musicians now earn less through selling CDs and streaming services, generating revenue from live performances can be critical (Papies & van Heerde, 2017). Our results reveal that factors for generating revenue from live performances differ from musicians’ commonly held beliefs. In addition, we suggest that success factors for a musician on the street may also be relevant for increasing consumers’ consumption of their music online.

Conceptual framework

Theoretical model of why consumers contribute to buskers

We use theoretically motivated variables to gain a better understanding of why consumers pay for free street music. The PWYW literature points to the relevance of the visibility of the payment (Kim et al., 2009; Roy, 2016). Many consumers strive to uphold social norms and may want to signal their commitment to society. In this context, we identify that being with another person or in a crowd of people surrounding a musician may influence consumer responses to buskers.

Furthermore, the donation literature suggests that feelings such as compassion, guilt, empathy, sympathy, and joy may influence altruistic behavior (Basil et al., 2008; Goenka & van Osselaer, 2019; Stellar et al., 2017). In this context, we investigate how weather, the day of the week, the presence of children in musicians’ groups, and gender of the consumer influence donation behavior. Finally, we explore the role of a busker’s performance quality based on the theory of reciprocity.

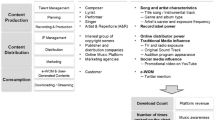
Figure 1 outlines the model of theoretically meaningful factors. As these theoretically derived variables do not provide a comprehensive or inclusive set of factors that drive consumer donations to buskers, we used semi-structured interviews with buskers and consumers as well as experience reports to generate a set of 11 control variables. Appendix 1 gives detailed insight into these controls and illustrates prior beliefs of buskers.

Fig. 1

Conceptual framework

Musician-specific factors

Quality of music ( +): In line with the theory of reciprocity (Bar-Tal, 1976), we predict that consumers are more likely to value a service and reward the effort of street musicians if the music quality is high. In reciprocal situations, individuals make a mental contract where they give with the expectation of receiving personal benefit to an equal extent. Prior empirical literature also points to the importance of music quality for a musician’s success (Papies & van Heerde, 2017).

Child musicians ( +): We suspect that more consumers will donate to child musicians because children possess characteristics that induce adults to protect and care for them, independent of their current parental status (Kringelbach et al., 2008; Li et al., 2019). Allegedly, parenting motivation is the basis for emotions such as empathy and compassion, which result in altruistic behavior.

Large audience ( +): Consumers’ willingness to donate is also influenced by both the recognition of the donation (e.g., Winterich et al., 2013) and the behavior of others (Shang et al., 2008). When consumers stand in a large audience around the musician, the principle of social recognition (Wedekind, 1998) suggests that more consumers donate because they expect that they will be perceived more favorably by those around them and gain a social advantage. Having good social standing may compensate for the financial loss of the donation (Nowak & Sigmund, 1998). In addition, the consensus bias effect suggests that consumers may identify with the audience, (sub)consciously feeling compelled to donate when others do (Shang et al., 2008) and possibly feeling embarrassed if they do not do so (Dahl et al., 2001).

Environmental factors

Weather [cloudy, precipitation ( +)]: We predict that cloudy weather and precipitation positively influence donation behavior, as bad weather could evoke empathy and compassion in consumers when they see musicians performing outside. In addition, the theory of reciprocity (Bar-Tal, 1976) suggests that consumers are likely to reward higher effort and consumers may believe it requires more effort to deliver a good performance in bad weather than it does in fair weather conditions. Previous research in marketing shows that weather influences consumer behavior (e.g., Moon et al., 2018; Rind, 1996) but this effect has not been studied with respect to donations.

Temperature [cold ( +)]: Relatedly, we expect that cold temperatures will lead to more consumer donations. In addition, homeostasis theory (Parker & Tavassoli, 2000) suggests that consumers who are physically cold are more likely to respond favorably to emotionally warm stimuli (e.g., music) (Bruno et al., 2017).

Day of the week [Sunday ( +)]: We expect that emotional responses such as empathy, compassion, and guilt are amplified on Sundays, leading to more donations than on any other day of the week. The salience of religions and religious norms, which is stronger on Sundays, can strengthen feelings like empathy and the willingness to do good for society. This “Sunday effect” on donation has been supported by prior empirical literature, albeit in different contexts (Martin & Randal, 2009).

Consumer-specific factors

Consumer is in company ( +): Again, from the theory of social recognition, we anticipate that consumers give more when accompanied by a friend, colleague, or family member.

Gender [women: ( +)]: We predict that more women donate than men. Women generally score higher in empathy and are therefore more likely to donate (Willer et al., 2015). Women are also socialized differently than men. Longstanding social norms and gender roles lead to unconscious biases that women should be friendlier and more caring than men (Winterich et al., 2009). This expectation may pressure women to display traits of fairness and empathy by giving donations. Although the empirical literature on donations and gender differences is abundant (Mesch et al., 2015), the results are mixed and have not been applied to the context of buskers.

Study 1: field study

Research design

We assembled a unique dataset by counting the number of consumers (out of 80,471 consumers, 49% males) who donated to 72 street musicians in the city center of Cologne. The focus on one city is critical, as it enabled us to observe some musicians on different days.

To prevent our presence from affecting the buskers and consumers, we conducted observations from angles where the consumers and musicians would not notice us. The observations occurred from mid-December 2016 to March 2017, and all observations were made by a coauthor and an additional observer between 10:00 a.m. and 9:00 p.m.

Sampling strategy

To generate a sample of consumers and buskers, we first identified public busking locations in the city center, such as shopping streets, side streets, and public squares. We then randomly chose one of these locations at different times on different days.

Strategy for determining busker success

To determine how successful a busker was, we counted the number of consumers who donated to the busker in 10-min windows (e.g., from 10:20 a.m. to 10:30 a.m.)—a timeframe sufficient to approximate the musician’s success. We verified this sufficiency with a random sample of 15 musicians who we observed for two to three consecutive 10-min timeslots at the same location. A t-test did not indicate a significant absolute deviance of more than two donations across the timeslots (p = 0.437; SD = 1.49).

Underlying assumptions

Our identification strategy rests on the assumption that our observations are allocated randomly across musicians and consumers. Specifically, we do not assume that only successful musicians self-select by choosing to play only under conditions that increase their earnings (e.g., playing at specific spots). Conducting our study in Cologne helps, as buskers in Cologne must change locations every 30 min by law, which creates the opportunity for a quasi-randomized sample. Similarly, we do not assume that potential drivers (e.g., bad weather) change the average share of generous consumers in the population of pedestrians. Note: We control for the exact number of passersby. We are also aware that our assumptions may be violated under certain conditions and discuss these in the limitations section of this paper.

Data collection and operationalization

Data collection required two observers. The first observer counted the number of consumers who donated within 10-min intervals (our dependent variable) and noted observable personal characteristics of the donating consumers (e.g., gender). The second observer used a mechanical frequency counter to tally the number of male and female pedestrians who walked by during the 10-min interval.

The observers also noted environmental factors (e.g., weather) and conducted brief interviews with the buskers after each observation period to determine musician-specific factors (e.g., age).

After the 10-min interval, one of the observers took a sample video of the musician and secured permission to use the video anonymously in our study. In a later step, three professional musicians watched the video of each musician and evaluated the music quality on a 7-point scale. The answers of the three evaluators were averaged with a sufficient inter-coder reliability (Cronbach’s α = 0.794; Fleiss-Kappa: p < 0.01). Table 1 provides a more detailed overview of the measurement of all variables.

Table.1 Measurements

Summary statistics

This study covers a total of 80,471 consumers and 72 buskers observed in 122 10-min intervals, yielding an average observation time of 17 min. Forty buskers were observed only once, and the remaining 32 were observed in up to five time intervals. Buskers who were observed more than once were observed again on average after 10 days. The unit of analysis is the number of female and male donors per observation period. This yields 244 unique observations. Appendix 2 provides summary statistics for potential success factors. Appendix 3 gives an overview of the observed buskers over time and a histogram of the number of donating consumers. Appendix 4 provides correlations of all variables.

Model specification

Equation 1 gives the econometric specification of our regression model. The dependent variable “musician success” measures the absolute number of male and female consumers (g) who donate to the street musician (s) during the observation period (o). We measured the dependent variable separately for men and women to identify the effect of consumer gender. Consequently, we use 244 unique observations to estimate the model. The independent variables comprise musician characteristics (m), consumer characteristics (c), environmental characteristics (e), and controls (k). 

$$\begin{aligned}{\text{MusicianSuccess}}_{\text{gso}} &=\alpha_{\text{s }}+ {\textstyle\sum_{\mathrm{m}=1}^{\mathrm{M}}}{\beta }_{1,m} {\text{MusicianCharacteristics}}_{\text{s}}\\&+ {\textstyle\sum_{\mathrm{e}=1}^{\mathrm{E}}}{\beta }_{2,e} {\text{EnvironmentCharacteristics}}_{\text{go}}\\&+ {\textstyle\sum_{\mathrm{c}=1}^{\mathrm{C}}}{\beta }_{3,c} {\text{ConsumerCharacteristics}}_{\text{gso}}\\&+ {\textstyle\sum_{\mathrm{k}=1}^{\mathrm{K}}}{\beta }_{4,k} {\mathrm{Controls}}_{\mathrm{gso}}+ {\varepsilon }_{\mathrm{gso}}\end{aligned}$$

(1)

with ${ \alpha }_{\mathrm{s }}= {\overline{\alpha }} +{\updelta }_{\mathrm{s}}, {\updelta }_{\mathrm{m}}\mathrm{ i}.\mathrm{i}.\mathrm{d}.\mathrm{ N}\left(0, {\upsigma }_{\text{gso}}^{2}\right)$ and ε _kbmi i.i.d. N(0,σ²_gso)

The parameter $\alpha_{\text{s}}$ denotes the intercept, and ε and $\updelta$ denote the error terms, which are assumed to be normally distributed. ${\upbeta }_{1,m}, {\upbeta }_{2,e},$ and ${\upbeta }_{3,c}$ are the estimated parameters of interest. ${\beta }_{4,k}$ designates the estimated control parameters.

By specifying a musician-specific constant $\alpha_{s}$, we control for musician-specific characteristics that are unobservable to us. Specifically, we capture their joint influence in the unobserved term ${\updelta }_{\mathrm{s}}$, which is assumed to be normally distributed with zero mean and variance ${\upsigma }^{2}$.

Regression results

Table 2 reports our estimates in determining the characteristics that are associated with the number of donations to street musicians. We estimate an additional model¹ to investigate the potential impact of consumers being accompanied and consumers’ ages (as control). The results of both models are highly consistent. Further, both models are highly significant, show good model fit, and do not yield multicollinearity issues (all VIFs < 10).

Table.2 Results of field study: consumer responses to buskers on the street

Musician, environment, and consumer characteristics

As expected, we find empirical evidence for the importance of high-quality execution. Street musicians are associated with more donations if the music quality is high (β = 0.745, p < 0.01). Child musicians receive significantly more donations than adult musicians (β = 3.86 = , p < 0.01), and a large audience is associated with the number of consumers who donate (β = 2.258, p < 0.01).

While results on weather conditions (e.g., rainy) are not significant (β = -0.999, p > 0.05), we do find an effect from temperature: the colder the weather, the more likely people seem to donate (β = -0.263, p < 0.01). Day of the week also has an effect; Sunday is associated with the highest number of donations (p < 0.01).

We also find support for the relevance of consumer-specific variables. More women donate than men (β = 0.978, p < 0.01), and more consumers in company donate than consumers who are alone (β = 0.245, p < 0.01).

Control variables

For the sake of brevity, we only highlight significant control variables but fully report all parameter estimates in Table 2. First, we find some evidence that consumers are most generous when classical music is played (compared to rock: β = -2.814, p < 0.10). Second, the location of the musician on the street has a significant impact; standing against a wall (β = -2.28, p < 0.01) or in the middle of the street (β = -2.480, p < 0.01) is associated with fewer donations than standing in a square. Third, more consumers seem to donate in March than in the reference category February (β = 2.612, p < 0.05). Fourth, background noise is negatively associated with donations (β = -1.447, p < 0.05). Fifth, the analysis reveals that the more people who walk by, the more donations the musicians receive (β = 0.007, p < 0.01). Finally, more consumers between 30 and 65 years of age donate than in any other age category (e.g., consumers from 18 to 30, β = -0.316, p < 0.01).

Robustness checks

We conducted several further tests to ensure robustness. First, following prior research (Stäbler & Fischer, 2020), we used an inductive approach to test for potential interaction effects among our focal variables (Appendix 5). None of the interactions were significant or met the statistical requirements. Second, instead of counting the number of consumers who donated while controlling for the number of pedestrians, we operationalized the dependent variable as the donation share (equal to the number of donating consumers divided by the number of pedestrians). Appendix 6 shows that the results are fully consistent with our main model. Third, we tested for omitted variable bias and included further control variables. We included a measurement of consumers’ familiarity with the busker as well as the time of the day. The variables did not add value to the model according to the likelihood ratio test. Fourth, we removed (blocks of) controls, and the results do not indicate any other conclusions (Appendix 7).

Study 2: controlled quasi-experiment

Objective

The main objective of the controlled quasi-experiment is to investigate whether the number of donations received on the street serve as a good predictor for whether consumers are willing to watch the video of the musician on an online video platform (see Fig. 1). In addition, we provide more detailed insights into which factors are relevant for both offline and online music consumption.

Research design and model

We enlisted 50 respondents (age, M = 31, SD = 12; males, 50%) from the University of Cologne campus, public places, and social media. Each respondent watched 20 videos taken from our street observations, resulting in 1000 observations. After each video, we asked respondents to rate their willingness to watch other videos of the musician on a 5-point single-item scale (M = 1.49, SD = 0.94). Respondents then provided socio-demographics and their general likelihood of watching videos online. We matched these data with the musician-specific data gathered in the field study. We used OLS regression to determine whether the number of offline donations predicted online success (model I) and how consumer, musician, and environmental characteristics that are applicable in online environments determine online success (model II).

Estimation results

Table 3 reports our estimates. First, we confirm that consumer offline responses predict consumers’ willingness to watch other videos of the musician (β^I = 0.033, p < 0.01). Second, we find that the critical success factors for street musicians in public spaces are mostly consistent with the success factors for musicians online. Music quality is a critical success factor not only for buskers on the street but also for musicians online (β^II = 0.134, p < 0.05). Furthermore, similar to the field study, female consumers are more likely to watch videos of buskers than male consumers are (β^II = 0.121, p < 0.05). Like in the field study, classical music is also more successful in an online context (rock music: β^II = -0.385, p < 0.05). However, we also find a driver that deviates from the offline setting. While more older consumers (30 to 65 years of age) donate on the street, younger consumers are more willing to watch videos online (β^II = -0.012, p < 0.01).

Table.3 Results of quasi-experiment: consumer responses to buskers on a video platform

Discussion

This study generates novel results, as we identify a significant number of factors that determine consumer responses to buskers. After observing 80,471 consumers and 72 musicians over several observation periods, we link variables related to the musician, consumers, and the environment to consumers’ donation behaviors. Through a controlled quasi-experiment with 1000 observations, we show that donation behavior in a public space also predicts a musician’s success online. Our findings have both theoretical and practical implications.

Theoretical implications

Our study makes important theoretical contributions to the limited knowledge about when and why consumers contribute to street musicians. We confirm that consumers are more willing to contribute to buskers if others witness the donation, both when consumers are accompanied by someone and when the audience size is larger. This finding is supported by theories of social recognition (Wedekind, 1998) and consensus bias effects (Shang et al., 2008). These results may also be due to consumers feeling embarrassed if they do not donate (Dahl et al., 2001).

We also add to the marketing literature by investigating how environmental characteristics influence donation behavior. We find that consumers are more likely to donate in cold weather, most likely because they feel greater sympathy for the musician or because consumers who are physically cold are more likely to respond favorably to emotionally warm stimuli (Bruno et al., 2017). This result is contradictory to weather studies in the (small business) literature that identified a negative effect of bad weather conditions on consumer tipping behavior in hotels (Rind, 1996) and shopping behavior in grocery stores (Moon et al., 2018). Furthermore, even though literature in the PWYW and small business domain (Kim et al., 2009) report controversial findings regarding the role of service quality, we find that quality matters for street music entrepreneurs. Finally, in line with recent findings in the PWYW literature (Santana & Morwitz., 2021), we confirm that more female consumers donate than male consumers.

Implications for marketing practice in public spaces

Our results may also be relevant to marketers of related businesses, such as fundraising companies and other kinds of street performers (e.g., dancers). These businesses and individuals could benefit from allocating working hours to Sundays, as the salience of religious norms, which is greater on Sundays, may amplify feelings like empathy and lead to more donations. Furthermore, we find that a large audience leads to more donations. Street artists could benefit from actively influencing the size of the crowd around them, perhaps by bringing fans and friends to their performances or advertising to notify fans about their performances.

Implications for the marketing of buskers

Simulation of the hourly earnings of a busker

To derive the practical significance of our results for buskers, we simulated the effects of our independent variables on a musician’s approximated hourly earnings (Fig. 2). Our interviews indicated an average single donation of 50 cents, allowing us to calculate average hourly earnings.

Fig. 2

Magnitude of driver effects: simulation of earnings per hour. Notes: We simulated the base scenario by setting all variables to their sample mean and extending the time frame from 10 min to 1 h. The average hourly earnings of a musician were calculated on the basis of insights from our interviews that an average single donation is 50 cents. We then changed only one of the main drivers while keeping all other factors constant. For metric variables, we increased the focal variable by 100%. For non-metric variables, we set the focal category to 1. For variables measured on a 7-point scale, we increased the variable by one point on the scale

Average hourly earnings of €23 are consistent with the insights from our interviews. The differences in the effect strength induced through the drivers are remarkable. If the quality of the music increases, earnings can rise to €28 per hour, and groups with children have the highest earnings €45 per hour. Sundays bring hourly earnings up to €36. The practical effects of control variables are also noteworthy. Whereas classical music generates up to €27 per hour, rock and jazz lower earnings to €11 per hour. Combining several success factors can increase earnings by more than €100. Figure 2 shows further effect sizes.

Concrete guidance for buskers

Several factors that drive consumer donations have strategic marketing implications, many of which challenge buskers’ prevalent views (see also Appendix 1). Contrary to street musicians’ belief that the most financially favorable genre is country and folk, classical music proves to be the most lucrative. Consumers may value the classical music genre because it is often perceived as more sophisticated and difficult to learn. In contrast to many musicians’ perceptions, the use of an amplifier does not increase donations. Furthermore, buskers who aspire to be successful on online video platforms should select videos on the basis of the success of their live performances.

Social costs and downsides of busking

Our findings also have downsides and social costs. For example, gender implications for donations could reinforce stereotypical behavior in society. If performers approach more women than men, women may come to think they should donate more often.

In addition, we would like to emphasize that while our findings indicate that child musicians receive the most donations, we do not encourage street performance by child musicians, except for entirely voluntary and recreational purposes such as Christmas caroling.

Lastly, as buskers are self-employed professionals (according to legislations in the USA and Europe), they need to declare income and pay taxes, particularly if income is high. Since authorities have difficulty capturing and controlling buskers’ income, tax evasion is a risk, resulting in a welfare loss for society and legal consequences for buskers.

Limitations and future research

While our study’s findings reveal valuable criteria relevant to street musicians’ success, its limitations offer avenues for further research. First, this study is limited to street musicians who we observed in a large city in Germany. A study across cultures might reveal intercultural differences that could be relevant for street musicians traveling around the world. Second, our study refers to several streams in the literature. We propose future research to disentangle consumer motivations with respect to paying for a performance versus helping the performer through a donation. Third, an area of interest might be to identify how external factors (e.g., temperature) influence consumer responses in an online scenario. Finally, buskers may strive to behave in an optimal way and want to adopt the best strategy to be successful. Our predefined assumptions relevant to the field study (p. 8) are violated if, for example, only very motivated or skilled musicians go out to play in low temperatures. The degree to which these cases exist is a challenging question, and we leave this open for further research.

Appendices

Appendix 1 Commonly held beliefs of musicians and consumers about success factors

Appendix 2 Descriptive statistics

Appendix 3 Observations per busker over time

Appendix 4 Correlation matrix of all variables

Appendix 5 Test for interaction effects

Following prior research (Stäbler & Fischer, 2020), we used an inductive approach and tested for potential interaction effects among our focal variables.

We first added each interaction effect separately to our base model and tested for this model extension using the likelihood ratio test. We then checked sample sizes of each interaction, which required a minimum sample size of 30 observations. When then checked.

whether the remaining candidate interactions satisfy standard collinearity requirements (VIF < 10). This leaves us with one interaction, for which we investigate stability across different models. The interaction effect was not stable across the models (i.e., in the extended model).

Consequently, none of the interactions was significant or met the statistical requirements (i.e., multicollinearity statistics, required sample sizes). We also tested for theoretically meaningful interaction of our focus variables and control variables. For example, as prior literature (Shang et al., 2008) points to the relevance of a match and mismatch of gender in the field of charitable fundraising, we tested whether more women donated if the musician was female. However, the interaction was not significant.

Appendix 6 Robustness check: alternative dependent variable

Appendix 7 Robustness check: removing blocs of control variables