Analysis of seafloor backscatter strength dependence on the survey azimuth using multibeam echosounder data

Abstract

The sediment backscatter strength measured by multibeam echosounders is a key feature for seafloor mapping either qualitative (image mosaics) or quantitative (extraction of classifying features). An important phenomenon, often underestimated, is the dependence of the backscatter level on the azimuth angle imposed by the survey line directions: strong level differences at varying azimuth can be observed in case of organized roughness of the seabed, usually caused by tide currents over sandy sediments. This paper presents a number of experimental results obtained from shallow-water cruises using a 300-kHz multibeam echosounder and specially dedicated to the study of this azimuthal effect, with a specific configuration of the survey strategy involving a systematic coverage of reference areas following “compass rose” patterns. The results show for some areas a very strong dependence of the backscatter level, up to about 10-dB differences at intermediate oblique angles, although the presence of these ripples cannot be observed directly—neither from the bathymetry data nor from the sonar image, due to the insufficient resolution capability of the sonar. An elementary modeling of backscattering from rippled interfaces explains and comforts these observations. The consequences of this backscatter dependence upon survey azimuth on the current strategies of backscatter data acquisition and exploitation are discussed.

Introduction

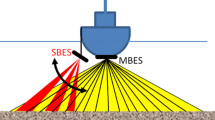
The composition of the seafloor is of high importance for a large number of scientific and engineering sectors operating in the sea, e.g. marine geology and biology, habitat mapping, hydrography, or cable-pipeline laying. For these purposes, acoustic remote sensing techniques can be useful to obtain information about the nature of the seafloor. Single- and multibeam echosounders (SBES, MBES) have been in common use for depth measurements for many decades; especially MBES can provide high spatial coverage with an excellent operational and economic efficiency. All echosounders can potentially determine the seafloor depth (from the signal flight time) and its reflectivity (from the received echo intensity) i.e. its capability to send back acoustical energy to the sonar. Reflectivity is objectively quantified by the backscatter strength (Urick 1983), depending on the following parameters: (a) sediment type and characteristics (roughness and impedance), (b) signal frequency, and (c) incidence angle. Backscatter strength (BS) can be measured by MBES over a wide range of beam angles across the seafloor; this capability has promoted the backscatter angular dependence as a key parameter in identifying seafloor type (Hughes Clarke 1994; Lurton and Lamarche 2015). The sediment classification potential of SBES and MBES is illustrated in various studies (Amiri-Simkooei et al. 2011; Canepa and Pouliquen 2005; Clarke 1994; De Moustier 1986; Fonseca and Mayer 2007; Hellequin et al. 2003; Lamarche et al. 2011; Simons and Snellen 2009; van; Walree et al. 2005; Weber and Ward 2015).

Therefore it is very important, when designing a survey and selecting potentially interesting areas, to take into account the impact of all possible factors affecting the parameters related to the backscatter strength. Survey azimuth is one of these factors. On an area with isotropic roughness and homogeneous sediment, no impact of survey lines direction is expected. On the contrary, on anisotropic and/or non-homogeneous areas, there can be a strong influence on the BS values. Past experiments have demonstrated that an azimuth dependence of BS can be expected both for seabed with sand waves (Boehme et al. 1985; Le Chenadec 2004; Richardson et al. 2001) and seabed covered with shells (Stanic et al. 1989); these case studies relied mainly on specific experimental configurations at low to medium sonar frequencies (20–150 kHz). In real survey conditions MBES-measured backscatter has been used to map and study large-scale seabed patterns (De Falco et al. 2015; Schmitt and Mitchell 2014). On the contrary, smaller bedforms (e.g. current sand ripples) often cannot be detected in bathymetry but may affect the backscatter intensity if they are well-defined throughout the survey area (Ferrini and Flood 2006).

In this paper we present observations of the survey azimuth effect on the backscatter strength, based on surveying areas around Brest (France) with different sediments types, using a Kongsberg EM 2040 MBES operated at 300 kHz. Each area has been surveyed from six different directions covering the whole azimuth range. This study is an extension of a previous work (Le Chenadec 2004) where a Simrad EM 1000 MBES (95 kHz) and an Edgetech DF 1000 sidescan sonar (100 kHz) were jointly used for surveying shallow sedimentary areas.

The purpose of this work is to illustrate the azimuth effect on seafloor reflectivity in real operational conditions, to interpret its existence in the light of available groundtruth elements, and to discuss its potential impact on current operations of reflectivity mapping with swath sonar systems (Lurton and Lamarche 2015). The paper is organized as follows. “Description of MBES and surveyed areas” section gives information about the surveyed areas and a brief description of the EM 2040 MBES. “Survey Methodology and MBES data processing” section provides details on the MBES data processing and the survey methodology. “Results” section presents the results of the processing, which are analyzed and discussed in “Discussion and interpretation” section together with modeling considerations. Finally, the main conclusions are summarized in “Conclusions” section.

N.B. In the text below, backscatter (or backscattering) refers to the physical phenomenon causing the incident wave to return to the source. Reflectivity is a more qualitative term, describing the ability of a material to reflect incident waves, conveniently usable in discussions. Finally Backscatter Strength (or BS) is the normalized in-dB quantity describing the ratio of backscattered to incident intensity (see e.g. Urick 1983).

Description OF MBES and surveyed areas

The data were collected using a Kongsberg EM 2040 multibeam echosounder installed on coastal R/V Thalia. EM 2040 can be operated at three frequencies: 200, 300, and 400 kHz. For standard survey operations, 300 kHz is used as it gives an optimum balance between high resolution and depth capability (Kongsberg 2012); only results obtained at this frequency are presented in this paper. EM 2040 has three transmit angular sectors across-track and three main modes of operation: “Central” (only the central sector is active), “Normal” (all three sectors are used at 300 kHz), and “Scanning”. The CW (continuous wave) pulse length values for the central sector are within the range 35–150 µs and for the ‘normal’ mode in the range 70–600 µs. The beam spacing in reception can be “Equiangular” or “Equidistant”. The exact settings of the EM 2040 configuration used per area for this study are detailed in Table 1. It has to be noted that the MBES used is a Dual Receiver system, completely beam roll- and pitch -stabilized.

Table 1 Details of the surveyed areas: water depth, sediment type and uniformity, EM 2040 MBES configuration (frequency; pulse length; transmit mode C = ”Central”, N = ”Normal”; beam repartition EA = ”Equiangular”, ED = “Equidistant”), dates of survey and ground-truthing (sediment sampling and video)

The surveys took place in June 2014, May 2015, and November 2015 offshore the harbour of Brest, France. The seven surveyed places are sketched in Fig. 1. Carré Renard is located inside the Bay of Brest while Camaret #2 and #3 are at the entrance of the Bay. Pierres Noires is further outside the Bay of Brest. The three remaining areas (Douarnenez #2, #3, and #4) are located in the Bay of Douarnenez. The survey sites were preselected using data from previous surveys, in order to be both as homogeneous and as flat as possible. Grab samples and videos were taken from each area to assist the interpretation of the results. The sediment types range from fine sand to coarse elements (shells, maerl) (see Table 1).

Fig. 1

Geographical location of the seven surveyed areas (Carré Renard, Camaret #2 and #3, Douarnenez #2, #3, and #4, Pierres Noires)

Survey methodology and MBES data processing

EM 2040 datagrams include the collected data as well as information about the system settings and survey status. The backscatter strength is logged under two different forms in various datagrams. In the first form called ‘Beam Intensity’, for each beam and each ping one single backscatter value is given: it is the result of first applying a moving average over the time series of amplitude samples and then selecting the maximum average level (Hammerstad 2000). In the second form ‘Seabed Image’, the data from the beam amplitude sample series are ranked in such a way that when fitted together the resulting array of signal samples represents a continuous set along the bottom with a fixed range step according to the signal sampling rate of the MBES and the mode it is used in (Hammerstad 2000). It has to be noted that the calculation of both forms assumes that the bottom is perfectly flat over the whole swath and perpendicular to the shortest range.

The Sonarscope ^® software (Augustin 2016) was used for processing the data presented here. In Sonarscope ^® the ‘Beam Intensity’ is imported directly from the MBES datagrams without any manipulation; while for the ‘Seabed Image’ one BS value per beam is calculated after averaging the non-overlapping samples that correspond to each beam. In this paper we have used the backscatter image resulting from the ‘Seabed Image’ as a first visual tool to estimate the homogeneity of each area. On the other hand, the backscatter strength from the ‘Beam Intensity’ is used for constructing the angular response plots of BS for the different incidence angles. The backscatter data that we have used were not compensated here for the MBES directivity pattern. This is not necessary since the purpose is to compare the seafloor response according to various azimuth angles; the comparative analysis remains valid if all measurements are affected by the same MBES directivity effect.

In the next sections, the measured BS values vs incidence angles have been computed under the simplifying approximation of a flat and horizontal seafloor interface. This is justified by the fact that the topography observed on the various areas (Figs. 3b, 4b, 5b, 6b, 7b, 8b, 9b, 10b) fulfills well this approximation: all the large-scale slopes stay below 1°.

The surveying principle for assessing the reflectivity dependence on survey azimuth is presented in Fig. 2a. The survey pattern (defined as a 12-point “compass rose”) features six survey lines with a nominal angle step of 30° covering all main azimuthal directions; practically the actual ship’s heading may slightly differ from these ideal values. As mentioned in “Description of MBES and surveyed areas” section, homogeneous areas were preselected based on previous survey data. Nevertheless, sea is a dynamic medium and the stability of seabed sediments over time always carries uncertainty. Based on this, we have specifically analyzed -in conjunction with the complete lines- the restricted datasets from the common part of all surveyed lines for each area. For perfectly straight survey lines the common part is visualized as a coloured polygon (see Fig. 2b). This common data subset analysis has two advantages: (a) the intersection is of small extent so it is likely spatially homogeneous, and (b) all surveyed lines have covered this very same part thus any comparisons are more reliable. Note that, in case of an inaccurate navigation, not all incidence angles may be present inside the common part along the six directions; however this did not happen significantly in the datasets presented here.

Fig. 2

a The six azimuth survey lines (“compass rose pattern”) per area with an angle step of 30°. b Example of the common part (yellow) of six actual survey lines accounting for the swath width of the surveyed tracks

Results

Result display

Five main plots have been created for each area (see e.g. Fig. 3) in order to illustrate both as clearly and completely as possible the survey azimuth influence on the backscatter strength. The first plot is a backscatter map for all survey lines, giving a first assessment of the area homogeneity and isotropy; the location of the grabs and videos collected is superimposed on this image. The second plot is the area bathymetry, all depth values being corrected for measurements from tide stations close to the surveyed areas. The third plot is the across track change in the backscatter strength vs incidence angle (angular response noted AR in the following) for the six different azimuths, considering data from the complete surveyed lines. The fourth plot is similar to the third one but restricted to the data from the common part of the survey lines. The last plot (already proposed in Le Chenadec 2004) is a polar representation of the same data summarizing the azimuth dependence of the backscatter strength: it allows easy viewing of the (an)isotropic nature of the seafloor, isotropic seafloor roughness being represented by regular and concentric circles in polar coordinates. Since each line was surveyed in only one (randomly chosen) direction (with the exception of Pierres Noires 2015), for constructing the complete polar plots we duplicated the results to cover both directions.

Fig. 3

Area Carré Renard (approx.size 450 × 450 m). a Backscatter image; b bathymetry; c BS vs incidence angle for the complete lines; d BS vs incidence angle for the common part; e BS vs azimuth in polar coordinates

Carré Renard

The plots for Carré Renard are shown in Fig. 3. The backscatter image (Fig. 3a) is uniform thus the area is probably homogeneous. Moreover the bathymetry of the area (Fig. 3b) is fairly flat (average depth 19.2 m) with nevertheless a depth range of 2 m. Figure 3a features the positions of the grab samples and videos taken in June 2014 and May 2015; in both cases the sediment type was found to be the same: silty gravelly sand mixed with coarse elements (such as maerl and shells). From the videos it can be observed that the seabed comprises of muddy gravel and muddy sandy gravel mixed with shells. The top layer of the seabed is colonized by brittle stars: the distribution of these shells and brittle stars is not uniform. Therefore, we cannot consider that the area is in principle homogeneous. Nevertheless, the backscatter image uniformity implies that the effect of this sediments variability on backscatter measurements is negligible. Figure 3c and d present the BS dependence on incidence angle, considering respectively the complete lines and only the common part. The two plots are very similar, confirming that the area is homogeneous across its whole extent. The curves in Fig. 3d are noisier than in Fig. 3c, probably due to the fact that the BS is averaged using a limited number of pings corresponding to the common part (approximately 60 pings). The change in the backscatter strength with azimuth is within 0.5 dB, hence negligible for most of the incidence angles, with the exception of incidence angles at ±10° and ±20° where the absolute maximum difference can reach 1 dB. Another observation from Fig. 3c, d and e is that the measurements between starboard and port show asymmetry. This is probably due to slight different sediment types between the seabed parts insonified by port and starboard. Furthermore, a hump of about 1 dB can be observed at −30°, with a slighter replica at +30°, which is presumably due to the MBES intrinsic response (since it can be observed on other areas as well). It can also be observed from Fig. 3e that the BS values for each incidence angle are very similar for all azimuth angles. So all these observations confirm that Carré Renard is a satisfactorily homogeneous, and isotropic area and that the effect of survey azimuth on backscatter strength is minimal.

Camaret #2

The second area (Camaret #2) consists of sand with grain size ranging from fine to medium. The video analysis reveals the existence of small-scale ripples. The backscatter image (Fig. 4a) shows patches with significantly different reflectivity. This indicates either a non-homogeneous seabed nature or the presence of topography anomalies. Furthermore, the plots in Fig. 4c and d are significantly different, especially at oblique angles where the dispersion reaches 7 dB at positive angles. Since the common part has small extent and uniform reflectivity, it can be expected to better describe the azimuth dependence of backscatter. On the contrary, the complete surveyed lines probably contain differences due to locally varying sediments. Figure 4d shows large differences in BS values for the different azimuths at incidence angles between ±5° and ± 40°. The trend is that the difference starts to increase from ±5° to ±20° (where the differences reach about 6 dB) and then gradually decreases; from ±40° till ±60° the difference vanishes. Also, the measurements show a difference between starboard and port. Figure 4e makes clear a polarization of the backscatter strength in the direction 0°–180°.

Fig. 4

Area: Camaret #2 (approx.size 450 × 450 m). a Backscatter image; b bathymetry; c BS vs incidence angle for the complete lines; d BS vs incidence angle for the common part; e BS vs azimuth in polar coordinates

Camaret #3

On the third area (Camaret #3) coarse material (maerl, shells) overlay sand and gravel. The area is flat with no noticeable features. The depth range is 1.8 m around an average of 21 m (Fig. 5b). Although the reflectivity image (Fig. 5a) looks uniform, the plots in Fig. 5c and d show some differences. Moreover, in this case a clear difference in BS values is observed between starboard and port. We hypothesize that these differences are due to alternating different sediment: denser concentrations of shells and hashed shells distributed in parallel bands are clearly visible in the videos. Here again the BS dispersion is higher over the complete lines; hence only the common part is considered for further analysis. The backscatter values from port side fluctuate less than the ones from starboard. Also a slight polarization of the backscatter strength in the direction 0°–180° is observed (Fig. 5e). These observations show that the area is not perfectly homogeneous.

Fig. 5

Area: Camaret #3 (approx.size 450 × 450 m). a Backscatter image; b bathymetry; c BS vs incidence angle for the complete lines; d BS vs incidence angle for the common part, e BS vs azimuth in polar coordinates

Douarnenez #2

For the fourth area (Douarnenez #2), the reflectivity (Fig. 6a) is uniform indicating a homogeneous sedimentary area. The grab sample and the video show the sediment type to be fine sand. Further analysis of the video reveals the presence of sand ripples at too small a scale to appear in the bathymetry map in Fig. 6b. The plots in Fig. 6c and d are very similar; this similarity implies that the anisotropy is stable across the whole area. As in the case of Camaret #2, in Fig. 6d a noticeable difference is observed in the backscatter values for the different azimuths for incidence angles from ±5° to ±40°. The trend of changes is similar to that observed in Camaret #2. The polarization of the backscatter strength is in the direction 150° to 330° (Fig. 6e).

Fig. 6

Area: Douarnenez #2 (approx.size 450 × 450 m). a Backscatter image; b bathymetry; c BS vs incidence angle for the complete lines; d BS vs incidence angle for the common part; e BS vs azimuth in polar coordinates

Douarnenez #3

The seabed of the fifth area (Douarnenez #3) is composed of silty sand. The backscatter image (Fig. 7a) shows a number of linear features with different backscatter strength values striping the area. The direction of the lines is West–East. Comparing backscatter and bathymetry maps (Fig. 7b) shows that the differences in reflectivity follow very slight bathymetry modulations. As a result, the plots in Fig. 7c and d are similarly chaotic regarding the behavior of the backscatter for different azimuths. In this case the differences in the common part are much larger than those observed for the complete lines. From Fig. 7d it is estimated that the difference in BS values can reach up to 5 dB at 20° incidence angle. Figure 7e shows a clear polarization of the backscatter strength values in the North–South direction at 20° incidence but also West–East at 40° and 50°.

Fig. 7

Area: Douarnenez #3 (approx.size 450 × 450 m). a Backscatter image; b bathymetry; c BS vs incidence angle for the complete lines; d BS vs incidence angle for the common part; e BS vs azimuth in polar coordinates

Douarnenez #4

The bathymetry map of Douarnenez #4 (Fig. 8b) shows a flat area with a depth range of 1 m around 29 m. The reflectivity image (Fig. 8a) is clearly not uniform with many areas of significantly different BS, indicating inhomogeneous substrates. Two grab samples were taken in the North and South parts of the compass rose pattern (green rectangles in Fig. 8). The North sample is silty sand, and the South one is coarse materials, confirming Douarnenez #4 heterogeneity. Following these observations, the large differences observed in the angular BS values for the different azimuths (Fig. 8c) were previsible. Thus, it is preferable to study the azimuth effect strictly on the common part of the surveyed lines (Fig. 8d), where the sediments must be coarse elements, based on their backscatter strength values. Figure 8d show differences of BS value magnitudes varying slightly over 1 dB for most angles, and up to 2 dB at 60°. In Fig. 8e most of the incidence angles follow a circular shape but slight anomalies still exist. Although these small variations remain may be not really significant, their comparison with those (showing a better regularity) of Carré Renard or Pierres Noires 2014 suggests that even the common part of Douarnenez #4 is not perfectly homogeneous and isotropic; this has been comforted by our video observations of this terrain patch.

Fig. 8

Area: Douarnenez #4 (approx.size 450 × 450 m). a Backscatter image; b bathymetry; c BS vs incidence angle for the complete lines; d BS vs incidence angle for the common part; e BS vs azimuth in polar coordinates

Pierres Noires

The Pierres Noires area is an important case since, like Carré Renard, it is used by the French Navy Hydrographic and Oceanographic Service (SHOM) for the bathymetric calibration of their high-frequency MBES. Comprised of silt, Pierres Noires is the deepest of all areas studied here, with an average depth of 61 m. Figures 9 and 10 show completely different results regarding the BS values obtained in June 2014 and November 2015. Although both reflectivity images (Figs. 9a and 10a) are uniform (homogeneous seabed) and the bathymetry has not changed (Figs. 9b and 10b) the backscatter was found to be azimuth independent in 2014 but highly varying with azimuth in 2015. In 2014, the seabed of the area is isotropic (concentric circles in Fig. 10e) while in 2015 a very strong polarization exists in the North–South direction (see Fig. 10e) where the BS variation can reach up to 11 dB at ±20°. Since the trend of changes is similar to that observed at Camaret #2 and Douarnenez #2 we hypothesize that this is due to the temporal formation of small ripples.

Fig. 9

Area: Pierres Noires in 2014 (approx.size 450 × 450 m). a Backscatter image; b bathymetry; c BS vs incidence angle for the complete lines; d BS vs incidence angle for the common part; e BS vs azimuth in polar coordinates

Fig. 10

Area: Pierres Noires in 2015 (approx.size 450 × 450 m). a Backscatter image; b bathymetry; c BS vs incidence angle for the complete lines; d BS vs incidence angle for the common part; e BS vs azimuth in polar coordinates. Dashed and solid lines indicate opposite directions

Also, Pierres Noires in 2015 is the only case where each azimuth angle was surveyed in both directions. The bold and the dashed lines in the plots of Fig. 10 correspond to opposite directions. In perfect navigation conditions and seafloor regularity, each line should show a similar behaviour for the two survey directions; however in the results plotted here, slight differences occur. They can be interpreted in two ways: imperfect navigation could cause the coverage of slightly different areas when sailing opposite directions; or the ripple profile could be slightly assymetrical and hence present a backscatter level depending on the direction of observations (steep flanks of a “factory roof” profile being seen alternatively from the port and starboard side of the ship); this explanation is supported by the slight asymmetry of the angular backscatter curves showing the maximum influence of ripples (corresponding to the North–South tracks).

Discussion and interpretation

Discussion of the results

The conclusions of the analysis of the previous section fall into three categories:

• Regardless of the seabed sediments, for homogeneous areas with no seabed formations (like Carré Renard or Pierres Noires in 2014) the effect of the survey azimuth on the backscatter level is minimal;

• For areas with small-scale sand ripples (Camaret #2, Douarnenez #2, and Pierres Noires in 2015) the BS presents a high dependence on survey azimuth over the incidence angle range ±20° to ± 40°; however the BS is independent of the azimuth in the range ± 40° to ± 60°;

• For non-homogeneous areas (Camaret #3, and Douarnenez #4) and for Douarnenez #3 where specific landforms are observed, no clear conclusions can be drawn.

The conclusions of the first and third cases were foreseeable. Here we focus on the second case, which has to do with the effect of sand ripples on the backscatter strength.

Underwater videos were taken in Camaret #2 and Douarnenez #2 during the compass rose survey. A still frame of the video from Camaret #2 (May 2015) presented in Fig. 11 shows that the inter-crest spacing of the ripples varies between 10 and 20 cm; no estimation could be done about the height of the ripples. Superimposed on the still video frame in Fig. 11 is the approximate beam footprint of the MBES at 20° incidence angle, determined from the beam aperture and the oblique range: for Tx and Rx beamwidths of 1° at 21-m depth the across track footprint is 41.5 cm and the along track footprint is 39 cm. So the typical beam footprint dimension is at least twice the characteristic wavelength of the ripples. Furthermore, the average distance between two consecutive pings was approximately 1 m (average survey speed 2.2 m/s and ping rate of two pings per second). The small-scale ripples cannot be resolved in the reflectivity mosaics or the bathymetry map using this acquisition configuration as they are not even visible in the “waterfall” displays of received pings, which provide the finest physical sampling of the recorded data. Therefore, without video observations, the presence of the ripples can only be detected as an effect on the backscatter values when changing azimuth.

Fig. 11

Camaret #2. Still frame (processed) from the video taken in May 2015. The black rectangle indicates the typical beam footprint extent at 20° incidence angle. The along and across track directions dimensions have been selected randomly just for illustration purposes.

One common observation from all areas with sand ripples is that the backscatter values are higher when surveying with the ship’s route following the ripple crests direction i.e. with the acrosstrack-formed beams normal to the ripples flanks. Ripples are formed with their crests perpendicular to the direction of the current. We checked the currents direction on the dates of our surveys and the polarization directions expected from these data (not shown here) match the ones observed in the polar plots. Therefore, the compass rose survey pattern can provide valuable information not only about the presence of ripples but also about their rough orientation.

Moreover in the angular response plots of Camaret #2, Douarnenez #2, and Pierres Noires in 2015 a very similar pattern is observed: the differences in the BS values for the various survey azimuths start to increase from ±~5°, reach a peak around ±~20° and then gradually decrease until reaching ±~40° beyond which convergence is achieved. Interestingly, the same patterns were observed with the same MBES operating at 200 and 400 kHz (results not shown here). The same behavior was observed also in the previous results of Le Chenadec (2004) where a lower frequency was used (~100 kHz). Therefore this observed angular behavior must be independent of the MBES characteristics and is most likely inherent to the shape and size of the ripples. This will be corroborated in the next section.

Interpretation of the results by interface backscatter modeling

Rippled seabed description and modeling hypothesis

Most of the modeling available today for seafloor backscatter (see e.g. Jackson and Richardson 2007) hypothesizes an isotropic roughness, with characteristics independent of azimuth direction. It is clear that this restriction is not relevant for interpreting the present set of data showing strong horizontal angle dependence at several locations.

The most probable cause of azimuth dependence, for the field data presented here, is the presence of ripple patches caused by tide currents, present in shallow water on sedimentary seabed especially when sand is dominant. A characteristic of this type of sedimentary landform is its relative regularity of organization: visual observations (Fig. 11) show that a given ripple field is usually characterized by a well-defined azimuthal orientation (imposed by the average local tide-current direction) and a pseudo-periodical behavior of the wave forms, with stable vertical amplitude. Hence, for our modeling purpose, a rippled seafloor can be described as the superimposition of a deterministic field of such waves and a random interface with a smaller-scale roughness. So we consider as first approach the organized ripple field as a periodical one-dimensional structure (horizontal wavelengths 10 cm–1 m; vertical amplitudes 1–10 cm) perturbed by a smaller-scale interface roughness, random and intrinsic to the sediment material.

A classical approach for such a rough surface is to mix the behavior of the backscatter by the interface considered both as locally flat (at the scale of the sand wave flanks) and rough (at the smaller scale of sediment rugosity), and the local tilting effect by the relief, which comes as a modulation of the incident angles. This is the fundamental idea behind the “composite roughness” approach of wave scattering, based on the coexistence of two scales of roughness (see Jackson and Richardson 2007).

For the present modeling approach, we use the classical angular splitting of the backscatter response (for the “rough flat” interface) in two complementary regimes: a “specular” lobe around normal incidence, representing the reflection by well-oriented mirror-like “facets” dominating the response; and a Lambert’s law component at oblique to grazing angles, comprising both the interface roughness effect and the sediment volume contribution. Note that such a model generalized under a phenomenological form involving a restricted number of parameters (Lamarche et al. 2011), is sufficiently versatile to be used to fit most practical results of angular backscatter measurement results.

Facet model component

For the steep angle sector, we adopt the “facet” model approach as described in (Brekhovskikh and Lysanov 1982—short-named below as BL82), which is valid under the hypotheses of a high-frequency signal and a smooth relief of the interface: this is indeed respected in our case where the signal wavelength (5 mm at 300 kHz) is indeed smaller than the ripple flanks extent and radius of curvature (see Fig. 11). The scatter response is then described as an incoherent summation of contributions from mirror-like reflectors, integrated over the effective tilt-angle sector of seafloor “facets” and weighted by (1) the average interface reflection coefficient and (2) the probability distribution function (PDF) of the interface slope angles (BL82, Eq. 9.9.9):

$${m_S}={(VF)^2}w( - \chi /q)$$

(1)

We have kept here the (BL82) original notations: m _S is the backscatter strength in natural units, V is the plane-wave amplitude reflection coefficient at the plane interface (classically considered as fluid–fluid), w is the interface slope PDF; χ and q are functions of the vector components of the incident and scattered waves; F is a geometrical term, function of χ and q (the complete forms of F, χ and q given in BL82 are not detailed here).

For a backscattered signal, under the hypothesis of a Gaussian and isotropic roughness, the PDF of the interface slope ζ is azimuth-independent and writes as:

$$w(\zeta ) = \frac{1}{{\sqrt {2\pi \delta ^{2} } }}\exp \left( { - \frac{{\zeta ^{2} }}{{2\delta ^{2} }}} \right)$$

(2)

where δ ² is the slope variance. The backscattering coefficient finally comes as the classical form (BL82, Eq. 9.9.14):

$${m_S}({\theta _0})=\frac{{{V^2}}}{{8\pi {\delta ^2}{{\cos }^4}{\theta _0}}}\exp \left( - \frac{{{{\tan }^2}{\theta _0}}}{{2{\delta ^2}}}\right)$$

(3)

where θ ₀ is the acoustic wave incidence angle onto the average interface; this expression can be conveniently approximated, for small values of θ ₀, as:

$${m_S}({\theta _0}) \approx \frac{{{V^2}}}{{8\pi {\delta ^2}}}\exp \left( - \frac{{\theta _{0}^{2}}}{{2{\delta ^2}}}\right)$$

(4)

What is proposed here is to extend this conceptual approach to the case of an interface relief with a profile describing roughly the small-scale tide-current ripples observed practically. A straightforward idea is to incorporate in the backscatter strength model of Eq. (1) a seabed-slope PDF describing the characteristics of a polarized sediment wave field, instead of the classical isotropic Gaussian.

In this approach, the facet slope PDF follows a dominant behavior imposed by the average profile of the ripple crosscut. This dominant distribution will be modified by a random distribution of the slopes around their average values. For instance, consider the naïve case of a saw-tooth profile for ripples, possibly asymmetrical. Such a perfect profile will show a PDF consisting in two Dirac-like components at the slope angles of both flanks of the ripples. More realistically, some random fluctuation happens around these to ideal flank slope angles; should this angle fluctuation be taken as Gaussian, the PDF will feature two normal-law components centered at the two flank average angles. This is illustrated in Fig. 12a.

Fig. 12

Sketches showing the cross-cut profile of the ripples (a, b), the ideal slope PDF (a ₁, b ₁) and the random slope PDF (a ₂, b ₂), for two idealized ripple shapes: asymmetrical saw-tooth (a) and rectified sine (b)

A more realistic ripple model could use a sine profile, or a rectified sine—the latter showing the difference between the sharp edges of the ripple crests opposed to the smooth relief of ripple troughs. In this case, the ideal PDF will be the one associated with the slopes of a sine function, which has an exact analytical expression: the maximum probability is obtained for the maximum slope angle of the sine wave, and is obviously zero outside this limit. To account for the random character of the slopes around the ideal shape, it is convenient to convolve this ideal PDF with e.g. a Gaussian PDF; the result is given in Fig. 12b, showing two smooth peaks centered on the maximum slope angles (which are not strictly maxima any more) with lower-probability values in the middle; this behavior is in good qualitative agreement with our experimental results presented in “Results” section.

The relevance of this intuitive physical model can be enhanced by a more quantitative observation of backscatter data recorded over ripple fields (Camaret #2, Douarnenez #2). Both show, for the maximum-amplitude response, a maximum level response at steep angles up to a limit around 20°–25°, followed by a sharp fall-off ending around 35°–40°. This is in excellent agreement with the commonly-known values (see e.g. Belderson et al. 1982) of slopes actually observed on sand waves and ripples: the angles of repose (i.e. the steepest angle that a sloping bed can attain without slumping) for sands lie typically in the range 20°–35°, depending on the grain-size composition. Hence the cut-off angle observed on our backscatter data is in agreement with this sand characteristic; this strongly supports the validity of the approach of steep angles by the facet-slope method based on a backscatter angle dependence following the slope angle distribution.

Up to now we have considered the case of ideally rectilinear ripples (in the horizontal plane), for which the facets model expects a backscatter response strictly in the vertical plane normal to the ripple crest direction. However this difficulty is avoided by considering the actual seabed geometry: sediment ripples are not rectilinear features, but rather sinuous, their crest lines oscillating smoothly around an average direction. Hence active facets are available outside the ideal orthogonal direction (Fig. 13). Under this simple hypothesis we consider that the slope PDF in a given azimuth direction is similar to the nominal one, although affected by the probability for the ripples to be well-oriented with respect to the azimuth angle of the sonar swath. Note that this azimuth-dependence effect is still enhanced by the effects of the sonar angle aperture (making it possible to intercept contributions from ripples slightly deviating from the nominal crest direction) and the sonar platform yaw (the actual vertical plane containing transmit and receive directivity lobe axes fluctuates around the average value given by the nominal heading).

Fig. 13

Sketch of the interception (red segments) of the ripple flank direction by the sonar beam, drawn in the horizontal plane: (a) rectilinear crests: only the orthogonal beam (ψ = 90°) can intercept well-oriented facets; (b) sinuous crests: the orthogonal beam intercepts a relative maximum of facets; when steered (ψ≠ 90°), this interception rate decreases progressively

A final effect to consider is that, seen from an “oblique” azimuth, the ripple field shows an apparent crest-spacing longer than broadside, increasing in 1/sinψ, where ψ is the horizontal angle between the sonar beam and the average line-of-crest. Said another way, the apparent ripple relief is smoother, and the apparent slopes are multiplied by a sinψ factor.

Finally we illustrate the above concepts by computing the theoretical BS for a rectified-sine profile. Such an ideal PDF is given by:

$$\begin{gathered} w(\zeta )=\frac{1}{{2\pi \sqrt {1 - {\zeta ^2}/\zeta _{0}^{2}} }}\quad {\text{if}}\,\left| \zeta \right|<{\zeta _0} \hfill \\ w(\zeta )=0\quad {\text{if}}\,\left| \zeta \right| \geqslant {\zeta _0} \hfill \\ \end{gathered}$$

(5)

where ${\zeta _0}$ is the nominal maximum slope value (see Fig. 12b), to be modulated by the sinψ factor caused by the horizontal steering as explained above. The random character of the slope distribution is obtained by convolving $w(\zeta )$with a Gaussian PDF; this operation does not give an exact analytical result, so it is done numerically. The final PDF is finally replaced in Eq. (1–3), and the resulting backscatter strength is computed and displayed in dB values. The graphical results of this process are sketched in Fig. 12 b ₁ and b ₂.

Lambert component

The facet approach presented above is valid only at steep enough angles for the concept of well-oriented mirror-like facets to be valid; at oblique incidences it is preferable to use a Lambert’s law description of the backscatter coefficient angle dependence:

$${m_S}(\theta )={m_0}{\cos ^2}\theta$$

(6)

or in dB:

$$BS(\theta )=B{S_0}+20\log (\cos \theta )$$

(7)

where BS ₀ = 10logm ₀ is the reference backscatter level depending on the signal frequency and seafloor characteristics. The incident angle dependence is taken here in cos² θ, which is very commonly used, although other power-law dependences can be proposed according to the interface characteristics (for instance a cosθ dependence, known as the Lommel-Silliger law, see BL82). This Lambert-like approach is a very common proxy for the results of elaborated theories classically used in the modeling of seafloor backscatter (e.g. Bragg’s scattering for the interface roughness, or Stockhausen for the sediment volume; see BL82, or Jackson and Richardson 2007) since it provides a grazing-angle decrease of the backscatter level sufficiently realistic for many purposes. It was considered here unnecessary to get into too detailed backscatter theory, and sufficient to limit the discussion to an elementary approach aimed at explaining the experimentally-observed convergence of BS(θ) at increasing oblique incidence angle toward a common limit whatever the azimuth angle.

This approach of backscatter dependence on oblique incidence angles by a Lambert’s law modulated by the local seafloor relief has already been used in previous works (see Tang et al. 2002, 2009) proving to be a good fundamental tool for modeling the backscatter from a ripple field: the cos² θ dependence is then considered locally, the incidence angle θ being controlled by the local slope of the interface. Using this method, Tang et al. (2009) show that the BS values along the ensonified swath follow convincingly the ripple relief evolution, and are in good agreement with experimental data. This approach is relevant for high-resolution imaging sonar, for which the resolution cell is smaller than the ripple wavelength scale and hence can follow the local slope variations: in this case the local values of backscatter reproduce the details of the terrain small-scale relief such as ripples, and this property can be used in order to retrieve the characteristics of the sand ripple field. On the other hand, if one is interested by an averaged value of backscatter over a rippled area (as this is typically the case for MBES mapping small-scale ripples with an insufficient resolution to resolve them), an average value should be considered, integrating over the incidence angles (accounting for the local ripple slopes $\zeta$ combined with the acoustical wave propagation angle θ upon incidence on the average seafloor) and weighted by the slope PDF $w(\zeta )$:

$${m_{Sav}}(\theta )={m_0}\int {{{\cos }^2}(\theta - \zeta )w(\zeta )d} \zeta$$

(8)

The issue is now how much this slope-averaged value of the BS observed at a given propagation angle differs from the one obtained with a ripple-free interface. The answer to this question depends on both the propagation angle and the maximum local slope value accounted for in the integral, and can be readily obtained by computing the m _Sav (θ) formula (8) above.

Numerical results are given in Fig. 14, depicting the difference (in dB) between “with” and “without” ripples, according to the propagation incidence angle and to the ripple slope maximum angle. The exercise has been conducted for two profiles of ripples: a saw-tooth and a rectified sine. For the sine profile, the difference in average BS (at a given propagation angle) caused by ripples is not greater than 1 dB in extreme case of 60° grazing angle and maximal slope of 30°; it is practically negligible for slope angles smaller than 15°. For the pessimistic case of a saw-tooth profile (since all the angles $\zeta$ are then equal to the maximum slope value), the differential values are slightly higher. It is interesting to note that for the steepest incidence angles, the presence of ripples tends to decrease the backscatter values (negative differential) while at more grazing angles ripples tend to increase the average backscatter level, the limit between the two regimes being approximately around 45°.

Fig. 14

Backscatter level differential caused by ripples on a seafloor with a Lambertian response. For each nominal incidence angle (horizontal axis), the difference is computed between the nominal Lambert’s law and its integration over the ripple slopes. The maximum slope angle of the ripples (vertical axis) varies from 0° (no ripples) to 30°. a sawtooth profile; b rectified-sine profile

So, practically, at most oblique and grazing angles where a Lambert model is relevant, the conclusion is that the ripple influence over the average BS is not significant. A corollary is that the azimuth dependence of average BS over an organized ripple field is expected to be negligible at oblique enough angles, since the BS level is almost insensitive to the presence of the ripples.

This prediction of a small impact of the ripple relief on the average backscatter at oblique-to-grazing angles is an important result for the interpretation of our experimental results. It is clear from the “Results” section that the azimuth impact observed over rippled sediment seafloors is very significant at steep angles, but disappears at incident angles exceeding 35–40° (cut-off angle in agreement with the slope flank angle limit) where the BS angular dependence follows the Lambert-like behavior valid for a non-rippled interface. This is coherent with the modeling approach presented here.

An obvious limitation to the elementary models used here is the absence of any shadowing effect, occurring when the propagation angle exceeds the local tangent-plane tilt of the facets orientated outwards the signal propagation direction. The existence of such shadows should be expected to cause azimuth-dependent effects, since the apparent slope of the ripples depends on the horizontal angle of observation. This phenomenon is not considered here; however this is consistent with our experimental data, for which the propagation angles are limited to typically 60° from vertical, leaving little chance of shadowing effects with usual sediment ripple slope values.

Synthesis

Finally the facets and Lambert components can be summed up into one resultant model, and applied to a ripple simplified configuration. Figure 15 presents their individual contributions and their summation into BS(θ, ψ). The computation was done for a rectified-sine profile with: ζ ₀ = 25° (modified by sin ψ); ψ = 15° and 90°; δ = 6°; V = 0.005; m ₀ = 0.002; θ = −60° to +60°.

Fig. 15

BS model synthesis for a rectified-sine-profile ripple field at two azimuth values 15° (dashed) and 90° (solid). The Facets and Lambert components are shown as individual (thin grey) and combined (thick black) contributions. Input parameters are given in the text

The computed model curves provide a result which is qualitatively very similar to the experimental results (Figs. 3, 4, 5, 6, 7, 8, 9, 10) presented in the previous parts of the paper. It makes clear the two distinct regimes observed on field data: a strong influence of the ripple slopes at steep angles, where a facets model is applicable; and an average decrease at oblique-to-grazing angles, conveniently described by a Lambert law with a negligible impact of the ripple presence. A more detailed quantitative agreement could be searched for, by improving the facet description and optimizing the various parameters of the elementary models; a special effort should bear on the ripple-field modeling, especially the local fluctuations of ripple directions in the horizontal plane. However the latter cannot really be ground-truthed, so it is not clear if such an exercise could inform further than what was presented above. This short section about the modeling of horizontal-angle dependence of BS from rippled seabed has been purposely limited to two simple and classical approaches of backscatter theory applied to an idealized interface roughness of parallel ripples typical of a sand seafloor; this relatively simple geometry makes it a good candidate for modeling, and our experimental results did correspond to this configuration. It is felt, however, that our approach makes possible a sufficient level of physical understanding of our experimental data, and provides results consistent with common observations. More sophisticated approaches are of course possible, but at the risk of a serious increase of the complexity in both the backscatter model and the sediment description in terms of geometrical and geoacoustical values.

Conclusions

In this paper, we have presented a study on the seabed backscatter strength dependence on survey azimuth, from data obtained in real surveying conditions. This particular issue may have not received all the attention it deserves, since it appears to be an important factor impacting the operations of backscatter data acquisition and processing which are today the objects of a standardization effort by the user’s community (Lurton and Lamarche 2015).

The experimental method proposed here is to survey an area from the six main azimuth directions forming a “compass rose” pattern. Surveys were conducted over seven areas around Brest, France, with various sediment types (from fine sand to coarse sedimentary material). A Kongsberg EM 2040 MBES was operated at 300 kHz for incident angles up to 60°. Various plots were used to assess the azimuth effect and the characteristics (homogeneity, isotropy) of each area. The data and parameters used for the assessment were: reflectivity; bathymetry; backscatter vs incidence angle at various azimuths; backscatter strength vs azimuth in polar coordinates. We analysed data coming both from complete survey lines and from the common part of the six lines. The latter provides the best homogeneity with respect to the sediment characteristics.

For flat areas covered with coarse material or silt, with no seabed landforms (e.g. sand ripples), the backscatter strength values for the different incidence angles were observed to be independent of the survey azimuth. Conversely, for areas covered with sand with tide-generated ripples, one same area may provide a number of different BS angular responses, depending on the sonar swath orientation. This phenomenon appears at moderate oblique incidence angles (5°–30°); in this angular range the differences in the backscatter strength values may reach 10 dB. In the 40°–60° range the azimuth dependence becomes negligible.

These experimental observations are in good agreement with modeling results based on the simplified (but classical) descriptions of facets theory (at steep angles) and Lambert’s law (at oblique angles). The results of this approach show a strong dependence of the facets component to a ripple-like organization of the roughness, and a negligible dependence of the Lambert regime on the presence of ripples; this is in good agreement with the field data. Our analysis was restricted to the case of idealized ripple profiles (rectified-sine) on a sand seabed. We expect that other organized roughness patterns caused by different seafloor types should lead to similar phenomena, explainable by using the same modeling tools favoring the geometrical side of things; however this remains to be demonstrated.

The consequences of these observations on the interpretation of sonar reflectivity data are important. In many cases the existence of a roughness polarization cannot be reliably inferred directly from the raw sonar data (bathymetry or reflectivity), since the corrugations may happen at a scale comparable or smaller than the signal footprint, and hence below the sensor’s resolution. Moreover such phenomena are expected to be time-dependent, at the time scale of tides and currents. This brings another factor in the seafloor interface description, to account for the roughness polarization. The “compass rose” method of surveying can provide valuable information both about the presence of small-scale ripples and their orientation; however it remains to be demonstrated if such a time-consuming survey strategy can be adopted as a routine procedure.

Repeated surveys aimed at monitoring the seafloor over a given area should be conducted using a line pattern following always the same azimuthal directions. On the other hand, controlled measurement at various azimuth angles should make it possible to retrieve characteristic features of the interface roughness. It is interesting to note that this method is used in radar monitoring of the sea-surface by satellite-borne ‘scatterometer’ radars retrieving wind direction from surface wave orientation (Elachi 1988).

The calibration of MBES for backscatter level measurements is an important still unresolved- issue (Lurton and Lamarche 2015). A promising approach could be in situ calibration on natural reference areas with known backscatter characteristics. Such an approach has multiple advantages: it is done over a target similar to the ones to be met under operation conditions, and the characteristics of the sonar upon calibration account for the specific installation environment. Also it can be integrated inside the bathymetry calibration operations. Therefore it is important to include a requirement, when identifying candidate reference area, that local backscatter strength has to be independent of the azimuth.

Finally, considering the high dispersion of backscatter-level results according to the survey azimuth, the direct comparison of field data with theoretical models assuming an isotropic roughness (and obviously the associated inversion processing) can lead to erroneous results if no preliminary estimation of a possible seabed-roughness polarization is made.