Effects of the concentrated mass and elastic support on dynamic and flutter behaviors of panel structures

Abstract

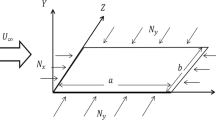
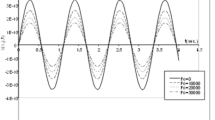
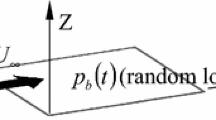
To research impacts of mass points and elastic supports on dynamic and aeroelastic properties of plate structures, a unified dynamic model concerning the plate structures with concentrated mass point or elastic support subjected to supersonic airflow is established in this paper. The energy approach is utilized to deduce energy functions of the dynamic system, and the nonlinear dynamic equations are further formulated based on the variational principle. Furthermore, several numerical calculations are implemented to validate the proposed formulations, and satisfactory agreements are exhibited between the calculated vibration and flutter solutions and data from the software and literature. Subsequently, impacts of the mass point and elastic support on vibration and flutter properties of panel structures are also presented and the detailed mechanisms are explained. It can be found that aeroelastic stability properties of panel structures are significantly raised with the location of the concentrated mass point or elastic support placed reasonably. This study provides a simple method for the flutter suppression of plates, which can be used in the mechanical design of these plate structures for the better dynamic performances.

Appendix A

The displacements of the panel structure are

$$\begin{gathered} u_{0} (x,y,t) = {\mathbf{H}}_{u} {\mathbf{q}}_{1} \hfill \\ v_{0} (x,y,t) = {\mathbf{H}}_{v} {\mathbf{q}}_{2} \hfill \\ w_{0} (x,y,t) = {\mathbf{H}}_{w} {\mathbf{q}}_{3} \hfill \\ \varphi_{0x} (x,y,t) = {\mathbf{H}}_{x} {\mathbf{q}}_{4} \hfill \\ \varphi_{0y} (x,y,t) = {\mathbf{H}}_{y} {\mathbf{q}}_{5} \hfill \\ \end{gathered}$$

(19)

The detailed expressions in these matrices of the panel structures are derived as

$${\mathbf{K}}^{l} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{uu} } & {{\mathbf{K}}_{uv} } & {\mathbf{0}} & {{\mathbf{K}}_{ux} } & {{\mathbf{K}}_{uy} } \\ {{\mathbf{K}}_{uv}^{{\text{T}}} } & {{\mathbf{K}}_{vv} } & {\mathbf{0}} & {{\mathbf{K}}_{vx} } & {{\mathbf{K}}_{vy} } \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{K}}_{ww} } & {{\mathbf{K}}_{wx} } & {{\mathbf{K}}_{wy} } \\ {{\mathbf{K}}_{ux}^{{\text{T}}} } & {{\mathbf{K}}_{vx}^{{\text{T}}} } & {{\mathbf{K}}_{wx}^{{\text{T}}} } & {{\mathbf{K}}_{xx} } & {{\mathbf{K}}_{xy} } \\ {{\mathbf{K}}_{uy}^{{\text{T}}} } & {{\mathbf{K}}_{vy}^{{\text{T}}} } & {{\mathbf{K}}_{wy}^{{\text{T}}} } & {{\mathbf{K}}_{xy}^{{\text{T}}} } & {{\mathbf{K}}_{yy} } \\ \end{array} } \right]$$

(20)

$${\mathbf{K}}^{nl} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{K}}_{uw}^{nl} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{K}}_{vw}^{nl} } & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{K}}_{wu}^{nl} } & {{\mathbf{K}}_{wv}^{nl} } & {{\mathbf{K}}_{ww}^{nl} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]$$

(21)

$$\begin{aligned} {\mathbf{K}}_{uu} & = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} A_{11} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right) + A_{66} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right) \hfill \\ + A_{16} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right) + A_{16} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right) \hfill \\ \end{gathered} \right]} } dxdy \\ & \quad + \int_{0}^{{L_{1} }} {\left( {\left. {k_{uy0} {\mathbf{H}}_{u}^{{\text{T}}} {\mathbf{H}}_{u} } \right|_{y = 0} + \left. {k_{{uyL_{2} }} {\mathbf{H}}_{u}^{{\text{T}}} {\mathbf{H}}_{u} } \right|_{{y = L_{2} }} } \right)} dx \\ & \quad + \int_{0}^{{L_{2} }} {\left( {\left. {k_{ux0} {\mathbf{H}}_{u}^{{\text{T}}} {\mathbf{H}}_{u} } \right|_{x = 0} + \left. {k_{{uxL_{1} }} {\mathbf{H}}_{u}^{{\text{T}}} {\mathbf{H}}_{u} } \right|_{{x = L_{1} }} } \right)} dy \\ \end{aligned}$$

(22)

$${\mathbf{K}}_{uv} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} A_{12} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right) + A_{66} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right) \hfill \\ + A_{16} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right) + A_{26} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(23)

$${\mathbf{K}}_{ux} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} B_{11} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial x}} \right) + B_{66} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial y}} \right) \hfill \\ + B_{16} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial x}} \right) + B_{16} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial y}} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(24)

$${\mathbf{K}}_{uy} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} B_{12} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial y}} \right) + B_{66} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial x}} \right) \hfill \\ + B_{16} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial x}} \right) + B_{26} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial y}} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(25)

$$\begin{aligned} {\mathbf{K}}_{vv} & = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} A_{22} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right) + A_{66} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right) \hfill \\ + A_{26} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right) + A_{26} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right) \hfill \\ \end{gathered} \right]} } dxdy \\ & \quad + \int_{0}^{{L_{1} }} {\left( {\left. {k_{vy0} {\mathbf{H}}_{v}^{{\text{T}}} {\mathbf{H}}_{v} } \right|_{y = 0} + \left. {k_{{vyL_{2} }} {\mathbf{H}}_{v}^{{\text{T}}} {\mathbf{H}}_{v} } \right|_{{y = L_{2} }} } \right)} dx \\ & \quad + \int_{0}^{{L_{2} }} {\left( {\left. {k_{vx0} {\mathbf{H}}_{v}^{{\text{T}}} {\mathbf{H}}_{v} } \right|_{x = 0} + \left. {k_{{vxL_{1} }} {\mathbf{H}}_{v}^{{\text{T}}} {\mathbf{H}}_{v} } \right|_{{x = L_{1} }} } \right)} dy \\ \end{aligned}$$

(26)

$${\mathbf{K}}_{vx} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} B_{12} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial x}} \right) + B_{66} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial y}} \right) \hfill \\ + B_{16} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial x}} \right) + B_{26} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial y}} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(27)

$${\mathbf{K}}_{vy} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} B_{22} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial y}} \right) + B_{66} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial x}} \right) \hfill \\ + B_{26} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial y}} \right) + B_{26} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial x}} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(28)

$$\begin{aligned} {\mathbf{K}}_{ww} & = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} K_{s} A_{44} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right) + K_{s} A_{55} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right) \hfill \\ + K_{s} A_{45} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right) + K_{s} A_{45} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right) \hfill \\ \end{gathered} \right]} } dxdy \\ & \quad + \int_{0}^{{L_{1} }} {\left( {\left. {k_{wy0} {\mathbf{H}}_{w}^{{\text{T}}} {\mathbf{H}}_{w} } \right|_{y = 0} + \left. {k_{{wyL_{2} }} {\mathbf{H}}_{w}^{{\text{T}}} {\mathbf{H}}_{w} } \right|_{{y = L_{2} }} } \right)} dx \\ & \quad + \int_{0}^{{L_{2} }} {\left( {\left. {k_{wx0} {\mathbf{H}}_{w}^{{\text{T}}} {\mathbf{H}}_{w} } \right|_{x = 0} + \left. {k_{{wxL_{1} }} {\mathbf{H}}_{w}^{{\text{T}}} {\mathbf{H}}_{w} } \right|_{{x = L_{1} }} } \right)} dy \\ & \quad + \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {\frac{{\lambda D_{1}^{{1}} }}{{L_{1}^{3} }}\left( {{\mathbf{H}}_{w}^{{\text{T}}} \frac{{\partial {\mathbf{H}}_{w} }}{\partial x}{\text{cos}}\theta_{air} + {\mathbf{H}}_{w}^{{\text{T}}} \frac{{\partial {\mathbf{H}}_{w} }}{\partial y}{\text{sin}}\theta_{air} } \right)} \right]} } dxdy \\ & \quad + k_{ps} {\mathbf{H}}_{w}^{{\text{T}}} {\mathbf{H}}_{w} \left| {_{{x = x_{p} ,{\kern 1pt} {\kern 1pt} y = y_{p} }} } \right. \\ \end{aligned}$$

(29)

$${\mathbf{K}}_{wx} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {K_{s} A_{55} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} ({\mathbf{H}}_{x} ) + K_{s} A_{45} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} ({\mathbf{H}}_{x} )} \right]} } dxdy$$

(30)

$${\mathbf{K}}_{wy} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {K_{s} A_{44} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} ({\mathbf{H}}_{y} ) + K_{s} A_{45} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} ({\mathbf{H}}_{y} )} \right]} } dxdy$$

(31)

$$\begin{aligned} {\mathbf{K}}_{xx} & = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} K_{s} A_{55} ({\mathbf{H}}_{x} )^{{\text{T}}} ({\mathbf{H}}_{x} ) + D_{11} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial x}} \right) + D_{66} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial y}} \right) \hfill \\ + D_{16} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial y}} \right) + D_{16} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial x}} \right) \hfill \\ \end{gathered} \right]} } dxdy \\ & \quad + \int_{0}^{{L_{1} }} {\left( {\left. {k_{xy0} {\mathbf{H}}_{x}^{{\text{T}}} {\mathbf{H}}_{x} } \right|_{y = 0} + \left. {k_{{xyL_{2} }} {\mathbf{H}}_{x}^{{\text{T}}} {\mathbf{H}}_{x} } \right|_{{y = L_{2} }} } \right)} dx \\ & \quad + \int_{0}^{{L_{2} }} {\left( {\left. {k_{xx0} {\mathbf{H}}_{x}^{{\text{T}}} {\mathbf{H}}_{x} } \right|_{x = 0} + \left. {k_{{xxL_{1} }} {\mathbf{H}}_{x}^{{\text{T}}} {\mathbf{H}}_{x} } \right|_{{x = L_{1} }} } \right)} dy \\ \end{aligned}$$

(32)

$${\mathbf{K}}_{xy} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} K_{s} A_{45} ({\mathbf{H}}_{x} )^{{\text{T}}} ({\mathbf{H}}_{y} ) + D_{12} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial y}} \right) + D_{66} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial x}} \right) \hfill \\ + D_{16} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial x}} \right) + D_{26} \left( {\frac{{\partial {\mathbf{H}}_{x} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial y}} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(33)

$$\begin{aligned} {\mathbf{K}}_{yy} & = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} K_{s} A_{44} ({\mathbf{H}}_{y} )^{{\text{T}}} ({\mathbf{H}}_{y} ) + D_{22} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial y}} \right) + D_{66} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial x}} \right) \hfill \\ + D_{26} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial y}} \right) + D_{26} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{y} }}{\partial x}} \right) \hfill \\ \end{gathered} \right]} } dxdy \\ & \quad + \int_{0}^{{L_{1} }} {\left( {\left. {k_{yy0} {\mathbf{H}}_{y}^{{\text{T}}} {\mathbf{H}}_{y} } \right|_{y = 0} + \left. {k_{{yyL_{2} }} {\mathbf{H}}_{y}^{{\text{T}}} {\mathbf{H}}_{y} } \right|_{{y = L_{2} }} } \right)} dx \\ & \quad + \int_{0}^{{L_{2} }} {\left( {\left. {k_{yx0} {\mathbf{H}}_{y}^{{\text{T}}} {\mathbf{H}}_{y} } \right|_{x = 0} + \left. {k_{{yxL_{1} }} {\mathbf{H}}_{y}^{{\text{T}}} {\mathbf{H}}_{y} } \right|_{{x = L_{1} }} } \right)} dy \\ \end{aligned}$$

(34)

$${\mathbf{K}}_{uw}^{nl} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} A_{66} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right){\mathbf{q}}_{3} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right) + \frac{{A_{11} }}{2}\left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right){\mathbf{q}}_{3} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right) \hfill \\ + \frac{{A_{12} }}{2}\left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right){\mathbf{q}}_{3} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(35)

$${\mathbf{K}}_{wu}^{nl} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} A_{66} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right) + A_{66} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial y}} \right) \hfill \\ + A_{11} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right) + A_{12} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{u} }}{\partial x}} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(36)

$${\mathbf{K}}_{vw}^{nl} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} A_{66} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right){\mathbf{q}}_{3} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right) + \frac{{A_{22} }}{2}\left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right){\mathbf{q}}_{3} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right) \hfill \\ + \frac{{A_{12} }}{2}\left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right){\mathbf{q}}_{3} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(37)

$${\mathbf{K}}_{wv}^{nl} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} A_{66} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right) + A_{66} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial x}} \right) \hfill \\ + A_{22} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right) + A_{12} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{v} }}{\partial y}} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(38)

$${\mathbf{K}}_{ww}^{nl} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} \frac{{A_{11} }}{2}\left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right){\mathbf{q}}_{3} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right) + \frac{{A_{22} }}{2}\left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right){\mathbf{q}}_{3} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right) \hfill \\ + \frac{{A_{12} }}{2}\left( {\left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right){\mathbf{q}}_{3} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right) + \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right){\mathbf{q}}_{3} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)} \right) \hfill \\ + A_{66} \left( {\left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right){\mathbf{q}}_{3} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right) + \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial y}} \right){\mathbf{q}}_{3} {\mathbf{q}}_{3}^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\mathbf{H}}_{w} }}{\partial x}} \right)} \right) \hfill \\ \end{gathered} \right]} } dxdy$$

(39)

The rigidity parameters are given as

$$\begin{aligned} A_{ij} & = \sum\limits_{k = 1}^{n} {\overline{Q}_{ij} } (z_{k + 1} - z_{k} ),\quad B_{ij} = \frac{1}{2}\sum\limits_{k = 1}^{n} {\overline{Q}_{ij} } \left( {z_{k + 1}^{2} - z_{k}^{2} } \right), \\ D_{ij} & = \frac{1}{3}\sum\limits_{k = 1}^{n} {\overline{Q}_{ij} } \left( {z_{k + 1}^{3} - z_{k}^{3} } \right). \\ \end{aligned}$$

$${\mathbf{M}} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{uu} } & {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{M}}_{ux} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{vv} } & {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{M}}_{vy} } \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{M}}_{ww} } & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{M}}_{ux}^{{\text{T}}} } & {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{M}}_{xx} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{vy}^{{\text{T}}} } & {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{M}}_{yy} } \\ \end{array} } \right]$$

(40)

$${\mathbf{M}}_{uu} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{0} ({\mathbf{H}}_{u} )^{{\text{T}}} ({\mathbf{H}}_{u} )} } dxdy + m_{s} {\mathbf{H}}_{u}^{{\text{T}}} {\mathbf{H}}_{u} \left| {_{{x = x_{m} ,{\kern 1pt} {\kern 1pt} y = y_{m} }} } \right.$$

(41)

$${\mathbf{M}}_{ux} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{1} ({\mathbf{H}}_{u} )^{{\text{T}}} ({\mathbf{H}}_{x} )} } dxdy$$

(42)

$${\mathbf{M}}_{vv} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{0} ({\mathbf{H}}_{v} )^{{\text{T}}} ({\mathbf{H}}_{v} )} } dxdy + m_{s} {\mathbf{H}}_{v}^{{\text{T}}} {\mathbf{H}}_{v} \left| {_{{x = x_{m} ,{\kern 1pt} {\kern 1pt} y = y_{m} }} } \right.$$

(43)

$${\mathbf{M}}_{vy} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{1} ({\mathbf{H}}_{v} )^{{\text{T}}} ({\mathbf{H}}_{y} )} } dxdy$$

(44)

$${\mathbf{M}}_{ww} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{0} ({\mathbf{H}}_{w} )^{{\text{T}}} ({\mathbf{H}}_{w} )} } dxdy + m_{s} {\mathbf{H}}_{w}^{{\text{T}}} {\mathbf{H}}_{w} \left| {_{{x = x_{m} ,{\kern 1pt} {\kern 1pt} y = y_{m} }} } \right.$$

(45)

$${\mathbf{M}}_{xx} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{2} ({\mathbf{H}}_{x} )^{{\text{T}}} ({\mathbf{H}}_{x} )} } dxdy$$

(46)

$${\mathbf{M}}_{yy} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{2} ({\mathbf{H}}_{y} )^{{\text{T}}} ({\mathbf{H}}_{y} )} } dxdy$$

(47)

$${\mathbf{C}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{C}}_{ww} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]$$

(48)

$${\mathbf{C}}_{ww} = \frac{{\sqrt {\mu \lambda \rho_{1} hD_{1}^{1} /M_{\infty } } }}{{L_{1}^{2} }}\int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {{\mathbf{H}}_{w}^{{\text{T}}} } } {\mathbf{H}}_{w} dxdy$$

(49)