Performance-aware design for piezoelectric energy harvesting optimisation via finite element analysis

Abstract

Most of the optimisation studies of Vibration Energy Harvesters (VEHs) account for a single output quantity, e.g. frequency bandwidth or maximum power output, but this approach does not necessarily maximise the system efficiency. In those applications where VEHs are suitable sources of energy, to achieve optimal design it is important to consider all these performance indexes simultaneously. This paper proposes a robust and straightforward multi-objective optimisation framework for Vibration Piezoelectric Energy Harvesters (VPEHs), considering simultaneously the most crucial performance indexes, i.e., the maximum power output, efficiency, and frequency bandwidth. For the first time, a rigorous formulation of efficiency for Multi-Degree of Freedom (MDOF) VPEHs is here proposed, representing an extension of previous definitions. This formulation lends itself to the optimisation of FE and MDOF harvesters models. The optimisation procedure is demonstrated using a planar-shape harvester and validated against numerical results. The effects of changing some structural parameters on the harvester performance are investigated via sensitivity analysis. The results show that the proposed methodology can effectively optimise the global performance of the harvester, although this does not correspond to an improvement of every single index. Furthermore, the optimisation of each performance index individually results in a variety of design configurations that greatly differs from one another. It is here demonstrated that the design obtained with the multi-objective function here proposed is similar to the design obtained when optimising the efficiency.

1 Introduction

In recent years, low-powered devices such as Wireless Sensor Networks (WSNs) for structural health monitoring, industry monitoring process, and environmental measurements have been proposed to be employed in different industrial sectors (Baire et al. 2019; Ruiz-Garcia et al. 2009; Jiao et al. 2020). These sensors, often located in remote or difficult access locations, are commonly powered by chemical batteries, which have the main drawback of a limited lifespan. In order to increase their autonomy and reduce maintenance costs, some authors suggested powering the WSNs using Energy Harvesters (EHs) (Noel et al. 2017, Knight et al. 2008). The EHs are able to extract energy from different sources in the surrounding environment (i.e., solar, thermal, and mechanical power) (Shaikh and Zeadally 2016). Ambient vibrations are ubiquitous, therefore VEHs represent a promising way to power small electronic devices such as WSNs (Adu-Manu et al. 2018, Safaei et al. 2019).

VEHs can exploit different transduction mechanisms (Wei and Jing 2017), with VPEHs (Sezer and Koç 2021; Moheimani and Fleming 2006) receiving great interest, thanks to their high power density (Safaei et al. 2019). VPEHs are typically used in applications where a small amount of power - in the order of milliwatt - is required (Sarker et al. 2019; Sezer and Koç 2021; Covaci and Gontean 2020). The most studied configuration is the beam shape which has been extensively studied from an analytical, numerical, and experimental point of view (Sodano et al. 2004; Erturk and Inman 2008a, 2009; Ajitsaria et al. 2007; Tan et al. 2016; Cho et al. 2014; Patel et al. 2011). One of the main problems of the VPEHs is the limited operational frequency bandwidth (Tran et al. 2018) out of which no significant power output is produced. Therefore, different approaches and design solutions have been proposed in the literature to tackle this problem. Some authors (Wu et al. 2014; Rezaeisaray et al. 2015; Toyabur et al. 2018) proposed to adopt multi-degree of freedom VPEHs. These harvesters can exploit the higher modes to improve the system frequency bandwidth. However, very complex designs are involved (Covaci and Gontean 2020) and a significant amount of power is produced only around the first modes, limiting the practical usage of such systems. Malaji and Ali (2017) and Upadrashta and Yang (2016), proposed multi-modal array systems to face the problem. The multi-modal array system is composed of several independent VPEHs, thus, it offers a wider frequency range by exploiting the resonance of each independent resonator. Nevertheless, the energy density of the overall system is reduced, due to the increased size and weight (Covaci and Gontean 2020). Other authors (Challa et al. 2008, Karadag and Topaloglu 2017, Senthilkumar et al. 2019), instead, studied tuneable devices, i.e., VPEHs, where the resonance frequency is controlled by changing one or more structural parameters to match the excitation frequency. This is a promising approach to face the frequency bandwidth problem, however, some produced energy is consumed by the tuning control system. Moreover, the necessity of an electronic controller increases the overall system complexity (Maamer et al. 2019). An alternative approach to increase the bandwidth of VPEHs is based on the use of structural non-linearities (Vijayan et al. 2015; Erturk and Inman 2011; Zhou et al. 2020; Li et al. 2018; Dai et al. 2020). The presence of non-linearities in energy harvesters is typically associated with a wider frequency bandwidth (Tran et al. 2018; Wei and Jing 2017), but its dynamic response is more complex and may result in the co-existence of multiple steady-state responses. Although high amplitude oscillations are preferred, in some regions of the frequency response, these may be difficult to attain. This can lead to a deceivingly large bandwidth of non-linear VPEHs, whereas, in practice, the linear harvesters can outperform the non-linear counterparts (Zhao and Erturk 2013; Cammarano et al. 2014).

Despite many attempts to meliorate the harvesters frequency bandwidth, the problem is far to be solved. Moreover, the proposed designs are very dissimilar from the others (Reddy et al. 2016; Lu et al. 2020; Wang et al. 2018), which could undermine the standardisation process of VEHs.

Some harvesters are also very complex (Salmani et al. 2019; Kuang and Zhu 2017; Qian et al. 2019; Qing et al. 2021) thus, in recent years, FE packages have been increasingly adopted in VPEHs literature. Zhu et al. (2009) proposed for the first time a study of VPEHs using FE commercial software.

Upadrashta and Yang (2015) developed a FE VPEH with non-linear magnetic interaction. In order to reduce the computational burden, the authors proposed simplifying the non-linear interaction between the mechanical oscillator and the magnets via non-linear springs. Finite Element Analysis (FEA) is also used by Kuang and Zhu (2017), who studied a mechanically plunked VPEH for knee-joint motion. Further examples of the use of FEA for VPEHs in the literature can be found in Qian et al. (2021), He et al. (2020), Kim et al. (2020), Tian et al. (2020), Upadrashta and Yang (2018), Shi et al. (2020), Caetano and Savi (2019), Caetano and Savi (2021). In the aforementioned works, the authors demonstrated that commercial FE software can be used reliably to predict the mechanical and electrical response of VPEHs and evaluate their performance.

However, the ultimate goal of the VEHs is to produce as much energy as possible for the widest possible frequency bandwidth, thus in the literature, the harvesters analysis has been accompanied by optimisation procedures to improve their performance (Sarker et al. 2019). Many examples of optimised VPEHs can be found in the literature (Kim et al. 2015; Shu and Lien 2006; Wickenheiser and Garcia 2010; Onsorynezhad et al. 2020; Rui et al. 2018; Townsend et al. 2019; Qian et al. 2018; Salmani et al. 2019; Wang et al. 2019). Nevertheless, the most interesting form of optimisation implements specific optimisation methods, and it requires the definition of objective functions, equality and inequality constraints, boundaries, and design variables (Caetano and Savi 2021; Townsend et al. 2019; Qian et al. 2019, 2018; Salmani et al. 2019; Wang et al. 2019). This kind of procedure allows for managing many parameters in a single optimisation process and exploits the algorithm to reduce the overall computational time (Kaveh and Talatahari 2010).

In this context, the definition of the objective function represents one of the most important aspects. In the literature, efficiency has been recognised as an important figure of merit for the optimisation of the VEHs performance (Aboulfotoh and Twiefel 2018; Yang et al. 2017). Richards et al. (2004) investigated the efficiency of a micro-scale VPEH, providing a definition of efficiency based on the electro-mechanical coupling and the quality factor. Shu and Lien (2006) studied the efficiency of a rectified VPEH, providing a definition that can be used in steady-state conditions. Kim et al. (2015) proposed a closed-form solution to compute the efficiency of a base excited bi-morph VPEH that accounts for the additional degree of freedom of the primary vibrating structure. The authors demonstrated that the optimal electrical load that maximises power output is quite different from the electrical load that maximises efficiency. Recently, Yang et al. (2017) proposed another formulation of efficiency for VPEHs: their definition of efficiency depends on the phase shift between the input force and the structural response of the system. Their results were validated experimentally.

The optimisation of VPEHs in the literature is mostly focused on the maximisation of power output and frequency bandwidth. Only a few studies consider the optimisation of the dynamic efficiency of the harvester and, to the best of the authors’ knowledge, none optimise the efficiency together with the maximum power output and the frequency bandwidth. This is mostly due to the lack of a definition of efficiency that can be used effectively with MDOF VEHs, with direct implications for the possibility of optimising complex geometries for vibration energy harvesting.

This work presents a multi-objective optimisation framework that can be applied to any VEHs geometry and optimises at the same time maximum power output, frequency bandwidth, and efficiency.

The proposed framework uses a novel definition of efficiency which is an extension of the definitions previously proposed for single-degree of freedom systems. Therefore, the novelty of this work lays not only in the proposed optimisation framework, but also in a novel matrix formulation of efficiency that can easily be used with FE models of VEHs and can directly drive the design process.

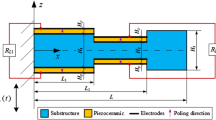
Here, a planar-shaped energy harvester (see Fig. 1) is used to prove the optimisation capabilities of the proposed framework.

2 Methodology

This section introduces the methodology of this study: firstly the FE model of VPEH is described, and then the optimisation problem, along with its objectives functions, is illustrated. The section concludes with the mathematical comparison between the proposed efficiency and a previous definition available in the literature.

2.1 Finite element model and optimisation parameters

The VPEH is composed of three main components: the sub-structural material (bronze), the piezoelectric laminate patch (PZT-5H), and the electric circuit which is modelled through an ideal resistor. The structure is constrained at the bottom extremity and is base excited in the horizontal direction as depicted in Fig. 1. The piezoelectric layer is applied to the lower part of the harvester where higher stress is expected.

Fig. 1

Graphical representation of the uni-morph VPEH. The figure shows the geometry and the main dimensions of the harvester which are considered in the optimisation study

A FE model of the harvester has been created in ANSYS by using SOLID45, SOLID5, and CIRCU94 elements: the former two are 3D structural and piezoelectric elements with 8 nodes, whereas the latter is a simplified electric element representing the ideal resistor. The voltage Degrees of Freedom (DOF) of the nodes, constituting the upper and lower surfaces of the piezoelectric material, are constrained to two separate nodes with the intent to reproduce two electrodes. Then, the resistor is connected to them to simulate the electrical circuit, as shown in Fig. 2. In addition, one end of the resistor is grounded to evaluate the overall electrical voltage (Upadrashta and Yang 2015).

Fig. 2

Finite element model of VPEH: the voltage DOFs of the nodes of the circuit element are coupled to the voltage DOFs of the upper and lower surface of the piezoelectric material

The following geometric parameters are used to drive the optimisation procedure: length h, width b, thickness of the sub-structural material t and piezoelectric patch $t_{p}$, angle of inclination $\theta$, and the trapezoid base angle $\varphi$ which are graphically shown in Fig. 1.

Table 1 Lower and upper bounds, and original configuration ($P_{0}$) of the parameters, i.e., design variables, adopted in the optimisation framework for the VPEH

Table 1 represents the lower and upper bounds, and the original configuration ($P_{0}$) of the parameters involved in the optimisation procedure, named design variables. The parameters f and g, instead, can be represented with the following expressions: $f = 1/6 h \sin (\theta )$ and $g = 2/3 h \sin (\theta )$; this keeps them proportional to the starting configuration and allows omitting additional parameters from the already complex optimisation procedure. The piezoelectric, elastic anisotropic, and dielectric matrices adopted in the FE model are obtained from (Yang 2006), while the properties of the sub-structural material are: Young modulus $E=100$ GPa, Poisson coefficient $\nu =0.34$, density $\rho =8000$ $kg/m^{3}$, and global structural damping of $2\%$. A converge analysis, needed to assess the quality of the mesh (Whiteley 2017), is carried out: 4000 elements with two layers per material are found to be a good trade-off between computational burden and the quality of the results.

2.2 Optimisation algorithm

The literature offers different algorithms for solving optimisation problems; between them, the heuristic methods provide faster convergence to an approximate global solution, reducing the overall computational burden (Kaveh and Talatahari 2010; Hassan et al. 2005). This is extremely important for optimisation procedures which adopt FEA for the evaluation of the objective function, as in the case proposed in this work. Many heuristic method for optimisation have been proposed in the literature and between them it is possible to find: Artificial Bee Colony (ABC) algorithm (Karaboga and Akay 2009), Genetic Algorithm (GA) (Mühlenbein 1997), Tabu Search (TS) algorithm (Chelouah and Siarry 2000), Particle Swarm Optimisation(PSO) (Kennedy and Eberhart 1995),Cuckoo Search (CS) algorithm (Yang and Deb 2009; Cuong-Le et al. 2021), Gravitational Search Algorithm (Rashedi et al. 2009), Grey Wolf Optimiser (GWO) (Mirjalili et al. 2014; Thobiani et al. 2022), etc. The proposed optimisation framework relies on the PSO method as it is more prone to solve the non-linear global optimisation problems (Biswal et al. 2016; Lindfield and Penny 2017; Shi and Eberhart 1998). Inspired by the nature, it tries to emulate the movement of birds using particles (Kennedy and Eberhart 1995; Shi and Eberhart 1998): these particles, which initially populate the whole design domain uniformly, converge to an optimum condition during the iteration process. In particular, the PSO procedure updates their position and velocity at each iteration; this allows identifying better combinations of the design values which minimises the objective function F. The iterative procedure ends when the variation of the objective function value does not exceed the prescribed function tolerance. The method was improved and modified by many authors: the version adopted in this work considers the modifications suggested by Mezura-Montes and Coello Coello (2011) and Pedersen (2010) which are implemented in the MATLAB function particleswarm. Finally, the parameters utilised in the analysis are: self- and social-adjustment correction factors $c_{1}=c_{2}=1.49$, inertia $W = 1.1$, swarm size $N=30$, function tolerance equal to $10^{-6}$, and maximum number of iterations equal to 1000 as suggested by the MATLAB built-in function.

2.3 Objective functions and constraints

Fig. 3

Optimisation framework - flowchart. The process is repeated until the convergence of the PSO algorithm

A schematic representation of the proposed optimisation methodology is depicted in Fig. 3: the figure shows how FE calculations, single-, and multi-objective functions are implemented in the framework. First, the starting values of the design variables, i.e. the initial particle positions, are defined by the PSO algorithm; these values are randomly determined and cover uniformly the design space. Then, the i-th particle position is passed to the optimisation framework and a non-linear inequality constraint is applied: it guarantees the creation of a non-broken mesh in the FE environment. The constraint is implemented through the definition of a penalty function as reported by the following equation:

$$\begin{aligned} F_{val} = \left\{ \begin{array}{cc} F({\mathbf {x}})&{} \quad \varphi \ge \frac{\pi }{2} \\ F({\mathbf {x}})&{} \quad h \le \frac{19}{40} b \tan (\varphi ) \quad \& \quad \varphi< \frac{\pi }{2} \\ 0 &{} \quad h > \frac{19}{40} b \tan (\varphi ) \quad \& \quad \varphi < \frac{\pi }{2} \end{array} \right. \end{aligned}$$

(1)

where:

• $F({\mathbf {x}})$ represents a generic objective function;

• ${\mathbf {x}}$ denotes the design variables vector as described in Table 1.

Afterwards, for each particle, the framework starts the FEA: firstly the FE model is created, and then modal and harmonic analyses are performed. The modal analysis allows identifying the first natural frequency of the VPEH; this permits locating a well-defined “frequency window” on which to perform the harmonic analysis, reducing the overall computational burden. It is worth noticing that the model is fully parametric, hence a change in the design variables results in reshaping the FE model and its mesh. The latter is defined so that the number of elements is kept constant for any possible system configuration inside the boundaries prescribed by Table 1. After the post-processing analysis, the framework computes three separate single-objective functions, $F_1({\mathbf {x}})$, $F_2({\mathbf {x}})$, and $F_3({\mathbf {x}})$, and combines them in the multi-objective function $F_4({\mathbf {x}})$. This procedure is repeated for each particle, improving its position at each iteration, as described in the PSO method (Kennedy and Eberhart 1995).

The first and second functions, $F_1({\mathbf {x}})$ and $F_2({\mathbf {x}})$, represent the maximum power and the frequency bandwidth at the half-power of the first resonance, respectively. Thus, they can be easily obtained from the power variation on frequency, which can be computed with the expression: $P = \frac{|V|^2}{2R}$. $F_3({\mathbf {x}})$, instead, represents the efficiency $\eta$ of the harvester at the first resonance. To evaluate the third objective function, the authors propose a novel matrix formulation of the efficiency. The definition is based on the energy balance principle, and it operates under the assumption of harmonic loading and steady-state conditions. Considering the Equations of Motion (EoM) of the electro-mechanical FE model (Ansys 2020; Allik and Hughes 1970):

$$\mathbf{M}\mathbf{\ddot{u}}+\mathbf{C}\mathbf{\dot{u}}+\mathbf{K}\mathbf{u} = \mathbf{Q}$$

(2)

the steady-state energy contributions per cycle $T_p = \frac{2 \pi }{\Omega }$ can be computed as follows:

$$\begin{aligned} \int_{0}^{T_{p}} \mathbf{\dot{u}}^{T}\mathbf{M}\mathbf{\ddot{u}} \, dt = -\frac{i \Omega^{2} \pi}{2}[\mathbf{U}^{T}\mathbf{M}\mathbf{\bar{U}} -\mathbf{\bar{U}}^{T}\mathbf{M}\mathbf{U}] \end{aligned}$$

(3a)

$$\begin{aligned} \int_{0}^{T_{p}} \mathbf{\dot{u}}^{T}\mathbf{K}\mathbf{u} \, dt = \frac{i \pi}{2} [\mathbf{U}^{T}\mathbf{K}\mathbf{\bar{U}}-\mathbf{\bar{U}}^{T}\mathbf{K}\mathbf{U}] \end{aligned}$$

(3b)

$$\begin{aligned} \int_{0}^{T_{p}} \mathbf{\dot{u}}^{T}\mathbf{C}\mathbf{\dot{u}} \, dt = \frac{\Omega \pi}{2} [\mathbf{U}^{T}\mathbf{C}\mathbf{\bar{U}}+\mathbf{\bar{U}}^{T}\mathbf{C}\mathbf{U}] \end{aligned}$$

(3c)

$$\begin{aligned} \int_{0}^{T_{p}} \mathbf{\dot{u}}^{T}\mathbf{Q} \, dt = \frac{i \pi}{2} [\mathbf{U}^{T}\mathbf{\bar{Q}}-\mathbf{\bar{U}}^{T}\mathbf{Q}] \end{aligned}$$

(3d)

where $\mathbf{M}$, $\mathbf{C}$, $\mathbf{K}$, and $\mathbf{Q}$ are respectively the generalised mass, damping, stiffness, and force matrices, $\mathbf{U}$ denotes the complex steady state solution of response $\mathbf{u}$, $T_p$ indicates the period and ${\bar{ {\bullet }}}$ symbolises the complex conjugated operator. FE software, like ANSYS, allows exporting the global matrices of their models, thus, these matrices can be easily implemented in the expressions of Eq.  3. However, the same global matrix could contain contributions coming from different physical aspects, e.g. the stiffness matrix $\mathbf{K}$ presents both piezoelectric and mechanical stiffness contributions. For the considered VPEH, the energy contributions coming from the viscous and electrical damping must be divided: the first one represents the energy lost in the harvesting process while the second one identifies the system energy output. Separating the structural and electrical components, the generalised damping matrix and load vector (Ansys 2020) of the VPEH become:

$$\begin{aligned} {\mathbf{C}} = \begin{bmatrix} { {\mathbf{C_{v}}}} &{} { {\mathbf{0}}}\\ { {\mathbf{0}}} &{} \mathbf{0} \end{bmatrix} + \begin{bmatrix} { {\mathbf{0}}} &{} { {\mathbf{0}}}\\ { {\mathbf{0}}} &{} -\mathbf{C_{vh}} \end{bmatrix} + \frac{1}{\Omega^{2}} \begin{bmatrix} { {\mathbf{0}}} &{} { {\mathbf{0}}}\\ { {\mathbf{0}}} &{} \mathbf{C_{r}} \end{bmatrix}\end{aligned}$$

(4a)

$$\begin{aligned} { {\mathbf{Q}}} = \begin{Bmatrix} { {\mathbf{0}}} \\ \mathbf{L_{a}} \\ \end{Bmatrix} + \begin{Bmatrix} \mathbf{Q_{a}} \\ { \mathbf{0}} \\ \end{Bmatrix} \end{aligned}$$

(4b)

where $\mathbf{C_{v}}$, $\mathbf{C_{vh}}$, and $\mathbf{C_{r}}$ denote the viscous, dielectric, and electric damping matrices while $\mathbf{Q_{a}}$ and $\mathbf{L_{a}}$ represent the structural and electrical load vectors. The efficiency can be computed by considering the input and output energy contributions: the first one is identified as the energy dissipated by the resistor, hence the energy contribution of $\mathbf{C_{r}}$, while the second one is represented by the energy associated to the external structural loads $\mathbf{Q_{a}}$. The final definition of efficiency can be written as:

$$\begin{aligned} \eta = \frac{1}{i \Omega }\frac{[\mathbf{ {U}}^{T} {\mathbf{C_{r}}^{*}}{\bar{ \mathbf{U}}}+{\bar{ \mathbf{U}}}^{T} {\mathbf{C_{r}}^{*}}{\mathbf{U}}]}{[{ \mathbf{U}}^{T}{\bar{\mathbf {Q}}_{\mathbf{a}}^{*}}-{\bar{ \mathbf{U}}}^{T} {\mathbf{Q_{a}}^{*}}]} \end{aligned}$$

(5)

where the matrices ${C_{r}^{*}}$ and ${Q_{a}^{*}}$ are:

$$\begin{aligned} {\mathbf{C_{r}}^{*}} = \begin{bmatrix} { \mathbf{0}} &{} { \mathbf{0}}\\ { \mathbf{0}} &{} \mathbf {C_{r}} \end{bmatrix} \end{aligned}$$

(6a)

$$\begin{aligned} {\mathbf{Q_{a}}^{*}} = \begin{Bmatrix} \mathbf{Q_{a}} \\ { \mathbf{0}} \\ \end{Bmatrix} \end{aligned}$$

(6b)

The matrix formulation of Eq. 5 represents an extension of previous definitions of efficiency: it can be used with MDOF and FE models of VEHs.

Finally, the multi-objective function $F_4(\mathbf{x})$ can be obtained with the following expression:

$$\begin{aligned} F_4({ \mathbf{x}})= w_{1}\frac{F_1({ \mathbf{x}})}{P_{opt}}+w_{2}\frac{F_2({ \mathbf{x}})}{\delta _{opt}}+w_{3}\frac{F_3({ \mathbf{x}})}{\eta _{opt}} \end{aligned}$$

(7)

where: w is the weighting factor while $P_{opt}$, $\eta _{opt}$, and $\delta _{opt}$ are, respectively, the optimum power, efficiency, and frequency bandwidth at the first resonance of the harvester. The first two values are obtained by optimising the single associated objective functions, while $\eta _{opt}$ is set equal to 1, as the maximum possible efficiency. Finally, it should be noted that the sum of $w_1$, $w_2$, and $w_3$ is set equal to 1. The authors want to stress the generality of the approach: indeed, both the optimisation framework and the efficiency formulation can be applied to any externally excited VEH.

2.4 Efficiency: comparison with previous definitions

The formulation of efficiency here proposed is based on the computation of the energy contributions per cycle. Such contributions are now compared to the existing definitions suggested by Yang et al. (2017). A mechanical single degree of freedom energy harvester is considered to carry out the comparison; for more detail about the system, the reader should refer to Yang et al. (2017). To proceed with the comparison, the input and output energies per cycle $T_p = \frac{2 \pi }{2 \Omega }$ are considered. The authors defined the input energy with the following expression:

$$\begin{aligned} E_{in,1} = \frac{1}{2}\frac{\pi }{\Omega }m|{\ddot{Z}}||{\dot{Y}}| \sin {\phi _{z}} \end{aligned}$$

(8)

while the output energy is described by the equation:

$$\begin{aligned} E_{out,1} = \frac{\pi }{\Omega }\frac{V_{RMS}^2}{R} = \frac{\pi |V|^2}{2 \Omega R} \end{aligned}$$

(9)

where Z and Y represent the complex amplitude of relative and base displacements of the VPEHs, m indicates the tip mass, $\phi _z$ is the phase of the relative coordinate, and the subscript $\bullet _1$ denotes that the definitions belong to the above-mentioned work of Yang et al. (2017). Through mathematical manipulation, Equation 8 becomes:

$$\begin{aligned} E_{in,1} = \frac{\pi }{2} m |{\ddot{Y}}| \Im {(Z)} \end{aligned}$$

(10)

when ${\ddot{Z}} = -\Omega ^2 Z$ and a real ¹ constant acceleration ${\ddot{Y}}$ is applied to the system.

The equation of motion of the system can be rewritten in matrix form:

$$\begin{aligned} \begin{bmatrix} m &{} 0 \\ 0 &{} 0 \end{bmatrix} \begin{Bmatrix} \ddot{z}\\ {\ddot{V}} \end{Bmatrix} + \begin{bmatrix} c &{} 0 \\ -\alpha &{} C_{0} \end{bmatrix} \begin{Bmatrix} {\dot{z}}\\ {\dot{V}} \end{Bmatrix} + \begin{bmatrix} k &{} \alpha \\ 0 &{} \frac{1}{R} \end{bmatrix} \begin{Bmatrix} z \\ V \end{Bmatrix} = \begin{Bmatrix} -m{\ddot{Y}} \\ 0 \end{Bmatrix} \end{aligned}$$

(11)

where $\alpha$, $C_0$, c, and k denote respectively, the force factor, the clamped capacitance, the damping, and the stiffness of the VPEH.

To identify the matrix which represents the power output of the system, the same reasoning adopted in Sect. 2.3 can be now applied. From Eq.  11 it is clear that the effect of the resistance is only contained in the stiffness matrix, hence, it must be used to compute the energy output per cycle of the considered harvester. The energy input per cycle, instead, is unequivocally described by the load vector. Therefore, Eq. 5 can be adjusted by accounting for Eq. 3b and 3d, and the energy contributions over one cycle $Tp = \frac{2 \pi }{2 \Omega }$ can be defined in matrix form as:

$$\begin{aligned} {E_{in,2} = \frac{i \pi }{4} [{ \mathbf{U}}^{T}{\bar{ \mathbf{Q}}}-{\bar{\mathbf {U}}}^{T}{\mathbf {Q}}]} \end{aligned}$$

(12a)

$$\begin{aligned} {E_{out,2} = \frac{i \pi }{4} [{\mathbf {U}}^{T}{ \mathbf{K}}{\bar{ \mathbf{U}}}-{\bar{ \mathbf{U}}}^{T}{ \mathbf{K}}{\mathbf {U}}]} \end{aligned}$$

(12b)

where the subscript $\bullet _2$ represents the definition of the energy contributions belonging to this work. By identifying the matrices through the analogy between Eq. 11 and Eq. 2, and applying a real constant acceleration ${\ddot{Y}}$, it is possible to achieve the following representation of the energy input:

$$\begin{aligned} E_{in,2} = i \frac{\pi }{4} m |{\ddot{Y}}| ({\bar{Z}}-Z) = \frac{\pi }{2} m |{\ddot{Y}}| \Im {(Z)} \end{aligned}$$

(13)

On the other hand, the energy output can be revised by considering the matrix multiplication:

$$\begin{aligned} {E_{out,2} = i \frac{\pi }{4} \alpha \left( Z {\bar{V}} - {\bar{Z}} V\right) } \end{aligned}$$

(14)

Solving Eq. 11 at the steady-state condition for a sinusoidal input excitation, the following expression of complex relative displacement Z can be obtained:

$$\begin{aligned} Z = \frac{1}{\alpha } \left( C_p - i\frac{1}{R \Omega }\right) V \end{aligned}$$

(15)

By substituting Eq. 15 in Eq. 14, it is possible to obtain:

$$\begin{aligned} E_{out,2} = \frac{\pi |V|^2}{2 \Omega R} \end{aligned}$$

(16)

Eq. 13 and Eq. 16 represent the energy contributions which are used for the computation the efficiency. Such energy contributions are exactly equal to the ones provided by Yang et al. (2017) (see Eqs. 8 and 9). This demonstrates that the proposed matrix formulation of efficiency represents an extension of previous definitions available in the literature.

3 Framework validation

In this section, the proposed optimisation framework is analytically validated. The validation aims to demonstrate that, for a generic VEH, the framework optimal solution coincides with the analytical one.

Although Erturk and Inman (2008b) demonstrated that the piezoelectric effect cannot be accurately modelled as viscous damping, the simplest model of VEH can be represented with an additional damper, as shown in Fig. 4. This model can be advantageously reproduced, both analytically and in FE environment, without introducing consistent approximation differences between the two representations, thus it is adopted for the validation procedure. The model is constituted by a base excited cantilevered beam with length L, width B, and thickness H. Two parallel dampers are applied to the beam tip: one represents the viscous dissipation effect caused by the structure, while the other one simulates the presence of a generic transducer.

Its equation of motion can be analytically described under the Euler-Bernoulli beam assumption considering the vertical displacement q(z, t) as the sum of the base $q_{b}(t)$ and relative $q_{rel}(z,t)$ displacements, and the dampers external force $f(z,t) = -(c_{m}+c_{e}) {\dot{q}}(z,t) \delta _{D}(z-L)$ applied on the tip. The resulting expression is described by Eq. 17, where $\mu$ is the density per unit length, E identifies the elastic modulus, $I=(H^3B)/12$ is the area moment of inertia, $c_m$ and $c_e$ represent the mechanical and equivalent electrical damping coefficients, and $\delta _{D}(z)$ denotes the Delta Dirac function.

$$\begin{aligned} \mu \frac{\partial ^{2} q_{rel}(z,t)}{\partial t^{2}} + (c_m+c_e)\frac{\partial q_{rel}(z,t)}{\partial t} \delta _{D}(z-L)+ E I \frac{\partial ^{4} q_{rel}(z,t)}{\partial z^{4}} = - \mu \frac{\partial ^{2} q_{b}(z,t)}{\partial t^{2}} - (c_m+c_e)\frac{\partial q_{b}(z,t)}{\partial t} \delta _{D}(z-L) \end{aligned}$$

(17)

Fig. 4

Simplified model of cantilevered VEH

By applying the expansion theorem, the eigenfunctions orthogonality property, and a harmonic excitation $q_{b}(t) = Q_{b,0} e^{i\Omega t}$, it is possible to obtain the system steady-state response:

$$\begin{aligned} Q_{rel,0}(z) = \sum _{r=1}^{n}\frac{Q_{b,0}(\frac{\nu _r}{\psi _r}\Omega ^2-i\Omega \frac{c_m+c_e}{\psi _r \mu }\phi _r(L))}{\omega _r^2-\Omega ^2+i2\zeta _r\omega _r\Omega } \phi _r(z) \end{aligned}$$

(18)

where $Q_{rel,0}$ is the harmonic complex relative displacement, $\Omega$ is the external forcing frequency, and n is the total number of modes considered. Additional terms and expressions, here not described, are reported in Appendix A for completeness.

The objective function considered for the optimisation process is the power output of the electrical damper, and the design variable is represented by its damping coefficient $c_e$. Analytically, it can be represented as:

$$\begin{aligned} P(c_e) = \frac{c_e \Omega ^2 |Q_{abs,0}|^2}{2} \end{aligned}$$

(19)

where, $Q_{abs,0}=Q_{rel,0}+Q_{b,0}$. Using the analytical expression of Eq. 18 and considering only the first modal contribution, it is possible to derive a closed-form expression for the optimum value of the electrical damping. This assumption holds if the system first mode is excited, thus, an excitation frequency equal to the first natural frequency, $\Omega = \omega _1$, is used. Under these conditions, the optimum electrical damping for the analytical model becomes: $c_{e_{opt}} = c_{m}$. The analytical derivation of the optimum value $c_{e_{opt}}$ and the numerical data adopted in the analysis are fully described in Appendix A.

Finally, an equivalent FE model is developed in ANSYS by using BEAM3 elements to model the beam, and COMBIN14 elements to model the equivalent electrical and mechanical dampers. The same objective function, i.e. the electrical damper power output, is optimised utilising the optimisation framework and the FE model, with parameter bounds $c_e = [0;1]$ Ns/m and no constraints.

Fig. 5

Electric power output of the analytical and FE models for $\Omega = \omega _1$

Figure 5 compares the trends of the electrical power output for the FE and analytical models. The dashed-dotted vertical line graphically represents the optimal condition identified by the optimisation framework for the FE model, which numerically corresponds to 0.5021 Ns/m. This value is very close to the analytical counterpart, which is exactly 0.5 Ns/m. Thus, having an error of only $0.4\%$, the optimisation framework can be considered validated.

4 Results and discussion

The methodology described in Sect. 2 is adopted to optimise the planar-shaped VPEH. A constant acceleration of 0.2 g is utilised to excite the system. First, the single objective functions $F_{1}({ \mathbf{x}})$, $F_{2}({\mathbf {x}})$, and $F_{3}({\mathbf {x}})$ are maximised separately: this step is necessary to identify the optimal design conditions for the sensitivity analysis and to determine the values $P_{opt}$ and $\delta _{opt}$ adopted in Eq. 7. Then, the multi-objective function $F_{4}({\mathbf {x}})$ is optimised by setting the weighting factors $w_{1}$, $w_{2}$, and $w_{3}$ equal to 1/3.

Fig. 6

Optimal designs of the VPEH: a optimum power output $F_1({\mathbf {x}})$, b optimum frequency bandwidth $F_2({\mathbf {x}})$, and c optimum multi-objective function $F_4({\mathbf {x}})$

Table 2 Optimal design variables and function value for the objective functions $F_{1}({\mathbf {x}})$, $F_{2}({\mathbf {x}})$, $F_{3}({\mathbf {x}})$, and $F_{4}({\mathbf {x}})$

Fig. 7

Sensitivity analysis of parameters for the first $F_1(\mathbf{x})$ and second $F_2(\mathbf{x})$ objective function around the optimum conditions. The dashed line denotes the application of a non-linear constraint which prevents the computation of the objective function

Figure 6 and Table 2 describe the results of the optimisation process. As shown in the figure, the adoption of different objective functions produces dissimilar shapes: the optimisation of $F_1({\mathbf {x}})$ generates a perpendicular and large VPEH while the optimisation of the $F_2({\mathbf {x}})$ originates a thick, tiny, and very inclined harvester. $F_3({\mathbf {x}})$ and $F_4({\mathbf {x}})$ produce similar results, and in comparison with the previous cases, larger width and smaller inclination angles are achieved. The multi-objective function tries to obtain a harvester which maintains all the good properties of the previously presented optimal designs: it reveals a change of $-89\%$ in power output, $+79\%$ in frequency bandwidth, and $+2711\%$ in the efficiency with respect to the starting configuration $P_{0}$. This shows two important results: firstly the multi-objective function is dominated by efficiency and secondly the optimisations of efficiency $F_3({\mathbf {x}})$ and power output $F_1({\mathbf {x}})$ lead to completely different optimal conditions. The first result has important implications in studies of optimal design: in fact, engineering applications of VPEHs need to know which are the driving factors of similar multi-objective optimisation. The second one, instead, demonstrates that not only the optimal electrical conditions (Kim et al. 2015) but also the optimal structural conditions for the maximisation of efficiency are very dissimilar from the ones necessary to optimise the maximum power output of the harvester.

In order to better understand the effect of the design parameters on the harvester performance, sensitivity analyses of $F_{1}({\mathbf {x}})$, $F_{2}({\mathbf {x}})$, and $F_{3}({\mathbf {x}})$ are carried out around their optimal design conditions. The results are graphically reported in Figs. 7 and 8.

From the inspection of Fig. 7, it is clear that the power output is maximised when the harvester structural dimensions are enlarged.

Fig. 8

Sensitivity analysis of parameters for the third $F_3(\mathbf{x})$ objective function around the optimum conditions

Indeed, $F_1({\mathbf {x}})$ is influenced by three main factors: the area of piezoelectric material, the system structural response, and the resistance. The former, according to the fundamental constitutive equations, is proportional to the power output, thus, h, b, and $\varphi$ are increased as much as possible in the optimisation procedure. Moreover, $\varphi$ intensifies the equivalent tip mass of the harvester, thus, larger stress and higher power output are produced when this parameter is magnified. The thicknesses follow a different path: when $t_{p}$ is reduced, the stress in the piezoelectric material is maximised, while, when t is increased, the tip mass effect, hence the power output, is enhanced. Therefore, the optimisation process returns a high value of t and a low value of $t_p$ to improve the function $F_1({\mathbf {x}})$. On the other hand, the angle $\theta$ affects the system structural response: the more the harvester is inclined, the more the axial modes influence its dynamics. This increases its first resonant frequency, lowering the power peak and raising the half-power frequency bandwidth. It is worth noticing that the polarisation of the piezoelectric patch is directed along its thickness (mode 3-1). This makes the system capable of extracting more energy when the material is stressed with bending deformation: such condition is maximised at $\theta = 90^{\circ }$ as well as the optimisation procedure returned. Finally, the resistance R controls the power output according to the expression $\frac{|V|^2}{2R}$: two extreme conditions, named open- and short-circuit conditions, exist. The first one is obtained when $R \rightarrow \infty$: in this case, the equivalent electrical circuit is open and no power is produced. The second one occurs when $R \rightarrow 0$: here, no voltage drop is produced across the resistance, thus, no power output is generated. Hence, for the function $F_1({\mathbf {x}})$, the optimum is achieved between these two conditions, particularly at $R = 2323$ $\Omega$.

The sensitivity analysis of the single-objective function $F_2(x)$ shows similar results: here, the optimisation tends to reduce the dimensions of the harvester, so h, b, and $\varphi$ are pushed against the lower bounds while the thicknesses t, and $t_{p}$ are maximised. Such a condition corresponds to the most rigid configuration of the harvester and allows for a boost of the associated frequency bandwidth. Once again, the parameter $\theta$ affects the system dynamics: the more the harvester is inclined, the higher the associated frequency bandwidth is. Therefore, the angle $\theta$ is curbed as much as possible in the optimisation procedure to maximise $F_2(\mathbf{x})$. Finally, the resistance R shows the same effects as before: it allows us to find the optimal condition for the power output between two extremes, maximising the frequency bandwidth for $R =2148$ $\Omega$.

Finally, Figure 8 describes the effect of the harvester parameters on the single-objective function $F_3({\mathbf {x}})$. The electrical parameter R exhibits a strong effect on the function, with the optimum condition identified at $R = 1078$ $\Omega$. The geometric parameters, instead, show a weaker effect than the electrical one: particularly, the angle $\theta$ has almost no effect on the efficiency. This agrees with its physical interpretation: in fact, the more the system is inclined, the less energy is harvested, but, at the same time, also less mechanical energy is transferred to the harvester, making the balance of the two quantities equal to zero. The other geometrical parameters reveal little effect on $F_3({\mathbf {x}})$: between them, only the angle $\varphi$ shows a steep reduction when it is increased over $90^{\circ }$ ($\approx 0.7$ in relative scale). This is due to the change in the piezoelectric and structural material area: indeed, by increasing the angle $\varphi$, the equivalent harvester tip mass and piezoelectric material area are increased. In the efficiency context, the first one means higher input energy, while the second one indicates higher output energy. When $\varphi$ is lower than $90^{\circ }$, an increase of the angle has a favourable net balance on the output energy side, thus the efficiency is increased. This trend is inverted when the angle reaches the value of about $90^{\circ }$ and explains the inversion of the trend reported in Fig. 8.

5 Conclusions

In this paper, a multi-objective optimisation framework is presented for the optimal design of VEH with complex geometries. The proposed framework optimises the maximum power output, frequency bandwidth, and efficiency of the harvester at the same time. For this purpose, a novel matrix formulation of the efficiency that can be applied to finite element models is derived, and its capabilities are numerically tested. In addition, it is mathematically demonstrated that the proposed definition of efficiency represents an extension of the existing definitions found in the literature.

The capabilities of the framework are assessed considering a planar-shape VPEH in conjunction with FEA. The study shows that the optimal design of VPEHs is strongly affected by the definition of the objective function. The numerical results also demonstrate that the proposed multi-objective function is dominated by efficiency: in fact, efficiency has a stronger effect on the multi-objective function when compared to the other performance indexes. In other words, the optimal geometry obtained by optimising only the efficiency is very similar to the multi-objective optimisation results. It is worth mentioning that, the optimisations of power output and efficiency separately, instead, produce profoundly different geometries. Finally, the sensitivity analysis suggests that all the structural parameters strongly affect the proposed objective functions, except $\theta$ which does not affect the efficiency because it has a similar influence on the input and output power. In conclusion, this analysis clearly demonstrates that the proposed framework can be used to obtain optimal designs for VPEH with complex geometries.

Appendices

Appendices

A- Validation Process

The eigenfunction associated with the problem boundary conditions described in Sect. 3 for the r-th mode is:

$$\begin{aligned}&\phi_r(z) = \sinh (\beta _{r}z) - \sin (\beta _{r}z) + \sigma _r (\cos (\beta _{r}z) - \cosh (\beta _{r}z)) \end{aligned}$$

(A.1)

where the eigenvalues $\beta _r$ can be obtained from the characteristic equation:

$$\begin{aligned} \cos (\beta _r z)\cosh (\beta _r z)-1=0 \end{aligned}$$

(A.2)

Consider the Eq. A.1, the terms $\sigma _r$ and $\beta _r$ can be represented as follows:

$$\begin{aligned} \sigma _r= & {} \frac{\sin (\beta _{r}L)+\sinh (\beta _{r}L)}{\cos (\beta _{r}L)+\cosh (\beta _{r}L)} \end{aligned}$$

(A.3)

$$\begin{aligned} \beta _r= & {} \left( \frac{\mu \omega _r^2}{E I} \right) ^\frac{1}{4} \end{aligned}$$

(A.4)

Where $\omega _r$ is the r-th natural frequency of the system. Then, the steady state solution described by Eq. 18, can be computed by considering the following term:

$$\begin{aligned} \zeta _r = \frac{(c_m+c_e)\phi _{r}^{2}(L)}{2 \omega _r \psi _r \mu } \end{aligned}$$

(A.5)

Where $\psi _r$ and $\nu _r$ are obtained from the integration and the application of the orthogonality property:

$$\begin{aligned} \psi _r= & {} \int _{0}^{L}\phi _{r}^2(z) dz \end{aligned}$$

(A.6)

$$\begin{aligned} \nu _r= & {} \int _{0}^{L}\phi _{r}(z) dz \end{aligned}$$

(A.7)

By considering Eqs. 18 and 19 and looking for the maximum of power, it is possible to obtain a general expression of the optimum damping coefficient as a function of $\Omega$:

$$\begin{aligned} c_{e}(\Omega ) = \frac{\sqrt{\Omega ^4\mu ^2\psi _1^2+\Omega ^2c_m^2\phi _1^4-2\Omega ^2\mu ^2\omega _1^2\psi _1^2+\mu ^2\omega _1^4\psi _1^2}}{\Omega \phi _1^2} \end{aligned}$$

(A.8)

where, $\psi _1$, $\phi _1$, $\omega _1$ have been computed considering the first mode and $z=L$. Finally, for $\Omega = \omega _1$, the optimum electrical damping coefficient becomes $c_{e_{opt}} = c_m$.

The numerical values adopted for the analysis are: H = 2 mm, B = 20 mm, L = 100 mm, E = 210 MPa, $c_m$ = 0.5 Ns/m, and $\mu$ = 0.3120 kg/m, and $Q_{b,0}$ = 1 mm.