Nonlinear size-dependent modeling and dynamics of nanocrystalline arc resonators

Abstract

The adequate modeling of the micro/nano arc resonators' dynamics is vital for their successful implementation. Here, a size-dependent model, wherein material structure, porosity, and micro-rotation effects of the grains are considered, is derived by combining the couple stress theory, multi-phase model, and the classical Euler–Bernoulli beam model, aiming to characterize the frequency tunability of micro/nano arc resonators as monitoring either the axial load or the electrostatic force for the first time. The arc dimensions are optimized to show various phenomena in the same arc, namely snap-through, crossing, and veering. The first three natural frequencies are monitored, showing the size dependency on the frequency tuning, snap-through/back, and pull-in instability as shrinking the scale from micro- to nano-scale. Significant changes in the static snap-through and pull-in voltages and the resonance frequencies were shown as scale shrinks. A dynamic analysis of the resonator's vibration shows a dramatic effect of the size-dependency as shrinking dimensions around the veering zone.

1 Introduction

Micro and nanoelectromechanical systems (MEMS/NEMS) have drawn significant attention in recent decades thanks to their high sensitivity, small size, and low power consumption. Dynamics of micro/nanoresonators, linear and nonlinear, have been studied theoretically and experimentally in the literature showing their potential exploitation for several applications (Raman et al. 2008; Kenig et al. 2009; Tamayo et al. 2013; Asadi et al. 2018; Hajjaj et al. 2019c). More specifically, bistable MEMS/NEMS resonators have extensively been used in numerous potential applications, like sensing (Zhao et al. 2018; Hajjaj et al. 2019c), filtering (Hafiz et al. 2017), logic devices (Hafiz et al. 2016), signal processing (Nguyen 2007), and energy harvesting (Ando et al. 2012). Bistable resonators could be realized in different configurations, including the buckled beams (Lacarbonara et al. 1998; Hajjaj et al. 2016; Fu et al. 2019; Erbil et al. 2020) and the intentionally fabricated curved beams (shallow arch beams) (Hajjaj et al. 2015; Tella et al. 2017; Ouakad and Najar 2019). Initially curved resonators were among the more investigated and exploited structures in the literature due to their rich and complex static and dynamic behavior (Tajaddodianfar et al. 2015a; Alcheikh et al. 2017; Hajjaj et al. 2017b; Alneamy et al. 2020).

These bistable structures' main characteristic is the double-well potential known by two stable positions. A third unstable state encounters the two local stable positions recognized as snap-through motion. This could be static or dynamic and was studied deeply in the literature for the case of initially buckled resonators (arches) electrostatically actuated (Zhang et al. 2007; Das and Batra 2009; Ouakad and Younis 2014). Studies showed that an electrostatically actuated arch beam could exhibit snap-through motion under specific actuation and geometric conditions. Ouakad et al. (Ouakad et al. 2009) investigated the occurring of the snap-through bifurcation on an initially curved beam electrostatically actuated. The initial rise, thickness, and transduction gaps are the main influencing parameters for the occurring of the snap-through motion. To examine the static snap-through and pull-in bifurcations for MEMS arch resonators under electrostatic force, several studies developed reduced-order models based on Galerkin discretization (Ouakad et al. 2009; Farokhi et al. 2016; Hajjaj et al. 2017a). Snap-through motion was recently proposed in different potential applications, like energy harvesting, filtering, and sensing (Ouakad and Younis 2014; Zhang et al. 2018b). Initially curved beam also showed a high tunability with a static DC electrostatic force (Ouakad et al. 2009; Tajaddodianfar et al. 2015a). For arches exhibiting snap-through bifurcations, the frequencies' tunability is dominated by the quadratic nonlinearity before snap-through (from arch shape and the electrostatic force). In contrast, the frequencies' tunability is dominated after snap-through by cubic nonlinearity (from the midplane stretching).

High tunability of the resonant frequencies with axial load is another attractive feature of initially curved resonators (Hajjaj et al. 2015, 2017a). The initial rise is demonstrated to hugely affect the tunability behavior of different frequencies of the arch beam. Hajjaj et al. (2017a) showed experimentally and theoretically the different tunability shapes as changing the beam geometry as tuning its axial load. Indeed, altering the axial load (leading to changing the arch curvature) could monitor the coupling among different vibration modes. The coupling could be linear (e.g., mode localization and veering) and nonlinear (mainly internal resonance). Particularly, the phenomenon of frequency veering has been deeply studied in the classical structural dynamic and have been reported in cable–spring system (Cheng and Perkins 1992), plates (Leissa 1974), curved beams (Petyt and Fleischer 1971), sagged cables (Rega 2012), carbon nanotubes (Ouakad and Younis 2011), and curved cylinders (Dawe 1974). Veering is characterizing by two frequencies deviating with high curvature after approaching as tuning a control parameter. Veering, occurring among symmetric and/or antisymmetric modes, is characterized by mode hybridization where both involved modes are influenced by the shape of each other. At the macro-scale, Lacarbonara et al. (Lacarbonara et al. 2005) investigated the veering phenomena numerically by introducing imperfection to the initially curved beam by considering linear and torsional springs at the boundaries. In MEMS and NEMS, the veering phenomenon was associated mostly with the mode-localization phenomenon arising in weakly coupled systems (Wang et al. 2012; Erbes et al. 2014). Most recent, veering for internally coupled modes in micromachined systems was reported for arc and V-shaped resonators with high stiffness tuning (Hajjaj et al. 2017a, b; Alcheikh et al. 2020; Ouakad et al. 2021). Hajjaj et al. (2017a) examined theoretically and experimentally the veering of arc MEMS resonators. The dynamic around the veering zone was demonstrated good capabilities to build tunable bandpass filters (Hajjaj et al. 2017b). V-shaped MEMS resonators were recently shown to demonstrate veering and crossover phenomena as tuning their axial stress (Alcheikh et al. 2020; Ouakad et al. 2021). One should mention that the veering phenomenon was also investigated for slightly curved double clamped CNTs (Sazonova et al. 2004; Ouakad and Younis 2011). More recently, Hajjaj and co-authors (Ramini et al. 2016a; Hajjaj et al. 2017a, b; Alcheikh et al. 2019) investigated the veering phenomenon experimentally and theoretically in the case of MEMS arc resonators electrostatically actuated and electrothermally tuned and demonstrated it in sensing and filtering applications. Tuning the axial load of arch resonators leads to the monitoring of the ratio between different vibration modes. A commensurate ratio between different participating modes is necessary for nonlinear energy transfer from the actuated mode to a new participating mode, known as internal resonance. Hence, different internal resonances were deeply studied numerically and experimentally as tuning the ratio between different modes (Hajjaj et al. 2018a, 2019a; Alfosail et al. 2019). The multiple scales techniques were numerically and widely used to characterize the different instability regions during the nonlinear interaction (Alfosail et al. 2019; Hajjaj et al. 2019b). Internal resonance was used recently in various potential applications, like sensing (Hacker and Gottlieb 2012; Zhang et al. 2018a; Xia et al. 2020), synchronization (Pu et al. 2018), and communication (Antonio et al. 2012; Hajjaj et al. 2018b).

The various dynamic phenomena of crossing, veering, snap-through, and static pull-in of MEMS/NEMS curved resonators have mostly been investigated theoretically based on the classical theories of continuum mechanics. This raises many questions about the reliability of this approach to model the behaviors of these resonators accurately at smaller scales. Indeed, designing mechanical systems at the nano-scale results in the presence of significant effects due to the size dependency and material structure [35], in addition to other effects including surface elasticity (Larkin et al. 2020), surface roughness (Nikpourian et al. 2019; Rojas et al. 2020), and van der Waals forces (Esfahani et al. 2019a; Nikpourian et al. 2019).

Shrinking mechanical systems to smaller scales results in the limitations of classical continuum mechanics theories owing to the assumption of the point mass representation of small particles to represent the system. These tiny particles should be represented as nano-volume elements, and hence several degrees of freedom should be considered. To this end, nano-systems are generally dependent on the material size. As a result, many nonclassical continuum mechanics theories, like strain gradient theory, nonlocal elasticity theory, and couple stress theory (Yang et al. 2008; Wang et al. 2011; Baghani 2012; Shaat and Abdelkefi 2015, 2017; Shaat et al. 2016; Ghommem and Abdelkefi 2017) were developed and exploited to intensively investigate the mechanics and dynamics of various MEMS and NEMS devices. In addition to the material size effect due to the small size of the system, the material structure should be considered due to the heterogeneous nature of structures composed of nanomaterials (Shaat and Abdelkefi 2015, 2016). Indeed, micro-/nano-systems are generally made of nanostructured materials, which are known for their ultra-small heterogeneity sizes and their ultra-high interface areas (Zhang et al. 2010). For instance, the interface to the grain ratio for nanocrystalline materials becomes significant, and hence the material cannot be represented as a single entity due to the difference in the material properties of the grain and interface and the possible presence of porosity (Gleiter 2000). To consider the material structure and size effects in this study, the multi-phase model and couple stress theory will be implemented based on the strategy proposed in (Shaat and Abdelkefi 2017). One should mention that few new models were developed recently to examine the static and dynamic behavior of the MEMS/NEMS resonators electrostatically actuated, accounting for fringing, viscoelastic, and size effects (Rahaeifard et al. 2012; Belardinelli et al. 2014; Farokhi and Ghayesh 2017; Farokhi et al. 2017, 2018; Ghayesh and Farokhi 2017; Esfahani et al. 2019b). Belardinelli et al. (2014) exploited the strain-gradient theory to examine the response of the fixed–fixed microbeam. Rahaeifard et al. (2012) evaluated the size-dependent deflection and the pull-in using the modified couple stress theory. Farokhi et al. (2017) developed a new electrostatic model to analyze the pull-in characteristics and nonlinear behavior of initially curved CNT based on 3D finite element analysis.

In previous works, curved resonators have been profoundly studied in the macro- and micro-scale. However, few studies have been done analytically and experimentally into arch resonators in the nano-scale (Ouakad and Younis 2011; Tajaddodianfar et al. 2015b, 2016; Kazmi et al. 2017). Kazmi et al. (Kazmi et al. 2017) studied NESS curved resonators' tunability electrostatically actuated with different arch dimensions. Tadajaddofier et al. (Tajaddodianfar et al. 2015b, 2016) investigated numerical approaches the investigate the dynamic of nano-resonators and the numerical prediction of chaos behavior. In this work, the aim is to analytically study the effects of shrinking the arc resonator from micro- to nano-scale as well as to characterize their frequency tunability and nonlinear behaviors. The micro/nano arc dimensions are optimized to be able to show several phenomena in the same arc: crossing, veering, and snap-through. Also, new models have to be developed considering the material size effects. For the first time, the size-dependency will be investigated for arc resonators and their static and dynamic behaviors as tuning either the applied electrostatic force and/or the axial compressive load. The size dependency will also be investigated on the dynamic response of the arc resonator as experiencing linear coupling via veering phenomenon and nonlinear coupling via internal resonance phenomenon.

2 System's modeling

2.1 Size-dependent governing equations and boundary conditions

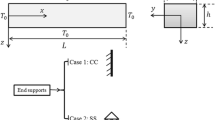
The structure under consideration consists of an initially curved fixed–fixed arc beam made of nanocrystalline silicon, as shown in Fig. 1. This curved beam is actuated with a half electrode configuration, allowing the activation of both symmetric and antisymmetric modes. The stationary electrode and the arc beam are separated with a gap of width d at the clamping ends. The arc beam is driven electrostatically by a DC bias voltage V_DC, an AC harmonic voltage of amplitude V_AC, and a frequency $\widehat{\Omega }$.

Fig. 1

Schematic of a fixed–fixed arc resonator with half-electrode configuration

The original shape ${\widehat{w}}_{a,0}(\widehat{x})$ of the fixed–fixed arc beam is governed by Eq. (1) as follows:

$$\hat{w}_{a,0} \left( {\hat{x}} \right) = \left( {\hat{b}_{0} - R_{a} + \sqrt {R_{a}^{2} - \left( {\hat{x} - \frac{L}{2}} \right)^{2} } } \right)$$

(1)

where $\widehat{x}$ denotes the position along the beam length, R_a represents the arc radius, ${\widehat{b}}_{0}$ is the arc midpoint rise, h is the arc thickness, and L represents its length. The arch beam, with a width b and a moment of inertia I, has a rectangular crosssection $A=bh$. The arc beam specifications for MEMS, MEMS/NEMS, and NEMS devices are provided in Table 1.

Table 1 Arc resonator geometrical properties at MEMS, MEMS/NEMS, and NEMS scales

Consider an Euler–Bernoulli beam with an initial curvature under axial load $\widehat{N}$, and electrostatic force, and undergoing a transverse displacement ${\widehat{w}}_{a}(\widehat{x}, \widehat{t})$. One should note that the transverse vibration is defined with respect to the initial curved shape. The initially curved beam theory concurs with the theory of shallow arches based on the following assumptions: the shear deformation, longitudinal inertia, and rotary inertia are negligible. To derive the equation of motion governing the transverse vibration of the arc beam, the extended Hamilton's principle is employed:

$$\mathop \smallint \limits_{{t_{0} }}^{{t_{1} }} \left( {\delta T - \delta U + \delta W_{NC} } \right)d\hat{t} = 0$$

(2)

where T, U, and W_NC refer to the kinetic energy, the potential energy, and the virtual work of the nonconservative forces (damping and electrostatic forces).

The alteration of the kinetic energy is given as:

$$\delta T = \rho A\mathop \smallint \limits_{0}^{L} \left( {v_{{\hat{t}}} \delta v_{{\hat{t}}} + \hat{w}_{{a,\hat{t}}} \delta \hat{w}_{{a,\hat{t}}} } \right)d\hat{x}$$

(3)

where $v(\widehat{x}, \widehat{t})$ represents the axial displacement, and ρ is the mass density.

Considering classical couple stress theory, the alteration of the potential energy (restoring energy) is written as (Shaat and Abdelkefi 2017):

$$\delta U = \mathop \smallint \limits_{V}^{c} \left( {\sigma \delta \varepsilon + \mu_{xy} \delta R_{yx} } \right)dV + \hat{N} \delta v\left( {L,\hat{t}} \right)$$

(4)

In Eq. (4), $\varepsilon$ represents the axial strain accounting for the axial strain of the centerline of the beam and the curvature of the arc midplane. $\sigma$ denotes the bulk stress defines as (Shaat and Abdelkefi 2017):

$$\sigma = \frac{{2\mu \left( {1 - \nu } \right)}}{1 - 2\nu }\varepsilon$$

(5)

In Eq. (5), ν denotes Poisson ratio while µ represents the shear modulus. ${\mu }_{xy}$ denotes the couple stress defined as ${\mu }_{xy}=\mu {l}^{2}\frac{{\partial }^{2}{\widehat{w}}_{a}}{\partial {\widehat{x}}^{2}}$, and ${R}_{yx}$ represents the rotation gradient defined as ${R}_{yx}=-\frac{{\partial }^{2}{\widehat{w}}_{a}}{\partial {\widehat{x}}^{2}}$. l denotes the couple stress parameter (Shaat and Abdelkefi 2017). More details about the derivation of the additional stiffness due to the couple stress theory and description of the multi-phase modeling to determine the nanocrystalline silicon effective material properties can be found in (Shaat and Abdelkefi 2017).

Following the same strategy proposed in (Hajjaj et al. 2017a, 2019a, b), the equation of motion governing the transverse vibration of the fixed–fixed arc beam, ${\widehat{w}}_{a}(\widehat{x},\widehat{t})$, can be expressed as:

$$\begin{gathered} \rho bh\frac{{\partial^{2} \hat{w}_{a} }}{{\partial \hat{t}^{2} }} + D\frac{{\partial^{4} \hat{w}_{a} }}{{\partial \hat{x}^{4} }} + \hat{c}\frac{{\partial \hat{w}_{a} }}{{\partial \hat{t}}} = \left\{ {\left( {\frac{{\partial^{2} \hat{w}_{a} }}{{\partial \hat{x}^{2} }} + \frac{{d^{2} \hat{w}_{a,0} }}{{d\hat{x}^{2} }}} \right) \times \left[ {\hat{N} + \frac{DA}{{2{ }L{ }I}}\mathop \smallint \limits_{0}^{L} \left( {\left( {\frac{{\partial \hat{w}_{a} }}{{\partial \hat{x}}}} \right)^{2} + 2\frac{{\partial \hat{w}_{a} }}{{\partial \hat{x}}}\frac{{d\hat{w}_{a,0} }}{{d\hat{x}}}} \right)d\hat{x}} \right]} \right\} \hfill \\ + \frac{1}{2}\epsilon b\frac{{\left( {V_{DC} + V_{AC} \cos (\hat{\Omega }\hat{t}} \right))^{2} }}{{\left( {d - \hat{w}_{a} - \hat{w}_{a,0} } \right)^{2} }}U_{s} \left( {\hat{x} - \frac{L}{2}} \right) \hfill \\ \end{gathered}$$

(6)

The arc beam is subjected to the following boundary conditions:

$$\hat{w}_{a} \left( {0,\hat{t}} \right) = \hat{w}_{a} \left( {L,\hat{t}} \right) = 0;{\text{ and }}\left. {\frac{{\partial \hat{w}_{a} }}{{\partial \hat{x}}}} \right|_{{\left( {0,\hat{t}} \right)}} = \left. {\frac{{\partial \hat{w}_{a} }}{{\partial \hat{x}}}} \right|_{{\left( {L,\hat{t}} \right)}} = 0$$

(7)

In Eq. (6), $\widehat{c}$, ${U}_{s}$, $\epsilon$ and denote the damping coefficient, the unit-step function to define the half electrode configuration, and the permittivity of the dielectric vacuum between the beam and the electrode, correspondingly. The term D represents the modified beam's stiffness, which includes the couple stress effects, ${D}_{CS}$, in addition to the beam's original stiffness, ${D}_{C},$ based on the effective material properties (Shaat and Abdelkefi 2017; Larkin et al. 2018).

$$D = D_{C} + D_{CS} ;D_{C} = \frac{{2\mu I\left( {1 - \nu } \right)}}{1 - 2\nu };D_{CS} = bh\mu L^{2}$$

(8)

Equations (6) and (7) are normalized using the following nondimensional parameters:

$$w_{a} = \frac{{\hat{w}_{a} }}{d}{ ; }x = \frac{{\hat{x}}}{L}{ ; }t = \frac{{\hat{t}}}{T}{; }w_{a,0} = \frac{{\hat{w}_{a,0} }}{d}{\text{; and }}b_{0} = \frac{{\hat{b}_{0} }}{d}$$

(9)

where $T=\sqrt{\frac{\rho bh{L}^{4}}{D}}$ is the timescale.

Inserting Eq. (9) into Eqs. (6) and (7), the dimensionless equation of motion with the associated boundary conditions are obtained:

$$\begin{gathered} \frac{{\partial^{2} w_{a} }}{{\partial t^{2} }} + \frac{{\partial^{4} w_{a} }}{{\partial x^{4} }} + c\frac{{\partial w_{a} }}{\partial t} = \left( {\left( {\frac{{\partial^{2} w_{a} }}{{\partial x^{2} }} + \frac{{d^{2} w_{a,0} }}{{dx^{2} }}} \right)\left[ {N_{non} + \alpha_{1} \mathop \smallint \limits_{0}^{1} \left[ {\frac{{\partial w_{a} }}{\partial x}^{2} + 2\frac{{\partial w_{a} }}{\partial x}\frac{{dw_{a,0} }}{dx}} \right]dx} \right]} \right) \hfill \\ + \alpha_{2} \frac{{\left( {V_{DC} + V_{AC} \cos (\Omega t} \right))^{2} }}{{\left( {1 - w_{a} - w_{a,0} } \right)^{2} }}U_{s} \left( {x - 0.5} \right) \hfill \\ \end{gathered}$$

(10)

$$w_{a} \left( {0,t} \right) = w_{a} \left( {1,t} \right) = 0;{\text{ and }}\left. {\frac{{\partial w_{a} }}{\partial x}} \right|_{{\left( {0,t} \right)}} = \left. {\frac{{\partial w_{a} }}{\partial x}} \right|_{{\left( {1,t} \right)}} = 0$$

(11)

The parameters appearing in Eq. (10) are described as follow:

$$c = \frac{{L^{4} }}{{DT_{s} }}\hat{c}; \alpha_{1} = 6\frac{{d^{2} }}{{h^{2} }};N_{non} = \frac{{L^{2} }}{D}\hat{N}_{0} ;\alpha_{2} = \frac{{\varepsilon bL^{4} }}{{2Dd^{3} }};{\Omega } = T_{s} \hat{\Omega }$$

(12)

2.2 Determination of the static position and natural frequencies

To examine the alteration of the arc beam resonance frequencies due to the tuning of the axial load, N_non, and bias voltage, V_DC, the equation of motion should be first linearized around the static position. The equation of motion describing the static configuration is given by dropping the time-dependent terms from Eq. (10):

$$\frac{{d^{4} w_{a,s} }}{{dx^{4} }} = \left( {\left( {\frac{{d^{2} w_{a,s} }}{{dx^{2} }} + \frac{{d^{2} w_{a,0} }}{{dx^{2} }}} \right)\left[ {N_{non} + \alpha_{1} \mathop \smallint \limits_{0}^{1} \left[ {\left( {\frac{{dw_{a,s} }}{dx}} \right)^{2} + 2\frac{{dw_{a,s} }}{dx}\frac{{dw_{a,0} }}{dx}} \right]dx} \right]} \right) + { }\alpha_{2} \frac{{V_{DC}^{2} }}{{\left( {1 - w_{a,s} - w_{a,0} } \right)^{2} }}U_{s} \left( {x - 0.5} \right)$$

(13)

Equation (13) is associated with the following boundary conditions:

$$w_{a,s} \left( 0 \right) = w_{a,s} \left( 1 \right) = 0{\text{ and }}\left. {\frac{{dw_{a,s} }}{dx}} \right|_{x = 0} = \left. {\frac{{dw_{a,s} }}{dx}} \right|_{x = 1} = 0$$

(14)

To evaluate the static behavior of the arc beam, Eq. (13) is discretized using the Galerkin method yielding a reduced-order model (ROM). Thus, the static response is estimated as:

$$w_{a,s} \left( x \right) = \mathop \sum \limits_{i = 1}^{k} a_{i} \varphi_{i} \left( x \right)$$

(15)

a_i (i = 1,2…k) represent the dimensionless constant modal coordinates and φ_i(x) (i = 1,2..k) denote the exact mode shapes of the unactuated fixed–fixed arc beam (Hajjaj et al. 2017a). Next, by multiplying Eq. (13) by ${\left(1-{w}_{a,s} -{w}_{a,0}\right)}^{2}$, substituting the static deflection by Eq. (14), multiplying Eq. (13) by φ_j(x) and integrating it along the arc beam, k algebraic equation as a function of the nondimensional constant modal coordinates will result. The algebraic equations system is then solved using Newton–Raphson method.

Next, the harmonic and damping terms are dropped from Eq. (10) to determine the system's resonant frequencies. Then, the arc beam deflection, w(x,t), is assumed as:

$$w_{a} \left( {x,t} \right) = w_{a,s} \left( x \right) + w_{a,d} \left( {x,t} \right)$$

(16)

w_a,d(x,t) represents a small dynamic deflection of the arc beam around its static position. Linearizing the equation of motion, the following dynamic equation with the associated boundary conditions are obtained (Hajjaj et al. 2017a):

$$\frac{{\partial^{2} w_{a,d} }}{{\partial t^{2} }} + \frac{{\partial^{4} w_{a,d} }}{{\partial x^{4} }} = \left[ {N_{non} + \alpha_{1} \mathop \smallint \limits_{0}^{1} \left[ {\left( {\frac{{dw_{a,s} }}{dx}} \right)^{2} + 2\frac{{dw_{a,s} }}{dx}\frac{{dw_{a,0} }}{dx}} \right]dx} \right]\frac{{\partial^{2} w_{a,d} }}{{\partial x^{2} }} + 2\alpha_{1} \mathop \smallint \limits_{0}^{1} \left[ {\left( {\frac{{dw_{a,s} }}{dx} + \frac{{dw_{a,0} }}{dx}} \right)\frac{{\partial w_{a,d} }}{\partial x}} \right]dx\left( {\frac{{d^{2} w_{a,s} }}{{dx^{2} }} + \frac{{d^{2} w_{a,0} }}{{dx^{2} }}} \right) + 2\alpha_{2} \frac{{V_{DC}^{2} }}{{\left( {1 - w_{a,s} - w_{a,0} } \right)^{3} }}U_{s} \left( {x - 0.5} \right)w_{a,d}$$

(17)

$$w_{a,d} \left( {0,t} \right) = w_{a,d} \left( {1,t} \right) = 0{\text{ and }}\left. {\frac{{\partial w_{a,d} }}{\partial x}} \right|_{x = 0,t} = \left. {\frac{{\partial w_{a,d} }}{\partial x}} \right|_{x = 1,t} = 0$$

(18)

The eigenfrequencies of the arc beam are determined using the Galerkin discretization for the linear equation of motion shown in Eq. (17). Toward this, the small dynamic deflection can be expressed as:

$$w_{a,d} \left( {x,t} \right) = \mathop \sum \limits_{i = 1}^{k} q_{i} \left( t \right)\varphi_{i} \left( x \right)$$

(19)

where q_i(t) (i = 1,2..k) refer to the dimensionless modal coordinates (Hajjaj et al. 2017a).

Substituting Eq. (19) into Eq. (17), multiply the outcome by the mode shape φ_j, and integrate over the beam domain yield the following ordinary differential equation:

$${\ddot q_j} = - \mathop \smallint \limits_0^1 {\varphi _j}\left( {\mathop \sum \limits_{i = 1}^k {q_i}{\varphi _i}^{\left( {iv} \right)}} \right)dx + \left[ {{N_{non}} + {\alpha _1}\mathop \smallint \limits_0^1 \left[ {{{\left( {\frac{{d{w_{a,s}}}}{{dx}}} \right)}^2} + 2\frac{{d{w_{a,s}}}}{{dx}}\frac{{d{w_{a,0}}}}{{dx}}} \right]dx} \right]\mathop \smallint \limits_0^1 {\varphi _j}\left( {\mathop \sum \limits_{i = 1}^k {q_i}\varphi _i^{''}} \right)dx + 2{\alpha _1}\mathop \smallint \limits_0^1 \left[ {\left( {\frac{{d{w_{a,s}}}}{{dx}} + \frac{{d{w_{a,0}}}}{{dx}}} \right)\mathop \sum \limits_{i = 1}^k {q_i}{\varphi _i}'} \right]dx\mathop \smallint \limits_0^1 {\varphi _j}\left( {\frac{{{d^2}{w_{a,s}}}}{{d{x^2}}} + \frac{{{d^2}{w_{a,0}}}}{{d{x^2}}}} \right)dx + \mathop \smallint \limits_0^1 {\varphi _j}\frac{{2{\alpha _2}{V_{DC}}^2}}{{{{\left( {1 - {w_{a,s}} - {w_{a,0}}} \right)}^3}}}\left( {\mathop \sum \limits_{i = 1}^k {q_i}{\varphi _i}} \right){U_s}\left( {x - 0.5} \right)dx$$

(20)

Using four modes in the Galerkin discretization, the Jacobian of the four equations is computed for each N_non and/or V_DC, and find the corresponding eigenvalues. The number of exact modes needed to simulate the resonator static and dynamic behaviors was conducted by a convergence analysis. At constant N_non and/or V_DC, the resonators' natural frequencies can be computed by taking these eigenvalues' square-root.

2.3 Nonlinear size-dependent reduced-order model

By fixing the axial load N_non near the veering zone, the arc beam's dynamic response is simulated by discretizing the equation of motion using a Galerkin procedure. Hence, the arc deflection is expressed as follows:

$$w_{a} \left( {x,t} \right) = \mathop \sum \limits_{i = 1}^{k} u_{i} \left( t \right)\phi_{i} \left( x \right)$$

(21)

where u_i(t)(i = 1…k) are the dimensionless modal coordinates and ${\phi }_{i}(x)$ (i = 1…k) are the new mode shapes of the arc beam at a constant axial load N_non and DC bias V_DC.

After that, the equation of motion is multiplied by ${\left(1-{w}_{a}-{w}_{a,0}\right)}^{2}$ to reduce the computational costs (i.e., the electrostatic force term will not involve complicated numerical integration), following (Ramini et al. 2016b; Hajjaj et al. 2017a). Then, by substituting Eq. (21) into Eq. (10), multiplying by ϕ_j(x) and integrating along the arc beam, k equations governing u_i(t) are obtained as follows:

$$\mathop \sum \limits_{i = 1}^{k} M_{ij} \left( u \right)\ddot{u}_{i} \left( t \right) + \mathop \sum \limits_{i = 1}^{k} C_{ij} \left( u \right)\dot{u}_{i} \left( t \right) + \mathop \sum \limits_{i = 1}^{k} K_{ij} \left( u \right)u_{i} \left( t \right) = F_{\Gamma j} \left( u \right) + Fe_{j} \left( t \right)\quad \forall \left( {j = 1 \ldots k} \right)$$

(22)

where ${M}_{ij}$,${C}_{ij}$, ${K}_{ij}$, ${F}_{\Gamma j}$, and $F{e}_{j}$ are set of integrals defined in the Appendix. The value of these integrals are first calculated over the beam domain according to the Eqs. (23)–(28) (reduction procedure). Next, the obtained set of nonlinear differential equations of u_i(t)(i = 1..k) is integrated in time using four exact mode shapes and the Runge–Kutta technique.

3 Size-dependent and material structure effects on the system's dynamics

It has been demonstrated in previous works that the grain radius and/or the porosity fraction affect the stiffness of the nanocrystalline silicon material, and hence its mechanical behaviors (Shaat and Abdelkefi 2015, 2016; Ghommem and Abdelkefi 2017). In this work, the influence of the size and material structure will be examined on the static and dynamic behaviors of the MEMS and NEMS arc beam resonators as considering two different porosity factors (f_3p = 0% and f_3p = 10%, with f_3p denoting the void volume fraction (Shaat and Abdelkefi 2017)) and two grain radii R = 100 nm and R = 2 nm. Here, CM denotes the classical beam theory, while CS denotes the couple stress theory's inclusion. The nanocrystalline silicon properties used in this work are provided in Table 2.

Table 2 The nanocrystalline silicon properties for different grain radii (Larkin et al. 2018)

4 Size and porosity effects on the static response and snap through

The impacts of the size of the electromechanical system and its material structure on the static deflection of the system are examined. Various sizes of MEMS, MEMS/NEMS, and NEMS arc shallow beams are considered, and then Eq. (13) is solved for different V_DC values. The plotted curves in Fig. 2 demonstrate the static deflection of arc beams, having the same parameters given in Table 1 but with different initial rises and thicknesses, at the midpoint as varying the DC bias voltage. This selection is carried out in order to study arches without snap-through motion. The static response shows the presence of single stable branches for all sizes and different material properties. A saddle-node bifurcation bounds the response at critical V_DC voltage: pull-in (PI), as shown in Fig. 2a.

Fig. 2

Static deflection of arc shallow beams under varying electrostatic load for different porosity and grain radius: a MEMS, b₀ = 2 µm, h = 2 µm, b MEMS/NEMS, b₀ = 0.2 µm, h = 0.2 µm, c MEMS/NEMS, b₀ = 35 nm, h = 35 nm. The filled scatters refer to the classical theory, while the empty scatters refer to the coupled stress theory's inclusion. Label PI denotes the pull-in instability. The axial load is set at zero value for these results

As shown in Fig. 2a, the size dependency effects due to the couple stress theory are negligible for electrostatically actuated systems at the micro-scale. Conversely, the material structure of the nanocrystalline material has a strong effect on the system's static deflection and pull-in voltage. Indeed, a reduction in the grain size results in a reduction in the overall stiffness of the system and consequently the static pull-in voltage. Concerning the porosity influences, it is clear from Fig. 2a that the porosity has a considerable effect on the static deflection and pull-in voltage even the system's size is in the micro-scale. These results demonstrate the importance of exactly determining the material structure of the nanocrystalline material to avoid any underestimation of the Young's modulus of the material. Shrinking the system to smaller scales, it follows from Fig. 2b and c that the couple stress have an important effect on the static response of the arc beam, particularly when smaller dimensions take place. The coupling effect due to the material structure and size may result in erroneous estimation of the couple stress parameter and the porosity or grain size of the material. Inspecting Fig. 2b, some curves are almost the same, but they represent different scenarios of the couple stress parameter, porosity fraction, and grain size. For example, the static deflection and pull-in voltage are almost similar for the case of small grain radius with couple stress and no porosity and the case of big grain radius without couple stress and porosity. These results show the importance of accurately determining the porosity fraction and grain size and the inclusion of the couple stress effect on the static deflection and pull-in voltage of these systems at micro-/nano-scale. One should mention that, at the nano-scale, the couple stress dominates the system's response and its effect is stronger than the porosity and grain size.

Next, the static deflection of arc beams at the midpoint as varying the DC voltage is plotted in Fig. 3 for the beam parameters given in Table 1. The static response indicates the presence of two stable branches for all sizes and different material properties. Three saddle nodes bifurcations bound the two stable branches at critical V_DC voltages: snap-through (ST), snap-back (SB), and pull-in, as shown in Fig. 3a. It should be mentioned that the beams' sizes (presented in Table 1) are carefully chosen to get the snap-through and snap-back bifurcation points. It follows from Fig. 2 that considering the same arc beams with lower initial rises (relatively with the thickness) will lead to suppressing the bistability of the arc resonators.

Fig. 3

Static deflection of shallow arc beams under varying electrostatic load for various porosity and grain radius. a MEMS, b MEMS/NEMS, c MEMS/NEMS. The arc beam parameters are given in Table 1. The filled scatters refer to the classical theory, while the empty scatters refer to the coupled stress theory's inclusion. Label PI, SB, and ST denote the pull-in, snap-back, and snap-through instabilities. The axial load is set at zero value for these results

Figure 3 shows clearly that the influence of the size dependency, namely, the inclusion of the couple stress effects, depends highly on the resonator's size. For the micro-scale size, similar to Fig. 2a, it is indicated from Fig. 3a that the size dependence through the inclusion of the couple stress theory has a negligible influence on the three bifurcation points of the studied arc shallow resonator, the snap-through/back voltages and the pull-in voltage. Hence, the size dependence can be ignored at the micro-scale. When the dimensions of the system are reduced to smaller scales, it can be seen from Fig. 3b-c that a dramatic effect of the inclusion of the couple stress theory on the arc resonators static behavior. For the MEMS/NEMS scales, the pull-in voltages increase by 47% for f_3p = 10% and 51% for f_3p = 0% as taking account of the couple stress effect. For the same porosity and as increasing the radius size from 2 to 100 nm, the pull-in voltage rises by 66.66%. Increasing the grain size leads to stiffening more of the beam. The snap-through/back voltages increase by almost the same percentage. Decreasing the resonator's size to the NEMS scale increases the pull-in and the snap-through/back voltages by 330% for f_3p = 10% and 344% for f_3p = 0%. For f_3p = 0% and R = 2 nm, and as increasing the radius size from 2 to 100 nm, the pull-in and the snap-through/back voltages increase by 320%. These results prove that as the beam's dimensions decrease, the classical continuum mechanics theory reaches its limit of applicability, and the couple stress effect becomes more significant. Also, one can note how an increase in porosity and/or grain radius also decreases the beam's rigidity, and hence can deflect with higher values at smaller DC values.

4.1 Material size and structure effects on the natural frequencies

After analyzing the influence of the material structure and size on the static response and pull-in of shallow arc beams, their effects on their resonant frequencies are determined. In Fig. 4, the variations of the three lowest resonant frequencies (the first two symmetric modes (f₁ and f₃) and the first antisymmetric mode (f₂)) of the shallow arc beam as changing the V_DC are depicted. The frequencies decrease as increasing the electrostatic force until an inflection point, whereafter, the frequencies start to increase until reaching the pull-in bifurcation. In Fig. 5, the variations of the three lowest resonant frequencies of the shallow arc beam as varying the V_DC are showed. The frequencies decrease as increasing the electrostatic force until reaching almost zero values around the fundamental frequency around the snap-through bifurcation. Next, the frequencies start to increase until reaching pull-in instability. At pull-in and going backward with the DC bias voltage, the resonant frequencies decrease until zero values are reached around the fundamental frequency at the snap-back bifurcation. While at the micro-scale, the effect of the size dependency is negligible, as decreasing the resonator dimensions, the effects of the size dependency not only change the snap-through/back and pull-in voltages but also the resonant frequency values.

Fig. 4

Variation of the three lowest natural frequencies of the arc beam with V_DC for various porosity and grain radius. a MEMS, b₀ = 2 µm, h = 2 µm. b-c MEMS/NEMS, b₀ = 0.2 µm, h = 0.2 µm, b Classical model, c Classical model with couple stress. d-e MEMS/NEMS, b₀ = 35 nm, h = 35 nm. d Classical model and e Classical model with couple stress. The filled scatters in (a) refer to the classical theory, while the empty scatters refer to the coupled stress theory's inclusion. Label f₁, f₂, and f₃ refer to the first symmetric, first antisymmetric, and second symmetric modes. The axial load is set at zero value for these results

Fig. 5

Variation of the three lowest natural frequencies of the arc beam with V_DC for various porosity and grain radius. a MEMS, f_3p = 0%, R = 100 nm, b MEMS, f_3p = 10%, R = 100 nm, c MEMS, f_3p = 0%, R = 2 nm, d MEMS/NEMS, f_3p = 0%, R = 100 nm, e MEMS/NEMS, f_3p = 10%, R = 100 nm, f MEMS/NEMS, f_3p = 0%, R = 2 nm, g NEMS, f_3p = 0%, R = 100 nm, NEMS, h f_3p = 10%, R = 100 nm, and i NEMS, f_3p = 0%, R = 2 nm. The arc beam parameters are given in Table 1. The filled scatters refer to the classical theory, while the empty scatters refer to the inclusion of the coupled stress theory. Label f₁, f₂, and f₃ refer to the first symmetric, first antisymmetric and second symmetric modes. The corresponding mode shapes are given as inset in (a). The axial load is set at zero value for these results

Figures 4d–c and 5g-i show clearly that the inclusion of the couple stress may lead to a dramatic impact of the variation of the frequencies at the nano-scale. These results show again the possible discrepancies that can be obtained due to the size dependency effects, which may lead to erroneous detection of the resonance frequencies and the pull-in instability.

Next, the variations of the three lowest resonant frequencies as varying the axial load, namely increasing the compressive load,for V_DC = 0 V are studied in order to examine the size-dependent effects on the arc beam performance. For all three considered designs, the arc resonator's geometric parameters are carefully chosen to activate the veering phenomenon. Indeed, as tuning the axial load, the fundamental frequency, f₁, increases, while the first antisymmetric and symmetric modes, f₂ and f₃, decrease. Increasing more the compressive load results in the crossover among the first symmetric and antisymmetric modes, as shown in Fig. 6. Increasing the axial load beyond the crossing zone, the frequencies depart from each other without mode hybridization (i.e., the first symmetric mode continues to increase while the first antisymmetric mode decreases). Increasing more the compressive load, the first two symmetric modes get closer to each other before they deviate with high curvature. After that, both modes change directions, and each continues along the path that the other mode would have taken if they crossed—this is known as veering phenomenon. Around veering, both modes hybridize, as shown in the mode shapes of Fig. 6a. After veering, the first frequency takes the mode shape of the third resonance frequency, while the thirst mode will take the hybridized mode combining both two symmetric mode shapes. Figure 6a shows a validation of the numerical results with experimental results presented in (Hajjaj et al. 2017a), where the veering was demonstrated numerically and experimentally for similar MEMS arc resonators electrothermally tuned. Here for comparison purposes, the corresponding induced compressive load is estimated for each applied electrothermal voltage according to the procedure described in (Hajjaj et al. 2017a).

Fig. 6

Variation of the three lowest natural frequencies of the shallow arc beam with the nondimensional axial load N_non illustrating the crossover and veering phenomena. a MEMS, f₃ = 0%, R = 100 nm, b MEMS, f₃ = 10%, R = 100 nm, c MEMS/NEMS, f₃ = 0%, R = 100 nm, d MEMS/NEMS, f₃ = 10%, R = 100 nm, e NEMS, f₃ = 0%, R = 100 nm, f NEMS, f₃ = 10%, R = 100 nm. The scatter (stars) in (a) presents the experimental data presented in Hajjaj et al. (2017a). The arc beam parameters are given in Table 1. The bias DC voltage V_DC is equal to 0 V. The dashed lines represent the classical theory, while the continuous lines represent the coupled stress theory's inclusion. Label f₁, f₂, and f₃ refer to the first symmetric, first antisymmetric, and second symmetric modes. The corresponding mode shapes are given as inset in (a)

Figure 6a and b show the negligible effect of the inclusion of the couple stress theory at the micro-scale. Shrinking more the arc dimensions, the size dependency effects clearly significantly impact the frequency tuning. As the figures show the nondimensional axial load, the dimensional axial load needed to reach the veering zone is increased by 95% in the case of the NEMS scale and 54% in the MEMS/NEMS scale, while it did not exceed 1% at the micro-scale, as including the effect of the couple stress theory. Concerning the porosity effects, the porosity results in a reduction in the three resonant frequencies due to the softening effect, as shown in Fig. 6. It is also clear that both the crossing and veering phenomena need high nondimensional axial load values.

Next, the frequency variation of the first three resonance frequencies with the nondimensional axial load using the half-electrode configuration and when V_DC = 1.25 V is studied with respect to the couple stress effect. Figure 7 shows the alteration of the frequencies of the arc resonator at nano-scale for two cases: without the inclusion of the couple stress theory (Fig. 7a) and with the inclusion of the couple stress theory (Fig. 7b). The V_DC is fixed to 1.25 V in order to be away from the snap-through motion for both cases. Figure 7a demonstrates the strong effect of the applied DC bias on the crossing phenomenon that is transformed into veering. This finding could be explained by the antisymmetric static shaped due to the half-electrode configuration. However, including the size dependency effect, the applied DC effect is weakened due to the stiffness increase of the structure to the electrostatic load, and hence the crossing phenomenon takes place, as depicted in Fig. 7b.

Fig. 7

Variation of the three lowest resonant frequencies of the arc beam with the nondimensional axial load N_non at a constant DC bias voltage V_DC = 1.25 V at nano-scale (NEMS case). a Classical model, f_3p = 0%, R = 100 nm, b Classical model with couple stress, f_3p = 0%, R = 100 nm. The arc beam parameters are given in Table 1. The dashed lines represent the classical theory, while the continuous lines represent the coupled stress theory's inclusion. The veering between the two lowest frequencies results from the non-symmetric static deflection of the arc beam because of the applied bias electrostatic force by the half-electrode configuration

4.2 Arc shallow nanobeams' performance and dynamics

After investigating the influence of material structure and size dependency on the system's static and frequency tuning, the nonlinear dynamics performance of the shallow arc beam subjected to an electrostatic force is explored. The vibratory motion of the shallow arc beam is computed at zero axial load and for different harmonic excitations around the first resonant frequency. The effects of size dependency are chosen to be studied at the micro/nano-scale to make more comparable electrostatic voltages. The DC bias is fixed at V_DC = 3 V. Figure 8 shows that as increasing the AC harmonic excitation, the frequency response of the arc beam goes from linear to nonlinear response, exhibiting softening; since the response is dominated by the quadratic nonlinearity. The plotted curves in Fig. 8 clearly depict the influences of the size dependency on the needed AC voltages to drive the resonator nonlinearly. As looking at the case of V_AC = 0.25 V, including the couple stress theory leads to changing the arc beam's strongly nonlinear response to a purely linear response. This result can be explained due to the high stiffness induced by the couple stress effect, and hence lower amplitudes take place. In addition, as revealed from the linear analysis, the size dependency effects lead to a hardening impact in the resonance region due to the increase in the effective stiffness. These results show the significance of considering the size-dependent effects as modeling these kinds of shallow arc systems at small scales.

Fig. 8

Dynamic frequency response of MEMS/NEMS arc shallow beam for various AC harmonic excitations under an axial load N_non = 0, an electrostatic load V_DC = 3 V, f_3p = 0%, and R = 100 nm. a Classical model, b Classical model with couple stress. The arc beam parameters are given in Table 1. The nonlinear arc behavior shows a softening response dominated by the quadratic nonlinearities

Next, the shallow arc beam is excited around the veering zone for various excitation forces. Around the veering zone, as exciting the beam nonlinearly, the band is created by the combination of the softening, first mode, and hardening, third mode. As approaching the veering zone, Figs. 9a-d show how both frequencies approach each other until combining at veering (Fig. 9d). The nonlinear excitation around veering leads to the 1:1 internal resonance (nonlinear coupling between modes), showing the energy transfer between modes as excited nonlinearly. As was obvious in Figs. 2a, 5a, and 6a, the size-dependent quantities of the micro arc beam have negligible influence on the static and dynamic of the arc beam as tuning either the bias DC voltage or the axial load. The above clarify the results of the nonlinear response shown in Fig. 9. Indeed, Fig. 9, displaying the dynamic frequency response of MEMS arc beam at veering under an electrostatic load: V_DC = 20 V and V_AC = 10 V, shows the negligible effect of the size dependency on the dynamic response around the veering response. Hence, neglecting the effect of the coupled stress theory as simulating the response of microbeam even at linear (veering) and nonlinear (internal resonance) modal coupling will not affect the analysis. At the micro/nano-scale, the effect of size dependency is more dramatic, as presented in Fig. 10. The inclusion of the couple stress affects the nonlinear interaction between modes and shrinks the band of interaction between both modes. To get the same band, higher AC voltages are needed in the couple stress theory case as a result of the structure's stiffening. After veering, the two modes change characteristics, and the third mode (or the new hybridized mode) shows a high amplitude of motion compared to the first mode.

Fig. 9

Dynamic frequency response of MEMS arc beam at veering under an electrostatic load, V_DC = 20 V and V_AC = 10 V: a N_non = 300, b N_non = 350, c N_non = 380, d N_non = 400. The arc beam parameters are given in Table 1. The filled scatters refer to the classical theory, while the empty scatters refer to the coupled stress theory's inclusion. The softening behavior denotes the first symmetric mode response. Hardening behavior represents the second symmetric mode response

Fig. 10

Dynamic frequency response of MEMS/NEMS arc beam under different AC harmonic excitation and a constant V_DC = 3 V and axial load N_non = 400. a Classic theory and b Classic theory with couple stress theory. The arc beam parameters are given in Table 1. As increasing the AC voltages, the arc response goes from linear to nonlinear behaviors

5 Conclusions

In this work, the effects of the size dependency on the static and nonlinear dynamics behaviors of shallow arc beams at different sizes were deeply investigated. It was shown that the size dependency dramatically affected the snap-through/back and static pull-in voltages that exceed 300%, while the latter showed a negligible effect at the micro-scale. At the micro/nano-scales, the size dependency strongly impacts the veering loads and the dynamic and nonlinear vibrations. The applied axial load needed to be tuned by 95% to reach the veering zone as including the coupled stress theory at the nano-scale. In a nutshell, neglecting the coupled stress theory's inclusion could lead to wrong characterization and modelization of the nano shallow arches' different features. The size dependence was showing at 1:1 nonlinear interaction between the two symmetric modes. This needs an in-depth study on the size dependency at different internal resonances that the arc resonator could exhibits: 2:1 and 3:1 internal resonances. It should be mentioned that this study was restricted to the inclusion of the couple stress theory and material structure caused by the porosity. However, the inclusion of the surface elasticity effect would have a strong and more dramatic impact on the arc beams' static and dynamic responses as operated nonlinearly and at veering zones.

Appendix

The integrals appeared in Eq. (21) are defined as:

$$M_{ij} \left( u \right) = \mathop \smallint \limits_{0}^{1} \left[ {\phi_{i} \left( x \right)\phi_{j} \left( x \right)\left( {1 - w_{a} - w_{a,0} } \right)^{2} } \right]dx$$

(23)

$$C_{ij} \left( u \right) = c\mathop \smallint \limits_{0}^{1} \left[ {\phi_{i} \left( x \right)\phi_{j} \left( x \right)\left( {1 - w_{a} - w_{a,0} } \right)^{2} } \right]dx$$

(24)

$$K_{ij} \left( u \right) = \mathop \smallint \limits_{0}^{1} \left[ {\phi_{i}^{{\left( {iv} \right)}} \left( x \right)\phi_{j} \left( x \right)\left( {1 - w_{a} - w_{a,0} } \right)^{2} } \right]dx$$

(25)

$$Fe_{j} \left( t \right) = \alpha_{2} (V_{DC} + V_{AC} Cos\left( {\Omega t} \right))^{2} \mathop \smallint \limits_{0}^{1} \phi_{j} \left( x \right)U_{s} (x - 0.5)dx$$

(26)

$$F_{{\Gamma}{j}} \left( u \right) = \alpha_{1} \Gamma \left( u \right)\mathop \smallint \limits_{0}^{1} \left[ {\phi_{j} \left( x \right)\left( {w_{a}^{\prime\prime} + w_{a,0} ^{\prime\prime}} \right)\left( {1 - w_{a} - w_{a,0} } \right)^{2} } \right]dx$$

(27)

where $\Gamma$ is given by:

$$\Gamma \left( u \right) = N_{non} + \mathop \smallint \limits_{0}^{1} \left( {w_{a} ^{\prime}} \right)^{2} dx + 2\mathop \smallint \limits_{0}^{1} w_{a} ^{\prime}w_{a,0} ^{\prime}\left( x \right)dx$$

(28)