Elastic buckling of nanoplates based on general third-order shear deformable plate theory including both size effects and surface effects

Abstract

A unified plate model predicting the buckling behaviors is proposed by incorporating both surface and size effects into the general third-order plate theory (GTPT). From the minimum potential energy principle, the governing equations are implemented with presenting the corresponding boundary conditions. Analytic buckling loads for rectangular nanoplates are obtained by considering different boundary conditions. The surface effects, size effects and geometric sizes of nanoplates on the plate instability loads are discussed by using four types of single crystalline metallic nano-materials, gold, silver, copper and nickel. The study reveals that the GTPT is more accurate in predicting the buckling behaviors of nanoplates than the Reddy’s plate theory when surface effects are considered due to the fact that the GTPT can freely satisfy the strain condition on plate surfaces. Further discussion shows that the nonlocal strain gradient GTPT predicts a higher critical buckling load of a nanoplate with increasing high order scale parameter while a lower critical buckling load with increasing nonlocal parameter than the classical GTPT. Moreover, it is found that the increasing in length-to-thickness ratios of the nanoplates enhances the influence of surface effects on the critical buckling loads.

Graphical abstract

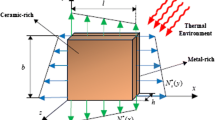
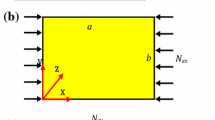
A nanoplate with significant surface stresses and the effects on dimensionless critical buckling load factor

Appendices

Appendix 1

The coefficients in Eq. (19) are.

$$ \begin{gathered} A_{{xx}} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left[ {\frac{{E\left( {R_{1} - z} \right)^{2} }}{{1 - \upsilon ^{2} }} + \frac{{2\upsilon \tau ^{s} z\left( {R_{1} - z} \right)}}{{\left( {1 - \upsilon } \right)h}}} \right]} dz + \left( {\lambda ^{s} + 2\mu ^{s} } \right)\left\{ {\left[ {R_{1} \left( {\frac{h}{2}} \right) - \frac{h}{2}} \right]^{2} + \left[ {R_{1} \left( { - \frac{h}{2}} \right) + \frac{h}{2}} \right]^{2} } \right\} \hfill \\ B_{{xx}} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left[ {\frac{{E\upsilon \left( {R_{1} - z} \right)^{2} }}{{1 - \upsilon ^{2} }} + \frac{{2\upsilon \tau ^{s} z\left( {R_{1} - z} \right)}}{{\left( {1 - \upsilon } \right)h}}} \right]} dz + \left( {\lambda ^{s} + \tau ^{s} } \right)\left\{ {\left[ {R_{1} \left( {\frac{h}{2}} \right) - \frac{h}{2}} \right]^{2} + \left[ {R_{1} \left( { - \frac{h}{2}} \right) + \frac{h}{2}} \right]^{2} } \right\} \hfill \\ C_{{xx}}^{i} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\frac{{ER_{i} \left( {R_{1} - z} \right)}}{{1 - \upsilon ^{2} }}dz} + \left( {\lambda ^{s} + 2\mu ^{s} } \right)\left\{ {R_{i} \left( {\frac{h}{2}} \right)\left[ {R_{1} \left( {\frac{h}{2}} \right) - \frac{h}{2}} \right] + R_{i} \left( { - \frac{h}{2}} \right)\left[ {R_{1} \left( { - \frac{h}{2}} \right) + \frac{h}{2}} \right]} \right\} \hfill \\ D_{{xx}}^{i} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\frac{{ER_{i} \left( {R_{1} - z} \right)}}{{1 - \upsilon ^{2} }}dz} + \left( {\lambda ^{s} + \tau ^{s} } \right)\left\{ {R_{i} \left( {\frac{h}{2}} \right)\left[ {R_{1} \left( {\frac{h}{2}} \right) - \frac{h}{2}} \right] + R_{i} \left( { - \frac{h}{2}} \right)\left[ {R_{1} \left( { - \frac{h}{2}} \right) + \frac{h}{2}} \right]} \right\} \hfill \\ E_{{xx}} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {2G\left( {R_{1} - z} \right)^{2} dz} + \left( {2\mu ^{s} - \tau ^{s} } \right)\left\{ {\left[ {R_{1} \left( {\frac{h}{2}} \right) - \frac{h}{2}} \right]^{2} + \left[ {R_{1} \left( { - \frac{h}{2}} \right) + \frac{h}{2}} \right]^{2} } \right\} \hfill \\ F_{{xx}}^{i} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {GR_{i} \left( {R_{1} - z} \right)dz} + \frac{1}{2}\left( {2\mu ^{s} - \tau ^{s} } \right)\left\{ {R_{i} \left( {\frac{h}{2}} \right)\left[ {R_{1} \left( {\frac{h}{2}} \right) - \frac{h}{2}} \right] + R_{i} \left( { - \frac{h}{2}} \right)\left[ {R_{1} \left( { - \frac{h}{2}} \right) + \frac{h}{2}} \right]} \right\} \hfill \\ G_{{xx}}^{i} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left[ {\frac{{ER_{i} \left( {R_{1} - z} \right)}}{{1 - \upsilon ^{2} }} + \frac{{2\upsilon \tau ^{s} zR_{i} }}{{\left( {1 - \upsilon } \right)h}}} \right]} dz + \left( {\lambda ^{s} + 2\mu ^{s} } \right)\left\{ {R_{i} \left( {\frac{h}{2}} \right)\left[ {R_{1} \left( {\frac{h}{2}} \right) - \frac{h}{2}} \right] + R_{i} \left( { - \frac{h}{2}} \right)\left[ {R_{1} \left( { - \frac{h}{2}} \right) + \frac{h}{2}} \right]} \right\} \hfill \\ H_{{xx}}^{i} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left[ {\frac{{\upsilon ER_{i} \left( {R_{1} - z} \right)}}{{1 - \upsilon ^{2} }} + \frac{{2\upsilon \tau ^{s} zR_{i} }}{{\left( {1 - \upsilon } \right)h}}} \right]} dz + \left( {\lambda ^{s} + \tau ^{s} } \right)\left\{ {R_{i} \left( {\frac{h}{2}} \right)\left[ {R_{1} \left( {\frac{h}{2}} \right) - \frac{h}{2}} \right] + R_{i} \left( { - \frac{h}{2}} \right)\left[ {R_{1} \left( { - \frac{h}{2}} \right) + \frac{h}{2}} \right]} \right\} \hfill \\ I_{{xx}}^{{ij}} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\frac{{ER_{i} R_{j} }}{{1 - \upsilon ^{2} }}} dz + \left( {\lambda ^{s} + 2\mu ^{s} } \right)\left[ {R_{i} \left( {\frac{h}{2}} \right)R_{j} \left( {\frac{h}{2}} \right) + R_{i} \left( { - \frac{h}{2}} \right)R_{j} \left( { - \frac{h}{2}} \right)} \right]\quad \hfill \\ J_{{xx}}^{{ij}} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\frac{{\upsilon ER_{i} R_{j} }}{{1 - \upsilon ^{2} }}} dz + \left( {\lambda ^{s} + \tau ^{s} } \right)\left[ {R_{i} \left( {\frac{h}{2}} \right)R_{j} \left( {\frac{h}{2}} \right) + R_{i} \left( { - \frac{h}{2}} \right)R_{j} \left( { - \frac{h}{2}} \right)} \right]\quad \hfill \\ K_{{xx}}^{i} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {2GR_{i} \left( {R_{1} - z} \right)dz} + \left( {2\mu ^{{ss}} - \tau ^{s} } \right)\left\{ {R_{i} \left( {\frac{h}{2}} \right)\left[ {R_{1} \left( {\frac{h}{2}} \right) - \frac{h}{2}} \right] + R_{i} \left( { - \frac{h}{2}} \right)\left[ {R_{1} \left( { - \frac{h}{2}} \right) + \frac{h}{2}} \right]} \right\} \hfill \\ L_{{xx}}^{{ij}} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {GR_{i} R_{j} dz} + \left( {\mu ^{{ss}} - \frac{1}{2}\tau ^{s} } \right)\left[ {R_{i} \left( {\frac{h}{2}} \right)R_{j} \left( {\frac{h}{2}} \right) + R_{i} \left( { - \frac{h}{2}} \right)R_{j} \left( { - \frac{h}{2}} \right)} \right] \hfill \\ S_{{xx}}^{i} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\kappa G\frac{{dR_{i} }}{{dz}}\frac{{dR_{1} }}{{dz}}dz} \hfill \\ T_{{xx}}^{{ij}} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\kappa G\frac{{dR_{i} }}{{dz}}\frac{{dR_{j} }}{{dz}}dz} \hfill \\ \end{gathered} $$

where $i,j = 1,2,3$

Appendix 2

The coefficient of matrix K are

$$ \begin{gathered} K_{ij} = \int_{0}^{{L_{x} }} {\int_{0}^{{L_{y} }} {\left( {1 - l^{2} \nabla^{2} } \right)\left[ {I_{xx}^{ij} \frac{{d^{3} X_{m} }}{{dx^{3} }}Y_{n} + L_{xx}^{ij} \frac{{dX_{m} }}{dx}\frac{{d^{2} Y_{n} }}{{dy^{2} }} - T_{xx}^{ij} \frac{{dX_{m} }}{dx}Y_{n} } \right]\frac{{dX_{m} }}{dx}Y_{n} dxdy} } \quad \left( {i,j = 1,2,3} \right) \hfill \\ K_{{i\left( {j + 3} \right)}} = \int_{0}^{{L_{x} }} {\int_{0}^{{L_{y} }} {\left( {1 - l^{2} \nabla^{2} } \right)\left[ {\left( {J_{xx}^{ij} + L_{xx}^{ij} } \right)\frac{{dX_{m} }}{dx}\frac{{d^{2} Y_{n} }}{{dy^{2} }}} \right]\frac{{dX_{m} }}{dx}Y_{n} dxdy} } \quad \left( {i,j = 1,2,3} \right) \hfill \\ K_{{\left( {i + 3} \right)j}} = \int_{0}^{{L_{x} }} {\int_{0}^{{L_{y} }} {\left( {1 - l^{2} \nabla^{2} } \right)\left[ {\left( {J_{xx}^{ij} + L_{xx}^{ij} } \right)\frac{{d^{2} X_{m} }}{{dx^{2} }}\frac{{dY_{n} }}{dy}} \right]X_{m} \frac{{dY_{n} }}{dy}dxdy} } \quad \left( {i,j = 1,2,3} \right) \hfill \\ K_{{\left( {i + 3} \right)\left( {j + 3} \right)}} = \int_{0}^{{L_{x} }} {\int_{0}^{{L_{y} }} {\left( {1 - l^{2} \nabla^{2} } \right)\left[ {I_{xx}^{ij} X_{m} \frac{{d^{3} Y_{n} }}{{dy^{3} }} + L_{xx}^{ij} \frac{{d^{2} X_{m} }}{{dx^{2} }}\frac{{dY_{n} }}{dy} - T_{xx}^{ij} X_{m} \frac{{dY_{n} }}{dy}} \right]X_{m} \frac{{dY_{n} }}{dy}dxdy} } \quad \left( {i,j = 1,2,3} \right) \hfill \\ K_{7j} = \int_{0}^{{L_{x} }} {\int_{0}^{{L_{y} }} {\left( {1 - l^{2} \nabla^{2} } \right)\left[ {C_{xx}^{j} X_{m} \frac{{d^{4} Y_{n} }}{{dy^{4} }} + \left( {D_{xx}^{j} + 2F_{xx}^{j} } \right)\frac{{d^{2} X_{m} }}{{dx^{2} }}\frac{{d^{2} Y_{n} }}{{dy^{2} }} - T_{xx}^{1j} \frac{{d^{2} X_{m} }}{{dx^{2} }}Y_{n} } \right]X_{m} Y_{n} dxdy} } \quad \left( {j = 1,2,3} \right) \hfill \\ K_{{7\left( {j + 3} \right)}} = \int_{0}^{{L_{x} }} {\int_{0}^{{L_{y} }} {\left( {1 - l^{2} \nabla^{2} } \right)\left[ {C_{xx}^{j} \frac{{d^{4} X_{m} }}{{dx^{4} }}Y_{n} + \left( {D_{xx}^{j} + 2F_{xx}^{j} } \right)\frac{{d^{2} X_{m} }}{{dx^{2} }}\frac{{d^{2} Y_{n} }}{{dy^{2} }} - T_{xx}^{1j} X_{m} \frac{{d^{2} Y_{n} }}{{dy^{2} }}} \right]X_{m} Y_{n} dxdy} } \quad \left( {j = 1,2,3} \right) \hfill \\ K_{77} = \int_{0}^{{L_{x} }} {\int_{0}^{{L_{y} }} {\left( {1 - l^{2} \nabla^{2} } \right)\left[ \begin{gathered} A_{xx} \left( {\frac{{d^{4} X_{m} }}{{dx^{4} }}Y_{n} + \frac{{d^{4} Y_{n} }}{{dy^{4} }}X_{m} } \right) + 2\left( {B_{xx} + E_{xx} } \right)\frac{{d^{2} X_{m} }}{{dx^{2} }}\frac{{d^{2} Y_{n} }}{{dy^{2} }} \hfill \\ - \left( {2\tau^{s} + S_{xx}^{1} } \right)\left( {X_{m} \frac{{d^{2} Y_{n} }}{{dy^{2} }} + \frac{{d^{2} X_{m} }}{{dx^{2} }}Y_{n} } \right) \hfill \\ \end{gathered} \right]X_{m} Y_{n} dxdy} } \hfill \\ \end{gathered} $$

where $K_{{\left( {i + 3} \right)\left( {j + 3} \right)}}$ is $K_{44}$ for i = j = 1, $K_{54}$ for i = 2 and j = 1, and so on.