Nonlinear stability analysis of FGM shallow arches under an arbitrary concentrated radial force

Abstract

The nonlinear in-plane buckling behaviour of pinned-pinned shallow circular arches made of functionally graded material (FGM) is investigated using a one-dimensional Euler–Bernoulli model. The effect of the bending moment on the membrane strain is included. The material properties vary along the thickness of the arch. The external load is a radial concentrated force at an arbitrary position. The pre-buckling and buckled equilibrium equations are derived using the principle of virtual work. Analytical solutions are given for both bifurcation and limit point buckling. Comprehensive studies are performed to find the effect of various parameters on the buckling load and on the behaviour. The major findings: (1) arches have multiple stable and unstable equilibria; (2) when the load is at the crown, the lowest buckling load is related to bifurcation buckling for most geometries and material compositions but when the external force is replaced, only limit point buckling is possible; (3) the position of the load has huge influence on the buckling load; (4) such arches are sensitive to small loading imperfections when loaded in the vicinity of the crown. The paper intends to improve and extend the existing knowledge about the behaviour of pinned-pinned shallow FGM arches under arbitrary concentrated radial load.

1 Introduction

Curved members are frequently used in engineering structures, like in bridges or roofs, because of their favourable load carrying capabilities. In practise, arches may be supported by pins at the ends to the ground or to adjacent members. Such members are often made of functionally graded material (FGM) with material properties continuously varying over the cross section.

Comprehensive studies on the in-plane buckling of arches were published in the past (Timoshenko and Gere 1961; Szeidl 1975; Simitses 1976; Bradford et al. 2002; Simitses and Hodges 2006; Bazant and Cedolin 2010). It is therefore well-known that geometrically nonlinear model is needed when analysing the stability of shallow members because the deformations prior to buckling can be significant and the behaviour can become nonlinear. Since then, various circular arch problems with numerous methods have been solved. Articles Plaut (2015a, b) focus on the critical displacements instead of critical forces. The analytical solutions are given for limit point buckling with pinned boundary conditions. Paper Silveira et al. (2013) presents a new numerical strategy for the nonlinear equilibrium and stability analysis of slender curved elements under unilateral constraints. It clarifies the influence of the foundation position and its stiffness on the nonlinear behavior and stability. Study (Zhou et al. 2015) report about analytical solutions of the stability and remote, unconnected equilibria of arbitrary shallow arches with non-symmetric geometric imperfections. In Asgari et al. (2014), a procedure is presented to trace the primary equilibrium path of functionally graded, pinned shallow arches under in-plane thermal load using the nonlinear Donnell shell theory. Investigations on the static buckling behaviour of steel arches with elastic horizontal and rotational end restraints with simulations and experiments can be found in Han et al. (2016). The authors of (Tsiatas and Babouskos 2017) develop an integral equation solution to the linear and nonlinear behaviour of thin shallow arches with varying cross section under a central concentrated load. The coupled differential equations are solved with the analog equation method. In Abdelgawad et al. (2013) the conditions of the static and dynamic snap-through of shallow arches resting on a two-parameter elastic foundation are studied. Article Rastgo et al. (2005) report on the thermal in- and out-of-plane buckling of FGM curved beams using the Galerkin method. Contributions (Liu and Jeffers 2017; Liu et al. 2017b; Liu and Jeffers 2018) present the isogeometric analysis of FG structural members, including snap-through instabilities in thermal environment.

Analytical solutions for pinned-pinned and fixed-fixed shallow arches subjected to a vertical dead load at the crown point are provided in Bradford et al. (2002) and Pi and Bradford (2008). Moreover, paper Pi et al. (2008) generalizes the results achieved in Bradford et al. (2002) for the case when the ends of the arch are rotationally restrained (there are pins with linear torsional springs). Further studies are published in Pi and Bradford (2012a) under the assumption that the torsional springs at the ends are different. Similar investigations, though, with a refined model are presented in Kiss (2014), Kiss and Szeidl (2015a) and Kiss and Szeidl (2015b) valid for cross sectional inhomogeneity.

Articles (Ting Yan et al. 2017, 2018a, b, c) report on the static stability of non-uniform shallow arches made of homogeneous material. Non-uniformity means three constant stiffness regions along the length of the arch. The Euler–Bernoulli hypothesis is used to find analytical solutions. Concentrated, distributed loads and various support conditions are investigated with geometrical imperfections also included. It is found that arches with stiffer center are favourable compared to arches with softer center. Studies (Bateni and Eslami 2014, 2015; Babaei et al. 2018) focus on the stability of FGM arches. Comprehensive analytical investigations are presented for both central concentrated and constant distributed loads using the classical shallow arch theory.

Despite concentrated crown load is really preferred in the literature, in practice, the load may act elsewhere. However, the influence of the load position has been under much less investigations. Early results for homogeneous members (Schreyer 1972; Plaut 1979) show the influence of the load position on the buckling load of shallow arches. The later article neglects the effect of axial compressive force and so overestimates the buckling load. Recently, some progress has been made in Pi et al. (2017) and Liu et al. (2017a). The authors have presented and evaluated an analytical Euler–Bernoulli model—the same as in Bradford et al. (2002)—to find the nonlinear equilibria and buckling load of fixed-fixed and pinned-fixed homogeneous shallow arches under arbitrary concentrated radial load. The authors have found that such arches have multiple stable equilibria and the load position has significant effects on the in-plane behaviour.

Based on the above literature research, in this paper it is intended to find how pinned-pinned FGM shallow arches behave when loaded by an arbitrary concentrated radial load. A refined single-layer Euler–Bernoulli theory is used and the equilibrium equations are gained from the principle of virtual work. Analytical solutions are provided for both limit point and bifurcation buckling to find the lowest buckling loads and nonlinear equilibria. Comprehensive studies are carried out to show the effect of certain geometric and material parameters on the buckling load and behaviour. The paper intends to improve and extend the existing results about pinned-pinned shallow arches under arbitrary concentrated radial load. The model introduced has further potential applications to dynamic problems, axially FG beams, non-shallow arches and to various structures and mechanisms with multiple stable configurations. Moreover, the analytical solutions can be used as benchmark for numerical solutions.

2 Mechanical model

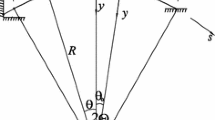
A pinned-pinned circular shallow arch is considered. The (E-weighted) centroidal axis is shown in Fig. 1, where the initial radius of curvature is $\rho$, the included angle is $\theta =2\vartheta$, the length of the arch is S while $\varphi$ and s are the angle and arc coordinates. The radial concentrated load P is applied at $\varphi =\alpha$. The arch has uniform, symmetric cross section made of FGM with the material composition being independent of $\xi$. The material properties, like the Young modulus E, are assumed to follow a power-law distribution along the thickness as (Babaei et al. 2018)

$$\begin{aligned} E(\zeta )=(E_c-E_m)\left( \frac{\zeta }{b} \right) ^k + E_m \end{aligned}$$

(1)

with subscripts c and m noting the ceramic and metallic constituents while b is the height of the cross section and k is the volume fraction index. Axis $\eta$ is a major principal axis. Using the Euler–Bernoulli hypothesis, the longitudinal normal strain at an arbitrary point is (Kiss and Szeidl 2015b)

$$\begin{aligned} \varepsilon _{\xi }=\frac{\rho }{\rho +\zeta }\left[ \frac{{\mathrm {d}}u}{ {\mathrm {d}}s}+\frac{w}{\rho }+\zeta \left( \frac{{\mathrm {d}}u}{\rho {\mathrm {d}}s }-\frac{{\mathrm {d}}^{2}w}{{\mathrm {d}}s^{2}}\right) \right] +\frac{1}{2}\left( \frac{u}{\rho }-\frac{{\mathrm {d}}w}{{\mathrm {d}}s}\right) ^{2}, \end{aligned}$$

(2)

with

$$\begin{aligned} \varepsilon _{L}=\frac{{\mathrm {d}}u}{{\mathrm {d}}s}+\frac{w}{\rho }\;,\qquad \kappa =\frac{{\mathrm {d}}u}{\rho {\mathrm {d}}s}-\frac{{\mathrm {d}}^{2}w}{\mathrm {d }s^{2}}\quad {\text {and}}\quad \psi = \frac{u}{\rho }-\frac{{\mathrm {d}}w}{ {\mathrm {d}}s}. \end{aligned}$$

(3)

Here $\varepsilon _{L}$ is the strain on the centroidal axis according to the classical linear theory (Timoshenko and Gere 1961), $\kappa$ is the curvature and $\psi$ is the mid-plane rotation about $\eta$. Therefore, the membrane strain at an arbitrary point on the centroidal axis ($\zeta =0$) is given by (Kiss and Szeidl 2015a; Pi and Bradford 2012b)

$$\begin{aligned} \varepsilon _{m}=\frac{{\mathrm {d}}u}{{\mathrm {d}}s}+\frac{w}{\rho }+\frac{1}{2} \left( \frac{u}{\rho }-\frac{{\mathrm {d}}w}{{\mathrm {d}}s}\right) ^{2} \end{aligned}$$

(4)

where u and w are the circumferential and lateral displacements. The third term on the right side is the source of nonlinearity—moderately large rotations are assumed. The E-weighted first moment of the cross section to $\eta$ on the centroidal axis vanishes: $Q_{e}=0$—see Eq. (7).

Fig. 1

The 1D beam model and the symmetric cross section

The material behaviour is assumed to be linearly elastic and isotropic, thus according to the Hooke law, the axial force N and the bending moment M can be expressed as (Kiss and Szeidl 2015b)

$$\begin{aligned} N= A_{e}\varepsilon _{m}-\frac{I_{e} }{\rho }\left( \frac{1}{\rho }\frac{{\mathrm {d}}u}{{\mathrm {d}}s}-\frac{\mathrm {d }^{2}w}{{\mathrm {d}}s^{2}}\right) ,\;\;\;M= -I_{e}\left( \frac{{\mathrm {d}}^{2}w}{{\mathrm {d}}s^{2}}+\frac{ w}{\rho ^{2}}\right) ,\;\;N+\frac{M}{\rho }=A_{e}\varepsilon _{m}. \end{aligned}$$

(5)

Thus, the effect of the bending moment on the membrane strain is accounted—see "Inner forces in terms of displacements" section in "Appendix" for the details. In the recent articles (Pi et al. 2008; Liu et al. 2017a; Ting Yan et al. 2018d) the following approximations can be found:

$$\begin{aligned} N\gg \frac{M}{\rho },\quad N=A_{e}\varepsilon _{m},\quad M=-I_{e}\frac{{\mathrm {d}}^{2}w}{{\mathrm {d}}s^{2}}. \end{aligned}$$

(6)

In the above equations

$$\begin{aligned} \left( A_{e},Q_{e},I_{e}\right) =\int _{A}E\times \left( \,1,\zeta ,\zeta ^{2}\right) \,{\mathrm {d}}A \end{aligned}$$

(7)

are the E-weighted area, E-weighted first moment- and moment of inertia to major principal axis $\eta .$

3 Pre and post-buckling equilibrium

Since the pre-buckling deformations are significant for shallow arches (Dimopoulos and Gantes 2008a, b), these effects must be included. The principle of virtual work is used to find the nonlinear pre-buckling equilibrium configuration of pinned-pinned shallow arches under an arbitrary concentrated radial load. This principle requires that

$$\begin{aligned} \int _{V}\sigma _{\xi }\delta \varepsilon _{\xi }\,{\mathrm {d}}V-P\left. \delta w\right| _{\varphi =\alpha }=0 \end{aligned}$$

(8)

to be satisfied for every kinematically admissible virtual field $\delta ()$. From this principle—with the details gathered in "Pre-buckling equilibrium equations" section in "Appendix"—the following equilibrium equations are found

$$\begin{aligned} \frac{{\mathrm {d}}N}{{\mathrm {d}}s}+\frac{1}{\rho }\left[ \frac{{\mathrm {d}}M}{ {\mathrm {d}}s}-\left( N+\frac{M}{\rho }\right) \psi \right]= & {} 0, \end{aligned}$$

(9)

$$\begin{aligned} \frac{{\mathrm {d}}}{{\mathrm {d}}s}\left[ \frac{{\mathrm {d}}M}{{\mathrm {d}}s}-\left( N+\frac{M}{\rho }\right) \psi \right] -\frac{N}{\rho }= & {} 0. \end{aligned}$$

(10)

In terms of strains and displacements—see "Pre-buckling equilibrium equations" section in "Appendix"—these become

$$\begin{aligned} \varepsilon _{m}^{^{\prime }}=0,\;\;\;\;\;\;\; W^{''''}+\left( \chi ^{2}+1\right) W^{^{\prime \prime }}+\chi ^{2}W=\chi ^{2}-1,\, \end{aligned}$$

(11)

with $W=w/\rho$, $U=u/\rho$ being dimensionless displacements, ${\mathrm {d}} ()/{\mathrm {d}}s=\left( {}\right) ^{^{\prime }}$, and

$$\begin{aligned} \chi ^{2}=1-\mu \varepsilon _{m};\qquad \mu =\frac{A_{e}\rho ^{2}}{I_{e}}=\frac{\rho ^{2}}{r^{2}};\qquad \lambda =\sqrt{\mu }\vartheta ^2. \end{aligned}$$

(12)

All of Eq. (12) depend on the material composition and geometry, and $\lambda$ is the (E-weighted) modified slenderness of the arch (Liu et al. 2017a). So, the effect of the geometry and material distribution is incorporated into the model through these parameters, with r being the (E-weighted) radius of gyration of the cross section about its major principal axis $\eta$. Equation (11)$_1$ expresses that the membrane strain is constant while Eq. (11)$_2$ is comparable to the likes of (Bateni and Eslami 2014; Ting Yan et al. 2018d). The major reasons of the differences: the simplification $\rho +\zeta \simeq \rho$ is not implied throughout this model, the effect of the circumferential displacement field u is kept in $\psi$ when deriving Eq. (11)$_2$ and the inequality $N\gg M/\rho$ is not considered.

Differential equations (11) are paired with boundary and (dis-)continuity conditions. The displacements and bending moment are zero at the supports, while all fields are continuous at the tip of the external force except the shear force distribution which has a discontinuity with magnitude P. Recalling Eqs. (5), all these conditions can be given in terms of the dimensionless lateral displacement as

$$\begin{aligned} \left. W\right| _{\varphi =-\vartheta }= & {} \left. W^{^{\prime \prime }}\right| _{\varphi =-\vartheta }=\left. W\right| _{\varphi =\vartheta }=\left. W^{^{\prime \prime }}\right| _{\varphi =\vartheta }=0, \end{aligned}$$

(13)

$$\begin{aligned} \left. W\right| _{\varphi =-\alpha }= & {} \left. W\right| _{\varphi =+\alpha }\qquad \left. W^{^{\prime }}\right| _{\varphi =-\alpha }=\left. W^{\prime }\right| _{\varphi =+\alpha }, \end{aligned}$$

(14)

$$\begin{aligned} \left. W^{^{\prime \prime }}\right| _{\varphi =-\alpha }= & {} \left. W^{^{\prime \prime }}\right| _{\varphi =+\alpha }\qquad -\left. W^{^{^{\prime \prime \prime }}}\right| _{\varphi =-\alpha }+\left. W^{^{\prime \prime \prime }}\right| _{\varphi =+\alpha }=-\frac{2 {\mathcal {P}}}{\vartheta }, \end{aligned}$$

(15)

where ${\mathcal {P}}$ is the dimensionless load defined by ${\mathcal {P}}=\frac{P\rho ^{2}\vartheta }{2I_{e}}$.

To find the post-buckling equilibrium state, let us decompose the typical quantities. Let, e.g., the total lateral displacement be $w^{*}=w+w_{b}$, where w is the pre-buckling- and $w_b$ is the buckling displacement. With this rule, similarly as in "Inner forces in terms of displacements" section in "Appendix", the following expressions are found for the buckling strain, axial force and bending moment:

$$\begin{aligned} \varepsilon _{\xi b}= & {} \frac{\rho }{\rho +\zeta }\left[ \frac{{\mathrm {d}}u_{b}}{ {\mathrm {d}}s}+\frac{w_{b}}{\rho }+\zeta \frac{{\mathrm {d}}\psi _{b}}{{\mathrm {d}}s }\right] +\psi \psi _{b}, \end{aligned}$$

(16)

$$\begin{aligned} \varepsilon _{mb}= & {} \frac{{\mathrm {d}}u_{b}}{{\mathrm {d}}s}+\frac{w_{b}}{\rho } +\left( \frac{u}{\rho }-\frac{{\mathrm {d}}w}{{\mathrm {d}}s}\right) \left( \frac{ u_{b}}{\rho }-\frac{{\mathrm {d}}w_{b}}{{\mathrm {d}}s}\right) , \end{aligned}$$

(17)

$$\begin{aligned} \varepsilon _{Lb}= & {} \frac{{\mathrm {d}}u_b}{{\mathrm {d}}s}+\frac{w_b}{\rho }\;,\qquad \kappa _{b}=\frac{{\mathrm {d}}u_b}{\rho {\mathrm {d}}s}-\frac{{\mathrm {d}}^{2}w_b}{ {\mathrm {d}}s^{2}},\quad \psi _{b}= \frac{u_b}{\rho }-\frac{ {\mathrm {d}}w_b}{{\mathrm {d}}s}, \end{aligned}$$

(18)

$$\begin{aligned} N_{b}= & {} A_{e}\varepsilon _{mb}-\frac{M_{b}}{\rho },\qquad M_{b}=-I_{e}\left( \frac{{\mathrm {d}}^{2}w_{b}}{{\mathrm {d}}s^{2}}+\frac{w_{b}}{\rho ^{2}}\right) . \end{aligned}$$

(19)

Applying the principle of virtual work for the buckled equilibrium configuration

$$\begin{aligned} \int _{V}\sigma _{\xi }^{*}\delta \varepsilon _{\xi }^{*}\,{\mathrm {d}} V-P^{*}\left. \delta w^{*}\right| _{\varphi =\alpha }=0 \end{aligned}$$

(20)

has to be fulfilled. Following the integration by parts theorem, as detailed in "Buckled equilibrium configuration" section in "Appendix", it is found that the inner forces should satisfy equilibrium equations

$$\begin{aligned} \frac{{\mathrm {d}}N_{b}}{{\mathrm {d}}s}+\frac{{\mathrm {d}}M_{b} }{{\rho\mathrm {d}}s}-\left( \frac{N+N_b}{\rho}+\frac{M+M_b}{\rho^2 }\right) \psi _{b}= & {} 0\;, \end{aligned}$$

(21a)

$$\begin{aligned} \frac{{\mathrm {d}}^{2}M_{b}}{{\mathrm {d}}s^{2}}-\frac{N_{b}}{\rho }-\frac{ {\mathrm {d}}}{{\mathrm {d}}s}\left[ \left( N+N_{b}+\frac{M+M_{b}}{\rho } \right) \psi _{b}+\left( N_{b}+\frac{M_{b}}{\rho }\right) \psi \right]= & {} 0. \end{aligned}$$

(21b)

As shown in "Buckled equilibrium configuration" section in "Appendix", these relations can be given in terms of the kinematical quantities as

$$\begin{aligned} \varepsilon _{m\,b}^{^{\prime }}= & {} 0, \end{aligned}$$

(22)

$$\begin{aligned} W_{b}^{^{\prime \prime \prime \prime }}+(\chi ^{2}+1)W_{b}^{^{\prime \prime }}+\chi ^{2}W_{b}=\mu \varepsilon _{mb}\left[ 1-\left( W^{^{\prime \prime }}+W\right) \right] \;,\qquad W_{b}= & {} w_{b}/\rho . \end{aligned}$$

(23)

These results are again comparable to the achievements of (Pi et al. 2008; Bateni and Eslami 2014). The related boundary and continuity conditions are

$$\begin{aligned} \left. W_{b}\right| _{\varphi =-\vartheta }=\left. W_{b}^{^{\prime \prime }}\right| _{\varphi =-\vartheta }=\left. W_{b}\right| _{\varphi =\vartheta }=\left. W_{b}^{^{\prime \prime }}\right| _{\varphi =\vartheta }=0, \end{aligned}$$

(24)

$$\begin{aligned} \left. W_{b}\right| _{\varphi =-\alpha }= & {} \left. W_{b}\right| _{\varphi =+\alpha }\qquad \left. W_{b}^{^{\prime }}\right| _{\varphi =-\alpha }=\left. W_{b}^{\prime }\right| _{\varphi =+\alpha }, \end{aligned}$$

(25)

$$\begin{aligned} \left. W_{b}^{^{\prime \prime }}\right| _{\varphi =-\alpha }= & {} \left. W_{b}^{^{\prime \prime }}\right| _{\varphi =+\alpha }\qquad \left. W_{b}^{^{^{\prime \prime \prime }}}\right| _{\varphi =-\alpha }=\left. W_{b}^{^{\prime \prime \prime }}\right| _{\varphi =+\alpha } \end{aligned}$$

(26)

with all the fields being continuous at $\varphi =\alpha$ as there is no load increment.

4 Analytical solutions

4.1 Pre-buckling state

The general solution satisfying equation (11)$_2$ is

$$\begin{aligned} W(\varphi )=\frac{\chi ^{2}-1}{\chi ^{2}}+X_{1}\cos \varphi +X_{2}\sin \varphi -\frac{X_{3}}{\chi ^{2}}\cos \chi \varphi -\frac{X_{4}}{\chi ^{2}}\sin \chi \varphi . \end{aligned}$$

(27)

Plugging it to conditions (13)–(14), a system of linear algebraic equations can be set for the constants $X_{i}$. The closed-form solutions are given in "Coefficients in the pre-buckling displacement field and the pre-buckling average strain" section in "Appendix".

Since the membrane strain is constant on the centroidal axis, it is therefore equal to the average membrane strain:

$$\begin{aligned} \varepsilon _{m}=\frac{1}{2\vartheta }\int _{-\vartheta }^{\vartheta }\varepsilon _{m}(\varphi ){\mathrm {d}}\varphi ={\text {constant}}. \end{aligned}$$

(28)

Recalling Eq. (4), the nonlinear equilibrium condition for pinned-pinned shallow arches is found to be

$$\begin{aligned} \int _{-\vartheta }^{\vartheta }\varepsilon _{m}(\varphi ){\mathrm {d}}\varphi \simeq \int _{-\vartheta }^{\vartheta }\left[ U^{^{\prime }}+W+\frac{1}{2} \left( W^{^{\prime }}\right) ^{2}\right] {\mathrm {d}}\varphi -2\vartheta \varepsilon _m =K_{0}+K_{1} {\mathcal {P}}+K_{2}{\mathcal {P}}^{2}. \end{aligned}$$

(29)

Here, the effect of the circumferential displacement on the rotation field was dropped. This assumption is generally accepted for shallow arches (Ting Yan et al. 2018a). The constants $K_{0}$, $K_{1}$ and $K_{2}$ are given in "Coefficients in the pre-buckling displacement field and the pre-buckling average strain" section in "Appendix".

4.2 Buckled equilibrium

It is well known (Bradford et al. 2002) that for certain shallow arches it is possible that the pre-buckling equilibrium path changes to an infinitesimally close orthogonal path with $\varepsilon _{mb}=0$. Based on Eq. (23), this phenomenon is characterized by the homogeneous equation

$$\begin{aligned} W_{b}^{^{\prime \prime \prime \prime }}+(1+\chi ^{2})W_{b}^{^{\prime \prime }}+\chi ^{2}W_{b}=0\;, \end{aligned}$$

(30)

whose general solution is

$$\begin{aligned} W_{b}(\varphi )=F_{1}\cos \varphi +F_{2}\sin \varphi +F_{3}\sin \chi \varphi +F_{4}\cos \chi \varphi ;\;\; F_i \in {\mathbb {R}} . \end{aligned}$$

(31)

Equation (31) and boundary conditions (24) determine a homogeneous linear system of algebraic equations. The lowest physically possible nontrivial solution is $\sin \chi \vartheta =0$$\rightarrow$$\chi \vartheta =\pi$ (Bradford et al. 2002).

Therefore, the (critical) buckling strain for bifurcation buckling is

$$\begin{aligned} \varepsilon _{m}=-\frac{1}{\mu }\left[ \left( \frac{ \mathfrak {\pi }}{\vartheta }\right) ^{2}-1\right] , \end{aligned}$$

(32)

with the associated antisymmetric buckled arch shape being $W_{b}(\varphi )=F_{3}\sin ({\pi \varphi }/{\vartheta })$. Plugging Eq. (32) to (29) yields the buckling load for bifurcation buckling.

From (17), the average buckling strain for shallow arches is

$$\begin{aligned} \frac{1}{2\vartheta }\int _{-\vartheta }^{\vartheta }\varepsilon _{mb}(\varphi ){\mathrm {d}}\varphi \simeq \frac{1}{2\vartheta }\int _{-\vartheta }^{\vartheta }\left[ U_{b}^{^{\prime }}+W_{b}+W^{^{\prime }}W_{b}^{^{\prime }}\right] {\mathrm {d}} \varphi , \end{aligned}$$

(33)

which has to vanish for bifurcation buckling. The first term on the right is zero because of the supports. Since the pre-buckling and buckling lateral displacements are orthogonal for bifurcation buckling, the third term is as well zero, meaning that the second term should also vanish. This buckling displacement, however, vanishes only if $W_{b}(\varphi )=-W_{b}(\varphi )$, i.e., when the buckling displacement is antisymmetric in $\varphi$. It is only possible for radial loads exerted at the crown. Hence, if the position of the load is arbitrary $(\varphi =\alpha \ne 0)$, bifurcation buckling can not occur for pinned-pinned shallow arches.

However, when there is strain increment after buckling, equation (23) governs the problem. The general solution to this inhomogeneous differential equation is

$$\begin{aligned} W_{b}(\varphi )& = {} Y_{1}\cos \varphi +Y_{2}\sin \varphi +Y_{3}\sin \chi \varphi +Y_{4}\cos \chi \varphi \\&\quad - \frac{\mu \varepsilon _{mb}}{2\chi ^{3}}\left( \frac{2}{\chi }+X_{3}\varphi \sin \chi \varphi -X_{4}\varphi \cos \chi \varphi \right) . \end{aligned}$$

(34)

With the boundary- (24) and continuity conditions (25–(26), determination of the constants $Y_{i}$ is possible with the results provided in "Coefficients in the buckling displacement and average buckling strain increment" section in "Appendix". Furthermore, using kinematical equations (17)–(18) with (22) leads to

$$\begin{aligned} \varepsilon _{mb}\simeq \frac{1}{2\vartheta }\int _{-\vartheta }^{\vartheta }\left( U_{b}^{^{\prime }}+W_{b}+W^{^{\prime }}W_{b}^{^{\prime }}\right) {\mathrm {d}} \varphi \end{aligned}$$

(35)

which is the nonlinear relationship between the strain parameter $\chi$ and the dimensionless load ${\mathcal {P}}$. Thus, a quadratic equation

$$\begin{aligned} L_{0}+L_{1}\mathcal {P+}L_{2}{\mathcal {P}}^{2}=0 \end{aligned}$$

(36)

is achieved with constants $L_{0},L_1$ and $L_2$ defined in "Coefficients in the post-buckling average strain" section in "Appendix". Solutions for limit point buckling can be evaluated in terms of the geometry and material distribution by solving nonlinear Eqs. (29) and (36) simultaneously.

5 Results and discussion

To verify the new model, first, the commercial finite element software Abaqus 6.13 (Abaqus 2017) was used. A square cross section was considered with r being 0.108 m and the constant Young modulus E of 200 GPa. In the one-dimensional, geometrically nonlinear beam model eighty B21 elements and the Static, Riks step were used. The boundary and load conditions were assigned in polar coordinate system. The equilibrium paths are shown by diamond symbols on Figs. 5, 6 and a very good correlation is found between the current model and the Abaqus computations. Some further comparisons were also carried out with focus on the buckling loads. The typical values are gathered in Table 1.

Table 1 Comparison of the results with Abaqus

Table 2 Verification of the results with Bateni and Eslami (2014) when $\vartheta ^2 \rho /b=8.5$; $\alpha =0$

Some additional comparisons were performed with the analytical results of (Bateni and Eslami 2014) valid for FG arches under crown load. The arch with rectangular cross section is made of Silicon nitride $Si_3N_4$ and stainless steel SUS304. The Young modulus of the ceramic and metallic parts are $E_c=348.43$ GPa and $E_m=201.04$ GPa. Four power law indices were selected. A very good agreement was found as shown in Table 2. Using the same geometry and materials, further 3D Abaqus computations were also performed using C3D8R elements. The body was composed of 25 perfectly tied layers along the thickness with the effective material parameters being constant in each layer. Results are shown in Table 3.

Table 3 Comparisons with 3D Abaqus computations

Evaluation of the new model reveal that when the load is central, there are three typical kinds of behaviour. The geometrical limits for these are almost constant in the slenderness as shown in Fig. 2a. When $\lambda (\mu =10^{3} \ldots 10^{6})\approx \lambda <3.91$, there is no buckling. After that, there is possibly limit point buckling with symmetric buckled shape and then, for most arches ($\lambda >\approx 9.81$), bifurcation buckling occurs first with antisymmetric buckled shape. When the external load is placed elsewhere, there is either no buckling or limit point buckling. The slenderness limits against the load position between these two ranges are shown in Fig. 2b for three magnitudes of $\mu$.

Fig. 2

Typical buckling ranges for a central load; b arbitrary load

To demonstrate the significant effect of the modified slenderness and the load position on the nonlinear in-plane behaviour of shallow arches, some the typical equilibrium paths for $S/r=200$ are shown in Figs. 3, 4, 5 and 6 with $W_{\alpha }=W(\varphi =\alpha )/(1-\cos \vartheta )$ as the dimensionless displacement at the tip of the load and $\varepsilon _{str.}= \left( 2\pi {r}/{S} \right) ^2$ being the second mode buckling strain of a pin-ended column under compression with the same cross section and material distribution as the selected arch (Bradford et al. 2002). Structural members with $\lambda =3.1$ show no buckling behaviour. There is nonlinear bending only, and the load position already has visible influence on the equilibrium path (Fig. 3). When the slenderness is set to 6.1, one upper and one lower limit point appear (Fig. 4) with two stable and one unstable branch. The buckling load increases with the selected load positions and the critical (buckling) strain is always less than for a straight member.

Fig. 3

Effect of load position on arches with $\lambda =3.1$: dimensionless load in terms of a dimensionless displacement; b strain ratio

Fig. 4

Effect of load position on arches with $\lambda =6.1$: dimensionless load in terms of a dimensionless displacement; b strain ratio

Fig. 5

Effect of load position on arches with $\lambda =10.1$: dimensionless load in terms of a dimensionless displacement; b strain ratio

Increasing the slenderness to 10.1 (Fig. 5) reveals that the number of limit points increase with $\lambda$. Although there is still one upper and one lower limit point when the load is at the crown, there are two upper and two lower limits for any other load position. When $\alpha =0$, there are two further bifurcation points, one on the primary stable and one on the remote stable branch. The critical strain for bifurcation buckling is lower and thus, it occurs first. However, for other load position parameters, there is only limit point buckling. The number of equilibrium branches also increases when $\alpha \ne 0$: two stable ones (primary and remote) and three unstable ones can be found. One typical load is related to two stable and three unstable equilibrium points. It is also noticed that meanwhile the lowest buckling loads for $\alpha =0$ and 0.6 are almost identical, the in-plane behaviour is completely different. At $\varepsilon _m/\varepsilon _{str.}=1$ there is an intersection point of the typical curves in Fig. 5b and the lowest critical strain is always less than $\varepsilon _{str}$. Further upper and lower limit points and equilibrium branches appear when $\lambda =14.3$ with bifurcation points located on the stable branches for crown loads as shown in Fig. 6. The total number of limit points for α > 0 is now six, with additional equilibrium branches. From the previous figures it is understood that the modified slenderness and the load position both have significant effects on the nonlinear behaviour: on the number of equilibrium branches, on the number of limit points and on the critical loads.

Fig. 6

Effect of load position on arches with $\lambda =14.3$: dimensionless load in terms of a dimensionless displacement; b strain ratio

Some related arch shapes in the pre-buckling equilibrium are shown in Fig. 7 with normalized displacements ${\bar{W}}$ against the arc coordinate s. The effect of both the slenderness and the load position are clearly visible.

Fig. 7

Some arch shapes: normalized displacement in terms of arc coordinate

The effect of the load position parameter on the buckling load is evaluated in Figs. 8 and 9. Because the end supports are identical, only positive parameters are selected. When $\mu =10^3$ and $\vartheta =0.4$ the buckling load gradually increases with $\alpha$. Otherwise, for any other selected parameter set, replacing the load from the crown causes the lowest buckling load decrease for a while. This decrease is more remarkable when $\mu$ is smaller and $\vartheta$ is greater. Overall, it can be seen, the load position can almost halve the buckling load compared to ${\mathcal {P}}(\alpha =0)={\mathcal {P}}(0)$. After reaching this lower limit, there is an increase and the load bearing capabilities of arches become even better when the load is placed in the direct vicinity of the supports. The effect of the load position and included angle have the greatest influence when $\mu =10^{3}$ and least when $\mu =10^{5}.$

Fig. 8

Effect of load position on buckling load when a$\mu =10^3$; b$\mu =10^4$

Fig. 9

Effect of load position on buckling load when $\mu =10^5$

Next, the lowest critical loads are shown in Figs. 10 and 11 in terms of $\lambda$ and $\vartheta$ for arches with $S/r=100$ and 200. Initially, the critical load increases steeply and after reaching the peak, there is a slow decrease. It is also visible that a small imperfection in the load position—e.g., $\alpha /\vartheta =0.1$ instead of 0—has quite a huge impact for most parameter sets. Increasing the ratio S / r shifts the typical curves to the left (buckling occurs for lower angles). It can be concluded that, independently of the load position parameter, arches with the same slenderness (or included angle) have better load carrying capabilities when S / r is greater.

Fig. 10

Buckling loads when $S/r=100$: in terms of a modified slenderness; b semi-vertex angle

Fig. 11

Buckling loads when $S/r=200$: in terms of a modified slenderness; b semi-vertex angle

In Figs. 12, 13 and 14 it is investigated how the dimensionless buckling load varies with the semi-vertex angle and the modified slenderness. Three magnitudes of parameter $\mu$ are selected: $10^{3},10^{4},10^{5}$ and four load positions are chosen for the illustrations: $\alpha /\vartheta =\left\{ 0;0.1;0.3;0.6\right\} .$

Fig. 12

Lowest critical load if $\mu =10^3$: in terms of a modified slenderness; b semi-vertex angle

Fig. 13

Lowest critical load if $\mu =10^4$: in terms of a modified slenderness; b semi-vertex angle

Fig. 14

Lowest critical load if $\mu =10^5$: in terms of a modified slenderness; b semi-vertex angle

There are many common findings in these diagrams. For lowest $\lambda , \vartheta$ parameters, there is no buckling. When the load is at the crown, limit point buckling occurs first for small angles, then bifurcation type is dominant. When the load is replaced from the crown, only limit point buckling can occur. Due to a small perturbation in the load position parameter around the crown, (e.g., $\alpha /\vartheta =0.1$—it is only $5\%$ of the included angle), for a short while, the typical buckling load is actually unchanged but with $\vartheta$ or $\lambda$ increasing, the effect of this small imperfection becomes really considerable. Depending on the parameters, the dimensionless buckling load can decrease by up to $20\%$ compared to crown load. When the load position parameter is changed from zero, the critical load decreases for a while but after that there is an increase. This finding is in accord with Figs. 8 and 9. There is always an intersection between the curves for $\alpha =0$ and $\alpha \ne 0$ in the figures. Thus, for certain arches, the buckling loads might be identical but with completely different buckled shapes and nonlinear behaviour.

When comparing Figs. 12, 13 and 14 it is visible that increasing $\mu$ makes the curves shift to the left: buckling behaviour appears for smaller angles and the related buckling load increases for any given $\vartheta$ and $\alpha$. When the semi-vertex angle and the load position are both prescribed, we find greater buckling loads when $\mu$ is greater. When $\alpha =0$ the findings correspond with the results in Kiss and Szeidl (2015b) valid for pinned-pinned shallow arches under a central concentrated load.

The next example attempts to demonstrate the possible effect of the material distribution on the buckling load. The arch with rectangular cross section is made of Silicon nitride $Si_3N_4$ and stainless steel SUS304. The material distribution follows the Voigt rule of Eq. (1). If $k=0$, the arch is made of ceramic, while if $k=10^5$ (tends to infinity) the material is pure steel with one thin ceramic layer at the top. The power law index k is varied continuously between 0 and 5. In Fig. 15a it is shown how the ratios $A_e(k\ne 0)/A_e({k=10^5})$; $I_e(k\ne 0)/I_e({k=10^5})$—defined by Eq. (7)—depend on the power law index. The maximum value is 1.77 times of the homogeneous steel for both, and remain considerably above 1 between $k=0 \ldots 5$. In Fig. 15b it is shown how the radius of the centroidal axis changes with the material distribution. The plotted ratio depends on $\rho /b$, but overall, this effect is not relevant. Next, it is investigated how the material distribution affects the buckling load. For $k=10^5$, S / r was set to 200 and $r=0.108$ m, as formerly. Various central angles, load positions and radius/cross sectional height ratios were selected, and it is found that the results plotted in Fig. 16, i.e., the critical load ratio $P(k\ne 0)/P(k=10^5)$, are independent of these with a good accuracy. It is also clear that the power law index has a huge impact on the lowest critical load.

Fig. 15

Variation of some cross sectional properties: a$A_e(k), I_e(k)$b$\rho (k)$

Fig. 16

The effect of material distribution on the buckling load

6 Conclusions

The nonlinear in-plane buckling behaviour of FGM shallow circular arches under an arbitrary concentrated radial load was investigated using a refined beam model. The effect of the bending moment on the membrane strain was accounted. The pre-buckling and buckled equilibrium equations were obtained from the principle of virtual work. Analytical solutions to these equations were presented for both bifurcation and limit point buckling. Parametric studies revealed that arches have multiple stable and unstable equilibrium branches. When the load is at the crown, the lowest buckling load is generally related to bifurcation buckling but for most arches and any other load positions, there is only limit point buckling. Changing the position of the load can almost halve the critical load compared to a force exerted at the crown. Moving the load close to the support causes the buckling load become even multiple times of crown load. Most arches are sensitive to small loading imperfections when the load is in the vicinity of the crown. This phenomenon requires further thorough investigations. The effect of the load position can become quite considerable as the load carrying capabilities decrease rapidly. The effects of various geometrical and material parameters on the behaviour and buckling load were shown through comprehensive studies.

Appendix

1.1 Inner forces in terms of displacements

Comparing Eqs. (2)–(4) and (7) yields the axial force and bending moment as in Eq. (5):

$$\begin{aligned} N& = {} \int _{A}\sigma _{\xi }\,{\mathrm {d}}A=\int _{A}E\varepsilon _{\xi }\,\mathrm {d }A=\int _{A}E\frac{\rho }{\rho +\zeta }\,{\mathrm {d}}A\varepsilon _{L}+\int _{A}E\zeta \frac{\rho }{\rho +\zeta }\,{\mathrm {d}}A\kappa +\int _{A}E\,{\mathrm {d}}A\frac{1}{2}\psi ^{2} \\ & \simeq {} A_{e}\varepsilon _{L}-\frac{I_{e}}{\rho }\kappa +A_{e}\frac{1}{2}\psi ^{2}=A_{e}\varepsilon _{m}-\frac{I_{e}}{\rho }\kappa \;, \end{aligned}$$

(37)

$$\begin{aligned} M& = {} \int _{A}\sigma _{\xi }\,{\mathrm {d}}A=\int _{A}E\varepsilon _{\xi }\zeta \, {\mathrm {d}}A=\int _{A}E\left( \frac{\rho }{\rho +\zeta }\left( \varepsilon _{L}+\zeta \kappa \right) +\frac{1}{2}\psi ^{2}\right) \zeta \,{\mathrm {d}}A \\& = {} \int _{A}E\frac{\rho }{\rho +\zeta }\,{\mathrm {d}}A\varepsilon _{L}+\int _{A}E\zeta ^{2}\frac{\rho }{\rho +\zeta }\,{\mathrm {d}}A\kappa +\int _{A}E\zeta \,{\mathrm {d}}A\frac{1}{2}\psi ^{2} \\& \simeq {} -\frac{I_{e}}{\rho }\left( \frac{{\mathrm {d}}u}{{\mathrm {d}}s}+\frac{w}{ \rho }\right) -I_{e}\frac{{\mathrm {d}}}{{\mathrm {d}}s}\left( \frac{{\mathrm {d}}w}{ {\mathrm {d}}s}-\frac{u}{\rho }\right) =-I_{e}\left( \frac{{\mathrm {d}}^{2}w}{ {\mathrm {d}}s^{2}}+\frac{w}{\rho ^{2}}\right) \;. \end{aligned}$$

(38)

Therefore

$$\begin{aligned} N& = {} A_{e}\left( \frac{{\mathrm {d}}u}{{\mathrm {d}}s}+\frac{w}{\rho }+\frac{1}{2} \psi ^{2}\right) +\frac{I_{e}}{\rho }\frac{{\mathrm {d}}}{{\mathrm {d}}s}\left( \frac{{\mathrm {d}}w}{{\mathrm {d}}s}-\frac{u}{\rho }\right) \\& = {} \frac{I_{e}}{\rho ^{3}}\left[ \left( \frac{A_{e}\rho ^{2}}{I_{e}}-1\right) \left( u^{^{\prime }}+w\right) +w^{^{\prime \prime }}+w\right] +\frac{1}{2} \psi ^{2}\left( \frac{A_{e}\rho ^{2}}{I_{e}}-1+1\right) \frac{I_{e}}{\rho ^{2}} \\& = {} \frac{I_{e}}{\rho ^{2}}\left( \frac{A_{e}\rho ^{2}}{I_{e}}-1\right) \left( \frac{1}{\rho }\left( u^{^{\prime }}+w\right) +\frac{1}{2}\psi ^{2}\right) + \frac{I_{e}}{\rho ^{3}}\left( w^{^{\prime \prime }}+w\right) \\& = {} \frac{I_{e}}{\rho ^{2}}\left( \frac{A_{e}\rho ^{2}}{I_{e}}-1\right) \varepsilon _{m}-\frac{M}{\rho }\simeq A_{e}\varepsilon _{m}-\frac{M}{\rho } \;. \end{aligned}$$

(39)

It can easily be shown that similar relations can be set up for the increments $N_b$ and $M_b$ as given by Eq. (19).

1.2 Pre-buckling equilibrium equations

With ${\mathrm {d}}V=\left( 1+{\zeta }/{\rho }\right) {\mathrm {d}}s\,{\mathrm {d}}A$ being the infinitesimal volume element, the first term in the principle of virtual work (8) can be expanded by recalling Eqs. (2)–( 7) as

$$\begin{aligned} \int _{V}\sigma _{\xi }\delta \varepsilon _{\xi }\,{\mathrm {d}}V& = {} \int _{\mathcal { L}}\int _{A}\left( 1+\frac{\zeta }{\rho }\right) \sigma _{\xi }\left[ \frac{ \rho }{\rho +\zeta }\left( \frac{{\mathrm {d}}\delta u}{{\mathrm {d}}s}+\frac{ \delta w}{\rho }+\zeta \frac{{\mathrm {d}}\delta \psi }{{\mathrm {d}}s}\right) +\psi _{\,}\delta \psi \right] {\mathrm {d}}A\,{\mathrm {d}}s \\& = {} \int _{{\mathcal {L}}}\left\{ \int _{A}\sigma _{\xi }{\mathrm {d}}A\left( \frac{ {\mathrm {d}}\delta u}{{\mathrm {d}}s}+\frac{\delta w}{\rho }\right) +\int _{A}\zeta \sigma _{\xi }{\mathrm {d}}A\frac{{\mathrm {d}}\delta \psi }{ {\mathrm {d}}s}+\int _{A}\left( 1+\frac{\zeta }{\rho }\right) \sigma _{\xi \,} {\mathrm {d}}A\psi \left( \frac{\delta u}{\rho }-\frac{{\mathrm {d}}\delta w}{ {\mathrm {d}}s}\right) \right\} {\mathrm {d}}s \\& = {} \int _{{\mathcal {L}}}\left[ N\left( \frac{{\mathrm {d}}\delta u}{{\mathrm {d}}s}+ \frac{\delta w}{\rho }\right) +M\frac{{\mathrm {d}}\delta \psi }{{\mathrm {d}}s} +\left( N+\frac{M}{\rho }\right) \psi \left( \frac{\delta u}{\rho }-\frac{ {\mathrm {d}}\delta w}{{\mathrm {d}}s}\right) \right] {\mathrm {d}}s. \end{aligned}$$

(40)

Integrating now by parts yields

$$\begin{aligned}&-\int _{{\mathcal {L}}}\left( \frac{{\mathrm {d}}N}{{\mathrm {d}}s}+\frac{1}{\rho } \frac{{\mathrm {d}}M}{{\mathrm {d}}s}-\frac{1}{\rho }\left( N+\frac{M}{\rho } \right) \psi \right) \delta u{\mathrm {d}}s-\int _{{\mathcal {L}}}\left( \frac{ {\mathrm {d}}^{2}M}{{\mathrm {d}}s^{2}}-\frac{N}{\rho }-\frac{{\mathrm {d}}}{\mathrm {d }s}\left( N+\frac{M}{\rho }\right) \psi \right) \delta w{\mathrm {d}}s \\&\quad -\left. \left[ \frac{{\mathrm {d}}M}{{\mathrm {d}}s}-\left( N+\frac{M}{\rho } \right) \psi \right] \delta w\right| _{s=-\rho \vartheta }+\left. \left[ \frac{{\mathrm {d}}M}{{\mathrm {d}}s}-\left( N+\frac{M}{\rho }\right) \psi \right] \delta w\right| _{s=\rho \vartheta } \\&\quad +\left\{ \left. \left[ \frac{{\mathrm {d}}M}{{\mathrm {d}}s}-\left( N+\frac{M}{ \rho }\right) \psi \right] \right| _{s=+\rho \alpha }-\left. \left[ \frac{{\mathrm {d}}M}{{\mathrm {d}}s}-\left( N+\frac{M}{\rho }\right) \psi \right] \right| _{s=-\rho \alpha }-P\right\} \left. \delta w\right| _{s=\rho \alpha } \\&\quad + \left. N\delta u\right| _{s=-\rho \vartheta }+\left. N\delta u\right| _{s=\rho \vartheta }+\left. M\right| _{s=\rho \vartheta }\left. \delta \psi \right| _{s=\rho \vartheta }-\left. M\right| _{s=-\rho \vartheta }\left. \delta \psi \right| _{s=-\rho \vartheta }=0. \end{aligned}$$

(41)

The arbitrariness of the virtual displacements $\delta u$, $\delta w$ gives the pre-buckling equilibrium equations (9). Plugging (5) to (9)$_1$ yields that the membrane strain is constant:

$$\begin{aligned} \left( A_{e}\varepsilon _{m}\right) ^{^{\prime }}-A_{e}\varepsilon _{m}\psi \simeq A_{e}\varepsilon _{m}' =0. \end{aligned}$$

(42)

The following transformations on Eq. (9)$_2$, with Eqs. (2)–(5)

$$\begin{aligned}&\frac{N}{\rho }=\frac{A_{e}}{\rho }\varepsilon _{m}-\frac{M}{\rho ^{2}}= \frac{I_{e}}{\rho ^{3}}\frac{A_{e}\rho ^{2}}{I_{e}}\varepsilon _{m}-\frac{M}{ \rho ^{2}}=\frac{I_{e}}{\rho ^{3}}\mu \varepsilon _{m}+\frac{I_{e}}{\rho ^{4} }\left( w^{\prime {\prime }}+w\right) \;, \end{aligned}$$

(43)

$$\begin{aligned}&-\frac{I_{e}}{\rho ^{4}}\left( w^{^{\prime \prime \prime \prime }}+w^{^{\prime \prime }}\right) -\frac{I_{e}}{\rho ^{4}}\frac{A_{e}\rho ^{2} }{I_{e}}\rho \varepsilon _{m}\psi ^{\prime }-\frac{I_{e}}{\rho ^{3}}\mu \varepsilon _{m}-\frac{I_{e}}{\rho ^{4}}\left( w^{^{\prime \prime }}+w\right) =0\;, \\&\left( w^{^{\prime \prime \prime \prime }}+w^{^{\prime \prime }}\right) +\rho \mu \varepsilon _{m}\left( \psi ^{^{\prime }}+1\right) +\left( w^{^{\prime \prime }}+w\right) =0\;, \end{aligned}$$

(44)

$$\begin{aligned}&\rho \varepsilon _{m}\left( 1+\psi ^{^{\prime }}\right) =\rho \varepsilon _{m}\left[ 1+\frac{1}{\rho }\left( u^{^{\prime }}-w^{^{\prime \prime }}\right) \right] =\rho \varepsilon _{m}\left[ 1+\frac{1}{\rho }\left( \rho \varepsilon _{m}-w-\frac{1}{2}\psi ^{2}\rho -w^{^{\prime \prime }}\right) \right] \\&\quad \approx \rho \varepsilon _{m}\left( 1+\varepsilon _{m}\right) -\varepsilon _{m}\left( w+w^{^{\prime \prime }}\right) \approx \rho \varepsilon _{m}-\varepsilon _{m}\left( w^{^{\prime \prime }}+w\right) \;, \end{aligned}$$

(45)

lead to

$$\begin{aligned} w^{^{\prime \prime \prime \prime }}+2w^{^{\prime \prime }}+w-\mu \varepsilon _{m}\left( w^{^{\prime \prime }}+w\right) =-\mu \rho \varepsilon _{m} \end{aligned}$$

(46)

which is identical to (11)$_2$.

1.3 Coefficients in the pre-buckling displacement field and the pre-buckling average strain

The coefficients in the pre-buckling displacement field (27) are given by

$$\begin{aligned} X_{1}&=\frac{-1}{\cos \vartheta }-\frac{H\sin \vartheta \cos \alpha +\cos \vartheta \sin \alpha }{2\cos \vartheta \left( \chi ^{2}-1\right) }\times{\mathcal {P}}=X_{11}+X_{12}{\mathcal {P}}, \end{aligned}$$

(47)

$$\begin{aligned} X_{2}&=\frac{H\cos \alpha \sin \vartheta +\sin \alpha \cos \vartheta }{2\left( \chi ^{2}-1\right) \sin \vartheta }{\mathcal {P}}=X_{22}{\mathcal {P}}, \end{aligned}$$

(48)

$$\begin{aligned} X_{3}&=\frac{-1}{\cos \chi \vartheta }-\chi \frac{H\sin \chi \vartheta \cos \chi \alpha +\cos \chi \vartheta \sin \chi \alpha }{2\cos \chi \vartheta \left( \chi ^{2}-1\right) }\times{\mathcal {P}}=X_{31}+X_{32}{\mathcal {P}}, \end{aligned}$$

(49)

$$\begin{aligned} X_{4}&=\chi \frac{H\sin \chi \vartheta \cos \chi \alpha +\cos \chi \vartheta \sin \chi \alpha }{2\sin \chi \vartheta \left( \chi ^{2}-1\right) }{\mathcal {P}} =X_{42}{\mathcal {P}}, \end{aligned}$$

(50)

with

$$\begin{aligned} H(\varphi )=\left\{ \begin{array}{cc} -1 &{} {\text {if }}\varphi \in \left[ -\vartheta ;\alpha \right] \\ +1 &{} {\text {if }}\varphi \in \left[ \alpha ;\vartheta \right] . \end{array} \right. \end{aligned}$$

(51)

Closed-form solutions to the constants $K_{0}$, $K_{1}$ and $K_{2}$ in (29) can be found after evaluating the integrals

$$\begin{aligned} K_{0}& = {} \int _{-\vartheta }^{\vartheta }\left( \frac{\chi ^{2}-1}{\chi ^{2}} +X_{11}\cos \varphi -\frac{X_{31}}{\chi ^{2}}\cos \chi \varphi \right) {\mathrm {d}}\varphi \\&\quad +\frac{1}{2}\int _{-\vartheta }^{\vartheta }\left( \frac{ \sin \varphi }{\cos \vartheta }-\frac{\sin \chi \varphi }{\chi \cos \chi \vartheta }\right) ^{2}{\mathrm {d}}\varphi -2\vartheta \varepsilon _{m},\end{aligned}$$

(52)

$$\begin{aligned} K_{1}& = {} \int _{-\vartheta }^{\vartheta }\left( X_{12}\cos \varphi +X_{22}\sin \varphi -\frac{X_{32}}{\chi ^{2}}\cos \chi \varphi -\frac{X_{42}}{\chi ^{2}} \sin \chi \varphi \right) {\mathrm {d}}\varphi \\&\quad +\int _{-\vartheta }^{\vartheta }\left( \frac{-X_{12}\chi \sin \varphi +X_{22}\chi \cos \varphi +X_{32}\sin \chi \varphi -X_{42}\cos \chi \varphi }{ \chi }\right) \\&\quad \times \left( \frac{-X_{11}\chi \sin \varphi +X_{31}\sin \chi \varphi }{\chi }\right) {\mathrm {d}}\varphi , \end{aligned}$$

(53)

$$\begin{aligned} K_{2}& = {} \frac{1}{2}\int _{-\vartheta }^{\vartheta }\left( X_{12}\cos \varphi +X_{22}\sin \varphi -\frac{X_{32}}{\chi ^{2}}\cos \chi \varphi -\frac{X_{42} }{\chi ^{2}}\sin \chi \varphi \right) ^{2}{\mathrm {d}}\varphi . \end{aligned}$$

(54)

If $\alpha =0$, the above solutions are identical to those in Kiss and Szeidl (2015b) set up for a concentrated load at the crown.

1.4 Buckled equilibrium configuration

Expanding Eq. (20), the principle of virtual work for the buckled configuration is

$$\begin{aligned} \,\int _{V}\sigma _{\xi }\delta \varepsilon _{\xi b}\,{\mathrm {d}} V+\int _{V}\sigma _{\xi \,b}\delta \varepsilon _{\xi b}{\mathrm {d}}V-P\left. \delta w_{b}\right| _{s=\rho \alpha }=0\;. \end{aligned}$$

(55)

The pre-buckling equilibrium state is already known, thus the variation of such quantities is identically zero. Based on Eq. (16), the variation of the total axial strain is

$$\begin{aligned} \delta \varepsilon _{\xi }^{*}=\delta \varepsilon _{\xi \,b}=\delta \varepsilon _{\xi \,b}^{1}+\delta \varepsilon _{\xi \,b}^{2} \end{aligned}$$

with

$$\begin{aligned} \delta \varepsilon _{\xi \,b}^{1}=\frac{\rho }{\rho +\zeta }\left( \delta \varepsilon _{L\,b}+\zeta \delta \kappa _{b}\right) +\psi \delta \psi _{b};\qquad \delta \varepsilon _{\xi \,b}^{2}=\psi _{b}\delta \psi _{b}. \end{aligned}$$

(56)

So the principle of virtual work is

$$\begin{aligned} 0=-\int _{V}\sigma _{\xi }\delta \varepsilon _{\xi \,b}^{2}{\mathrm {d}} V-\int _{V}\sigma _{\xi \,b}\delta \varepsilon _{\xi \,b}^{1}\,{\mathrm {d}} V-\int _{V}\sigma _{\xi \,b}\delta \varepsilon _{\xi \,b}^{2}\,{\mathrm {d}}V+P\left. \delta w_{b}\right| _{s=\rho \alpha }. \end{aligned}$$

(57)

Integrating the first three terms by parts while using kinematical Eqs. (16)–(19) result the following relations

$$\begin{aligned} \int _{V}\sigma _{\xi }\delta \varepsilon _{\xi \,b}^{2}{\mathrm {d}}V& = {} \int _{ {\mathcal {L}}}\int _{A}\left( 1+\frac{\zeta }{\rho }\right) \sigma _{\xi }\delta \varepsilon _{\xi \,b}^{2}{\mathrm {d}}A\,{\mathrm {d}}s=\int _{{\mathcal {L}} }\left( N+\frac{M}{\rho }\right) \psi _{b}\left( \frac{\delta u_{b}}{\rho }- \frac{{\mathrm {d}}\delta w_{b}}{{\mathrm {d}}s}\right) {\mathrm {d}}s \\& = {} \int _{{\mathcal {L}}}\frac{1}{\rho }\left( N+\frac{M}{\rho }\right) \psi _{b}\delta u_{b}{\mathrm {d}}s+\int _{{\mathcal {L}}}\left[ \frac{{\mathrm {d}}}{ {\mathrm {d}}s}\left( N+\frac{M}{\rho }\right) \psi _{b}\right] \delta w_{b} {\mathrm {d}}s-\left. \left( N+\frac{M}{\rho }\right) \psi _{b}\right. \left. \delta w_{b}\right| _{s=\rho \alpha } \\&\quad +\left. \left( N+\frac{M}{\rho }\right) \psi _{b}\delta w_{b}\right| _{s=-\rho \vartheta }-\left. \left( N+\frac{M}{\rho }\right) \psi _{b}\delta w_{b}\right| _{s=\rho \vartheta }\;, \end{aligned}$$

(58)

moreover

$$\begin{aligned} \int _{V}\sigma _{\xi \,b}\delta \varepsilon _{\xi \,b}^{1}\,{\mathrm {d}} V& = {} \int _{{\mathcal {L}}}\int _{A}\left( 1+\frac{\zeta }{\rho }\right) \sigma _{\xi \,b}\left[ \frac{\rho }{\rho +\zeta }\left( \frac{{\mathrm {d}}\delta u_{b}}{{\mathrm {d}}s}+\frac{\delta w_{b}}{\rho }+\zeta \frac{{\mathrm {d}}\delta \psi _{b}}{{\mathrm {d}}s}\right) +\psi \delta \psi _{b}\right] {\mathrm {d}}A\, {\mathrm {d}}s \\& = {} \int _{{\mathcal {L}}}\left\{ N_{b}\left( \frac{{\mathrm {d}}\delta u_{b}}{\mathrm { d}s}+\frac{\delta w_{b}}{\rho }\right) +M_{b}\frac{{\mathrm {d}}}{{\mathrm {d}}s} \left( \frac{\delta u_{b}}{\rho }-\frac{{\mathrm {d}}\delta w_{b}}{{\mathrm {d}}s} \right) +\left( N_{b}+\frac{M_{b}}{\rho }\right) \psi \left( \frac{\delta u_{b}}{\rho }-\frac{{\mathrm {d}}\delta w_{b}}{{\mathrm {d}}s}\right) \right\} \, {\mathrm {d}}s \\& = {} -\int _{{\mathcal {L}}}\frac{{\mathrm {d}}N_{b}}{{\mathrm {d}}s}\delta u_{b}{\mathrm {d}} s-\left. N_{b}\delta u_{b}\right| _{s=-\rho\vartheta}+\left[ \left. N_{b}\right| _{s=-\rho \alpha }-\left. N_{b}\right| _{s=+\rho \alpha }\right] \left. \delta u_{b}\right| _{s=\rho \alpha }+\left. N_{b}\delta u_{b}\right| _{s=\rho\vartheta } \\&\quad +\int _{{\mathcal {L}}}\frac{N_{b}}{\rho }\delta w_{b}\,{\mathrm {d}}s-\int _{ {\mathcal {L}}}\frac{1}{\rho }\frac{{\mathrm {d}}M_{b}}{{\mathrm {d}}s}\delta u_{b} {\mathrm {d}}s-\int _{{\mathcal {L}}}\frac{{\mathrm {d}}^{2}M_{b}}{{\mathrm {d}}s^{2}} \delta w_{b}{\mathrm {d}}s+\left. M_{b}\delta \psi _{b}\right| _{s=\rho\vartheta }-\left. M_{b}\delta \psi _{b}\right| _{s=-\rho\vartheta } \\&\quad -\left. \frac{{\mathrm {d}}M_{b}}{{\mathrm {d}}s}\delta w_{b}\right| _{s=-\rho\vartheta }+\left[ \left. \frac{{\mathrm {d}}M_{b}}{{\mathrm {d}}s} \right| _{s=-\rho \alpha }-\left. \frac{{\mathrm {d}}M_{b}}{{\mathrm {d}}s} \right| _{s=+\rho \alpha }\right] \left. \delta w_{b}\right| _{s=\rho \alpha }+\left. \frac{{\mathrm {d}}M_{b}}{{\mathrm {d}}s}\delta w_{b}\right| _{s=\rho\vartheta } \\&\quad +\int _{{\mathcal {L}}}\frac{1}{\rho }\frac{{\mathrm {d}}}{{\mathrm {d}}s}\left( N_{b}+ \frac{M_{b}}{\rho }\right) \psi \delta u_{b}{\mathrm {d}}s+\int _{{\mathcal {L}}} \left[ \frac{{\mathrm {d}}}{{\mathrm {d}}s}\left( N_{b}+\frac{M_{b}}{\rho }\right) \psi \right] \delta w_{b}{\mathrm {d}}s-\left. \left( N_{b}+\frac{M_{b}}{\rho } \right) \psi \delta w_{b}\right| _{s=-\rho\vartheta }^{s=\rho\vartheta }\;, \end{aligned}$$

(59)

and finally, the third term in (57) is the same as (40) but for the increments. Altogether, because of the arbitrariness of the virtual quantities, the buckled equilibrium is governed by Eq. (21)

After substituting (5) and (19), Eq. (21)$_1$ becomes

$$\begin{aligned} \frac{{\mathrm {d}}}{{\mathrm {d}}s}\left( A_{e}\varepsilon _{mb}\right) -\frac{1}{ \rho }\left( A_{e}\varepsilon _{m}\psi _{b}\right) =0 \end{aligned}$$

where the second term can be dropped, so $\varepsilon _{mb}'=0$. Furthermore, Eq. (21) simplifies to

$$\begin{aligned} -\frac{{\mathrm {d}}^{2}M_{b}}{{\mathrm {d}}s^{2}}+\frac{N_{b}}{\rho }+\left( N+ \frac{M}{\rho }\right) \frac{{\mathrm {d}}\psi _{b}}{{\mathrm {d}}s}+\left( N_{b}+ \frac{M_{b}}{\rho }\right) \frac{{\mathrm {d}}\psi }{{\mathrm {d}}s}=0, \end{aligned}$$

(60)

or identically

$$\begin{aligned} A_{e}\varepsilon _{m}\frac{{\mathrm {d}}\psi _{b}}{{\mathrm {d}}s} +A_{e}\varepsilon _{mb}\frac{{\mathrm {d}}\psi }{{\mathrm {d}}s}=\mu \frac{I_{e}}{ \rho ^{2}}\left( \varepsilon _{m}\frac{{\mathrm {d}}\psi _{b}}{{\mathrm {d}}s} +\varepsilon _{mb}\frac{{\mathrm {d}}\psi }{{\mathrm {d}}s}\right) . \end{aligned}$$

(61)

Further recalling Eq. (19), the manipulations

$$\begin{aligned}&\frac{I_{e}}{\rho ^{4}}\left( w_{b}^{^{\prime \prime \prime \prime }}+w_{b}^{^{\prime \prime }}\right) +\frac{I_{e}}{\rho ^{4}}\left( w_{b}^{^{\prime \prime }}+w_{b}\right) +\mu \frac{I_{e}}{\rho ^{3}} \varepsilon _{mb}+\mu \frac{I_{e}}{\rho ^{3}}\varepsilon _{m}\psi _{b}^{^{\prime }}+\mu \frac{I_{e}}{\rho ^{3}}\varepsilon _{mb}\psi ^{^{\prime }}=0\,, \end{aligned}$$

(62)

$$\begin{aligned}&w_{b}^{^{\prime \prime \prime \prime }}+2w_{b}^{^{\prime \prime }}+w_{b}+\mu \rho \varepsilon _{mb}\left( 1+\psi ^{^{\prime }}\right) +\mu \rho \varepsilon _{m}\psi _{b}^{^{\prime }}=0\,, \\&\mu \rho \varepsilon _{mb}\left( 1+\psi ^{^{\prime }}\right) \simeq \mu \rho \varepsilon _{mb}\left[ 1-\frac{1}{\rho }\left( w^{^{\prime \prime }}+w\right) \right] =\mu \rho \varepsilon _{mb}-\mu \varepsilon _{mb}\left( w^{^{\prime \prime }}+w\right) \,, \\&\mu \rho \varepsilon _{m}\psi _{b}^{\prime }\simeq -\mu \varepsilon _{m}\left( w_{b}^{^{\prime \prime }}+w_{b}\right) \, \end{aligned}$$

(63)

lead to

$$\begin{aligned} w_{b}^{^{\prime \prime \prime \prime }}+\left( 2-\mu \varepsilon _{m}\right) w_{b}^{^{\prime \prime }}+\left( 1-\mu \varepsilon _{m}\right) w_{b}=-\mu \rho \varepsilon _{mb}-\mu \varepsilon _{mb}\left( w^{^{\prime \prime }}+w\right) \end{aligned}$$

(64)

that is identical to (23).

1.5 Coefficients in the buckling displacement and average buckling strain increment

With the decomposition $Y_{i}=\varepsilon _{mb}\left( Y_{i1}+Y_{i2}{\mathcal {P}}\right)$ and Eq. (51), for $i=1,2$, the coefficients in Eq. (34) are as follows:

$$\begin{aligned} Y_{1i}= \,& {} \frac{\mu H}{2\chi ^{2}\left( 1-\chi ^{2}\right) \cos \vartheta } \times \left[ B_{3i}\left( \cos \chi \alpha \cos \alpha \cos \vartheta +H\chi \sin \chi \alpha \cos \alpha \sin \vartheta \right. \right. \\&- \left. H\cos \chi \alpha \sin \alpha \sin \vartheta -H\cos \chi \vartheta +\chi \sin \chi \alpha \cos \vartheta \sin \alpha \right) +A_{3i}\left( H\cos \chi \alpha \sin \alpha \sin \vartheta \right. \\&- \left. H\cos \chi \vartheta -\chi \sin \chi \alpha \cos \vartheta \sin \alpha -\cos \chi \alpha \cos \alpha \cos \vartheta -H\chi \sin \chi \alpha \cos \alpha \sin \vartheta \right) \\&+ B_{4i}\left( H\sin \chi \vartheta -\chi \cos \chi \alpha \cos \vartheta \sin \alpha -H\chi \cos \chi \alpha \cos \alpha \sin \vartheta +\cos \alpha \cos \vartheta \sin \chi \alpha \right. \\&- \left. H\sin \alpha \sin \vartheta \sin \chi \alpha \right) +A_{4i}\left( \chi \cos \chi \alpha \cos \vartheta \sin \alpha -H\sin \chi \vartheta \right. \\&+ \left. \left. H\chi \cos \chi \alpha \cos \alpha \sin \vartheta -\cos \alpha \cos \vartheta \sin \chi \alpha +H\sin \alpha \sin \vartheta \sin \chi \alpha \right) +2\left( i-2\right) \right] , \\ Y_{2i}= \,& {} \frac{\mu }{2\chi ^{2}\left( \chi ^{2}-1\right) \sin \vartheta } \times \left[ B_{3i}\left( \cos \chi \alpha \cos \alpha \cos \vartheta +H\chi \sin \chi \alpha \cos \alpha \sin \vartheta \right. \right. \\&- \left. H\cos \chi \alpha \sin \alpha \sin \vartheta -\cos \chi \vartheta +\chi \sin \chi \alpha \cos \vartheta \sin \alpha \right) +A_{3i}\left( H\cos \chi \alpha \sin \alpha \sin \vartheta +\cos \chi \vartheta \right. \\&- \left. \cos \chi \alpha \cos \alpha \cos \vartheta -H\chi \sin \chi \alpha \cos \alpha \sin \vartheta -\chi \sin \chi \alpha \cos \vartheta \sin \alpha \right) +B_{4i}\left( \sin \chi \vartheta \right. \\&- \left. \chi \cos \chi \alpha \cos \vartheta \sin \alpha -H\chi \cos \chi \alpha \cos \alpha \sin \vartheta +\cos \alpha \cos \vartheta \sin \chi \alpha -H\sin \alpha \sin \vartheta \sin \chi \alpha \right) \\&+A_{4i}\left( \sin \chi \vartheta +H\chi \cos \chi \alpha \cos \alpha \sin \vartheta +\chi \cos \chi \alpha \cos \vartheta \sin \alpha \right. \\&-\left. \left. \cos \alpha \cos \vartheta \sin \chi \alpha +H\sin \alpha \sin \vartheta \sin \chi \alpha \right) \right] , \\ Y_{3i}= \,& {} \frac{\mu H}{4\chi ^{4}\sin \chi \vartheta \left( 1-\chi ^{2}\right) }\times \left[ B_{3i}H\left( -1+\chi \right) \left( 1+\chi \right) \left( \alpha \chi \sin \chi \vartheta +H\vartheta \chi \sin \chi \vartheta +H\cos \chi \vartheta \right. \right. \\&- \left. H\cos \chi \vartheta \cos ^{2}\chi \alpha +\sin \chi \vartheta \sin \chi \alpha \cos \chi \alpha \right) +A_{3i}\left( 1-\chi \right) \left( 1+\chi \right) \left( \alpha \chi \sin \chi \vartheta +H\vartheta \chi \sin \chi \vartheta \right. \\&+ \left. H\cos \chi \vartheta -H\cos \chi \vartheta \cos ^{2}\chi \alpha +\sin \chi \vartheta \sin \chi \alpha \cos \chi \alpha \right) +\left( 0.5H+0.5\right) B_{4i}\left( \chi -1\right) \left( 1+\chi \right) \\&\times \left( \chi \vartheta \cos \chi \vartheta +\chi \alpha \cos \chi \vartheta -\sin \chi \vartheta \cos ^{2}\chi \alpha -\cos \chi \alpha \cos \chi \vartheta \sin \chi \alpha \right) \\&+\left( -0.5H+0.5\right) B_{4i}\left( \sin \chi \vartheta \cos ^{2}\chi \alpha +\chi \alpha \cos \chi \vartheta +\chi \vartheta \cos \chi \vartheta -\chi ^{2} \cos ^{2}\chi \alpha \sin \chi \vartheta \right. \\&- \left. 4\chi ^{2}\sin \chi \vartheta -\cos \chi \alpha \cos \chi \vartheta \sin \chi \alpha +\chi ^{2}\cos \chi \alpha \cos \chi \vartheta \sin \chi \alpha -\chi ^{3}\vartheta \cos \chi \vartheta -\chi ^{3}\alpha \cos \chi \vartheta \right) \\&+\left( 0.5H+0.5\right) A_{4i}\left( \chi ^{3}\vartheta \cos \chi \vartheta -\sin \chi \vartheta \cos ^{2}\chi \alpha +\chi ^{2}\cos \chi \alpha \cos \chi \vartheta \sin \chi \alpha +\chi \alpha \cos \chi \vartheta \right. \\&-\left. \chi \vartheta \cos \chi \vartheta -\chi ^{3}\alpha \cos \chi \vartheta +\chi ^{2}\cos ^{2}\chi \alpha \sin \chi \vartheta -\cos \chi \alpha \cos \chi \vartheta \sin \chi \alpha +4\chi ^{2}\sin \chi \vartheta \right) +A_{4i} \\&\times \left. \left( 0.5 -0.5H\right) \left( \chi -1\right) \left( 1+\chi \right) \left( \chi \alpha \cos \chi \vartheta -\chi \vartheta \cos \chi \vartheta -\cos \chi \alpha \cos \chi \vartheta \sin \chi \alpha +\sin \chi \vartheta \cos ^{2}\chi \alpha \right) \right] , \\ Y_{4i}= \,& {} \frac{\mu }{4\chi ^{4}\cos \chi \vartheta \left( \chi ^{2}-1\right) } \times \left[ \left( 0.5H+0.5\right) B_{3i}\left( \chi -1\right) \left( 1+\chi \right) \right. \left( \alpha \chi \sin \chi \vartheta +\vartheta \chi \sin \chi \vartheta \right. \\&+ \left. \cos \chi \vartheta -\cos \chi \vartheta \cos ^{2}\chi \alpha +\sin \chi \vartheta \sin \chi \alpha \cos \chi \alpha \right) +4\left( i-2\right) +\left( 0.5H+0.5\right) A_{3i} \\&\times \left( \cos \chi \vartheta -\cos \chi \vartheta \cos ^{2}\chi \alpha +\vartheta \chi ^{3}\left( \sin \chi \vartheta \right) -5\chi ^{2}\cos \chi \vartheta +\chi ^{2}\cos \chi \vartheta \cos ^{2}\chi \alpha \right. \\&+\left. \sin \chi \vartheta \sin \chi \alpha \cos \chi \alpha -\chi ^{2}\sin \chi \vartheta \sin \chi \alpha \cos \chi \alpha +\alpha \chi \sin \chi \vartheta -\vartheta \chi \sin \chi \vartheta -\alpha \chi ^{3}\sin \chi \vartheta \right) \\&+ \left( 0.5-0.5H\right) B_{3i}\left( \alpha \chi ^{3}\sin \chi \vartheta +\vartheta \chi ^{3}\sin \chi \vartheta -\sin \chi \vartheta \sin \chi \alpha \cos \chi \alpha -5\chi ^{2}\cos \chi \vartheta -\alpha \chi \sin \chi \vartheta \right. \\&+ \left. \chi ^{2}\cos \chi \vartheta \cos ^{2}\chi \alpha +\chi ^{2}\sin \chi \vartheta \sin \chi \alpha \cos \chi \alpha +\cos \chi \vartheta -\cos \chi \vartheta \cos ^{2}\chi \alpha -\vartheta \chi \sin \chi \vartheta \right) \\&+\left( 0.5-0.5H\right) A_{3i}\left( 1-\chi \right) \left( 1+\chi \right) \left( \alpha \chi \sin \chi \vartheta \cos ^{2}\chi \alpha +\alpha \chi \sin \chi \vartheta \sin ^{2}\chi \alpha \right. \\&- \left. \vartheta \chi \cos ^{2}\chi \alpha \sin \chi \vartheta -\vartheta \chi \sin \chi \vartheta \sin ^{2}\chi \alpha -\sin ^{2}\chi \alpha \cos \chi \vartheta +\sin \chi \vartheta \sin \chi \alpha \cos \chi \alpha \right) \\&+ HB_{4i}\left( \chi ^{2}-1\right) \left( H\chi \vartheta \cos \chi \vartheta +\chi \alpha \cos \chi \vartheta -H\sin \chi \vartheta \cos ^{2}\chi \alpha -\cos \chi \alpha \cos \chi \vartheta \sin \chi \alpha \right) \\&+ \left. A_{4i}H\left( 1-\chi ^{2}\right) \left( H\chi \vartheta \cos \chi \vartheta +\chi \alpha \cos \chi \vartheta -H\sin \chi \vartheta \cos ^{2}\chi \alpha -\cos \chi \alpha \cos \chi \vartheta \sin \chi \alpha \right) \right] . \end{aligned}$$

1.6 Coefficients in the post-buckling average strain

The constants $L_0$, $L_1$ and $L_2$ in (36) are defined by

$$\begin{aligned} L_{0}= \,& {} -2\vartheta +\int _{-\vartheta }^{\vartheta }\left( \frac{\chi ^{2}-1}{\chi ^{2}}+X_{11}\cos \varphi +X_{21}\sin \varphi -\frac{X_{31}}{\chi ^{2}}\cos \chi \varphi -\frac{X_{41}}{\chi ^{2}}\sin \chi\varphi \right) {\mathrm {d}}\varphi \\&+ \int _{-\vartheta }^{\vartheta }\left( \frac{\chi ^{2}-1}{\chi ^{2}}+X_{11} \cos \varphi +X_{21}\sin \varphi -\frac{X_{31}}{\chi ^{2}}\cos \chi \varphi -\frac{X_{41}}{\chi ^{2}}\sin \chi\varphi \right) ^{^{\prime }} \\&\times \left[ Y_{11}\cos \varphi +Y_{21}\sin \varphi +Y_{31}\sin \chi \varphi +Y_{41} \cos \chi \varphi \right. \\&- \left. \frac{\mu }{2\chi ^{3}}\left( \frac{2}{\chi }+X_{31}\varphi \sin \chi \varphi -X_{41}\varphi \cos \chi \varphi \right) \right] {\mathrm {d}} \varphi , \end{aligned}$$

(65)

$$\begin{aligned} L_{1}= \,& {} \int _{-\vartheta }^{\vartheta }\left( \frac{\chi ^{2}-1}{\chi ^{2}} +X_{12}\cos \varphi +X_{22}\sin \varphi -\frac{X_{32}}{\chi ^{2}}\cos \chi \varphi -\frac{X_{42}}{\chi ^{2}}\sin \chi \varphi \right) {\mathrm {d}}\varphi \\&+ \int _{-\vartheta }^{\vartheta }\left( \frac{\chi ^{2}-1}{\chi ^{2}}+X_{11} \cos \varphi +X_{21}\sin \varphi -\frac{X_{31}}{\chi ^{2}}\cos \chi \varphi -\frac{X_{41}}{\chi ^{2}}\sin \chi \varphi \right) ^{^{\prime }} \\&\times \left[ Y_{12}\cos \varphi +Y_{22}\sin \varphi +Y_{32}\sin \chi \varphi +Y_{42} \cos \chi \varphi \right. \\&- \left. \frac{\mu }{2\chi ^{3}}\left( \frac{2}{\chi }+X_{32}\varphi \sin \chi \varphi -X_{42}\varphi \cos \chi \varphi \right) \right] {\mathrm {d}} \varphi \\&+ \int _{-\vartheta }^{\vartheta }\left( \frac{\chi ^{2}-1}{\chi ^{2}}+X_{12} \cos \varphi +X_{22}\sin \varphi -\frac{X_{32}}{\chi ^{2}}\cos \chi \varphi -\frac{X_{42}}{\chi ^{2}}\sin \chi \varphi \right) ^{^{\prime }} \\&\times \left[ Y_{11}\cos \varphi +Y_{21}\sin \varphi +Y_{31}\sin \chi \varphi +Y_{41} \cos \chi \varphi \right. \\&- \left. \frac{\mu }{2\chi ^{3}}\left( \frac{2}{\chi }+X_{31}\varphi \sin \chi \varphi -X_{41}\varphi \cos \chi \varphi \right) \right] {\mathrm {d}} \varphi , \end{aligned}$$

(66)

$$\begin{aligned} L_{2}= \,& {} \int _{-\vartheta }^{\vartheta }\left( \frac{\chi ^{2}-1}{\chi ^{2}} +X_{12}\cos \varphi +X_{22}\sin \varphi -\frac{X_{32}}{\chi ^{2}}\cos \chi \varphi -\frac{X_{42}}{\chi ^{2}}\sin \chi \varphi \right) ^{^{\prime }} \\&\times \left[ Y_{12}\cos \varphi +Y_{22}\sin \varphi +Y_{32}\sin \chi \varphi +Y_{42} \cos \chi \varphi \right. \\&-\left. \frac{\mu }{2\chi ^{3}}\left( \frac{2}{\chi }+X_{32}\varphi \sin \chi \varphi -X_{42}\varphi \cos \chi \varphi \right) \right] {\mathrm {d}} \varphi . \end{aligned}$$

(67)