1 Introduction

The optimization of reinforced concrete (RC) frames and structures under different load combinations remains an important problem today. In situ, structures are loaded by variable and repeated quasi-static loads within a known domain. These loads are not described by history in time, but only by their given combinations according to Eurocode or any other standard.

Usually the combinations of these loads are assumed to be independent (Guerra and Kiousis 2006; Guerra et al. 2011), but this is only true for linear systems. Relatively few papers take into account the mutual interaction of load combinations for nonlinear systems such as RC frames. This interaction can be determined either by manually analysing load histories, which is a labour intensive task, without any guarantee of encountering the worst case scenarios of independent loads, or by performing a shakedown analysis (SDA) for the entire class of loadings (Aliawdin 2005; Atkociunas 2011; Cyras 1983; König 1987; Nguyen 2006; Weichert and Maier 2002; Weichert and Ponter 2009). An example of an optimized shakedown approach for steel frames was published by Atkociunas and Venskus (2011). Alawdin and Bulanov (2014) performed a shakedown limit analysis of RC frames and Alawdin and Urbańska (2013, 2015) applied the same method to composite structures. Optimal design has been achieved by various methods of nonlinear programming (Borino 2014), including genetic algorithms (Conceição 2009).

The design of elastic–plastic RC frames is usually carried out using BS EN 1992-1-1, Eurocode 2: Design of concrete structures (2004) (EC2) or other standards. The algorithms for strength and stiffness evaluation of RC structural elements, however, are not fully described in these standards. The analysis and design of such structures has been reported by various investigators (Czarnecki and Staszczuk 1997; Korentz 2014; Narayanan and Roberts 1991; Nielsen and Hoang 2011). Furthermore, the stiffness and capacity of concrete-filled double-skin tube columns under axial compression was investigated by Tan and Zhang (2010).

In this paper, a SDA and optimization of RC frames is proposed for the general nonlinear problem and a simplified linear case. The duality of the linear programming problem is presented in static and kinematic formulations. The methodology, algorithms and implementation of RC frame weight optimization are discussed with numerical examples.

The continuous optimization solution gives the optimal reinforcement cross-sectional area and member sizing. This allows the designing of reinforcement bars from manufacturers’ catalogues using a mixed-integer nonlinear programming approach.

2 Mathematical model of shakedown optimization of RC frames

2.1 General mathematical model and assumptions

The mathematical models in this paper assume small displacements. The modelling employs linear and nonlinear programming theories and the finite element method.

The distribution of frame element parameters (limit inner forces) is optimized at shakedown under strength constraints when load variation, material parameters and lengths L k of all elements k are known (k ∊ K).

The general problem of the shakedown optimization of RC structures under loads \(\varvec{F}\), which vary in the domain \(\varOmega (\varvec{F})\), is formulated as follows: find a vector of limit forces \(\varvec{S}_{0} = (\varvec{S}_{0k} ,k \in K)\) of the RC sections, and a vector of residual forces \(\varvec{S}_{r}\), such that

$${\rm find} \quad \hbox{min}\,f_{0} ({\mathbf{S}}_{0} ),$$
(1)
$${\rm subj.\,to} \quad \varvec{AS}_{r} = {\mathbf{0}},$$
(2)
$$\phi = {\mathbf{f}}({\mathbf{S}}_{e} + {\mathbf{S}}_{r} ) -{\varvec{\varGamma S}}_{0} \le {\mathbf{0}},$$
(3)
$$\varvec{S}_{e} = \varvec{\alpha F},$$
(4)
$$\varvec{B}_{F} \varvec{F} \le \varvec{C}_{F} ,$$
(5)
$$\varvec{S}_{0}^{ - } \le \varvec{S}_{0} \le \varvec{S}_{0}^{ + } ,$$
(6)

where \(f_{0} ({\mathbf{S}}_{0} )\) is a criterion of optimization, \(\varvec{\alpha}\) is an influence matrix of internal elastic forces \(\varvec{S}_{e}\), \(\varvec{S}_{0}^{ - }\) and \(\varvec{S}_{0}^{ + }\) are constraints of the limit forces \(\varvec{S}_{0}\), \({\varvec{\Gamma}}\) is the configuration matrix of element limit forces, ϕ and \(\varvec{f}\) are yield and strength functions of the Sect. (2.2), respectively, \(\varvec{B}_{F}\) and \(\varvec{C}_{F}\) are, respectively, the matrix and vector of linear inequalities that define the domain \(\varOmega (\varvec{F})\) as a convex polyhedron of varying (uncertain) loads \(\varvec{F}\). This domain may also be described as the polytope \(\varOmega (\varvec{F},\varvec{F}_{l} ,l \in L)\) with the l vertices corresponding to the load combinations \(\varvec{F}_{l} ,l \in L.\) Aliawdin (2005) derives the polyhedron/polytope from the load combinations.

The limit forces \(\varvec{S}_{0}\) depend on the sizes of the element sections, which are continuous variables, and the reinforcement areas are integer variables.

The optimal limit force distribution at shakedown is a common optimization problem. It can be formulated as Eqs. (1)–(6), where a set of critical load combinations \(\varvec{F}_{l} ,l \in L,\) may be chosen by the procedure suggested by Aliawdin (2005). Therefore, the vector of loads \(\varvec{F}\) will be neglected from here on, and in a similar way the vector of unknown internal forces \(\varvec{S}_{e}\) will be replaced by the set J of known vectors of critical internal forces,

$$\varvec{S}_{ej} = \varvec{\alpha F}_{j} ,\quad j \in J .$$
(7)

For load domain \(\varOmega (\varvec{F})\), the procedure of choosing \(\varvec{F}_{l} ,\;\;l \in L\) was suggested by Aliawdin (2005). In particular, the polyhedron \(\varOmega (\varvec{F})\) becomes the parallelepiped with bounds \(\varvec{F}_{inf}\) and \(\varvec{F}_{sup}\),

$${\mathbf{F}}_{{\text{inf}}} \le {\mathbf{F}} \le {\mathbf{F}}_{{\text{sup}}} ,$$
(8)

and the set of internal force combinations \(\varvec{S}_{ej} ,j \in J\), are defined by simple formulae (Atkociunas 2011; Cyras 1969), so these variables are known.

2.2 Yielding conditions of RC cross-sections

\(\varvec{S}_{0k} = (M_{0k} ,N_{0k} ),k \in K,\) are functions of cross-sectional geometry and material properties. These functions may be linear or nonlinear; they are presented in Fig. 1 for rectangular doubly RC cross-sections. The functions were derived by Czarnecki and Staszczuk (1997) and later adapted to Eurocode 2 by Korentz (2014), thus they are not investigated further here.

Fig. 1
figure 1

Strength locus, interaction curves of a rectangular doubly symmetrically reinforced cross-section

Full size image

In Fig. 1, there are six unique points where interaction curves intersect each other. These intersection points represent different states of RC cross-section. Point 1: the tension failure state of the cross-section; Point 2: the point where the parabolic curve (2–6) intersects the line (1–2); Point 3: the point where the parabolic curve (6–3) intersects the line (3–4); Point 4: compressive failure followed by the rapid increase of axial force (M ≠ 0); Point 5: pure compression failure (M = 0); Point 6: balanced failure, assuming that the tensile steel reaches its yield strength and the compressed concrete reaches its compressive strain limit (ɛ cu  = 0.0035) simultaneously. The dashed lines between line segments 2–6 and 6–3 show the linearized forms of the nonlinear strength locus curves. In the case of asymmetric reinforcement, this interaction locus would have different upper and lower parts.

The points of intersection of each interaction curve are provided in Table 1, sourced from Czarnecki and Staszczuk (1997) and Korentz (2015).

Table 1 Intersection points of interaction curves (Czarnecki and Staszczuk 1997; Korentz 2015)
Full size table

The coefficients α, β, k 1 can be determined from the following formulae:

$$\alpha = f_{yd} A_{s1} /k_{1} ;$$
(19)
$$\beta = a_{1} /k_{1} ;$$
(20)
$$k_{1} = \eta f_{cd} bd.$$
(21)

Here, η is a coefficient defining effective strength and if η = 1.0 then \(f_{ck} \le 50\;\text{MPa}\) (Eurocode 2), where f ck is the cylindrical characteristic compressive concrete strength after 28 days of curing; f cd is the computational concrete strength, for C30/37 it is \(f_{cd} = 20\;{\text{MPa}}\); b is the width of the cross-section, see Fig. 2; d is the distance from the top of the section to the tensioning reinforcement, see Fig. 2; ξ lim is the limiting value of the relative height of the compression zone, for the C30/37 and reinforcement class B400 it is ξ lim  = 0.534.

Fig. 2
figure 2

Reinforcement design of a rectangular eccentrically compressed cross-section (doubly symmetrically reinforced); a large eccentricity, b small eccentricity

Full size image

From these intersection points (Table 1) one can derive linear functions that provide a linear approximation of the strength locus of a rectangular doubly reinforced cross-section (see Fig. 2). These functions in linear form can be written as follows:

$$M + \left( {\frac{{a_{1} - d}}{2}} \right)N + A_{s1} f_{yd} \left( {a_{1} - d} \right) \ge 0;$$
(22)
$$M + \left( {\frac{{a_{1} - d + d\xi_{lim} }}{2}} \right)N + A_{s1} f_{yd} \left( {a_{1} - d} \right) - a_{1} \eta f_{cd} bd\xi_{lim} \ge 0;$$
(23)
$$M + \left( {\frac{{2d\xi_{lim} - d - a_{1} }}{4}} \right)N + A_{s1} f_{yd} \left( {a_{1} - d} \right) - \frac{{bd\eta f_{cd} \xi_{lim} \left( {d - a_{1} } \right)}}{4} \ge 0;$$
(24)
$$\begin{aligned} &M + \left( { - \frac{{\left( {\left( {a_{1} - d} \right)\left( {8A_{s1} f_{yd} - a_{1} b\eta f_{cd} + bd\eta f_{cd} } \right)} \right)}}{{\left( {4\left( {4A_{s1} f_{yd} - a_{1} b\eta f_{cd} + bd\eta f_{cd} } \right)} \right)}}} \right)N + A_{s1} f_{yd} \left( {a_{1} - d} \right) + \hfill \\ &\quad + \frac{{\left( {\frac{{b\eta f_{cd} \left( {a_{1} + d} \right)}}{2}} \right)\left( {a_{1} - d} \right)\left( {8A_{s1} f_{yd} - b\eta f_{cd} \left( {a_{1} - d} \right)} \right)}}{{4\left( {4A_{s1} f_{yd} - b\eta f_{cd} \left( {a_{1} - d} \right)} \right)}} - \frac{{b\eta f_{cd} \left( {a_{1}^{2} - d^{2} } \right)}}{8} - \frac{{a_{1} bd\eta f_{cd} }}{4} \ge 0; \hfill \\ \end{aligned}$$
(25)
$$M + \frac{d}{2}N - \frac{{d\left( {2A_{s1} f_{yd} + bd\eta f_{cd} } \right) - a_{1} bd\eta f_{cd} }}{2} \ge 0;$$
(26)
$$- M + \left( {\frac{{a_{2} - d}}{2}} \right)N + A_{s2} f_{yd} \left( {a_{2} - d} \right) \ge 0;$$
(27)
$$- M + \left( {\frac{{a_{2} - d + d\xi_{lim} }}{2}} \right)N + A_{s2} f_{yd} \left( {a_{2} - d} \right) - a_{2} \eta f_{cd} bd\xi_{lim} \ge 0;$$
(28)
$$- M + \left( {\frac{{2d\xi_{lim} - d - a_{2} }}{4}} \right)N + A_{s2} f_{yd} \left( {a_{2} - d} \right) - \frac{{bd\eta f_{cd} \xi_{lim} \left( {d - a_{2} } \right)}}{4} \ge 0;$$
(29)
$$\begin{aligned} &- M + \left( { - \frac{{\left( {\left( {a_{2} - d} \right)\left( {8A_{s2} f_{yd} - a_{2} b\eta f_{cd} + bd\eta f_{cd} } \right)} \right)}}{{\left( {4\left( {4A_{s2} f_{yd} - a_{2} b\eta f_{cd} + bd\eta f_{cd} } \right)} \right)}}} \right)N + A_{s2} f_{yd} \left( {a_{2} - d} \right) + \hfill \\ &\quad \; + \frac{{\left( {\frac{{b\eta f_{cd} \left( {a_{2} + d} \right)}}{2}} \right)\left( {a_{2} - d} \right)\left( {8A_{s2} f_{yd} - b\eta f_{cd} \left( {a_{2} - d} \right)} \right)}}{{4\left( {4A_{s2} f_{yd} - b\eta f_{cd} \left( {a_{2} - d} \right)} \right)}} - \frac{{b\eta f_{cd} \left( {a_{2}^{2} - d^{2} } \right)}}{8} - \frac{{a_{2} bd\eta f_{cd} }}{4} \ge 0; \hfill \\ \end{aligned}$$
(30)
$$- M + \frac{d}{2}N - \frac{{d\left( {2A_{s2} f_{yd} + bd\eta f_{cd} } \right) - a_{2} bd\eta f_{cd} }}{2} \ge 0.$$
(31)

2.3 Modified mathematical model

If the optimization criterion is a linear function, \(f_{0} ({\mathbf{S}}_{0} ) = {\mathbf{L}}^{T} {\mathbf{S}}_{0}\), and the RC sections have linear strength functions, then the mathematical formulation of the optimal design of an RC frame subjected to cyclic loading, expressed as a limit (shakedown) analysis, reads:

$${\rm find} \quad \hbox{min}\,\,\varvec{L}^{T} \varvec{S}_{0} ,$$
(32)
$${\rm subj.\,to} \quad \varvec{AS}_{r} = {\mathbf{0}},$$
(33)
$$\begin{aligned} \varvec{\varphi }_{j} = {\varvec{\Gamma}}\varvec{S}_{0} -\varvec{\varPhi}\varvec{S}_{r} -\varvec{\varPhi}\varvec{S}_{ej} - {\mathbf{B}} \ge {\mathbf{0}}, \\ \quad j \in J, \\ \end{aligned}$$
(34)
$$- {\mathbf{S}}_{0} \le - {\mathbf{S}}_{0}^{ - } ,$$
(35)
$${\mathbf{S}}_{0} \le\, {\mathbf{S}}_{0}^{ + } .$$
(36)

The dual (kinematic) formulation of the mathematical model (32)–(36), can be written as follows: Find

$$\begin{aligned} \hbox{max} \left( {\sum\limits_{j \in J} {(\varvec{\varPhi S}_{ej} - {\mathbf{B}})^{T}\varvec{\lambda}_{j} } } \right. \hfill \\ \quad \quad \quad \left. { + ({\mathbf{S}}_{0}^{ - } )^{T} {\varvec{\uplambda}}^{ - } - ({\mathbf{S}}_{0}^{ + } )^{T} {\varvec{\uplambda}}^{ + } } \right), \hfill \\ \end{aligned}$$
(37)
$${\rm subj.\,to}\quad\sum\limits_{j \in J} {\varvec{\varPhi}^{T}\varvec{\lambda}_{j} + \varvec{A}^{T} \varvec{u}_{r} } = {\mathbf{0}}\text{,}$$
(38)
$$\sum\limits_{j \in J} {\varvec{\varGamma}^{T}\varvec{\lambda}_{j} + {\varvec{\uplambda}}^{ - } - {\varvec{\uplambda}}^{ + } = \varvec{L}} ,$$
(39)
$$\varvec{\lambda}_{j} \ge {\mathbf{0}}\text{,}\quad \, j \in J,$$
(40)
$${\varvec{\uplambda}}^{ - } \le {\mathbf{0},}$$
(41)
$${\varvec{\uplambda}}^{ + } \le {\mathbf{0}}{\mathbf{.}}$$
(42)

Here, \({\mathbf{L}} = (L_{k} ,\;k \in K)\), \(\varvec{S}_{0} = (S_{0k} ,\;k \in K)\), L k is the sum of the lengths of the k elements with the same limiting generalised force, k ∊ K, S 0k is the limiting generalised force of the k-th element, \(\varvec{S}_{0}\) is a vector of the limiting generalised forces, \(\varvec{S}_{r}\) is a vector of residual generalised forces, \(\varvec{S}_{ej}\) is a vector of elastic generalised forces at load locus apex j ∊ J, \(\varvec{\lambda}_{j}\) is a vector of plastic multipliers, \(\, j \in J\), \({\varvec{\uplambda}}^{ - }\) and \({\varvec{\uplambda}}^{ + }\) are vectors of multipliers according to the constraints (35)–(36), \(\varvec{u}_{r}\) is a vector of residual displacements, \(\varvec{\varPhi} = diag\varvec{\varPhi}_{i}\) is a quasi-diagonal matrix of the linear yielding conditions (22)–(31), where \(\varvec{\varPhi}_{i}\) is the matrix of coefficients of the linear yielding conditions of the i-th section, \(\varvec{B} = \left[ {\begin{array}{*{20}c} {\varvec{B}_{1} } & {\varvec{B}_{2} } & \cdots & {\varvec{B}_{i} } \\ \end{array} } \right]^{T}\) is a vector of the free units of linear yielding conditions (22)–(31). See Table 2 for the matrix \(\varvec{\varPhi}_{i}\) and vector B of free units and linear yielding conditions for the i-th section.

Table 2 Quasi-diagonal matrix of linear yielding conditions \(\left( {\varvec{\varPhi}_{i} } \right)\) and the vector of free units \(\left( \varvec{B} \right)\) for the i-th cross-section
Full size table

The problem of structural optimization at shakedown is stated as follows: given the load variation bounds \({\text{F}}_{sup} \;{\text{and}}\;{\text{F}}_{inf}\), find the vector of limit forces \(\varvec{S}_{0} ,\) satisfying the optimisation criterion and the constraints of shakedown and construction requirements (Atkociunas and Venskus 2011).

The limit forces S 0k , k ∊ K of elements and the vectors of plastic multipliers \(\varvec{\lambda}_{j} \ge {\mathbf{0}},\;j \in J\) are unknowns in problem (32)–(36). The limit forces S 0k are components of vector \(\varvec{S}_{0}\). Conditions (35), (36), which restricts the maximum (\(- {\mathbf{S}}_{0}^{ - }\)) and minimum (\({\mathbf{S}}_{0}^{ + }\)) values of limit forces \(\varvec{S}_{0}\), performs the function of constructive constraint (Atkociunas 2011).

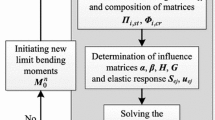
The general solution of the problem (32)–(36) can be derived in the following order. The geometrical parameters of the rectangular cross-section—height h, width b, and reinforcement clearances a 1 and a 2, are known and constant. The initial limit forces \(S_{ok}^{0}\), i.e., moments \(M_{ok}^{0}\) and axial forces \(N_{ok}^{0}\) (k ∊ K), are prescribed. The design of the steel reinforcement \(A_{s1}^{0}\) and \(A_{s2}^{0}\) is performed according to the scheme in Fig. 3. The initial influence matrices \(\varvec{\alpha}^{0} ,\;\varvec{\beta}^{0} ,\;\varvec{G}^{0} ,\;\varvec{H}^{0}\) are calculated, then the problem (32)–(36) is solved. Later, when a new distribution of limit moments \(M_{ok}^{new}\) and axial forces \(N_{ok}^{new}\) (k ∊ K) is determined, the new reinforcement design is implemented and new \(A_{s1}^{new}\) and \(A_{s2}^{new}\) are obtained. Updated influence matrices \(\varvec{\alpha}^{new} ,\;\varvec{\beta}^{new} ,\;\varvec{G}^{new} ,\;\varvec{H}^{new}\) are computed for the next iteration. From these matrices, the elastic response is determined, which consists of displacements \(\varvec{u}_{ej}\) and internal forces \(\varvec{S}_{ej}\).

Fig. 3
figure 3

Flowchart of the principal procedure for finding the optimal limit moments distribution

Full size image

For the linear yield conditions (34), the residual displacements \(\varvec{u}_{r} = \varvec{H\lambda }\) and residual internal forces \(\varvec{S}_{r} = \varvec{G\lambda }\) can be expressed by influence matrices of residual displacements (43) and forces (44):

$$\varvec{H} = \left( {\left( {\varvec{AD}^{ - 1} \varvec{A}^{T} } \right)^{ - 1} \varvec{AD}^{ - 1} } \right)\varvec{\varPhi},$$
(43)
$$\varvec{G} = \varvec{D}^{ - 1} \varvec{A}^{T} \varvec{H} - \varvec{D}^{ - 1}\varvec{\varPhi}.$$
(44)

Problem (32)–(36) is solved, therefore, in an iterative approach. The process is deemed to be finished when selected cross-sectional characteristics are within a prescribed tolerance (eps, see Fig. 3) of those from the previous iteration, giving the optimal solution \(S_{ok}^{*}\), \(\lambda_{j}^{*}\), k ∊ K, j ∊ J of the problem (32)–(36). Having obtained this solution, it is possible to indirectly calculate the volume of the frames (32); as described by Atkociunas and Karkauskas (2010) and Atkociunas (2011).

Remark 2.1

A solution of problem (32)–(36) may have J l active inequalities (34) for a single element cross-section subject to J l loads. This regime of plastic yielding is termed sign-changing. In such a case we may calculate this element cross-section as being elastic.

Remark 2.2

Inequalities (34) generally depend on the domain \(\varOmega (\varvec{F})\) of loading (Aliawdin 2005; Aliawdin and Kasabutski 2009); the checking of this effect may be a problem addressed in Eurocode’s future variants.

Remark 2.3

In the formulation of problem (32)–(36), one may include not only the unknown load, but also any other actions, material properties or geometrical imperfections of the structure (e.g., see Elishakoff et al. 2013).

The influence matrices \(\varvec{\alpha}\), of the elastic internal forces, and \(\varvec{\beta}\), of the elastic displacements, are generally calculated by

$$\varvec{\alpha}= \varvec{D}^{ - 1} \varvec{A}^{T} \left( {\varvec{AD}^{ - 1} \varvec{A}^{T} } \right)^{ - 1} ,$$
(45)
$$\varvec{\beta}= \left( {\varvec{AD}^{ - 1} \varvec{A}^{T} } \right)^{ - 1} ,$$
(46)

where \(\varvec{A}\left\{ {L_{k} } \right\}\) is matrix of coefficients of equilibrium equations and \(\varvec{D}\left\{ {I_{tr} ,A_{tr} ,E_{comp} } \right\}\) is a flexibility matrix of the transformed cross-section; see Atkociunas and Karkauskas (2010), Atkociunas (2011) and Liepa et al. (2014). The transformation of the cross-section needs to be performed because RC cross-sections are composed of two materials. Their geometrical characteristics, such as moment of inertia I tr and area of cross-section A tr , can be determined using methods described by Beardmore (2011). The elastic modulus of composite material E comp is determined according to the Derivation of the Rule of Mixtures and Inverse rule of Mixtures (accessed 2015). The principal scheme of the optimization of the limiting-moment distribution procedure is illustrated in Fig. 3.

3 Design of RC cross-section: main rules

The design of reinforcement for an eccentrically compressed rectangular cross-section (Fig. 2) is carried out according to the Eurocode 2 recommendations. The flowchart of the implemented design procedure is shown in Fig. 4.

Fig. 4
figure 4

Flowchart of the reinforcement design procedure

Full size image

Here, M 0 and N 0 are, respectively, the limiting moment and limiting axial force of the RC cross-section; e is the ratio of internal forces (eccentricity of axial force from the centre of the cross-section); e1 and e2 are eccentricities (refer to Fig. 2); b is the width of the RC cross-section; h is the height of the RC cross-section; d is the distance of the designed reinforcement bar’s centre to the opposite outside layer of the RC element; \(a_{1}\,{\text{and}}\,a_{2}\) are the clearance distances of reinforcement; f yd is the designed yield strength of steel reinforcement; κ s i the reduction coefficient of steel reinforcement yield strength; x eff is an effective height of the compressive concrete zone; x eff,lim is the limit of the effective height of the compressive concrete zone; x’ is the equivalent height of the compressive concrete zone; ρ is the ratio of required reinforcement; ρ min is the minimal ratio of required reinforcement; ρ max is the maximal allowed ratio of required reinforcement.

4 Example of shakedown analysis

A two-storey RC plane frame is subjected to two independent loads: a vertical live load F 1 (0 kN ≤ F 1 ≤ 160 kN) and a horizontal wind load F 2 (−120 kN ≤ F 2 ≤ 100 kN), see Fig. 5. The load combinations with applied load impact coefficients are shown in Table 3. No load combination coefficients were applied. The task is to find an optimal solution to the problem (32)–(36) for determining the distribution of limit moments on the frame at shakedown.

Fig. 5
figure 5

Computational scheme of the frame structure

Full size image
Table 3 Load combinations
Full size table

The load variation ranges can be described as a locus, as in Fig. 6.

Fig. 6
figure 6

Load variation locus

Full size image

The impact coefficients of the loads were assigned arbitrarily, but can be determined according to the requirements of the standards.

The discrete model of the frame structure is shown in Fig. 7. The frame is discretized into eight finite beam elements (number in square), each with two sections. The frame is k = 6 times statically indeterminate, it has n = 24 internal forces, and m = 18 possible directions of nodal displacements (i.e., degrees of freedom \(\text{DOF = 18}\)). Each finite element has two bending moments (one per section) and an axial force (one per element).

$$\begin{aligned} &F_{1,sup} = 160\;\text{kN}; \\ & F_{1,inf} = 0\;\text{kN}; \\ \\ & F_{2,sup} = 100\;\text{kN}; \\ & F_{2,inf} = - 120\;\text{kN}; \\ \\ &\varvec{F} = \left[ {F_{1} \quad F_{2} } \right]^{T} \\ &\varvec{F}_{sup} = \left[ {160\quad 100} \right]^{T} ; \\ &\varvec{F}_{inf} = \left[ {0\quad - 120} \right]^{T} . \\ \end{aligned}$$
Fig. 7
figure 7

Discrete model of the frame and possible directions of nodal displacements

Full size image

5 Solution

The initial geometrical parameters of the sections and reinforcement cross-sectional areas, designed according to the initial limiting bending moments and axial forces, are presented in Table 4.

Table 4 Initial and optimal section properties
Full size table

The optimal solution of problem (32)–(36) for the frame in question was obtained after eight iterations. The value of the optimal criterion function after eight iterations was \(f* = { 1} . 8 6 3 3 ,\) see Fig. 8. The final value was 1.17 % larger than the initial value of the optimal criterion function after the first iteration, f 0 = 1.8415. This small difference, however, produces a significant change (>65 %) in the reinforcement areas for all cross-sections. Table 4 presents the optimal reinforcement cross-sectional areas and geometrical parameters of frame cross-sections.

Fig. 8
figure 8

Optimal solution convergence during the iterative procedure

Full size image

From Table 4, the initial reinforcements of the four sections are:

  • M 01: \(A_{s1,1}^{0} = A_{s2,1}^{0} = 12.19\;{\text{cm}}^{ 2} ,\) which can be designed as \(2 \times 2\emptyset 28\) (2 × 12.32 cm2)Footnote 1;

  • M 02: \(A_{s1,2}^{0} = A_{s2,2}^{0} = 5.0\;{\text{cm}}^{ 2} ,\) which can be designed as \(2 \times 2\emptyset 18\) (2 × 5.08 cm2) (see footnote 1);

  • M 03: \(A_{s1,3}^{0} = A_{s2,3}^{0} = 3.96\;{\text{cm}}^{2} ,\) which can be designed as \(2 \times 2\emptyset 16\) (2 × 4.02 cm2) (see footnote 1);

  • M 04: \(A_{s1,4}^{0} = A_{s2,4}^{0} = 12.84\;{\text{cm}}^{2} ,\) which can be designed as \(2 \times 2\emptyset 32\) (2 × 16.08 cm2) (see footnote 1).

Likewise, the optimal reinforcements of these sections are:

  • M 01: \(A_{s1,1}^{*} = A_{s2,1}^{*} = 62.29\;{\text{cm}}^{ 2} ,\) which can be designed as \(2 \times 5\emptyset 40\) (2 × 62.85 cm2) (see footnote 1);

  • M 02: \(A_{s1,2}^{*} = A_{s2,2}^{*} = 16.58\;{\text{cm}}^{2} ,\) which can be designed as \(2 \times 3\emptyset 28\) (2 × 18.48 cm2) (see footnote 1);

  • M 03: \(A_{s1,3}^{*} = A_{s2,3}^{*} = 12.76\;{\text{cm}}^{2} ,\) which can be designed as \(2 \times 3\emptyset 25\) (2 × 14.73 cm2) (see footnote 1);

  • M 04: \(A_{s1,4}^{*} = A_{s2,4}^{*} = 30.88\;{\text{cm}}^{ 2} ,\) which can be designed as \(2 \times 3\emptyset 36\) (2 × 30.54 cm2) (see footnote 1).

Solving the optimization problem allows us to efficiently design a cross-section by choosing the closest to the optimal area required for reinforcement.

Figures 9 and 10 shows how the strength loci of every section changes during iterative optimization at shakedown. Both the initial and optimal limits of the internal forces (Table 4) are within the strength locus.

Fig. 9
figure 9

Iterative changes of the strength loci of section with limiting bending moment a M 01, b M 02

Full size image
Fig. 10
figure 10

Iterative changes of the strength loci of section with limiting bending moment a M 03, b M 04

Full size image

6 Conclusions

In this paper, we proposed a nonlinear mathematical model of shakedown and optimization of RC plane frames under variable and repeated uncertain loads, and also presented a linearized version. Mechanisms of system collapse at shakedown such as plastic yielding and sign-changing were analysed, and the plastic redistribution of forces in such structures were found. The conditions of element strength were derived according to Eurocode 2. A duality of the linear programming problem was shown here for the static and kinematic formulations. The methodology, algorithms and implementation of the optimization of RC frame weights was presented and illustrated by a numerical example. The results showed that updated strength conditions can be used in the optimization of doubly RC cross-sections of frames.

The optimal solution for the plane frame under variable and repeated loading was obtained by solving a mixed-integer optimization problem, which required choosing the reinforcement bars from a manufacturer’s catalogue.

The optimal reinforcement was implemented as doubly symmetrically distributed bars. By analysing the reinforcement design procedure, we find that large eccentricities of internal forces can occur in the designed section because of applied shakedown loads. In most cases for the same type of frames, the doubly symmetrical reinforcement is the optimal solution.

Further investigation is needed that takes into account the effect of shear forces in the frame elements, torsion and bidirectional bending moments for the three dimensional frames, and implementation of transverse reinforcement design of the frame elements in shakedown conditions.

A dependence of element strength conditions on the domain of loading may need to be addressed in Eurocode’s future revisions.

As well as modelling loading, the formulation proposed here is amenable to including other actions and environmental influences, material properties, and geometrical data.