Active constrained layer damping of geometrically nonlinear vibrations of smart laminated composite sandwich plates using 1–3 piezoelectric composites

Abstract

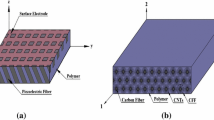
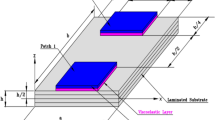
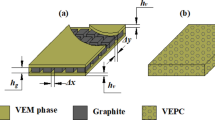
This paper deals with the analysis of active constrained layer damping (ACLD) of geometrically nonlinear vibrations of sandwich plate with orthotropic laminated composite faces separated by a flexible core. The constraining layer of the ACLD treatment is composed of the vertically/obliquely reinforced 1–3 piezoelectric composites. The Golla–Hughes–McTavish method has been implemented to model the constrained viscoelastic layer of the ACLD treatment in time domain. The first-order shear deformation theory and the Von Kármán type nonlinear strain displacement relations are used for analyzing this coupled electro-elastic problem. A three dimensional finite element model of smart laminated composite sandwich plate integrated with ACLD patches has been developed to investigate the performance of these patches for controlling the geometrically nonlinear vibrations of the plates. The numerical results indicate that the ACLD patches significantly improve the damping characteristics of the sandwich plates with laminated cross-ply and angle-ply facings for suppressing their geometrically nonlinear vibrations. Particular emphasis has been placed on investigating the effect of the variation of piezoelectric fiber orientation angle on the performance of the ACLD treatment.

Appendix

In Eq. (28), the matrices $\left[ {{\text{Z}}_{1} } \right],\,\left[ {{\text{Z}}_{2} } \right],\,\left[ {{\text{Z}}_{3} } \right],\,\left[ {{\text{Z}}_{4} } \right],\, \left[ {{\text{Z}}_{5} } \right],\,\left[ {{\text{Z}}_{6} } \right],\,\left[ {{\text{Z}}_{7} } \right],\,\left[ {{\text{Z}}_{8} } \right],\,\left[ {{\text{Z}}_{9} } \right]$ and $\left[ {{\text{Z}}_{10} } \right]$ are given by

$$ \begin{aligned} \left[ {{\text{Z}}_{1} } \right] & = {\left[ \begin{array}{lllll} [{{\bar{\text{Z}}}_{1} }] & \widetilde{0} & \widetilde{0} & \widetilde{0} & \widetilde{0} \\ \end{array} \right]} \\ \left[ {{\text{Z}}_{2} } \right] & = {\left[\begin{array}{lllll} ( - {\text{h}}_{\text{c}}){\text{I}}& \left[ {{\bar{\text{Z}}}_{2} } \right] & \widetilde{0} & \widetilde{0} & \widetilde{0} \\ \end{array} \right]} \\ \left[ {{\text{Z}}_{3} } \right] & = {\left[\begin{array}{lllll} ({\text{h}}_{\text{c}} ){\text{I }} & \widetilde{0} & \left[ {{\bar{\text{Z}}}_{3} } \right]& \widetilde{0} & \widetilde{0}\\ \end{array}\right]} \\ \left[ {{\text{Z}}_{4} } \right] & = {\left[\begin{array}{lllll} ({\text{h}}_{\text{c}} ){\text{I }} & \widetilde{0} & ({\text{h}}){\text{I }}& ({\text{h}}_{\text{v}} ){\text{I}} & \left[ {{\bar{\text{Z}}}_{5} } \right]\\ \end{array} \right]} \\ \left[ {{\text{Z}}_{5} } \right] & = {\left[\begin{array}{llllllllll} \overline{\text{I}} & \overline{0} & \overline{0} & \overline{0} & \overline{0} & {\text{z}}\overline{\text{I}}& \overline{0} & \overline{0} & \overline{0} & \overline{0} \\ \end{array}\right]} \\ \left[ {{\text{Z}}_{6} } \right] & = {\left[\begin{array}{llllllllll} \overline{0} & \overline{\text{I}} & \overline{0} & \overline{0} & \overline{0} & ({-{\text{h}}_{\text{c}}})\overline{\text{I}} & ({\text{z}} + {\text{h}}_{\text{c}} )\overline{\text{I}} & \overline{0} & \overline{0}& \overline{0} \\ \end{array}\right]} \\ \left[ {{\text{Z}}_{7} } \right] & = {\left[\begin{array}{llllllllll} \overline{0}& \overline{0} & \overline{\text{I}} & \overline{0} & \overline{0} & ({{\text{h}}_{\text{c}} })\overline{\text{I}}& \overline{0} & ({\text{z}}-{\text{h}}_{\text{c}} )\overline{\text{I}} & \overline{0}& \overline{0} \\ \end{array} \right]} \\ \left[ {{\text{Z}}_{8} } \right] & = {\left[\begin{array}{llllllllll} \overline{0} & \overline{0} & \overline{0} & \overline{\text{I}} & \overline{0} & ({{\text{h}}_{\text{c}} })\overline{\text{I}} & \overline{0}& ({\text{h}})\overline{\text{I}} & ({\text{z}}-{\text{h}}_{\text{c}} - {\text{h}})\overline{\text{I}} & \overline{0} \\ \end{array}\right]} \\ \left[{{\text{Z}}_{9}}\right] & = {\left[\begin{array}{llllllllll} \overline{0} & \overline{0} & \overline{0} & \overline{0} & \overline{\text{I}} & \left( {{\text{h}}_{\text{c}} } \right)\overline{\text{I}} & \overline{0} & ({\text{h}})\overline{\text{I}} & {\text{h}}_{\text{v}} \overline{\text{I}} & ({\text{z}} - {\text{h}}_{\text{c}} - {\text{h}} - {\text{h}}_{\text{v}} )\overline{\text{I}}\\ \end{array}\right]} \\ \end{aligned} $$

where

$$ \left[ {\overline{\text{Z}}_{1} } \right] = \left[ {\begin{array}{llll}{\text{z}} & 0 & 0 & 0 \\ 0& Z & 0 & 0\\ 0 & 0& Z&0\\ 0 & 0& 0 & 1 \\ \end{array}}\right], \quad \left[ {\overline{\text{Z}}_{2} } \right] = \left[\begin{array}{cccc}({{\text{z}} - {\text{h}}_{\text{c}} } ) & 0 &0 & 0 \\ 0 & {({\text{z}} - {\text{h}}_{\text{c}} )} & 0 & 0 \\ 0 & 0 & {({{\text{z}} - {\text{h}}_{\text{c}} } ) } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right], \quad [ {\overline{\text{Z}}_{3} } ] = \left[ {\begin{array}{cccc} ( {{\text{z}} + {\text{h}}_{\text{c}} }) & 0 & 0 & 0 \\ 0 & { ({\text{z}} + {\text{h}}_{\text{c}} )} & 0 & 0 \\ 0 & 0 & {({{\text{z}} + {\text{h}}_{\text{c}} })} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}}\right], \quad [{\overline{\text{Z}}_{5}}] = \left[ \begin{array}{cccc} ({{\text{z}} - {\text{h}}_{\text{c}} - {\text{h}} - {\text{h}}_{\text{v}} } ) & 0 & 0 & 0 \\ 0 & ({\text{z}} - {\text{h}}_{\text{c}} - {\text{h}} - {\text{h}}_{\text{v}} ) \\ & 0 & 0 \\ 0 & 0 & {( {{\text{z}} - {\text{h}}_{\text{c}} - {\text{h}} - {\text{h}}_{\text{v}} }) } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right], \quad {\text{I}} = \left[ {\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} }\right], \quad \overline{\text{I}} = \left[ {\begin{array}{ll} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],\quad \overline{0} = \left[ {\begin{array}{ll} 0 & 0 \\ 0 & 0 \\ \end{array} }\right], \quad \widetilde{0} = \left[ \begin{array}{llll} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array}\right] $$

The various submatrices $\left[ {{\mathbf{B}}_{tbi} } \right],\,\left[ {{\mathbf{B}}_{rbi} } \right],\,\left[ {{\mathbf{B}}_{tsi} } \right]$ and $\left[ {{\mathbf{B}}_{rsi} } \right]$ appearing in Eq. (29)

$$ \begin{gathered} \left[{{\mathbf{B}}_{tbi}} \right] = \left[{\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{{\partial n_{i}}}{\partial x} } & 0 & 0 \\ \end{array}} \\ {\begin{array}{*{20}c} 0 & { \frac{{\partial n_{i}}}{\partial y}} & 0 \\ \end{array}} \\ {\begin{array}{*{20}c} {\frac{{\partial n_{i}}}{\partial y}} & {\frac{{\partial n_{i}}}{\partial x}} & 0 \\ \end{array}} \\ {\begin{array}{*{20}c} 0 & { 0} & { 0} \\ \end{array}} \\ \end{array}} \right],\,\left[{{\mathbf{B}}_{tsi}} \right] = \left[{\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & {\frac{{\partial n_{i}}}{\partial x}} \\ \end{array}} \\ {\begin{array}{*{20}c} 0 & 0 & {\frac{{\partial n_{i}}}{\partial y}} \\ \end{array}} \\ \end{array}} \right] \hfill \\ \left[{{\mathbf{B}}_{rbi}} \right] = \left[{\begin{array}{*{20}c} {\begin{array}{*{20}c} {\widehat{{{\mathbf{B}}_{rbi}}}} & {\check{0}} & {\check{0}} \\ \end{array} \begin{array}{*{20}c} {\check{0}} & {\check{0}} \\ \end{array}} \\ {\begin{array}{*{20}c} {\check{0}} & {\widehat{{{\mathbf{B}}_{rbi}}}} & {\check{0}} \\ \end{array} \begin{array}{*{20}c} {\check{0}} & {\check{0}} \\ \end{array}} \\ {\begin{array}{*{20}c} {\check{0}} & {\check{0}} & {\widehat{{{\mathbf{B}}_{rbi}}}} \\ \end{array} \begin{array}{*{20}c} {\check{0}} & {\check{0}} \\ \end{array}} \\ {\begin{array}{*{20}c} {\check{0}} & {\check{0}} & {\check{0}} \\ \end{array} \begin{array}{*{20}c} {\widehat{{{\mathbf{B}}_{rbi}}}} & {\check{0}} \\ \end{array}} \\ {\begin{array}{*{20}c} {\check{0}} & {\check{0}} & {\check{0}} \\ \end{array} \begin{array}{*{20}c} {\check{0}} & {\widehat{{{\mathbf{B}}_{rbi}}}} \\ \end{array}} \\ \end{array}} \right],\,\widehat{{{\mathbf{B}}_{rbi}}} = \left[{\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{{\partial n_{i}}}{\partial x} } & 0 & 0 \\ \end{array}} \\ {\begin{array}{*{20}c} 0 & { \frac{{\partial n_{i}}}{\partial y}} & 0 \\ \end{array}} \\ {\begin{array}{*{20}c} {\frac{{\partial n_{i}}}{\partial y}} & {\frac{{\partial n_{i}}}{\partial x}} & 0 \\ \end{array}} \\ {\begin{array}{*{20}c} 0 & { 0} & { 1} \\ \end{array}} \\ \end{array}} \right],\,\check{0} = \left[{\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array}} \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array}} \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array}} \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array}} \\ \end{array}} \right] \hfill \\ \left[{{\mathbf{B}}_{rsi}} \right] = \left[{\begin{array}{*{20}c} {\begin{array}{*{20}c} {\check{\rm I} } & {{{\ddot{0}}} } & {{{\ddot{0}}}} \\ \end{array} \begin{array}{*{20}c} {{{\ddot{0}}} } & {{{\ddot{0}}}} \\ \end{array}} \\ {\begin{array}{*{20}c} {{{\ddot{0}}} } & {\check{\rm I} } & {{{\ddot{0}}}} \\ \end{array} \begin{array}{*{20}c} {{{\ddot{0}}}} & { {{\ddot{0}}}} \\ \end{array}} \\ {\begin{array}{*{20}c} {{{\ddot{0}}} } & {{{\ddot{0}}} } & {\check{\rm I}} \\ \end{array} \begin{array}{*{20}c} {{{\ddot{0}}} } & {{{\ddot{0}}}} \\ \end{array}} \\ {\begin{array}{*{20}c} {{{\ddot{0}}} } & {{{\ddot{0}}} } & {{{\ddot{0}}}} \\ \end{array} \begin{array}{*{20}c} {\check{\rm I} } & {{{\ddot{0}}}} \\ \end{array}} \\ {\begin{array}{*{20}c} {{{\ddot{0}}} } & {{{\ddot{0}}} } & {{{\ddot{0}}}} \\ \end{array} \begin{array}{*{20}c} {{{\ddot{0}}} } & {\check{\rm I}} \\ \end{array}} \\ {\begin{array}{*{20}c} {\widehat{{{\mathbf{B}}_{rsi}}}} & {{{\ddot{0}}}} & {{{\ddot{0}}}} \\ \end{array} \begin{array}{*{20}c} {{{\ddot{0}}}} & {{{\ddot{0}}}} \\ \end{array}} \\ {\begin{array}{*{20}c} {{{\ddot{0}}}} & {\widehat{{{\mathbf{B}}_{rsi}}}} & {{{\ddot{0}}}} \\ \end{array} \begin{array}{*{20}c} {{{\ddot{0}}}} & {{{\ddot{0}}}} \\ \end{array}} \\ {\begin{array}{*{20}c} {{{\ddot{0}}}} & {{{\ddot{0}}}} & {\widehat{{{\mathbf{B}}_{rsi}}}} \\ \end{array} \begin{array}{*{20}c} {{{\ddot{0}}}} & {{{\ddot{0}}}} \\ \end{array}} \\ {\begin{array}{*{20}c} {{{\ddot{0}}}} & {{{\ddot{0}}}} & {{{\ddot{0}}}} \\ \end{array} \begin{array}{*{20}c} {\widehat{{{\mathbf{B}}_{rsi}}}} & {{{\ddot{0}}}} \\ \end{array}} \\ {\begin{array}{*{20}c} {{{\ddot{0}}}} & {{{\ddot{0}}}} & {{{\ddot{0}}}} \\ \end{array} \begin{array}{*{20}c} {{{\ddot{0}}}} & {\widehat{{{\mathbf{B}}_{rsi}}}} \\ \end{array}} \\ \end{array}} \right],\,\widehat{{{\mathbf{B}}_{rsi}}} = \left[{\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & {\frac{{\partial n_{i}}}{\partial x}} \\ \end{array}} \\ {\begin{array}{*{20}c} 0 & 0 & {\frac{{\partial n_{i}}}{\partial y}} \\ \end{array}} \\ \end{array}} \right],\, {\ddot{0}} = \left[{\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array}} \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array}} \\ \end{array}} \right] \hfill \\ \end{gathered} $$

The various rigidity matrices and the rigidity vectors for electro-elastic coupling appearing in the above elemental matrices are given by

$$ \begin{aligned} \left[ {{\mathbf{D}}_{{{\mathbf{tb}}}}^{{\mathbf{b}}} } \right] & = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{b}}}^{{\mathbf{b}}} } \right]^{{\mathbf{k}}} {\mathbf{dz}},\,\left[ {{\mathbf{D}}_{{{\mathbf{trb}}}}^{{\mathbf{b}}} } \right] = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{b}}}^{{\mathbf{b}}} } \right]^{{\mathbf{k}}} \left[ {{\mathbf{Z}}_{{\mathbf{1}}} } \right]{\mathbf{dz}},\,\left[ {{\mathbf{D}}_{{{\mathbf{ts}}}}^{{\mathbf{b}}} } \right] = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{s}}}^{{\mathbf{b}}} } \right]^{{\mathbf{k}}} {\mathbf{dz}}, \\ \left[ {{\mathbf{D}}_{{{\mathbf{trs}}}}^{{\mathbf{b}}} } \right] & = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{s}}}^{{\mathbf{b}}} } \right]^{{\mathbf{k}}} \left[ {{\mathbf{Z}}_{5} } \right]{\mathbf{dz}},\,\left[ {{\mathbf{D}}_{{{\mathbf{rrb}}}}^{{\mathbf{b}}} } \right] = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {{\mathbf{Z}}_{{\mathbf{1}}} } \right]^{{\mathbf{T}}} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{s}}}^{{\mathbf{b}}} } \right]^{{\mathbf{k}}} \left[ {{\mathbf{Z}}_{{\mathbf{1}}} } \right]{\mathbf{dz}}, \\ \left[ {{\mathbf{D}}_{{{\mathbf{rrs}}}}^{{\mathbf{b}}} } \right] & = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {{\mathbf{Z}}_{{\mathbf{5}}} } \right]^{{\mathbf{T}}} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{s}}}^{{\mathbf{b}}} } \right]^{{\mathbf{k}}} \left[ {{\mathbf{Z}}_{{\mathbf{5}}} } \right]{\mathbf{dz}} \\ \left[ {{\mathbf{D}}_{{{\mathbf{tb}}}}^{{\mathbf{t}}} } \right] & = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{b}}}^{{\mathbf{t}}} } \right]^{{\mathbf{k}}} {\mathbf{dz}},\,\left[ {{\mathbf{D}}_{{{\mathbf{trb}}}}^{{\mathbf{t}}} } \right] = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{b}}}^{{\mathbf{t}}} } \right]^{{\mathbf{k}}} \left[ {{\mathbf{Z}}_{{\mathbf{3}}} } \right]{\mathbf{dz}},\,\left[ {{\mathbf{D}}_{{{\mathbf{ts}}}}^{{\mathbf{t}}} } \right] = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{s}}}^{{\mathbf{t}}} } \right]^{{\mathbf{k}}} {\mathbf{dz}}, \\ \left[ {{\mathbf{D}}_{{{\mathbf{trs}}}}^{{\mathbf{t}}} } \right] & = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{s}}}^{{\mathbf{t}}} } \right]^{{\mathbf{k}}} \left[ {{\mathbf{Z}}_{{\mathbf{7}}} } \right]{\mathbf{dz}},\,\left[ {{\mathbf{D}}_{{{\mathbf{rrb}}}}^{{\mathbf{t}}} } \right] = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {{\mathbf{Z}}_{{\mathbf{3}}} } \right]^{{\mathbf{T}}} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{s}}}^{{\mathbf{t}}} } \right]^{{\mathbf{k}}} \left[ {{\mathbf{Z}}_{{\mathbf{3}}} } \right]{\mathbf{dz}}, \\ \left[ {{\mathbf{D}}_{{{\mathbf{rrs}}}}^{{\mathbf{t}}} } \right] & = \mathop \sum \limits_{{{\mathbf{k}} = {\mathbf{1}}}}^{{\mathbf{n}}} \int \limits_{{{\mathbf{h}}_{{\mathbf{k}}} }}^{{{\mathbf{h}}_{{{\mathbf{k}} + {\mathbf{1}}}} }} \left[ {{\mathbf{Z}}_{{\mathbf{7}}} } \right]^{{\mathbf{T}}} \left[ {\overline{{\mathbf{C}}}_{{\mathbf{s}}}^{{\mathbf{t}}} } \right]^{{\mathbf{k}}} \left[ {{\mathbf{Z}}_{{\mathbf{7}}} } \right]{\mathbf{dz}} \\ \left[ {{\mathbf{D}}_{ts}^{b} } \right] & = \left[ {{\mathbf{C}}_{s}^{b} } \right]{\text{h}},\, \left[ {{\mathbf{D}}_{ts}^{c} } \right] = 2\left[ {{\mathbf{C}}_{s}^{c} } \right]{\text{h}}_{\text{c}} ,\, \left[ {{\mathbf{D}}_{ts}^{t} } \right] = \left[ {{\mathbf{C}}_{s}^{t} } \right]{\text{h}}, \left[ {{\mathbf{D}}_{ts}^{v} } \right] = \left[ {{\mathbf{C}}_{s}^{v} } \right]{\text{h}}_{\text{v}} , \left[ {{\mathbf{D}}_{ts}^{p} } \right] = \left[ {{\mathbf{C}}_{s}^{p} } \right]{\text{h}}_{\text{p}} \\ \left[ {{\mathbf{D}}_{tbs}^{p} } \right] & = \left[ {{\mathbf{D}}_{bs}^{p} } \right]{\text{h}}_{p} ,\, \left[ {{\mathbf{D}}_{trbs}^{p} } \right] = \,\int \limits_{{h_{5} }}^{{h_{6} }} \left[ {{\mathbf{C}}_{bs}^{p} } \right]\left[ {{\mathbf{Z}}_{10} } \right]{\text{d}}z,\, \left[ {{\mathbf{D}}_{rtbs}^{p} } \right] = \,\int \limits_{{h_{5} }}^{{h_{6} }} \left[ {{\mathbf{Z}}_{5} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{bs}^{p} } \right]{\text{d}}z \\ \left[ {{\mathbf{D}}_{rrbs}^{p} } \right] & = \int \limits_{{h_{5} }}^{{h_{6} }} \left[ {{\mathbf{Z}}_{5} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{bs}^{p} } \right]\left[ {{\mathbf{Z}}_{10} } \right]{\text{d}}z,\, \left[ {{\mathbf{D}}_{trb}^{b} } \right] = \int \limits_{{h_{1} }}^{{h_{2} }} \left[ {{\mathbf{C}}_{b}^{b} } \right]\left[ {{\mathbf{Z}}_{1} } \right]{\text{d}}z,\,\left[ {{\mathbf{D}}_{trb}^{c} } \right] = \int \limits_{{h_{2} }}^{{h_{3} }} \left[ {{\mathbf{C}}_{b}^{c} } \right]\left[ {{\mathbf{Z}}_{2} } \right]{\text{d}}z \\ \left[ {{\mathbf{D}}_{trb}^{t} } \right] & = \int \limits_{{h_{3} }}^{{h_{4} }} \left[ {{\mathbf{C}}_{b}^{t} } \right]\left[ {{\mathbf{Z}}_{3} } \right]{\text{d}}z, \left[ {{\mathbf{D}}_{trb}^{v} } \right] = \int \limits_{{h_{4} }}^{{h_{5} }} \left[ {{\mathbf{C}}_{b}^{v} } \right]\left[ {{\mathbf{Z}}_{4} } \right]{\text{d}}z,\,\left[ {{\mathbf{D}}_{trb}^{p} } \right] = \int \limits_{{h_{5} }}^{{h_{6} }} \left[ {{\mathbf{C}}_{b}^{p} } \right]\left[ {{\mathbf{Z}}_{5} } \right]{\text{d}}z \\ \left[ {{\mathbf{D}}_{rrb}^{b} } \right] & = \int \limits_{{h_{1} }}^{{h_{2} }} \left[ {{\mathbf{Z}}_{1} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{b}^{b} } \right]\left[ {{\mathbf{Z}}_{1} } \right]{\text{d}}z,\,\left[ {{\mathbf{D}}_{rrb}^{c} } \right] = \int \limits_{{h_{2} }}^{{h_{3} }} \left[ {{\mathbf{Z}}_{2} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{bs}^{p} } \right]\left[ {{\mathbf{Z}}_{2} } \right]{\text{d}}z,\,\left[ {{\mathbf{D}}_{rrb}^{t} } \right] = \int \limits_{{h_{3} }}^{{h_{4} }} \left[ {{\mathbf{Z}}_{3} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{bs}^{p} } \right]\left[ {{\mathbf{Z}}_{3} } \right]{\text{d}}z \\ \left[ {{\mathbf{D}}_{rrb}^{v} } \right] & = \int \limits_{{h_{4} }}^{{h_{5} }} \left[ {{\mathbf{Z}}_{4} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{bs}^{p} } \right]\left[ {{\mathbf{Z}}_{4} } \right]{\text{d}}z,\,\left[ {{\mathbf{D}}_{rrb}^{p} } \right] = \int \limits_{{h_{5} }}^{{h_{6} }} \left[ {{\mathbf{Z}}_{5} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{bs}^{p} } \right]\left[ {{\mathbf{Z}}_{5} } \right]{\text{d}}z,\, \left[ {{\mathbf{D}}_{trs}^{b} } \right] = \int \limits_{{h_{1} }}^{{h_{2} }} \left[ {{\mathbf{C}}_{s}^{b} } \right]\left[ {{\mathbf{Z}}_{6} } \right]{\text{d}}z \\ \left[ {{\mathbf{D}}_{trs}^{c} } \right] & = \int \limits_{{h_{2} }}^{{h_{3} }} \left[ {{\mathbf{C}}_{s}^{c} } \right]\left[ {{\mathbf{Z}}_{7} } \right]{\text{d}}z,\,\left[ {{\mathbf{D}}_{trs}^{t} } \right] = \int \limits_{{h_{3} }}^{{h_{4} }} \left[ {{\mathbf{C}}_{s}^{t} } \right]\left[ {{\mathbf{Z}}_{8} } \right]{\text{d}}z,\,\left[ {{\mathbf{D}}_{trs}^{v} } \right] = \int \limits_{{h_{4} }}^{{h_{5} }} \left[ {{\mathbf{C}}_{s}^{v} } \right]\left[ {{\mathbf{Z}}_{9} } \right]{\text{d}}z,\,\left[ {{\mathbf{D}}_{trs}^{p} } \right] = \int \limits_{{h_{5} }}^{{h_{6} }} \left[ {{\mathbf{C}}_{s}^{p} } \right]\left[ {{\mathbf{Z}}_{10} } \right]{\text{d}}z, \\ \left[ {{\mathbf{D}}_{rrs}^{b} } \right] & = \int \limits_{{h_{1} }}^{{h_{2} }} \left[ {{\mathbf{Z}}_{6} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{s}^{b} } \right]\left[ {{\mathbf{Z}}_{6} } \right]{\text{d}}z,\left[ {{\mathbf{D}}_{rrs}^{c} } \right] = \int \limits_{{h_{2} }}^{{h_{3} }} \left[ {{\mathbf{Z}}_{7} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{s}^{c} } \right]\left[ {{\mathbf{Z}}_{7} } \right]{\text{d}}z, \\ \left[ {{\mathbf{D}}_{rrs}^{t} } \right] & = \int \limits_{{h_{3} }}^{{h_{4} }} \left[ {{\mathbf{Z}}_{8} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{s}^{t} } \right]\left[ {{\mathbf{Z}}_{8} } \right]{\text{d}}z,\,\left[ {{\mathbf{D}}_{rrs}^{v} } \right] = \int \limits_{{h_{4} }}^{{h_{5} }} \left[ {{\mathbf{Z}}_{9} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{s}^{v} } \right]\left[ {{\mathbf{Z}}_{9} } \right]{\text{d}}z,\,\left[ {{\mathbf{D}}_{rrs}^{p} } \right] = \int \limits_{{h_{5} }}^{{h_{6} }} \left[ {{\mathbf{Z}}_{10} } \right]^{\text{T}} \left[ {{\mathbf{C}}_{s}^{p} } \right]\left[ {{\mathbf{Z}}_{10} } \right]{\text{d}}z \\ \left\{ {{\mathbf{D}}_{tb}^{p} } \right\} & = - \int \limits_{{h_{5} }}^{{h_{6} }} {\raise0.7ex\hbox{${\left\{ {{\mathbf{e}}_{b} } \right\}}$} \!\mathord{\left/ {\vphantom {{\left\{ {{\mathbf{e}}_{b} } \right\}} {{\text{h}}_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{h}}_{p} }$}} {\text{d}}z,\, \left\{ {{\mathbf{D}}_{ts}^{p} } \right\} = - \int \limits_{{h_{5} }}^{{h_{6} }} {\raise0.7ex\hbox{${\left\{ {{\mathbf{e}}_{s} } \right\}}$} \!\mathord{\left/ {\vphantom {{\left\{ {{\mathbf{e}}_{s} } \right\}} {{\text{h}}_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{h}}_{p} }$}} {\text{d}}z,\,\left\{ {{\mathbf{D}}_{rb}^{p} } \right\} = - \int \limits_{{h_{5} }}^{{h_{6} }} \left[ {{\mathbf{Z}}_{5} } \right]^{\text{T}} {\raise0.7ex\hbox{${\left\{ {{\mathbf{e}}_{b} } \right\}}$} \!\mathord{\left/ {\vphantom {{\left\{ {{\mathbf{e}}_{b} } \right\}} {{\text{h}}_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{h}}_{p} }$}} {\text{d}}z \\ \left\{ {{\mathbf{D}}_{rs}^{p} } \right\} & = - \int \limits_{{h_{5} }}^{{h_{6} }} \left[ {{\mathbf{Z}}_{10} } \right]^{\text{T}} {\raise0.7ex\hbox{${\left\{ {{\mathbf{e}}_{s} } \right\}}$} \!\mathord{\left/ {\vphantom {{\left\{ {{\mathbf{e}}_{s} } \right\}} {{\text{h}}_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{h}}_{p} }$}} {\text{d}}z, \\ \end{aligned} $$