1 Introduction

Nowadays, an issue of interest in the field of nanoscience and nanotechnology is the fabrication of nanomaterials with desired properties from the knowledge of their internal nanostructures characteristics. The Hall–Petch to Reversed Hall–Petch Relationship (HPR-to-RHPR) has been extensively used, with some success, to predict nanomaterials mechanical properties (or yield stress) from the knowledge of nanostructure sizes, (Hall 1951; Petch 1953; Zhao 2006). The HPR-to-RHPR in its original form is more suitable when dealing with “instantaneous” relationships between grain sizes and yield stresses, (Tengen et al. 2008a). To deal with values that change with time, the relationship has to be modified, (Tengen et al. 2010). It should, thus, be remarked that the (modified) HPR-to-RHPR uses the knowledge obtained from the characterisation of grain sizes to predict overall properties mechanical properties, such as yield stress. Thus, an approach to the issue of predicting nanomaterials overall properties (or stabilities) from the knowledge of the internal nanostructure characteristics has been to start with the understanding (or characterisation) of the internal nanostructures, and then followed by relating the characteristics, in “some sense”, to the overall observed macroscopic properties.

Quite a large number of research works have been done on these characterisations (i.e. on the understanding of the characteristics) of nanostructures; and more advanced works are still being done due to constant advancement in microscopy technology. Several approaches have being used to relate nanomaterials characteristics, in some sense, to overall mechanical properties, some of which are given here. Firstly, it is noted, (Tengen et al. 2010), that during plastic deformation of coarse-grain materials into nanomaterials, the larger-softer grains may predominantly accommodate a larger amount of the plastic strain. This issue has been handled, (Tengen et al. 2010), by considering local information about a grain, such as individual grain size, critical grain size, Grain Boundary (GB) mobility function, random grain size fluctuation and rate of grain rotation. Such a consideration, (Tengen et al. 2010), revealed the normal, anomalous and homologous temperature behaviours of nanomaterials mechanical properties. The second school of thought, (Kim and Estrin 2005, 2008), approach the deformation problems in nanomaterials from the phase-mixture point of view; whereby nanomaterials grains are assumed to be made up of two phases: the softer GB and harder Grain Interiors (GI) phases. Here, (Kim and Estrin 2005, 2008), the grain stress or strain is considered to be made up of contributions from GI and GB. Another school of thought, (Tengen 2008), proposes that a grain’s neighbours should impart different “deformation” forces on that grain, with the resultant (or number) of the deformation forces depending on the grain contact number. A grain contact number is the number of faces on that grain which represents the number of nearest neighbouring grains, (Tengen 2008). Thus, the major accommodation of plastic strain by the larger softer grains can be explained, from forces consideration, to be due to the larger number of neighbours (or faces). This last proposal is not yet rigorously verified since the directions of the forces around a particular grain, from the neighbours, are unknown and are random. Detail investigation on this face-force consideration is subject to further research where results from the present study may be useful.

The basis of this face-force proposition is that if a nanomaterial is made up of grains with faces on them, then the sum of the faces on all the grains can be obtained. Similarly, nanomaterials overall property (e.g. overall force on nanomaterial) can be obtained as the “sum in some sense” of the properties of (e.g. forces on) the internal structures, (Tengen et al. 2008a, 2010; Tengen and Iwankiewicz 2010). Thus, it is logical to claim that there exists some relationship(s) between these two sums (i.e. sum of total number of features and sum of properties of nanostructures). The rest of this present paper deals with further effort aimed at understanding the temporal and thermal evolution of the statistics of the sum of the features on all the grains.

Models for the sum of all features, herein called overall or cumulative features, on all the grains have been proposed and tested, (Tengen 2008, 2009; Tengen and Iwankiewicz 2006), under instantaneous/static conditions where grain growth was assumed not to occur. The present paper proposes theoretically modified models for the evolution of the cumulative features’ statistics that account for grain growth. The proposed theoretically modified models result in system of differential equations that are solved simultaneously as initial-to-intermediate value problems. The initial and intermediate values are some data obtained at some time-points from nanocrystalline aluminium samples during grain growth. Thus, models for different grain growth mechanisms are also useful in this study.

Various mechanisms have been identified to be responsible for grain growth in nanomaterials, (Tengen 2008; Tengen et al. 2007, 2008b). This includes the curvature-driven Grain Boundary Migration (GBM) where larger grains gradually consume smaller grains by atoms diffusion through the GB; mis-orientation angle driven Grain Rotation Coalescence (GRC) mechanism where two neighbouring grains rotate and only coalesce when the mis-orientation angle between them is zero; the T1 event where some grains which are initially neighbours separate along common GB and move apart while some grains that are initially not neighbours move towards each other to form common GB; and the T2 events where smaller 3-sided grains disappear from the nanomaterials. Model for grain growth as a function of grain size, that involves the different grain growth mechanisms, has been dealt with, (Tengen 2008; Tengen et al. 2007, 2008b). The effect of the different mechanisms of grain growth, as a function of grain size, on nanomaterials mechanical properties, such yield stress and internal energy, have also been studied, (Tengen et al. 2008a, 2010; Tengen and Iwankiewicz 2010). The present paper studies the effects of the different mechanisms of grain growth and temperature on the cumulative features on all the grains in nanomaterials, which have not been considered in the previous works.

Before continuing, let’s introduce some nanomaterials grains’ features/characteristics. The number of faces or triple junctions per grain or grain size is herein called the number of features per nanostructure or the nanostructure characteristics: see Fig. 1 for sample nanomaterials showing these features on their grains. The number of faces, f, per grain are usually obtained from 3-D experiments and analyses; the number of sides or number of triple junctions or number of vertices, s, per grain are mostly used when undertaking 2-D and/or 3-D space analyses; and the size (radius) of a grain, r, is applicable for all the dimensional spaces i.e. 1-D, 2-D and/or 3-D analyses. The term, “size”, is used in this report to represent Lebesgue measure which stands for length in 1-D, area in 2-D, and volume in 3-D.

Fig. 1
figure 1

Grains in Nanocrystalline aluminium sample showing features such as faces and sides or junctions

Full size image

It is found in the literature that there are fundamentally three different ways of expressing grain growth phenomena using the three grain features or characteristics: Firstly, Hillert suggested a model, (Hillert 1965), that predicts how the grain radius (diameter) evolves with time as a function of the grain radius. This has been modified, (Tengen 2008; Tengen et al. 2007, 2008b), to.

$$ \, dr = M_{0} (T)\left( {1 + \frac{c}{r}} \right)\left( {\frac{1}{{r_{c} }} - \frac{1}{r}} \right)dt + b\sqrt r dW(t) + (a + 1)rdN(t) $$
(1)

where r is grain radius, \( M_{0} (T)\left( {1 + \left[ {C/r} \right]} \right) \) is GB mobility function which accounts for the fact that the GB mobility decreases during grain growth, \( M_{0} (T) \) is temperature dependent part of the GB mobility; a, b and c are constants, r c is the local critical grain size which is the size of a grain that neither grows nor shrinks and it is also known as the average size of the nearest neighbouring (surrounding) grains, dW(t) and dN(t) are respectively the increments of Weiner and stochastic counting processes within an infinitesimal time interval.

Secondly, the Von Neumann-Mullins law, (Von Neumann 1952; Mullins 1956; Mullins and Vinals 2002), expresses the evolution of the area of a grain as a function of the number of triple junctions only (i.e. as a function of the number of sides of the grains only). This von Neumann-Mullins relationship has been modified, (Gottstein et al. 2005), to

$$ \frac{dA_{s}}{dt} = \frac{{M_{b} }}{{1 + \frac{1}{\Uplambda }}}\left( {2\pi - s\left[ {\pi - 2\theta } \right]} \right) $$
(2)

where M b is the reduced GB mobility which is a product of GB mobility with the GB surface tension, Λ is the product of the triple junction mobility and the grain size divided by the GB mobility, s is the number of triple junction and θ is the contact angle at a triple junction.

And thirdly (Rivier 1983), proposed a relationship for the evolutions of the grain volume as a function of the number of faces per grain alone given by expression (3). Glazier, (Glazier and Prause 2002; Glazier 1993; Weaire and Glazier 1993; Glazier and Weaire 1992), later modified Rivier’s expression to (4) stating that Rivier’s expression gives grain growth exponent value of 0.33 or 1/3 instead of 0.5 that had been obtained in experiments. The issue about variable growth exponents obtained in experiments and simulations have been explained, (Tengen et al. 2007), to be due to variable initial grain size dispersions or initial dispersions of number of features per grain in nanomaterials. The expressions are

$$ \left[ {\frac{{dV_{f} }}{dt}} \right] = k\left( {F - F_{0} } \right) $$
(3)
$$ V_{f}^{ - 1/3} \left[ {\frac{{dV_{f} }}{dt}} \right] = k\left( {F - F_{0} } \right) $$
(4)

where k is termed Glazier-Rivier diffusion term, F is number of faces on a grain, F 0 is local critical number of faces per grain which is the number of faces that a grain that possesses it does not grow nor shrink at that instant and it is the mean number of faces on surrounding grains, V f is volume of an F-faced grain. Note that F 0 varies during grain growth. It is stated, (Glazier and Prause 2002; Glazier 1993; Weaire and Glazier 1993; Glazier and Weaire 1992), that F 0  = 〈F 2〉/〈F〉2 but it is derived in (Weaire and Glazier 1993) that, F 0  = 〈F 2〉/〈F〉. These conflicting reports led to a further literature search. This resulted, (Garboczi et al. 1995; Morhac and Morhacova 2000), in another finding that the relationship between the average number of faces of grains adjacent to an f-faced grain (i.e. the local critical number of faces per grain), F 0 , and the face number on that grain, F, is similar to Aboav-Weaire relation in two dimensions given for constant C1 and C2 as F = C 1 + C 2 /F 0 . These varying relationships between F 0 and F should have variable impacts when they are employed in models. Kumar et al., (Kumar et al. 2003), also noted that discrepancies exist when comparing results from many sources, and even results from the same authors. Thus, most models discuss the revealed trends; an approach adopted for this paper. Without further questioning, the relationship stated in (Glazier and Prause 2002; Glazier 1993; Weaire and Glazier 1993; Glazier and Weaire 1992), F 0  = 〈F 2〉/〈F〉 2 is termed CASE 1 and the derivation in (Weaire and Glazier 1993) which, F 0  = 〈F 2〉/〈F〉 is termed CASE 2 in the present report. These two cases are tested here.

Another observation is that the evolution of grain area has not yet been given as a function of number of faces per grain, and evolution of grain volume has not yet been expressible as a function of number of sides per grain. An issue is that if there exist strong mathematical relations between radius, area and volume, then why is it that one and only one random feature appears in each expressions of the evolution of grain size; and that a feature is not yet replaced by the other feature (i.e. “marginal” relationship is used instead of “joint” relationship)? Answers to this concern may further explain why deviations have been frequently encountered while verifying different models of grain growth from both simulations and experiments e.g. while verifying the Von Neumann-Law using the evolution of mean grain size or evolution of number of faces per grain. Resolving these issues is not the subject matter of the present paper.

The subject matter of the present paper is the impact of different grain growth mechanisms and temperature on the cumulative features on nanostructures. Using the degeneracy properties of the probability product density, the statistics of the cumulative nanostructure features on grains in nanomaterials has been proposed to be given by, (Tengen 2008, 2009; Tengen and Iwankiewicz 2006),

$$ {\mathbf{E}}\left[ {dF_{p} (R)} \right] = {\mathbf{E}}\left[ {F_{i} (R)} \right]v(R)dR $$
(5)
$$ {\mathbf{E}}\left[ {\left\{ {dF_{p} (R)} \right\}^{m} } \right] = {\mathbf{E}}\left[ {\left\{ {F_{i} } \right\}^{m} } \right]v(R)dR $$
(6)
$$ {\mathbf{E}}\left[ {dF_{p} (R_{1} )dF_{p} (R_{2} )} \right] = {\mathbf{E}}\left[ {\left\{ {F_{i} } \right\}^{2} } \right]v(R_{1} )v(R_{2} )dR_{1} dR_{2} {\text{ for }}R_{1} \ne R_{2} $$
(7)
$$ d\sigma_{{F_{p} }}^{2} (R) = 7[F(R)^{2} ]v(R)dR $$
(8)

where F p (R) is number of features of all grains (i.e. cumulative features) in nanomaterials, F i (R) is the number of features per grain, v(R) is the mean occurrence rate of grains or mean population density (or sparseness) and R is a “size” term i.e. dR is the size of a “section” of the entire nanomaterials. Note that the above position vector R is interpreted for Von-Neumann-Schvindlerman model as R = R(x,y) = (x,y)↔dR = (dx,dy) = dA and for Rivier-Glazier model as R = R(x,y,z) = (x,y,z)↔dR = (dx,dy,dz) = dV. Expressions (5)–(8) were previously tested, (Tengen 2008, 2009; Tengen and Iwankiewicz 2006), under static conditions. The objective of the present paper is to study the time evolution of these expressions (5)–(8). Thus, without loss of generality, dR is assumed to be change in grain size.

2 Method

To derive expressions (5)–(8), the entire nanomaterial has to be divided into contiguous sub-regions or sub-materials such that dR represents the increment in individual grain size. This division criterion is to ensure that regularity condition of the probability density function holds. Thus, for a 1-D nanostructure, dR is the change in “length or radius” of an individual grain; in 2-D, dR is the change in “area” while in 3-D, dR is the change in “volume”. To get the modified statistical expressions of the time evolution of the cumulative features on all grains, one of the two approaches given below can be employed: i.e. either employing exact expressions or approximate ones.

The exact approach involves applying Ito’s differential rule, (Iwankiewicz and Nielsen 1999), on expression (1) to obtain the expressions for the evolution of the second moment (area) or third moment (volume) of grain size. This derived expression is equated with expression (2) or (3) respectively, and the rule governing the Ito’s equation for moment, (Iwankiewicz and Nielsen 1999), is applied so as to get the relationship between moment of s and r; or F and r. The relationships between the first moments are given by

$$ \frac{{M_{b} }}{{1 + \frac{1}{\Uplambda }}}\left( {2\pi - s\left[ {\pi - 2\theta } \right]} \right) = 2\pi \left[ {2M\left( {\frac{r}{{r_{c} }} - 1} \right) + b^{2} r + \left( {3 + 4a + a^{2} } \right)r^{2} \mu + {\text{const}}_{s} } \right] $$
(9)
$$ k\left( {F - F_{0} } \right) = \frac{4}{3}\pi \left[ {3M\frac{{r^{3} }}{{r_{c} }} + 3r^{2} (b^{2} - M) + \left( {7 + 12a + 6a^{2} + a^{3} } \right)r^{3} \mu + {\text{const}}_{F} } \right] $$
(10)

where μ is the rate of coalescence events of grains and const i are constants of integration. The constant of integration is obtained from the fact that if the rates of change (or the derivatives) of two variables (A and B) are the same, then one of the variables is equal to the other plus a constant (i.e. A = B+Constant). Practically, the constant of integration is a normalisation parameter that depends on the type of material under consideration. It may be interpreted as being related the energy associated with the grain growth mechanisms where there is no change in grain size, such as during the rotation of the grain before coalescence, during T1 event and/or during T2 events. This is typically the change in “driving” force at constant grain size i.e. the First Theorem of Complementary Energy, (Tengen and Iwankiewicz 2010; B.W Young, Energy Methods of Structural Analysis, Theory, Worked Examples And Problems, The Macmillan Press Ltd 1981). The expression for the moments of s or F given in expressions (9)–(14), together with the equation for increment of grain area or grain volume respectively, obtained by Ito’s stochastic differential rule, are substituted into expressions (5)–(8) to obtain the expression for the time evolution of the statistics of the cumulative features. This approach is exact and involves the use of very lengthy equations. On applying the Von-Neumann-Schvindlerman model, (Von Neumann 1952; Mullins 1956; Mullins and Vinals 2002; Gottstein et al. 2005), the lengthy expressions for the time evolution of the statistics of cumulative features, s are

$$ {\mathbf{E}}\left[ {dS_{p} (R)} \right] = {\mathbf{E}}\left[ {S_{i} (R)} \right]v(R)dR = \left\{ {{\text{Const}}_{VNS} - A_{VNS} {\mathbf{E}}\left[ {2M\left( {\frac{\text{r}}{{{\text{r}}_{\text{c}} }} - 1} \right) + b^{2} r + D_{VNS} \, r^{2} } \right]} \right\}* \, {\mathbf{E}}\left\{ {2M\left( {\frac{\text{r}}{{{\text{r}}_{\text{c}} }} - 1} \right) + b^{2} r + D_{VNS} \, r^{2} } \right\}v(r)dt $$
(11)
$$ {\mathbf{E}}\left[ {\left\{ {dS_{p} (R)} \right\}^{2} } \right] = {\mathbf{E}}\left[ {\left\{ {S_{i} (R)} \right\}^{2} } \right] \, v(R)dR = \left\{ {{\text{Const}}_{VNS}^{2} - 2({\text{Const}}_{VNS}^{{}} )A_{VNS} {\mathbf{E}}\left[ {2M(\frac{\text{r}}{{{\text{r}}_{\text{c}} }} - 1) + b^{2} r + D_{VNS} r^{2} } \right]} \right. + A^{2}_{VNS} {\mathbf{E}}\left\{ {4M^{2} \left( {\left[ {\frac{\text{r}}{{{\text{r}}_{\text{c}} }}} \right]^{2} - 2\frac{\text{r}}{{{\text{r}}_{\text{c}} }} + 1} \right) + b^{4} r^{2} + D_{VNS}^{2} r^{4} + 2b^{2} D_{VNS} r^{3} } \right. \left. { + 4M\left[ {b^{2} \frac{{{\text{r}}^{ 2} }}{{{\text{r}}_{\text{c}} }} + D_{VNS} \frac{{{\text{r}}^{ 3} }}{{{\text{r}}_{\text{c}} }} - b^{2} r - D_{VNS} r^{2} } \right]} \right\}* \, {\mathbf{E}}\left\{ {2M\left( {\frac{\text{r}}{{{\text{r}}_{\text{c}} }} - 1} \right) + b^{2} r + D_{VNS} \, r^{2} } \right\}v(r)dt $$
(12)

where

$$ {\text{Const}}_{VNS} = \frac{1}{{\left[ {\pi - 2\theta } \right]}}\left\{ {2\pi - A_{VNS} {\text{const}}_{s} } \right\}, \quad {\text{A}}_{VNS} = \left[ {1 + \frac{1}{\Uplambda }} \right]\frac{2\pi }{{M_{b} }}, \quad {\text{ D}}_{VNS} = \left( {3 + 4a + a^{2} } \right)\mu $$

And the following two expressions are obtained on applying Rivier Glazier model:

$$ {\mathbf{E}}\left[ {dF_{p} (R)} \right] = {\mathbf{E}}\left[ {F_{i} (R)} \right]v(R)dR = {\mathbf{E}}\left\{ {A_{{RG}} \left[ {3M\frac{{r^{3} }}{{r_{c} }} + {\text{3}}\left( {{\text{b}}^{{\text{2}}} {\text{ - M}}} \right){\text{ }}r^{2} + D_{{RG}} {\text{ }}r^{3} } \right] + Const_{2} } \right\}{\text{ }}*{\mathbf{E}}\left\{ {3M\frac{{r^{3} }}{{r_{c} }} + {\text{3}}\left( {{\text{b}}^{{\text{2}}} {\text{ - M}}} \right){\text{ }}r^{2} + D_{{RG}} {\text{ }}r^{3} } \right\}v(r)dt $$
(13)
$$ {\mathbf{E}}\left[ {\left\{ {dF_{p} (R)} \right\}^{2} } \right] = {\mathbf{E}}\left[ {\left\{ {F_{i} (R)} \right\}^{2} } \right]v(R)dR = {\mathbf{E}}\left\{ {A_{RG}^{2} \left( {9M^{2} \frac{{r^{6} }}{{r_{c}^{2} }} + 6M} \right.\left[ { 3\left( {{\text{b}}^{ 2} - {\text{M}}} \right)\frac{{r^{5} }}{{r_{c}^{2} }} + D_{RG} \frac{{r^{6} }}{{r_{c} }}} \right] + \, 9\left( {{\text{b}}^{ 2} - {\text{M}}} \right)^{2} r^{4} + 6\left( {{\text{B}}^{ 2} - {\text{M}}} \right)D_{RG} r^{5} + D_{RG}^{2} r^{6} } { + 2{\text{Const}}_{2} *\left[ {3M\frac{{r^{3} }}{{r_{c} }} + 3\left( {{\text{b}}^{ 2} - {\text{M}}} \right) \, r^{2} + D_{RG} r^{3} } \right] + {\text{Const}}_{2}^{2} } \right\}*{\mathbf{E}}\left\{ {3M\frac{{r^{3} }}{{r_{c} }} + 3\left( {{\text{b}}^{ 2} - {\text{M}}} \right)r^{2} + D_{RG} r^{3} } \right\}v(r)dt $$
(14)

where

$$ {\text{const}}_{RG} = \frac{4\pi }{3k}{\text{const}}{}_{F} + {\text{F}}_{\text{o}} , \quad A_{RG} = \frac{4\pi }{3k}, \quad {\text{D}}_{RG} = \, \left( {7 + 12a + 6a^{2} + a^{3} } \right)\mu $$

The second approach is to use approximate and simpler expressions obtained from experiments. Such an expression for the relationship between F and r has been given, (Glazier and Prause 2002; Glazier 1993; Weaire and Glazier 1993; Glazier and Weaire 1992), as Vf 1/3 = R1/3αF. Searching the literature, no similar relationship between s and R was found. The statistical expressions for the time evolution of the cumulative number of features on grains is obtained by substituting the Right Hand Side of expressions (2) or (3) for dR in expressions (5)–(8). Considering the relationship Vf 1/3 = R1/3 α F and also the fact Vf 1/3 = R1/3 α r, (note the difference between r and R), it follows that rαF ↔ r n α F n. The resulting expressions for the statistics of the cumulative features from this approach are given by

$$ {\mathbf{E}}\left[ {dF_{p} (R)} \right] = {\mathbf{E}}\left[ {F_{i} (R)} \right]v(R)dR = k\left\langle r \right\rangle \left[ {\left\langle r \right\rangle - {{\left\langle {r^{2} } \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {r^{2} } \right\rangle } {\left\langle r \right\rangle }}} \right. \kern-\nulldelimiterspace} {\left\langle r \right\rangle }}} \right]v(r)dt $$
(15)
$$ {\mathbf{E}}\left[ {\left\{ {dF_{p} (R)} \right\}^{m} } \right] = {\mathbf{E}}\left[ {\left\{ {F_{i} } \right\}^{m} } \right]v(R)dR = k\left\langle {r^{m} } \right\rangle \left[ {\left\langle r \right\rangle - {{\left\langle {r^{2} } \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {r^{2} } \right\rangle } {\left\langle r \right\rangle }}} \right. \kern-\nulldelimiterspace} {\left\langle r \right\rangle }}} \right]v(r)dt $$
(16)
$$ {\mathbf{E}}\left[ {dF_{p} (R_{1} )dF_{p} (R_{2} )} \right] = {\mathbf{E}}\left[ {\left\{ {F_{i} } \right\}^{2} } \right] \, v(R_{1} )v(R_{2} )dR_{1} dR_{2} {\text{ for }}R_{1} \ne R_{2} = k^{2} \left\langle {r^{2} } \right\rangle \left[ {\left( {\left\langle {r{}_{1}} \right\rangle - {{\left\langle {r_{1}^{2} } \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {r_{1}^{2} } \right\rangle } {\left\langle {r_{1} } \right\rangle^{{}} }}} \right. \kern-\nulldelimiterspace} {\left\langle {r_{1} } \right\rangle^{{}} }}} \right)} \right]\left[ {\left( {\left\langle {r_{2} } \right\rangle - {{\left\langle {r_{2}^{2} } \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {r_{2}^{2} } \right\rangle } {\left\langle {r_{2} } \right\rangle }}} \right. \kern-\nulldelimiterspace} {\left\langle {r_{2} } \right\rangle }}} \right)} \right] \, v(r_{1} )v(r_{2} )dt_{1} dt_{2} $$
(17)
$$ \sigma_{{F_{p} }}^{2} (R) = 7[F(R)^{2} ]v(R)dR = 7k\left\langle {r^{2} } \right\rangle \left[ {\left\langle r \right\rangle - {{\left\langle {r^{2} } \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {r^{2} } \right\rangle } {\left\langle r \right\rangle }}} \right. \kern-\nulldelimiterspace} {\left\langle r \right\rangle }}} \right]v(r)dt $$
(18)

Observe that expressions (9)–(14) from the “exact” approach and (15)–(18) from the “approximate” approach are functions of grain size, “r”. They, i.e. either expressions (9)–(14) or (15)–(18), are solved simultaneously with expressions for the moments of grain size. Different mechanisms of grain growth are obtained by filtering expression (1). The mechanisms of grain growth that are considered when dealing with the “approximate” approach are the GBM process, GRC process and TOTAL process which is when GRC and GBM occurs simultaneously. Due to the inclusion of the “constant of integration” when using “exact” expressions (9)–(14), more grain growth mechanisms are explicitly considered i.e. T1 events, T2 events, GMB only, GRC only and TOTAL Process. T1 events and the process of rotating grains before coalescence which occur without any change in grain sizes are explained, (Tengen and Iwankiewicz 2010), to be given by the First Theorem of Complementary Energy. The First Theorem of Complementary energy gives the work done on nanomaterials by a changing force at constant displacement (i.e. constant grain size), (Tengen and Iwankiewicz 2010; B.W Young, Energy Methods of Structural Analysis, Theory, Worked Examples And Problems, The Macmillan Press Ltd 1981). T2 event is an instantaneous event that is assumed to be represented by the GRC mechanisms. Thus, the use of the “Exact” expressions (9)–(14) has an added advantage because it explicitly considers more mechanisms of grain growth.

3 Testing proposed models on Nanocrystalline aluminium

(Kumar et al. 2003), also noticed the existence of discrepancies when comparing experimental and simulation data from different (and, sometimes, the same) sources. They, (Kumar et al. 2003), explained that the reason is partly because of the limitations of available experimental tools to image and record, during deformation, the deformation processes at nanometer resolution. They, (Kumar et al. 2003) further explained that in order to overcome such limitations, attempts have been made to visualize defect nucleation at the atomic level in nanaocrsytalline metals using the Bragg-Nye soap bubble raft model (Bragg and Nye 1947; Gouldstone et al. 2001; Van Vliet et al. 2003), which is a two-dimensional (2-D) analog to fcc metals (Gouldstone et al. 2001; Van Vliet et al. 2003). The soap bubble raft has been used, (Van Vliet et al. 2003), to assess whether the deformation mechanisms in polycryattline nanometals vary with grain size. Readers interested in the soap buble raft experiments are referred to the original paper (Kumar et al. 2003; Bragg and Nye 1947; Gouldstone et al. 2001; Van Vliet et al. 2003). It should be remarked that the present paper also makes use of some trends/data obtained from soap bubbles or soap frost (Tengen et al. 2008b; Hillert 1965; Von Neumann 1952; Mullins 1956; Glazier and Prause 2002). The data/trends are given in the next two paragraphs.

The number of grains in the aggregate (grain density) is known, (Glazier and Prause 2002; Glazier 1993; Weaire and Glazier 1993; Glazier and Weaire 1992), to decrease during grain growth: grain growth is as a result of mass/atoms transfer through grain boundaries where larger grains consume smaller grains or by coalescence of grains. The relationship of the varying grain density is related to the mean number of faces per grain given by, (Tengen and Iwankiewicz 2006), v(r) = λ ′ e β{3−〈F〉}, where λ′ is the (number) density of grains corresponding to minimum mean number of faces per grain i.e. the highest grain number density, and β is a constant that accounts for the rate at which v(r) decreases as 〈F〉 increases during grain growth.

3.1 Set of constraints

It is reported that, (Tengen and Iwankiewicz 2006; Saito 1998), F(R) ∈ [3,36] and that, (Tengen and Iwankiewicz 2006; Glazier and Prause 2002; Glazier 1993; Weaire and Glazier 1993; Glazier and Weaire 1992; Saito 1998), {when 〈F〉 = 3, v(d) = 7000 and F p (d) = 21000}; and that {when 〈F〉 = 15.05 then v(d) = 96.63 and F p (d) = 1454.19}. Using this data with λ′ = 7000 it follows that β = 0.3554.

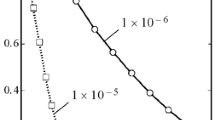
The results obtained from the present study are presented in the figures below. These results are from the “approximate” approach and from Rivier-Glazier’s model of grain growth. Thus, the results may be approximations too, and as such, emphases are paid on the trends of the results. Since there are variable relationships between the local critical number of faces per grain, F0, and the number of faces on per grain, F, results are presented here for two cases: CASE 1: F 0  = 〈F 2〉/〈F〉 2 and CASE 2: F 0  = 〈F 2〉/〈F〉. The dispersions, CV, of the grain features are obtained from the general formula 〈F 2〉 =(CV 2 + 1) 〈F〉2. The linear relationship, (Glazier and Prause 2002; Saito 1998), between grain size and the number of faces per grain used in the present report is F = (r/r 0 ) + (r 0 −1) with r o  = 3 nm. Note that F = r 0 when r = r 0 . The values of the diffusion term k given by the Rivier-Glazier’s model of grain growth are calibrated depending on the types of mechanisms of grain growth; and in such a way that the plots from the models should coincide with the experimental observations given in the preceding paragraph as sets of constraints. The rationale for variable k is that various grain growth mechanisms affect grain growth differently. The values of Glazier-Rivier’s constant, k, obtained for the various grain growth mechanisms and for the different cases that give plots that approximate to the sets of constraint data are kTOTAL,CASE1 = 1.43 × 10−6, kGBM,CASE1 = 9.6 × 10−6, kGRC,CASE1 = 2.14 × 10−6, kTOTAL,CASE2 = 1.32 × 10−6, kGBM,CASE2 = 2.32 × 10−6 and kGRC,CASE2 = 4.97 × 10−7. The labels on the plots are TOTALT, GBMT and GRCT. They plots should be interpreted as the values of the variables on the vertical axes as functions of horizontal axes variables at “T” Kelvin due to TOTAL Process, GBM only and GRC only respectively.

These major observations will not be repeated again under each result. Firstly, it should be remarked that the observed natures and extents of the evolutions of the statistics of the cumulative features depend strongly on the values of k: a slight change in k results in significant change in statistics of the cumulative number of faces on all grains. Secondly, the observed results also depend very strongly of the form of the local critical number of faces per grain (i.e. they depend on the cases: CASE 1 or CASE 2). And thirdly, the results depend on the type of grain growth mechanism under consideration and also on the annealing temperature.

It can be observed from Fig. 2a that the mean number of faces per grain increases constantly throughout grain growth for all the mechanisms of grain growth, an observation also made by others, (Rivier 1983; Glazier and Prause 2002; Glazier 1993; Weaire and Glazier 1993; Glazier and Weaire 1992; Garboczi et al. 1995; Morhac and Morhacova 2000; Saito 1998). It can be observed, Fig. 2a, that the extents to which grain growth occurs under various temperature conditions (i.e. “extent” is determined by the mean number of faces per grain) are higher for the TOTAL process than when other mechanisms of grain growth were to occur alone. This is due to the fact that during the TOTAL process, all the grain growth mechanisms take place simultaneously. At 500°K or lower temperature (Fig. 2a), the evolution of the mean number of faces per grain due to mis-orientation angle driven GRC only is larger than that due to the curvature driven GBM process only. This can be explained to be due to the fact that the GRC process is a mis-orientation angle driven mechanism whereby the mis-orientation is not affected by temperature. The GBM process is atom-diffusion based process whose rate depends of the annealing temperature given in the form of Arrhenius equation. The extent of grain growth changes at 700°K or higher temperatures when comparing GBM only and GRC only. This is due to the fact that at higher temperature, more thermal energy is available in the system leading to more diffusion of atoms. The lower rate of growth due to the GRC process at larger grain sizes is due to the fact that it becomes difficult for the grains to rotate at the larger sizes or higher number of faces per grain.

Fig. 2
figure 2

Evolution during grain growth of a mean number of faces per grain as function of time, b grain number density as function of time and c density of grain as a function of mean number of faces per grain

Full size image

It can also be observed from Fig. 2b that the density of grains in the nanomaterials sample decrease with time, an observation also made by others, (Rivier 1983; Glazier and Prause 2002; Glazier 1993; Weaire and Glazier 1993; Glazier and Weaire 1992). It should be observed that the higher the temperature the less dense (i.e. number density) the system becomes. This is due to the fact that more grain growth tends to occur thus, leading to a reduction in the number of grains in the material at higher temperature. The reduction in the density of grains at the same mean number of faces per grain but at higher temperature, Fig. 2c, indicates that the density of the grains in nanomaterials is simultaneously affected by many factors such as temperature, mean number of faces per grain, mechanisms of grain growth. This can also be explained to be partly due to the fact that other mechanisms of grain growth occur at constant number of faces per grain, such as T1 and T2 events. Furthermore, from the thermodynamics point of view, an increase in temperature makes materials/systems to become less dense. Finally, it should be remarked that the results in Fig. 2 are similar for the two CASES of critical number of faces per grain.

The evolutions of the mean cumulative number of faces on all the grains are given in Fig. 3. It can be observed that, for all the grain growth mechanisms and for the two cases, increasing the annealing temperature results in increase in mean cumulative number of faces on grains. This can be seen from the fact that the curves of results at higher temperatures lie above those at lower temperature. This can be explained to be due to the fact that more grain growth occurs (i.e. mean number of faces per grain increases) with little change in density of grains at higher temperature, see Fig 3a, b.

Fig. 3
figure 3

The evolution during grain growth of the sum of features on all the grains in the nanomaterial sample as functions of a mean number of faces per grain and CASE 1; b mean number of faces per grain and CASE 2, c density of grain CASE 1 and d density of grain CASE 2

Full size image

It should be remarked that in nanomaterials, the increase in the mean number of features per grain (i.e. grain growth) is always accompanied by a decrease in the grain number-density. It should be observed that the cumulative features on grains as a function of mean number of features per grain decrease continuously for the TOTAL process and GBM-only process throughout grain growth for the two CASES of local critical number of faces per grain. Larger decrease is observed for the TOTAL process than for the GBM only. This can be explained to be due to the fact that during grain growth the rate of decrease in the density of the grains in nanomaterials is larger for the TOTAL process than for the GBM only. It should be further recalled that it can be observed from expressions (5)–(8) that the cumulative number of features is affected simultaneously by mean number of features per grain, the grain density in nanomaterials and the size of the nanomaterials. The word “simultaneous” is very important observation in the previous statement. In the present situation, the sizes of the nanomaterials remain constant.

The nature of evolution of the cumulative number of features on all the grains as a function of grain density is also given in Fig. 3c. It can be observed that the cumulative feature decreases as the density of the grain decreases. This density-to-cumulative feature relationship can be easily explained from the following ideal example: Suppose that a section of nanomaterials were made up of two 3-faced grains. Then the total number of faces on the two grains is six. If the two grains were to coalesce along a common grain boundary during GRC process, then this will result in a section with one grain that has at total of five (5) faces. Thus, the evolution of the system is such that an initial system with two grains and a total of 6 faces grows to a final system made up of one grain with a total of 5 faces i.e. a reduction in number density leads to a reduction in the total number of faces on all the grain.

The trends for the evolution of the cumulative number of features as a function of the mean number of features per grain due to GRC only are seen to depend on the CASES, see Fig. 3a (i.e. it depends on the form of the mean local critical number of faces per grain). In CASE 1, it decreases as grain grows right up the point where the mean number of faces per grain is about 10–14, and then increases steadily. In CASE 2, it decreases steadily throughout the grain growth period. The reason for the decrease shown in CASE 1 where the mean number of features per grain is <10 and the observations in CASE 2 have already been explained in the previous paragraph. The observations in CASE 1, when the mean number of faces per grain is greater than the value at the turning point (i.e. >10-to-16 faces per grain), can be can be attributed to the presence of other mechanisms of grain growth such as T1 and T2 events which are implicit/inherited in the GRC process. Suppose, for example, that T2 event were to occur in a nanomaterial whose mean number of faces per grain is greater than 16. Further suppose, for example, that the nanomaterial is made up of two grains: one which is 31-faced grain and the other which is 3-faced grain making an average of 17 faces per grain. At the beginning of the occurrence of T2 event, the 3-faced grain disappears from the nanomaterial leaving one grain with an average of 31 faces. This “disappearance” of grain does not imply that “matter has been destroyed” nor that the grain has left the nanomaterial sample. The disappearance is due to the fact that it becomes difficult to monitor/trace the 3-faced grain throughout the nanomaterials during the evolution process. Due to the fact that matter is not destroyed, there will come a time whereby the disappeared grain gets attached to the 31-faced grain thus increasing the number of faces on the 31-faced grain to a value greater than 31 e.g. if coalescence occurs along a common grain boundary, then the number of faces changes from 31 to 33. Thus, there is an increase in mean number of faces per grain at constant density. It is, but, obvious that if the number-density of the grain in nanomaterial is constant then an increase in the mean number of faces per grain results in increase in the total number of faces on all the grains.

The evolution of the dispersion of the cumulative features on all grains is given in Fig. 4. It can be observed that the dispersions increase as grains grow, reaching a maximum and the decrease steadily. This nature of evolution (or behaviour) is similar to Hall–Petch-to-Reverse-Hall–Petch relationship. More resemblance to the HPR to RHPR can be achieved with proper choice of K. Thus, there might be some correlation between the dispersion of the cumulative features on all of the grains and the yield stress of nanomaterials. Verification is subject of future publication.

Fig. 4
figure 4

Evolution of dispersion, CV, of the cumulative features as a function of mean number of features (faces) per grain for a all the mechanisms of grain growth for CASE 1; b GBM only for CASE1; c GRC only for CASE 1and (d) all mechanisms at different temperature for CASE 2

Full size image

4 Conclusion

It can be concluded that models for the evolution of the statistics of the cumulative features on the all the grains in nanomaterial have been proposed and tested.

The evolution of mean number of faces per grain has been shown to increase constantly during grain growth.

The density of grain has been shown to decrease steadily for all grain growth mechanisms.

It the observed natures and extents of the evolutions of the statistics of cumulative features depend strongly on the values of k.

It is also observed that the results also depend very strongly of the form of the local critical number of faces per grain (i.e. they depend on the cases: CASE 1 or CASE 2).

It has been also shown that different mechanisms of grain growth and annealing temperatures impart different natures of evolution on the statistics of the cumulative features. The increase in temperature results in increase in mean number of features per grain, a decrease in grain density, an increase in cumulative features on grain and varying evolution of dispersion of cumulative features depending on grain growth mechanisms.

The mean cumulative number faces on all the grains have been shown to decrease steadily for TOTAL and GBM only and for the two cases. It also decreases steadily for GRC only in CASE 2. For CASE 1, it decreases reaching a minimum value and then increase steadily when grain growth is due to GRC only. This later observation in CASE 1 due to GRC only has been explained to be due to the presence of other grain growth mechanisms, such as T2 events, which are implicit in the GRC models.

The dispersion of the cumulative features has been shown to evolve in a manner similar to the mechanical properties given by the Hall–Petch to reverse-Hall–Petch relationships.

The results presented are for approximate expressions, and, hence, the results are surely approximation too.

Since reasonable explanations have made, by considering different grain growth mechanisms, about the “variable” or contradictory results from the different CASES, it can be concluded that results from various sources can be described as “not agreeing” only when the processing conditions, processing “routes” and the nature of evolution of the internal constituents of nanomaterials are exactly the same. Hence, processing route, processing conditions and the nature of evolution of the constituents of nanomaterials are simultaneously vital when designing or characterising nanomaterials.