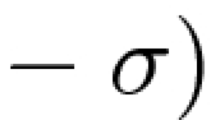Abstract
In this paper we establish sufficient conditions for the oscillation of all solutions of equation
via comparison with some first order delay difference equations whose oscillatory characters are known. The presented criterion is easily verifiable. Examples are also given to illustrate the main result.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we assume that p and q are sequences of positive real numbers, \(\tau \in \mathbb {N}=\{0,1,2,\dots ,\}\). We consider the linear fourth-order difference equation of the form
where \(n\in \mathbb {N}_{n_0}=\{n_0,n_0+1,\dots \}\) and \(n_0 \in \mathbb {N}\), \(\varDelta \) is the forward difference operator defined by \(\varDelta x(n)=x(n+1)-x(n)\). By a solution of equation (E) we understand a sequence x of real numbers, that is defined for \(n\ge n_0-\tau \) and satisfies the equation for sufficiently large n. A solution is nonoscillatory if it is eventually positive or eventually negative. Otherwise, the solution is said to be oscillatory. We call equation (E) oscillatory if all its solutions are oscillatory.
The background of difference equations and discrete oscillation theory can be found in the monographs of Agarwal [1] and Agarwal, Bohner, Grace and O’Regan [2]. In recent years, the study of oscillatory and asymptotic behavior of solutions of second order difference equations has received great attention. Compared to this, the study of higher-order difference equations receives considerably less attention in literature. Some recent results for the oscillation of third-order difference equations can be found in [3, 6, 7, 9, 12, 13, 24, 25], and for fourth-order in [4, 10, 16, 18, 23]. In particular, in [7] and [13], the authors studied oscillation and asymptotic properties of solutions of the three-term difference equation
by assuming the coefficient of the damping term is nonnegative. In [12], the difference equation
with positive coefficient p was investigated. In these papers the comparison theorems with suitable first-order difference equations were used. It seemed to be natural to continue the research in the case of higher-order equations especially since fourth-order differential and difference equations often occur as models in mathematical biology, economics and engineering (for example see [4, 5, 8, 26]).
In [15], the authors investigated the oscillatory behavior of solutions of the fourth order difference equations with damping
under the assumption that the auxiliary third order difference equation
is nonoscillatory.
The purpose of this paper is to study the oscillation of equation (E). Since for three-terms equations it is difficult to introduce the classification of nonoscillatory solutions, first we prove two lemmas that allow us to rewrite equation (E) in equivalent form as a two-terms equation with quasidifferences. Then, in our main result we give sufficient conditions for the oscillation of all solutions of equation (E) in terms of the two associated first order delay difference equations. Applying the appropriate criteria to these delay difference equations allows us to obtain new, easily verifiable oscillation results for equation (E) (see Theorem 2.10). It is worth noticing, that in this criterion the explicit form of solutions of the auxiliary equations is not needed. Numerical methods are frequently used in the investigation of the properties of the solutions of differential and difference equations. However, such methods are difficult to apply when investigating the oscillation of solutions. Our results may be helpful in the interpretation of numerical solutions, see Examples 3.1 and 3.2.
Let us recall some results that will be used in the sequel.
Lemma 1.1
[14, Corollary 7.6.1] Let a be a sequence of non-negative real numbers and let k be a positive integer such that
for large n. Then the difference inequality
has an eventually positive solution if and only if the difference equation
has an eventually positive solution.
The next result follows from [19, Theorem 1].
Lemma 1.2
Consider the equation
where c, b are eventually positive sequences. If
then for any real constant \(\beta \) there exists a solution v of equation (1.1) which converges to \(\beta \) at infinity.
Lemma 1.3
[18] Consider the difference equation
where a, b, c are sequences of positive real numbers and \(f:\mathbb {N}\times \mathbb {R}\rightarrow \mathbb {R}\).
Assume that
and \(u f(n,u)>0\) for all \(u\ne 0\), \(n\in \mathbb {N}\) hold. Let x be an eventually positive solution of (1.2). Then exactly one of the following statements holds for all sufficiently large n:
-
(i)
\(x(n)>0\), \(\varDelta x(n)>0\), \(\varDelta (c(n)\varDelta x(n))>0\) and \(\varDelta (b(n)(\varDelta (c(n)\varDelta x(n)))) >0\);
-
(ii)
\(x(n)>0\), \(\varDelta x(n)>0\), \(\varDelta (c(n)\varDelta x(n))<0\) and \(\varDelta (b(n)(\varDelta (c(n)\varDelta x(n))))>0\).
2 Main results
We start this section with two lemmas, which allow us to rewrite equation (E) in equivalent binomial form in terms of solutions of two auxiliary linear equations. Because the proofs of these lemmas are technically complicated, they are presented in Sect. 4.
Lemma 2.1
If z is an eventually positive solution of equation
then the equality
holds for any sequence x and for large n.
Lemma 2.2
If z is an eventually positive solution of equation (2.1) and equation
has an eventually positive solution v, then the equality
holds for any sequence x and for large n .
Applying (2.4) to equation (E) we get
Therefore, if z and v are eventually positive solutions of the equations (2.1) and (2.3) respectively, then, by Lemmas 2.1 and 2.2, equation (E) can be written in the form

The question arises whether equations (2.1) and (2.3) have eventually positive solutions. The lemma below presents a possible criterion.
Lemma 2.3
Assume \(\beta , \gamma \in (0,\infty )\) and
Then there exist an eventually positive solution z of (2.1) and an eventually positive solution v of (2.3) such that
Proof
By [22, Theorem 1] there exists a solution z of (2.1) such that \(\lim \nolimits _{n\rightarrow \infty }z(n)=\gamma \). That means, that there exists an index \(n_1>n_0\) such that \(z(n)>0\) and satisfies equality (2.1) for any \(n\ge n_1\). Hence, by (2.1), we have \(\varDelta ^3z(n)<0\) for \(n\ge n_1\). The convergence of z(n) implies
Since \(\varDelta ^3z(n)<0\) for \(n\ge n_1\), we get \(\varDelta ^2z(n)>0\) for \(n\ge n_1\). Analogously \(\varDelta z(n)<0\) eventually.
By [20, Lemma 6] the series \(\sum _{k=1}^\infty \sum _{n=k}^\infty \varDelta ^2z(n+1)\) is convergent. Using [20, Lemma 3] we get
Let, for \(n\ge n_1\),
Then, by (2.6), we have
where \(L=\gamma ^2z(n_1+1)\). Hence, from Lemma 1.2, we get the existence of a solution v of (2.3) such that \(\lim \limits _{n\rightarrow \infty }v(n)=\beta \). \(\square \)
Based on Trench [27], we say that a linear difference operator
is in canonical form if \(\sum \nolimits _{n=n_0}^{\infty }\frac{1}{r_j(n)}=\infty \) for \(j=1,\dots , m-1\), where \(r_j\) are eventually positive real sequences. The sequences \(L_ix\) are called quasidifferences of x.
The quasidifferences in equation () have the form
Note, that if z and v are solutions of the equations (2.1) and (2.3) respectively, and both converge to positive constants, then
and then the linear operator
in () is in canonical form, which means equation () is in canonical form.
Hence, by Lemma 1.3, we get the following classification of the nonoscillatory solutions of ().
Lemma 2.4
Assume that condition (2.5) is satisfied. Let x be an eventually positive solution of equation (). Then there exists \(n_2\ge n_0\) such that for all \(n\ge n_2\)
and either
or
In summary, we get the following remark.
Remark 2.5
If condition (2.5) holds, then the three-term difference equation (E) can be rewritten as a two-terms equation of the form (), which is in the canonical form.
Our goal is to present an easily verifiable oscillation criterion for equation (E). In our investigation we utilize the form (). Using the comparison theorem we will deduce the oscillation of (E) from the oscillation of certain first-order difference equations whose properties are well-explored.
Let z be a solution to equation (2.1) which tends to a positive constant and let v be a solution to equation (2.3) which tends to a positive constant. Then there exist positive constants \(z^{*}\), \(z^{**}\), \(v^{*}\), \(v^{**}\) and \(n_3 \in \mathbb {N}\) such that
for \(n \ge n_3\).
Assuming
we define sequences \(K_1, K_2\) by
where \(n_4=\max \{n_2,n_3\}+\tau +3\) and \(n_2\) as in Lemma 2.4. It is easy to see that condition (2.9) is equivalent to
Theorem 2.6
Assume that conditions (2.5) and (2.10) hold. If the following delayed equations with unknown sequence u
and
are oscillatory, then equation (E) is also oscillatory.
Proof
Assume to the contrary that there exists an eventually positive solution x to (E). Let x be such a solution. Notice that x is also an eventually positive solution to (). Let z be a positive decreasing solution of (2.1). According to Lemma 2.4 we consider two cases.
Case I. Assume conditions (2.7) and (2.8) hold. Summation of the both sides of () from \(s\ge n_4\) to infinity, leads to equality
From the above, by properties of the sequence \(L_3x\), we get
Since the sequence \(L_1x\) is a positive sequence, x is increasing,
and consequently
Summing the above inequality from n to infinity, we obtain
Again by (2.8),
By properties of the sequence \(L_2x\), we have
Combining the above two inequalities, we obtain
that is
Hence, using (2.8) we get
Based on the sequence \(L_1x\) properties, we have
for \(n > n_4\). Therefore
Combining (2.13) with (2.14), we get
that is
for \(n\ge n_4+\tau \). Using the definition of \(K_1\), this leads to inequality
By assumption, the sequence x is an eventually positive solution of inequality (2.15). By virtue of Lemma 1.1, it is also an eventually positive solution of equation (2.11). This contradicts that all solutions of (2.11) are oscillatory.
Case II. Set \(u(n):=L_3x(n)\). Let conditions (2.7) and (2.8) hold. Thus the the sequence \(L_2x\) is positive for \(n\ge n_4\). Hence, the following estimation holds
From the properties of the sequence \(L_3x\), we have
Combining the above two inequalities, we get
Summing both sides of the above inequality from \(n_4\) to \(k-1\), we obtain
Since the sequence \(L_1x\) is positive for \(n\ge n_4\), we have
On the other hand, again by (2.8), we get
The above and inequalities (2.16), (2.17) imply
By summation of both sides of the above inequality from \(n_4\) to \(n-1\), we obtain
Sequence x is positive for \(n\ge n_4\) hence \(\sum \nolimits _{k=n_4}^{n-1}\varDelta x(k)=x(n)-x(n_4)\le x(n)\). Consequently
Since the sequence \(L_3x\) is decreasing,
Hence,
Using the definition of u, equation () takes the form
We get
Hence, using (2.8) we get
Finally, using the definition of \(K_2\), we obtain
Since u is an eventually positive solution of the above inequality, by Lemma 1.1 it is also an eventually positive solution of equation (2.12). In that way there is contradiction with the assumption that all solutions of equation (2.12) are oscillatory. \(\square \)
Applying well-known oscillation criteria for first-order delay difference equations to equations (2.11) and (2.12) (see [11] and [17]), we obtain the following oscillation criteria for equation (E).
Corollary 2.7
Assume (2.5) and (2.10) are satisfied. If for \(j=1,2\)
then equation (E) is oscillatory.
If \(\tau >0\), then we can also use the following criterion.
Corollary 2.8
Assume (2.5) and (2.9) are satisfied. If for \(j=1,2\)
then equation (E) is oscillatory.
Note, that in the above results the explicit form of the eventually positive solutions of (2.1) and (2.3) are needed. But, it is well known, that it is difficult to find the explicit form of solutions of second and third order linear difference equations with variable coefficients. Therefore, we present a criterion in which the assumptions depend only on the coefficients p and q of the equation (E). First we prove a simple lemma.
Lemma 2.9
Then \(\lim \nolimits _{n\rightarrow \infty }K_j(i)=\infty \) for \(j=1,2\).
Proof
Let \(j=1\). Define a sequence Q by
Using discrete L’Hospital’s rule we obtain
Since \(\lim \nolimits _{n \rightarrow \infty } n^3q(n)=\infty \) we get \(\lim \nolimits _{n\rightarrow \infty } nQ(n)= \infty \). Hence
Let \(j=2\). It is easy to verify that
Since \(\lim \nolimits _{n \rightarrow \infty } n^3q(n)=\infty \) we get \(\lim \limits _{n\rightarrow \infty } K_2(n)= \infty \). \(\square \)
Combining Lemma 2.9 and Corollary 2.7 we get the following oscillation criterion.
Theorem 2.10
Assume (2.5), (2.10), and (2.18). Then equation (E) is oscillatory.
To verify conditions (2.5) and (2.10) the tests presented in [21] may be useful. For example, applying [21, Lemma 4.4] or [21, Lemma 4.5] we get the following results
Corollary 2.11
Assume (2.18) and
Then equation (E) is oscillatory.
Corollary 2.12
Assume (2.18) and
Then equation (E) is oscillatory.
3 Examples
By using computer algebra systems there is always possible to find recursively an approximate solution of the considered equation, but sometimes it is very difficult to determine whether the approximate solution is oscillatory or not. In many cases, it is rather easy to use our last criterion to verify that the considered equation is oscillatory. Such cases are shown in the following examples.
Example 3.1
Consider the following equation of type (E):
where \(n\ge 2\),
Using the iterative scheme
we solve (3.1) with the following initial conditions
Except for the initial conditions all computed values of x are rounded to the nearest integer number. As we see in Table 1, the obtained terms of this solution are positive until the 88th term, then negative. The next sign change of terms is on 346th term, next on 900th term and so on. Since the length of intervals with one sign are increasing, the oscillations of the solutions are not easily visible.
On the other hand, it is easy to verified that
Hence, by Theorem 2.10 all solutions of equation (3.1) are oscillatory.
Example 3.2
Consider fourth-order trinomial difference equations of the form
where \(a,b, \alpha , \beta >0\), \(\tau \in \mathbb {N}\). It is easy to see that if \(\alpha >3\) and \(2<\beta <3\), then conditions (2.5), (2.9) and (2.18) are satisfied. Hence, by Theorem 2.10 all solutions of equation (3.2) are oscillatory.
For a numerical solution of (3.2), we set \(a = 10, \;b = 5, \tau = 2, \alpha = 5, \beta =2,5\). The recurrence formula for the equation takes the form
Taking the initial values
we get a solution x whose trajectory from \(n=1\) to \(n=150\) is shown in Fig. 1. To show the oscillatory nature of this solution, we present its graph divided into four parts with increasingly larger scales.
Solution plot of Eq. (3.2) from Ex. 2
The graph from Fig. 1 divided into four parts
4 Proofs of Lemmas
Proof of Lemma 2.1
Let z be an eventually positive solution of equation (2.1). From the left hand side of (2.2), using (2.1), we obtain
Proof of Lemma 2.2
We start from the right hand side of (2.4):
Applying (2.2) to the first term of the last equality and combining together the second and third term we obtain
Now we transform separately the third term of the above expression
Hence, we obtain
From (2.3) we conclude that \(\varDelta ^2 z(n+1) \frac{v(n+1)}{z(n+1)z(n+2)} +\varDelta \left( \frac{\varDelta v(n)}{z(n+1)}\right) =0\) and finally we get
\(\square \)
5 Conclusions
In this paper, we have studied the oscillation of a fourth-order delay three-terms equation (E). Our comparison method is based on the canonical representation () of equation (E) and the existence of positive solutions satisfying the auxiliary equations (2.1) and (2.3). We have deduced the oscillation of equation (E) from the oscillation of certain first-order difference equations. Note, that even when we do not know the exact solutions of the auxiliary equation (2.1) or (2.3), we can easily verify the conditions presented in our criterion.
References
R.P. Agarwal, Difference Equations and Inequalities (Marcel Dekker, New York, 1992)
R.P. Agarwal, M. Bohner, S.R. Grace, D. O’Regan, Discrete Oscillation Theory Equations and Inequalities (Hindawi, New York, 2005)
M.F. Aktas, A. Tiryaki, A. Zafer, Oscillation of third-order nonlinear delay difference equations. Turk. J. Math. 36, 422–436 (2012). https://doi.org/10.3906/mat-1010-67
D.R. Anderson, F. Minhǒs, A discrete fourth-order Lidstone problem with parameters. Appl. Math. Comput. 214(2), 523–533 (2009). https://doi.org/10.1016/j.amc.2009.04.034
M. Artzroumi, Generalized stable population theory. J. Math. Biol 21, 363–381 (1985). https://doi.org/10.1007/BF00276233
M. Bohner, C. Dharuman, R. Srinivasan, E. Thandapani, Oscillation criteria for third-order nonlinear functional difference equations with damping. Appl. Math. Inf. Sci. 11(3), 669–676 (2017). https://doi.org/10.18576/amis/110305
M. Bohner, S. Geetha, S. Selvarangam, E. Thandapani, Oscillation of third-order delay difference equations with negative damping term. Ann. Univ. Mariae Curie-Sklodowska Sect. A 72(1), 19–28 (2018). https://doi.org/10.17951/a.2018.72.1.19
Ch. Hou, S.S. Cheng, Asymptotic dichotomy in a class of fourth-order nonlinear delay differential equations with damping, Abstr. Appl. Anal., Art. ID 484158, 7 pp. (2009). https://doi.org/10.1155/2009/484158
Z. Došlá, A. Kobza, On third-order linear difference equations involving quasi-differences. Adv. Differ. Equ., Article ID 65652 (2006). https://doi.org/10.1155/ADE/2006/65652
Z. Došlá, J. Krejčová, Oscillation of a class of the fourth-order nonlinear difference equations. Adv. Differ. Equ. 2012, 99 (2012). https://doi.org/10.1186/1687-1847-2012-99
L.H. Erbe, B.G. Zhang, Oscillation of discrete analogues of delay equations. Differ. Integral Equ. 2, 300–309 (1989)
A. Gleska, M. Migda, Asymptotic properties of nonoscillatory solutions of third-order delay difference equations. in Differential and Difference Equations with Applications. Springer Proceedings in Mathematics Statistics, 230, Springer, Cham, 327–337 (2018)
A. Gleska, M. Migda, Properties of solutions of third-order trinomial difference equations with deviating arguments. in Proceedings of the International Conference on Numerical Analysis and Applied Mathematics 2016, Book Series: AIP Conference Proceedings Volume: 1863 Article Number: UNSP 140006-1 (2017)
I. Györi, G. Ladas, Oscillation Theory of Delay Differential Equations with Applications (Clarendon Press, Oxford, 1991)
S. Jaikumar, K. Alagesan, G. Ayyappan, New oscillation criteria for fourth order delay difference equations with damping. Malaya J. Matematik 8, 838–844 (2020). https://doi.org/10.26637/MJM0803/0018
J. Krejčová, A comparison theorem for oscillation of fourth-order difference equations. Tatra Mt. Math. Publ. 63, 175–182 (2015). https://doi.org/10.1515/tmmp-2015-0029
G. Ladas, Ch.G. Philos, Y.G. Sficas, Sharp conditions for the oscillation of delay difference equations. J. Appl. Math. Simul. 2, 101–111 (1989). https://doi.org/10.1155/S1048953389000080
M. Migda, A. Musielak, E. Schmeidel, On a clss of fourth-order nonlinear difference equations. Adv. Differ. Equ., 23–36 (2004). https://doi.org/10.1155/s1687183904308083
M. Migda, Asymptotic behaviour of solutions of nonlinear delay difference equations. Fasc. Math. 31, 57–62 (2001)
J. Migda, Asymptotic properties of solutions of nonautonomous difference equations. Arch. Math. (Brno) 46, 1–11 (2010)
J. Migda, Iterated remainder operator, tests for multiple convergence of series and solutions of difference equations. Adv. Differ. Equ. 2014(189), 1–18 (2014). https://doi.org/10.1186/1687-1847-2014-189
M. Migda, J. Migda, On the asymptotic behavior of solutions of higher order nonlinear difference equations. Nonlinear Anal. 47, 4687–4695 (2001). https://doi.org/10.1016/S0362-546X(01)00581-8
J. Migda, M. Migda, M. Zdanowicz, Asymptotic properties of solutions to fourth order difference equations. J. Comput. Appl. Math. 362, 68–82 (2019). https://doi.org/10.1016/j.cam.2019.05.018
S.H. Saker, Oscillation of a certain class of third order nonlinear difference equations. Bull. Malays. Math. Sci. Soc. 35, 651–669 (2012)
S.H. Saker, J.O. Alzabut, A. Mukheimer, On the oscillatory behavior for a certain class of third order nonlinear delay difference equations. Electron. J. Qual. Theory Differ. Equ. 67, 16 (2010). https://doi.org/10.14232/ejqtde.2010.1.67
R.B. Stein, An analysis of oscillations in neuro-muscular systems. J. Math. Biol. 2, 87–105 (1975). https://doi.org/10.1007/BF00275922
W.F. Trench, Canonical forms and principal systems for general disconjugate equations. Trans. Am. Math. Soc. 189, 319–327 (1974)
Acknowledgements
The first author was partially supported by the Ministry of Science and Higher Education of Poland (04/43/SPAB/0113).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Migda, M., Schmeidel, E., Zdanowicz, M. et al. Oscillation results via comparison theorems for fourth-order delay three-terms difference equations. Period Math Hung 86, 395–412 (2023). https://doi.org/10.1007/s10998-022-00479-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10998-022-00479-1