Abstract
We present a version of an unpublished result of A.L.S. Corner on p-adic modules with anti-isomorphic endomorphism algebras. The result gives a complete description of necessary conditions for two such modules to have anti-isomorphic endomorphism algebras and a sufficient condition is also given. A main difference in the current version is that extensive use is made of our ability to describe certain homomorphism groups.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Throughout let R and Q denote the ring of p-adic integers and the field of p-adic numbers respectively and for rings T, S we write  if there is an anti-isomorphism from T onto S. As usual End(X) denotes the R-endomorphism algebra of X and we use the terminology ‘G is a p-adic module’ as a shorthand for saying ‘G is a module over the ring of p-adic integers’.
if there is an anti-isomorphism from T onto S. As usual End(X) denotes the R-endomorphism algebra of X and we use the terminology ‘G is a p-adic module’ as a shorthand for saying ‘G is a module over the ring of p-adic integers’.
Corner proved the result stated below sometime around 1961/62 but never published it. The only version [1] that exists is in Corner’s handwriting and corresponds to the reference [U4] in the listing of Corner’s unpublished works in [8]. This present work is based on the original but many of the arguments used there have been modified to reflect the advances that have been made in our understanding of the structure of homomorphism groups in more recent years.
Theorem 1.1
(A.L.S. Corner) Let G, H be p-adic modules with anti-isomorphic endomorphism algebras,  . Then either
. Then either
-
(I)
\(G \cong H \cong \bigoplus \nolimits _r R\) or \(G \cong H \cong \bigoplus \nolimits _r \mathbb {Z}(p^\infty )\) for some integer r,or
-
(II)
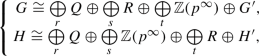
for integers r, s, t and either
-
(a)
\(G', H'\) are isomorphic finite p-groups or
-
(b)
there is a sequence of finite cyclic groups \(\langle a_j\rangle \) with exponents tending to infinity such that \(\prod \nolimits _{j=1}^\infty \langle a_j\rangle = P \ge G',H' \ge T\), the torsion submodule of P and \(G'/T, H'/T\) are divisible. Thus, \(G',H'\) are submodules of D, where D/T is the maximal divisible submodule of P/T.
If \(r \ge 1\) then \(G', H'\) are p-groups; if \(s \ge 1\) or \(t \ge 1\), then \(G', H'\) are finite p-groups.
Note that an immediate consequence of this result is that if G, H are p-groups with anti-isomorphic endomorphism rings then G is actually isomorphic to H. In addition, the rank of G is either finite or the continuum \(2^{\aleph _0}\); moreover either G is divisible or it has no elements of infinite height, i.e., G is a separable p-group.
Corner also provided a sufficient condition for anti-isomorphism of endomorphism algebras but we will defer discussion of this until later.
There have been several other approaches to this question of determining necessary conditions for p-adic modules to have anti-isomorphic endomorphism algebras. Most notably, Gabriella d’Este [3] proved in 1978 that for torsion p-adic modules (i.e., p-groups)  if, and only if, G is torsion-compact. She also established a number of interesting results in both the non-local and non-torsion situations. However, to date no result seems to be known which has the generality of Corner’s original theorem.
if, and only if, G is torsion-compact. She also established a number of interesting results in both the non-local and non-torsion situations. However, to date no result seems to be known which has the generality of Corner’s original theorem.
Corner also introduced the following terminology which we shall continue to use: if G, H are R-modules, then we say that the module G is opposed under \(\omega \) to H if there exists an R-algebra anti-isomorphism \(\omega :\mathrm{End}(G) \rightarrow \mathrm{End}(H)\); in this situation we say that G (and of course H) is opposable. The relationship is clearly symmetrical and, as above, we write 
Otherwise our teminology is standard and follows that of Fuchs [5,6,7]; standard notions in Abelian group and module theory may be found in these works and also in [11]. In particular, if G is a torsion R-module, then G is an Abelian p-group and the rank of G is the cardinality of a maximal independent subset consisting only of elements of order a power of p; equivalently the rank of G is then the vector-space dimension of its socle G[p]—see, for example, [5, Section 16]. We have used the terminology ‘semi-standard’ to denote a torsion R-module G having the property that each Ulm invariant \(f_G(n)\), with \(n < \omega \), is finite; equivalently a basic submodule B of G is of the form \(B = \bigoplus _{n < \omega }B_n\) where each \(B_n\) is a homocyclic p-group of exponent n and finite (possibly zero) rank.
2 Basic facts about p-adic modules
In this section we highlight some basic facts relating to modules over the ring R of p-adic integers. These results are well known and we mostly omit proofs or just give a reference to standard material.
A key tool in our approach to proving Corner’s result is, inevitably, based on an idea going back to Kaplansky’s work on torsion modules over a complete discrete valuation ring [11, §19]: if e is an idempotent in the endomorphism ring of a module M, then the rings \(e\mathrm{End}(M)e\) and \(\mathrm{End}(e(M))\) are isomorphic.
Proposition 2.1
Suppose that \(A, A'\) are R-modules and \(\omega : \mathrm{End}(A) \rightarrow \mathrm{End}(A')\) is an anti-isomorphism. If A has a decomposition \(A = B \oplus C\), then \(A'\) has a decomposition \(A' = B' \oplus C'\), and \(\omega \) induces an anti-isomorphism  . In particular, a direct summand of an opposable module is opposable.
. In particular, a direct summand of an opposable module is opposable.
Proof
If \(\pi \) is the projection of A onto B along C, then \(\pi ' = \omega (\pi )\) is an idempotent in \(\mathrm{End}(A')\) and gives rise to a decomposition \(A' = B' \oplus C'\) where \(B' = \omega (\pi )(B)\). However, \(\mathrm{End}(B') = \mathrm{End}(\pi '(A')) \cong \pi '\mathrm{End}(A')\pi ' = \omega (\pi \mathrm{End}(A)\pi ) = \omega (\mathrm{End}(\pi (A)))\). Thus, \(\omega \) induces an anti-isomorphism  . The final statement is immediate. \(\square \)
. The final statement is immediate. \(\square \)
Our next result, which is contained in Corner’s original manuscript, is simple but extremely useful.
Lemma 2.2
Let G, H be opposed under \(\omega \) and let \(\alpha _1, \alpha _2\) be two projections of G. Set \(A_i = \alpha _i(G), \beta _i = \omega (\alpha _i)\) and \(B_i = \beta _i(H)\). Then if \(\mathrm{Hom}(A_1, A_2) = 0\), we have \(\mathrm{Hom}(B_2, B_1) = 0\).
Proof
Let \(\beta :B_2 \rightarrow B_1\) be an arbitrary homomorphism. Extend \(\beta \) to the whole of H by defining \(\beta (1 - \beta _2)(H) = 0\). Then an easy check gives that \(\beta = \beta _1\beta \beta _2\). Now taking images under \(\omega ^{-1}\) and setting \(\alpha = \omega ^{-1}(\beta )\), we get \(\alpha = \omega ^{-1}(\beta _1\beta \beta _2) = \omega ^{-1}(\beta _2)\omega ^{-1}(\beta )\omega ^{-1}(\beta _1) = \alpha _2\alpha \alpha _1\) and so \(\alpha \) is a homomorphism \(:A_1 \rightarrow A_2\). Hence \(\alpha \) must be the zero homomorphism and thus, \(\beta = 0\) since \(\omega ^{-1}\) is an anti-isomorphism. \(\square \)
-
The nonzero indecomposable p-adic modules are \(R, Q, \mathbb {Z}(p^\infty )\) and \(\mathbb {Z}(p^n)\) for each \(n \ge 1\). An indecomposable p-adic module has a commutative endomorphism ring which has rank 1 as a p-adic module; the possible rings are just \(R,Q,R,\mathbb {Z}(p^n)\) respectively. If X is an indecomposable R-module, then it follows from Proposition 2.1 and the structure of the endomorphism rings of \(R,Q,\mathbb {Z}(p^\infty ),\mathbb {Z}(p^n)\) as given above that:
-
If X is opposed to Y, then Y is indecomposable.
-
If \(X \in \{Q, \mathbb {Z}(p^n) \ n\ge 1 \}\) and X is opposed to Y, then \(X \cong Y\).
-
If R is opposed to Y then either \(Y \cong R\) or \(Y \cong \mathbb {Z}(p^\infty )\).
-
If \(\mathbb {Z}(p^\infty )\) is opposed to Y then either \(Y \cong \mathbb {Z}(p^\infty )\) or \(Y \cong R\).
We remark that the main source of problems in trying to establish Corner’s theorem derives from the fact that R may be opposed to either R itself or to \(\mathbb {Z}(p^\infty )\).
Our next basic results focus on the structure of homomorphism groups and proofs of these may be found in [5, Chapter VIII] or [7, Chapter 7].
-
\((\bullet \ X)\) If either A or C is a torsion-free and divisible R-module, then \(\mathrm{Hom}(A,C)\) is always torsion-free and divisible.
-
\((\bullet \ Y)\) If \(\mathrm{End}(A)\) is torsion-free divisible, then A is torsion-free divisible.
-
\((\bullet \ Z)\) If A is divisible then \(\mathrm{Hom}(A,C)\) is torsion-free.
-
\((\bullet \ W)\)\(\mathrm{Hom}(\mathbb {Z}(p^\infty ), \bigoplus \nolimits _{\lambda } \mathbb {Z}(p^\infty )) \cong \widehat{\bigoplus \nolimits _{\lambda } R}\).
We require one further elementary result and include the proof for the convenience of the reader.
Lemma 2.3
If G is a reduced R-module having a summand isomorphic to R, then \(\mathrm{Hom}(G, R) \cong \prod \nolimits _{\lambda } R\) for some cardinal \(\lambda \ne 0\).
Proof
Observe firstly that \(\mathrm{Hom}(G, R) \cong \mathrm{Hom}(G/tG, R)\) always holds so there is no loss in assuming that G is torsion-free. Thus, G has the form \(G = D \oplus X\) where D is divisible and X is reduced; note that \(X \ne 0\) since G has a summand isomorphic to R. Clearly \(\mathrm{Hom}(G, R) = \mathrm{Hom}(X, R)\). However, since X is torsion-free, it has a free basic submodule B of rank \(\lambda \) say and \(0 \rightarrow B \rightarrow X \rightarrow D \rightarrow 0\) is an exact sequence where D is torsion-free divisible. Since R is complete, \(\mathrm{Ext}(D, R) = 0\) and it follows that \(\mathrm{Hom}(X, R) = \mathrm{Hom}(B, R) \cong \prod \nolimits _{\lambda }R \). \(\square \)
We finish this section with a simple property of R-modules having torsion basic submodules; this result will be useful in the final stages of our arguments.
Lemma 2.4
If the torsion module B is basic in the R-module G and \(G/B \cong \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\oplus \bigoplus \nolimits _{\mu }Q\), then \(\mathrm{Hom}(G, \mathbb {Z}(p^\infty ))\) has a summand of the form \(\prod \nolimits _{\lambda } R \oplus \prod \nolimits _{\mu }Q\).
Proof
Consider the pure exact sequence \(0 \rightarrow B \rightarrow G \rightarrow G/B \rightarrow 0\) and apply the functor \(\mathrm{Hom}(-, \mathbb {Z}(p^\infty ))\) to obtain the pure exact sequence
Now
since it is straightforward to show, using the completeness of R, that \(\mathrm{Ext}^1 (Q, R) = 0\) and hence \(\mathrm{Hom}(Q, Q/R) \cong Q\). Now the latter is algebraically compact and pure in \(\mathrm{Hom}(G, \mathbb {Z}(p^\infty ))\) and so it is a summand. \(\square \)
2.1 Some cardinality relationships
In this subsection we isolate some arguments that will appear a number of times in our later discussions. The main results that we shall need are all well known but it is not easy to give specific references to them. Since they are reasonably easy to demonstrate, we give the short proofs.
Proposition 2.5
Suppose \(\lambda , \mu \) are cardinals.
-
(i)
If \(\bigoplus \nolimits _{\lambda } Q \cong \prod \nolimits _{\mu } Q\) and \(\prod \nolimits _{\lambda }Q \cong \bigoplus \nolimits _{\mu }Q\), then \(\lambda = \mu \) is finite.
-
(ii)
If \(\prod \nolimits _{\lambda } R \cong \widehat{\bigoplus \nolimits _{\mu }R}\), then \(\mu = 2^{\lambda }\) if \(\mu \) is infinite; if \(\mu \) is finite then \(\mu = \lambda \).
Proof
-
(i)
The module \(\prod \nolimits _{\mu } Q\) is the vector space dual of the Q-space \(\bigoplus \nolimits _{\mu }Q\). If \(\mu \) is infinite then so too is \(\lambda \) and the first isomorphism in (i) gives \(\lambda = \dim \bigoplus \nolimits _{\lambda } Q = \dim \prod \limits _{\mu } Q = |Q|^{\mu } = 2^{\mu }\), while the second isomorphism gives \(\mu = \dim \bigoplus \limits _{\mu } Q = \dim \prod \nolimits _{\lambda } Q = |Q|^{\lambda } = 2^{\lambda }\)—here we are using the classical result on the dimension of the dual space of an infinite-dimensional vector space, see, for example, [10, Chapter IX, Theorem 2]. So \(\lambda = 2^{\mu }\) and \(\mu = 2^{\lambda }\) which yields \(\lambda = 2^{2^{\lambda }}\)—contradiction. Hence \(\lambda , \mu \) are both finite and their equality is then immediate.
-
(ii)
The submodule \(\bigoplus \nolimits _{\mu }R\) is pure and dense in its completion \(\widehat{\bigoplus \nolimits _{\mu }R}\) and so
$$ \widehat{\bigoplus \nolimits _{\mu }R}/p(\widehat{\bigoplus \nolimits _{\mu }R}) \cong \bigoplus \nolimits _{\mu }R/p(\bigoplus \nolimits _{\mu }R) \cong \bigoplus \nolimits _{\mu }\mathbb {Z}(p).$$However, \(\prod \nolimits _{\lambda }R /p(\prod \nolimits _{\lambda } R) \cong \prod \nolimits _{\lambda }\mathbb {Z}(p)\) and so it follows from the isomorphism in (ii) that \(\prod \nolimits _{\lambda }\mathbb {Z}(p) \cong \bigoplus \nolimits _{\mu }\mathbb {Z}(p)\). If \(\lambda \) is infinite then so too is \(\mu \) and we have, on equating cardinalities, that \(\mu = 2^{\lambda }\), as required. If \(\mu \) is finite, then \(\widehat{\bigoplus \nolimits _{\mu }R} = \bigoplus \nolimits _{\mu }R\) and it follows immediately that \(\mu = \lambda \).
\(\square \)
We shall also need the following result which can be derived in greater generality from [9, Proposition 1.2]; we give a simple version adequate for our purposes.
Lemma 2.6
\(\mathrm{Hom}(\prod \nolimits _{\lambda } R, R) \cong \prod \nolimits _{2^{\lambda }} R\) if \(\lambda \) is infinite; if \(\lambda \) is finite then \(\mathrm{Hom}(\prod \nolimits _{\lambda } R, R) \cong \prod \nolimits _{\lambda } R\).
Proof
Since R is complete and \(\lambda \) is infinite, \(\prod \nolimits _{\lambda } R\) is of the form \( \widehat{\bigoplus \nolimits _{\kappa } R}\) for some infinite cardinal \(\kappa \). Then, reducing modulo p, we get \(\prod \nolimits _{\lambda } \mathbb {Z}(p) \cong \widehat{\bigoplus \nolimits _{\kappa } R}/p\widehat{\bigoplus \nolimits _{\kappa } R} \cong \bigoplus \nolimits _{\kappa } \mathbb {Z}(p)\). Since \(\lambda \) is infinite, \(\kappa = 2^{\lambda }\). Thus, \(\mathrm{Hom}(\prod \nolimits _{\lambda } R, R) = \mathrm{Hom}(\hat{F}, R)\) where F is free of rank \(\kappa = 2^{\lambda }\). However, as the quotient \(\hat{F}/F\) is torsion-free and R is complete, \(\mathrm{Ext}(\hat{F}/F, R) = 0\) and so \(\mathrm{Hom}(\hat{F}, R) = \mathrm{Hom}(F, R) \cong \prod \nolimits _{2^{\lambda }}R\). The situation when \(\lambda \) is finite is straightforward since, in that case, \(\prod \nolimits _{\lambda } R\) is just the free R-module of rank \(\lambda \). \(\square \)
.
2.2 The fundamental relations
Suppose that G, H are R-modules which are opposed under the anti-isomorphism \(\omega \). We shall use the following notation: if \(\phi \in \mathrm{End}(G)\), then \(\phi ' = \omega (\phi )\) is the corresponding element of \(\mathrm{End}(H)\). For simplicity of notation and when there is no danger of confusion, we shall often write \(E = \mathrm{End}(G), E' = \mathrm{End}(H) = \omega (E)\).
If we assume that G is indecomposable then, as we have shown in the previous section, Corner’s result holds when the module G is assumed to be indecomposable. So from here on we assume that G, and hence H, is decomposable.
Assume \(\pi \) is an indecomposable idempotent of \(E = \mathrm{End}(G)\), so that \(\pi (G)\) is an indecomposable R-module, then as we have seen in Proposition 2.1, there is an indecomposable idempotent \(\pi ' \in E' = \mathrm{End}(H)\). Since \(\omega \) is an anti-isomorphism, we get isomorphisms \(E\pi \cong \pi 'E'\) and \(\pi E \cong E'\pi '\). Since the relationships \(\mathrm{Hom}(\pi (G), G) \cong \mathrm{End}(G)\pi \), \(\mathrm{Hom}(G, \pi (G)) \cong \pi \mathrm{End}(G)\) always hold for an idempotent \(\pi \in \mathrm{End}(G)\), we have the following Fundamental Relations for an indecomposable idempotent \(\pi \) and its image \(\pi '\) under the anti-isomorphism \(\omega \):
The main thrust of the rest of our approach to proving Corner’s result will be in applying these Fundamental Relations in a systematic way.
Before proceeding to the next section where we introduce a series of reductions, we give four useful consequences of the Fundamental Relations relating to direct sums of a fixed indecomposable module.
Proposition 2.7
If \(G = \bigoplus \nolimits _{\lambda }Q\) and G is opposed to H, then \(G \cong H\) and \(\lambda \) is finite.
Proof
By \((\bullet X)\), \(\mathrm{End}(G)\) is divisible and torsion-free and so it follows from \((\bullet Y)\) that H must be torsion-free and divisible, so that \(H = \bigoplus \nolimits _{\mu }Q\) for some cardinal \(\mu \). It follows from the Fundamental Relations that \(\prod \nolimits _{\lambda }Q \cong \mathrm{Hom}(G, Q) \cong \mathrm{Hom}(Q, H) \cong \bigoplus \nolimits _{\mu }Q\) and also \(\bigoplus \nolimits _{\lambda }Q \cong \mathrm{Hom}(Q, G) \cong \mathrm{Hom}(H, Q) \cong \prod \nolimits _{\mu }Q\). It follows immediately from Proposition 2.5 (i) that \(\lambda = \mu \) is finite and \(G \cong H\). \(\square \)
Proposition 2.8
Suppose \(G = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\) and  for some R-module H. Then either \(H = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\) or \(H = \bigoplus \nolimits _{\lambda }R\) and in both cases \(\lambda \) must be finite.
for some R-module H. Then either \(H = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\) or \(H = \bigoplus \nolimits _{\lambda }R\) and in both cases \(\lambda \) must be finite.
Proof
G has a projection \(\pi \) onto a summand isomorphic to \(\mathbb {Z}(p^\infty )\) and this gives rise to a summand \(\pi '(H)\) of H which may be isomorphic to either \(\mathbb {Z}(p^\infty )\) or to R. From the Fundamental Relations we have two scenarios to consider:
-
Case (a):
\(\mathrm{Hom}(\mathbb {Z}(p^\infty ), G) \cong \mathrm{Hom}(H, \mathbb {Z}(p^\infty ))\) and \(\mathrm{Hom}(G, \mathbb {Z}(p^\infty )) \cong \mathrm{Hom}(\mathbb {Z}(p^\infty ), H)\).
-
Case (b):
\(\mathrm{Hom}(\mathbb {Z}(p^\infty ), G) \cong \mathrm{Hom}(H, R)\) and \(\mathrm{Hom}(G, \mathbb {Z}(p^\infty )) \cong \mathrm{Hom}(R, H)\).
In Case (a) we have by \((\bullet \ W)\) that \(\mathrm{Hom}(H, \mathbb {Z}(p^\infty )) \cong \mathrm{Hom}(\mathbb {Z}(p^\infty ), \bigoplus \nolimits _{\lambda } \mathbb {Z}(p^\infty )) \cong \widehat{\bigoplus \nolimits _{\lambda } R}\); in particular \(\mathrm{Hom}(H, \mathbb {Z}(p^\infty ))\) is torsion-free and reduced. Now if H is not torsion divisible, then it has a summand isomorphic to one of \(\mathbb {Z}(p^n)\) (for some n), R or Q. The first of these possibilities would yield a torsion direct summand of \(\mathrm{Hom}(H, \mathbb {Z}(p^\infty ))\) and the third would yield a summand isomorphic to Q since, as noted in the Proof of Lemma 2.4, \(\mathrm{Hom}(Q, \mathbb {Z}(p^\infty )) \cong Q\), hence neither can occur. If H has a summand isomorphic to R, then \(\mathrm{Hom}(H, \mathbb {Z}(p^\infty ))\) would have a summand isomorphic to \(\mathbb {Z}(p^\infty )\) which is also impossible. Hence H is torsion divisible and of the form \(H = \bigoplus \nolimits _{\mu } \mathbb {Z}(p^\infty )\) for some cardinal \(\mu \). The Fundamental Relations in this case then reduce to \(\prod \nolimits _\lambda R \cong \widehat{\bigoplus \nolimits _{\mu } R}\) and \(\widehat{\bigoplus \nolimits _{\lambda } R} \cong \prod \nolimits _{\mu } R\). It follows immediately from Proposition 2.5 that \(\lambda = \mu \) is finite.
In Case (b) \(H \cong \mathrm{Hom}(G, \mathbb {Z}(p^\infty )) = \prod \nolimits _{\lambda }R\) and \(\mathrm{Hom}(\mathbb {Z}(p^\infty ), G) = \widehat{\bigoplus \nolimits _{\lambda }R} \cong \mathrm{Hom}(H, R)\). Thus, we have by Lemma 2.6 above that \(\widehat{\bigoplus \nolimits _{\lambda }R} \cong \prod \nolimits _{2^{\lambda }}R\) if \(\lambda \) is infinite; if \(\lambda \) is finite, the latter term is just the product of \(\lambda \) copies of R. However, \(\lambda \) infinite is impossible since it would then follow from Proposition 2.5 (ii) that \(\lambda = 2^{2^{\lambda }}\). Thus, we conclude that \(\lambda \) is finite and \(H = \bigoplus \nolimits _{\lambda }R\). \(\square \)
Proposition 2.9
If G is a reduced torsion-free R-module and  for some R-module H, then G is free of finite rank r and either \(H \cong G\) or \(H \cong \bigoplus \nolimits _{r}\mathbb {Z}(p^\infty )\).
for some R-module H, then G is free of finite rank r and either \(H \cong G\) or \(H \cong \bigoplus \nolimits _{r}\mathbb {Z}(p^\infty )\).
Proof
Since G is reduced torsion-free, it has a summand R and this gives rise to a summand of H which can be either R or \(\mathbb {Z}(p^\infty )\). The Fundamental Relations then give either (i) \(\mathrm{Hom}(R, G) \cong \mathrm{Hom}(H, R)\) and \(\mathrm{Hom}(G, R) \cong \mathrm{Hom}(R, H)\) or (ii) \(\mathrm{Hom}(R, G) \cong \mathrm{Hom}(H, \mathbb {Z}(p^\infty ))\) and \(\mathrm{Hom}(G, R) \cong \mathrm{Hom}(\mathbb {Z}(p^\infty ), H)\).
In the first case this yields \(G \cong \mathrm{Hom}(H, R)\) and \(H \cong \mathrm{Hom}(G, R)\). However, since G is torsion-free reduced, it has a free basic submodule B, of rank r say and it follows from Lemma 2.3 that \( H \cong \mathrm{Hom}(G, R) = \mathrm{Hom}(B, R) \cong \prod \nolimits _{r}R \). If r is infinite, substituting for H will give that \(G \cong \mathrm{Hom}(H, R) \cong \prod \nolimits _{2^{r}}R\) , the last equality coming from Proposition 2.6. Substituting now for G we get \(H \cong \mathrm{Hom}(G, R) \cong \prod \nolimits _{2^{2^{r}}} R\) and a simple calculation of cardinalities shows this cannot hold. Hence r is finite and \(B = G \cong H\).
In the second case we see that \(G \cong \mathrm{Hom}(H, \mathbb {Z}(p^\infty ))\) is torsion-free and reduced and so the argument in the proof of Case (b) of Proposition 2.8 gives us that H is torsion divisible, say \(H = \bigoplus \nolimits _{\mu }\mathbb {Z}(p^\infty )\) for some \(\mu \). As  and \(H = \bigoplus \nolimits _{\mu }\mathbb {Z}(p^\infty )\), it now follows from Proposition 2.8 that G is either free of rank \(\mu \) or torsion divisible of rank \(\mu \); in both cases \(\mu \) is finite.
and \(H = \bigoplus \nolimits _{\mu }\mathbb {Z}(p^\infty )\), it now follows from Proposition 2.8 that G is either free of rank \(\mu \) or torsion divisible of rank \(\mu \); in both cases \(\mu \) is finite.
This completes the proof of the proposition. \(\square \)
Proposition 2.10
Suppose that G is opposed to H and \(G = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^n)\) for some \(\lambda \ge 1\) and n a fixed positive integer. Then \(G \cong H\) and \(\lambda \) is finite.
Proof
Since \(p^nG = 0, p^n\mathrm{End}(G) = 0\) also and the anti-isomorphism between \(\mathrm{End}(G)\) and \(\mathrm{End}(H)\) implies that \(p^n\mathrm{End}(H) = 0\); in particular, \(p^n1_H = 0\) and thus, \(p^nH = 0\). Moreover, H cannot have a summand \(\mathbb {Z}(p^k)\) for any \(k < n\) since it would follow from Proposition 2.1 that G has then a summand opposed to \(\mathbb {Z}(p^k)\)—impossible since the only R-module oppose to \(\mathbb {Z}(p^k)\) is \(\mathbb {Z}(p^k)\) itself. So \(H = \bigoplus \nolimits _{\mu }\mathbb {Z}(p^n)\) for some \(\mu \ge 1\). By the Fundamental Relations, \(\mathrm{Hom}(G, \mathbb {Z}(p^n)) \cong \mathrm{Hom}(\mathbb {Z}(p^n), H)\) and \(\mathrm{Hom}(\mathbb {Z}(p^n), G) \cong \mathrm{Hom}(H, \mathbb {Z}(p^n))\). Thus, we have \( G = G[p^n] \cong \mathrm{Hom}(G, \mathbb {Z}(p^n)) \cong \mathrm{Hom}(\mathbb {Z}(p^n), H)\) and \(H = H[p^n] \cong \mathrm{Hom}(\mathbb {Z}(p^n), H) \cong \mathrm{Hom}(G, \mathbb {Z}(p^n)) \cong \prod \nolimits _{\lambda }\mathbb {Z}(p^n)\). So

Thus, \(\mu = \lambda \) if \(\lambda \) is finite; \(\mu = 2^{\lambda }\) if \(\lambda \) is infinite. However, \(G \cong \mathrm{Hom}(\mathbb {Z}(p^n), H)\) is then homocyclic of rank \(\mu \) or \(2^{\mu }\) depending on whether \(\mu \) is finite or infinite. It then follows that \(\lambda = \mu \) if \(\mu \) is finite. However, if \(\mu \) is infinite, we are forced to conclude that \(\lambda \) is also infinite leading to the absurdity that \(\mu = 2^{\lambda } = 2^{2^{\mu }}\). Thus, we must have \(\lambda = \mu \) and then \(G \cong H\), as required. \(\square \)
3 Some reductions
For our first reduction we consider the possibility that G has a summand D which is of the form \(D = \bigoplus \nolimits _{\lambda }Q\) and \(G = D \oplus G_1\), where \(G_1\) has no summand isomorphic to Q. Then H has a summand K with  . Now it follows from Proposition 2.7 that \(D \cong K\) and \(\lambda \) is finite. Furthermore, if \(H = K \oplus H_1\) and \(H_1\) has a summand isomorphic to Q, then \(G_1\) would also have a summand isomorphic to Q since
. Now it follows from Proposition 2.7 that \(D \cong K\) and \(\lambda \) is finite. Furthermore, if \(H = K \oplus H_1\) and \(H_1\) has a summand isomorphic to Q, then \(G_1\) would also have a summand isomorphic to Q since  —contradiction. So \(H_1\) has no summands isomorphic to Q.
—contradiction. So \(H_1\) has no summands isomorphic to Q.
Thus, we have our first reduction:
-
(I)
If \(G = D \oplus G_1\) where \(0 \ne D\) is torsion-free divisible and \(G_1\) has no summands isomorphic to Q, then if
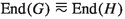 , we have \(H = D' \oplus H_1\) where \(D' \cong D\) is a finite-dimensional Q-space,
, we have \(H = D' \oplus H_1\) where \(D' \cong D\) is a finite-dimensional Q-space, 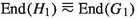 and \(H_1\) has no summands isomorphic to Q. For our second reduction we focus on the situation where \(G_1\) has no summands isomorphic to Q, \(G_1 = C \oplus G_2\), \(0 \ne C = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\) and \(G_2\) is reduced. Now if \(\pi \) is an idempotent corresponding to the summand C and
and \(H_1\) has no summands isomorphic to Q. For our second reduction we focus on the situation where \(G_1\) has no summands isomorphic to Q, \(G_1 = C \oplus G_2\), \(0 \ne C = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\) and \(G_2\) is reduced. Now if \(\pi \) is an idempotent corresponding to the summand C and 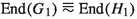 , the corresponding idempotent \(\pi '\) gives rise to a summand \(0 \ne D\) of \(H_1\), say \(H_1 = D \oplus H_2\), and the endomorphism rings of corresponding summands are anti-isomorphic:
, the corresponding idempotent \(\pi '\) gives rise to a summand \(0 \ne D\) of \(H_1\), say \(H_1 = D \oplus H_2\), and the endomorphism rings of corresponding summands are anti-isomorphic: 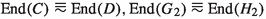 . Moreover, as \(\mathrm{Hom}(C, G_2) = 0\) it follows from Lemma 2.2 that \(\mathrm{Hom}(H_2, D) = 0\). Since \(0 \ne C = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\), it follows from Proposition 2.8 that either \(D= \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\) or \(D = \bigoplus \nolimits _{\lambda }R\); in both cases \(\lambda \) must be finite. The first option is impossible since \(\mathrm{Hom}(X, \mathbb {Z}(p^\infty )) \ne 0\) for all nonzero R-modules X. Hence \(D = \bigoplus \nolimits _{\lambda }R\) where \(\lambda \) is finite and
. Moreover, as \(\mathrm{Hom}(C, G_2) = 0\) it follows from Lemma 2.2 that \(\mathrm{Hom}(H_2, D) = 0\). Since \(0 \ne C = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\), it follows from Proposition 2.8 that either \(D= \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\) or \(D = \bigoplus \nolimits _{\lambda }R\); in both cases \(\lambda \) must be finite. The first option is impossible since \(\mathrm{Hom}(X, \mathbb {Z}(p^\infty )) \ne 0\) for all nonzero R-modules X. Hence \(D = \bigoplus \nolimits _{\lambda }R\) where \(\lambda \) is finite and 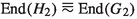 . Note that \(H_2\) cannot have a summand isomorphic to R: if it did, then \(0 = \mathrm{Hom}(H_2, D)\) would have a summand \(\mathrm{Hom}(R, D) \cong D\), contrary to \(0 \ne D\). Thus, we have our second reduction:
. Note that \(H_2\) cannot have a summand isomorphic to R: if it did, then \(0 = \mathrm{Hom}(H_2, D)\) would have a summand \(\mathrm{Hom}(R, D) \cong D\), contrary to \(0 \ne D\). Thus, we have our second reduction: -
(II)
If \(G = \bigoplus \nolimits _{r}Q \oplus \bigoplus \nolimits _{t}\mathbb {Z}(p^\infty )\oplus G_2\), where \(0 \ne r,t\), \(G_2\) is reduced and
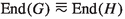 , then \(H = \bigoplus \nolimits _{r}Q \oplus \bigoplus \nolimits _{t}R \oplus H_2\), r, t are finite, \(H_2\) has no summand isomorphic to R or Q and \(H_2\) is opposed to \(G_2\). We want to make one further reduction to enable us to reduce the problem to its core case. In the situation above, the module \(G_2\) may have a summand isomorphic to R. In order to handle this situation we need to develop a further basic result.
, then \(H = \bigoplus \nolimits _{r}Q \oplus \bigoplus \nolimits _{t}R \oplus H_2\), r, t are finite, \(H_2\) has no summand isomorphic to R or Q and \(H_2\) is opposed to \(G_2\). We want to make one further reduction to enable us to reduce the problem to its core case. In the situation above, the module \(G_2\) may have a summand isomorphic to R. In order to handle this situation we need to develop a further basic result.
Proposition 3.1
Suppose that X, Y are R-modules with  and X is reduced and has a summand isomorphic to R. Then either (i) \(Y \cong X\) and both are free of finite rank or (ii) \(X = \bigoplus \nolimits _{\lambda }R \oplus X_1, Y = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\oplus Y_1\) where \(\lambda \) is finite and neither \(X_1\) nor \(Y_1\) have a summand isomorphic to R.
and X is reduced and has a summand isomorphic to R. Then either (i) \(Y \cong X\) and both are free of finite rank or (ii) \(X = \bigoplus \nolimits _{\lambda }R \oplus X_1, Y = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\oplus Y_1\) where \(\lambda \) is finite and neither \(X_1\) nor \(Y_1\) have a summand isomorphic to R.
Proof
Since X is opposed to Y and X has a summand isomorphic to R, Y has a summand isomorphic to either R or \(\mathbb {Z}(p^\infty )\). The Fundamental Relations then present two possibilities:
-
(i)
\(\mathrm{Hom}(R, X) \cong \mathrm{Hom}(Y, R)\) and \(\mathrm{Hom}(X, R) \cong \mathrm{Hom}(R, Y)\),
-
(ii)
\(\mathrm{Hom}(R, X) \cong \mathrm{Hom}(Y, \mathbb {Z}(p^\infty ))\) and \(\mathrm{Hom}(X, R) \cong \mathrm{Hom}(\mathbb {Z}(p^\infty ), Y)\).
Case (i). By Lemma 2.3 we get \(\prod \nolimits _{\lambda }R \cong \mathrm{Hom}(X, R) \cong \mathrm{Hom}(R, Y) \cong Y\) for some cardinal \(\lambda \ne 0\). So Y is torsion-free reduced and it follows from Proposition 2.9 that \(X \cong Y \cong \bigoplus \nolimits _{\lambda }R\) for some finite \(\lambda \); the possibility arising in Proposition 2.9 that \(X \cong \bigoplus \nolimits _{r}\mathbb {Z}(p^\infty )\) cannot occur since X is reduced.
Case (ii). Since X is reduced and X, Y are opposed, Y cannot have a summand isomorphic to Q. Suppose then that \(Y = D \oplus Y_1\), where \(Y_1\) is reduced and \(D = \bigoplus \nolimits _{\mu }\mathbb {Z}(p^\infty )\). In this case the Fundamental Relations and Lemma 2.3 yield
By \((\bullet W)\) we then have \(\widehat{\bigoplus \nolimits _{\mu }R} \cong \prod \nolimits _{\lambda }R\) and it follows by Proposition 2.5 (ii) that \(\mu = \lambda \) if \(\mu \) is finite; but \(\mu = 2^{\lambda }\) if \(\mu \) is infinite.
Note also that the Fundamental Relations also give
so that \(X \cong \prod \nolimits _{\mu }R \oplus X_1\), where \(X_1 \cong \mathrm{Hom}(Y_1, \mathbb {Z}(p^\infty ))\).
Consider firstly the situation where \(\mu \) is finite. In this case we have \(X = \bigoplus \nolimits _{\mu }R \oplus X_1\) and \(Y = \bigoplus \nolimits _{\mu }\mathbb {Z}(p^\infty )\oplus Y_1\), where \(Y_1\) is reduced. However, \(Y_1\) cannot have a summand isomorphic to R, for if it did, then \(X_1 \cong \mathrm{Hom}(Y, \mathbb {Z}(p^\infty ))\) would have a summand isomorphic to \(\mathbb {Z}(p^\infty )\) contradicting the fact that X is reduced. It also follows that \(X_1\) cannot have a summand isomorphic to R: if it did then \(\mathrm{Hom}(X, R) \cong \mathrm{Hom}(\mathbb {Z}(p^\infty ), Y)\) would have a free summand of rank greater than \(\mu \) which is impossible since \(\mathrm{Hom}(\mathbb {Z}(p^\infty ), Y_1) = 0\) as \(Y_1\) is reduced.
To establish the proposition it remains to handle the case in which \(\mu \) is infinite. We claim that this case cannot occur.
Now \(X \cong \prod \nolimits _{\mu }R \oplus X_1\) and so it follows by using Lemma 2.6 that \(|\mathrm{Hom}(X, R)| \ge |\mathrm{Hom}(\prod \nolimits _{\mu }R, R)| = |\prod \nolimits _{2^{\mu }}R|\). But \(\mathrm{Hom}(X, R) = \prod \nolimits _{\lambda }R\), so \(|\mathrm{Hom}(X, R)| = (2^{\aleph _0})^{\lambda } = 2^{\lambda } = \mu \). However, \(|\prod \nolimits _{2^{\mu }}R| = (2^{\aleph _0})^{2^{\mu }} = 2^{2^{\mu }}\) leading to the contradiction that \(\mu \ge 2^{2^{\mu }}\). So the case with \(\mu \) infinite cannot occur. \(\square \)
For our next reduction we consider the situation where \(G_2\) is reduced and has a summand isomorphic to R, \(G_2\) is opposed to \(H_2\) but \(H_2\) does not have a summand isomorphic to either R or Q. It follows from Proposition 3.1 above that either \(G_2\) is free of finite rank and isomorphic to \(H_2\)—impossible in the present situation as \(H_2\) has no free summands—or \(G_2= \bigoplus \nolimits _{\lambda }R \oplus G_3\) for some finite \(\lambda \) and \(G_3\) does not have a summand isomorphic to R. Now this decomposition of \(G_2\) gives a corresponding decomposition of \(H_2\) as \(H_2 = A \oplus H_3\), where A is opposed to \(\bigoplus \nolimits _{\lambda }R\) and \(H_3\) is opposed to \(G_3\). It follows from Proposition 2.9 that either A is free of finite rank \(\lambda \) or \(A = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\). As \(G_3\) does not have a summand isomorphic to R, \(\mathrm{Hom}(G_3, R) = 0\) and so \(\mathrm{Hom}(G_3, \bigoplus \nolimits _{\lambda }R) = 0\). It follows now from Lemma 2.2 that \(\mathrm{Hom}(A, H_3) = 0\) so that A is clearly not free. Hence we must have \(A = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\) and \(H_2 = \bigoplus \nolimits _{\lambda }\mathbb {Z}(p^\infty )\oplus H_3\), where \(H_3\) is opposed to \(G_3\). Note also that \(H_3\) cannot have a summand isomorphic to \(\mathbb {Z}(p^\infty )\) since \(\mathrm{Hom}(A, H_3) = 0\); as \(H_2\) does not have a summand isomorphic to Q, the same is true of \(H_3\). Thus, we have that \(H_3\) is reduced.
Thus, we have our third reduction:
(III) Assume \(G = \bigoplus \nolimits _{r}Q \oplus \bigoplus \nolimits _{t}\mathbb {Z}(p^\infty )\oplus \bigoplus \nolimits _{s}R \oplus G_3\), where \(0 \ne r,s,t\), \(G_3\) is reduced and has no summand isomorphic to R, and  . Then \(H = \bigoplus \nolimits _{r}Q \oplus \bigoplus \nolimits _{t}R \oplus \bigoplus \nolimits _{s}\mathbb {Z}(p^\infty )\oplus H_3\), r, s, t are finite, \(H_3\) is reduced and has no summand isomorphic to R, and \(H_3\) is opposed to \(G_3\).
. Then \(H = \bigoplus \nolimits _{r}Q \oplus \bigoplus \nolimits _{t}R \oplus \bigoplus \nolimits _{s}\mathbb {Z}(p^\infty )\oplus H_3\), r, s, t are finite, \(H_3\) is reduced and has no summand isomorphic to R, and \(H_3\) is opposed to \(G_3\).
We have now reached the core of the proof of Corner’s theorem. To simplify notation in the next subsection we will write G, H for \(G_3, H_3\), respectively.
3.1 Reduced groups with no summand \({\mathbf {R}}\)
Suppose now that G is a reduced group which does not have a summand isomorphic to R.
Recall that basic submodules of R-modules exist and have the form \(B = B_0 \oplus \bigoplus \nolimits _{n \ge 1}B_n\), where \(B_0\) is a free R-module and each \(B_n\) is a direct sum (possibly zero) of cyclic groups \(\mathbb {Z}(p^n)\).
Proposition 3.2
If G is a reduced R-module which does not have a summand isomorphic to R and B is a basic submodule of G, then (i) G/tG is divisible and (ii) \(G/B \cong (tG/B) \oplus D\), where tG/B is torsion divisible and D is torsion-free divisible isomorphic to G/tG.
Proof
-
(i)
Let \(G/tG = D \oplus F\), where D is divisible and F is torsion-free reduced. Since G has no summand isomorphic to R, \(\mathrm{Hom}(G,R) = 0\) and hence it follows that \(\mathrm{Hom}(G/tG,R) = 0\). Thus, \(\mathrm{Hom}(F, R) = 0\) which forces \(F = 0\) since F is torsion-free and reduced.
-
(ii)
If B is basic in G then \(B_0\) must be zero for otherwise G would have a summand isomorphic to R. Thus, B is torsion and G/B is divisible. Furthermore, tG/B is pure in G/B since tG is pure in G and so tG/B is divisible. Thus, \(G/B = tG/B \oplus D\) and since \(D \cong G/tG\), it follows from part (i) that D is divisible.
\(\square \)
Notice that Proposition 3.2 tells us that if G is a reduced R-module which does not have a summand isomorphic to R and B is a basic submodule of G, then B is, in fact, precisely a basic submodule of tG. Before we can exploit this situation further, we need a result on p-groups which we establish below.
Proposition 3.3
If G is opposed to H and G, H are reduced R-modules with torsion basic submodules B, C respectively, then \(B \cong C\) and both are semi-standard.
Proof
Let \(B = \bigoplus \nolimits _{n \ge 1}B_n, C = \bigoplus \nolimits _{n \ge 1}C_n\), where \(B_n\) is homocyclic of exponent n and rank \(\lambda _n\), \(C_n\) is homocyclic of exponent n and rank \(\mu _n\); of course, some of the \(\lambda _n, \mu _n\) may be zero. If \(\lambda _n \ne 0\), then \(G = B_n \oplus G'\) and since  , we have \(H = A_n \oplus H'\) for some \(A_n\) with
, we have \(H = A_n \oplus H'\) for some \(A_n\) with  . It follows from Proposition 2.10 that \(B_n \cong A_n\) and \(\lambda _n\) is finite. Hence \(0 < \lambda _n = f_G(n-1) \le f_H(n-1) = \mu _n\). Now reverse roles noting that \(\mu _n \ne 0\) and begin with a decomposition of H as \(H = C_n \oplus H''\). By a similar argument we get \(0 < \mu _n = f_H(n-1)\le f_G(n-1)\) and so \(\mu _n \le \lambda _n \le \mu _n\) for all nonzero \(\lambda _n, \mu _n\). Furthermore, these cardinals are finite, so the nonzero Ulm invariants of B, C are equal and all are finite, hence \(B \cong C\) and both are semi-standard. \(\square \)
. It follows from Proposition 2.10 that \(B_n \cong A_n\) and \(\lambda _n\) is finite. Hence \(0 < \lambda _n = f_G(n-1) \le f_H(n-1) = \mu _n\). Now reverse roles noting that \(\mu _n \ne 0\) and begin with a decomposition of H as \(H = C_n \oplus H''\). By a similar argument we get \(0 < \mu _n = f_H(n-1)\le f_G(n-1)\) and so \(\mu _n \le \lambda _n \le \mu _n\) for all nonzero \(\lambda _n, \mu _n\). Furthermore, these cardinals are finite, so the nonzero Ulm invariants of B, C are equal and all are finite, hence \(B \cong C\) and both are semi-standard. \(\square \)
Note that if a direct sum of cyclic groups B is semi-standard, then it can be expressed either in the form \(B = \bigoplus \nolimits _{i = 1}^N \langle b_{n_i}\rangle \) where N is finite or as \(B = \bigoplus \nolimits _{i = 1}^\infty \langle b_i\rangle \) and each \(\langle b_i\rangle \) is cyclic of order \(p^{n_i}\) with \(n_1 \le n_2 \le \cdots \).
Let us return now to the situation where G, H are reduced R-modules with torsion basic submodules B, C respectively. If G, H are opposed then by Proposition 3.3\(B \cong C\) and both are semi-standard. First we dispose of the situation where B is bounded. Here it follows that \(B = G\) and \(C= H\) since bounded pure submodules are summands. Thus, \(G \cong H\) and since G is semi-standard and bounded, it is a finite p-group. This corresponds to Case (a) of (II) in the statement of Corner’s theorem.
For the remaining case, B and hence, of course, C are both unbounded. Then there is a sequence of cyclic direct summands of B of increasing orders, say \(\langle b_i\rangle \) is such a summand where \(b_i\) is of order \(n_i\) and \(n_1 \le n_2 \le \cdots \). Thus, \(B = \bigoplus \nolimits _{i = 1}^\infty \langle b_i\rangle \) is basic in G and so the p-adic completions of B, G coincide and G may be regarded as a pure submodule of the product \(P = \prod \nolimits _{i = 1}^\infty \langle b_i\rangle \). Thus, \(B \le tG \le tP\). Our objective is to show that the equality \(tG = tP\) holds.
If \(\mathbf {x} = (x_1, x_2, \dots )\) is an arbitrary element of tP, then there is an integer k, dependent on \({\mathbf{x}}\), such that \(o(\mathbf {x}) \le p^{n_k}\); for a given \(\mathbf {x}\) fix such a k. Then the components \(x_i\) of \(\mathbf {x}\) satisfy, for some suitable integers \(r_i < p^{n_k}\),

Now define endomorphisms \(\alpha _{ij}\) of B by

and extend these to endomorphisms of G by setting \(\alpha _{ij}(1 - \alpha _j)(G) = 0\).
Suppose we have shown that for all i, \(\mathrm{End}(G)\) contains an endomorphism \(\alpha \) such that \(\alpha _i\alpha = r_i\alpha _{ik}\), where \(\alpha _i\) denotes the projection mapping taking an element \(g \in G\) onto its \(i^{th}\) component regarding g as an element of \(P = \prod \nolimits _{i = 1}^\infty \langle b_i\rangle \). Then if \(g = \alpha (b_k)\), then \(g \in tG\) and, furthermore,

Since the last display is precisely the value \(x_i\), we conclude that \(\mathbf {x} = g \in tG\) and so \(tP = tG = \bar{B}\), the torsion-completion of B.
If \(tG = tP\) then \(G/tG = G/tP \le P/tP\) and as G/tG is divisible, as noted in Proposition 3.2 above, we have \(G/tP \le D/tP\), where the latter is the maximal divisible submodule of P/tP. Thus, the requirement in Case (b) of (II) in the statement of Corner’s theorem will hold.
The remainder of this section is devoted to showing that G has the appropriate endomorphism \(\alpha \). Not surprisingly, the key to establishing this lies in the fact that G is opposed to H.
Note that the endomorphisms \(\alpha _i, \alpha _{ij}\) of G satisfy the relations

Let \(\Phi \) denote the anti-isomorphism  and denote by \(\beta _i, \beta _{ji}\) the images \(\Phi (\alpha _i), \Phi (\alpha _{ij})\); then if \(\beta _i = \Phi (\alpha _i)\), the image \(\beta _i(H)\) is a direct summand, \(\langle c_i\rangle \) say, of H with \(o(c_i) = p^{n_i}\). Furthermore, the uniqueness of opposition of modules of the form \(\bigoplus \nolimits _{\nu }\langle b_{\nu }\rangle \), where each \(b_{\nu }\) has order \(p^{n_i}\) (Proposition 2.10) and \(\nu \) indexes all such summands in a direct decomposition of B, means that the corresponding summand \(\bigoplus \nolimits _{\nu }\langle c_{\nu }\rangle \) contains all such summands of order \(p^{n_i}\) from a decomposition of H. It follows from a result of Szele [5, Theorem 33.2] that the submodule \(C = \bigoplus \nolimits _{i=1}^\infty \langle c_{i}\rangle \) is a basic submodule of H. Also if \(\gamma = \Phi (\alpha _{ij})\), we have \(\beta _j\gamma \beta _i = \gamma \) and it follows exactly as in Kaplansky’s proof of Theorem 28 in [11] that, absorbing units if necessary, \(\gamma = \beta _{ji}\). Hence the analogues of the equations displayed above hold with the \(\alpha _i\) replaced by \(\beta _i\) and the \(\alpha _{ij}\) replaced by \(\beta _{ji}\).
and denote by \(\beta _i, \beta _{ji}\) the images \(\Phi (\alpha _i), \Phi (\alpha _{ij})\); then if \(\beta _i = \Phi (\alpha _i)\), the image \(\beta _i(H)\) is a direct summand, \(\langle c_i\rangle \) say, of H with \(o(c_i) = p^{n_i}\). Furthermore, the uniqueness of opposition of modules of the form \(\bigoplus \nolimits _{\nu }\langle b_{\nu }\rangle \), where each \(b_{\nu }\) has order \(p^{n_i}\) (Proposition 2.10) and \(\nu \) indexes all such summands in a direct decomposition of B, means that the corresponding summand \(\bigoplus \nolimits _{\nu }\langle c_{\nu }\rangle \) contains all such summands of order \(p^{n_i}\) from a decomposition of H. It follows from a result of Szele [5, Theorem 33.2] that the submodule \(C = \bigoplus \nolimits _{i=1}^\infty \langle c_{i}\rangle \) is a basic submodule of H. Also if \(\gamma = \Phi (\alpha _{ij})\), we have \(\beta _j\gamma \beta _i = \gamma \) and it follows exactly as in Kaplansky’s proof of Theorem 28 in [11] that, absorbing units if necessary, \(\gamma = \beta _{ji}\). Hence the analogues of the equations displayed above hold with the \(\alpha _i\) replaced by \(\beta _i\) and the \(\alpha _{ij}\) replaced by \(\beta _{ji}\).
Now the map \(\beta ': C \rightarrow \langle c_k\rangle \) given by \(\beta ' = \bigoplus \nolimits _{i = 1}^\infty r_i\beta _{ki}\) extends to a map \(\beta :H \rightarrow \langle c_k\rangle \) with \(\beta \upharpoonright C = \beta '\) since \(\langle c_k\rangle \) is a complete R-module and C is basic in H. Direct calculation gives that \(\beta \beta _i = r_i\beta _{ki}\) for each \(i = 1,2, \dots \). Hence if we set \(\alpha = \Phi ^{-1}(\beta )\), we get for each i that \(\alpha _i\alpha = r_i\alpha _{ik}\) so that the required mapping \(\alpha \) exists. Thus, we have established that \(tG = tP = \bar{B}\), the torsion-completion of B. A similar result holds of course for H by interchanging the roles of G and H.
Summarising, we have established Case II (b) of Corner’s result Theorem 1.1.
We can obtain some additional information on the submodules we labelled \(G_3, H_3\) when the integers r, s, t appearing in the decompositions

are nonzero.
Suppose firstly that \(r \ne 0\); we claim that \(G_3\) (and hence of course \(H_3\)) is torsion. The module \(X = Q \oplus G_3\) being a summand of an opposable module, is itself opposable by some module Y. Then Y decomposes as \(Y = Q \oplus Z\) for some R-module Z, by the uniqueness of opposition of torsion-free divisible modules Proposition 2.7 and Z is opposed to \(G_3\); in particular, Z is reduced, \(\mathrm{Hom}(Q, Z) = 0\) and thus, \(\mathrm{Hom}(G_3, Q) = 0\). However, if \(G_3\) is not torsion, we know that \(G_3/tG_3\) is nonzero divisible and hence \(\mathrm{Hom}(G_3, Q) = \mathrm{Hom}(G_3/tG_3, Q) \ne 0\)—contradiction. So in this case \(G_3\) is necessarily torsion.
Suppose now that \(s\ge 1\), then \(A = \mathbb {Z}(p^\infty )\oplus G_3\) is opposed by some module W and we know that W is then of the form \(\mathbb {Z}(p^\infty )\oplus Z\) or \(R \oplus Z\), for some R-module Z. The first possibility cannot happen since \(\mathrm{Hom}(\mathbb {Z}(p^\infty ), G_3) = 0\) would imply that \(\mathrm{Hom}(Z, \mathbb {Z}(p^\infty )) = 0\) and this can never occur. Thus, \(W = R \oplus Z\) for some Z which is opposed to \(G_3\). It follows from the Fundamental Relations that \(\mathrm{Hom}(A, \mathbb {Z}(p^\infty )) \cong \mathrm{Hom}(R, W) = R \oplus Z\). So \(R \oplus Z \cong R \oplus \mathrm{Hom}(G_3, \mathbb {Z}(p^\infty ))\) and since free summands of finite rank have the cancellation property, we conclude that \(Z \cong \mathrm{Hom}(G_3, \mathbb {Z}(p^\infty ))\). Furthermore, since Z is opposed to \(G_3\) it has no summand isomorphic to R or Q. Now if \(G_3\) has an unbounded basic submodule B, then \(G_3/B\) has a summand of the form \(tG_3/B = \bar{B}/B \cong \bigoplus \nolimits _\lambda \mathbb {Z}(p^\infty )\) for some \(\lambda \ne 0\). It follows from Lemma 2.4 that \(G_3\) must have a summand isomorphic to R—contradiction. Hence \(G_3\) is itself bounded and, as noted in Proposition 3.3, it is also semi-standard so that it is in fact finite. It follows then that \(H_3\) is also finite.
The case in which \(t \ge 1\) is essentially identical: one can simply interchange the roles played by \(G_3\) and \(H_3\) in the previous argument.
3.2 A sufficient condition
In Corner’s handwritten manuscript a partial converse is stated at the end of his statement of Theorem 1.1: “Conversely, if G and H are related as above, then  provided in case (b) of (II) that \(G'\) and \(H'\) are fully invariant submodules of D.”No proof of the claim is provided but the key idea he intended to use is probably that which is contained in the publication [2]; we remark that the result in [2] shows that there is no possibility of strengthening Theorem 1.1 to a statement saying that \(G'\) and \(H'\) are isomorphic. Indeed, as explained in [2, Section 3], the examples contained in that work show that Kaplansky’s hope of using some sort of duality to clarify the situation was unfounded.
provided in case (b) of (II) that \(G'\) and \(H'\) are fully invariant submodules of D.”No proof of the claim is provided but the key idea he intended to use is probably that which is contained in the publication [2]; we remark that the result in [2] shows that there is no possibility of strengthening Theorem 1.1 to a statement saying that \(G'\) and \(H'\) are isomorphic. Indeed, as explained in [2, Section 3], the examples contained in that work show that Kaplansky’s hope of using some sort of duality to clarify the situation was unfounded.
We shall merely look at the situation that occurs in relation to condition (II) Case (b) in terms of sufficiency; the other situations are standard and derive easily from the fact that \(R, \mathbb {Z}(p^\infty )\) and finite p-groups possess an anti-isomorphism. Suppose then that X is a fully invariant submodule of D obeying the conditions of (II) Case (b). It is easy to see that D corresponds to the p-adic completion of T and so any endomorphism of T extends uniquely to an endomorphism of D, which in turn restricts to an endomorphism of X since X is, by assumption, fully invariant in D. Thus, if \(\theta \in \mathrm{End}(T)\), there is a unique \(\phi \in \mathrm{End}(X)\) with \(\phi \upharpoonright T = \theta \). Also if \(\phi \in \mathrm{End}(X)\), then \(\phi \) restricts to a unique endomorphism of T since if \(\phi \upharpoonright T = 0\) then \(\phi \) induces a map \(X/T \rightarrow X\) and this later must be the zero map since X/T is divisible while X is reduced. It follows that in this situation we have a ring isomorphism \(\mathrm{End}(X) \cong \mathrm{End}(T)\); in particular if G, H are any pair of submodules obeying the conditions of (II) Case (b), then there is a ring isomorphism \(\Psi :\mathrm{End}(G) \cong \mathrm{End}(H)\).
Assume for the moment that we have an anti-isomorphism \(\Phi :\mathrm{End}(T) \rightarrow \mathrm{End}(T)\), then the composition \(\Psi ^{-1}\Phi \Psi \) is easily seen to be an anti-isomorphism \(\mathrm{End}(G) \rightarrow \mathrm{End}(H)\). Thus, to establish the sufficiency of the conditions it suffices to show T has an anti-automorphism. Since T is the maximal torsion subgroup of a direct product of cyclic p-groups of increasing order, T is a torsion-complete group and may be viewed as \(T = \bar{B}\), where B is the corresponding direct sum of the cyclic groups. The existence of such an anti-automorphism is well known with a proof being given in [2, Theorem 3.2]; alternative proofs may be found in [3] or [4].
References
A.L.S. Corner, On p-adic modules with anti-isomorphic endomorphism rings, undated hand-written manuscript from the period 1961/62
A.L.S. Corner, B. Goldsmith, S. Wallutis, Anti-isomorphisms and the failure of duality, pp. 315–323 in Models, Modules and Abelian Groups, (editors R. Göbel and B. Goldsmith) Walter de Gruyter, Berlin - New York, 2008
G. D’Este, Abelian groups with anti-isomorphic endomorphism rings. Rend. Sem. Mat. Univ. Padova 60, 55–75 (1978)
K. Faltings, On the automorphism group of a reduced primary abelian group. Trans. Am. Math. Soc. 165, 1–25 (1972)
L. Fuchs, Infinite Abelian Groups, vol. I (Academic Press, New York - London, 1970)
L. Fuchs, Infinite Abelian Groups, vol. II (Academic Press, New York - London, 1973)
L. Fuchs, Abelian Groups (Springer International Publishing, Switzerland, 2015)
B. Goldsmith, Anthony Leonard Southern Corner 1934–2006, in Models, Modules and Abelian Groups. ed. by R. Göbel, B. Goldsmith (Walter de Gruyter, Berlin - New York, 2008), pp. 1–7
B. Goldsmith, P. Zanardo, Maximal relatively divisible submodules. Houston J. Math. 39, 387–394 (2013)
N. Jacobson, Lectures in Abstract Algebra, vol. II (Linear Algebra, Van Nostrand, New York, 1953)
I. Kaplansky, Infinite Abelian Groups, University of Michigan Press, Ann Arbor, 1954 and 1969
Acknowledgements
We would like to express our thanks to Enrico Gregorio for providing us with the macro to produce the elegant version of the symbol  which replaced our original rather clumsy one.
which replaced our original rather clumsy one.
Funding
Open Access funding provided by the IReL Consortium.
Author information
Authors and Affiliations
Corresponding author
Additional information
In Memoriam Peter Vámos.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Noel White passed away on 1st September 2021 after a long illness.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Goldsmith, B., White, N. Corner’s theorem on modules with anti-isomorphic endomorphism algebras. Period Math Hung 85, 227–239 (2022). https://doi.org/10.1007/s10998-022-00453-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10998-022-00453-x



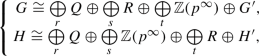
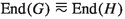 , we have
, we have 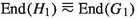 and
and 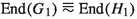 , the corresponding idempotent
, the corresponding idempotent 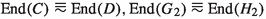 . Moreover, as
. Moreover, as 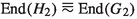 . Note that
. Note that 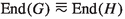 , then
, then