Roots of crosscap slides and crosscap transpositions

Abstract

Let $N_{g}$ denote a closed nonorientable surface of genus g. For $g \ge 2$ the mapping class group $\mathcal {M}(N_{g})$ is generated by Dehn twists and one crosscap slide (Y-homeomorphism) or by Dehn twists and a crosscap transposition. Margalit and Schleimer observed that Dehn twists on orientable surfaces have nontrivial roots. We give necessary and sufficient conditions for the existence of roots of crosscap slides and crosscap transpositions.

1 Introduction

Let $N_{g, s}^{n}$ be a connected nonorientable surface of genus g with s boundary components and n punctures, that is a surface obtained from a connected sum of g projective planes $N_{g}$ by removing s open disks and specifying the set $\Sigma = \lbrace p_{1}, \ldots , p_{n} \rbrace$ of n distinguished points in the interior of $N_{g}$. If s or/and n equals zero, we omit it from notation. The mapping class group $\mathcal {M}(N_{g, s}^{n})$ consists of isotopy classes of self-homeomorphisms $h: N_{g,s}^{n} \rightarrow N_{g,s}^{n}$ fixing boundary components pointwise and such that $h(\Sigma ) = \Sigma$. The mapping class group $\mathcal {M}(S_{g,s}^{n})$ of an orientable surface is defined analogously, but we consider only orientation-preserving maps. If we allow orientation-reversing maps, we obtain the extended mapping class group $\mathcal {M}^{\pm }(S_{g,s}^{n})$. By abuse of notation, we identify a homeomorphism with its isotopy class.

In the orientable case, the mapping class group $\mathcal {M}(S_{g})$ is generated by Dehn twists [3]. As for nonorientable surfaces, Lickorish proved that Dehn twists alone do not generate $\mathcal {M}(N_{g})$, $g \ge 2$. This group is generated by Dehn twists and one crosscap slide (Y-homeomorphism) [4].

A presentation for $\mathcal {M}(N_{g})$ using these generators was obtained by Stukow [14]. This presentation was derived from the presentation given by Paris and Szepietowski [9], which used as generators Dehn twists and yet another homeomorphisms of nonorientable surfaces, so-called crosscap transpositions.

Margalit and Schleimer discovered a surprising property of Dehn twists: in the mapping class group of a closed orientable surface $S_{g}$ of genus $g \ge 2$, every Dehn twist has a nontrivial root [5]. It is natural to ask if crosscap slides and crosscap transpositions also have a similar property. The main goal of this paper is to prove the following:

Main Theorem

In $\mathcal {M}(N_{g})$ a nontrivial root of a crosscap transposition (resp. crosscap slide) exists if and only if $g \ge 5$ or $g = 4$ and the complement of the support of this crosscap transposition [or crosscap slide] is orientable.

2 Preliminaries

2.1 Crosscap transpositions and crosscap slides

Let $N = N_{g}$ be a nonorientable surface of genus $g \ge 2$. Let $\alpha$ and $\mu$ be two simple closed curves on N intersecting in one point, such that $\alpha$ is two-sided and $\mu$ is one-sided. A regular neighborhood of $\mu \cup \alpha$ is homeomorphic to the Klein bottle with a hole denoted by K. A convenient model of K is a disk with 2 crosscaps, see Fig. 1. In this figure shaded disks represent crosscaps, thus the boundary points of these disks are identified by the antipodal map.

Fig. 1

A crosscap transposition and a crosscap slide

A crosscap transposition $U_{\mu ,\alpha }$ specified by $\mu$ and $\alpha$ is a homeomorphism of K which interchanges two crosscaps keeping the boundary of K fixed [9]. It may be extended by the identity to a homeomorphism of N. If $t_{\alpha }$ is the Dehn twist about $\alpha$ (with the direction of the twist indicated by small arrows in Fig. 1), then $Y_{\mu ,\alpha } = t_{\alpha }U_{\mu ,\alpha }$ is a crosscap slide of $\mu$ along $\alpha$, that is the effect of pushing $\mu$ once along $\alpha$ keeping the boundary of K fixed. Note that $U_{\mu ,\alpha }^{2}=Y_{\mu ,\alpha }^{2}=t_{\partial K}$.

Remark 2.1

If g is odd, then the complement of K in $N_g$ is a nonorientable surface $N_{g-2,1}$, thus in this case every two crosscap slides [or crosscap transpositions] are conjugate. If g is even, then the complement of K in $N_g$ can be either a nonorientable surface $N_{g-2,1}$ or an orientable surface $S_{\frac{g-2}{2},1}$, therefore in the mapping class group of a surface of even genus two conjugacy classes of crosscap slides and crosscap transpositions exist.

2.2 Notation

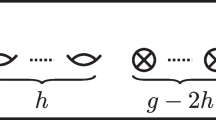
Represent $N_g$ as a connected sum of g projective planes and let $\mu _1,\ldots ,\mu _{g}$ be one-sided circles that correspond to crosscaps as indicated in Fig. 2. By abuse of notation, we identify $\mu _i$ with the corresponding crosscap.

Fig. 2

A nonorientable surface $N_g$

If $\alpha _1,\ldots ,\alpha _{g-1}$ are two-sided circles indicated in the same figure, then for each $i=1,\ldots ,g-1$ by $t_{\alpha _i},u_i,y_i$ we denote the Dehn twist about $\alpha _i$, the crosscap transposition $U_{\mu _{i+1},\alpha _i}$, and the crosscap slide $Y_{\mu _{i+1},\alpha _i}$, respectively.

2.3 Relations in the mapping class group of a nonorientable surface

A full presentation for $\mathcal {M}(N_{g})$ is given in [9, 14]. Among others, the following relations hold in $\mathcal {M}(N_{g})$:

• (R1) $u_{i}u_{j} = u_{j}u_{i}$ for $i,j = 1, \ldots , g-1, \ |i-j|>1$,

• (R2) $u_{i}u_{i+1}u_{i} = u_{i+1}u_{i}u_{i+1}$ for $i=1,\ldots , g-2$,

• (R3) $\left( u_{1}u_2 \cdots u_{g-1}\right) ^{g} = 1$,

• (R4) $t_{\alpha _{i}}u_{j} = u_{j}t_{\alpha _{i}}$ and hence $y_{i}u_{j} = u_{j}y_{i}$ for $i,j=1, \ldots , g-1, \ |i-j|>1$.

It is straightforward to check that relations (R1)–(R3) imply

• (R5) $\left( u_{1}^{2}u_{2}\cdots u_{g-1}\right) ^{g-1} = 1$.

Geometrically $u_{1}u_2\cdots u_{g-1}$ is a cyclic rotation of $\mu _1,\mu _2,\ldots ,\mu _{g}$ and $u_{1}^{2}u_{2}\cdots u_{g-1}$ is a cyclic rotation of $\mu _2,\mu _3,\ldots ,\mu _{g}$ around $\mu _1$. In particular,

• (R6) $\left( u_{1}u_2 \cdots u_{g-1}\right) ^{g} = \left( u_{1}^{2}u_{2} \cdots u_{g-1}\right) ^{g-1} = t_{\partial N_{g,1}}$ in $\mathcal {M}(N_{g,1})$.

We also have the following chain relation between Dehn twists (Proposition 4.12 of [1]): if $k \ge 2$ is even and $c_{1}, \ldots , c_{k}$ is a chain of simple closed curves on a surface S, such that the boundary of a closed regular neighborhood of their union is isotopic to d, then

• (R7) $\left( t_{c_{1}}t_{c_{2}}\cdots t_{c_{k}}\right) ^{2k+2} = t_{d}$.

3 Proof of Main Theorem

Remark 3.1

Automorphisms of $H_{1}(N_{g}; \mathbb {R})$ induced by crosscap transpositions and crosscap slides have determinant equal to $-1$, so if a root of a crosscap slide or a crosscap transposition exists, it must be of odd degree.

Note that in order to prove Main Theorem, it is enough to prove it for some (arbitrary chosen) representatives of conjugacy classes of crosscap slides and crosscap transpositions (see Remark 2.1).

Let u and y be respectively a crosscap transposition and a crosscap slide supported in the same Klein bottle $K\subset N_g$ and let $\delta =\partial K$. In particular, $u^2=y^2=t_{\delta }$. If $N\setminus K$ is nonorientable, then we assume that $u=u_1$, $y=y_1$ and K is a Klein bottle which contains $\mu _1$ and $\mu _2$ (Fig. 2).

3.1 The case of ${g\ge 5}$ odd

Let $p,q \in \mathbb {Z}$ be such that $2p + q(g-2) = 1$. By relations (R6) and (R1),

$$\begin{aligned} \begin{aligned} u_{1}^{2}&=t_\delta =\left( u_{3}u_4 \cdots u_{g-1}\right) ^{g-2}\\ u_{1}^{2p}&=\left( u_{3}u_4 \cdots u_{g-1}\right) ^{p(g-2)}\\ u_{1}&=\left( \left( u_{3}u_4\cdots u_{g-1}\right) ^{p}u_{1}^{q}\right) ^{g-2}. \end{aligned} \end{aligned}$$

Analogously, by relations (R6), (R1) and (R4), $y_{1} = \left( \left( u_{3}u_4\cdots u_{g-1}\right) ^{p}y_{1}^{q}\right) ^{g-2}$.

3.2 The case of ${g \ge 6}$ even and ${N_{g} \backslash K}$ nonorientable

Let $p,q \in \mathbb {Z}$ be such that $2p + q(g-3) = 1$. By relations (R6) and (R1),

$$\begin{aligned} \begin{aligned} u_{1}^{2}&=t_\delta =\left( u_{3}^{2}u_{4} \cdots u_{g-1}\right) ^{g-3}\\ u_{1}^{2p}&=\left( u_{3}^{2}u_{4} \cdots u_{g-1}\right) ^{p(g-3)}\\ u_{1}&=\left( \left( u_{3}^{2}u_{4} \cdots u_{g-1}\right) ^{p}u_{1}^{q}\right) ^{g-3}. \end{aligned} \end{aligned}$$

Analogously, by relations (R6), (R1) and (R4), $y_{1} = \left( \left( u_{3}^{2}u_{4} \cdots u_{g-1}\right) ^{p}y_{1}^{q}\right) ^{g-3}$.

3.3 The case of ${g \ge 4}$ even and ${N_{g} \backslash K}$ orientable

Suppose now that $N_g\setminus K$ is orientable. If $c_{1}, \ldots , c_{g-2}$ is a chain of two-sided circles in $N_g\setminus K$, then by relation (R7),

$$\begin{aligned} \begin{aligned} u^{2}&=t_{\partial K}=\left( t_{c_{1}}t_{c_{2}}\cdots t_{c_{g-2}}\right) ^{2g-2}\\ \left( u^{2}\right) ^{\frac{g}{2}}&=\left( \left( t_{c_{1}}t_{c_{2}}\cdots t_{c_{g-2}}\right) ^{2g-2}\right) ^{\frac{g}{2}}\\ u&=\left( \left( t_{c_{1}}t_{c_{2}}\cdots t_{c_{g-2}}\right) ^{g}u^{-1}\right) ^{g-1}. \end{aligned} \end{aligned}$$

Analogously, $y = \left( \left( t_{c_{1}}t_{c_{2}}\cdots t_{c_{g-2}}\right) ^{g}y^{-1}\right) ^{g-1}$.

3.4 The case of $g=2$

Crosscap slides and crosscap transpositions are primitive in $\mathcal {M}(N_{2})$ because [4]

$$\begin{aligned} \begin{aligned} {\mathcal {M}}(N_{2})&\cong \left\langle t_{\alpha _{1}}, y_{1} \;|\;t_{\alpha _{1}}^{2} = y_{1}^{2} = (t_{\alpha _{1}}y_{1})^{2} = 1 \right\rangle \\&\cong \left\langle t_{\alpha _{1}}, u_{1} | \ t_{\alpha _{1}}^{2} = u_{1}^{2} = (t_{\alpha _{1}}u_{1})^{2} = 1 \right\rangle \cong \mathbb {Z}_{2} \oplus \mathbb {Z}_{2}. \end{aligned} \end{aligned}$$

3.5 The case of $g=3$

Remark 3.2

It is known that the mapping class group $\mathcal {M}(N_{3})$ is hyperelliptic [15] and has the central element $\varrho$ such that $\mathcal {M}(N_{3})/\langle \varrho \rangle$ is the extended mapping class group $\mathcal {M}^{\pm }(S_{0}^{3,1})$ of a sphere with 4 punctures. Two upper subscripts mean that we have four punctures on the sphere, but one of them must be fixed. This implies [2] that the maximal finite order of an element in $\mathcal {M}^{\pm }(S_{0}^{3,1})$ is 3, and hence the maximal finite order of an element in $\mathcal {M}(N_{3})$ is 6. Moreover, each of two rotations of order 3 in $\mathcal {M}^{\pm }(S_{0}^{3,1})$ are conjugate, which easily implies that each of two elements of order 6 in $\mathcal {M}(N_{3})$ are conjugate. The details of the proof of the last statement are completely analogous to that used in [12], hence we skip them.

The same conclusion can also be obtained purely algebraically: it is known [11] that $\mathcal {M}(N_{3})\cong \mathrm {GL}(2,\mathbb {Z})$ and the maximal finite order of an element in $\mathrm {GL}(2,\mathbb {Z})$ is 6. Moreover, there is only one conjugacy class of such elements in $\mathrm {GL}(2,\mathbb {Z})$—for details see for example Theorem 2 of [7].

We will show that crosscap transpositions do not have nontrivial roots in $\mathcal {M}(N_{3})$. Suppose that $x \in \mathcal {M}(N_{3})$ exists such that $x^{2k+1} = u_{1}$, where $k\ge 1$ (see Remark 3.1). Then

$$\begin{aligned} x^{2(2k+1)}=x^{4k+2}=u_1^2=t_\delta =1. \end{aligned}$$

Note that the order of x can not be odd (because otherwise $u_1=x^{2k+1}=1$), it can not equal 2 (because otherwise $x=u_1$), and it is not divisible by 4. Hence, by Remark 3.2, x has order 6. Moreover, by relation (R7),

$$\begin{aligned} \left( t_{\alpha _1}t_{\alpha _2}\right) ^6=t_d=1, \end{aligned}$$

where d is a boundary of a closed regular neighborhood of $\alpha _1\cup \alpha _2$. Hence x is conjugate to $t_{\alpha _1}t_{\alpha _2}$ and this contradicts Remark 3.1, because Dehn twists induce automorphisms of $H_1(N_3;\mathbb {R})$ with determinant equal to 1 and $x^{2k+1}=u_{1}$.

In the case of a crosscap slide the argument is completely analogous, hence we skip the details.

3.6 The case of $g=4$ and ${N_{4} \backslash K}$ nonorientable.

If $N_{4} \backslash K$ is nonorientable, then $\delta$ cuts $N_4$ into two Klein bottles with one boundary component: K and $K_1$. Moreover, as was shown in Appendix A of [13],

$$\begin{aligned} \begin{aligned} \mathcal {M}(K)&=\left\langle t_{\alpha _{1}}, u_{1} \ | \ u_{1}t_{\alpha _{1}} = t_{\alpha _{1}}^{-1}u_{1}\right\rangle \\ \mathcal {M}(K_1)&=\left\langle t_{\alpha _{3}}, u_{3} \ | \ u_{3}t_{\alpha _{3}} = t_{\alpha _{3}}^{-1}u_{3}\right\rangle . \end{aligned} \end{aligned}$$

By abuse of language, we say that $t_{\alpha _1}^ku_1^m\in \mathcal {M}(K)$ interchanges $\mu _1$ and $\mu _2$ if and only if m is odd. Equivalently, elements of $\mathcal {M}(K)$ which does not interchange $\mu _1$ and $\mu _2$ are precisely elements of the twist subgroup of $\mathcal {M}(K)$ (that is the subgroup of index 2 generated by Dehn twists). In the same way we define the notion of interchanging $\mu _3$ and $\mu _4$ for elements of $\mathcal {M}(K_1)$.

If $x \in \mathcal {M}(N_{4})$ exists such that $x^{2k+1} = u_{1}$ and $k\ge 1$ (see Remark 3.1), then

$$\begin{aligned} x^{4k+2}=u_1^2=t_\delta . \end{aligned}$$

In particular, x commutes with $t_\delta$ and

$$\begin{aligned} t_\delta =xt_{\delta }x^{-1}=t_{x(\delta )}^{\pm }. \end{aligned}$$

By Proposition 4.6 of [13], up to isotopy of $N_4$, $x(\delta )=\delta$. Because $u_1$ does not interchange two sides of $\delta$ and does not reverse the orientation of $\delta$, x has exactly the same properties. Therefore, we can assume that x is composed of maps of K and $K_1$. Moreover $u_1=x^{2k+1}$ interchanges $\mu _1$ and $\mu _2$ and does not interchange $\mu _3$ and $\mu _4$, hence

$$\begin{aligned} \begin{aligned} x&=t_{\alpha _{1}}^{k_{1}}u_{1}^{2m_{1}+1}t_{\alpha _{3}}^{k_{2}}u_{3}^{2m_{2}}= t_{\alpha _{1}}^{k_{1}}u_{1}t_{\alpha _{3}}^{k_{2}}t_{\delta }^{m_1+m_2}\\ x^2&=t_{\alpha _{3}}^{2k_{2}}t_{\delta }^{2m_1+2m_2+1}. \end{aligned} \end{aligned}$$

But then

$$\begin{aligned} t_\delta =(x^2)^{2k+1}=t_{\alpha _{3}}^{2k_{2}(2k+1)}t_{\delta }^{(2m_1+2m_{2}+1)(2k+1)} \end{aligned}$$

and Proposition 4.4 of [13] implies that $k_2=0$ and $(2m_1+2m_{2}+1)(2k+1)=1$ which is a contradiction.

In the case of a crosscap slide the argument is completely analogous, hence we skip the details.

Remark 3.3

As was shown by McCullough, Rajeevsarathy [6] and independently by Monden [8], roots of Dehn twists constructed by Margalit and Schleimer [5] are of maximal possible degree. Since the geometric nature of our constructions of roots of crosscap slides and crosscap transpositions is quite similar to that of Margalit and Schleimer, it is natural to ask if the roots constructed in the proof of Main Theorem are also of maximal degree. We plan to answer this question in subsequent work, but it turns out that even in the case of Dehn twists on nonorientable surfaces, the study of possible degrees of their roots is significantly more complicated than in the orientable case—see for example Sect. 4 [10].

4 Roots of elementary braids in the mapping class group of n-punctured sphere

Margalit and Schleimer observed in [5] that if $g\ge 5$, then roots of elementary braids in $\mathcal {M}(S_{0}^g)$ exist. Main Theorem implies slightly stronger version of that result.

Corollary 4.1

An elementary braid in the mapping class group $\mathcal {M}(S_{0}^n)$ or in the extended mapping class group $\mathcal {M}^\pm (S_{0}^n)$ of n-punctured sphere has a nontrivial root if and only if $n \ge 5$.

Proof

By Proposition 2.4 of [9], there is a monomorphism

$$\begin{aligned} \varphi :\mathcal {M}^{\pm }(S_{0}^g)\rightarrow \mathcal {M}(N_g) \end{aligned}$$

which is induced by blowing up each puncture to a crosscap. In particular, this monomorphism sends elementary braids to crosscap transpositions. Moreover, all roots of crosscap transpositions constructed in the proof of Main Theorem are elements of $\varphi (\mathcal {M}(S_{0}^g))$. $\square$