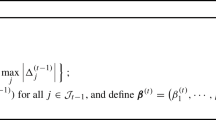Abstract
In this paper, we propose systematic approaches for learning imbalanced data based on a two-regime process: regime 0, which generates excess zeros (majority class), and regime 1, which contributes to generating an outcome of one (minority class). The proposed model contains two latent equations: a split probit (logit) equation in the first stage and an ordinary probit (logit) equation in the second stage. Because boosting improves the accuracy of prediction versus using a single classifier, we combined a boosting strategy with the two-regime process. Thus, we developed the zero-inflated probit boost (ZIPBoost) and zero-inflated logit boost (ZILBoost) methods. We show that the weight functions of ZIPBoost have the desired properties for good predictive performance. Like AdaBoost, the weight functions upweight misclassified examples and downweight correctly classified examples. We show that the weight functions of ZILBoost have similar properties to those of LogitBoost. The algorithm will focus more on examples that are hard to classify in the next iteration, resulting in improved prediction accuracy. We provide the relative performance of ZIPBoost and ZILBoost, which rely on the excess kurtosis of the data distribution. Furthermore, we show the convergence and time complexity of our proposed methods. We demonstrate the performance of our proposed methods using a Monte Carlo simulation, mergers and acquisitions (M&A) data application, and imbalanced datasets from the Keel repository. The results of the experiments show that our proposed methods yield better prediction accuracy compared to other learning algorithms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Most canonical classifiers assume that the number of examples in each of the different classes is approximately the same. Unfortunately, class imbalances are present in many real-life situations (Fernández et al., 2018). Class imbalance refers to the dominance of one class (i.e., the majority class) over the other (i.e., the minority class). It occurs when the prior probability of belonging to the majority class is significantly higher than that of belonging to the minority class (Koziarski et al., 2021). The presence of class imbalance is known to deteriorate the prediction of the minority class (Thanathamathee & Lursinsap, 2013). The minority class is usually overlooked. One of the main issues in imbalance problems is that, despite its rareness, the minority class is generally of more interest from an application perspective, as it may contain important and useful knowledge (Krawczyk, 2016). Thus, it is necessary to correct the prediction of the minority class. Furthermore, because any dataset with an unequal class distribution is technically considered imbalanced, proposing new learning methods for imbalanced data is an important topic in the machine learning community.
In this study, we propose systematic approaches to learning imbalanced data. The systematic imbalanced learning method allows us to think more mechanistically about the data generation processes used to produce imbalanced examples. For instance, in the case of the survival rate of sea turtle eggs, ones are recorded for survivors and zeros for hatchlings who did not survive to adulthood. Since the estimated survival rate of hatchlings is about 0.1% (1 one and 999 zeros), the zero (failure) examples outnumber the one (success) examples (Janzen, 1993); the case of successful hatchlings can be characterized as an imbalanced classification. In this case, the survival process consists of two regimes. First, on the beach, hatchlings must escape natural predators, such as birds, crabs, raccoons, and foxes, to make it to the sea (regime 0); second, once in the water, few hatchlings survive to adulthood as a result of anthropogenic activities, such as overexploitation for food, the pet trade, and the threat of global climate change (regime 1) (Stanford et al., 2020). Turtles typically experience the highest mortality rates during the hatchling and early life stages (Gibbons, 1987; Heppell et al., 1996; Perez-Heydrich et al., 2012); the majority of the class (i.e., excessive zeros) is generated in regime 0. However, the survival rate increases rapidly as turtles grow and age (Brooks et al., 1988; Congdon et al., 1994); after passing the first hurdle (regime 0), the minority class (i.e., ones) enters into regime 1. Thus, the minority class comprises survivors, whereas the majority class consists of hatchlings who either failed to approach the water or did not survive to adulthood in the water. Nature operates in this way.
Therefore, in some cases, it is ideal to propose a method that generates two models (regimes). First, a probit (or logit) model is generated for the excessive zero examples (e.g., predicting whether a hatchling will escape from predators); this is identified as regime 0 for the majority class. Then, another probit (or logit) model is generated for the underrepresented examples (e.g., predicting whether or not those hatchlings who graduate from the first regime would survive to adulthood); this is identified as regime 1 for the minority class. Finally, the two models are combined. Notably, each of the two models may use a different set of predictors. In the above example, the factors related to natural predators are more critical to survival in regime 0 than in regime 1. Similarly, the factors related to human activities are more critical to survival in regime 1 than in regime 0. For more details, see Fig. 1.
We argue that systematic approaches that rely on data-generating processes may be appropriate for imbalance learning in particular cases (e.g., survival of sea turtle eggs). We then develop zero-inflated probit boost (ZIPBoost) and zero-inflated logit boost (ZILBoost) methods to account for imbalance learning based on two distinct regimes. More specifically, the proposed ZIPBoost (ZILBoost) uses a two-regime process that combines a split probit (logit) model for regime 0 with an ordinary probit (logit) model for regime 1. Since boosting (e.g., LogitBoost and AdaBoost) is known to improve accuracy compared with a single classifier, we combine a boosting strategy (incremental learning rules) with the framework of the two-regime process.
Notably, we show that the weight functions of ZIPBoost have the desired properties for achieving good predictive performance. Similar to AdaBoost, the weight functions upweight misclassified examples and downweight correctly classified examples. We present these properties as propositions. The properties make the algorithm focus more on misclassified examples during iterations, resulting in a reduction in errors. Since ZIPBoost involves updating two functions—one for probabilities in the split probit model and the other for probabilities in the ordinary probit model—we apply cyclic coordinate descent, which is a repeated application of the Newton–Raphson method. In the case of imbalanced data, it is known that the logit model outperforms the probit model for a leptokurtic distribution (a distribution with positive excess kurtosis), whereas the probit model is preferred for a platykurtic distribution (a distribution with negative excess kurtosis) (Chen & Tsurumi, 2010). Thus, we also introduce the ZILBoost algorithm, wherein the two probit models in ZIPBoost are replaced with two logit models. We show that the weight functions of ZILBoost have similar properties to LogitBoost. The weight functions upweight examples that have low confidence (i.e., the fitted values are around zero) and downweight examples that have high confidence (i.e., the fitted values are not around zero). These properties imply that the algorithm will prioritize examples that are hard to classify in the next iteration, leading to improved prediction accuracy. Like ZIPBoost, ZILBoost requires updating two functions, and thus, we employ cyclic coordinate descent. We use a simulation to demonstrate that the excess kurtosis of the data distribution determines the relative performance of ZIPBoost and ZILBoost. In addition, we present the convergence and time complexity of the proposed methods.
We demonstrate the performance of our proposed methods using experiments by a Monte Carlo simulation, a real data application for predicting M&A outcomes, and imbalanced datasets from the Keel repository. For comparison, we consider standard learning algorithms, including Adaboost, Logitboost, and Probitboost, and existing approaches for learning imbalanced data, such as AdaC2, SMOTEBoost, and generative adversarial networks (GANs). The results from the experiments show that our proposed methods provide the best prediction accuracy. We believe that when data are generated from a two-regime process, our proposed methods outclass existing methods in terms of predictive performance.
To implement the proposed methods, it is necessary to have prior information on two different sets of predictors that affect the probabilities of belonging to either regime 0 or 1. If researchers do not have access to knowledge of the optimal predictor splits, they can empirically determine the splits that provide the best predictive performance on data. However, we note that this data-driven approach to the predictor splits may be computationally expensive. For more details, please see Sect. 5.3. Furthermore, the proposed methods can be generalized to multiclass problems, but we note that other updating schemes should be employed to reduce the computational burden. This study also provides the possibility for future work on the refinement functions of the proposed methods.
This paper is organized as follows. We review the existing approaches to imbalanced learning in Sect. 2. In Sect. 3, we set up the problem. In Sect. 4, we introduce the proposed methods (ZIPBoost and ZILBoost). We present experiments in Sect. 5. In Sect. 6, we conclude the paper with suggestions for future work.
2 Related work
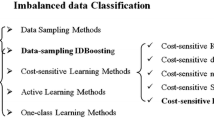
Numerous efforts have been made in the machine learning community to classify the minority class correctly in the presence of class imbalance. A large number of techniques can be broadly categorized into four groups based on how they tackle the class imbalance problem (Fernández et al., 2018).
First, data-level approaches try to rebalance the class distribution by resampling the imbalanced examples (e.g., Batista et al., 2004; Fernández et al., 2008; Koziarski & Woźniak, 2017; Napierała et al., 2010; Stefanowski & Wilk, 2008). Notably, data-level approaches include sampling methods consisting of oversampling, undersampling, and a combination of both. Oversampling attempts to increase the size of the minority class, whereas undersampling discards the examples in the majority class. Among the sampling methods, the Synthetic Minority Over-sampling TEchnique (SMOTE), proposed by Chawla et al. (2002), is quite popular. SMOTE generates synthetic minority examples through linear interpolation. However, the presence of disjoint data distribution and outliers is known to hinder improvements in classification using synthetic examples (Koziarski, 2020). Recently, the GANs approach has been adopted to deal with the imbalance problem (e.g., Frid-Adar et al., 2018). The GANs approach consists of the following two components (Huang et al., 2022): (1) a generator that attempts to generate data similar to the real imbalanced data, and (2) a discriminator that attempts to discriminate between the real imbalanced data and the generated data. Unlike conventional oversampling methods used to address class imbalance, GANs may not suffer from overfitting, because their training is based on adversarial learning between the two components. Data-level approaches do not require modification of the learning algorithm, because sampling methods alter data distribution to train a classifier under class balance. However, the sampling methods have a limitation in that the resampled data may follow a distribution that is different from that of the original data (Sun et al., 2015).
Second, algorithm-level approaches aim to modify existing classification algorithms to bias learning toward the minority class (e.g., Barandela et al., 2003; Lin et al., 2002; Liu et al., 2000). For instance, a support vector machine (SVM), one of the popular classification methods, can be combined with different classification strategies, such as kernel modifications and weighting schemes based on the importance of each example for classification, to alleviate the tendency to classify a minority example as the majority class while learning imbalanced data (Hwang et al., 2011; Liu & He, 2022). For algorithmic approaches, it is vital to have sufficient knowledge of the causes of bias from the underlying mechanisms of the original algorithms so that appropriate modifications can be considered (Krawczyk, 2016). Without a precise identification of the reasons for a failure in classifying the minority class, classifiers still tend to predict the majority class at the cost of losing the minority class’s predictive power.
Third, cost-sensitive approaches consist of a combination of data-level transformations and algorithm-level adaptations (e.g., Chawla et al., 2008; Lee et al., 2020; Ling et al., 2006; Zhang et al., 2008). The classification algorithm is biased toward the minority class by adding costs to instances and is modified to account for misclassification costs. More precisely, to build a cost-sensitive classifier, different misclassification costs for different classes are incorporated into the learning process, such as making the cost of misclassifying a minority example at a higher level than that of misclassifying a majority example. One of the cost-sensitive approaches is the cost-sensitive decision tree, in which different misclassification costs can be used for splitting or pruning criteria (López et al., 2012). However, the major drawback of this approach is that it assumes a known cost matrix that is unknown in most cases (Krawczyk et al., 2014; Pei et al., 2021; Saber et al., 2020; Sun et al., 2007). The cost-sensitive approach has difficulty finding the optimal cost matrix to handle the class imbalance problem (Ren et al., 2022).
Fourth, ensemble-based approaches are hybrid methods that usually combine an ensemble learning algorithm with a data-level (or cost-sensitive) approach (e.g., Wang & Japkowicz, 2010; Wang et al., 2014). For example, ensemble-based approaches include combinations of cost-sensitive approaches with boosting or bagging, which are ensemble learning algorithms designed to improve predictive accuracy. This combination processes imbalanced data before utilizing multiple learning algorithms. To accept costs in the training process, cost-sensitive ensembles guide cost minimization using the ensemble learning algorithm (Galar et al., 2012). Despite this, ensemble learning methods, such as boosting and bagging, can play a role only in producing more accurate predictions than stand-alone learning algorithms. Specifically, unless the combined data-level (or cost-sensitive) approach appropriately addresses the imbalance problem, ensemble-based approaches are unable to resolve the imbalance problem. For example, cost-sensitive ensembles still require an optimal cost matrix.
However, the existing approaches do not account for the possibility that two different types of zeros exist, as they do not distinguish between zeros that may stem from regime 0 (e.g., a hatchling that did not escape from predators on the beach) and zeros generated from regime 1 (e.g., a hatchling that graduated from the first regime but did not ultimately survive to adulthood in the water). In other words, the existing approaches assume that only one regime generates the majority and minority classes. Departing from the existing approaches, we propose systematic approaches to address the imbalance problem for classification by assuming that two distinct regimes produce the majority and minority classes.
3 Problem setup
In this section, we describe the two-regime process and illustrate how boosting can be applied to the process.
3.1 The two-regime process
In this study, we assume that the sample is obtained from a two-regime process: regime 0, which generates excess zeros, and regime 1, which contributes to generating a minority class. We present the distribution of fictitious data from the two-regime process in Fig. 1. We consider the fictitious data to be imbalanced, as an outcome of 0 significantly outweighs an outcome of 1: Among the 500 examples, 400 examples (80%) have an outcome of 0, while only 100 examples (20%) have an outcome of 1. The majority class is an outcome of 0. This two-regime process assumes the following: (1) For the instances of the outcome of 0, regime 0 generates the gray portion (300 examples, representing the excess zeros) and regime 1 generates the black portion (100 examples), and (2) for the instances of the outcome of 1, regime 1 generates the black portion (100 examples, representing the minority class). Thus, in this two-regime process, zeros are composed of two parts: gray and black portions of the zero bar. The black portions of the zero and one bars indicate the examples in regime 1, which passed the first hurdle (regime 0). Notably, in the absence of excess zeros (i.e., without the gray portion), the data would seem balanced, since the zero and one bars have the same height with 100 examples for each outcome. In this case, canonical classifiers, including ordinary probit or logit models, would perform well in predicting outcomes. However, in the presence of a gray portion, it becomes essential to differentiate between the gray portion and the black portion of the zero bar. To this end, a systematic approach is required to identify whether examples belong to the gray portion or black portion of the zero and one bars, as well as to ascertain whether examples in the black portion have an outcome of 0 or 1.
More specifically, let us consider a sample of \(N\) observed units with binary outcomes 0 and 1 and assume that a zero outcome is inflated. To put it differently, the sample represents a class imbalance whose majority is a zero outcome. In this setting, let \({q}^{*}\) be a latent variable to represent the propensity of regime 1 as.
where \({\varvec{x}}\) indicates a vector of covariates that cause inflated zeros for the majority class, \({\varvec{\beta}}\) is a vector of coefficients, and \(u\) represents the error term. Equation (1) represents the splitting equation (SE), which accounts for excess zeros. For example, the SE identifies whether a hatchling will reach the water or not. Depending on the value of \({q}^{*}\), we define the two regimes indicated by \(q\in \{\text{0,1}\}\) such that a unit with \({q}^{*}\le 0\) belongs to regime 0 (i.e., \(q=0\)), and the observed zero turns out to be an inflated case, and if a unit has \({q}^{*}>0\), we may observe one of the possible outcomes, 0 or 1, in regime 1 (i.e., \(q=1\)). The probability of belonging to regime 1 is defined as
For those with \(q=1\), the observed outcome is determined by the underlying latent variable \({\widetilde{y}}^{*}\) defined as follows:
where \({\varvec{z}}\) indicates a vector of covariates that generate the minority class, \({\varvec{\gamma}}\) is a vector of coefficients, and \(\varepsilon \) represents the error term. We refer to Eq. (2) as the outcome equation (OE) (Hill et al., 2011). For example, the OE identifies whether a hatchling will survive to adulthood or not. To state it differently, depending on the value of \({\widetilde{y}}^{*}\) for those with \(q=1\), one of the possible outcomes is observed. Under regime 1, the possible outcomes, \(\widetilde{y}\), are defined as follows:
Notably, zero outcomes can be generated from either \(q\) in the SE or \(\widetilde{y}\) in the OE, but it is not distinguishable. The full probabilities for observed outcomes, \(y\), are then jointly based on the results from the SE and OE:
The SE and OE can be modeled using probit or logit models. The choice between probit and logit models depends on the characteristics of the data distribution. For example, if the data distribution exhibits negative excess kurtosis, a probit model is preferred over a logit model, while a logit model is deemed more suitable for data with positive excess kurtosis (Chen & Tsurumi, 2010). When the probit model is applied, Eq. (3) becomes
where \(\varPhi (\cdot )\) is the cumulative distribution function of the standard univariate normal distribution. Notably, it is shown that the parameters of Eq. (4) are consistently and efficiently estimated through maximum likelihood estimation (Harris & Zhao, 2007). Based on the probabilities in Eq. (4), the log-likelihood function to find an optimal solution is defined as.
where \({f}_{1}\left({\varvec{x}}\right)={{\varvec{x}}}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}\), \({f}_{2}\left({\varvec{z}}\right)={{\varvec{z}}}^{\boldsymbol{^{\prime}}}{\varvec{\gamma}}\), and \(f\in \{{f}_{1}\left({\varvec{x}}\right),{f}_{2}\left({\varvec{z}}\right)\}\).
If the SE and OE are modeled by the logit model, Eq. (4) can be rewritten as
and the log-likelihood function is
where \({f}_{1}\left({\varvec{x}}\right)={{\varvec{x}}}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}\), \({f}_{2}\left({\varvec{z}}\right)={{\varvec{z}}}^{\boldsymbol{^{\prime}}}{\varvec{\gamma}}\), and \(f\in \{{f}_{1}\left({\varvec{x}}\right),{f}_{2}\left({\varvec{z}}\right)\}\).
3.2 Boosting with cyclic coordinate descent
Boosting is an ensemble method that combines many weak classifiers to generate a powerful learning rule (Oentaryo et al., 2014). Notably, it is widely acknowledged that ensembles of many classifiers, such as boosting, often exhibit higher prediction accuracy compared to individual models that produce a single classifier (Guelman, 2012; Provost & Domingos, 2003; Ren et al., 2016). Thus, we employ boosting to update \({f}_{1}\left(\mathbf{x}\right)\) and \({f}_{2}\left(\mathbf{z}\right)\) to obtain the final classifier.
To this end, we use the expected negative log-likelihood as a loss function, denoted as \(E\left[-l\left(f\right)|{\varvec{x}},{\varvec{z}}\right]\). Hence, the expected log-likelihood maximization problem becomes the expected negative log-likelihood minimization problem, and the minimizer \({f}_{1}^{*}\left({\varvec{x}}\right)\) and \({f}_{2}^{*}\left({\varvec{z}}\right)\) of \(E\left[-l\left(f\right)|{\varvec{x}},{\varvec{z}}\right]\) is the maximizer of the expected log-likelihood.
In the iterative process of updating \({f}_{1}\left({\varvec{x}}\right)\) and \({f}_{2}\left({\varvec{z}}\right)\), we use a cyclic coordinate descent algorithm. This sequential update involves updating one of them while keeping the other fixed at each iteration, reducing multivariate optimization to sequential univariate (Tang & Wu, 2014). Owing to computational efficiency, cyclic coordinate descent has gained popularity for solving problems with more than one parameter (Massias et al., 2020; Saha & Tewari, 2013). In each update of \({f}_{1}\left({\varvec{x}}\right)\) and \({f}_{2}\left({\varvec{z}}\right)\), the Newton–Raphson method is applied (Wu, 2013; Wu & Lange, 2010).
To minimize the expected negative log-likelihood, the update schemes based on the Newton–Raphson method at iteration \(m\) are defined as follows:
where \(D\left(.\right)\) and \(H\left(.\right)\) are the gradient and Hessian of the objective function, respectively. Given initial values of 0 for \({f}_{1}^{0}({\varvec{x}})\) and \({f}_{2}^{0}({\varvec{z}})\), the final values after \(M\) iterations are \({f}_{1}^{M}\left({\varvec{x}}\right)={\sum }_{m=1}^{M}{f}_{1}^{m}({\varvec{x}})\) and \({f}_{2}^{M}\left({\varvec{z}}\right)={\sum }_{m=1}^{M}{f}_{2}^{m}({\varvec{z}})\), and the predicted probabilities of observing each possible outcome for unit \(i\) are calculated based on \({f}_{1}^{M}\left({\varvec{x}}\right)\) and \({f}_{2}^{M}\left({\varvec{z}}\right)\). The final classifier is \(\widehat{y}=\) \(\underset{j\in \left\{\text{0,1}\right\}}{\text{argmax}}\text{Pr}(y=j|{\varvec{x}},{\varvec{z}})\), where \(\widehat{y}\) represents the predicted outcome and \(j\) indicates possible outcomes.
4 Proposed methods
In this section, we propose two novel methods, ZIPBoost and ZILBoost, that integrate the two-regime process with boosting techniques to reduce the misclassification of the minority class. We also show the convergence of the proposed methods.
4.1 ZIPBoost
ZIPBoost consists of two types of iterations: one with respect to the SE and the other with respect to the OE. The objective function in ZIPBoost is the expected negative log-likelihood, \(E\left[-l\left(f\right)|{\varvec{x}},{\varvec{z}}\right]\), where \(l\left(f\right)\) is defined as in Eq. (5). Like AdaBoost, the observation weights for the SE and OE increase when units are misclassified and decrease for units that are correctly classified.
4.1.1 Splitting equation iterations
ZIPBoost starts by fitting the SE, \({f}_{1}\left({\varvec{x}}\right)\). We use \({f}_{x}={f}_{1}({\varvec{x}})\) and \({f}_{z}={f}_{2}({\varvec{z}})\) interchangeably for simplicity in notation. Using the properties of the cumulative distribution function and the probability distribution function of the standard normal distribution, we can infer that \(\varPhi \left(-f\left(\cdot \right)\right)= 1-\varPhi \left(f\left(\cdot \right)\right)\), \(\varphi \left(-f\left(\cdot \right)\right)=\varphi \left(f\left(\cdot \right)\right),\) and \({\varphi }{\prime}\left(f\left(\cdot \right)\right)=-f\left(\cdot \right)\varphi \left(f\left(\cdot \right)\right)\), where \(\varPhi \left(\cdot \right)\) represents the standard normal cumulative distribution function and \(\varphi \left(\cdot \right)\) indicates the standard normal probability density function. We also assume the natural logarithm for the negative log-likelihood function for simplicity. The gradient of the objective function is defined as
For the derivation of the gradient \(D\left({f}_{x}\right)\), please see Appendix A.
In addition, the Hessian is defined as
Equation (8) indicates that when \(y=0\), \(h\left({f}_{x}\right)\) can be written as \(h\left({f}_{x}\right)=-\frac{\left\{{f}_{x}\varphi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)\left[1-\varPhi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)\right]-{\varphi }^{2}\left({f}_{x}\right){\varPhi }^{2}\left({f}_{z}\right)\right\}}{{\left\{1-\varPhi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)\right\}}^{2}}\) and when \(y=1\), \(h\left({f}_{x}\right)\) can be written as \(h\left({f}_{x}\right)=-\frac{\left\{-{f}_{x}\varphi \left({f}_{x}\right)\varPhi \left({f}_{x}\right)-{\varphi }^{2}\left({f}_{x}\right)\right\}}{{\left\{\varPhi \left({f}_{x}\right)\right\}}^{2}}.\) Therefore,
where \({G}_{0}\left({f}_{x}\right)=-{f}_{x}+{f}_{x}\varPhi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)+\varphi \left({f}_{x}\right)\varPhi \left({f}_{z}\right),\) \({G}_{1}\left({f}_{x}\right)={f}_{x}\varPhi \left({f}_{x}\right)+\varphi \left({f}_{x}\right)\), and \({G}_{0}\left({f}_{x}\right)=-{f}_{x}+\varPhi \left({f}_{z}\right){G}_{1}\left({f}_{x}\right)\).
Descent methods require convexity of the loss function to guarantee optimality. The convexity can be proven by showing that the Hessian of \(E\left[-l\left(f\right)|{\varvec{x}}\right]\) is positive definite. However, the Hessian in Eq. (9) is indefinite, since \(h\left({f}_{x}\right)>0\) if \({f}_{x}\le 0\) but \(h\left({f}_{x}\right)<0\) if \({f}_{x}>0\) when \(y=1\). This means that our algorithm can converge to saddle points (Dauphin et al., 2014). Thus, we use the absolute value of the Hessian to force the matrix to be positive definite. Notably, for the non-convex functions in the Newton–Raphson method, the eigenvalues of the Hessian can be replaced with absolute values (Paternain et al., 2019; Wright & Nocedal, 2006). In our setting, since the Hessian is a \(1\times 1\) matrix and the eigenvalue is the value of the Hessian itself, the modification is achieved by taking the absolute value, represented as \(|h\left({f}_{x}\right)|\).
Based on the gradient and the modified Hessian, the Newton–Raphson method is applied to minimize the expected negative log-likelihood as follows:
where \({E}_{w}(\cdot |{\varvec{x}})\) indicates the weighted conditional expectation such that \({E}_{w}\left(g\left({\varvec{x}},y\right)|{\varvec{x}}\right)=\frac{\text{E}\left[\text{w}\left({\varvec{x}}, y\right)\text{g}\left({\varvec{x}},y\right)|{\varvec{x}}\right]}{\text{E}\left[\text{w}\left({\varvec{x}},y\right)|{\varvec{x}}\right]},\boldsymbol{ }\text{with w}\left({\varvec{x}}, y\right)>0\).
Furthermore, the weights are expected to increase for misclassification but decrease for correct classification. Thus, we provide the property of the weight function, \(|h\left({f}_{x}\right)|\):
When \(y=0,\) Eq. (10) becomes
The weight function with \(y=0\) upweights the misclassified units and downweights the units that are correctly classified. We summarize these properties in the following propositions:
Proposition 1
(Correct classification) We have \(\underset{{f}_{x}\to -\infty }{\text{lim}}W\left({f}_{x}\right)=0\).
Proposition 2
(Correct classification) Given \({f}_{z}\ll -N\), where \(N\) is an arbitrarily large positive number, \(\underset{{f}_{x}\to \infty }{\text{lim}}W\left({f}_{x}\right)=0\).
Proposition 1 holds because \(\varphi \left({f}_{x}\right)\to 0\) and \(\left({f}_{x}\right)\to 0\), and Proposition 2 holds because \(\varphi \left({f}_{x}\right)\to 0\) and\(\varPhi \left({f}_{x}\right)\to 1\), but\(\varPhi \left({f}_{z}\right)\approx 0\).
Proposition 3
(Misclassification) Given \({f}_{z}\gg N\), where \(N\) is an arbitrarily large positive number, \(\underset{{f}_{x}\to \infty }{\text{lim}}W\left({f}_{x}\right)=1\).
Proof
Given \({f}_{z}\gg N\), \(\underset{{f}_{x}\to \infty }{\text{lim}}W\left({f}_{x}\right)=\underset{{f}_{x}\to \infty }{\text{lim}}\left|\frac{-{f}_{x}\varphi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)+{f}_{x}\varphi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)+{\varphi }^{2}\left({f}_{x}\right){\varPhi }^{2}\left({f}_{z}\right)}{{\left\{1-\varPhi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)\right\}}^{2}}\right|=\frac{0}{0}\), which is an indeterminate form, since \(\varPhi \left({f}_{x}\right)\varPhi ({f}_{z}) \to 1\) and \(\varphi \left({f}_{x}\right)\to 0\) as \({f}_{x}\to \infty \). Thus, following Zheng and Liu (2012), we apply L’Hôpital’s rule repeatedly:
where the second, sixth, ninth, and tenth equations hold by L’Hôpital’s rule. □
Propositions 1 and 2 provide the weight functions with \(y=0\) in the SE iterations when a unit is correctly classified (i.e., the predicted outcome is 0). As \({f}_{x}\) decreases, it is more likely that the unit is identified as an inflated case, resulting in the correct classification. In such a case, the weight function downweights the unit. When \({f}_{x}\) increases, the algorithm will correctly classify the unit only if \({f}_{z}\) is sufficiently small (i.e., \(\varPhi \left({f}_{z}\right)\approx 0)\). It implies that when \({f}_{z}\) is smaller than an arbitrarily large negative number, \(-N\), the weight for the unit decreases as \({f}_{x}\) increases. On the other hand, Proposition 3 provides the weight function with \(y=0\) in the case of misclassification. When \({f}_{x}\) increases and a sufficiently large value of \({f}_{z}\) (i.e., \(\varPhi \left({f}_{z}\right)\approx 1)\) is given, it is more likely that the unit is misclassified as an outcome of 1, and hence, its weight is increased.
When \(y=1,\) Eq. (10) becomes
The weight function with \(y=1\) increases the weights for the misclassified units and decreases the weights for the units that are correctly classified. We summarize these properties in the following propositions:
Proposition 4
(Correct classification) We have \(\underset{{f}_{x}\to \infty }{\text{lim}}W\left({f}_{x}\right)=0.\)
The proof of Proposition 4 is trivial because \(\varphi \left({f}_{x}\right)\to 0\).
Proposition 5
(Misclassification) We have \(\underset{{f}_{x}\to -\infty }{\text{lim}}W\left({f}_{x}\right)=1\).
Proof
The proof of Proposition 5 is similar to that of Proposition 3. For more details, please see Appendix B.
Proposition 4 provides the weight function with \(y=1\) for correct classification. An increase in \({f}_{x}\) indicates a higher likelihood of passing the first hurdle (regime 0), and hence, the weight for the unit is decreased. Proposition 5 shows the weight function with \(y=1\) in the case of misclassification. When \({f}_{x}\) decreases, it is more likely that the unit, whose actual outcome is 1, is mistakenly identified as an inflated case. In such a case, our algorithm will increase its weight in the next iteration.
4.1.2 Outcome equation iterations
Next, the algorithm updates \({f}_{2}\left({\varvec{z}}\right)\) based on the previously updated \({f}_{1}\left({\varvec{x}}\right)\). The gradient of the objective function is defined as
We provide details on the derivation of the gradient \(D\left({f}_{z}\right)\) in Appendix A.
Furthermore, the Hessian is defined as
When \(y=0, h\left({f}_{z}\right)\) in Eq. (11) becomes \(h\left({f}_{z}\right)=-\frac{\left\{{f}_{z}\varphi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)\left[1-\varPhi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)\right]-{\varphi }^{2}\left({f}_{z}\right){\varPhi }^{2}\left({f}_{x}\right)\right\}}{{\left\{1-\varPhi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)\right\}}^{2}}\), and when \(y=1,\) it becomes \(h\left({f}_{z}\right)=-\frac{\left\{-{f}_{z}\varphi \left({f}_{z}\right)\varPhi \left({f}_{z}\right)-{\varphi }^{2}\left({f}_{z}\right)\right\}}{{\left\{\varPhi \left({f}_{z}\right)\right\}}^{2}}\). Therefore, the Hessian can be rewritten as
where \({G}_{0}\left({f}_{z}\right)=-{f}_{z}+{f}_{z}\varPhi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)+\varphi \left({f}_{z}\right)\varPhi \left({f}_{x}\right),\) \({G}_{1}\left({f}_{z}\right)={f}_{z}\varPhi \left({f}_{z}\right)+\varphi \left({f}_{z}\right)\), and \({G}_{0}\left({f}_{z}\right)=-{f}_{z}+\varPhi \left({f}_{x}\right){G}_{1}\left({f}_{z}\right)\).
Like in Sect. 4.1.1, the Hessian in Eq. (12) is not positive definite, which means that our objective function, \(E\left[-l\left(f\right)|{\varvec{z}}\right]\), is not convex. Thus, we use the modified Hessian by using the absolute value of the Hessian.
Based on the gradient and the modified Hessian, the Newton–Raphson method is applied to minimize the negative log-likelihood with \({f}_{2}({\varvec{z}}\)) as follows:
where \({E}_{w}(\cdot |{\varvec{z}})\) indicates the weighted conditional expectation such that \({E}_{w}\left(g\left({\varvec{z}}, y\right)|{\varvec{z}}\right)=\frac{\text{E}\left[\text{w}\left({\varvec{z}}, y\right)\text{g}\left({\varvec{z}},y\right)|{\varvec{z}}\right]}{\text{E}\left[\text{w}\left({\varvec{z}},y\right)|{\varvec{z}}\right]},\) with \(\text{w}\left({\varvec{z}}, y\right)>0\).
Furthermore, we provide the properties of the weight function, \(|h\left({f}_{z}\right)|\), which is defined as
The weight function with \(y=0\) can be rewritten as
and has the properties of increasing the weights for the misclassified units and decreasing the weights for the correctly classified units as follows:
Proposition 6
(Correct classification) We have \(\underset{{f}_{z}\to -\infty }{\text{lim}}W\left({f}_{z}\right)=0\).
Proposition 7
(Correct classification) Given \({f}_{x}\ll -N,\) where \(N\) is an arbitrarily large positive number,\(\underset{{f}_{z}\to \infty }{\text{lim}}W\left({f}_{z}\right)=0\).
Proposition 6 holds because \(\varphi \left({f}_{z}\right)\to 0\) and \(\varPhi \left({f}_{z}\right)\to 0\), and Proposition 7 holds because \(\varphi \left({f}_{z}\right)\to 0\) and \(\varPhi \left({f}_{z}\right)\to 1\), but \(\varPhi \left({f}_{x}\right)\approx 0\).
Proposition 8
(Misclassification) Given \({f}_{x}\gg N,\) where \(N\) is an arbitrarily large positive number, \(\underset{{f}_{z}\to \infty }{\text{lim}}W\left({f}_{z}\right)=1\).
Proof
The proof of Proposition 8 is similar to that of Proposition 3. For more details, please see Appendix B.
Propositions 6 and 7 provide the weight functions with \(y=0\) in the OE iterations in the case of correct classification. As \({f}_{z}\) decreases, our algorithm predicts an outcome of 0 for the unit, implying that the observed outcome and the predicted outcome are identical. Thus, its weight is decreased. When \({f}_{z}\) increases, correct classification occurs only if \({f}_{x}\) is sufficiently small (i.e., \(\varPhi \left({f}_{x}\right)\approx 0\)). In other words, for a given \({f}_{x}\) smaller than an arbitrarily large negative number, \(-N\), the weight for the unit is decreased, as the unit is identified as an inflated case. However, with a sufficiently large value of \({f}_{x}\)(i.e., \(\varPhi \left({f}_{x}\right)\approx 1\)), an increase in \({f}_{z}\) implies a higher possibility of being misclassified as an outcome of 1 and the weight for the unit is increased, as shown in Proposition 8.
The weight function with \(y=1\) can be rewritten as
and we provide the properties that upweight the misclassified units and downweight the units as follows:
Proposition 9
(Correct classification) \(\underset{{f}_{z}\to \infty }{\text{lim}}W\left({f}_{z}\right)=0\).
It is easy to see that Proposition 9 holds because \(\varphi \left({f}_{z}\right)\to 0\).
Proposition 10
(Misclassification)\(\underset{{f}_{z}\to -\infty }{\text{lim}}W\left({f}_{z}\right)=1\).
Proof
To prove Proposition 10, we apply L’Hôpital’s rule repeatedly since we have an indeterminate form due to the fact that \(\varPhi \left({f}_{z}\right)\to 0\) and \(\varphi \left({f}_{z}\right)\to 0\) as \({f}_{z}\to -\infty \). Please see Appendix B.
Proposition 9 provides the weight function with \(y=1\) in the OE iterations for correct classification. As \({f}_{z}\) increases, it is more likely that the predicted outcome of the unit is 1, leading to a decrease in the corresponding weight. On the other hand, Proposition 10 shows a decrease in weights for misclassification. When \({f}_{z}\) decreases, the unit is more likely to be misclassified as an outcome of 0. In such a case, our algorithm will increase its weight.
4.1.3 Pseudo-code for ZIPBoost
We summarize the proposed algorithm ZIPBoost by presenting the pseudo-code in Algorithm 1. The algorithm requires a set of samples \(\left({{\varvec{x}}}_{i},{{{\varvec{z}}}_{i},y}_{i}\right)\) for \(i\in \{1,\dots ,N\}\), where \({{\varvec{x}}}_{i}\) and \({{\varvec{z}}}_{i}\) are sets of variables for the SE and OE, respectively, and the maximum number of iterations, \(M\). In Step A, we set the initial fitted values of \({f}_{1}^{0}\left({{\varvec{x}}}_{i}\right)\) and \({f}_{2}^{0}\left({{\varvec{z}}}_{i}\right)\) to zero.
Next, in Step B, we run the ZIPBoost iterations to sequentially update the fitted values for the SE (Lines 3–6) and for the OE (Lines 7–10). More precisely, for each iteration of \(m\in \{1,\dots ,M\}\), we first run the SE iterations with the transformed response \({q}_{i,se}^{m}\) in Line 3 and weights for the SE \({w}_{i,se}^{m}\) in Line 4, which are defined as follows:
and
where \({G}_{0}\left({f}_{x}\right)=-{f}_{x}+{f}_{x}\varPhi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)+\varphi \left({f}_{x}\right)\varPhi \left({f}_{z}\right),\) \({G}_{1}\left({f}_{x}\right)={f}_{x}\varPhi \left({f}_{x}\right)+\varphi \left({f}_{x}\right)\), and \({G}_{0}\left({f}_{x}\right)=-{f}_{x}+\varPhi \left({f}_{z}\right){G}_{1}\left({f}_{x}\right)\).
Since the update scheme is based on the Newton–Raphson method, the classifier can be obtained by fitting a weighted least square regression of the transformed response \({q}_{i,se}^{m}\) on \({{\varvec{x}}}_{i}\) with the weight \({w}_{i,se}^{m}\). Thus, the optimal classifier, \({g}^{m}({\varvec{x}};\beta )\) in Line 5, is
Based on \({g}^{m}({{\varvec{x}}}_{i};\beta )\), we update the probability for the SE, \({f}_{1}^{m}({{\varvec{x}}}_{i})\), in Line 6. Then, we have
Given \({f}_{1}^{m}({{\varvec{x}}}_{i})\), we run the OE iterations to update \({f}_{2}\left({{\varvec{z}}}_{i}\right)\) with the transformed response \({y}_{i,oe}^{m}\) in Line 7 and weights \({w}_{i,oe}^{m}\) in Line 8, which are defined as
and
where \({G}_{0}\left({f}_{z}\right)=-{f}_{z}+{f}_{z}\varPhi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)+\varphi \left({f}_{z}\right)\varPhi \left({f}_{x}\right),\) \({G}_{1}\left({f}_{z}\right)={f}_{z}\varPhi \left({f}_{z}\right)+\varphi \left({f}_{z}\right)\), and \({G}_{0}\left({f}_{z}\right)=-{f}_{z}+\varPhi \left({f}_{x}\right){G}_{1}\left({f}_{z}\right)\).
Like in the SE iterations, we fit a weighted least square regression of the transformed response \({y}_{i,oe}^{m}\) on \({{\varvec{z}}}_{i}\) with the weight \({w}_{i,oe}^{m}\). The optimal classifier for the OE, \({g}^{m}({{\varvec{z}}}_{i};\gamma )\) in Line 10, is
We update the probability for the OE, \({f}_{2}^{m}({{\varvec{z}}}_{i})\), in Line 6 as follows:
In Step C, after \(M\) iterations, the probability of belonging to each class can be calculated based on the fitted values of \({f}_{1}^{M}\left({{\varvec{x}}}_{i}\right)\) and \({f}_{2}^{M}\left({{\varvec{z}}}_{i}\right)\). Using these estimated final values, the final probability and the corresponding predicted class for unit \(i\) are produced.
We note that assuming \(k\ll N\) (sample size is much larger than number of variables), the overall time complexity of ZIPBoost is \(O({k}^{2}NM)\), where the bottleneck is the estimation of \({g}^{m}({{\varvec{x}}}_{i};\beta )\) and \({g}^{m}({{\varvec{z}}}_{i};\gamma )\) in Lines 5 and 9, requiring build of weighted least square regression in each iteration of Step B, where each estimation requires \(O({k}^{2}N)\) steps.
During iterations, the weights might become extremely small, especially in regions where units are perfectly classified, leading to potential computational problems. More precisely, in cases of perfect classification, in which the weights are too small (i.e., the weights are close to zero since they are bounded to zero), the denominator of the transformed response can be such a small value that the transformed response is not well defined. To avoid the numerical problems involved in defining the transformed response, we adopt a lower threshold of 2 \(\times machine-zero\) on the weights, following the work of Friedman et al. (2000). In addition, the transformed response can become extreme values, resulting in numerical instability. To be specific, the transformed responses for SE and OE in ZIPBoost can be rewritten as \({q}_{i,se}=\frac{1}{\left|{f}_{x}+\frac{\varphi \left({f}_{x}\right)}{\phi \left({f}_{x}\right)}\right|}\) and \({y}_{i,oe}=\frac{1}{\left|{f}_{z}+\frac{\varphi \left({f}_{z}\right)}{\phi \left({f}_{z}\right)}\right|}\) when \(y=1\), respectively. If \({f}_{x}\) or \({f}_{z}\) is too small, \({q}_{i,se}\) or \({y}_{i,oe}\) becomes very large. When \(y=0\), we have \({q}_{i,se}=\frac{-1}{\left|{-f}_{x}+\frac{\varphi \left({f}_{x}\right)\phi \left({f}_{z}\right)}{1-\phi \left({f}_{x}\right)\phi \left({f}_{z}\right)}\right|}\) and \({y}_{i,oe}=\frac{-1}{\left|{-f}_{z}+\frac{\varphi \left({f}_{z}\right)\phi \left({f}_{x}\right)}{1-\phi \left({f}_{x}\right)\phi \left({f}_{z}\right)}\right|}\). For a unit with large \({f}_{x}\) and \({f}_{z}\) values, \({q}_{i,se}\) and \({y}_{i,oe}\) become quite small. Therefore, we enforce the working responses to fall in the interval of \(\left[-4, 4\right]\), which was derived according to Friedman et al. (2000). This interval shows that we construct the transformed responses with a lower threshold of -4 and an upper threshold of 4.
4.2 ZILBoost
ZILBoost also proceeds with the iterations for the SE and OE sequentially, utilizing the expected negative log-likelihood, \(E\left[-l\left(f\right)|{\varvec{x}},{\varvec{z}}\right]\), where \(l\left(f\right)\) is defined as Eq. (7), serving as the objective function. The weight function operates similarly to LogitBoost: The observation weights increase for those with \({f}_{1}({\varvec{x}})\) or \({f}_{2}\left({\varvec{z}}\right)\) close to zero, whereas the weights decrease for those with \({f}_{1}({\varvec{x}})\) or \({f}_{2}\left({\varvec{z}}\right)\) far from zero.
4.2.1 Splitting equation iterations
The algorithm starts by updating \({f}_{1}\left({\varvec{x}}\right)\). The gradient of the objective function is defined as
and the Hessian is defined as
The derivation of the gradient \(D\left({f}_{x}\right)\) is provided in Appendix A.
Equation (17) indicates that when \(y=0\), \(h\left({f}_{x}\right)\) can be written as
and when \(y=1\), \(h\left({f}_{x}\right)\) can be written as
Therefore,
where \(L\left({f}_{x}\right)={\left(1+\text{exp}\left(-{f}_{x}\right)\right)}^{-3}{\left(1+\text{exp}\left(-{f}_{z}\right)\right)}^{-1}\left(\text{exp}\left(-{f}_{x}\right)-1\right)+{\left(1+\text{exp}\left(-{f}_{x}\right)\right)}^{-4}{\left(1+\text{exp}\left(-{f}_{z}\right)\right)}^{-2}\).
Since we cannot guarantee the positive definiteness of the Hessian in Eq. (19), we replace \(h\left({f}_{x}\right)\) with its absolute value in our algorithm. Based on the gradient and the modified Hessian, the Newton–Raphson method is applied to minimize the expected negative log-likelihood as follows:
where \({E}_{w}(\cdot |{\varvec{x}})\) indicates the weighted conditional expectation such that \({E}_{w}\left(g\left({\varvec{x}},y\right)|{\varvec{x}}\right)=\frac{\text{E}\left[\text{w}\left({\varvec{x}}, y\right)\text{g}\left({\varvec{x}},y\right)|{\varvec{x}}\right]}{\text{E}\left[\text{w}\left({\varvec{x}},y\right)|{\varvec{x}}\right]},\boldsymbol{ }\text{with w}\left({\varvec{x}}, y\right)>0\).
The weight function of ZILBoost, \(|h\left({f}_{x}\right)|\), is similar to that of LogitBoost in that the algorithm upweights the units that are hard to classify (i.e., the fitted values are around zero) and downweights the units that can be classified with high confidence (i.e., the fitted values are not around zero).
From Eq. (18), we can infer that the weight function with \(y=1\) is similar to the probability distribution function (PDF) of the logistic distribution with a location parameter of 0 and a scale parameter of 1. The PDF of the logistic distribution has the maximum probability at the center of 0 and is symmetric around zero. Consequently, the maximum weights will be assigned to units whose fitted values are zero.
Next, we provide the property of the weight function, \(|h\left({f}_{x}\right)|\), when \(y=0\) and \({f}_{z}\gg N\). In this case, whether a unit is misclassified depends on the value of \({f}_{x}\) because \({f}_{z}\) is greater than an arbitrarily large positive number, resulting in \({\left(1+\text{exp}\left(-{f}_{z}\right)\right)}^{-1}\) being approximately 1. Assuming this, let us rewrite the weight function as follows:
Let \(1+\text{exp}\left(-{f}_{x}\right)=K\). Then, we can rewrite Eq. (20) as
which is similar to the PDF of the logistic distribution with a location parameter of 0 and a scale parameter of 1.
In addition, we provide the property of the weight function with \(y=0\) and \({f}_{z}\ll -N\). In this case, \({f}_{x}\) does not play an important role in the classification because the negative value of \({f}_{z}\) indicates that the predicted class for a unit would be zero. This means that \({f}_{z}\) is smaller than an arbitrarily large negative number such that \({\left(1+\text{exp}\left(-{f}_{z}\right)\right)}^{-1}\approx 0\), which reduces the weight function to zero.
4.2.2 Outcome equation iterations
Next, the algorithm updates \({f}_{z}\) given the updated value of \({f}_{x}\). For updating \({f}_{z}\), the gradient of the objective function is defined as
For the derivation of the gradient \(D\left({f}_{z}\right)\), please see Appendix A.
The Hessian is defined as
According to Eq. (21), when \(y=0\), \(h\left({f}_{z}\right)\) can be rewritten as
and when \(y=1\), \(h\left({f}_{z}\right)\) can be rewritten as
Thus, the Hessian of the objective function is as follows:
where \(L\left({f}_{z}\right)={\left(1+\text{exp}\left(-{f}_{z}\right)\right)}^{-3}{\left(1+\text{exp}\left(-{f}_{x}\right)\right)}^{-1}\left(\text{exp}\left(-{f}_{z}\right)-1\right)+{\left(1+\text{exp}\left(-{f}_{z}\right)\right)}^{-4}{\left(1+\text{exp}\left(-{f}_{x}\right)\right)}^{-2}\).
As before, we use the modified Hessian, given that the Hessian in Eq. (22) is not positive definite. Based on the gradient and the modified Hessian, we apply the Newton–Raphson method to minimize the expected negative log-likelihood as follows:
where \({E}_{w}(\cdot |{\varvec{z}})\) indicates the weighted conditional expectation such that \({E}_{w}\left(g\left({\varvec{z}},\text{y}\right)|{\varvec{z}}\right)=\frac{\text{E}\left[\text{w}\left({\varvec{z}},\text{ y}\right)\text{g}\left({\varvec{z}},\text{y}\right)|{\varvec{z}}\right]}{\text{E}\left[\text{w}\left({\varvec{z}},\text{y}\right)|{\varvec{z}}\right]},\boldsymbol{ }\text{with w}\left({\varvec{z}},\text{ y}\right)>0\).
Since the Hessian serving as the weight function in Eq. (22) is akin to the one in Eq. (19) used during the SE iterations, it is easy to see that the update for \({f}_{z}\) results in increased weights for units having high classification confidence and decreased weights for those with low classification confidence.
4.2.3 Pseudo-code for ZILBoost
In this section, we summarize the ZILBoost algorithm through pseudo-code in Algorithm 2. The pseudo-code of ZILBoost is similar to that of ZIPBoost presented in Sect. 4.1.3 except the formulas for the transformed response variables, \({q}_{i,se}^{m}\) and \({y}_{i,oe}^{m}\), and the weight functions, \({w}_{i,se}^{m}\) and \({w}_{i,oe}^{m}\). For the SE iterations, the transformed response and the weight function are defined as
and
where \(L\left({f}_{i,x}^{m-1}\right)={\left(1+\text{exp}\left(-{f}_{1}^{m-1}\left({{\varvec{x}}}_{i}\right)\right)\right)}^{-3}{\left(1+\text{exp}\left(-{f}_{2}^{m-1}\left({{\varvec{z}}}_{i}\right)\right)\right)}^{-1}\left(\text{exp}\left(-{f}_{1}^{m-1}\left({{\varvec{x}}}_{i}\right)\right)-1\right)+{\left(1+\text{exp}\left(-{f}_{1}^{m-1}\left({{\varvec{x}}}_{i}\right)\right)\right)}^{-4}{\left(1+\text{exp}\left(-{f}_{2}^{m-1}\left({{\varvec{z}}}_{i}\right)\right)\right)}^{-2}\). Using \({q}_{i,se}^{m}\) and \({w}_{i,se}^{m}\), we obtain the optimal classifier by fitting a weighted least square regression such that
For the OE iterations, the algorithm uses the following transformed response and the weight function:
and
where \(L\left({f}_{i,z}^{m-1}\right)={\left(1+\text{exp}\left(-{f}_{2}^{m-1}\left({{\varvec{z}}}_{i}\right)\right)\right)}^{-3}{\left(1+\text{exp}\left(-{f}_{1}^{m}\left({{\varvec{x}}}_{i}\right)\right)\right)}^{-1}\left(\text{exp}\left(-{f}_{2}^{m-1}\left({{\varvec{z}}}_{i}\right)\right)-1\right)+{\left(1+\text{exp}\left(-{f}_{2}^{m-1}\left({{\varvec{z}}}_{i}\right)\right)\right)}^{-4}{\left(1+\text{exp}\left(-{f}_{1}^{m}\left({{\varvec{x}}}_{i}\right)\right)\right)}^{-2}\). Like in the OE, we fit a weighted least square regression to obtain the optimal classifier as
After \(M\) iterations, using \({f}_{1}^{M}\left({{\varvec{x}}}_{i}\right)\) and \({f}_{2}^{M}\left({{\varvec{z}}}_{i}\right)\), the probabilities of belonging to each class can be calculated, and the corresponding predicted class for unit \(i\) is determined.
Similar to ZIPBoost, assuming \(k\ll N\) (the sample size is much larger than the number of variables), the overall time complexity of ZILBoost is \(O({k}^{2}NM)\).
Similar to ZIPBoost, we set a lower threshold of the weights as 2 \(\times machine-zero\). Furthermore, the transformed responses for SE and OE in ZILBoost can be defined as \({q}_{i,se}=1+\text{exp}(-{f}_{x})\) and \({y}_{i,oe}=1+\text{exp}(-{f}_{z})\) when \(y=1\). In this case, they become very large values with a small value \({f}_{x}\) or \({f}_{z}\). For \(y=0\), \({q}_{i,se}=-\left(1+\text{exp}\left(-{f}_{x}\right)\right)\left(1-{\left(1+\text{exp}\left(-{f}_{x}\right)\right)}^{-1}{\left(1+\text{exp}\left(-{f}_{x}\right)\right)}^{-1}\right)/\left|-1+\text{exp}\left(-{f}_{x}\right)+{\left(1+\text{exp}\left(-{f}_{x}\right)\right)}^{-1}{\left(1+\text{exp}\left(-{f}_{z}\right)\right)}^{-1}\right|\) and \({y}_{i,oe}=-\left(1+\text{exp}\left(-{f}_{z}\right)\right)\left(1-{\left(1+\text{exp}\left(-{f}_{z}\right)\right)}^{-1}{\left(1+\text{exp}\left(-{f}_{x}\right)\right)}^{-1}\right)/|-1+\text{exp}\left(-{f}_{z}\right)+{\left(1+\text{exp}\left(-{f}_{z}\right)\right)}^{-1}{\left(1+\text{exp}\left(-{f}_{x}\right)\right)}^{-1}|\) so that the transformed responses can be extremely small while having large values of \({f}_{x}\) and \({f}_{z}\). Thus, to maintain numerical stability, we limit the range of the working responses to \(\left[-4, 4\right]\).
4.3 Convergence of proposed methods
ZIPBoost and ZILBoost follow the modified Newton method, \({f}_{x}^{m+1}={f}_{x}^{m}-\frac{D\left({f}_{x}^{m}\right)}{\left|H\left({f}_{x}^{m}\right)\right|}\) for SE and \({f}_{z}^{m+1}={f}_{z}^{m}-\frac{D\left({f}_{z}^{m}\right)}{\left|H\left({f}_{z}^{m}\right)\right|}\) for OE, where \(D\left({f}_{x}^{m}\right)=\frac{\partial E[-l(f)|{\varvec{x}}] }{\partial {f}_{x}}\), \(H\left({f}_{x}^{m}\right)=\frac{\partial }{\partial {f}_{x}}\left[\frac{\partial E[-l(f)|{\varvec{x}}] }{\partial {f}_{x}}\right]\), \(D\left({f}_{z}^{m}\right)=\frac{\partial E[-l(f)|{\varvec{z}}] }{\partial {f}_{z}}\), and \(H\left({f}_{z}^{m}\right)=\frac{\partial }{\partial {f}_{z}}\left[\frac{\partial E[-l(f)|{\varvec{z}}] }{\partial {f}_{z}}\right]\). Here, we show the convergence of the proposed methods to a local minimum. As the iterations for the splitting equation and OE in the proposed methods rely on the same updated scheme, we provide only the convergence for the spitting equation iteration, \({f}_{x}^{m}\), because the convergence for the OE iteration is similar.
Let us define a function \(g\left({f}_{x}^{m}\right)={f}_{x}^{m}-\frac{D\left({f}_{x}^{m}\right)}{\left|H\left({f}_{x}^{m}\right)\right|}\) to have \({f}_{x}^{m+1}=g\left({x}_{k}\right)\). For the convergence, we use the fact that \(g\left({f}_{x}^{m}\right)\) is a contraction in a neighborhood of a local minimum. We define a contraction in Definition 1.
Definition 1
A function \(g(x)\) is called a contraction in the interval \([a,b]\) if there exists a number \(L\in [\text{0,1})\) such that
for any \(x,y\in [a,b]\).
However, in our setting, it is challenging to apply Definition 1 directly to prove that \(g\left({f}_{x}^{m}\right)\) is a contraction. Thus, we rely on Theorem 1, which is equivalent to Definition 1 (For more details, please see Babajee & Dauhoo, 2006).
Theorem 1
(Babajee & Dauhoo, 2006). If \(g\) is differentiable and a number \(L\in [\text{0,1})\) exists such that \(\left|{g}{\prime}\left(x\right)\right|\le L\) for all \(x\in [a,b]\), then \(g\) is a contraction on \([a,b]\).
Proof
Let \(x,y\in [a,b]\) and assume \(x<y\). According to the mean value theorem, we have \(\frac{g\left(x\right)-g\left(y\right)}{x-y}={g}{\prime}(c)\) for some \(c\in (x,y)\). If \(\left|{g}{\prime}\left(x\right)\right|\le L \text{for all }x\in [a,b]\), then \(\left|{g}{\prime}\left(c\right)\right|\le L\).
Therefore, we have \(\left|\frac{g\left(x\right)-g\left(y\right)}{x-y}\right|\le L\), and equivalently, \(\left|g\left(x\right)-g\left(y\right)\right|\le L(x-y)\), which is the definition of the contraction. □
Based on Theorem 1, we now show that the iteration \(g({f}_{x}^{m})\) converges to a local minimum by following Süli and Mayers (2003, Theorem 1.5).
Theorem 2
Let \({f}_{x}^{*}\) be the actual solution of \(D\left({f}_{x}^{*}\right)=0\), and assume \(\left|{f}_{x}^{0}-{f}_{x}^{*}\right|<\delta \), where \({f}_{x}^{0}\) is an initial guess and \(\delta \) is an arbitrary positive number. If \(g\left({f}_{x}^{m}\right)\) is a contraction on \(\left({f}_{x}^{*}-\delta , {f}_{x}^{*}+\delta \right)\), the iteration converges to \({f}_{x}^{*}\).
Proof
Let us assume there exists a solution \({f}_{x}^{*}\) satisfying the following three conditions: (i) \({\left.\frac{\partial E[-l(f)|{\varvec{x}}] }{\partial {f}_{x}}\right|}_{{f}_{x}={f}_{x}^{*}} =D\left({f}_{x}^{*} \right)=0\), (ii) \({\left.\frac{{\partial }^{2}E[-l(f)|{\varvec{x}}] }{{\partial }^{2}{f}_{x}}\right|}_{{f}_{x}={f}_{x}^{*}}=H\left({f}_{x}^{*}\right)>0\), (iii) \(\frac{{\partial }^{3}E[-l(f)|{\varvec{x}}] }{{\partial }^{3}{f}_{x}}\) is bounded near \(\overline{x }\). We also assume that an initial guess \({f}_{x}^{0}\) is sufficiently close to the solution \({f}_{x}^{*}\) satisfying \(\left|{f}_{x}^{0}-{f}_{x}^{*}\right|<\delta \). We note that the standard Newton method also requires this assumption for convergence (Casella & Bachmann, 2021).
First, we show \(g({f}_{x}^{m})\) is a contraction using Theorem 1. We know that \(g({f}_{x}^{m})\) is differentiable since the third-order derivatives can be defined.Footnote 1 Then, there exists a number \(L\in [\text{0,1})\) such that \(\left|{g}{\prime}\left({f}_{x}^{m}\right)\right|\le L\) for all \({f}_{x}\in [{f}_{x}^{*}-\delta , {f}_{x}^{*}+\delta ]\). With \({g}{\prime}\left({f}_{x}^{m}\right)=1-\frac{H\left({f}_{x}^{m}\right)}{\left|H\left({f}_{x}^{m}\right)\right|}+\frac{D\left({f}_{x}^{m} \right)\frac{H\left({f}_{x}^{m}\right)}{\left|H\left({f}_{x}^{m}\right)\right|}{\left. \frac{{\partial }^{3}E[-l(f)|{\varvec{x}}] }{{\partial }^{3}{f}_{x}}\right|}_{{f}_{x}={f}_{x}^{m}}}{{\left(\left|H\left({f}_{x}^{m}\right)\right|\right)}^{2}}\), we can show \(\underset{{f}_{x}\to {f}_{x}^{*}}{\text{lim}}{g}{\prime}\left({f}_{x}^{m}\right)=0\), since the first and second terms converge to 1 and 0, respectively, because \(D\left({f}_{x}^{*} \right)=0\) and \(H\left({f}_{x}^{*}\right)>0\). This result implies that \({g}{\prime}\left({f}_{x}^{m}\right)\) is near zero for \({f}_{x}\) around \({f}_{x}^{*}\), and there exists an interval \([{f}_{x}^{*}-\delta , {f}_{x}^{*}+\delta ]\) where \(\left|{g}{\prime}\left({f}_{x}^{m}\right)\right|<L<1\) for all \({f}_{x}\in [{f}_{x}^{*}-\delta , {f}_{x}^{*}+\delta ]\). This means that the assumptions of Theorem 1 hold, and hence, we conclude that \(g({f}_{x}^{m})\) is a contraction on \([{f}_{x}^{*}-\delta , {f}_{x}^{*}+\delta ]\).
Next, we show that the iteration \(g({f}_{x}^{m})\) converges to \({f}_{x}^{*}\). For \({f}_{x}^{*}\), we have \(g\left({f}_{x}^{*}\right)={f}_{x}^{*}-\frac{D\left({f}_{x}^{*}\right)}{\left|H\left({f}_{x}^{*}\right)\right|}={f}_{x}^{*}\) since \(D\left({f}_{x}^{*}\right)=0\) and \(H\left({f}_{x}^{*}\right)>0\). Thus,
Since \(L<1\), we have \(\underset{m\to \infty }{\text{lim}}\left|{f}_{x}^{m}-{f}_{x}^{*}\right|=0\), implying that \({f}_{x}^{m}\to {f}_{x}^{*}\). Therefore, the iteration by the modified Newton method leads to convergence to \({f}_{x}^{*}\). □
5 Computational experiment
In this section, we show that our proposed methods outperform other boosting methods, such as AdaBoost, LogitBoost, ProbitBoost, AdaC2, SMOTEBoost, and GANs, using a Monte Carlo Simulation, a real data application for predicting M&A outcomes, and imbalanced datasets from the Keel repository. We implemented all algorithms in R (version 4.2.2) on a Mac-OS system with M1 and 16 GB RAM.
5.1 Monte Carlo simulation
We simulate hypothetical data with the zero-inflated case to demonstrate the performance of ZIPBoost and ZILBoost. We include AdaBoost (Freund & Schapire, 1996), LogitBoost (Friedman et al., 2000), ProbitBoost (Zheng & Liu, 2012), AdaC2 (Sun et al., 2007), SMOTEBoost (Chawla et al., 2003), and GANs (Goodfellow et al., 2014) as benchmark models. AdaBoost, LogitBoost, and ProbitBoost update classifiers based on prediction error without accounting for class imbalance. AdaC2 is a variant of AdaBoost with unequal misclassification costs for majority and minority classes. In addition to AdaC2, several other cost-sensitive learning algorithms based on AdaBoost have been proposed, such as AdaCost, AdaC1, and AdaC3. However, this simulation study considers only AdaC2 as one of the benchmark models since previous research shows that AdaC2 outperforms other modifications of AdaBoost (e.g., Sun et al., 2007; Yin et al., 2013). Since AdaC2 embeds unequal misclassification costs for each class in a cost matrix, we select costs that maximize the F-scoreFootnote 2 in the training data following Sun et al. (2007). Meanwhile, SMOTEBoost, a combination of SMOTE (an oversampling method) and boosting, requires the oversampling rate, which is the ratio of the number of synthetic minority examples to that of the original minority examples (Gao et al., 2014), and the number of nearest neighbors. Based on prior studies (e.g., Wei et al., 2021), we set the oversampling rate to the rounded-down value of the imbalance ratio (IR)—that is, the ratio of the number of the majority examples to that of the minority examples. Along with the oversampling rate, the synthetic examples were generated based on the five nearest neighbors. To train weak learners with the synthetic examples, we experimented with various learning algorithms, including classification and regression tree (CART), C.50 Decision Tree (DT), Random Forest (RF), Naïve Bayes (NB), and SVM. We also considered combinations of GANs and learning algorithms as benchmarks. Specifically, we trained the GANs to generate synthetic examples and, thus, balance distributions across the two classes. We applied learning algorithms, including the generalized boost method (GBM), logit, DT, RF, and SVM, for classification after adding the synthetic examples to the dataset.
We generated the dataset 1,000 times following the data-generating process (DGP):
For \(i\in \{1,\dots , 1000\}\),
We examined the performance under various proportions of the minority class in the data, which are 5%, 10%, 20%, 30%, and 40%, by adjusting the parameter values. Specifically, we set \({\beta }_{1}\), \({\beta }_{2},{\beta }_{3}, {\gamma }_{1},{\gamma }_{2},\) and \({\gamma }_{3}\) to 0.5, –3.5, –1.5, –2, 1.5, and 0.5, respectively, across all cases. In addition, we adjusted the values of \({\beta }_{0}\) and \({\gamma }_{0}\) to change the proportions of the minority class: \(\left({\beta }_{0},{\gamma }_{0}\right)=(-5,-5)\) for the 5% minority examples, \(\left({\beta }_{0},{\gamma }_{0}\right)=(-3,-2.5)\) for the 10% minority examples, \(\left({\beta }_{0},{\gamma }_{0}\right)=(-1.5, 0.1)\) for the 20% minority examples, \(\left({\beta }_{0},{\gamma }_{0}\right)=(\text{0,1}.5)\) for the 30% minority examples, and \(\left({\beta }_{0},{\gamma }_{0}\right)=(2, 2.5)\) for the 40% minority examples. In addition, \({x}_{i1},{x}_{i2}\), \({x}_{i3}, {z}_{i1},{z}_{i2},\) and \({z}_{i3}\) are iid with \(N\left(\text{0,2}\right)\), and \({u}_{i}\) and \({\varepsilon }_{i}\) are iid with \(N\left(\text{0,1}\right).\) The observed outcome \({y}_{i}\) is determined as
We considered a zero outcome as the majority class. To assess the predictive performance of our proposed methods against other benchmark methods, we used the first 500 observations as the training set and the remaining 500 observations as the test set. The predictive performance was measured by F-scores and Matthews correlation coefficient (MCC) in the training and test data. The F-score is widely considered an appropriate measure for handling imbalance problems since it does not rely on the true negative rate (Waegeman et al., 2014). While prioritizing accurate predictions for the minority class, we aimed to maintain precision in the majority class. Therefore, we used the F-scores measured in both the minority class and the majority class. For instance, the F-score measured in the minority class indicates that the minority class is considered the positive class so that the proportion of correctly classified majority examples does not affect the F-score. To examine the average performance over all classes, we considered a macro F-score that averages the F-scores measured in each class. All the F-scores range from 0 to 1, with a higher value indicating better accuracy.
In addition to the F-scores, we evaluated the classification performance using MCC. Since the MCC is calculated based on all the information in the confusion matrix, it has been regarded as a summary of a model’s predictive performance and is thus widely used in the presence of class imbalance (Boughorbel et al., 2017). The MCC can take a value from –1 to 1, implying that with the correct classification for all examples, the value of the MCC is equal to 1, while a value below zero indicates that the classifier performs worse than a random classifier.
Regarding predictors, our proposed approaches considered \({x}_{1},{x}_{2}\), and \({x}_{3}\) for the SE iterations and \({z}_{1},{z}_{2},\) and \({z}_{3}\) for the OE iterations, assuming that \({x}_{1},{x}_{2}\), and \({x}_{3}\) are predictors that may generate the inflated zeros in regime 0, and \({z}_{1},{z}_{2},\) and \({z}_{3}\) predict the minority class in regime 1. Other benchmark models utilized all predictors, \({x}_{1},{x}_{2}\), \({x}_{3}, {z}_{1},{z}_{2},\) and \({z}_{3}\), to construct the final classifiers.
We first illustrate the performance of ZIPBoost and ZILBoost over several iterations in Fig. 2. To this end, we provide the F-scores measured on each class and the macro F-score at each number of iterations. Notably, ZIPBoost and ZILBoost provided rapid convergence, attributed to the sequential application of the Newton–Raphson method to update the probability function of the SE and OE.
We note that early stopping conditions can be added to the algorithms of the proposed methods. Notably, the proposed methods show the rapid convergence, which is the advantage of the Newton method (Rohde & Wand, 2016). Given this quick convergence of the proposed methods, an extensive number of iterations may be unnecessary. Thus, in practice, an early stopping condition can be integrated into the algorithms of the proposed methods in many ways. First, one of the possible conditions is to stop iterations when all gradients for SE and OE reach zero, because a zero gradient indicates that no further improvement is possible (London et al., 2023). Second, early stopping can also be done using a validation set (Drucker, 2002). Generally, algorithms aim for optimal performance on unseen data. Thus, we can choose a subsample from the training data for a validation set and limit the iteration to a point where the predictive performance of the algorithm hits its maximum or its error rate approaches a minimum on the validation set.
The results of the simulation using the test data are presented in Table 1. To save space, we reported the performance of the proposed methods on the training data and training time in Appendix C1. The number of iterations for each boosting method was set to 100. Across all datasets, our algorithms returned the final classifier within 1 s, similar to AdaBoost, LogitBoost, and ProbitBoost, regardless of the proportions of the minority class. Using AdaC2, we did not find large differences in training time across the proportions of the minority class. It required about 7–8 s to generate the final classifier, starting with a cost matrix search. The training time of SMOTEBoost varied based on the learning algorithms and the proportions of the minority examples. When synthetic examples were generated from the 10% minority examples and CART was used to construct the classifier from augmented data, the final classifier was provided within 2 s. However, the training time of SMOTEBoost-SVM exceeded 14 s when the size of the minority class comprised 30% of the dataset. GANs required the longest training time, ranging from about 6–29 s in most cases, except when synthetic examples were generated from the 20% minority examples.
In terms of predictive performance, we found that the prediction accuracy for the minority class from most of the models improved with an increase in the proportion of the minority class. AdaBoost, SMOTEBoost-C.50, and SMOTEBoost-RF achieved perfect classifications in the training data, regardless of the proportions of the minority class. AdaC2 resulted in perfect classifications when the proportion of the minority class was less than or equal to 20%. SMOTEBoost-SVM achieved a macro F-score of 1 and an MCC of 1 when the size of the minority class was extremely small (i.e., 5% minority examples), whereas GANs-RF produced zero classification error when the number of minority examples was greater than or equal to 20% of the dataset. ZIPBoost and ZILBoost showed moderate performance across all proportions of the minority examples.
Using the test data, our proposed methods showed superior predictive performance compared to the benchmark models for both classes. The proposed methods produced maximum F-scores for both classes and the macro F-score and MCC across all cases. We also found that the performance of the two proposed methods was similar. This may be due to the fact that the data-generating process for the OE follows a normal distribution with zero excess kurtosis. For more details, see Appendix D, where we discuss the relative performance of ZIPBoost and ZILBoost depending on the excess kurtosis of the OE data-generating process. The results indicate that our proposed methods improved the accuracy of predicting the minority class without significant sacrifice in predicting the majority class, in comparison to the benchmark models. Even the benchmark models that achieved perfect classifications on the training data exhibited less accuracy than the proposed methods in terms of the macro F-score and MCC.
Classifiers built using conventional boosting methods are trained to minimize overall misclassification error at the expense of neglecting the minority class (Song et al., 2011; Sun et al., 2007). AdaC2 also requires obtaining a cost matrix based on an F-score from the training data without considering the inherent class imbalance, which may result in overfitting. Furthermore, oversampling methods, including SMOTE and GANs, may not be optimal for handling imbalance problems in the presence of two distinct DGPs. SMOTE is vulnerable to disjoint data distributions (Koziarski, 2020), which the two-regime process may cause, and GANs can fail to learn the true distribution of the minority class (Yang & Zhou, 2021), which results in synthetic examples that inadequately represent the minority class.
Therefore, our proposed methods outperform the benchmark methods because the benchmark methods do not reflect the existence of the two-regime process that causes the excess zeros.
5.2 M&A data
We examine the performance of ZIPBoost and ZILBoost using real data to predict M&A outcomes. Notably, most M&A deals end up being successful, making failures relatively rare occurrences. Nevertheless, the misclassification of the failures can induce substantial costs because it may be accompanied by missed opportunities to look for other potential deals (Lee et al., 2020).
We considered M&A deals spanning from 2009 to 2014. The information on M&A deals was collected from the Securities Data Company’s (SDC) U.S. Mergers and Acquisitions database and coupled with financial data from Compustat. To construct the final sample, we started by retaining the first takeover announcement during the sample period. We also excluded cases in which the acquirer and target firm tickers were identical. Since Compustat provides financial information for public firms, being matched with Compustat lets us restrict our sample to the takeover whose acquirer and target firm were both publicly held. Finally, we included only deals with a completed or withdrawn status. The final sample consists of 411 completed deals and 56 withdrawn takeover deals.
In this application, the target variable is whether a takeover was completed successfully or withdrawn. We assign values of zero and one to represent successful and withdrawn takeovers, respectively, and this leads to a zero-inflated case in which approximately 86% of the sample has zero outcomes. Notably, based on the previous study (Lee et al., 2020), we assumed that the completion of takeovers may be caused by either deals’ characteristics or financial characteristics of the acquirer or target firm. More specifically, some takeovers may be completed mainly due to deal characteristics, whereas others were completed based on financial characteristics, without deal characteristics forcing the decision. For example, the presence of a termination fee may lead to the completion of a takeover (Butler & Sauska, 2014). On the other hand, without such a termination fee, the decision to complete the deal may hinge on the financial performance of the acquirer or target firm, possibly leading to deal withdrawal. Thus, we included two types of predictors: (1) M&A-related predictors to account for successfully completed cases (zeros; majority class) and (2) financial performance-related predictors to account for withdrawn cases (ones; minority class).
The majority of completed cases (SE) are likely to be driven by factors associated with M&A-related predictors based on the literature review (Bugeja, 2005; Gao et al., 2021; Renneboog & Vansteenkiste, 2019; Renneboog & Zhao, 2014; Stahl et al., 2012). More specifically, hostile deals may face resistance from target firms (Renneboog & Zhao, 2014; Stahl et al., 2012), making nonhostile deals more likely to succeed. Tender offers also convey confidence in the deal (Renneboog & Vansteenkiste, 2019). We considered additional factors that can affect the probability of completing a deal, such as its relative, which indicates the risk to which an acquirer and target firm can be exposed (Gao et al., 2021), and an increase in the target firm’s share price prior to a merger announcement, which reduces the probability of bid competition and price revision (Bugeja, 2005). Thus, \({q}^{*}\) is likely to be related to the presence of a termination fee, a termination fee imposed on the acquirer, a termination fee imposed on the target firm, a hostile deal, a tender offer, and relative deal size (i.e., deal size related to the size of the acquirer) and the target firm’s share price one day prior to the announcement. In mathematical notation, for each M&A deal \(i\), we assumed the following data-generating process for SE:
where \({\text{fee}}_{i}\) indicates a dummy variable for the presence of a termination fee, \({\text{fee}}_{\text{acq},i}\) is a termination fee imposed on the acquirer, \({\text{fee}}_{\text{target},i}\) is a termination fee imposed on the target firm, \({\text{hostile}}_{i}\) indicates hostile deals, \({\text{tender}}_{i}\) indicates tender offers, \({\text{dealsize}}_{i}\) represents relative deal size, \({\text{share}}_{i}\) indicates the target firm’s share price one day prior to the announcement, and \({u}_{i}\) is random error.
Regarding the withdrawn cases (OE) conditional on M&A-related predictors, the existing literature typically focuses on financial predictors (Baker & Wurgler, 2006; Rodrigues & Stevenson, 2013). We used financial characteristics of the acquirer and target firms, such as dividend per share, the ratio of inventory to total assets, the market-to-book ratio, the price-to-earnings ratio, the growth rate in sales over the past year, the ratio of capital expenditure to operating revenue, invested capital turnover, dividend yield, and the logarithm of total assets. Following Lee et al. (2020), we used the difference in financial performance between the acquirer and the target firm to measure the dyadic relationship between them, since the extent of this difference can be used to predict the completion of deals. More precisely, the purpose of M&As between two firms (i.e., acquirers and target firms) is to strategically combine their resources. Such interfirm relationships require firms to get better at identifying the potential sources of dyadic conflict that arise during M&A negotiations (Lee et al., 2020). This implies that evaluating these dyadic conflicts is important when assessing why two firms engaged in a takeover process, which could be either completed or withdrawn. Thus, \({\widetilde{{y}_{i}}}^{*}\) is likely to be associated with dividend, the ratio of inventory to total assets, the market-to-book ratio, the price-to-earnings ratio, the growth rate in sales, the ratio of capital expenditure to operating revenue, capital turnover, dividend yield, and total assets. In mathematical notation, for each M&A deal \(i\), we assumed the following data-generating process for OE:
where \({\text{dividend}}_{i}\) indicates dividend per share, \({\text{inventory}}_{i}/{\text{assets}}_{i}\) indicates the ratio of inventory to total assets, \(\text{M}/\text{B} {\text{ratio}}_{i}\) represents the market-to-book ratio, \(\text{P}/\text{E} {\text{ratio}}_{i}\) represents the price-to-earnings ratio, \({\text{growth}}_{i}\) indicates the growth rate in sales over the past year, \({\text{expenditure}}_{i}/{\text{revenue}}_{i}\) indicates the ratio of capital expenditure to operating revenue, \(\text{capital} {\text{turnover}}_{i}\) indicates invested capital turnover, \({\text{yield}}_{i}\) represents dividend yield, \(\text{log}\left({\text{assets}}_{i}\right)\) indicates the log of total assets, and \({\varepsilon }_{i}\) is random error. Based on \({q}_{i}^{*}\) and \({\widetilde{{y}_{i}}}^{*}\), the outcome of deal \(i\), \({y}_{i}\), is determined as
To demonstrate the predictive performance of our proposed approaches, we used the examples from 2009 to 2012 as the training set (314 deals: 273 completed and 41 withdrawn) and the examples from 2013 and 2014 as the test set (153 deals: 138 completed and 15 withdrawn). The goal of this application was to predict the outcomes of M&A deals in 2013 and 2014. As in the simulation study, we considered the following benchmark models: AdaBoost, LogitBoost, ProbitBoost, AdaC2, SMOTEBoost, and GANs. We also considered different learning algorithms to build classifiers using SMOTEBoost and GANs. For AdaC2, we derived the cost matrix based on the F-score. For SMOTEBoost, the oversampling rate was fixed to 500, which is a rounded-down value of the IR in the training data, with five nearest neighbors. To train GANs, we used a batch size of 20 since we had only 41 withdrawn cases in the training set. In terms of predictors, the benchmark models used all M&A- and financial-related variables.
The results of this application are presented in Table 2. Using the training data, we computed the training times: 0.551 s for AdaBoost, 0.049 s for LogitBoost, 0.101 s for ProbitBoost, 6.845 s for AdaC2, 3.723 s for SMOTEBoost-C.50, 7.987 s for GANs-GBM, 0.216 s for ZIPBoost, 0.199 s for ZILBoost, 1.970 s for SMOTEBoost-CART, 3.025 s for SMOTEBoost-RT, 4.087 s for SMOTEBoost-NB, 3.226 s for SMOTEBoost-SVM, 3.410 s for GANs-Logit, 3.413 s for GANs-DT, 4.058 s for GANs-RF, and 3.406 s for GANs-SVM. Notably, the proposed methods produced a final classifier within 1 s.
For brevity, we present results for the test data only. The findings revealed that ZIPBoost performed best in terms of prediction accuracy for the minority class (i.e., failure of M&A deals) and average performance across both classes. It had the highest F-score of 0.619, along with a macro F-score of 0.779 and an MCC of 0.597. ZILBoost’s predictive performance was moderate, yielding a macro F-score of 0.724 and an MCC of 0.482. Since ZIPBoost relies on the probit model, distributions that favor the probit may lead to better performance of ZIPBoost than ZILBoost. By contrast, for distributions favoring the logit, ZILBoost, based on the logit model, may outperform ZIPBoost.
As detailed in Appendix D1, the OE data-generating process determines the performance of the proposed algorithms. When the OE data-generating process is based on positive excess kurtosis (i.e., leptokurtic—sharply peaked with heavy tails), ZILBoost performs better than ZIPBoost. Conversely, when this process is based on negative excess kurtosis (i.e., platykurtic—the curve has a flat peak and more dispersed values with lighter tails), ZIPBoost exhibits superior performance to ZILBoost. Thus, we can infer that M&A data may be generated by a platykurtic distribution, which is flatter than a normal distribution with fewer values in the tails.
It is also worth mentioning that GANs, a recently adopted method for tackling the imbalance problem, performed better than all other benchmark models. When a decision tree was employed to construct the classifier, GANs provided the second-highest macro F-score (0.761) and MCC (0.553). Moreover, GANs with SVM had the highest F-scores measured in the majority class. Nevertheless, of the systematic approaches, ZIPBoost was the best predictor of M&A deal failure without losing predictive accuracy for successful deals compared to the benchmark models.
As a robustness check, we motivate the adopted predictor splitting (in SE and OE) and evaluate the effect of this predictor split (and its possible variants) on the performance of the proposed algorithms. The performance distributions of predictors splitting rules are shown in Fig. 3. The performance distributions were evaluated on the basis of their macro F-scores. In this figure, each box represents the minimum (bottom whisker), the 25th percentile (box base), the median (bold line), the 75th percentile (box top), the maximum (top whisker), and outliers (dots located outside the whisker). The red dashed line in each part of the figure indicates the performance-adopted predictors (before predictor splitting) based on the literature review.
In Experiment 1, we examined various splits in question by relocating predictors adopted for SE into OE. The number of predictors in OE ranged from 10 to 15. For instance, we started with splits involving 1 predictor moving from SE to OE, resulting in 10 predictors in OE. To this end, we had 7 candidate predictors for splits. When 2 predictors in SE were added to OE, resulting in 11 predictors in OE, we considered 21 candidate predictors for splits. For each split candidate, we obtained a macro F-score produced by ZIPBoost only, as it showed better predictive performance than ZILBoost for the adopted predictor splitting. We grouped the candidates based on the number of predictors in OE and plotted their distributions of macro F-scores in Fig. 3a. Notably, we did not report cases with more than 14 predictors in OE, as they predicted all examples as the majority class, making it impossible to obtain a macro F score. We also did not consider cases in which all predictors were contained in either SE or OE.
In Experiment 2, we examined all possible candidates for splits that had predictors related to OE in SE. Similar to Experiment 1, we allowed SE to have a varying number of predictors (8–15). Starting with 9 candidates where one predictor in OE was shifted to SE, we obtained macro F-scores produced by ZIPBoost for each candidate. We repeated this process until 8 out of 9 predictors in OE were contained in SE. The distributions of macro F-scores by the number of predictors in SE are shown in Fig. 3b. As in Experiment 1, we excluded splits where all predictors were in one of SE or OE.
In Fig. 3a, the results of Experiment 1 show that all boxplots are below the red dashed line. This means that the adopted predictor splitting (based on the literature review) outperforms all possible splitting cases. Unlike Experiment 1, Experiment 2 shows that when the number of predictors in SE is between 9 and 13, the top whisker of the boxplots is above the red dashed line. This suggests that, in some cases, variant splitting performs better than the adopted predictor splitting using prior knowledge. However, the medians (or 75th percentile) in all cases remain below the red dashed line. Thus, we found that a systematic approach leveraging prior knowledge about predictor splitting can significantly improve imbalanced learning.
5.3 Keel repository
As previously mentioned, the proposed methods require prior information about the data-generating processes for SE and OE. However, prior knowledge is not always available in practice. In such cases, researchers can turn to data-driven approaches to identify optimal predictor splits. We show the effectiveness of the proposed methods in terms of predictive performance with data-driven predictor splits using 36 imbalanced datasets from the Keel repository; please see the following link: https://sci2s.ugr.es/keel/imbalanced.php. We considered datasets with an IR between 1.5 and 9 (Fernández et al., 2008) and the first part of the datasets whose IR is higher than 9 (Fernández et al., 2008, 2009). Notably, to reduce complexity, we focused on the datasets with fewer than 9 predictors. A summary of the datasets is provided in Table 3.
Each dataset was randomly split into 50% training and 50% test sets. In this experiment, we did not consider the selection of predictors for simplicity purposes, implying that all predictors in each dataset were used. Notably, for the proposed methods, we relied on the split of predictors for SE and OE using the training set, aiming to maximize the macro F-score among the possible splits since the DGP in most datasets was unknown. For \(k\) predictors, we examine \({2}^{k}-2\) possible splits. We did not consider splits where all predictors belonged to either OE or SE. More precisely, we measured the macro F-score using the training set for each candidate for the splits, and the optimal split was identified based on the highest macro F-score. In addition, we generated synthetic examples for SMOTE and GANs to balance the number of examples between the majority and minority classes.
We obtained the macro F-score for each model on each test set to compare the proposed methods with other benchmark models. The results of our experiments are summarized in Fig. 4. The bars show the number of datasets in which a particular model outperformed others in the macro F-score (i.e., the number of outperformed cases). We defined outperformance as the algorithm achieving the highest macro F-score for a given data set. It is important to note that some models failed to generate final classifiers for certain datasets that lack predictor variation. More precisely, in ecoli1, ecoli2, ecoli-0_vs_1, ecoli-0-1-3-7_vs_2-6, ecoli4, and yeast-2_vs_4 datasets, classifiers were not defined from LogitBoost, ProbitBoost, ZILBoost, ZIPBoost, and GANs-SVM. In addition, SMOTEBoost-NB failed to provide predictions for the ecoli-0-1-3-7_vs_2-6 data. In these cases, we were not able to calculate F-scores. Thus, we excluded models that failed to generate final classifiers from empirical evaluations. For more details, see Appendix E1. In the table, “N.A.” indicates cases in which the model failed to produce the final classifier.
Results of the experiments. SMOTEB-c50, SMOTEB-RF, SMOTEB-NB, GANs-RF, SMOTEB-CART, SMOTEB-SVM, GANs-DT, GANs-SVM, GANs-Logit, and GANs-GBM refer to SMOTEBoost with C.50 Decision Tree (DT), SMOTEBoost with Random Forest (RF), SMOTEBoost with Naïve Bayes (NB), GANs with Random Forest (RF), SMOTEBoost with classification and regression tree (CART), SMOTEBoost with Support Vector Machine (SVM), GANs with DT, GANs with SVM, GANs with logit, and GANs with the generalized boost method, respectively
In Fig. 4, the total number of outperformed cases across the models is greater than 36, the number of datasets we used for this experiment. This is because in some datasets, more than one model had the maximum F-score. For example, in the new-thyroid2 data, ZIPBoost, ZILBoost, AdaBoost, AdaC2, SMOTEBoost-SVM, GANs-RF, and GANs-SVM produced the maximum F score of 0.984. In such cases, we considered it an outperformed case for all models with the maximum F score.
The dark gray bars represent the proposed methods, ZIPBoost and ZILBoost, while the light gray bars indicate the benchmark models. We arranged the bars from the highest to the lowest number of outperformed cases. Figure 4 shows that ZIPBoost achieved the best predictive performance in 12 out of 36 datasets, while ZILBoost produced the best performance in 8 out of 36 datasets, similar to SMOTEBoost-C.50, which outperformed all other benchmark models. These results show the effectiveness of the proposed methods compared to other benchmark models in handling imbalanced data.
6 Conclusions and future work
The learning problems of imbalanced data have been widely discussed in the machine learning community because standard learning algorithms pay less attention to classifying the minority class in such datasets. With the present study, we hope to contribute to this community by proposing a systematic approach to learning imbalanced data.
In contrast to existing studies, the proposed approach described in this paper assumes the existence of two distinct regimes (two-regime process). Regime 0 identifies the inflated zeros, and regime 1 identifies the minority class. More specifically, our model generates two models (regimes). First, a probit (or logit) model is generated for the excessive zero examples, which is identified as regime 0 for the majority class. Then, another probit (or logit) model is generated for the underrepresented examples, which is identified as regime 1 for the minority class. Notably, each of the two models may use a different set of predictors. Thus, our model embraces two distinct regimes that describe majority and minority classes, allowing us to flexibly account for the DGP of the imbalance class.
Because boosting is known for its enhanced accuracy compared to single classifiers, we integrated incremental learning rules into the framework for the proposed approach. More specifically, the proposed ZIPBoost (ZILBoost) algorithm uses a combination of a split probit (logit) model for regime 0 and a traditional probit (logit) model for regime 1 through a boosting strategy. We implement boosting to obtain final probabilities, distinguishing whether a unit belongs to regime 1 (i.e., SE iterations) or is classified as the minority class (i.e., OE iterations). ZIPBoost relies on the probit model to estimate probabilities, while ZILBoost employs the logit model. Furthermore, in this study we show that the OE data-generating process determines the performance of the proposed algorithms. When dealing with imbalanced data, ZILBoost performs better than ZIPBoost when the OE data-generating process exhibits positive excess kurtosis. In contrast, ZIPBoost is preferred when this process is characterized by negative excess kurtosis (Chen & Tsurumi, 2010).
Using Monte Carlo simulation, we showed that in terms of the predictive performance on the test data, ZIPBoost and ZILBoost surpass standard learning algorithms, including AdaBoost, LogitBoost, and ProbitBoost, as well as existing approaches for learning imbalanced data, such as AdaC2, SMOTEBoost, and GANs. The results of the simulation show that in a particular case in which the majority class is related to two distinct DGPs, the proposed systematic approaches can result in an improvement of prediction accuracy for the minority class without sacrificing the predictive power for the majority class.
In the real data application, we considered the classification of M&A outcomes in which the majority class was successful takeovers. Successful takeovers may arise from two different motivations, either related to M&A deal characteristics or the dyadic relationship between the acquirer and the target firm. On the other hand, the failure of M&A deals can occur if the acquirer may not expect any gain from the deal due to financial differences with the target firm, especially when deal characteristics do not force its completion. Thus, we assumed that the financial performances of the acquirer and target firm might be important for predicting the failure of M&A deals, whereas deal characteristics may affect their success. From a modeling point of view, M&A-related predictors were considered in the SE iterations to account for successfully completed cases (zeros; majority class) and 2) financial performance-related predictors in the OE iterations to account for withdrawn cases (ones; minority class). As a result, we found that ZIPBoost achieved the best prediction accuracy for the minority class, with the highest F-score measured in the minority class. At the same time, it produced the highest macro F-score and MCC, suggesting that ZIPBoost can predict the failure of M&A deals more accurately without compromising predictive performance for successful takeovers compared to other benchmark models.
It is important to note that our proposed method requires two sets of predictors, one for SE and the other for OE. In other words, researchers should know which factors are critical for representing the majority class (i.e., inflated case), as well as which factors predict the minority class. This is because the systematic approaches leverage prior information about how the data were generated—the proposed methods require knowledge about the data-generating process. Thus, the proposed methods may not be suitable for exploratory analyses. However, given appropriate sets of predictors based on prior knowledge, we believe that the proposed methods, which are systematic approaches that accommodate the dominance of one class, can outperform existing learning methods in terms of their predictive performance on imbalanced data.
When researchers lack prior information about how the data were generated, however, the optimal predictor selection for both SE and the OE should be determined from the data. Thus, data-driven modeling as a preprocessing step for predictor selection is necessary for the application of our proposed methods to any dataset. To demonstrate this data-driven approach, in this study, we selected 36 imbalanced datasets from the Keel repository. The results of the experiments show the effectiveness of the proposed methods based on data-driven strategies compared with other benchmark models in handling imbalanced data. Not surprisingly, data-driven modeling is computationally very expensive, and thus, in these experiments, we focused on the datasets with a number of predictors less than 10 in order to reduce computational costs. Notably, data-driven strategies may not be appropriate in cases with a large number of predictors.
This study opens the possibility for future work in multiclass problems. The proposed methods can be extended to classification problems with more than two classes, as discussed in Appendix F. However, for such extensions, the update schemes reliant on the Newton–Raphson method may be computationally too expensive since the gradient and Hessian functions should be defined for each class over iterations. Thus, other update schemes—for example, the application of gradient boosting, which requires only the defining gradient—can be explored in future work for multiclass cases with class imbalance. Finally, we propose a possible idea for future work involving refinement functions. In this study, we assume that the observed outcome of \(y\) is the realization of two separated latent equations, (1) and (2), with uncorrelated error terms. However, in certain cases, it may be necessary to assume that \(u\) and \(\varepsilon \) are related. To address this, ZIPBoost based on a bivariate normal distribution with correlation coefficients seems appropriate to extend the model to correlate the two error terms.
Availability of data and material
We have used simulated data and open data sources.
Code availability
The R code is available in the online supplement.
Notes
The third derivative of the objective function for ZIPBoost is \(\frac{{f}_{x}\varphi ({f}_{x})\varPhi ({f}_{x})(y-\varPhi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)\left(\varPhi \left(-{f}_{x}\right)+\varPhi \left({f}_{x}\right)\varPhi \left(-{f}_{z}\right)\right)+{\varphi }^{2}\left({f}_{x}\right)\varPhi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)\left(\varPhi \left(-{f}_{x}\right)+\varPhi \left(-{f}_{x}\right)\varPhi \left(-{f}_{z}\right)\right)+\varphi \left({f}_{x}\right)\varPhi \left({f}_{x}\right)\left(y-\varPhi \left({f}_{x}\right)\varPhi \left({f}_{z}\right)\right)\left(-\varphi \left({f}_{x}\right)+\varphi \left({f}_{x}\right)\varPhi \left(-{f}_{z}\right)\right)+{\varphi }^{2}\left({f}_{x}\right)\left(y-\varPhi \left(-{f}_{x}\right)\varPhi \left({f}_{z}\right)\right)\left(\varPhi \left(-{f}_{x}\right)+\varPhi \left({f}_{x}\right)\varPhi \left(-{f}_{z}\right)\right)}{{\left\{\varPhi \left(-{f}_{x}\right)+\varPhi \left({f}_{x}\right)\varPhi \left(-{f}_{z}\right)\right\}}^{2}{\varPhi }^{2}\left({f}_{x}\right)}\) for the splitting equation, and for the outcome equation,
$$\frac{{f}_{z}\varphi ({f}_{z})\varPhi ({f}_{z})(y-\varPhi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)\left(\varPhi \left(-{f}_{x}\right)+\varPhi \left({f}_{x}\right)\varPhi \left(-{f}_{z}\right)\right)+{\varphi }^{2}\left({f}_{z}\right)\varPhi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)\left(\varPhi \left(-{f}_{x}\right)+\varPhi \left(-{f}_{x}\right)\varPhi \left(-{f}_{z}\right)\right)-{\varphi }^{2}\left({f}_{z}\right)\varPhi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)\left(y-\varPhi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)\right)+{\varphi }^{2}\left({f}_{z}\right)\left(y-\varPhi \left({f}_{z}\right)\varPhi \left({f}_{x}\right)\right)\left(\varPhi \left(-{f}_{x}\right)+\varPhi \left({f}_{x}\right)\varPhi \left(-{f}_{z}\right)\right)}{{\left\{\varPhi \left(-{f}_{x}\right)+\varPhi \left({f}_{x}\right)\varPhi \left(-{f}_{z}\right)\right\}}^{2}{\varPhi }^{2}\left({f}_{z}\right)}.$$The objective function for ZILBoost has the third derivative since, for the splitting equation, we have, \(\frac{\left(\text{exp}\left(4{f}_{x}\right)-\left(\text{exp}\left({f}_{z}\right)+2\right)\text{exp}\left(3{f}_{x}\right)-6\left(\text{exp}\left({f}_{z}\right)+1\right)\text{exp}\left(2{f}_{x}\right)-\left(\text{exp}\left({f}_{z}\right)+1\right)(\text{exp}\left({f}_{z}\right)+2\right)\text{exp}\left({f}_{x}\right)+\text{exp}\left(2{f}_{z}\right)+2\text{exp}\left({f}_{z}\right)+1))\text{exp}\left({f}_{x}+{f}_{z}\right) }{{\left(\text{exp}\left({f}_{x}\right)+1\right)}^{3}{\left(\text{exp}\left({f}_{x}\right)+\text{exp}\left({f}_{z}\right)+1\right)}^{3}}\) when \(y=0\), and \(-\frac{\left(\text{exp}\left({f}_{x}\right)-1\right)\text{exp}\left({f}_{x}\right)}{{\left(\text{exp}\left({f}_{x}\right)+1\right)}^{3}}\) when \(y=1\). For the outcome equation, we have, \(\frac{\left(\text{exp}\left(4{f}_{z}\right)-\left(\text{exp}\left({f}_{x}\right)+2\right)\text{exp}\left(3{f}_{z}\right)-6\left(\text{exp}\left({f}_{x}\right)+1\right)\text{exp}\left(2{f}_{z}\right)-\left(\text{exp}\left({f}_{x}\right)+1\right)(\text{exp}\left({f}_{x}\right)+2\right)\text{exp}\left({f}_{z}\right)+\text{exp}\left(2{f}_{x}\right)+2\text{exp}\left({f}_{x}\right)+1))\text{exp}\left({f}_{x}+{f}_{z}\right) }{{\left(\text{exp}\left({f}_{z}\right)+1\right)}^{3}{\left(\text{exp}\left({f}_{x}\right)+\text{exp}\left({f}_{z}\right)+1\right)}^{3}}\), when \(y=0\), and \(-\frac{\left(\text{exp}\left({f}_{z}\right)-1\right)\text{exp}\left({f}_{z}\right)}{{\left(\text{exp}\left({f}_{z}\right)+1\right)}^{3}}\) when \(y=1\).
References
Alashwali, F., & Kent, J. T. (2016). The use of a common location measure in the invariant coordinate selection and projection pursuit. Journal of Multivariate AnalySis, 152, 145–161. https://doi.org/10.1016/j.jmva.2016.08.007
Babajee, D. K. R., & Dauhoo, M. Z. (2006). An analysis of the properties of the variants of Newton’s method with third order convergence. Applied Mathematics and Computation, 183(1), 659–684. https://doi.org/10.1016/j.amc.2006.05.116
Baker, M., & Wurgler, J. (2006). Investor sentiment and the cross-section of stock returns. The Journal of Finance, 61(4), 1645–1680. https://doi.org/10.1111/j.1540-6261.2006.00885.x
Barandela, R., Sánchez, J. S., García, V., & Rangel, E. (2003). Strategies for learning in class imbalance problems. Pattern Recognition, 36(3), 849–851. https://doi.org/10.1016/S0031-3203(02)00257-1
Batista, G. E., Prati, R. C., & Monard, M. C. (2004). A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explorations Newsletter, 6(1), 20–29. https://doi.org/10.1145/1007730.1007735
Boughorbel, S., Jarray, F., & El-Anbari, M. (2017). Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE, 12(6), e0177678. https://doi.org/10.1371/journal.pone.0177678
Brooks, R. J., Galbraith, D. A., Nancekivell, E. G., & Bishop, C. A. (1988). Developing management guidelines for snapping turtles. General Technical Report RM-Rocky Mountain Forest and Range Experiment Station, US Department of Agriculture, Forest Service (USA).
Bugeja, M. (2005). The “independence” of expert opinions in corporate takeovers: Agreeing with directors’ recommendations. Journal of Business Finance & Accounting, 32(9–10), 1861–1885. https://doi.org/10.1111/j.0306-686X.2005.00650.x
Butler, F. C., & Sauska, P. (2014). Mergers and acquisitions: Termination fees and acquisition deal completion. Journal of Managerial Issues, 44–54.
Casella, F., & Bachmann, B. (2021). On the choice of initial guesses for the Newton-Raphson algorithm. Applied Mathematics and Computation, 398, 125991. https://doi.org/10.1016/j.amc.2021.125991
Chawla, N. V., Lazarevic, A., Hall, L. O., & Bowyer, K. W. (2003). SMOTEBoost: Improving prediction of the minority class in boosting. In European conference on principles of data mining and knowledge discovery (pp. 107–119). Springer. https://doi.org/10.1007/978-3-540-39804-2_12
Chawla, N. V., Bowyer, K. W., Hall, L. O., & Kegelmeyer, W. P. (2002). SMOTE: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research, 16, 321–357. https://doi.org/10.1613/jair.953
Chawla, N. V., Cieslak, D. A., Hall, L. O., & Joshi, A. (2008). Automatically countering imbalance and its empirical relationship to cost. Data Mining and Knowledge Discovery, 17(2), 225–252. https://doi.org/10.1007/s10618-008-0087-0
Chen, G., & Tsurumi, H. (2010). Probit and logit model selection. Communications in Statistics—Theory and Methods, 40(1), 159–175. https://doi.org/10.1080/03610920903377799
Congdon, J. D., Dunham, A. E., & Sels, R. V. L. (1994). Demographics of common snapping turtles (Chelydra serpentina): Implications for conservation and management of long-lived organisms. American Zoologist, 34(3), 397–408. https://doi.org/10.1093/icb/34.3.397
Copas, J. B. (1988). Binary regression models for contaminated data. Journal of the Royal Statistical Society: Series B (methodological), 50(2), 225–253.
Dauphin, Y. N., Pascanu, R., Gulcehre, C., Cho, K., Ganguli, S., & Bengio, Y. (2014). Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. Advances in Neural Information Processing Systems, 27.
Drucker, H. (2002). Effect of pruning and early stopping on performance of a boosting ensemble. Computational Statistics & Data Analysis, 38(4), 393–406. https://doi.org/10.1016/S0167-9473(01)00067-6
Fernández, A., García, S., Galar, M., Prati, R. C., Krawczyk, B., & Herrera, F. (2018). Learning from imbalanced data sets (Vol. 10, pp. 978–3). Springer.
Fernández, A., del Jesus, M. J., & Herrera, F. (2009). Hierarchical fuzzy rule based classification systems with genetic rule selection for imbalanced datasets. International Journal of Approximate Reasoning, 50(3), 561–577. https://doi.org/10.1016/j.ijar.2008.11.004
Fernández, A., García, S., del Jesus, M. J., & Herrera, F. (2008). A study of the behaviour of linguistic fuzzy rule based classification systems in the framework of imbalanced data-sets. Fuzzy Sets and Systems, 159(18), 2378–2398. https://doi.org/10.1016/j.fss.2007.12.023
Freund, Y., & Schapire, R. E. (1996). Experiments with a new boosting algorithm. In International conference on machine learning (Vol. 96, pp. 148–156).
Frid-Adar, M., Diamant, I., Klang, E., Amitai, M., Goldberger, J., & Greenspan, H. (2018). GAN-based synthetic medical image augmentation for increased CNN performance in liver lesion classification. Neurocomputing, 321, 321–331. https://doi.org/10.1016/j.neucom.2018.09.013
Friedman, J., Hastie, T., & Tibshirani, R. (2000). Special invited paper. Additive logistic regression: A statistical view of boosting. Annals of Statistics, 337–374.
Galar, M., Fernandez, A., Barrenechea, E., Bustince, H., & Herrera, F. (2012). A review on ensembles for the class imbalance problem: Bagging-, boosting-, and hybrid-based approaches. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 42(4), 463–484. https://doi.org/10.1109/TSMCC.2011.2161285
Gao, M., Hong, X., Chen, S., Harris, C. J., & Khalaf, E. (2014). PDFOS: PDF estimation based over-sampling for imbalanced two-class problems. Neurocomputing, 138, 248–259. https://doi.org/10.1016/j.neucom.2014.02.006
Gao, N., Hua, C., & Khurshed, A. (2021). Loan price in mergers and acquisitions. Journal of Corporate Finance, 67, 101754. https://doi.org/10.1016/j.jcorpfin.2020.101754
Gibbons, J. W. (1987). Why do turtles live so long? BioScience, 37(4), 262–269. https://doi.org/10.2307/1310589
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., & Bengio, Y. (2014). Generative adversarial nets. In Advances in Neural Information Processing Systems, 27.
Guelman, L. (2012). Gradient boosting trees for auto insurance loss cost modeling and prediction. Expert Systems with Applications, 39(3), 3659–3667. https://doi.org/10.1016/j.eswa.2011.09.058
Harris, M. N., & Zhao, X. (2007). A zero-inflated ordered probit model, with an application to modelling tobacco consumption. Journal of Econometrics, 141(2), 1073–1099. https://doi.org/10.1016/j.jeconom.2007.01.002
Heppell, S. S., Crowder, L. B., & Crouse, D. T. (1996). Models to evaluate headstarting as a management tool for long-lived turtles. Ecological Applications, 6(2), 556–565. https://doi.org/10.2307/2269391
Hill, D. W., Bagozzi, B. E., Moore, W. H., & Mukherjee, B. (2011). Strategic incentives and modeling bias in ordinal data: The zero-inflated ordered probit (ZiOP) model in political science. In New faces in political methodology meeting (Vol. 30). Penn State.
Huang, Y., Fields, K. G., & Ma, Y. (2022). A tutorial on generative adversarial networks with application to classification of imbalanced data. Statistical Analysis and Data Mining: THe ASA Data Science Journal, 15(5), 543–552. https://doi.org/10.1002/sam.11570
Hwang, J. P., Park, S., & Kim, E. (2011). A new weighted approach to imbalanced data classification problem via support vector machine with quadratic cost function. Expert Systems with Applications, 38(7), 8580–8585. https://doi.org/10.1016/j.eswa.2011.01.061
Janzen, F. J. (1993). An experimental analysis of natural selection on body size of hatchling turtles. Ecology, 74(2), 332–341. https://doi.org/10.2307/1939296
Koziarski, M. (2020). Radial-based undersampling for imbalanced data classification. Pattern Recognition, 102, 107262. https://doi.org/10.1016/j.patcog.2020.107262
Koziarski, M., Bellinger, C., & Woźniak, M. (2021). RB-CCR: Radial-Based Combined Cleaning and Resampling algorithm for imbalanced data classification. Machine Learning, 110(11), 3059–3093. https://doi.org/10.1007/s10994-021-06012-8
Koziarski, M., & Woźniak, M. (2017). CCR: A combined cleaning and resampling algorithm for imbalanced data classification. International Journal of Applied Mathematics and Computer Science. https://doi.org/10.1515/amcs-2017-0050
Krawczyk, B. (2016). Learning from imbalanced data: Open challenges and future directions. Progress in Artificial Intelligence, 5(4), 221–232. https://doi.org/10.1007/s13748-016-0094-0
Krawczyk, B., Woźniak, M., & Schaefer, G. (2014). Cost-sensitive decision tree ensembles for effective imbalanced classification. Applied Soft Computing, 14, 554–562. https://doi.org/10.1016/j.asoc.2013.08.014
Lee, K., Joo, S., Baik, H., Han, S., & In, J. (2020). Unbalanced data, type II error, and nonlinearity in predicting M&A failure. Journal of Business Research, 109, 271–287. https://doi.org/10.1016/j.jbusres.2019.11.083
Lin, J., Zhong, C., Hu, D., Rudin, C., & Seltzer, M. (2020). Generalized and scalable optimal sparse decision trees. In International conference on machine learning (pp. 6150–6160). PMLR.
Lin, Y., Lee, Y., & Wahba, G. (2002). Support vector machines for classification in nonstandard situations. Machine Learning, 46(1), 191–202. https://doi.org/10.1023/A:1012406528296
Ling, C. X., Sheng, V. S., & Yang, Q. (2006). Test strategies for cost-sensitive decision trees. IEEE Transactions on Knowledge and Data Engineering, 18(8), 1055–1067. https://doi.org/10.1109/TKDE.2006.131
Liu, B., Ma, Y., & Wong, C. K. (2000). Improving an association rule based classifier. In European conference on principles of data mining and knowledge discovery (pp. 504–509). Springer. https://doi.org/10.1007/3-540-45372-5_58
Liu, G., Wu, J., & Zhou, Z. H. (2012). Key instance detection in multi-instance learning. In Asian conference on machine learning (pp. 253–268). PMLR.
Liu, X., & He, W. (2022). Adaptive kernel scaling support vector machine with application to a prostate cancer image study. Journal of Applied Statistics, 49(6), 1465–1484. https://doi.org/10.1080/02664763.2020.1870669
London, B., Lu, L., Sandler, T., & Joachims, T. (2023). Boosted off-policy learning. In International conference on artificial intelligence and statistics (pp. 5614–5640). PMLR.
López, V., Fernández, A., Moreno-Torres, J. G., & Herrera, F. (2012). Analysis of preprocessing vs. cost-sensitive learning for imbalanced classification: Open problems on intrinsic data characteristics. Expert Systems with Applications, 39(7), 6585–6608. https://doi.org/10.1016/j.eswa.2011.12.043
Massias, M., Vaiter, S., Gramfort, A., & Salmon, J. (2020). Dual extrapolation for sparse generalized linear models. Journal of Machine Learning Research, 21(234), 1–33.
Napierała, K., Stefanowski, J., & Wilk, S. (2010). Learning from imbalanced data in presence of noisy and borderline examples. In International conference on rough sets and current trends in computing (pp. 158–167). Springer. https://doi.org/10.1007/978-3-642-13529-3_18
Oentaryo, R., Lim, E. P., Finegold, M., Lo, D., Zhu, F., Phua, C., Cheu, E. Y., Yap, G. E., Sim, K., Nguyen, M. N., Perera, K., Neupane, B., Faisal, M., Aung, Z., Woon, W. L., Chen, W., Patel, D., & Berrar, D. (2014). Detecting click fraud in online advertising: A data mining approach. Journal of Machine Learning Research, 15(1), 99–140.
Paternain, S., Mokhtari, A., & Ribeiro, A. (2019). A Newton-based method for nonconvex optimization with fast evasion of saddle points. SIAM Journal on Optimization, 29(1), 343–368.
Pei, W., Xue, B., Shang, L., & Zhang, M. (2021). Genetic programming for development of cost-sensitive classifiers for binary high-dimensional unbalanced classification. Applied Soft Computing, 101, 106989. https://doi.org/10.1016/j.asoc.2020.106989
Perez-Heydrich, C., Jackson, K., Wendland, L. D., & Brown, M. B. (2012). Gopher tortoise hatchling survival: Field study and meta-analysis. Herpetologica, 68(3), 334–344. https://doi.org/10.1655/HERPETOLOGICA-D-11-00046.1
Provost, F., & Domingos, P. (2003). Tree induction for probability-based ranking. Machine Learning, 52(3), 199–215. https://doi.org/10.1023/A:1024099825458
Ren, D., Qu, F., Lv, K., Zhang, Z., Xu, H., & Wang, X. (2016). A gradient descent boosting spectrum modeling method based on back interval partial least squares. Neurocomputing, 171, 1038–1046. https://doi.org/10.1016/j.neucom.2015.07.109
Ren, Z., Zhu, Y., Kang, W., Fu, H., Niu, Q., Gao, D., Yan, K., & Hong, J. (2022). Adaptive cost-sensitive learning: Improving the convergence of intelligent diagnosis models under imbalanced data. Knowledge-Based Systems, 241, 108296. https://doi.org/10.1016/j.knosys.2022.108296
Renneboog, L., & Vansteenkiste, C. (2019). Failure and success in mergers and acquisitions. Journal of Corporate Finance, 58, 650–699. https://doi.org/10.1016/j.jcorpfin.2019.07.010
Renneboog, L., & Zhao, Y. (2014). Director networks and takeovers. Journal of Corporate Finance, 28, 218–234. https://doi.org/10.1016/j.jcorpfin.2013.11.012
Rodrigues, B. D., & Stevenson, M. J. (2013). Takeover prediction using forecast combinations. International Journal of Forecasting, 29(4), 628–641. https://doi.org/10.1016/j.ijforecast.2013.01.008
Rohde, D., & Wand, M. P. (2016). Semiparametric mean field variational Bayes: General principles and numerical issues. Journal of Machine Learning Research, 17(1), 5975–6021.
Saber, M. A. S., Ghorbani, M., Bayati, A., Nguyen, K. K., & Cheriet, M. (2020). Online data center traffic classification based on inter-flow correlations. IEEE Access, 8, 60401–60416. https://doi.org/10.1109/ACCESS.2020.2983605
Saha, A., & Tewari, A. (2013). On the nonasymptotic convergence of cyclic coordinate descent methods. SIAM Journal on Optimization, 23(1), 576–601. https://doi.org/10.1137/110840054
Song, J., Lu, X., Liu, M., & Wu, X. (2011). Stratified normalization LogitBoost for two-class unbalanced data classification. Communications in Statistics-Simulation and Computation, 40(10), 1587–1593. https://doi.org/10.1080/03610918.2011.589332
Stahl, G. K., Chua, C. H., & Pablo, A. L. (2012). Does national context affect target firm employees’ trust in acquisitions? Management International Review, 52(3), 395–423. https://doi.org/10.1007/s11575-011-0099-7
Stanford, C. B., Iverson, J. B., Rhodin, A. G., van Dijk, P. P., Mittermeier, R. A., Kuchling, G., & Walde, A. D. (2020). Turtles and tortoises are in trouble. Current Biology, 30(12), R721–R735. https://doi.org/10.1016/j.cub.2020.04.088
Stefanowski, J., & Wilk, S. (2008). Selective pre-processing of imbalanced data for improving classification performance. In International conference on data warehousing and knowledge discovery (pp. 283–292). Springer. https://doi.org/10.1007/978-3-540-85836-2_27
Süli, E., & Mayers, D. F. (2003). An introduction to numerical analysis. Cambridge University Press.
Sun, Y., Kamel, M. S., Wong, A. K., & Wang, Y. (2007). Cost-sensitive boosting for classification of imbalanced data. Pattern Recognition, 40(12), 3358–3378. https://doi.org/10.1016/j.patcog.2007.04.009
Sun, Z., Song, Q., Zhu, X., Sun, H., Xu, B., & Zhou, Y. (2015). A novel ensemble method for classifying imbalanced data. Pattern Recognition, 48(5), 1623–1637. https://doi.org/10.1016/j.patcog.2014.11.014
Tang, C. Y., & Wu, T. T. (2014). Nested coordinate descent algorithms for empirical likelihood. Journal of Statistical Computation and Simulation, 84(9), 1917–1930. https://doi.org/10.1080/00949655.2013.770514
Thanathamathee, P., & Lursinsap, C. (2013). Handling imbalanced data sets with synthetic boundary data generation using bootstrap re-sampling and AdaBoost techniques. Pattern Recognition Letters, 34(12), 1339–1347. https://doi.org/10.1016/j.patrec.2013.04.019
Waegeman, W., Dembczyński, K., Jachnik, A., Cheng, W., & Hüllermeier, E. (2014). On the Bayes-optimality of f-measure maximizers. Journal of Machine Learning Research, 15, 3333–3388.
Wang, B. X., & Japkowicz, N. (2010). Boosting support vector machines for imbalanced data sets. Knowledge and Information Systems, 25(1), 1–20. https://doi.org/10.1007/s10115-009-0198-y
Wang, S., Minku, L. L., & Yao, X. (2014). Resampling-based ensemble methods for online class imbalance learning. IEEE Transactions on Knowledge and Data Engineering, 27(5), 1356–1368. https://doi.org/10.1109/TKDE.2014.2345380
Wei, J., Feng, G., Lu, Z., Han, P., Zhu, Y., & Huang, W. (2021). Evaluating drug risk using GAN and SMOTE based on CFDA’s spontaneous reporting data. Journal of Healthcare Engineering. https://doi.org/10.1155/2021/6033860
Wright, S., & Nocedal, J. (2006). Numerical optimization. Springer Science, 35(67–68), 7. https://doi.org/10.1137/17M1150116
Wu, T. T. (2013). Lasso penalized semiparametric regression on high-dimensional recurrent event data via coordinate descent. Journal of Statistical Computation and Simulation, 83(6), 1145–1155. https://doi.org/10.1080/00949655.2011.652114
Wu, T. T., & Lange, K. (2010). Multicategory vertex discriminant analysis for high-dimensional data. The Annals of Applied Statistics, 4(4), 1698–1721. https://doi.org/10.1214/10-AOAS345
Xu, D. (2020). Modelling asset returns under price limits with mixture of truncated Gaussian distribution. Applied Economics, 52(52), 5706–5725. https://doi.org/10.1080/00036846.2020.1770682
Yang, H., & Zhou, Y. (2021). Ida-gan: A novel imbalanced data augmentation gan. In 2020 25th international conference on pattern recognition (ICPR) (pp. 8299–8305). IEEE. https://doi.org/10.1109/ICPR48806.2021.9411996
Yin, Q. Y., Zhang, J. S., Zhang, C. X., & Liu, S. C. (2013). An empirical study on the performance of cost-sensitive boosting algorithms with different levels of class imbalance. Mathematical Problems in Engineering. https://doi.org/10.1155/2013/761814
Zhang, S., Liu, L., Zhu, X., & Zhang, C. (2008). A strategy for attributes selection in cost-sensitive decision trees induction. In 2008 IEEE 8th international conference on computer and information technology workshops (pp. 8–13). IEEE. https://doi.org/10.1109/CIT.2008.Workshops.51.
Zheng, S., & Liu, W. (2012). Functional gradient ascent for Probit regression. Pattern Recognition, 45(12), 4428–4437. https://doi.org/10.1016/j.patcog.2012.06.006
Funding
None.
Author information
Authors and Affiliations
Contributions
Yeasung Jeong: Data curation, Resources, Formal Analysis, Investigation, Software, Visualization, Writing-original draft, and Writing-review & editing. Kangbok Lee: Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Writing-original draft, and Writing-review & editing. Young Woong Park: Validation and Writing-review & editing. Sumin Han: Conceptualization, Methodology, Validation, Writing-original draft, and Writing-review & editing.
Corresponding author
Ethics declarations
Conflict of interest
We have no conflict of interest to declare.
Ethical approval
Not Applicable.
Consent to participate
Not Applicable.
Consent for publication
Not Applicable.
Additional information
Editors: Nuno Moniz, Paula Branco, Luís Torgo, Nathalie Japkowicz, Michal Wozniak, Shuo Wang.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix A. Derivations of the gradients
In this appendix, we derive the gradients of the loss functions in ZIPBoost and ZILBoost. In ZIPBoost, the gradient for the OE iterations is defined as follows:
For the SE iterations, the gradient is obtained by
In ZILBoost, the gradient of the OE iterations is defined as
and the gradient of the SE iterations is as follows:
Appendix B. Proofs of propositions
Proposition 5. (Misclassification) we have \(\underset{{f}_{x}\to -\infty }{\text{lim}}W\left({f}_{x}\right)=1\).
Proof
Note that \(\underset{{f}_{x}\to -\infty }{\text{lim}}W\left({f}_{x}\right)=\underset{{f}_{x}\to -\infty }{\text{lim}}\left|\frac{{f}_{x}\varphi \left({f}_{x}\right)\varPhi \left({f}_{x}\right)+{\varphi }^{2}\left({f}_{x}\right)}{{\left\{\varPhi \left({f}_{x}\right)\right\}}^{2}}\right|=\frac{0}{0}\), which is an indeterminate form, since \(\varPhi \left({f}_{x}\right)\to 0\) and \(\varphi \left({f}_{x}\right)\to 0\) as \({f}_{x}\to -\infty \). As before, we apply L’Hôpital’s rule repeatedly:
where the second, fifth, seventh, and ninth equations hold by L’Hôpital’s rule. □
Proposition 8. (Misclassification) Given \( f_{x} \gg N,~ \) where N is an arbitrarily large positive number, \( \mathop {\lim }\limits_{{f_{z} \to \infty }} W\left( {f_{z} } \right) = 1 \).
Proof
Given \( f_{x} \gg N,~ \)\( \mathop {\lim }\limits_{{f_{z} \to \infty }} W\left( {f_{z} } \right) = \mathop {\lim }\limits_{{f_{z} \to \infty }} \left| {\frac{{ - \left\{ {f_{z} \varphi \left( {f_{z} } \right)\varPhi \left( {f_{x} } \right)\left[ {1 - \varPhi \left( {f_{z} } \right)\varPhi \left( {f_{x} } \right)} \right] - \varphi ^{2} \left( {f_{z} } \right)\varPhi ^{2} \left( {f_{x} } \right)} \right\}}}{{\left\{ {1 - \varPhi \left( {f_{z} } \right)\varPhi \left( {f_{x} } \right)} \right\}^{2} }}} \right| = \frac{0}{0} \), which is an indeterminate form, since \( \varPhi \left( {f_{z} } \right)\varPhi \left( {f_{x} } \right)~ \to 1 \) and \( \varphi \left( {f_{z} } \right) \to 0 \) as \( f_{z} \to \infty \) Therefore, we apply L’Hôpital’s rule repeatedly:
where the second, sixth, ninth, and tenth equations hold by L’Hôpital’s rule. □
Proposition 10. (Misclassification) \( \mathop {\lim }\limits_{{f_{z} \to - \infty }} W\left( {f_{z} } \right) = 1 \).
Proof
To prove Proposition 10, we apply L’Hôpital’s rule repeatedly since we have an indeterminate form due to the fact that \( \varPhi \left( {f_{z} } \right) \to 0~ \text{and}\, \varphi \left( {f_{z} } \right) \to 0 \, \text{as}\, f_{z} \to - \infty \).
where the second, fifth, seventh, and ninth equations hold by L’Hôpital’s rule. □
Appendix C. Simulation results using training data
3.1 Appendix C1 Monte Carlo Simulation results using training data
AdaBoost | LogitBoost | ProbitBoost | AdaC2 | SMOTEboost -C.50 | GANs-GBM | ZIPBoost | ZILBoost | |
|---|---|---|---|---|---|---|---|---|
5% minority examples | ||||||||
F-score: minority | 1.000 (0.000) | 0.729 (0.109) | 0.602 (0.113) | 1.000 (0.000) | 1.000 (0.000) | 0.194 (0.115) | 0.808 (0.136) | 0.907 (0.059) |
F-score: majority | 1.000 (0.000) | 0.985 (0.057) | 0.984 (0.004) | 1.000 (0.000) | 1.000 (0.000) | 0.963 (0.015) | 0.992 (0.005) | 0.996 (0.003) |
Macro F-score | 1.000 (0.000) | 0.857 (0.072) | 0.793 (0.057) | 1.000 (0.000) | 1.000 (0.000) | 0.578 (0.059) | 0.900 (0.070) | 0.951 (0.031) |
MCC | 1.000 (0.000) | 0.724 (0.131) | 0.597 (0.108) | 1.000 (0.000) | 1.000 (0.000) | 0.144 (0.127) | 0.766 (0.223) | 0.903 (0.061) |
Training Time (sec) | 0.625 (0.028) | 0.047 (0.023) | 0.113 (0.019) | 6.858 (0.205) | 4.616 (0.179) | 18.959 (3.468) | 0.419 (0.049) | 0.215 (0.025) |
10% minority examples | ||||||||
F-score: minority | 1.000 (0.000) | 0.712 (0.066) | 0.660 (0.061) | 1.000 (0.000) | 1.000 (0.001) | 0.502 (0.0124) | 0.887 (0.034) | 0.899 (0.035) |
F-score: majority | 1.000 (0.000) | 0.966 (0.008) | 0.961 (0.006) | 1.000 (0.000) | 1.000 (0.000) | 0.943 (0.011) | 0.986 (0.004) | 0.987 (0.005) |
Macro F-score | 1.000 (0.000) | 0.839 (0.036) | 0.811 (0.033) | 1.000 (0.000) | 1.000 (0.000) | 0.722 (0.066) | 0.936 (0.019) | 0.943 (0.020) |
MCC | 1.000 (0.000) | 0.682 (0.071) | 0.628 (0.063) | 1.000 (0.000) | 1.000 (0.001) | 0.451 (0.129) | 0.874 (0.037) | 0.887 (0.040) |
Training Time (sec) | 0.629 (0.030) | 0.066 (0.020) | 0.112 (0.023) | 7.536 (0.197) | 5.664 (0.202) | 13.267 (90.269) | 0.458 (0.054) | 0.229 (0.023) |
20% minority examples | ||||||||
F-score: minority | 1.000 (0.000) | 0.739 (0.045) | 0.709 (0.043) | 1.000 (0.000) | 1.000 (0.000) | 0.683 (0.072) | 0.905 (0.023) | 0.911 (0.025) |
F-score: majority | 1.000 (0.000) | 0.932 (0.010) | 0.928 (0.009) | 1.000 (0.000) | 1.000 (0.000) | 0.908 (0.024) | 0.975 (0.006) | 0.976 (0.007) |
Macro F-score | 1.000 (0.000) | 0.836 (0.026) | 0.819 (0.024) | 1.000 (0.000) | 1.000 (0.000) | 0.795 (0.046) | 0.940 (0.014) | 0.944 (0.016) |
MCC | 1.000 (0.000) | 0.672 (0.052) | 0.641 (0.047) | 1.000 (0.000) | 1.000 (0.000) | 0.594 (0.092) | 0.880 (0.028) | 0.888 (0.031) |
Training Time (sec) | 0.637 (0.031) | 0.078 (0.020) | 0.112 (0.028) | 8.039 (0.214) | 7.136 (0.303) | 17.526 (2.241) | 0.481 (0.051) | 0.242 (0.029) |
30% minority examples | ||||||||
F-score: minority | 1.000 (0.000) | 0.777 (0.032) | 0.755 (0.032) | 0.996 (0.047) | 1.000 (0.000) | 0.781 (0.039) | 0.919 (0.017) | 0.924 (0.018) |
F-score: majority | 1.000 (0.000) | 0.902 (0.013) | 0.899 (0.012) | 0.996 (0.063) | 1.000 (0.000) | 0.892 (0.022) | 0.965 (0.007) | 0.966 (0.008) |
Macro F-score | 1.000 (0.000) | 0.840 (0.021) | 0.827 (0.020) | 0.997 (0.048) | 1.000 (0.029) | 0.837 (0.029) | 0.942 (0.012) | 0.945 (0.013) |
MCC | 1.000 (0.001) | 0.680 (0.042) | 0.655 (0.040) | 0.992 (0.087) | 1.000 (0.000) | 0.679 (0.056) | 0.884 (0.023) | 0.890 (0.026) |
Training Time (sec) | 0.631 (0.038) | 0.073 (0.022) | 0.104 (0.023) | 7.871 (0.218) | 8.085 (0.447) | 22.289 (2.904) | 0.472 (0.045) | 0.238 (0.036) |
40% minority examples | ||||||||
F-score: minority | 1.000 (0.001) | 0.811 (0.026) | 0.795 (0.026) | 0.970 (0.107) | 1.000 (0.000) | 0.856 (0.021) | 0.933 (0.013) | 0.937 (0.014) |
F-score: majority | 1.000 (0.001) | 0.864 (0.017) | 0.861 (0.015) | 0.969 (0.172) | 1.000 (0.000) | 0.890 (0.015) | 0.953 (0.009) | 0.956 (0.010) |
Macro F-score | 1.000 (0.001) | 0.838 (0.019) | 0.828 (0.019) | 0.978 (0.122) | 1.000 (0.000) | 0.873 (0.017) | 0.943 (0.011) | 0.946 (0.012) |
MCC | 1.000 (0.002) | 0.677 (0.039) | 0.656 (0.037) | 0.929 (0.254) | 1.000 (0.000) | 0.749 (0.033) | 0.887 (0.021) | 0.893 (0.023) |
Training Time (sec) | 0.637 (0.041) | 0.076 (0.027) | 0.105 (0.029) | 8.008 (0.242) | 8.361 (0.402) | 28.856 (2.770) | 0.470 (0.050) | 0.240 (0.036) |
SMOTEBoost—Cart | SMOTEBoost -RF | SMOTEBoost -NB | SMOTEBoost -SVM | GANs-Logit | GANs-DT | GANs-RF | GANs-SVM | |
|---|---|---|---|---|---|---|---|---|
5% minority examples | ||||||||
F-score: minority | 0.997 (0.010) | 1.000 (0.000) | 0.575 (0.083) | 1.000 (0.003) | 0.129 (0.061) | 0.282 (0.203) | 0.997 (0.011) | 0.513 (0.161) |
F-score: majority | 1.000 (0.000) | 1.000 (0.000) | 0.966 (0.009) | 1.000 (0.000) | 0.769 (0.031) | 0.974 (0.007) | 1.000 (0.000) | 0.982 (0.005) |
Macro F-score | 0.998 (0.005) | 1.000 (0.000) | 0.770 (0.045) | 1.000 (0.002) | 0.449 (0.042) | 0.628 (0.103) | 0.998 (0.006) | 0.747 (0.082) |
MCC | 0.996 (0.010) | 1.000 (0.000) | 0.606 (0.071) | 1.000 (0.003) | 0.099 (0.121) | 0.120 (0.201) | 0.997 (0.011) | 0.496 (0.172) |
Training Time (sec) | 1.926 (0.134) | 2.952 (0.179) | 6.197 (0.179) | 6.910 (1.031) | 10.443 (3.462) | 10.453 (3.463) | 10.867 (3.478) | 10.460 (3.464) |
10% minority examples | ||||||||
F-score: minority | 0.992 (0.009) | 1.000 (0.000) | 0.687 (0.047) | 0.992 (0.011) | 0.356 (0.071) | 0.604 (0.134) | 0.999 (0.002) | 0.791 (0.047) |
F-score: majority | 0.999 (0.001) | 1.000 (0.000) | 0.945 (0.009) | 0.999 (0.001) | 0.762 (0.034) | 0.956 (0.009) | 1.000 (0.000) | 0.974 (0.005) |
Macro F-score | 0.996 (0.005) | 1.000 (0.000) | 0.816 (0.027) | 0.995 (0.006) | 0.559 (0.051) | 0.780 (0.070) | 1.000 (0.001) | 0.883 (0.026) |
MCC | 0.991 (0.010) | 1.000 (0.000) | 0.668 (0.045) | 0.991 (0.012) | 0.298 (0.110) | 0.565 (0.142) | 0.999 (0.002) | 0.767 (0.051) |
Training Time (sec) | 2.729 (0.169) | 3.854 (0.197) | 7.098 (0.217) | 11.573 (1.369) | 6.320 (0.467) | 6.331 (0.466) | 6.275 (0.480) | 6.343 (0.467) |
20% minority examples | ||||||||
F-score: minority | 0.993 (0.006) | 1.000 (0.000) | 0.779 (0.032) | 0.982 (0.011) | 0.593 (0.063) | 0.755 (0.050) | 1.000 (0.001) | 0.850 (0.032) |
F-score: majority | 0.998 (0.002) | 1.000 (0.000) | 0.928 (0.011) | 0.995 (0.003) | 0.800 (0.042) | 0.933 (0.013) | 1.000 (0.000) | 0.957 (0.010) |
Macro F-score | 0.996 (0.004) | 1.000 (0.000) | 0.853 (0.021) | 0.989 (0.007) | 0.697 (0.051) | 0.844 (0.030) | 1.000 (0.001) | 0.904 (0.020) |
MCC | 0.992 (0.007) | 1.000 (0.000) | 0.720 (0.038) | 0.977 (0.014) | 0.488 (0.084) | 0.691 (0.058) | 1.000 (0.001) | 0.809 (0.040) |
Training Time (sec) | 3.864 (0.211) | 4.941 (0.221) | 8.465 (0.271) | 14.391 (0.931) | 17.486 (2.758) | 17.496 (2.758) | 17.837 (2.761) | 17.509 (2.759) |
30% minority examples | ||||||||
F-score: minority | 0.994 (0.004) | 1.000 (0.000) | 0.819 (0.023) | 0.978 (0.010) | 0.725 (0.039) | 0.823 (0.031) | 1.000 (0.001) | 0.882 (0.025) |
F-score: majority | 0.998 (0.002) | 1.000 (0.000) | 0.912 (0.012) | 0.990 (0.005) | 0.825 (0.033) | 0.918 (0.015) | 1.000 (0.000) | 0.944 (0.014) |
Macro F-score | 0.996 (0.003) | 1.000 (0.000) | 0.865 (0.016) | 0.984 (0.008) | 0.775 (0.034) | 0.870 (0.022) | 1.000 (0.001) | 0.913 (0.019) |
MCC | 0.992 (0.006) | 1.000 (0.000) | 0.735 (0.032) | 0.968 (0.015) | 0.597 (0.053) | 0.744 (0.043) | 1.000 (0.001) | 0.829 (0.037) |
Training Time (sec) | 4.703 (0.224) | 5.744 (0.273) | 9.469 (0.263) | 14.387 (1.225) | 17.486 (3.314) | 17.496 (3.314) | 17.837 (3.309) | 17.509 (3.314) |
40% minority examples | ||||||||
F-score: minority | 0.994 (0.004) | 1.000 (0.000) | 0.846 (0.021) | 0.974 (0.009) | 0.806 (0.023) | 0.883 (0.021) | 1.000 (0.000) | 0.919 (0.017) |
F-score: majority | 0.996 (0.003) | 1.000 (0.000) | 0.893 (0.014) | 0.982 (0.006) | 0.840 (0.018) | 0.914 (0.014) | 1.000 (0.000) | 0.941 (0.013) |
Macro F-score | 0.995 (0.003) | 1.000 (0.000) | 0.870 (0.016) | 0.978 (0.008) | 0.823 (0.019) | 0.898 (0.017) | 1.000 (0.000) | 0.930 (0.014) |
MCC | 0.991 (0.006) | 1.000 (0.000) | 0.739 (0.032) | 0.956 (0.015) | 0.658 (0.035) | 0.799 (0.033) | 1.000 (0.001) | 0.862 (0.028) |
Training Time (sec) | 5.227 (0.242) | 6.104 (0.257) | 10.001 (0.292) | 12.070 (0.341) | 24.965 (3.112) | 24.974 (3.111) | 25.245 (3.102) | 24.983 (3.111) |
Appendix D. Comparison of ZILBoost and ZIPBoost
We conducted simulations based on different combinations of data-generating processes to investigate the relative performance of ZILBoost and ZIPBoost. Previous research has indicated that probit and logit models can be differentiated depending on the kurtosis of their data distribution (Chen & Tsurumi, 2010). More precisely, when data have positive excess kurtosis (i.e., leptokurtic data), the logit model outperforms the probit model; for data with negative excess kurtosis (i.e., platykurtic data), the probit model outperforms the logit model. Based on these previous findings, we considered two distributions—the Laplace distribution and a mixture of truncated normal distributions—to manipulate the kurtosis of the data. The Laplace distribution produces positive excess kurtosis (Alashwali & Kent, 2016), while a mixture of truncated normal distributions is flexible for generating data across a wide kurtosis range (Xu, 2020). For comparative purposes, we set the parameters for the mixture of truncated normal distributions to induce negative kurtosis.
In Scenario 1, echoing Chen and Tsurumi (2010), we generated data for both SE and OE from the Laplace distribution, resulting in positive kurtosis for both equations. Similarly, in Scenario 2, we derived data for SE and OE from a mixture of two truncated normal distributions, leading to negative kurtosis for both equations.
In Scenarios 3 and 4, we mixed the two distributions such that either SE or OE had positive kurtosis while the other had negative kurtosis. In Scenario 3, we generated data for SE from a mixture of two truncated normal distributions while deriving data for OE from the Laplace distribution. Thus, in this scenario, the excess SE and OE kurtoses were negative and positive, respectively. In Scenario 4, we generated data for SE from the Laplace distribution and derived data for OE from a mixture of two truncated normal distributions so that the excess SE and OE kurtoses were positive and negative, respectively.
Based on these scenarios, we generated 1,000 observations, with the first 500 used as the training set and the remaining 500 as the test set. The average ratio of the minority class was about 0.3. As expected, ZILBoost and ZIPBoost were preferable in Scenarios 1 and 2, respectively. In Scenarios 3 and 4, ZILBoost and ZIPBoost, respectively, were preferable. This suggests that the OE data–generating process determines the performance of the proposed algorithms.
Scenario 1. Excess kurtoses of SE and OE are positive:
where \(\left({\beta }_{0},{\beta }_{1}\right)=(0, 1)\), \(\left({\gamma }_{0},{\gamma }_{1}\right)=(0, 1)\), \({x}_{i}\sim L(0, 1)\), \({z}_{i}\sim L(\text{1,1})\), and \({u}_{i}\) and \({\varepsilon }_{i}\) are iid with \(N\left(\text{0,2}\right).\)
Scenario 2. Excess kurtoses of SE and OE are negative:
where \(\left({\beta }_{0},{\beta }_{1}\right)=(-1, 1)\), \(\left({\gamma }_{0},{\gamma }_{1}\right)=(0, 1)\), \({x}_{i}\) \(\sim \) 0.75 \(TN\left(-1, 2, \left[-2, 2\right]\right)+0.25TN\left(0, 1.5, \left[-\text{1,6}\right]\right)\), \({z}_{i}\sim \) 0.25 \(TN\left(-2, 1, \left[-3, 1\right]\right)+0.75TN\left(2, 1, \left[-\text{1,3}\right]\right)\), and \({u}_{i}\) and \({\varepsilon }_{i}\) are iid with \(N\left(\text{0,2}\right).\)
Scenario 3. Excess kurtoses of SE and OE are negative and positive, respectively:
where \(\left({\beta }_{0},{\beta }_{1}\right)=(0, 1)\), \(\left({\gamma }_{0},{\gamma }_{1}\right)=(0, 1)\), \({x}_{i}\) \({x}_{i}\) \(\sim \) 0.75 \(TN\left(-1, 2, \left[-2, 2\right]\right)+0.25TN\left(0, 1.5, \left[-\text{1,6}\right]\right)\), \({z}_{i}\sim L(\text{1,1})\), and \({u}_{i}\) and \({\varepsilon }_{i}\) are iid with \(N\left(\text{0,2}\right).\)
Scenario 4. Excess kurtoses of SE and OE are positive and negative, respectively.
where \(\left({\beta }_{0},{\beta }_{1}\right)=(0, 1)\), \(\left({\gamma }_{0},{\gamma }_{1}\right)=(0, 1)\), \({x}_{i}\sim L(\text{0,1})\), \({z}_{i}\sim \) 0.25 \(TN\left(-2, 1, \left[-3, 1\right]\right)+0.75TN\left(2, 1, \left[-\text{1,3}\right]\right)\), and \({u}_{i}\) and \({\varepsilon }_{i}\) are iid with \(N\left(\text{0,2}\right).\)
Due to space constraints, the simulation results presented in Appendix D1 focus on the performance of the test data. In this simulation, the overall performance measured by macro F-score and MCC depended on OE kurtosis signs. More specifically, we found that for Scenarios 1 and 2, the kurtosis of OE determined overall performance: When both equations provided positive excess kurtosis, ZILBoost produced more accurate predictions than ZIPBoost; with negative excess kurtosis, ZIPBoost was preferable. Similarly, for Scenarios 3 and 4, we discovered that relative performance relied on the kurtosis of OE. When OE exhibited positive kurtosis, ZILBoost provided better overall predictive performance, while negative OE kurtosis yielded a higher macro F-score and MCC in ZIPBoost. This is consistent with findings in the literature (Chen & Tsurumi, 2010).
Notably, ZILBoost showed better predictive performance for the minority class than ZIPBoost across all scenarios. In contrast, ZIPBoost outperformed ZILBoost in terms of majority-class F-scores. This implies that favor toward the minority class involves sacrificing the majority class’s predictive performance. This is consistent with the fact that the logit model is more robust to outliers than the probit model (Copas, 1988).
4.1 Appendix D1 Comparison of ZILBoost and ZIPBoost
Scenario 1 (Excess kurtoses of SE and OE are positive) | Scenario 2 (Excess kurtoses of SE and OE are negative) | |||
|---|---|---|---|---|
ZILBoost | ZIPBoost | ZILBoost | ZIPBoost | |
F-score: minority | 0.557 (0.030) | 0.386 (0.146) | 0.610 (0.028) | 0.563 (0.070) |
F-score: majority | 0.667 (0.047) | 0.764 (0.036) | 0.569 (0.066) | 0.692 (0.042) |
Macro F-score | 0.612 (0.028) | 0.575 (0.063) | 0.589 (0.039) | 0.627 (0.033) |
MCC | 0.278 (0.042) | 0.200 (0.083) | 0.243 (0.056) | 0.270 (0.049) |
Scenario 3 (Excess kurtoses of SE and OE are negative and positive, respectively) | Scenario 4 (Excess kurtoses of SE and OE are positive and negative, respectively) | |||
|---|---|---|---|---|
ZILBoost | ZIPBoost | ZILBoost | ZIPBoost | |
F-score: minority | 0.544 (0.058) | 0.481 (0.124) | 0.602 (0.028) | 0.535 (0.082) |
F-score: majority | 0.673 (0.048) | 0.727 (0.045) | 0.570 (0.064) | 0.699 (0.065) |
Macro F-score | 0.608 (0.038) | 0.604 (0.032) | 0.586 (0.036) | 0.617 (0.035) |
MCC | 0.253 (0.061) | 0.241 (0.072) | 0.253 (0.048) | 0.268 (0.047) |
Standard errors are in parentheses. Entries in bold indicate the best performance in each scenario.
Appendix E. Results for 36 imbalanced datasets
5.1 Appendix E1 Results of the experiments using test data
AdaBoost | LogitBoost | ProbitBoost | AdaC2 | SMOTEBoost -C.50 | GANs-GBM | ZIPBoost | ZILBoost | |
|---|---|---|---|---|---|---|---|---|
haberman | ||||||||
F-score: minority | 0.388 | 0.222 | 0.122 | 0.500 | 0.449 | 0.328 | 0.082 | 0.547 |
F-score: majority | 0.828 | 0.833 | 0.833 | 0.578 | 0.774 | 0.833 | 0.825 | 0.839 |
Macro F-score | 0.608 | 0.528 | 0.478 | 0.539 | 0.612 | 0.580 | 0.453 | 0.648 |
MCC | 0.258 | 0.183 | 0.127 | 0.221 | 0.224 | 0.235 | 0.046 | 0.328 |
iris0 | ||||||||
F-score: minority | 1.000 | 1.000 | 1.000 | 1.000 | 0.962 | 1.000 | 1.000 | 1.000 |
F-score: majority | 1.000 | 1.000 | 1.000 | 1.000 | 0.980 | 1.000 | 1.000 | 1.000 |
Macro F-score | 1.000 | 1.000 | 1.000 | 1.000 | 0.971 | 1.000 | 1.000 | 1.000 |
MCC | 1.000 | 1.000 | 1.000 | 1.000 | 0.943 | 1.000 | 1.000 | 1.000 |
new-thyroid1 | ||||||||
F-score: minority | 0.933 | 0.970 | 1.000 | 0.914 | 0.933 | 0.903 | 0.815 | 0.909 |
F-score: majority | 0.989 | 0.994 | 1.000 | 0.983 | 0.989 | 0.984 | 0.973 | 0.983 |
Macro F-score | 0.961 | 0.982 | 1.000 | 0.949 | 0.961 | 0.943 | 0.894 | 0.946 |
MCC | 0.925 | 0.965 | 1.000 | 0.902 | 0.925 | 0.887 | 0.807 | 0.893 |
new-thyroid2 | ||||||||
F-score: minority | 0.974 | 0.947 | 0.923 | 0.826 | 0.947 | 0.857 | 0.974 | 0.974 |
F-score: majority | 0.994 | 0.989 | 0.983 | 0.952 | 0.989 | 0.972 | 0.994 | 0.994 |
Macro F-score | 0.984 | 0.968 | 0.953 | 0.889 | 0.968 | 0.915 | 0.984 | 0.984 |
MCC | 0.969 | 0.936 | 0.906 | 0.800 | 0.936 | 0.834 | 0.969 | 0.969 |
ecoli1 | ||||||||
F-score: minority | 0.757 | N.A | N.A | 0.766 | 0.767 | 0.000 | N.A | N.A |
F-score: majority | 0.931 | N.A | N.A | 0.909 | 0.920 | 0.876 | N.A | N.A |
Macro F-score | 0.844 | N.A | N.A | 0.838 | 0.844 | 0.438 | N.A | N.A |
MCC | 0.688 | N.A | N.A | 0.711 | 0.702 | 0.000 | N.A | N.A |
ecoli2 | ||||||||
F-score: minority | 0.830 | N.A | N.A | 0.600 | 0.830 | 0.000 | N.A | N.A |
F-score: majority | 0.968 | N.A | N.A | 0.875 | 0.968 | 0.916 | N.A | N.A |
Macro F-score | 0.899 | N.A | N.A | 0.738 | 0.899 | 0.458 | N.A | N.A |
MCC | 0.799 | N.A | N.A | 0.551 | 0.799 | 0.000 | N.A | N.A |
ecoli3 | ||||||||
F-score: minority | 0.483 | 0.643 | 0.645 | 0.435 | 0.629 | 0.000 | 0.645 | 0.485 |
F-score: majority | 0.951 | 0.968 | 0.964 | 0.910 | 0.957 | 0.960 | 0.964 | 0.944 |
Macro F-score | 0.717 | 0.805 | 0.805 | 0.673 | 0.793 | 0.480 | 0.805 | 0.714 |
MCC | 0.437 | 0.612 | 0.620 | 0.418 | 0.614 | 0.000 | 0.620 | 0.444 |
ecoli-0_vs_1 | ||||||||
F-score: minority | 0.975 | N.A | N.A | 0.897 | 0.975 | 0.000 | N.A | N.A |
F-score: majority | 0.986 | N.A | N.A | 0.932 | 0.986 | 0.785 | N.A | N.A |
Macro F-score | 0.980 | N.A | N.A | 0.915 | 0.980 | 0.392 | N.A | N.A |
MCC | 0.961 | N.A | N.A | 0.842 | 0.961 | 0.000 | N.A | N.A |
yeast1 | ||||||||
F-score: minority | 0.750 | 0.784 | 0.734 | 0.758 | 0.800 | 0.745 | 0.494 | 0.538 |
F-score: majority | 0.932 | 0.939 | 0.918 | 0.905 | 0.932 | 0.901 | 0.840 | 0.818 |
Macro F-score | 0.841 | 0.861 | 0.826 | 0.832 | 0.866 | 0.823 | 0.667 | 0.678 |
MCC | 0.682 | 0.723 | 0.655 | 0.702 | 0.745 | 0.681 | 0.346 | 0.356 |
yeast3 | ||||||||
F-score: minority | 0.744 | 0.710 | 0.680 | 0.738 | 0.782 | 0.000 | 0.821 | 0.755 |
F-score: majority | 0.968 | 0.966 | 0.965 | 0.958 | 0.970 | 0.941 | 0.976 | 0.973 |
Macro F-score | 0.856 | 0.838 | 0.823 | 0.848 | 0.876 | 0.471 | 0.899 | 0.874 |
MCC | 0.712 | 0.678 | 0.652 | 0.716 | 0.755 | 0.000 | 0.798 | 0.749 |
pima | ||||||||
F-score: minority | 0.626 | 0.656 | 0.627 | 0.609 | 0.586 | 0.546 | 0.641 | 0.655 |
F-score: majority | 0.827 | 0.825 | 0.821 | 0.635 | 0.802 | 0.796 | 0.817 | 0.798 |
Macro F-score | 0.726 | 0.741 | 0.724 | 0.622 | 0.694 | 0.671 | 0.729 | 0.726 |
MCC | 0.458 | 0.482 | 0.450 | 0.349 | 0.390 | 0.350 | 0.459 | 0.457 |
glass0 | ||||||||
F-score: minority | 0.738 | 0.690 | 0.642 | 0.729 | 0.771 | 0.000 | 0.640 | 0.649 |
F-score: majority | 0.831 | 0.787 | 0.782 | 0.780 | 0.855 | 0.791 | 0.806 | 0.803 |
Macro F-score | 0.784 | 0.739 | 0.712 | 0.755 | 0.813 | 0.000 | 0.723 | 0.726 |
MCC | 0.584 | 0.501 | 0.431 | 0.577 | 0.639 | 0.000 | 0.446 | 0.454 |
glass1 | ||||||||
F-score: minority | 0.738 | 0.690 | 0.642 | 0.729 | 0.771 | 0.000 | 0.431 | 0.412 |
F-score: majority | 0.871 | 0.753 | 0.737 | 0.726 | 0.839 | 0.762 | 0.752 | 0.726 |
Macro F-score | 0.784 | 0.739 | 0.712 | 0.728 | 0.813 | 0.381 | 0.591 | 0.569 |
MCC | 0.584 | 0.501 | 0.431 | 0.577 | 0.639 | 0.000 | 0.198 | 0.145 |
glass6 | ||||||||
F-score: minority | 0.769 | 0.769 | 0.720 | 0.579 | 0.741 | 0.769 | 0.909 | 0.833 |
F-score: majority | 0.968 | 0.968 | 0.963 | 0.909 | 0.963 | 0.968 | 0.990 | 0.979 |
Macro F-score | 0.869 | 0.869 | 0.841 | 0.744 | 0.852 | 0.869 | 0.949 | 0.906 |
MCC | 0.740 | 0.740 | 0.684 | 0.558 | 0.710 | 0.740 | 0.903 | 0.812 |
glass-0-1-2-3 vs 4-5-6 | ||||||||
F-score: minority | 0.750 | 0.800 | 0.714 | 0.815 | 0.844 | 0.800 | 0.886 | 0.818 |
F-score: majority | 0.943 | 0.947 | 0.930 | 0.938 | 0.959 | 0.939 | 0.929 | 0.953 |
Macro F-score | 0.846 | 0.873 | 0.822 | 0.877 | 0.902 | 0.870 | 0.834 | 0.886 |
MCC | 0.706 | 0.747 | 0.650 | 0.769 | 0.803 | 0.744 | 0.668 | 0.773 |
wisconsin | ||||||||
F-score: minority | 0.958 | 0.934 | 0.938 | 0.946 | 0.963 | 0.938 | 0.882 | 0.944 |
F-score: majority | 0.981 | 0.970 | 0.973 | 0.974 | 0.983 | 0.969 | 0.950 | 0.974 |
Macro F-score | 0.969 | 0.952 | 0.955 | 0.960 | 0.973 | 0.953 | 0.916 | 0.959 |
MCC | 0.939 | 0.905 | 0.911 | 0.921 | 0.946 | 0.908 | 0.835 | 0.918 |
ecoli-0-1-3-7_vs_2-6 | ||||||||
F-score: minority | 0.667 | N.A | N.A | 0.500 | 0.400 | 0.000 | N.A | N.A |
F-score: majority | 0.993 | N.A | N.A | 0.970 | 0.978 | 0.986 | N.A | N.A |
Macro F-score | 0.830 | N.A | N.A | 0.735 | 0.689 | 0.493 | N.A | N.A |
MCC | 0.702 | N.A | N.A | 0.560 | 0.387 | 0.000 | N.A | N.A |
ecoli4 | ||||||||
F-score: minority | 0.727 | N.A | N.A | 0.750 | 0.783 | 0.000 | N.A | N.A |
F-score: majority | 0.981 | N.A | N.A | 0.981 | 0.984 | 0.966 | N.A | N.A |
Macro F-score | 0.854 | N.A | N.A | 0.866 | 0.883 | 0.483 | N.A | N.A |
MCC | 0.708 | N.A | N.A | 0.734 | 0.768 | 0.000 | N.A | N.A |
yeast-1_vs_7 | ||||||||
F-score: minority | 0.300 | 0.118 | 0.125 | 0.200 | 0.250 | 0.000 | 0.111 | 0.133 |
F-score: majority | 0.968 | 0.966 | 0.968 | 0.879 | 0.944 | 0.971 | 0.964 | 0.971 |
Macro F-score | 0.634 | 0.542 | 0.547 | 0.540 | 0.597 | 0.486 | 0.537 | 0.552 |
MCC | 0.285 | 0.111 | 0.138 | 0.156 | 0.200 | 0.000 | 0.092 | 0.180 |
abalone9-18 | ||||||||
F-score: minority | 0.194 | 0.550 | 0.579 | 0.312 | 0.346 | 0.391 | 0.650 | 0.619 |
F-score: majority | 0.964 | 0.974 | 0.977 | 0.919 | 0.950 | 0.918 | 0.980 | 0.977 |
Macro F-score | 0.579 | 0.762 | 0.778 | 0.616 | 0.648 | 0.654 | 0.815 | 0.798 |
MCC | 0.175 | 0.525 | 0.560 | 0.287 | 0.305 | 0.404 | 0.631 | 0.596 |
abalone19 | ||||||||
F-score: minority | 0.000 | 0.000 | 0.000 | 0.018 | 0.043 | 0.000 | 0.000 | 0.000 |
F-score: majority | 0.996 | 0.997 | 0.997 | 0.973 | 0.978 | 0.953 | 0.997 | 0.996 |
Macro F-score | 0.498 | 0.499 | 0.499 | 0.496 | 0.511 | 0.477 | 0.499 | 0.498 |
MCC | -0.002 | 0.000 | 0.000 | 0.010 | 0.045 | -0.025 | 0.000 | -0.004 |
yeast-0-5-6-7-9_vs_4 | ||||||||
F-score: minority | 0.519 | 0.500 | 0.432 | 0.476 | 0.484 | 0.000 | 0.655 | 0.612 |
F-score: majority | 0.945 | 0.955 | 0.957 | 0.901 | 0.931 | 0.948 | 0.960 | 0.960 |
Macro F-score | 0.732 | 0.727 | 0.695 | 0.689 | 0.708 | 0.000 | 0.807 | 0.786 |
MCC | 0.464 | 0.465 | 0.440 | 0.439 | 0.424 | 0.000 | 0.616 | 0.574 |
yeast-1-2-8-9_vs_7 | ||||||||
F-score: minority | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.286 |
F-score: majority | 0.986 | 0.989 | 0.989 | 0.967 | 0.975 | 0.989 | 0.989 | 0.934 |
Macro F-score | 0.493 | 0.495 | 0.495 | 0.484 | 0.488 | 0.495 | 0.495 | 0.635 |
MCC | -0.012 | 0.000 | 0.000 | -0.031 | -0.025 | 0.000 | 0.000 | 0.270 |
yeast-1-4-5-8_vs_7 | ||||||||
F-score: minority | 0.118 | 0.000 | 0.000 | 0.184 | 0.308 | 0.000 | 0.000 | 0.095 |
F-score: majority | 0.978 | 0.972 | 0.981 | 0.883 | 0.959 | 0.981 | 0.981 | 0.972 |
Macro F-score | 0.548 | 0.486 | 0.491 | 0.534 | 0.633 | 0.491 | 0.491 | 0.534 |
MCC | 0.121 | -0.026 | 0.000 | 0.194 | 0.290 | 0.000 | 0.000 | 0.071 |
yeast-2_vs_4 | ||||||||
F-score: minority | 0.739 | N.A | N.A | 0.754 | 0.745 | 0.000 | N.A | N.A |
F-score: majority | 0.974 | N.A | N.A | 0.967 | 0.972 | 0.953 | N.A | N.A |
Macro F-score | 0.857 | N.A | N.A | 0.861 | 0.859 | 0.477 | N.A | N.A |
MCC | 0.713 | N.A | N.A | 0.753 | 0.722 | 0.000 | N.A | N.A |
yeast-2_vs_8 | ||||||||
F-score: minority | 0.182 | 0.462 | 0.364 | 0.276 | 0.364 | 0.000 | 0.364 | 0.462 |
F-score: majority | 0.981 | 0.985 | 0.985 | 0.954 | 0.985 | 0.983 | 0.985 | 0.985 |
Macro F-score | 0.581 | 0.723 | 0.674 | 0.615 | 0.674 | 0.492 | 0.674 | 0.723 |
MCC | 0.188 | 0.461 | 0.397 | 0.271 | 0.397 | 0.000 | 0.397 | 0.461 |
yeast4 | ||||||||
F-score: minority | 0.378 | 0.294 | 0.074 | 0.373 | 0.417 | 0.000 | 0.074 | 0.316 |
F-score: majority | 0.984 | 0.983 | 0.983 | 0.967 | 0.981 | 0.982 | 0.983 | 0.982 |
Macro F-score | 0.681 | 0.639 | 0.528 | 0.670 | 0.699 | 0.491 | 0.528 | 0.649 |
MCC | 0.401 | 0.335 | 0.193 | 0.362 | 0.399 | 0.000 | 0.193 | 0.324 |
yeast5 | ||||||||
F-score: minority | 0.711 | 0.541 | 0.579 | 0.759 | 0.800 | 0.000 | 0.526 | 0.636 |
F-score: majority | 0.991 | 0.988 | 0.989 | 0.990 | 0.993 | 0.984 | 0.988 | 0.989 |
Macro F-score | 0.851 | 0.764 | 0.784 | 0.875 | 0.897 | 0.492 | 0.757 | 0.813 |
MCC | 0.704 | 0.556 | 0.591 | 0.761 | 0.794 | 0.000 | 0.535 | 0.628 |
yeast6 | ||||||||
F-score: minority | 0.500 | 0.400 | 0.240 | 0.364 | 0.545 | 0.000 | 0.000 | 0.478 |
F-score: majority | 0.988 | 0.986 | 0.987 | 0.960 | 0.986 | 0.986 | 0.986 | 0.983 |
Macro F-score | 0.744 | 0.693 | 0.613 | 0.662 | 0.766 | 0.493 | 0.493 | 0.731 |
MCC | 0.495 | 0.394 | 0.320 | 0.400 | 0.532 | 0.000 | 0.000 | 0.464 |
glass-0-1-6_vs_2 | ||||||||
F-score: minority | 0.182 | 0.000 | 0.000 | 0.190 | 0.200 | 0.118 | 0.235 | 0.100 |
F-score: Majority | 0.950 | 0.921 | 0.933 | 0.773 | 0.956 | 0.914 | 0.926 | 0.895 |
Macro F-score | 0.566 | 0.461 | 0.467 | 0.482 | 0.578 | 0.516 | 0.581 | 0.498 |
MCC | 0.142 | -0.079 | -0.066 | 0.121 | 0.180 | 0.036 | 0.167 | 0.006 |
glass-0-1-6_vs_5 | ||||||||
F-score: minority | 0.889 | 0.889 | 0.800 | 0.545 | 0.727 | 0.000 | 0.889 | 0.889 |
F-score: majority | 0.994 | 0.994 | 0.989 | 0.971 | 0.983 | 0.978 | 0.994 | 0.994 |
Macro F-score | 0.942 | 0.942 | 0.894 | 0.758 | 0.855 | 0.489 | 0.942 | 0.942 |
MCC | 0.889 | 0.889 | 0.807 | 0.542 | 0.743 | 0.000 | 0.889 | 0.889 |
glass2 | ||||||||
F-score: minority | 0.286 | 0.276 | 0.296 | 0.213 | 0.364 | 0.000 | 0.455 | 0.500 |
F-score: majority | 0.922 | 0.886 | 0.898 | 0.778 | 0.927 | 0.966 | 0.938 | 0.948 |
Macro F-score | 0.604 | 0.581 | 0.597 | 0.500 | 0.645 | 0.483 | 0.696 | 0.724 |
MCC | 0.234 | 0.239 | 0.261 | 0.186 | 0.329 | 0.000 | 0.438 | 0.480 |
glass4 | ||||||||
F-score: minority | 0.000 | 0.167 | 0.154 | 0.727 | 0.400 | 0.000 | 0.778 | 0.824 |
F-score: majority | 0.946 | 0.950 | 0.945 | 0.969 | 0.955 | 0.956 | 0.980 | 0.985 |
Macro F-score | 0.473 | 0.559 | 0.550 | 0.848 | 0.677 | 0.478 | 0.879 | 0.904 |
MCC | -0.042 | 0.153 | 0.118 | 0.712 | 0.365 | 0.000 | 0.757 | 0.810 |
glass5 | ||||||||
F-score: minority | 0.444 | 0.333 | 0.400 | 0.667 | 0.667 | 0.000 | 1.000 | 0.667 |
F-score: majority | 0.976 | 0.981 | 0.986 | 0.990 | 0.990 | 0.991 | 1.000 | 0.995 |
Macro F-score | 0.710 | 0.657 | 0.693 | 0.829 | 0.829 | 0.496 | 1.000 | 0.831 |
MCC | 0.522 | 0.337 | 0.395 | 0.700 | 0.700 | 0.000 | 1.000 | 0.704 |
shuttle-c0-vs-c4 | ||||||||
F-score: minority | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.991 |
F-score: majority | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.999 |
Macro F-score | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.995 |
MCC | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.991 |
shuttle-c2-vs-c4 | ||||||||
F-score: minority | 1.000 | 0.800 | 0.800 | 1.000 | 1.000 | 0.000 | 1.000 | 1.000 |
F-score: majority | 1.000 | 0.992 | 0.992 | 1.000 | 1.000 | 0.984 | 1.000 | 1.000 |
Macro F-score | 1.000 | 0.896 | 0.896 | 1.000 | 1.000 | 0.492 | 1.000 | 1.000 |
MCC | 1.000 | 0.810 | 0.810 | 1.000 | 1.000 | 0.000 | 1.000 | 1.000 |
SMOTEBoost-Cart | SMOTEBoost -RF | SMOTEBoost -NB | SMOTEBoost -SVM | GANs-Logit | GANs-DT | GANs-RF | GANs-SVM | |
|---|---|---|---|---|---|---|---|---|
haberman | ||||||||
F-score: minority | 0.521 | 0.300 | 0.493 | 0.430 | 0.282 | 0.319 | 0.286 | 0.242 |
F-score: majority | 0.781 | 0.752 | 0.841 | 0.802 | 0.754 | 0.802 | 0.815 | 0.792 |
Macro F-score | 0.651 | 0.526 | 0.667 | 0.616 | 0.518 | 0.560 | 0.550 | 0.517 |
MCC | 0.306 | 0.056 | 0.356 | 0.238 | 0.042 | 0.149 | 0.155 | 0.069 |
iris0 | ||||||||
F-score: minority | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
F-score: majority | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
Macro F-score | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
MCC | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
new-thyroid1 | ||||||||
F-score: minority | 0.994 | 0.994 | 1.000 | 1.000 | 0.994 | 0.972 | 0.995 | 1.000 |
F-score: majority | 0.970 | 0.970 | 1.000 | 1.000 | 0.970 | 0.848 | 0.968 | 1.000 |
Macro F-score | 0.982 | 0.982 | 1.000 | 1.000 | 0.982 | 0.910 | 0.981 | 1.000 |
MCC | 0.965 | 0.965 | 1.000 | 1.000 | 0.965 | 0.821 | 0.963 | 1.000 |
new-thyroid2 | ||||||||
F-score: minority | 0.923 | 0.923 | 0.884 | 0.974 | 0.974 | 0.857 | 0.973 | 0.974 |
F-score: majority | 0.983 | 0.983 | 0.971 | 0.994 | 0.994 | 0.972 | 0.994 | 0.994 |
Macro F-score | 0.953 | 0.953 | 0.927 | 0.984 | 0.984 | 0.915 | 0.983 | 0.984 |
MCC | 0.906 | 0.906 | 0.864 | 0.969 | 0.969 | 0.834 | 0.968 | 0.969 |
ecoli1 | ||||||||
F-score: minority | 0.824 | 0.776 | 0.737 | 0.721 | 0.727 | 0.703 | 0.780 | N.A |
F-score: majority | 0.940 | 0.924 | 0.896 | 0.904 | 0.919 | 0.916 | 0.929 | N.A |
Macro F-score | 0.882 | 0.850 | 0.817 | 0.812 | 0.823 | 0.809 | 0.855 | N.A |
MCC | 0.777 | 0.713 | 0.671 | 0.639 | 0.647 | 0.619 | 0.716 | N.A |
ecoli2 | ||||||||
F-score: minority | 0.815 | 0.815 | 0.759 | 0.793 | 0.680 | 0.696 | 0.800 | N.A |
F-score: majority | 0.965 | 0.965 | 0.950 | 0.957 | 0.944 | 0.952 | 0.969 | N.A |
Macro F-score | 0.890 | 0.890 | 0.854 | 0.875 | 0.812 | 0.824 | 0.885 | N.A |
MCC | 0.780 | 0.780 | 0.714 | 0.756 | 0.625 | 0.656 | 0.783 | N.A |
ecoli3 | ||||||||
F-score: minority | 0.595 | 0.562 | 0.000 | 0.606 | 0.625 | 0.462 | 0.455 | 0.621 |
F-score: majority | 0.950 | 0.954 | 0.960 | 0.957 | 0.961 | 0.955 | 0.962 | 0.964 |
Macro F-score | 0.772 | 0.758 | 0.480 | 0.782 | 0.793 | 0.708 | 0.708 | 0.792 |
MCC | 0.582 | 0.530 | 0.000 | 0.581 | 0.600 | 0.416 | 0.426 | 0.589 |
ecoli-0_vs_1 | ||||||||
F-score: minority | 0.963 | 0.951 | 0.951 | 0.975 | 0.962 | 1.000 | 1.000 | N.A |
F-score: majority | 0.978 | 0.971 | 0.971 | 0.986 | 0.979 | 1.000 | 1.000 | N.A |
Macro F-score | 0.971 | 0.961 | 0.961 | 0.980 | 0.970 | 1.000 | 1.000 | N.A |
MCC | 0.943 | 0.925 | 0.925 | 0.961 | 0.941 | 1.000 | 1.000 | N.A |
yeast1 | ||||||||
F-score: minority | 0.776 | 0.776 | 0.719 | 0.707 | 0.732 | 0.703 | 0.779 | 0.767 |
F-score: majority | 0.924 | 0.924 | 0.899 | 0.906 | 0.913 | 0.916 | 0.934 | 0.935 |
Macro F-score | 0.850 | 0.850 | 0.809 | 0.806 | 0.823 | 0.809 | 0.857 | 0.851 |
MCC | 0.713 | 0.713 | 0.638 | 0.619 | 0.652 | 0.619 | 0.715 | 0.703 |
yeast3 | ||||||||
F-score: minority | 0.791 | 0.750 | 0.232 | 0.705 | 0.702 | 0.798 | 0.708 | 0.721 |
F-score: majority | 0.971 | 0.966 | 0.288 | 0.960 | 0.966 | 0.975 | 0.969 | 0.969 |
Macro F-score | 0.881 | 0.858 | 0.260 | 0.832 | 0.834 | 0.886 | 0.838 | 0.845 |
MCC | 0.766 | 0.718 | 0.149 | 0.666 | 0.673 | 0.773 | 0.688 | 0.698 |
pima | ||||||||
F-score: minority | 0.654 | 0.630 | 0.649 | 0.608 | 0.641 | 0.602 | 0.634 | 0.588 |
F-score: majority | 0.826 | 0.814 | 0.821 | 0.796 | 0.817 | 0.798 | 0.828 | 0.795 |
Macro F-score | 0.740 | 0.722 | 0.735 | 0.702 | 0.729 | 0.700 | 0.731 | 0.692 |
MCC | 0.480 | 0.445 | 0.470 | 0.404 | 0.459 | 0.400 | 0.466 | 0.384 |
glass0 | ||||||||
F-score: minority | 0.795 | 0.815 | 0.611 | 0.790 | 0.650 | 0.684 | 0.779 | 0.441 |
F-score: majority | 0.870 | 0.887 | 0.604 | 0.872 | 0.791 | 0.826 | 0.876 | 0.787 |
Macro F-score | 0.833 | 0.851 | 0.607 | 0.831 | 0.721 | 0.755 | 0.828 | 0.614 |
MCC | 0.678 | 0.710 | 0.351 | 0.670 | 0.446 | 0.511 | 0.657 | 0.262 |
glass1 | ||||||||
F-score: minority | 0.704 | 0.773 | 0.308 | 0.531 | 0.418 | 0.514 | 0.667 | 0.562 |
F-score: majority | 0.853 | 0.878 | 0.698 | 0.800 | 0.735 | 0.743 | 0.831 | 0.813 |
Macro F-score | 0.779 | 0.826 | 0.503 | 0.666 | 0.576 | 0.628 | 0.749 | 0.688 |
MCC | 0.562 | 0.651 | 0.018 | 0.354 | 0.163 | 0.257 | 0.500 | 0.399 |
glass6 | ||||||||
F-score: minority | 0.741 | 0.800 | 0.769 | 0.762 | 0.667 | 0.769 | 0.833 | 0.857 |
F-score: majority | 0.963 | 0.974 | 0.968 | 0.974 | 0.958 | 0.968 | 0.979 | 0.984 |
Macro F-score | 0.852 | 0.887 | 0.869 | 0.868 | 0.812 | 0.869 | 0.906 | 0.921 |
MCC | 0.710 | 0.774 | 0.740 | 0.746 | 0.625 | 0.740 | 0.812 | 0.853 |
glass-0-1-2-3 vs 4-5-6 | ||||||||
F-score: minority | 0.732 | 0.810 | 0.667 | 0.800 | 0.744 | 0.629 | 0.667 | 0.683 |
F-score: majority | 0.936 | 0.953 | 0.926 | 0.947 | 0.936 | 0.927 | 0.926 | 0.925 |
Macro F-score | 0.834 | 0.882 | 0.796 | 0.873 | 0.840 | 0.778 | 0.796 | 0.804 |
MCC | 0.677 | 0.769 | 0.610 | 0.747 | 0.683 | 0.607 | 0.610 | 0.616 |
wisconsin | ||||||||
F-score: minority | 0.963 | 0.953 | 0.938 | 0.907 | 0.954 | 0.949 | 0.958 | 0.946 |
F-score: majority | 0.983 | 0.979 | 0.973 | 0.957 | 0.978 | 0.976 | 0.981 | 0.974 |
Macro F-score | 0.973 | 0.966 | 0.955 | 0.932 | 0.966 | 0.963 | 0.969 | 0.960 |
MCC | 0.946 | 0.932 | 0.911 | 0.864 | 0.933 | 0.925 | 0.939 | 0.922 |
ecoli-0-1-3-7_vs_2-6 | ||||||||
F-score: minority | 0.364 | 0.444 | N.A | 0.000 | 0.889 | 0.000 | 0.000 | N.A |
F-score: majority | 0.974 | 0.982 | N.A | 0.986 | 0.996 | 0.986 | 0.986 | N.A |
Macro F-score | 0.669 | 0.713 | N.A | 0.493 | 0.943 | 0.493 | 0.493 | N.A |
MCC | 0.354 | 0.429 | N.A | 0.000 | 0.891 | 0.000 | 0.000 | N.A |
ecoli4 | ||||||||
F-score: minority | 0.783 | 0.857 | 0.857 | 0.833 | 0.769 | 0.700 | 0.706 | N.A |
F-score: majority | 0.984 | 0.990 | 0.990 | 0.987 | 0.981 | 0.981 | 0.984 | N.A |
Macro F-score | 0.883 | 0.924 | 0.924 | 0.910 | 0.875 | 0.841 | 0.845 | N.A |
MCC | 0.768 | 0.849 | 0.849 | 0.824 | 0.761 | 0.685 | 0.727 | N.A |
yeast-1_vs_7 | ||||||||
F-score: minority | 0.211 | 0.258 | 0.126 | 0.303 | 0.111 | 0.000 | 0.235 | 0.267 |
F-score: majority | 0.929 | 0.946 | 0.286 | 0.946 | 0.964 | 0.971 | 0.971 | 0.975 |
Macro F-score | 0.570 | 0.602 | 0.206 | 0.624 | 0.537 | 0.486 | 0.603 | 0.621 |
MCC | 0.156 | 0.209 | 0.106 | 0.258 | 0.092 | 0.000 | 0.255 | 0.383 |
abalone9-18 | ||||||||
F-score: minority | 0.327 | 0.298 | 0.244 | 0.279 | 0.537 | 0.000 | 0.160 | 0.308 |
F-score: majority | 0.945 | 0.952 | 0.904 | 0.955 | 0.972 | 0.965 | 0.970 | 0.974 |
Macro F-score | 0.636 | 0.625 | 0.574 | 0.617 | 0.755 | 0.482 | 0.565 | 0.641 |
MCC | 0.285 | 0.252 | 0.205 | 0.234 | 0.509 | − 0.026 | 0.200 | 0.376 |
abalone19 | ||||||||
F-score: minority | 0.038 | 0.029 | 0.017 | 0.019 | 0.000 | 0.000 | 0.000 | 0.000 |
F-score: majority | 0.962 | 0.984 | 0.871 | 0.975 | 0.989 | 0.996 | 0.997 | 0.994 |
Macro F-score | 0.500 | 0.506 | 0.444 | 0.497 | 0.495 | 0.498 | 0.499 | 0.497 |
MCC | 0.047 | 0.023 | 0.012 | 0.011 | − 0.010 | − 0.003 | 0.000 | − 0.006 |
yeast-0-5-6-7-9_vs_4 | ||||||||
F-score: minority | 0.581 | 0.464 | 0.000 | 0.509 | 0.180 | 0.175 | 0.206 | 0.000 |
F-score: majority | 0.944 | 0.936 | 0.940 | 0.943 | 0.008 | 0.103 | 0.373 | 0.935 |
Macro F-score | 0.762 | 0.700 | 0.470 | 0.726 | 0.094 | 0.139 | 0.289 | 0.468 |
MCC | 0.535 | 0.402 | − 0.041 | 0.453 | 0.020 | − 0.029 | 0.112 | − 0.050 |
yeast-1-2-8-9_vs_7 | ||||||||
F-score: minority | 0.000 | 0.000 | 0.041 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
F-score: majority | 0.971 | 0.974 | 0.339 | 0.956 | 0.989 | 0.988 | 0.988 | 0.989 |
Macro F-score | 0.485 | 0.487 | 0.190 | 0.478 | 0.495 | 0.494 | 0.494 | 0.495 |
MCC | -0.028 | -0.026 | 0.002 | -0.038 | 0.000 | -0.007 | -0.007 | 0.000 |
yeast-1-4-5-8_vs_7 | ||||||||
F-score: minority | 0.279 | 0.303 | 0.079 | 0.238 | 0.000 | 0.000 | 0.000 | 0.000 |
F-score: majority | 0.952 | 0.965 | 0.170 | 0.951 | 0.981 | 0.981 | 0.979 | 0.981 |
Macro F-score | 0.616 | 0.634 | 0.124 | 0.595 | 0.495 | 0.495 | 0.490 | 0.495 |
MCC | 0.263 | 0.277 | 0.062 | 0.215 | 0.000 | 0.000 | -0.011 | 0.000 |
yeast-2_vs_4 | ||||||||
F-score: minority | 0.755 | 0.784 | 0.679 | 0.714 | 0.698 | 0.684 | 0.844 | NA |
F-score: majority | 0.972 | 0.976 | 0.961 | 0.965 | 0.972 | 0.975 | 0.985 | NA |
Macro F-score | 0.863 | 0.880 | 0.820 | 0.840 | 0.835 | 0.830 | 0.915 | NA |
MCC | 0.735 | 0.765 | 0.654 | 0.695 | 0.672 | 0.678 | 0.830 | NA |
yeast-2_vs_8 | ||||||||
F-score: minority | 0.364 | 0.364 | 0.111 | 0.308 | 0.364 | 0.364 | 0.364 | 0.364 |
F-score: majority | 0.985 | 0.985 | 0.966 | 0.981 | 0.985 | 0.985 | 0.985 | 0.985 |
Macro F-score | 0.674 | 0.674 | 0.538 | 0.644 | 0.674 | 0.674 | 0.674 | 0.674 |
MCC | 0.397 | 0.397 | 0.078 | 0.298 | 0.397 | 0.397 | 0.397 | 0.397 |
yeast4 | ||||||||
F-score: minority | 0.393 | 0.391 | 0.085 | 0.415 | 0.143 | 0.303 | 0.143 | 0.000 |
F-score: majority | 0.976 | 0.981 | 0.477 | 0.978 | 0.984 | 0.984 | 0.984 | 0.982 |
Macro F-score | 0.685 | 0.686 | 0.281 | 0.697 | 0.563 | 0.644 | 0.563 | 0.491 |
MCC | 0.370 | 0.376 | 0.079 | 0.394 | 0.273 | 0.360 | 0.273 | 0.000 |
yeast5 | ||||||||
F-score: minority | 0.750 | 0.784 | 0.378 | 0.735 | 0.579 | 0.323 | 0.452 | 0.345 |
F-score: majority | 0.992 | 0.992 | 0.942 | 0.991 | 0.989 | 0.986 | 0.988 | 0.987 |
Macro F-score | 0.871 | 0.888 | 0.660 | 0.863 | 0.784 | 0.654 | 0.720 | 0.666 |
MCC | 0.742 | 0.778 | 0.455 | 0.726 | 0.591 | 0.376 | 0.534 | 0.451 |
yeast6 | ||||||||
F-score: minority | 0.500 | 0.512 | 0.115 | 0.500 | 0.345 | 0.619 | 0.320 | 0.000 |
F-score: majority | 0.983 | 0.985 | 0.729 | 0.983 | 0.987 | 0.989 | 0.988 | 0.986 |
Macro F-score | 0.742 | 0.749 | 0.422 | 0.742 | 0.666 | 0.804 | 0.654 | 0.493 |
MCC | 0.488 | 0.497 | 0.176 | 0.488 | 0.376 | 0.608 | 0.431 | 0.000 |
glass-0-1-6_vs_2 | ||||||||
F-score: minority | 0.182 | 0.000 | 0.000 | 0.190 | 0.200 | 0.118 | 0.667 | 0.113 |
F-score: majority | 0.950 | 0.921 | 0.933 | 0.773 | 0.956 | 0.914 | 0.978 | 0.927 |
Macro F-score | 0.566 | 0.461 | 0.467 | 0.592 | 0.578 | 0.516 | 0.822 | 0.530 |
MCC | 0.142 | -0.079 | -0.066 | 0.121 | 0.180 | 0.036 | 0.656 | 0.060 |
glass-0-1-6_vs_5 | ||||||||
F-score: minority | 0.600 | 0.700 | 0.571 | 0.889 | 0.800 | 0.000 | 0.000 | 0.000 |
F-score: majority | 0.977 | 0.989 | 0.965 | 0.994 | 0.989 | 0.978 | 0.972 | 0.978 |
Macro F-score | 0.789 | 0.894 | 0.768 | 0.942 | 0.894 | 0.489 | 0.486 | 0.489 |
MCC | 0.591 | 0.807 | 0.611 | 0.889 | 0.807 | 0.000 | -0.022 | 0.000 |
glass2 | ||||||||
F-score: minority | 0.308 | 0.250 | 0.169 | 0.375 | 0.308 | 0.286 | 0.182 | 0.000 |
F-score: majority | 0.904 | 0.905 | 0.587 | 0.949 | 0.904 | 0.950 | 0.956 | 0.966 |
Macro F-score | 0.606 | 0.578 | 0.378 | 0.662 | 0.606 | 0.618 | 0.569 | 0.483 |
MCC | 0.273 | 0.195 | 0.140 | 0.328 | 0.273 | 0.236 | 0.147 | 0.000 |
glass4 | ||||||||
F-score: minority | 0.462 | 0.429 | 0.500 | 0.308 | 0.000 | 0.000 | 0.000 | 0.000 |
F-score: majority | 0.965 | 0.960 | 0.970 | 0.955 | 0.935 | 0.956 | 0.956 | 0.956 |
Macro F-score | 0.713 | 0.694 | 0.735 | 0.631 | 0.468 | 0.478 | 0.478 | 0.478 |
MCC | 0.473 | 0.412 | 0.560 | 0.295 | -0.050 | 0.000 | 0.000 | 0.000 |
glass5 | ||||||||
F-score: minority | 0.667 | 0.333 | 0.400 | 0.667 | 0.286 | 0.000 | 0.667 | 0.000 |
F-score: majority | 0.990 | 0.981 | 0.971 | 0.995 | 0.976 | 0.991 | 0.990 | 0.991 |
Macro F-score | 0.829 | 0.657 | 0.685 | 0.831 | 0.631 | 0.496 | 0.829 | 0.496 |
MCC | 0.700 | 0.337 | 0.486 | 0.704 | 0.296 | 0.000 | 0.700 | 0.000 |
shuttle-c0-vs-c4 | ||||||||
F-score: minority | 1.000 | 1.000 | 1.000 | 0.983 | 0.982 | 1.000 | 1.000 | 0.966 |
zF-score: majority | 1.000 | 1.000 | 1.000 | 0.999 | 0.999 | 1.000 | 1.000 | 0.998 |
Macro F-score | 1.000 | 1.000 | 1.000 | 0.991 | 0.991 | 1.000 | 1.000 | 0.982 |
MCC | 1.000 | 1.000 | 1.000 | 0.982 | 0.981 | 1.000 | 1.000 | 0.964 |
shuttle-c2-vs-c4 | ||||||||
F-score: minority | 1.000 | 1.000 | 1.000 | 1.000 | 0.800 | 0.571 | 1.000 | 1.000 |
F-score: majority | 1.000 | 1.000 | 1.000 | 1.000 | 0.992 | 0.976 | 1.000 | 1.000 |
Macro F-score | 1.000 | 1.000 | 1.000 | 1.000 | 0.896 | 0.774 | 1.000 | 1.000 |
MCC | 1.000 | 1.000 | 1.000 | 1.000 | 0.810 | 0.617 | 1.000 | 1.000 |
Appendix F. Extension to multiclass problems
To extend the application of ZILBoost and ZIPBoost to problems with more than two classes, we assume \(J+1\) classes (i.e., possible outcomes) by defining a discrete random variable \(y\) \(\in \{\text{0,1},\dots , J\}\) that is observable. In multiclass problems, we aim to obtain a final classifier for each class. Let \(q\) denote a binary variable indicating the split between regime 0 and 1 via the mapping of a latent variable \({q}^{*}\): \(q=1\) for \({q}^{*}>0\) and \(q=0\) for \({q}^{*}\le 0\). In this setting, \({q}^{*}\) represents the propensity of regime 1 as
\({q}^{*}={{\varvec{x}}}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}+u\),
where \({\varvec{x}}\) indicates a vector of covariates that creates inflated zeros for the majority class, \({\varvec{\beta}}\) is a vector of coefficients, and \(u\) represents the error term. This equation represents the SE, which accounts for excess zeros.
Conditional on \(q=1\), the multi-class outcomes under regime 1 are represented by a discrete variable \(\widetilde{y} \left(\widetilde{y}=\text{0,1},\dots ,J\right)\), which is generated by an OE model via a second latent variable \({\widetilde{y}}^{*}\):
\({\widetilde{y}}^{*}={{\varvec{z}}}{\prime}{\varvec{\gamma}}+\varepsilon \),
where \({\varvec{z}}\) indicates a vector of covariates that generate the minority class, \({\varvec{\gamma}}\) is a vector of coefficients, and \(\varepsilon \) represents the error term. We refer to the second equation as the OE. Then, for the multiclass extension, the mapping between \({\widetilde{y}}^{*}\) and \(\widetilde{y}\) is given by
where \({s}_{j}(j=1,\dots ,J-1)\) refer to the boundary parameters to be estimated in addition to \({\varvec{\gamma}}\). The full probabilities for the observed outcomes, \(y\), are then jointly based on the results of the SE and OE:
where \(j=1,\dots , J-1\). Based on probit models, the full probabilities can be written as follows:
where \(j=1,\dots , J-1\). The full probabilities for logit models are described as follows:
where \(j=1,\dots , J-1\). Let us define the binary variable \({y}_{j}=I(y=j)\), which allows us to formulate the log-likelihood function as follows:
\(l\left(f\right)={\sum }_{j=0}^{J}{y}_{j}\text{logPr}\left(y=j|{\varvec{x}}, {\varvec{z}}\right)\), where \(f\in \{{f}_{1,j=0}\left({\varvec{x}}\right), \dots , {f}_{1,j=J}\left({\varvec{x}}\right),{f}_{2,j=0}\left({\varvec{z}}\right),\dots , {f}_{2,j=J}\left({\varvec{z}}\right)\}\) with \({f}_{1,j}\left({\varvec{x}}\right)\) = \({{\varvec{x}}}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}\) and \({f}_{2,j}\left({\varvec{z}}\right)\) = \({{\varvec{z}}}^{\boldsymbol{^{\prime}}}{\varvec{\gamma}}\) for each possible outcome \(j\). Since we construct a final classifier for each class, a centering condition may help achieve numerical stability (Friedman et al., 2000). Thus, we modify the log-likelihood by adding the centering condition as follows:
The expected negative log-likelihood can be defined using the aforementioned log-likelihood function with the centering condition. Given the expected negative log-likelihood, we can fit weighted least square regressions for SE and OE for each class over \(M\) iterations using the following update schemes:
Notably, the values of the boundary parameters \({s}_{j}\) do not depend on the predictors; therefore, they can be estimated via maximum likelihood at the initial stage and remain fixed for the iterations. The predicted probabilities of observing each possible outcome \(j\) for unit \(i\) are calculated based on \({f}_{1,j}^{M}\left({\varvec{x}}\right)\) and \({f}_{2,j}^{M}\left({\varvec{z}}\right)\). At the \(M\) iteration, the final classifier is \(\underset{j\in \left\{0,\dots , J\right\}}{\text{argmax}}\text{Pr}(y=j|{\varvec{x}},{\varvec{z}})\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jeong, Y., Lee, K., Park, Y.W. et al. A systematic approach for learning imbalanced data: enhancing zero-inflated models through boosting. Mach Learn (2024). https://doi.org/10.1007/s10994-024-06558-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10994-024-06558-3