Learning de-biased regression trees and forests from complex samples

Abstract

Regression trees and forests are widely used due to their flexibility and predictive accuracy. Whereas typical tree induction assumes independently identically distributed (i.i.d.) data, in many applications the training sample follows a complex sampling structure. This includes unequal probability sampling, which is often found in survey data. Then, a ‘naive estimation’ that simply ignores the sampling weights may be substantially biased. This article analyzes the bias arising from a naive estimation of regression trees or forests under complex sample designs and proposes ways of de-biasing. This is achieved by bridging tree learning to survey statistics, due to the correspondence of the mean-squared-error criterion in regression trees and variance estimation. Transferring population variance estimation approaches from survey statistics to tree induction, indeed considerably reduces the bias in the resulting trees, both in predictions and the tree structure. The latter is particularly crucial if the trees are to be interpreted. Our methodology is extended to random forests, where we show on simulated data and a housing dataset that correcting for complex sample designs leads to overall much better predictive accuracy and more trustworthy interpretation. Interestingly, corrected forests can surpass forests learned on i.i.d. samples in terms of accuracy, which also has important implications for adaptive data collection approaches.

1 Introduction

In recent years machine learning (ML) methods have become ubiquitous in nearly all areas of science and society. They often achieve impressive accuracy gains compared to classical statistical learning methods, such as regression models, while also being flexible to many data situations. Whereas the advantages of applying ML are obvious, its often prevalent black-box nature raises problems regarding explainability and reproducibility. This hinders the immediate and general applicability of ML in critical domains; see, for instance, the intensive debate in official statistics on complementing the fundamental quality frameworks (Yung et al., 2022).

Regression trees and ensembles thereof are one of the most widely used supervised learning methods. Their popularity stems from their good ‘out of the box’ performance for most standard tabular data type prediction problems (Fernandez-Delgado et al., 2014). Trees¹ are often used due to their symbolic representability, making them easy to interpret. Decision forests, such as random forests (Breiman, 2001), on the other hand, are by themselves black-box models. However, in the last decades, methods for interpreting such forest methods, at least on a global level, became available, partly mitigating the black-box problem. They comprise techniques to interpret feature effects—e.g., individual conditional expectations (ICEs) plots (Goldstein et al., 2015) and partial dependence plots (PDPs) (Friedman, 2001)—as well as methods to interpret the contribution of features on the predictions (Shapley, 1953; Lundberg et al., 2018) and permutation feature importance (Fisher et al., 2019; Breiman, 2001). Interpretability is of particular importance in critical domains, as it allows judging if the implied relationships are reasonable and sound, or perhaps based on data artefacts.

One assumption that most ML models either explicitly or implicitly rely on is that the training data is independently and identically distributed (i.i.d). While for classical statistical methods, it is often well understood what happens when parts of this assumption are violated and how to counteract (e.g., mixed effect models to model correlated data in the context of regression models), the same is not true for ML methods. Here one often only can hope that the effect of violating the underlying assumptions will be mitigated by an increase in training data.

This article argues that such hope is unjustified in the case of complex sample designs², where observations are drawn with unequal probabilities. Depending on the concrete sample design, the bias of estimators does not necessarily disappear with an increase in sample size. This is highly relevant when ML is applied to survey data, as such data typically stems from complex sample designs with unequal selection probabilities. In order to enable the safe application of ML in areas that rely on survey data, such as social sciences or official statistics, the bias induced by complex sample designs needs to be understood and corrected.

Unequal probability sampling and the induced bias of estimators under complex sample designs have been studied extensively in the area of survey statistics, see e.g. Särndal et al. (2003); Valliant et al. (2018) for overviews. Many different correction methods exist for the estimation of totals, means, variances and regression estimators. However, little connection currently exists between ML and survey statistics, with Toth and Eltinge (2011); Breidt and Opsomer (2017); Dagdoug et al. (2021); McConville and Toth (2019); MacNell et al. (2023) being notable exceptions.³

We argue that bridging the theory of handling complex samples and ML is indispensable for a comprehensive analysis of survey data. In particular, this connection

• allows for a deeper understanding of when and why regression trees and forests might fail under complex sampling schemes, and how then their interpretations are biased;

• enables a direct extension of the correction methods found in the rich literature of survey statistics, leading to an unbiased analysis of trees and forests under complex sample designs;

• may moreover offer exciting opportunities in the domain of adaptive data collection in ML (e.g., Bayesian optimization).

The first two topics rely on the correspondence of the mean-squared-error (MSE) splitting criterion used in regression trees to population variance estimation, a problem already successfully studied in survey sampling literature (Swain & Mishra, 1994; Chaudhuri, 1978; Liu & Thompson, 1983). The third topic adopts from survey statistics the interesting perspective that unequal sampling weights do not only have to be seen as a disturbance. Instead, incorporating design-based sampling and estimation into machine learning algorithms in domains of adaptive data collection may increase their accuracy and stability, analogous to the increased accuracy of the Horvitz-Thompson estimator (Horvitz & Thompson, 1952) in sampling theory.

This article is structured as follows: Sect. 2 describes the setting of complex samples and introduces notations. Section 3 recalls some aspects from the methodology of regression trees relevant for deriving the bias introduced in trees when built on complex samples. There, we also propose several estimators for reducing bias in the splitting criterion. Section 4 extends the methodology to random forests. In Sect. 5 we show on multiple simulations that the correction approaches are an efficient way to reduce or remove bias. A real-world dataset is analyzed in Sect. 6. Section 7 undertakes an outlook on spill-over effects of our results on the topic of adaptive data collection (e.g., Bayesian optimization), while Sect. 8 generally concludes.

2 Complex samples

In this article, we are interested in supervised learning when given a complex sample. Hence we are interested in learning or approximating the unknown function f that maps elements x of a p-dimensional input space $\mathcal{X}$ to elements y of the outcome space $\mathcal{Y}$. In the following only the regression setting with $\mathcal{Y} = {\mathbb {R}}$ is considered. To learn f one is typically given a training sample $D = \{(x, y)_1, \cdots , (x, y)_n\}$ consisting of n labeled observations.

Special attention has to be paid to situations when the sampled units can not be assumed to be drawn independently and identically distributed (i.i.d.) from an infinite population domain. Typical violations of the standard i.i.d. assumption are unequal inclusion probabilities and sampling from a finite population domain, also implicitly inducing dependencies between the units drawn. More formally⁴, to specify a sample design, let $\mathcal{U} = \{1,\dots , N\}$ denote the collection of indices of all units, $\mathcal{S} \subset \mathcal{U}$ a random element describing the sample taken from $\mathcal{U}$ and ${\mathbb {P}}$ the distribution underlying $\mathcal{S}$. A sample design is said to be a Simple Random Sampling (SRS) when the underlying sampling process is such that, for all subsets of $\mathcal{U}$ with a fixed cardinality k, the probability to be sampled only depends on k; then the term SRS is also applied to the sample itself. Of particular interest are the so-called inclusion probabilities, giving for sets of indices the probability to be part of the drawn sample $\mathcal{S}$. In particular, denote, for every unit $i\in \mathcal{U}$, by $\pi _i = {\mathbb {P}}(i \in \mathcal{S})$ the (first order) inclusion probability of observation i, and by $\pi _{ij} = {\mathbb {P}}(i \in S \wedge j \in \mathcal{S})$ the joint inclusion probability of observations i and j, $i\not = j$. For SRS, one has, by definition,

$$\begin{aligned} \pi _i = \pi _j \quad \forall i,j \in \mathcal{U}\,, \end{aligned}$$

(1)

and

$$\begin{aligned} \pi _{ij} = \pi _{kl} \quad \forall i\not =j, k\not =l \in \mathcal{U}\,. \end{aligned}$$

(2)

If the first-order inclusion probabilities are different, i.e., if $\exists i,j: \pi _i \ne \pi _j$, one speaks of a complex sample (design).

The reasons for the emergence of complex samples are manifold. On the one hand, in some sampling situations, an involuntary sampling bias is introduced through effects such as selection bias. In this situation typically the $\pi$ are unknown.⁵

On the other hand, unequal sampling probabilities are commonly used in survey statistics or ecology research for practical reasons (Haziza & Beaumont, 2017) or to increase the accuracy and efficiency of resulting estimators (Schreuder et al., 2001; Horvitz & Thompson, 1952). In this situation, the $\pi$ are carefully constructed by the survey statistician and are typically known prior to the sampling step (Skinner & Wakefield, 2017). Common sampling schemes include cluster sampling, multi-stage sampling and probability-proportional-to-size sampling (Horvitz & Thompson, 1952; Valliant et al., 2018). Throughout this article, it is assumed that $\pi _i$ and ideally $\pi _{ij}$ are known for all $i\not =j \in U$.

Example: PPS sampling

For illustrative purposes, PPS (probability-proportional-to-size) sampling is used as a running example throughout this article, but the derived methodology also extends to other complex sampling schemes. In PPS sampling one relies on an auxiliary variable A that often is roughly proportional to the variable of interest y and known prior to the sampling step for all population units. Inclusion probabilities are constructed via

$$\begin{aligned} \pi _i = n \frac{a_i}{\sum _{j = 1}^N a_j}\,, \end{aligned}$$

(3)

giving observations with high values of a a higher probability of being included in the sample.⁶ For Eq. (3) to yield positive probabilities $a \ge 0$ is required. Given $\pi$, in finite sample domains, methods such as the pivotal method (Deville & Tille, 1998) can be used to draw PPS samples. Estimators that account for $\pi$, such as the Horvitz-Thompson mean estimator (Horvitz & Thompson, 1952),

$$\begin{aligned} {\bar{y}}_{HT} = \frac{1}{N}\sum _{i = 1}^n y_i \pi _i^{-1}\,, \end{aligned}$$

(4)

can reduce the variance greatly compared to estimators based on SRS (Valliant et al., 2018). Intuitively, as the extreme observations are more often included in the sample (but down-weighted), the samples are more similar and hence variance is reduced. However, if not corrected for, the estimates will be biased towards over-estimation.

One example of PPS sampling, to be continued in Sect. 6, is in the estimation of housing prices, where larger apartments should be included with higher probability, as otherwise, the estimates will vary a lot, depending on the inclusion of the larger and likely more expensive apartments. Therefore, PPS sampling can lead to more stable and accurate estimators. As an auxiliary variable A the number of square feet could be used if this information is available beforehand for all population units.

3 Regression trees

3.1 Regression tree induction

For deriving the bias of naive estimation and to correct for it, it is helpful to recall that tree induction relies on successively splitting such that the impurity is maximally reduced. Relying on the mean squared error (MSE), one obtains the reduction in MSE

$$\begin{aligned} \Delta (s) = \epsilon (c) - p(l)\epsilon (l) - p(r)\epsilon (r)\,, \end{aligned}$$

(5)

where s is the considered split point, $p(l), \, p(r)$ denote the probability of falling into the left child-node ($x_j \le s$) and right child-node ($x_j > s$), while $\epsilon (l), \epsilon (r)$ and $\epsilon (c)$ denote the MSE in the left and right child-nodes and the current node, respectively.

When using constant mean predictions in the leaf nodes, the MSE corresponds to the variance. Thus Eq. (5) can be written as

$$\begin{aligned} \Delta (s) = \sigma ^2(c) - p(l)\sigma ^2(l) - p(r)\sigma ^2(r)\,, \end{aligned}$$

(6)

where $\sigma ^2(l)$ and $\sigma ^2(r)$ are the sample variances in the left and right child-node resulting from the split.

After the optimal split is found, all observations with $x \le s$ are moved to the left child-node and to the right child-node otherwise. Then the child-nodes are split again. This recursive process is repeated until either no split improves the MSE-criterion or some stopping criteria is reached. Typical stopping criteria include a pre-specified minimum number of observations in either the current node or the resulting nodes after splitting or a minimum reduction in MSE. In practice, pruning techniques are typically used before using the tree for prediction, which can reduce overfitting (Rokach & Maimon, 2005).

After splitting is stopped, the current node becomes a leaf node and the mean ${\hat{y}}$ of all observations of the training sample falling into this leaf node is attached as the prediction value.

At prediction time, the test cases are propagated down the tree, until they reach a leaf node. Then the attached prediction value is used as a final prediction.

A nice property of regression trees is that the tree structure is easy to interpret, given that the trees are not too large. For test cases, one can simply follow the decisions at each node, and, with that path, one gets an explanation for the prediction that is being made.

A second advantage is that interaction effects do not need to be specified beforehand. Also, non-linear effects can be captured naturally, making regression trees very flexible models.

3.2 Regression trees built on complex samples

When given a complex sample, regression tree induction is affected in three ways, namely via

• #1 the MSE criterion (cf. Eq. 6), leading to a biased split point selection,

• #2 the estimated number of observations present in the current node, leading to incorrect stopping behavior,

• #3 and the prediction values attached to each leaf node.

In Toth and Eltinge (2011) the authors correct for #2 and #3, but show that the tree structure does not need to be adjusted for consistent models.⁷ While this is asymptotically true, we argue that if one is to interpret the regression tree on a given sample, which is one of the main selling points of regression trees in the first place, one must ensure that the structure is unbiased as well. Also, it is unclear how the asymptotic argument translates to a bias on smaller sample sizes.

In order to study and reduce the bias introduced by complex samples on all three levels #1, #2 and #3 listed above, we make use of survey statistics literature on variance estimation. Following Courbois and Urquhart (2004), the bias of the ‘naive’ population variance estimator $\widehat{\sigma ^2}_{Naive}$ with unequal probability sampling can be written as

$$\begin{aligned} {\mathbb {E}}(\sigma ^2 - \widehat{\sigma ^2}_{Naive}) = \frac{1}{n}\sum _{i=1}^Ny_i^2\left( \pi _i - \frac{n}{N}\right) - \frac{1}{n(n-1)} \sum _{j=1}^N\sum _{j\ne i}y_i y_j \left( \pi _{ij} - \frac{n(n-1)}{N(N-1)} \right) \,. \end{aligned}$$

(7)

This bias will, ceteris paribus, be low if the (first and second order) inclusion probabilities are close to SRS and thus the variance of $\pi$ is low. At the same time, the bias also depends on the correlation between Y and $\pi$. If inclusion probabilities vary randomly and are not correlated with the outcome, the bias is expected to be low, although still the variance of the estimator may be increased.

Hence, if the variance of $\pi$ is high, and, in addition, $\pi$ is correlated with the outcome, we expect the bias to be quite large. Also interestingly, the bias will not necessarily disappear with larger sample sizes but depends on the ratio n/N. For example, in the trivial case of $n = N$, the complex sample design has no effect, as all observations are drawn. On the other hand, if $n<< N$, finite sample effects disappear and the bias can become large.

3.3 De-biasing the MSE-criterion

Unbiased estimation of the population variance was studied in survey statistics literature.⁸ One such estimator is given by Chaudhuri (1978)

$$\begin{aligned} \widehat{\sigma ^2_{*}} = \frac{1}{2N^2}\sum \sum _{i \ne j}^n \frac{(y_i - y_j)^2}{\pi _{ij}}\,. \end{aligned}$$

(8)

Hence, if N and $\pi _{ij}$ are known, $\widehat{\sigma ^2_{*}}$ is an unbiased estimator for the population variance. This fact can be directly transferred to estimate the population variance in a given child-node, as used in the splitting criterion (cf. Eq. (6)). However, in contrast to population variance estimation in surveys with known population size, in the case of regression trees, N is typically not known for each possible node and needs to be estimated. Again relying on survey statistics literature, this can be achieved via ${\hat{N}} = \sum _{i = 1}^n \pi _i^{-1}$ (Toth & Eltinge, 2011).

While for larger datasets the bias introduced by estimating N will be small, for small nodes this bias is still expected to be an issue.

An alternative to $\widehat{\sigma ^2_{*}}$ is to rely on an Hájek-type approach, which is commonly used in mean estimation if the population size is unknown. The Hájek mean estimator

$$\begin{aligned} {\hat{y}}_{HJ} = \frac{\sum _{i=1}^n y_i w_i}{\sum _{i=1}^nw_i}\,, \end{aligned}$$

(9)

where $w_i = \pi _i^{-1}$, is known to be biased, but typically gives very accurate results (Särndal et al., 2003). Adapted to variance estimation the Hájek variance estimator becomes (Lumley, 2004)

$$\begin{aligned} \widehat{\sigma ^2}_{HJ} = \frac{\sum _{i=1}^nw_i (y_i - {\widehat{y}}_{HJ})^2}{\sum _{i=1}^nw_i}\,. \end{aligned}$$

(10)

In $\widehat{\sigma ^2}_{HJ}$ both ${\widehat{y}}_{HJ}$ and ${\widehat{N}} = \sum _{i=1}^nw_i$ are estimated. Hence, $\widehat{\sigma ^2}_{HJ}$ will not be unbiased, but is expected to greatly reduce bias compared to the naive estimator.

We, therefore, propose to replace the MSE-criterion with its Hájek-corrected version,

$$\begin{aligned} \Delta _{HJ}(s) = \widehat{\sigma ^2}_{HJ} - {\widehat{p}}_{HJ}(l) \, \widehat{\sigma ^2}_{HJ}(l) - {\widehat{p}}_{HJ}(r) \, \widehat{\sigma ^2}_{HJ}(r)\,, \end{aligned}$$

(11)

where ${\hat{p}}_{HJ}(l) = \sum _{i \in \mathcal{L}}^nw_i /( \sum _{i \in \mathcal{L}}^nw_i + \sum _{j \in \mathcal{R}}^nw_j)$ and ${\hat{p}}_{HJ}(r) = \sum _{i \in \mathcal{R}}^nw_i /( \sum _{i \in \mathcal{L}}^nw_i + \sum _{j \in \mathcal{R}}^nw_j)$ are the estimates for population fractions falling into the left and right child-node, with $\mathcal{L}$ and $\mathcal{R}$ being the sets of indices of observations in the left and right node, and $\widehat{\sigma ^2}_{HJ}(l), \widehat{\sigma ^2}_{HJ}(r)$ are the Hájek-variance estimates in the left and right child-nodes respectively.

Unbiased estimators may be obtained when N is known for all possible child-nodes, by replacing $\widehat{\sigma ^2}_{HJ}$ with $\widehat{\sigma ^2_{*}}$. However, this is seldom the case. Therefore, $\Delta _{HJ}(s)$ is a good alternative for most practical applications.

We note that $\widehat{\sigma ^2}_{HJ}$ is already often implicitly used in machine learning software to handle observation weights. This is interesting two-fold: Firstly, it gives a theoretical justification to the standard, commonly used, inverse weighting approach. Secondly, as $\widehat{\sigma ^2}_{HJ}$ is already implemented in many libraries, using the correction approaches is relatively straightforward. For example, the rpart R-library (Therneau & Atkinson, 2022) treats observation weights in this fashion and can be used to fit de-biased trees.

Figure 1 shows the de-biasing effect of different correction approaches on the split selection for simulated data, using a PPS design. As expected, for the naive estimation increasing the sample size does not lead to unbiased estimates and will often lead to a biased split point selection. The correction approaches will typically lead to correct selection. With an increase in n, the curves approach the population $\Delta (s)$ function. We especially note that $\Delta _{HJ}(s)$ greatly improves on the naive estimation in all settings and efficiently recovers the correct split selection. This result implies that, without correcting the split points, one cannot hope to get an unbiased tree structure. As the differences in trees are propagated downward due to their recursiveness, the structure will diverge even more in the following layers. If one is to interpret regression trees, we argue that the structure needs to be corrected as well. Section 6 will showcase this property on a real-world housing dataset.

Fig. 1

Comparison of different debiasing methods on simulated data: $\Delta (s)$ on the population (purple dotted), naive estimation on the sample (blue dashed), $\Delta _{HJ}(s)$ (green), using $\widehat{\sigma ^2_{*}}$ with N known (red solid) and $\widehat{\sigma ^2_{*}}$ with N estimated (yellow dashed). All correction methods greatly improve (i.e. are closer to the population curve) on naive estimation and converge towards the population $\Delta (s)$ with increasing n. The same is not true for the naive estimation, which remains biased with increasing n (Color figure online)

4 Random forests

Instead of using a single tree, random forests build an ensemble of trees, each generated on a bootstrap sample from the training data. Additional randomness is induced by limiting the candidate covariates for splitting at each node. This leads to de-correlation between trees, which can be shown to improve the generalization performance of the resulting ensemble (Breiman, 2001; Hastie et al., 2009). The random forest model with K trees can be written as

$$\begin{aligned} F_{RF}({\textbf{x}}) = \frac{1}{K} (f_1({\textbf{x}}, \Theta _1)+...+f_K({\textbf{x}}, \Theta _K))\,, \end{aligned}$$

(12)

where $f_1,..,f_K$ are trees and the bootstrap samples together with the drawn feature subsets are denoted as $\Theta _1, ..., \Theta _K$.

When given a complex sample, random forests are expected to be biased in their predictions. The complex sample influences each tree, and therefore also the ensemble will be biased. However, the degree of the bias is unclear and difficult to obtain analytically. Additionally, the bootstrap samples differ from the ones obtained under SRS. This suggests that random forests may be de-biased either on the individual tree level or through the bootstrap step, leading to the following two proposed de-biasing techniques.

4.1 Hájek-forests

One straightforward correction approach can be achieved by replacing the base learner in Eq. (12) with Hájek corrected trees. Bootstrapping and feature sub-setting then is performed as usual. As the bias in each tree is reduced, also the bias of the whole ensemble is expected to be reduced. In this approach, extreme observations will be present in most trees, but down-weighted, therefore advantages of the design-based approach are expected to carry over. As the individual trees are less biased, the random forest is expected to greatly reduce bias when compared to the naive random forest estimator.

However, one detail requires further consideration. Typically, the trees in random forests are grown until purity. While this may be a good idea generally, as it increases model variance further, for our correction approach this may lead to problems: if only one observation (or more generally a very small number of observations) is present in the leaf nodes, then the Hájek correction in the leaf nodes is virtually voided and extreme predictions occur. We therefore recommend setting the minimum node size higher than usual, e.g. to 2% of observations to avoid extreme behaviour, if extremely high target values are expected. Alternatively, our approach could be combined with the correction proposed in Dagdoug et al. (2021), which exploits the nearest-neighbor representation of random forests and allows direct down-weighting of over-sampled observations for the final prediction.

4.2 Bootstrap-corrected forests

A second approach is to incorporate the weights in the bootstrapping step. The rationale is straightforward: We draw observations $(x,y)_i$ with probability proportional to $\frac{1}{\pi _i}$ in each bootstrap step. That is, observations with high inclusion probability are down-weighted in the bootstrap samples and vice versa. Note that the R library ranger (Wright & Ziegler, 2017) allows for such weighted bootstrap samples by passing $\frac{1}{\pi _i}$ as case.weights. The resulting forest is expected to be unbiased, however, extreme observations will not be present in most trees, as they are heavily down-weighted.

This approach of inverse-probability weighting has also been used to deal with missing data, see Seaman and White (2013) for an overview. It has been applied to linear regression, quantile regression, and boosting in Nahorniak et al. (2015). Moreover, bootstrapping with inverse-probability weighting is reminiscent of PPS bootstrapping (Mecatti, 2000). Note, however, that Mecatti (2000) uses direct PPS weighting instead of inverse weighting, but the same rationale applies.

4.3 Interpreting random forests via partial dependence plots and permutation importance scores

One way to interpret random forests is via partial dependence plots (PDP) (Friedman, 2001). Partial dependence plots show the average marginal influence of a feature j, given by

$$\begin{aligned} {\widehat{PD}}(x)_j = \frac{1}{N}\sum _{i = 1}^N F_{RF}(x, x^{(-j)}_i)\,, \end{aligned}$$

(13)

where $F_{RF}(x, x^{(-j)}_i)$ is the random forest prediction using value x in covariate j and all other values as given in the dataset; N is the population size as above. PDPs allow for interpreting the effect of individual covariates on the outcome, without imposing any assumptions on the shape of the relationship (i.e., no need for linearity). Notably, the partial dependence function in Eq. (13) can also be defined for two features to assess interaction effects. To this end, one considers $F_{RF}(x_j, x_k, x^{(-j,k)}_i)$, that is, using value $x_j$ in covariate j, $x_k$ in covariate k, and all other values as given in the dataset.

As we reduce bias in $F_{RF}$, also the bias in ${\widehat{PD}}$ is expected to be reduced, and the interpretation of feature effects to be closer to the interpretation obtained by using an i.i.d. sample.

A popular measure for feature importance is the permutation feature importance (Breiman, 2001). The importance of a feature is measured as the relative increase in MSE after the given covariate is randomly shuffled. If the relationship between covariate and target is strong, the predictive performance will be more affected by shuffling.

We note that the effect of complex samples on importance measures is not trivial, and a comprehensive analysis of the bias must be left for future work. The next section therefore analyses the behaviour of random forests and their derived interpretation methods empirically.

5 Simulation study

In this section, we test the ability of the correction methods to produce valid predictions when learned on a complex sample. To this end, we differentiate between two settings. In scenario 1, we consider the setting where large values are mostly outliers and can not be predicted given the covariates. In scenario 2, we study a setting where large values are predictable. In both settings, we generate a population $\mathcal{U}$ of size $N = 1000n$. In this $N>> n$ setting, drawing without replacement is similar to drawing with replacement, and thus no finite data correction is necessary. In each setting a separate test set of size 1000 is drawn from the same distribution.

On each of the 100 repetitions in each scenario, the MSE on the test set of each method is compared to the MSE of a random forest learned from a SRS drawn from the same population, and the relative MSE is reported.

5.1 Scenario 1: noise

Data is generated under the model

$$\begin{aligned} X_1,\dots , X_{10}&\sim \mathcal{N}(0, 1)\\ Y&\sim LogNormal(X_1 + \dots + X_5, \eta ) \\ A&\sim \mathcal{N}(Y, 0.1). \end{aligned}$$

The LogNormal distribution is chosen to produce skewed data, similar to income-type data. This also leads to a high variance of $\pi$ as the ratio of the individual A-value and the sum of all A-values in Eq. (3)⁹. Skewness is varied via $\eta \in \{0.01, 0.5, 1, 2\}$, and the sample size via $n \in \{100, 500, 1000\}$. Large y-values have to be considered noise, as they can not be explained by the covariates, and we expect overfitting to occur.

The results are reported in Table 1. Depending on the skewness, the naive random forest shows much higher MSE values, due to the bias from oversampled large observations that must be seen as noise. For $\eta = 2$, the naive random forest virtually falls apart, and the MSE is over 1000 times higher on the same test set.

Using weighted bootstrapping (WB) drastically reduces the relative error and is only slightly worse than the random forest learned from a simple random sample on all settings, especially for moderate skewness and larger sample sizes.

The Hájek correction (HJ) also helps to reduce the relative error. If the minimum number of observations in the leaf nodes is set to 0.02n performance (HJreg) is similar to WB and better for the higher skewness settings if n is high enough. On the other hand, the Hájek correction without minimum node size (HJ) struggles in the settings with higher skewness and performs worse than WB overall, but is still much better compared to the naive estimator.

5.2 Scenario 2: high correlation

As a second scenario of skewed data, we generate data under the model

$$\begin{aligned} X_1,\dots , X_{10}&\sim LogNormal(0, 1)\\ Y&\sim \mathcal{N}(X_1 + \dots + X_5, \eta ) \\ A&\sim \mathcal{N}(Y, 0.1). \end{aligned}$$

with all other settings as above. The difference between the two models may seem subtle but is quite substantial. Under scenario 1, extreme values of y may be seen as noise and therefore not predictable. On the other hand, under scenario 2, the large values in y are based on the underlying relationship and hence carry valuable information for the model. Higher skewness in this case also increases correlation. Oversampling high values may, in this scenario, actually improve the model, compared to an estimator obtained under SRS, as it increases the probability that larger areas of the input space are covered.

The results are shown in Table 2. In this setting the naive estimator performs reasonably for low and moderate skewness and only falls apart for $\eta = 2$. This makes sense, as it is less important which area of the input space is over-sampled, as long as this area is modeled correctly.

All correction approaches do a good job and show performance similar to the SRS forest. In this scenario, increasing the minimum number of observations overall worsens performance for the Hájek correction. This is due to the fact that the input space can be modeled less granular. While this was a good idea for the previous setting, as it reduces overfitting, now it leads to underfitting.

An interesting result is that for high skewness, where PPS sampling in conjunction with WB or Hájek correction leads to a higher accuracy than learning on a SRS. The important implications of this result will be discussed in Sect. 7.

Table 1 Relative MSE of the different methods in simulation scenario 1, where high target values are outliers

Table 2 Relative MSE of the different methods in simulation scenario 2, where high target values are predictable

6 Seoul housing data

In this section, we showcase our correction approaches on a real-world housing dataset. The goal is to demonstrate differences in interpretation that one might obtain when using correction methods compared to the ‘naive’ estimators.

The dataset contains 2.65Mio houses/apartments that were sold between the years 2005 and 2023 in Seoul.¹⁰ The target variable is the price (SalePrice) and in total 29 covariates are present in the dataset. To make the analysis more tangible, we limit the used covariates to the size of the apartment in square meter (sqm), the size of the lot (lsqm), the year in which the house was built (YearBuilt) and the year in which the house was sold (YrSold), which we expect to be the most influential ones.

As no sampling weights are given in the dataset, we construct a complex sample structure by drawing a sample of size n from the dataset, with the following setup:

• generate an auxiliary variable $A \sim \mathcal{N}(SalePrice, 10000)$,

• sample n units with PPS sampling using the auxiliary variable A,

• separately sample n units using SRS sampling as a baseline.

We expect the dataset situation to be somewhat in between the two simulation scenarios: Very high prices are mostly based on their covariate values, but not all the variance can be explained, especially as important covariates to explain housing prices, such as the region of the apartment, are missing.

Fig. 2

Left: population tree on the South Korea housing data. Right: Hájek corrected tree. The values in the leaf nodes are given in ten million Wons

6.1 Regression tree interpretation

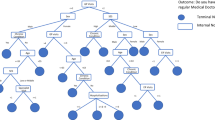
Figure 2 shows the Hájek corrected and the population trees for a PPS sample of size $n = 1000$. The Hájek corrected tree recovers the population tree very closely: the first split is identical, while the splits on the second level are similar, differentiating houses with a small lot and a bigger lot. While the splits $lsqm < 231$ and $sqm < 476$ are different, both separate very expensive houses from the other houses, as can be seen when looking at the leaf values. Overall, while the Hájek corrected tree is not identical, due to randomness in the sampling process, the interpretation is quite similar, nevertheless.

Figure 3 shows the naive tree learned on the same sample. It is clear that already the first split is very different, separating houses with large lots. In general, the whole tree focuses mostly on the more expensive houses, as also can be seen at the leaf node values, where no predictions smaller than 46 can be found. So, overall, the interpretation of the naive tree is very different from the population tree, as it focuses on the oversampled expensive houses.

When analyzing trees built on complex samples, correction methods are therefore crucial, which is in line with our expectation (cf. Sect. 3).

Fig. 3

Naive Tree on the housing dataset

Table 3 Relative MSE of the different random forest methods on the housing dataset

Fig. 4

Partial dependence curves for the different covariates (averaged over 100 runs). Shown are the ‘naive’ random forest (red solid), Hájek Forest (blue dashed), weighted bootstrap (purple dashed), and a random forest built upon a random sample (green dotted). While all show a similar pattern the correction approaches are much closer to the simple random sample version (Color figure online)

6.2 Random forest interpretation

Next, we compare the differences in the interpretation one obtains using different correction procedures for random forests. We interpret the random forest methods using partial dependence plots and permutation importance scores (cf. Subsect. 4.3). Using the complex sampling scheme specified above, we build naive, Hájek and weighted bootstrap corrected forests. As a baseline comparison, we also take a separate SRS and learn a plain random forest. Each setting is repeated 100 times and all scores are averaged over all runs.

Table 3 shows the average relative MSE for different choices of n. Interestingly, with increasing n both HJ and WB perform better than the SRS forest. This is analogous to simulation scenario 2 in Subsect. 5.2 and shows that a design-based sampling approach can improve the predictive accuracy of machine learning models when corrected for.

Fig. 5

Permutation feature importance scores of ‘naive’ random forest (red), Hájek Forest (blue), weighted bootstrap (purple), a random forest built upon a random sample (green) over 100 repetitions. The bars show the standard deviation over the repetitions (Color figure online)

6.2.1 Partial dependence plots

Figure 4 shows the PDP for the different methods. While there still is a difference between the SRS version, HJ, and WB, the correction leads to a more similar interpretation, whereas the naive forest is on some variables quite far off. This is especially the case for areas in the input space with fewer observations, for example, $YearBuilt < 1950$ where the naive forest heavily overestimates the prices, probably due to some very expensive houses that are over-sampled. PDP plots for interaction effects among two variables (not shown here) give a similar impression: the correction methods capture the interaction effects for SRS better than the naive forest.

6.2.2 Permutation importance scores

The permutation importance is shown in Fig. 5. It can be seen that the correction approaches are closer to the SRS forest overall. Smaller differences persist, for example in the covariate YrSold, where the Hájek correction is slightly further off compared to the naive forest. The WB approach appears to be the closest to SRS and can be a good choice when interpretation is of importance.

7 Outlook on adaptively collected data

As discussed above, complex sampling schemes can occur due to a great variety of reasons. One particular reason is when data is collected adaptively within a learning or optimization algorithm. The resulting samples typically are not i.i.d.. Such adaptively collected data is subtly ubiquitous in various subfields of data science and machine learning. We discuss three examples in brevity: Bayesian optimization (BO), self-training in semi-supervised learning (SSL), and bandit algorithms. All methods rely on refitting learners to artificially enhanced training data. These enhancements are based on pre-defined criteria to select data points rendering some data more likely to be added than others. Rodemann et al. (2022) empirically analyze the distance from the so-produced complex samples to i.i.d. samples by maximum mean discrepancy (Gretton et al., 2012). In order to deploy inverse probability weighting, inclusion probabilities have to be estimated. However, this is not a major issue, since explicit information on the inclusion mechanism is available; after all, the data is generated by the algorithm itself by means of selection criteria.

To make things more tangible, consider the case of BO first. It optimizes an unknown function by iteratively approximating it through a surrogate model, whose mean and standard error estimates are scalarized to a selection criterion (Snoek et al., 2012). The arguments of this criterion’s optima are evaluated and added to the training data. Rodemann (2021); Rodemann et al. (2022) propose to weight them by means of the surrogate model’s standard errors at the time of selection. For the case of deploying random forests as surrogate models, one can refit them by weighted drawing in the bootstrap sampling step. Refitting may be done iteratively aiming at speeding up the optimization or after convergence aiming at providing applicants with a (global) interpretable surrogate model.

Similarly, self-training in SSL selects instances from a set of unlabeled data, predicts its labels, and adds these pseudo-labeled data to the training data. Instances are selected according to a confidence measure, e.g. the predictive variance. Regions in the feature space where the model is very confident are thus over-represented in the selected sample. Rodemann et al. (2022) explicitly exploit the selection criteria to define weights used for resampling-based refitting of the model. The more confident the model is in the self-assigned labels, the lower their weights should be to counteract the selection bias.

Bandit algorithms also select data adaptively, resulting in a complex sampling scheme. Classical statistical approaches thus fail to provide valid confidence intervals. Zhang et al. (2021) propose adaptive weights for M-estimators (such as maximum-likelihood estimators) that allow for the construction of asymptotically valid confidence regions for a variety of inferential targets.

8 Conclusion

This article analyzes the bias introduced by complex samples in regression trees and forests, when not corrected for, both analytically and through simulation studies. We propose a Hájek type estimator to reduce bias in trees and two methods to reduce bias and improve predictive performance in random forests, which are easy to implement in current machine learning software. Our proposed correction approaches were found to improve predictive performance, as shown in simulation data and real-world data. Similarly, correction methods are equally crucial if one is to interpret trees and forests, as a naive estimator leads to flawed interpretation.

In this work, we studied the effect of complex samples on random forests and interpretation methods empirically, but an analytic study would be very interesting for future work. Similar to the analytic study of bias in trees, this could indicate the severity of the bias that is to be expected on a given dataset.

As an outlook, we sketched the connection between survey statistics and the ML area of adaptively collected data. As seen in this article, the design-based approach to survey statistics can lead to substantial improvements in machine learning models. Therefore, we believe this area to be very fruitful for future work.