Abstract
Classification and regression algorithms based on k-nearest neighbors (kNN) are often ranked among the top-10 Machine learning algorithms, due to their performance, flexibility, interpretability, non-parametric nature, and computational efficiency. Nevertheless, in existing kNN algorithms, the kNN radius, which plays a major role in the quality of kNN estimates, is independent of any weights associated with the training samples in a kNN-neighborhood. This omission, besides limiting the performance and flexibility of kNN, causes difficulties in correcting for covariate shift (e.g., selection bias) in the training data, taking advantage of unlabeled data, domain adaptation and transfer learning. We propose a new weighted kNN algorithm that, given training samples, each associated with two weights, called consensus and relevance (which may depend on the query on hand as well), and a request for an estimate of the posterior at a query, works as follows. First, it determines the kNN neighborhood as the training samples within the kth relevance-weighted order statistic of the distances of the training samples from the query. Second, it uses the training samples in this neighborhood to produce the desired estimate of the posterior (output label or value) via consensus-weighted aggregation as in existing kNN rules. Furthermore, we show that kNN algorithms are affected by covariate shift, and that the commonly used sample reweighing technique does not correct covariate shift in existing kNN algorithms. We then show how to mitigate covariate shift in kNN decision rules by using instead our proposed consensus-relevance kNN algorithm with relevance weights determined by the amount of covariate shift (e.g., the ratio of sample probability densities before and after the shift). Finally, we provide experimental results, using 197 real datasets, demonstrating that the proposed approach is slightly better (in terms of \(F_1\) score) on average than competing benchmark approaches for mitigating selection bias, and that there are quite a few datasets for which it is significantly better.

Similar content being viewed by others
Data availability
All the data used for this research are publicly available in the Web and cited in the article.
Code Availability
The source code implementing the proposed kNN method will be made available, upon acceptance, in a GitHub repository.
Notes
It is unclear whether or how importance weights may influence the kNN neighborhood indirectly via the distance function.
In general, the consensus and relevance weights of any training instance may depend not only on the training instance itself but on the query instance as well.
For brevity, we often refer to the features \({\textbf{x}}_i\) of a training instance
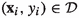 as a training instance \({\textbf{x}}_i\) whenever \(y_i\) is not pertinent to the discussion at hand and
as a training instance \({\textbf{x}}_i\) whenever \(y_i\) is not pertinent to the discussion at hand and  is clear from the context.
is clear from the context.Recall the multivariate Calculus notations \({\textbf{x}}^{\varvec{\alpha }} \triangleq \prod _{i=1}^{d} x_i ^{\alpha _i}\),
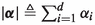 , \(\varvec{\alpha }! \triangleq \prod _{i=1}^d (\alpha _i!)\), and \(\max (\varvec{\alpha }) = \max \{ \alpha _i \}\) for any d—vector \(\varvec{\alpha }\) of non-negative integers.
, \(\varvec{\alpha }! \triangleq \prod _{i=1}^d (\alpha _i!)\), and \(\max (\varvec{\alpha }) = \max \{ \alpha _i \}\) for any d—vector \(\varvec{\alpha }\) of non-negative integers.For brevity, we ignore loss weights associated with queries that are used to weight the estimation loss for each query, since they only affect the score of kNN estimators but not their inner workings. Besides, it is not clear what loss function kNN estimators optimize.
For brevity, when convenient and there is no ambiguity, we drop from
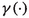 the arguments that do not affect its value.
the arguments that do not affect its value.Observe that since we assume
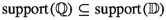 , it follows that the correction factor
, it follows that the correction factor 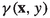 is well defined for any \(({\textbf{x}}, y)\) in the
is well defined for any \(({\textbf{x}}, y)\) in the  .
.The resampled dataset is generally smaller than the original training dataset in the sample selection bias scenario.
Empirical logloss comparison on four real datasets does not indicate preference of this proposed technique in Liu and Ziebart (2014) over instance reweighing.
For each cluster C in a clustering of the features of all the available instances \(S \cup U\), set
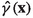 to
to 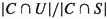 for each instance \({\textbf{x}}\) in the cluster C, i.e., set it to the ratio of the cluster’s empirical
for each instance \({\textbf{x}}\) in the cluster C, i.e., set it to the ratio of the cluster’s empirical  and
and 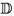 probabilities.
probabilities.Let \({\textbf{x}} \circ {\textbf{x}}'\) denote the Hadamard (component-wise) product of vectors \({\textbf{x}}\) and \({\textbf{x}}'\).
Source code implementation of our consensus–relevance kNN classifiers will be provided for review and upon publication.
The limit of 4,000 on the size of each seed dataset for these experiments is for computational expediency. Similar results were obtained for higher values.
We have not found any real datasets with selection bias probabilities in the literature or common Machine Learning dataset repositories.
Our choice of F is motivated by the logistic regression model, a ubiquitous model for estimating binary outcomes from continuous predictors.
These observations support sound aggregation of evaluation scores of kNN estimators trained and evaluated on family members of a collection of families.
Hyperparameters not explicitly fixed below, assume their default values of the kNN classifier in Pedregosa (2011). Unless specified otherwise, for computational expediency, we do not report experimental results with hyperparameter optimization.
Alternative importance weights considered (but not reported on in these experiments) included
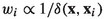 and
and 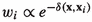 .
.Training and scoring each kNN estimator on each family member entails redundant computations and does not yield additional information. For example, the base estimator produces identical results on B-SCF and B-UNF family members, SkNN and base estimators produce identical results on B-UNF, etc.
An infallible sequence of estimates has accuracy, recall, precision, and \(F_1\) scores all equal to 1.
In order to simplify handling divisions by 0 when computing the normalized score–loss, we divide by the maximum of \(10^{-4}\) and the reference’s score–loss.
Unless stated otherwise, we take \(0/0 \triangleq 1\).
References
Abramson, I. S. (1982). On bandwidth variation in kernel estimates-a square root law. Annals of Statistics, 10(4), 1217–1223. https://doi.org/10.1214/aos/1176345986
Anava, O. & Levy, K. Y. (2016). k*-nearest neighbors: From global to local, NIPS. arXiv:1701.07266.
Balsubramani, A., Dasgupta, S., Freund, Y. & Moran, S. (2019). An adaptive nearest neighbor rule for classification, NIPS. arXiv:1905.12717.
Bhapkar, V. P. (1966). A note on the equivalence of two test criteria for hypotheses in categorical data. Journal of the American Statistical Association, 61(313), 228–235.
Bickel, S., Brückner, M., & Scheffer, T. (2009). Discriminative learning under covariate shift. JMLR, 10, 2137–2155.
Bishop, C. M. (1995). Neural networks for pattern recognition. Clarendon Press/Oxford.
Bouckaert, R. R. & Frank, E. (2004). Evaluating the replicability of significance tests for comparing learning algorithms, PAKDD.
Breiman, L., Meisel, W., & Purcell, E. (1977). Variable kernel estimates of multivariate densities. Technometrics, 19(2), 135–144.
Chaudhuri, K. & Dasgupta, S. (2014). Rates of convergence for nearest neighbor classification, NIPS. arXiv:1407.0067.
Chawla, N. V., Bowyer, K. W., Hall, L. O., & Kegelmeyer, W. P. (2002). Smote: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research, 16, 321–357. arXiv:1106.1813.
Chen, G., & Shah, D. (2018). Explaining the success of nearest neighbor methods in prediction. Foundations and Trends in Machine Learning, 10, 337–588. https://doi.org/10.1561/2200000064
Cortes, C., Mohri, M., Riley, M. & Rostamizadeh, A. (2008). Sample selection bias correction theory, Algorithmic Learning Theory (ALT). arXiv:0805.2775v1.
Cover, T., & Hart, P. (1967). Nearest neighbor pattern classification. IEEE Transactions on Information Theory, 13, 21–27.
Delgado, M. F., Cernadas, E., Barro, S., & Amorim, D. G. (2014). Do we need hundreds of classifiers to solve real world classification problems? JMLR, 15, 3133–3181.
Devroye, L., Györfi, L., & Lugosi, G. (1996). A probabilistic theory of pattern recognition. Springer.
Dheeru, D. & Karra Taniskidou, E. (2017). UCI machine learning repository. http://archive.ics.uci.edu/ml.
Dietterich, T. G. (1998). Approximate statistical tests for comparing supervised classification learning algorithms. Neural Computation, 10(7), 1895–1923. https://doi.org/10.1162/089976698300017197
Domeniconi, C., Peng, J., & Gunopulos, D. (2002). Locally adaptive metric nearest-neighbor classification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24, 1281–1285.
Dudani, S. A. (1976). The distance-weighted k-nearest-neighbor rule. IEEE Transactions on Systems, Man, and Cybernetics, SMC–6, 325–327.
Elkan, C. (2001). The foundations of cost-sensitive learning, IJCAI.
Fan, W., Davidson, I., Zadrozny, B. & Yu, P. S. (2005). An improved categorization of classifier’s sensitivity on sample selection bias, ICDM.
Geler, Z., Kurbalija, V., Radovanovic, M., & Ivanovic, M. (2015). Comparison of different weighting schemes for the knn classifier on time-series data. Knowledge and Information Systems, 48, 331–378.
Hall, P., Hu, T. C., & Marron, J. S. (1995). Improved variable window kernel estimates of probability densities. Annals of Statistics, 23(1), 1–10. https://doi.org/10.1214/aos/1176324451
Hall, P. A., & Kang, K.-H. (2005). Bandwidth choice for nonparametric classification. Annals of Statistics, 33(1), 284–306. https://doi.org/10.1214/009053604000000959
Hastie, T. J. & Tibshirani, R. (1995). Discriminant adaptive nearest neighbor classification. IEEE Transactions on Pattern Analysis and Machine Intelligence.
He, H., Bai, Y., Garcia, E. A. & Li, S. (2008). Adasyn: Adaptive synthetic sampling approach for imbalanced learning, IJCNN, 1322–1328.
Huang, J., Smola, A. J., Gretton, A., Borgwardt, K. M. & Schölkopf, B. (2006). Correcting sample selection bias by unlabeled data, NIPS.
Kouw, W. M. & Loog, M. (2018). An introduction to domain adaptation and transfer learning. CoRR. arXiv:1812.11806.
Krautenbacher, N., Theis, F. J., & Fuchs, C. (2017). Correcting classifiers for sample selection bias in two-phase case-control studies. Computational and Mathematical Methods in Medicine. https://doi.org/10.1155/2017/7847531
Kremer, J., Gieseke, F., Pedersen, K. S., & Igel, C. (2015). Nearest neighbor density ratio estimation for large-scale applications in astronomy. Astronomy and Computing, 12, 67–72. https://doi.org/10.1016/j.ascom.2015.06.005
Lemberger, P. & Panico, I. (2020). A primer on domain adaptation. arXiv:2001.09994.
Lin, Y. C., & Jeon, Y. (2006). Random forests and adaptive nearest neighbors. Journal of the American Statistical Association, 101, 578–590.
Liu, A. & Ziebart, B. D. (2014). Robust classification under sample selection bias, NIPS.
Mack, Y. & Rosenblatt, M. (1979). Multivariate k-nearest neighbor density estimates.
Mao, C., Hu, B., Chen, L., Moore, P. & Zhang, X. (2018). Local distribution in neighborhood for classification. arXiv:1812.02934v1.
Murphy, M. Z. (1987). The importance of sample selection bias in the estimation of medical care demand equations. Eastern Economic Journal, 13(1), 19–29.
Pedregosa, F., et al. (2011). Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12, 2825–2830.
Prasath, V. B. S. et al. (2017). Distance and similarity measures effect on the performance of k-nearest neighbor classifier: A review. arXiv:1708.04321v3.
Samworth, R. J. (2012). Optimal weighted nearest neighbour classifiers. Annals of Statistics, 40, 2733–2763.
scikit learn. scikit-learn: Machine learning in python (2020).
Scott, D. & Sain, S. (2005). Multi-dimensional density estimation. Data Mining and Data Visualization24.
Shimodaira, H. (2000). Improving predictive inference under covariate shift by weighting the log-likelihood function. Journal of Statistical Planning and Inference, 90(2), 227–244. https://doi.org/10.1016/s0378-3758(00)00115-4
Shringarpure, S., & Xing, E. (2014). Effects of sample selection bias on the accuracy of population structure and ancestry inference. G3: Genes, Genomes, Genetics, 4, 901–911. https://doi.org/10.1534/g3.113.007633
Silverman, B. W. (1998). Density estimation for statistics and data analysis. Chapman & Hall/CRC.
Storkey, A. (2009). Dataset Shift in Machine Learning, Ch. When Training and Test Sets Are Different: Characterizing Learning Transfer, 3–28.
Sugiyama, M., Nakajima, S., Kashima, H., von Bünau, P. & Kawanabe, M. (2007). Direct importance estimation with model selection and its application to covariate shift adaptation, NIPS.
Sugiyama, M., et al. (2009). A density-ratio framework for statistical data processing. IPSJ Transactions on Computer Vision and Applications, 1, 183–208. https://doi.org/10.2197/ipsjtcva.1.183
Sugiyama, M., Suzuki, T., & Kanamori, T. (2010). Density ratio estimation: A comprehensive review. Statistical Experiment and its Related Topics, 1703, 10–31.
Sun, X. & Yang, Z. (2008). Generalized mcnemar’s test for homogeneity of the marginal distributions, no. Statistics and Data Analysis Paper 382-2008 in SAS Global Forum 2008. http://www2.sas.com/proceedings/forum2008/382-2008.pdf.
Sun, W., Qiao, X., & Cheng, G. (2015). Stabilized nearest neighbor classifier and its statistical properties. Journal of the American Statistical Association, 111, 1–55. https://doi.org/10.1080/01621459.2015.1089772
Terrell, G. R., & Scott, D. W. (1992). Variable kernel density estimation. Annals of Statistics, 20(3), 1236–1265. https://doi.org/10.1214/aos/1176348768
Wang, J., Neskovic, P., & Cooper, L. (2006). Improving nearest neighbor rule with a simple adaptive distance measure. Pattern Recognition Letters, 28, 43–46. https://doi.org/10.1016/j.patrec.2006.07.002
Wettschereck, D. & Dietterich, T. G. (1993). Locally adaptive nearest neighbor algorithms, NIPS.
Wu, X., et al. (2007). Top 10 algorithms in data mining. Knowledge and Information Systems. https://doi.org/10.1007/s10115-007-0114-2
Zadrozny, B. (2004). Learning and evaluating classifiers under sample selection bias, ICML.
Zadrozny, B., Langford, J. & Abe, N. (2003). Cost-sensitive learning by cost-proportionate example weighting, ICDM, 435–442.
Acknowledgements
We thank the reviewers for their invaluable comments and suggestions for improving the presentation of the paper.
Funding
The author did not receive funding for conducting this study.
Author information
Authors and Affiliations
Contributions
KK is the sole contributor to this manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The author has no competing interests to declare that are relevant to the content of this article.
Ethical approval
The research for this manuscript did not involve any human subjects or animals.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Additional information
Editor: Xiaoli Fern.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix A Proofs
Appendix A Proofs
Lemma
(Shift Correction Lemma (Shimodaira, 2000)) Let  and
and  be two distributions such that
be two distributions such that  . Let f be a function defined on the support of
. Let f be a function defined on the support of  such that
such that  exists. If
exists. If  then
then

Furthermore,  .
.
Proof




The second part, follows from the linearity of expectation. This part is often used when analyzing the expected loss at a query for a random training dataset. \(\square \)
Shimodaira (2000) provides additional results regarding the asymptotic loss statistics under the correction factor  .
.
Lemma
Consider two integrable functions h and g and a sequence of i.i.d. r.v. \({\textbf{z}}_i\) from a distribution  . Suppose \(g({\textbf{z}}_1) \ne 0\). Then,
. Suppose \(g({\textbf{z}}_1) \ne 0\). Then,


Proof
By the Strong Law of Large Numbers ( ) we have
) we have


Since a.s. convergence implies convergence in probability, we have that

Since the function \(r(a,b)=a/b\) is continuous, provided \(b \ne 0\), invoking the Continuous Mapping Theorem on the last tuple of r.v., we get

Upon simplifying the LHS and RHS, we get

Since convergence in probability implies convergence in distribution, from the Portmanteau lemma we get that

\(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kalpakis, K. Consensus–relevance kNN and covariate shift mitigation. Mach Learn 113, 325–353 (2024). https://doi.org/10.1007/s10994-023-06378-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-023-06378-x



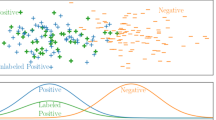

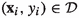 as a training instance
as a training instance  is clear from the context.
is clear from the context.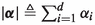 ,
, 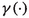 the arguments that do not affect its value.
the arguments that do not affect its value.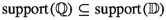 , it follows that the correction factor
, it follows that the correction factor 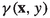 is well defined for any
is well defined for any  .
.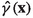 to
to 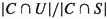 for each instance
for each instance  and
and  probabilities.
probabilities. was chosen to facilitate the 5x2cv paired t-test methodology (Dietterich,
was chosen to facilitate the 5x2cv paired t-test methodology (Dietterich, 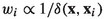 and
and 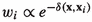 .
.