Bayesian mixture variational autoencoders for multi-modal learning

Abstract

This paper provides an in-depth analysis on how to effectively acquire and generalize cross-modal knowledge for multi-modal learning. Mixture-of-Expert (MoE) and Product-of-Expert (PoE) are two popular directions in generalizing multi-modal information. Existing works based on MoE or PoE have shown notable improvement on data generation, while new challenges such as high training cost, overconfident experts, and encoding modal-specific features also emerge. In this work, we propose Bayesian mixture variational autoencoder (BMVAE) which learns to select or combine experts via Bayesian inference. We show that the proposed idea can naturally encourage models to learn modal-specific knowledge and avoid overconfident experts. Also, we show that the idea is compatible with both MoE and PoE frameworks. When being a MoE model, BMVAE can be optimized by a tight lower bound and is efficient to train. The PoE BMVAE has the same advantages and a theoretical connection to existing works. In the experiments, we show that BMVAE achieves state-of-the-art performance.

1 Introduction

Objects or concepts in the real world can often be realized from different perspectives or modalities. For example, people can learn a new type of neural network by visually observing the architecture diagram or studying reports textually describing the model. To have comprehensive understanding, the ability to effectively generalize the knowledge across modalities is essential. While it is a trivial skill for human beings, how to make machines generalize heterogeneous information is still an open topic. In this work, we focus on learning generative models from multi-modal data without explicit supervision. The underlying challenges or criteria summarized by Shi et al. (2019) are as follows.

Coherent joint generation Given a randomly sampled latent vector, the model should be able to generate multi-modal data by transforming the vector and ensure the generated data describe the same objects or concepts. For example, a model can generate an arbitrary image and the associated texts describing the image content.

Coherent cross generation The model should be able to transfer modalities. For example, the model can generate text descriptions of a given image, and vice versa. It should also be applicable to data missing scenarios. Specifically, missing information is expected to be at least partially recovered by existing modalities.

Latent factorization The learned latent space can be decomposed into subspaces capturing shared and modality-specific features.

Synergy The quality of generation can be boosted when multiple modalities are observed.

To satisfy the criteria, one plausible solution is to build a variational encoder (Kingma & Welling, 2014) for each modality, and combine the encoders to obtain a joint posterior by Product-of-Experts (PoE) or Mixture-of-Experts (MoE) methods. MVAE (Wu & Goodman, 2018) is a representative PoE model, which has product of Gaussian experts as the joint posterior. Although MVAE does not focus on factorizing latent spaces by shared or private factors, it possesses a key benefit that the cross-modal generation can be effectively done without additional uni-modal encoders. In terms of MoE, the state-of-the-art model is MMVAE (Shi et al., 2019). MMVAE shows notable improvement over MVAE on cross-modality generation and satisfies the four proposed criteria. More importantly, experiments show that MMVAE can avoid over-confident experts which commonly exist in MVAE. However, MMVAE is relatively inefficient to train mainly due to the fact that the MoE posterior has no analytic form in most cases. To address the efficiency issue, a PoE model mmJSD (Sutter et al., 2020) has been proposed. However, the limitation being mmJSD accepts only the experts that follow Gaussian. Another recently proposed model, DMVAE (Daunhawer et al., 2020), shows remarkable performance on disentangling latent factors but is also constrained to employing Gaussian posteriors.

In general, PoE can be more efficient than MoE if all the experts are Gaussian, as there exists a closed-form joint posterior. However, for non-Gaussian experts, PoE can be intractable (Hinton, 2002). On the other hand, MoE is much easier to work with non-Gaussian experts through tractable training methods. The flexibility of assuming diverse distributions can potentially lead to better fit on the observed data.

In this work, we propose the Bayesian mixture variational autoencoder (BMVAE) for multi-modal learning. The idea comes from an assumption that uni-modal experts are not always equally reliable if modality-specific information exists. For example, an expert trained by image data is unlikely to learn sentence structures or tones of textual descriptions. Similarly, we may not expect an expert to learn all the details of images from textual descriptions. Therefore, to achieve high-quality generation, it is necessary to rely on certain clever ways to select suitable experts. Following this idea, BMVAE is designed to select experts for each latent dimension via Bayesian inference during learning. We show that BMVAE can be implemented given both MoE and PoE frameworks. When implemented as MoE, denoted by BMVAE$_M$, it has a clear connection to Bayesian Model Averaging (Hoeting et al., 1999) and shows the following advantages over MMVAE:

• BMVAE$_M$ shows improvement over MMVAE on coherent joint generation, coherent cross generation and synergy. Regarding the latent factorization criteria, BMVAE$_M$ naturally learns to disentangle and encode modality-specific features. Additionally, the degree of specificity is quantified for each latent dimension, making the representations more explainable.

• BMVAE$_M$ is more efficient to train. For data with M modalities, MMVAE requires $M^2$ passes through decoders during training, while BMVAE$_M$ only needs M passes.

• MMVAE needs to be learned by optimizing a looser lower bound, as the tighter bound empirically causes overconfident experts. We show that BMVAE$_M$ does not need to sacrifice the theoretical tightness to avoid the overconfidence issue.

For PoE-based BMVAE, denoted by BMVAE$_P$, we present connections between the proposed and existing models. Specifically, we show that the model can be regarded as generalized mmJSD with stochastic weights and a different sampling strategy. We also show that BMVAE$_P$ and BMVAE$_M$ can have equivalent joint posteriors in specific settings.

2 Background

Section 2.1 is an overview of the recently proposed works. Section 2.2 briefly reviews the idea of joint posteriors factorization via MoE and PoE. Sections 2.3 and 2.4 are the fundamentals of MMVAE. Section 2.5 introduces the mmJSD objectives.

2.1 Overview of recent works

Variational autoencoders (VAE) have been shown to be effective for multi-modal learning. An example is JMVAE (Suzuki et al., 2017) which is designed to model the joint distribution of modalities by following the VAE framework. Also, the model has the ability to handle missing modality at test (or prediction) time. The cost of handling missing data is that it requires an additional uni-modal encoder for each modality, and the uni-modal encoders are optimized to approximate the joint distribution. The TELBO model proposed by Vedantam et al. (2018) can be learned by optimizing a different objective, which can handle partially observed features by PoE inference networks. To obtain more effective latent factorization, Hsu and Glass (2018) propose PVAE which specifically learns shared and modality-specific representations. Similar to JMVAE, PVAE requires additionally training uni-modal encoders to handle missing modalities. Another work, MFM (Tsai et al., 2019), factorizes latent representations into discriminative and modality-specific factors, where discriminative factors are learned from labeled data. Instead of employing VAE, the authors propose multi-modal Wasserstein autoencoder for inference.

The works introduced above need additional data information, learning objectives, or uni-modal networks, which is a less ideal setting as discussed by Shi et al. (2019). By contrast, a more compact solution is MVAE proposed by Wu and Goodman (2018). MVAE is designed to model joint posterior via PoE architectures. Different from TELBO, an expert in MVAE is responsible for a whole modality instead of a single feature. As a result, MVAE shows competitive performance and does not need additional uni-modal encoders. Shi et al. (2019) report that MVAE could severely suffer from over-confident experts due to the product operations and propose MMVAE which models the joint posterior by MoE methods. Empirical results show that MMVAE can avoid aforementioned issues and outperform MVAE on data generation and modality transferring. Although MMVAE has several advantages over MVAE, it is less efficient to train. Since the joint posterior generated by MoE generally has no analytic form, the learning process would then rely on sampling-based methods having higher training cost. Besides, for data with M modalities, MMVAE requires $M^2$ passes through decoders during training. More recently, Sutter et al. (2020) propose mmJSD to address the efficiency issue by focusing on PoE-based dynamic prior. Instead of employing KL divergence for regularization, mmJSD applies JS divergence for both regularization and learning multi-modal information. To achieve efficient learning, mmJSD requires the prior and uni-modal posteriors to be Gaussian. Another PoE model proposed recently is DMVAE (Daunhawer et al., 2020). DMVAE focuses on not only efficient learning but also disentangling latent factors. Different from typical multi-modal VAEs, DMVAE requires additional loss functions and adversarial training approaches to learn disentangled features.

2.2 Factorized joint posteriors

Here we introduce the idea of factorizing posteriors via MoE and PoE for multi-modal learning. Given M-modalities data $\{x_1,\ldots ,x_M\}$ or $x_{1:M}$ for training, the parameterized likelihood $p_\varTheta$ and posterior $q_\varPhi$ are commonly modelled by deep neural networks with $\varTheta =\{\theta _1,\ldots ,\theta _M\}$ and $\varPhi = \{\phi _1,\ldots ,\phi _M\}$, respectively. In MMVAE, the joint posterior $q_{\varPhi }$ is designed to be factorized by a uniform combination of uni-modal posteriors. Namely, $q_{\varPhi }(z\mid x_{1:M}) = \sum _{m}\alpha _m \cdot q_{\phi _m}(z\mid x_m)$, where $\alpha _m = \frac{1}{M}$. Each uni-modal posterior $q_{\phi _m}$ is implemented by an encoder with corresponding modality as input.

Regarding PoE-based factorization, the most common form would be $q_{\varPhi }(z\mid x_{1:M}) = \prod _{m} q_{\phi _m}(z\mid x_m)$. In PoE settings, the experts are usually assumed to be Gaussian, as the joint distribution will also be Gaussian and thus can be learned efficiently. If the experts are non-Gaussian, training the PoE model generally becomes intractable (Hinton, 2002). On the contrary, we note that MoE models are more flexible on selecting distributions to fit data. If the weights $\alpha _{1:M}$ are constants or learnable parameters, the MoE joint posterior $q_{\varPhi }(z\mid x_{1:M})$ can be easily trained if sampling from $q_{\phi _m}(z\mid x_m)$ is efficient. Specifically, the gradient for learning $\phi _m$ can be estimated via Monte Carlo methods which can be applied to a wide range of distributions (Mohamed et al., 2020).

Another difference between MoE and PoE is the overconfidence issue. Shi et al. (2019) show that PoE could suffer from over-confident experts, which empirically leads to weak performance on modality transfer. Also, in order to let a PoE model be aware of missing modalities, training tricks involving artificial sub-sampling may be necessary (Wu & Goodman, 2018).

2.3 Importance weighted autoencoder for multi-modal learning

In the work of MMVAE, Shi et al. suggest that importance weighted autoencoder (IWAE) (Burda et al., 2016) could be more effective than vanilla VAE in multi-modal learning. Equation 1 is the objective function of IWAE for data with M-modalities.

$$\begin{aligned} {\mathscr {L}}_I = {\mathbb {E}}_{z^{1:K}\sim q_{\varPhi }(z\mid x_{1:M})}\left[ \log \sum _{k=1}^K \frac{1}{K} \frac{p_{\varTheta }(z^k, x_{1:M})}{q_{\varPhi }(z^k \mid x_{1:M})} \right] \end{aligned}$$

(1)

In Eq. 1, the hyper-parameter K is the number of samples from posterior $q_{\varPhi }$. Burda et al. (2016) theoretically prove that higher K improves tightness of a lower bound for variational inference. It potentially enhances the model to learn more informative latent representations and achieve better performance on data generation. When $K=1$, Eq. 1 is equivalent to the vanilla VAE.

In addition to improved performance over vanilla VAE in general cases, Shi et al. (2019) suggest that IWAE can be especially beneficial in multi-modal learning. Specifically, the estimated posteriors tend to have higher entropy, encouraging an uni-modal posterior (i.e. $q_{\phi _m}$) to assign higher probability to regions of other modalities.

2.4 Learning objectives of MMVAE

Here we briefly introduce MMVAE. Equation 2 is the proposed objective function for training. The function ${\mathscr {L}}_M$ has been shown to be a lower bound of log likelihood of observed data, i.e. ${\mathscr {L}}_M \le \log p(x_{1:M})$.

$$\begin{aligned} {\mathscr {L}}_{M} = \frac{1}{M}\sum ^M_{m=1}{\mathbb {E}}_{z^{1:K}_m\sim q_{\phi _m}}\left[ \log \frac{1}{K} \sum _{k=1}^K \frac{p_{\varTheta }(z^k_m, x_{1:M})}{q_{\varPhi }(z^k_m \mid x_{1:M})} \right] \end{aligned}$$

(2)

Shi et al. (2019) also reveal that there exists a tighter lower bound as shown in Eq. 3, where $L = K / M$ for having the same number of samples as Eq. 2.

$$\begin{aligned} {\mathscr {L}}_{T} = {\mathbb {E}}_{\begin{array}{c} z^{1:L}_1\sim q_{\phi _1}\\ \vdots \\ z^{1:L}_M\sim q_{\phi _M} \end{array}}\left[ \log \frac{1}{M} \sum ^M_{m=1} \frac{1}{L} \sum _{l=1}^L \frac{p_{\varTheta }(z^l_m, x_{1:M})}{q_{\varPhi }(z^l_m \mid x_{1:M})} \right] \end{aligned}$$

(3)

Optimizing ${\mathscr {L}}_T$ is more effective theoretically as ${\mathscr {L}}_M\le {\mathscr {L}}_T\le \log p(x_{1:M})$. However, empirical results show that optimizing ${\mathscr {L}}_T$ can lead to modality collapse in MMVAE, significantly degrading performance on multi-modal data generation. Specifically, the joint posterior ignores most experts during training and is then reduced to a uni-modal posterior generally.

A possible reason for the collapse could be the weights for gradients in IWAE. For example, let $z_1^{1:K}$ and $z_2^{1:K}$ be latent vectors sampled from $q_{\phi _1}$ and $q_{\phi _2}$ respectively. In ${\mathscr {L}}_T$, $z_1^{1:K}$ and $z_2^{1:K}$ can simultaneously exist inside the log summation. By the weight mechanism of IWAE, $z_1^{1:K}$ and $z_2^{1:K}$ receive gradients with different weights according to their contributions to the likelihood. If modality 1 has less contribution, $q_{\phi _1}$ would be gradually ignored due to decreasing gradients. On the contrary, in ${\mathscr {L}}_M$, samples inside the log summation must come from the same modality. The effect is that gradients from different modalities are forced to be equally weighed, preventing a modality from fading out due to weak update signals.

2.5 The mmJSD learning objectives

2.5.1 Standard mmJSD objective

Sutter et al. (2020) recently propose mmJSD as an objective for multi-modal learning. The differences between mmJSD and previous works are twofold. Firstly, the evidence lower bound (ELBO) is optimized via JS instead of KL divergence. Secondly, the joint posterior is combined with priors and serves as a so-called dynamic prior. Equation 4 is the objective, where $\sum ^P_{m=1} \pi _m = 1$ and function $f_{\mathscr {M}}$ defines a mixture distribution averaging uni-modal $q_{\phi _m}$ and parameterized prior $p_\varTheta (z)$.

$$\begin{aligned} \begin{aligned}&{\mathbb {E}}_{q_\phi }\left[ \log p_\varTheta (x_{1:M}\mid z) \right] - JS^{M+1}_{\pi }(\{q_{\phi _m}(z\mid x_m)\}^M_{m=1},p_\varTheta (z)) \\&\quad JS^P_\pi (\{r_m(z)\}^P_{m=1}) = \sum ^P_{m=1} \pi _m D_{KL}(r_m(z)\mid f_{\mathscr {M}}(\{r_v(z)\}^P_{v=1})) \end{aligned} \end{aligned}$$

(4)

For efficient training, $f_{\mathscr {M}}$ is restricted to be product of Gaussian. Namely, $f_{\mathscr {M}}(\{q_{\phi _m}(z\mid x_m)\}^M_{m=1},p_\varTheta (z)) = \prod _{m=1}^M q^{\pi _m}_{\phi _m}p^{\pi _{M+1}}_\varTheta$, where $q_{\phi _m}$ and $p_\varTheta$ are all Gaussian.

2.5.2 Modality-specific mmJSD objective

Sutter et al. (2020) also propose a variant of mmJSD focusing on learning shared and modality-specific latent factors. The idea is to let latent vectors z be concatenation of sub-vectors $\{s_m\}^M_{m=1}$ and c, where $\{s_m\}$ encodes features specific to the m-th modality, and c encodes modality-independent information. Equation 5 is the objective.

$$\begin{aligned} \begin{aligned}&\sum ^M_{m=1}{\mathbb {E}}_{q_{\phi _c}(c\mid x_{1:M})}\left[ {\mathbb {E}}_{q_{\phi _{s_m}}} \left[ \log p_\varTheta (x_m\mid s_m, c) \right] \right] \\&\quad - \sum ^M_{m=1} D_{KL}(q_{\phi _{s_m}}(s_m\mid x_m) ||p_\theta (s_m)) - JS^{M+1}_{\pi }(\{q_{\phi _{c_m}}(c\mid x_m)\}^M_{m=1},p_\theta (c)) \end{aligned} \end{aligned}$$

(5)

Although the objective is in a form of mmJSD, Sutter et al. show that the idea can also work on MMVAE and MVAE.

A limitation of the objective is that $\{s_m\}^M_{m=1}$ are constrained to have the same number of dimensions despite the fact that some modalities might be more complex than others. Besides, deciding the number of dimensions of $\{s_m\}^M_{m=1}$ or c requires additional experiments for validation.

3 The MoE Bayesian mixture variational autoencoder

In this section, we introduce the learning algorithms of BMVAE$_M$. The main ideas, dimension-wise mixture, stochastic weight inference and explicit regularization, are introduced in Sects. 3.1–3.3. The introductions are based on IWAE for generality and can easily fit VAE by setting $K=1$.

3.1 Dimension-wise MoE mixture

We first introduce the joint posterior in BMVAE$_M$. We follow the MoE framework but propose a different algorithm from MMVAE for mixing uni-modal experts. We note that the proposed method can naturally fit a tight lower bound ${\mathscr {L}}_T$ without modality collapse and is more computationally efficient.

In our method, the joint posterior $q_\varPhi$ is factorized by not only modality but also latent factor. Equation 6 is the factorization, where D is the number of dimensions of a latent vector.

$$\begin{aligned} \begin{aligned} q_\varPhi (z\mid x_{1:M})&= \prod _{d=1}^D q_{\varPhi ,d}(z_d\mid x_{1:M}) \\ q_{\varPhi ,d}(z_d\mid x_{1:M})&= \sum _{m=1}^M \alpha _{m,d} \cdot q_{\phi _{m,d}}(z_d\mid x_m) \end{aligned} \end{aligned}$$

(6)

Conceptually, we create D expert sets where each set has M experts to decide the value of one latent factor. It differs from MMVAE in two ways. The first difference is each latent factor has its own mixture weights $\alpha _{m,d}$ which can be $\frac{1}{M}$ or learned from data. The algorithms for learning the weights are discussed in Sect. 3.2. The second difference lies in the individually sampled latent factor. Specifically, the mixture weights $\alpha _{m,d}$ form a categorical distribution $C_{\alpha _d}(m)$ for latent dimension d. When we want to obtain a sample z from joint posterior $q_\varPhi$, the sampling process repeats Eq. 7 for $d=1,\ldots ,D$. Afterwards, we can concatenate the sampled $z_1,\ldots ,z_D$ to get z.

$$\begin{aligned} \begin{aligned} m&\sim C_{\alpha _d}(m) \\ z_d&\sim q_{\phi _{m,d}}(z_d\mid x_m) \end{aligned} \end{aligned}$$

(7)

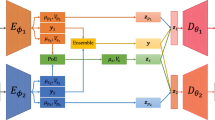
To train the IWAE, we conduct standard IWAE objective (i.e. ${\mathscr {L}}_I$) with $z^{1:K}$ sampled by the proposed method and apply reparameterization. Note that the number of parameters of encoders and decoders is the same as it is in MMVAE, as each expert here is responsible for only one factor. The comparison of encoding-decoding between BMVAE and MMVAE is illustrated in Fig. 1.

Fig. 1

Comparison of encoding and decoding between BMVAE and MMVAE

From Fig. 1a, we can see that a sampled z in BMVAE$_M$ is composed of factors generated by randomly chosen encoders. It can be regarded as a simulation of modality missing in training time. Additionally, we note that this mechanism has two merits.

Optimization with tight lower bound It can be seen that latent vectors sampled by our methods naturally contain outputs from multiple modalities. By taking derivative of the log summation term in ${\mathscr {L}}_I$, gradients through the outputs can be weighed differently. Compared with MMVAE optimized by ${\mathscr {L}}_T$, we find BMVAE$_M$ optimized by ${\mathscr {L}}_I$ does not suffer from modality collapse. The difference could come from the stochastic selection of experts. In ${\mathscr {L}}_T$, samples from all the experts simultaneously exist for decoding. If one of the experts, say $q_{\phi _1}$, is relatively powerful, the model could choose to rely on $q_{\phi _1}$ and ignore $q_{\phi _{2:M}}$. On the other hand, in BMVAE$_M$, experts are selected by binary indicators sampled from categorical distribution $C_{\alpha _d}(m)$. If $\alpha _{d}$ are all close to $\frac{1}{M}$, relying on a single modality could be risky, as there is a chance the corresponding expert is not selected. Therefore, the model does have motivation to make all experts similarly capable.

Reduced computational cost As illustrated in Fig. 1a, BMVAE$_M$ is similar to a multi-task autoencoder generating heterogeneous data by decoding a given latent code. Specifically, decoding during training BMVAE$_M$ is done by computing $p_{\theta _1}(x\mid z)$ and $p_{\theta _2}(x\mid z)$, where z is one of the sampled latent vectors. In MMVAE, decoding is done by computing $p_{\theta _1}(x\mid z_1)$, $p_{\theta _1}(x\mid z_2)$, $p_{\theta _2}(x\mid z_1)$ and $p_{\theta _2}(x\mid z_2)$, where $z_1$ and $z_2$ are sampled from modality 1 and 2, respectively. In summary, MMVAE requires $M^2$ passes through decoders while BMVAE$_M$ needs M passes.

3.2 Stochastic inference on mixture weights

In MMVAE, the mixture weights are constant $\frac{1}{M}$, which is reasonable as favoring a specific modality without concrete evidence could result in overconfident experts. In BMVAE$_M$, we note that using multiple sets of experts allows imbalanced mixture weights. In reality, the imbalance could have a connection with finding shared and private latent subspaces, which is beneficial to multi-modal learning. For example, assuming latent factor d encodes private features of modality 1, it is intuitive to expect $q_{\phi _{1,d}}$ to be able to make more reliable predictions and should have higher credibility, namely, $\alpha _{1,d} > \frac{1}{M}$.

To determine parameters $\alpha _{m,d}$, we propose learning them jointly with $\varTheta$ and $\varPhi$ by following the same IWAE objective. We assume $C_\alpha = \prod _{d=1}^D C_{\alpha _d}$, and denote a collection of D binary indicators sampled from $C_{\alpha _{1:D}}$ respectively as a symbol $m^\star$. The objective function after incorporating modality selection is shown in Eq. 8.

$$\begin{aligned} \begin{aligned}&{\mathbb {E}}_{\begin{array}{c} z^{1:K}\sim q_{\varPhi }\\ m^{\star ^{1:K}}\sim C_{\alpha } \end{array}}\left[ \log \sum _{k=1}^K \frac{1}{K} \frac{p_{\varTheta }(z^k, m^{\star ^k}, x_{1:M})}{q_{\varPhi }(z^k, m^{\star ^k} \mid x_{1:M})} \right] \\&\quad = {\mathbb {E}}_{\begin{array}{c} z^{1:K}\sim q_{\varPhi }\\ m^{\star ^{1:K}}\sim C_{\alpha } \end{array}}\left[ \log \sum _{k=1}^K \frac{1}{K} \frac{p_{\varTheta }(x_{1:M}\mid z^k, m^{\star ^k})p(z^k)C(m^{\star ^k})}{q_{\varPhi }(z^k \mid x_{1:M}, m^{\star ^k})C_\alpha (m^{\star ^k})} \right] \end{aligned} \end{aligned}$$

(8)

In Eq. 8, there are two additional assumptions. Firstly, we assume the prior p(z) is independent to modalities. Hence, $p(z\mid m^\star ) = p(z)$. Secondly, the categorical prior C can be factorized as $C = \prod _{d=1}^D C_d$. The parameters (i.e. mixture weights) of $C_d$ are all constants $\frac{1}{M}$. The reason for choosing $\frac{1}{M}$ is to provide uninformative prior. Also, it could encourage experts from different modalities to find shared features, which can improve performance on cross-modality generation.

To learn $C_\alpha$, we employ differentiable Gumbel-Softmax (Jang et al., 2017; Maddison et al., 2017) to approximate discrete samples generated by categorical distributions. In this work, we allocate M learnable parameters (i.e. $\alpha _d$) for each latent dimension. An indicator, m, for selecting modality in dimension d is sampled by Eq. 9 for $i=1,\ldots ,M$ with temperature $\tau _d$. The sampled M-dimensional vector is followed by straight-through trick (Jang et al., 2017) for being discrete. The general idea of the trick is to create a constant vector $m_c$ having the same size and values as $m_{1:M}$. A discrete indicator is then obtained via one_hot$(m_c) + m_{1:M} - m_c$. The result is one-hot encoded but the gradient will only pass through continuous $m_{1:M}$ since $m_c$ is constant.

$$\begin{aligned} \begin{aligned} m_i&= \frac{\exp ((\log (\alpha _{i,d}) + g_i) / \tau _d)}{\sum _{j=1}^M\exp ((\log (\alpha _{j,d}) + g_j) / \tau _d)} \\ g&= -\log (-\log (u)) \\ u&\sim Uniform(0, 1) \end{aligned} \end{aligned}$$

(9)

Another issue of learning with Eq. 9 is deciding the temperature $\tau _d$. High temperature can make the Gumbel-Softmax distribution more continuous and uniform. It helps finding shared information across modalities; however, it also increases the difficulty of encoding private features. On the contrary, low temperature leads to a more discrete distribution, which discourages the model from finding shared information. In order to find both shared and private information, we propose dimension-wise temperature, which includes both high and low $\tau _d$. We first decide lower and higher temperature bounds l and u. Then, we let $\tau _d=l+\frac{(u-l)(d-1)}{D-1}$ to ensure both high and low $\tau _d$ are included. As a result, the model can thereby find appropriate dimensions for encoding shared and private features.

3.3 Explicit regularization for inference

We find explicitly controlling optimization of mixture weights can make training easier and help strengthen shared features. To do this, we approximately decompose Eq. 8 into two terms as shown in Eq. 10.

$$\begin{aligned} \begin{aligned} F&= {\mathbb {E}}_{\begin{array}{c} z^{1:K}\sim q_{\varPhi }\\ m^{\star ^{1:K}}\sim C_{\alpha } \end{array}}\left[ \log \sum _{k=1}^K \frac{1}{K} \frac{p_{\varTheta }(x_{1:M}\mid z^k, m^{\star ^k})p(z^k)}{q_{\varPhi }(z^k \mid x_{1:M}, m^{\star ^k})} \right] \\ G&= {\mathbb {E}}_{m^{\star ^{1:K}}\sim C_{\alpha }}\left[ \log \sum _{k=1}^K \frac{1}{K} \frac{C(m^{\star ^k})}{C_\alpha (m^{\star ^k})} \right] \end{aligned} \end{aligned}$$

(10)

It can be observed that G is negative KL divergence $D_{KL}(C_\alpha \Vert C)$ if $K=1$. In practice, we find optimizing $D_{KL}(C_\alpha \Vert C)$ where C and $C_\alpha$ are both categorical distributions is more numerically stable, as there is an analytic form. The final objective of BMVAE$_M$ is Eq. 11, where the hyper-parameter $\lambda _c$ reweighs strength of the divergence. If $\lambda _c=1$, ${\mathscr {L}}_B$ is approximately the derived result in Eq. 8.

$$\begin{aligned} \begin{aligned} {\mathscr {L}}_B = F - \lambda _c \cdot D_{KL}(C_\alpha \Vert C) \end{aligned} \end{aligned}$$

(11)

In practice, we note that models trained with $\lambda _c=1$ do not necessarily realize multi-modal learning. For example, a model may learn to set $\alpha _{m,d}$ to either 1 or 0 for all d. Given $\sum ^M_{m=1}\alpha _{m,d}=1$, the binary weights turn BMVAE$_M$ into a concatenation of multiple uni-modal IWAE. To fix this, we simply raise the strength of $D_{KL}(C_\alpha \Vert C)$ to encourage $\alpha _{m,d} \approx \frac{1}{M}$. We find $\lambda _c$ in $\left[ 10, 15\right]$ helps the model learn both shared and private features from data.

4 The PoE Bayesian mixture variational autoencoder

In this section, we present our PoE-based BMVAE, namely BMVAE$_P$. The proposed model can be regarded as a generalized mmJSD with stochastic weights and a different sampling strategy. In Sect. 4.1, we first reveal an alternative form of mmJSD. The learning algorithm and objective of BMVAE$_P$ are introduced in Sect. 4.2. Finally, we show that there exists an equivalence between our MoE and PoE-based posteriors in Sect. 4.3.

4.1 The alternative form of mmJSD

Our PoE-based BMVAE is derived from the standard mmJSD objective but in a different form. Specifically, we find Eq. 4 is equivalent to the common ELBO with additional objectives.

Let the PoE joint posterior $\prod ^M_{m=1} q_{\phi _m}$ be $\bar{q}$, $\pi _q=\sum ^M_{m=1}\pi _m$, and $\pi _z = 1 - \pi _q$. The JS divergence term in Eq. 4 can be reorganized as follows.

$$\begin{aligned} \begin{aligned}&JS^{M+1}_\pi (\{q_{\phi _m}\}^M_{m=1}, p_\varTheta (z)) \\&\quad = \sum ^M_{m=1}\pi _m D_{KL}(q_{\phi _m}||\bar{q}^{\pi _q}p^{\pi _z}_\varTheta (z)) + \pi _z D_{KL}(p_\varTheta (z)||\bar{q}^{\pi _q}p^{\pi _z}_\varTheta (z)) \\&\quad = \sum ^M_{m=1}\pi _m \int _z q_{\phi _m} \log \frac{q^{\pi _q}_{\phi _m} q^{\pi _z}_{\phi _m}}{\bar{q}^{\pi _q}p^{\pi _z}_\varTheta (z)} \,dz + \pi _z \int _z p_\varTheta (z) \log \frac{p^{\pi _q}_\varTheta (z) p^{\pi _z}_\varTheta (z)}{\bar{q}^{\pi _q}p^{\pi _z}_\varTheta (z)} \,dz \\&\quad = \sum ^M_{m=1}\pi _m (\pi _q D_{KL}(q_{\phi _m}||\bar{q}) + \pi _z D_{KL}(q_{\phi _m}||p_\varTheta (z))) + \pi _z \pi _q D_{KL}(p_\varTheta (z)||\bar{q}) \end{aligned} \end{aligned}$$

(12)

By combining Eq. 12 with Eq. 4, we obtain the following objective equivalent to the standard mmJSD.

$$\begin{aligned} \begin{aligned}&\underbrace{{\mathbb {E}}_{z\sim q_\varPhi }\left[ \log p_\varTheta (x_{1:M}|z)\right] - \sum ^M_{m=1}\pi _m\pi _z D_{KL}(q_{\phi _m}||p_\varTheta (z))}_\text {Multi-modal ELBO}\\&\quad \underbrace{- \sum ^M_{m=1}\pi _m \pi _q D_{KL}(q_{\phi _m}||\bar{q}) - \pi _z \pi _q D_{KL}(p_\varTheta (z)||\bar{q})}_\text {Additional objectives} \end{aligned} \end{aligned}$$

(13)

Given that $p_\varTheta (z)$ mainly encodes prior knowledge of data, the first part of Eq. 13 simply combines M uni-modal VAEs without explicit cross-modalities alignment. Therefore, it can be seen that multi-modal learning is mostly realized by the additional objectives. The realization is also intuitive. The first KL divergence encourages uni-modal posteriors to learn cross-modality information from the joint posterior $\bar{q}$, and the second one regularizes the learned $\bar{q}$.

4.2 Stochastic and dimension-wise weights

Similar to the idea presented in Sect. 3, we propose inferring weights by latent dimension. To do this, we let the non-negative weights $\pi _{1:D} = \{\pi _1,\ldots ,\pi _D\}$ be D M-dimensional random variables instead of constant vectors. The weight $\pi _z$ remains a hyper-parameter. For dimension d, there is a constraint $\sum ^M_{m=1}\pi _{m,d} = 1$. Note that this constraint seems to violate the mmJSD objective since $\sum ^M_{m=1}\pi _{m,d} + \pi _z > 1$. However, as shown in Eq. 13, the violation simply increases the strength of regularization and additional objectives, which can be easily fixed by re-scaling the KL divergence terms.

To define a PoE-based joint posterior, we follow Eq. 6 but employ geometric rather than arithmetic mean. Given that $\pi _{1:M}$ are not necessarily discrete, we propose sampling $\pi _{1:M}$ from parameterized Dirichlet distributions. Equation 14 is the defined posterior in dimension d, where $\beta _d \in {\mathbb {R}}^M_{>0}$ are learnable parameters and inferred via reparameterization gradient for Dirichlet (Figurnov et al., 2018).

$$\begin{aligned} \begin{aligned} q_{\varPhi , d}(z_d \mid x_{1:M})&= \prod ^M_{m=1} q^{\pi _{m,d}}_{\phi _{m,d}}(z_d \mid x_m)\\ \pi _{1:M,d}&\sim Dir(\beta _d) \end{aligned} \end{aligned}$$

(14)

With the defined joint posterior, we present the objective ${\mathscr {L}}_P$ for learning BMVAE$_P$ in Eq. 15, where $\bar{q}$ is constructed by Eq. 14, $\lambda _{ab} = \pi _a\pi _b$, $\eta$ and $\beta _{prior}$ are hyper-parameters.

$$\begin{aligned} \begin{aligned} {\mathscr {L}}_P&= {\mathbb {E}}_{\pi \sim Dir}\underbrace{\left[ {\mathbb {E}}_{z\sim \bar{q}}\left[ \log p_\varTheta (x_{1:M}|z)\right] - \lambda _{zq} D_{KL}(\bar{q}||p_\varTheta (z))\right] }_\text {Multi-modal ELBO}\\&\quad - \sum ^M_{m=1}\lambda _{mq} D_{KL}(q_{\phi _m}||\bar{q})\\&\quad - \sum ^M_{m=1}\lambda _{mz} D_{KL}(q_{\phi _m}||p_\varTheta (z)) \\&\quad - \eta \sum ^D_{d=1} D_{KL}(Dir(\beta _d) || Dir(\beta _{prior})) \end{aligned} \end{aligned}$$

(15)

There are two differences between ${\mathscr {L}}_P$ and the alternative form of mmJSD (i.e. Eq. 13). The first one is the newly included KL divergence for inferring Dirichlet distributions. The second difference is we introduce weighted product of posteriors. Here we also reverse $D_{KL}(p_\varTheta (z)||\bar{q})$ to be consistent with the common ELBO form. The reason for shifting to multi-modal ELBO is that we find the learned $\pi$ are not meaningful when training with uni-modal ELBO. To see this, in uni-modal ELBO, the gradient propagated from reconstruction loss is not through $\pi$. Therefore, the learned $\pi$ only involves $D_{KL}(q_{\phi _m}||\bar{q})$ and $D_{KL}(Dir(\beta _d)||\beta _{prior})$, which includes insufficient data information.

4.3 On the equivalence of MoE and PoE-based joint posteriors

We show that there exists an equivalence between MoE and PoE joint posteriors in BMVAE. The equivalence originates from parameter settings of Dirichlet distributions. Let the weights $\pi _d \sim Dir(\beta _d)$ and $\beta _{m,d}$ for all $m\in \{1,\ldots ,M\}$ have similar values for simplicity. When $\beta _{m,d} > 1$, $\pi _d$ are likely to be close to the centre of the $(M-1)$-simplex in a sense of continuous weights (i.e. $\pi _{m.d} \approx \frac{1}{M}$). On the contrary, $\pi _d$ sampled with $\beta _{m,d} < 1$ tend to be in corners of the simplex, resulting in nearly discrete weights. Specifically, if $\beta _{m,d} \rightarrow {0}$, $\pi _{m,d}$ is either 1 or 0.

When $\pi _{m,d}$ are discrete, the MoE and PoE mixture methods of BMVAE become similar, as they both learn to stochastically select one expert for each latent dimension. Therefore, training BMVAE$_P$ with a constraint $\beta _d \ll 1$ would be close to training BMVAE$_M$ with additional objectives $D_{KL}(q_{\phi _m}||\bar{q})$ and $D_{KL}(q_{\phi _m}||p_\varTheta (z))$. It first implies that BMVAE$_P$ can approximate BMVAE$_M$ by constraining $\beta _d \ll 1$ and $\lambda _{mq}=\lambda _{mz}=0$. Secondly, it may raise a question that if we can equip BMVAE$_M$ with the additional objectives to improve MoE-based multi-modal learning. However, we find the two additional objectives empirically do not improve BMVAE$_M$ on the evaluation tasks we reveal in Sect. 6. Also, different from PoE, the joint posterior $\bar{q}$ has no analytic form, increasing computational cost of $D_{KL}(q_{\phi _m}||\bar{q})$ in the training stage.

5 Analysis of time and space complexity

We analyze complexity of training MMVAE, mmJSD, BMVAE$_M$ and BMVAE$_P$ in this section. We first discuss time complexity. Training the VAE-based models involves encoding, decoding, obtaining joint posteriors, sampling from posteriors, and KL divergence minimization. We define the upper bound of the cost of training an encoder or decoder as ${\mathscr {C}}_T$ including forward and backward passes. As an example, the cost of training a single-modality auto-encoder without variational inference is bounded by ${\mathscr {C}}_T + {\mathscr {C}}_T = 2{\mathscr {C}}_T$. As latent dimensions are assumed to be mutually independent in the discussed models, we note that the training procedures excluding encoding and decoding can be decomposed into dimension-wise operations with complexity O(D). The operations are enumerated as follows.

• Obtaining product of 2 Gaussian posteriors.

• Obtaining a categorical or Dirichlet posterior where the underlying encoder is a single-layer neural network.

• Sampling from a Gaussian or categorical posterior.

• Sampling from a mixture of posteriors.

• Estimating KL divergence between 2 Gaussian or categorical distributions.

With the enumerated upper bounds, we analyze training costs of the discussed models and summarize the results in Table 1.

MMVAE The cost of obtaining M posteriors is $M{\mathscr {C}}_T$. As MMVAE does not sample embeddings from a joint posterior but M posteriors, the cost of sampling is $MK\cdot O(D)$ where K is the sample size of IWAE. The MK embeddings are then decoded by M decoders, costing $M^2K{\mathscr {C}}_T$. Finally, the cost of estimating the sampling-based KL divergence for the MK embeddings is $MK\cdot O(D)$.

BMVAE$_M$ The cost of obtaining M posteriors and 1 categorical posterior is $M{\mathscr {C}}_T + O(D)$. Sampling from a mixture of posteriors of an IWAE-based BMVAE$_M$ costs $(M+1)K\cdot O(D)$. Different from MMVAE, the number of generated embeddings is K instead of MK. Therefore, the cost of decoding reduces to $MK{\mathscr {C}}_T$. Finally, the cost of the sampling-based KL divergence is $(M+1)K\cdot O(D)$ where the additional cost comes from the categorical distributions.

mmJSD The cost of encoding and decoding is $2M{\mathscr {C}}_T$. Obtaining the product of M Gaussian densities and a prior costs $(M+1)\cdot O(D)$. We assume the product of Gaussian is both used for the joint posterior and dynamic prior. Sampling from the joint posterior costs O(D) and estimating KL divergence between uni-modal posteriors and dynamic prior costs $M\cdot O(D)$ in total.

BMVAE$_P$ The cost of encoding and decoding is $2M{\mathscr {C}}_T + O(D)$ where O(D) comes from the Dirichlet distribution. The joint posterior is the weighted product of M Gaussian densities costing $M\cdot O(D)$. The embeddings for decoding are sampled from the joint posterior costing O(D). The cost of the KL divergence losses is $(M + M + 1)\cdot O(D)$ which can be observed from Eq. 15.

Table 1 Time complexity of multi-modal VAEs

For the analysis of space complexity, we define the upper bound of the cost of an encoder or decoder as ${\mathscr {C}}_S$. Other costs coming from the following components are assumed to have space complexity O(D).

• A single-layer neural network with D neurons.

• A D-dimensional embedding sampled from a posterior.

The costs of the discussed multi-modal VAEs are summarized in Table 2.

Table 2 Space complexity of multi-modal VAEs

6 Experiments

In Sects. 6.1 and 6.2, we compare BMVAE$_M$ with MMVAE following protocols and datasets proposed by Shi et al. (2019). The autoencoders are IWAE and the posteriors are Laplace distributions. In each evaluation task, the sample size K of IWAE is the value suggested by Shi et al. and applied to both MMVAE and BMVAE$_M$. In Sect. 6.3, we evaluate both BMVAE$_M$ and BMVAE$_P$ on a 3-modal dataset proposed by Sutter et al. (2020). For fair comparison, the posteriors are all Gaussian and the autoencoders used in testing include both VAE and IWAE. In Sect. 6.4, we evaluate models via MultiBench (Liang et al., 2021) measuring cross-modality generalization, training speed, and robustness. The tested datasets are more challenging, and the models for evaluations are not limited to MoE and PoE methods.

In each experiment, the models for comparison have the same uni-modal encoders and decoders. Our models are all trained by Adam optimizer (Kingma & Ba, 2015) with learning rate 0.001. The parameters $\lambda _c$ and $\eta$ for controlling mixture weights in BMVAE$_M$ and BMVAE$_P$ are decided via validation data. The parameter search space of $\lambda _c$ and $\eta$ is $\{0.01h, 0.1h, 0.5h\}$, where h is the average size of data. For example, if the training data are all $32\times 32$ images, $h=32\times 32$. The remaining parameters of BMVAE$_P$, $\lambda _{zq}$, $\lambda _{mz}$ and $\lambda _{mq}$, are set to be 1, $\frac{1}{M}$ and $\frac{1}{M}$ respectively. The parameters $\beta _{prior}$ of the Dirichlet prior is 0.5 in Sects. 6.1, 6.2, and 6.3. In Sect. 6.4, it is chosen from $\{0.5, 1, 10\}$ via validation. The training epochs are reported in respective subsections. We note that although BMVAE seems to be more complex than MMVAE in the aspect of mixture method, BMVAE can normally converge in fewer epochs.

6.1 MNIST-SVHN

The first dataset used for evaluation is MNIST-SVHN. It is constructed by pairing images depicting the same digit class from MNIST and SVHN. Examples are shown in Fig. 2. As can be seen that the modalities are both images but with distinct and more complicated styles.

Fig. 2

Examples of MNIST-SVHN data

Following the settings in the previous work, the encoders for MNIST and SVHN data are multi-layer perceptron (MLP) and convolutional neural network (CNN) respectively. The number of dimensions of a latent vector is 20. Likelihoods, prior and posteriors are all Laplace. The likelihoods are weighted to balance reconstruction errors. In particular, given SVHN are 3-channel 32$\times$32 images and MNIST are 1-channel 28$\times$28 images, the log likelihood of MNIST is multiplied by $\frac{32\times 32\times 3}{28\times 28}=3.92$. Latent classification and coherence of generations are used for evaluation as suggested by Shi et al. (2019). BMVAE and MMVAE are both trained for 30 epochs. The structures of uni-modal encoders and decoders are shown in Table 3.

Table 3 MNIST-SVHN encoders and decoders. Args: (kernel size, stride, padding)

6.1.1 Latent classification

The goal here is to examine whether the shared information (i.e. digit class) can be effectively learned by models by checking if the digits can be successfully recognized from latent vectors by linear classifiers. The assumption is that accurate recognition implies informative representations regarding shared information. Second, implication is that the information is encoded separately across latent dimensions as shallow classifiers are sufficient for the recognition task. The classification accuracy is listed in Table 4. To show the advantages of multi-modal architectures, performance of uni-modal VAE is also included.

Table 4 Digit classification accuracy

6.1.2 Coherence

Another evaluation metric is to examine coherence of joint and cross-modal generations. In general, coherence checks both shared and private information by observing the generated data. When evaluating random generation via coherence, the decoders are required to generate images given the same vector which is randomly sampled from prior. To achieve high scores, the generated images need to depict the same digit class. Also, styles of the images need to be consistent with the corresponding modality. In cross-modal coherence, the generation conditions on distinct modality rather than random noises. For example, given an SVHN image depicting digit “3”, we first input the image into SVHN encoder and let it generate a sampled latent vector. Afterwards, we let the MNIST decoder generate an image given the sampled latent vector and check if it also depicts “3” in MNIST-style. To recognize digits and styles from generated images, two CNN-based classifiers are trained by SVHN and MNIST datasets respectively. The score of coherence is estimated by the probability of correct digit matching. Evaluation results are shown in Table 5.

Table 5 Random and cross-modal coherence. M and S are abbreviations of MNIST and SVHN. S$\mid$M and M$\mid$S are generations given MNIST and SVHN, respectively

6.2 CUB image-captions

The other dataset used in the experiment is Caltech-UCSD Birds (CUB). It contains 11,788 photos of birds with captions describing birds’ visual characteristics. Examples are shown in Fig. 3. CUB dataset provides more challenges than MNIST-SVHN due to more complex data and heterogeneous modalities.

Fig. 3

Examples of CUB data

For evaluation on CUB, we follow the methods proposed by Shi et al. (2019) which focuses on coherence as CUB has no clear label information. Notably, the coherence discussed here is measured on a vector space. The details of the proposed evaluation are as follows.

Data generation For image data, the decoder actually outputs vectors in feature space of a pre-trained ResNet-101 He et al. (2016) instead of real images. The motivation is to avoid generating blurry images. The method of generation and reconstruction then becomes finding the most similar vector of a real photo on the feature space by Euclidean distance. Additionally, likelihood of the image decoder is Laplace distribution. For the caption data, the encoder and decoder are based on CNN. The likelihood of decoder is Categorical distribution. For other training details, the priors and posteriors are Laplace where the number of dimensions of latent vectors is 128. The training epochs for BMVAE and MMVAE are 30 and 50. The structures of uni-modal encoders and decoders are shown in Table 6.

Table 6 CUB encoders and decoders. CN: Conv2d. BN: BatchNorm2d. RE: RELU. Args: (kernel size, stride, padding)

Coherence To check whether a pair of generated image and caption matches, the proposed idea is to map generated images and captions into a common vector space. To do so, Shi et al. (2019) suggested employing Canonical Correlation Analysis (CCA). Specifically, generated images are converted into 2048-dimensional feature vectors by pre-trained ResNet-101. Generated captions are converted into 300-dimensional vectors by averaging word vectors trained by FastText Bojanowski et al. (2017). To do the mapping, two projection matrices $W_1\in {\mathbb {R}}^{2048\times 40}$ and $W_2\in {\mathbb {R}}^{300\times 40}$ are trained by maximizing correlations between $W_1^Ty_1$ and $W_2^Ty_2$, where $y_1$ and $y_2$ are the feature vectors. After training, when there are new pairs of feature vectors, we can do the projection by $W_1$ and $W_2$ and compute the correlation as the performance measurement. The random and cross-modal coherence results are shown in Table 7. Examples of cross-modal generation are also provided in Fig. 4.

Table 7 Correlation of images (I) and sentences (S) generations. The ground truth of random coherence is 0.273

Fig. 4

CUB generation results

6.3 MNIST-SVHN-Text

Here we evaluate our models with data having 3 modalities. The dataset for evaluation is MNIST-SVHN-Text proposed by Sutter et al. (2020). It is constructed by adding text modality on the MNIST-SVHN dataset, where the text data are character-level strings of digit names (e.g. ‘o’, ‘n’, ‘e’). In order to increase complexity of the text data, random numbers of space characters are dynamically inserted in front of the digit names.

In addition to datasets, a notable difference to the settings in Sect. 6.1 is that we conduct Gaussian instead of Laplace posteriors for fair comparisons with mmJSD and MVAE (Wu & Goodman, 2018). Models trained by the modality-specific framework reviewed in Sect. 2.5.2 are also included for comparisons. BMVAE, MVAE, MMVAE, mmJSD are trained for 50 epochs. The modality-specific versions of MVAE, MMVAE and mmJSD are trained for 100 epochs. The uni-modal encoders and decoders are shown in Table 8.

Table 8 MNIST-SVHN-Text encoders and decoders. Args: (kernel size, stride, padding)

6.3.1 Latent classification

The classification task is the same as the one introduced in Sect. 6.1.1. However, we can now examine the generated samples given data with multiple modalities. To obtain samples from BMVAE$_M$, we first construct a categorical distribution by normalizing $\alpha _{m,d}$ for each latent dimension. For example, if modality 1 and 3 are given, the parameters of the categorical distribution in dimension d are $\frac{\alpha _{1,d}}{\alpha _{1,d}+\alpha _{3,d}}$ and $\frac{\alpha _{3,d}}{\alpha _{1,d}+\alpha _{3,d}}$. Then, we can conduct ancestral sampling to obtain samples from BMVAE$_M$.

To obtain samples from BMVAE$_P$, we first sample mixture weights from the learned Dirichlet distributions. Then, as weighted product-of-Gaussian has an analytic form, we directly construct the joint posteriors to generate samples for BMVAE$_P$. The evaluation results are shown in Table 9.

Table 9 Classification accuracy of sampled latent vectors. The provided modalities include MNIST (M), SVHN (S) and Text (T). The modality specific (MS) objectives improve performance of MVAE, MMVAE, and mmJSD. BMVAE has particular advantages when multiple modalities are available

We first compare BMVAE$_M$ with other MoE models, and see that BMVAE$_M$ has a clear advantage when more modalities are given. Similar results can also be found from the comparisons between BMVAE$_P$ and other PoE models. The advantages could indicate effectiveness of the learned weights. More concretely, the ideal experts are correctly selected or properly weighted via the learned $\alpha$.

6.3.2 Coherence

The experiment settings are the same as Sect. 6.1.2 with an exception that we apply a different method for random generation for BMVAE. The motivation is that we observe the joint posteriors $q_\varPhi (z)$ are less similar to the prior p(z) after learning the data. To have more effective generation, we follow an idea proposed by Daunhawer et al. (2020) where ex-post estimation (Ghosh et al., 2020) is employed. Specifically, we find ${\hat{p}}(z)\approx q_\varPhi (z)$ via density estimation and draw samples from ${\hat{p}}(z)$ instead of p(z) for evaluating random coherence. In the experiments, we let ${\hat{p}}(z)$ be a 10-component Gaussian mixture model with diagonal covariance matrices. The results are shown in Table 10.

Table 10 Random (R) and cross-modal coherence with modalities MNIST (M), SVHN (S) and Text (T). The modality specific (MS) objectives does not always improve performance of MVAE, MMVAE, and mmJSD but is able to prevent a significant performance drop (e.g., the S$\mid$M column). BMVAE does not suffer from the issue and has advantages on performance when multiple modalities are available

The results in Table 10 also lead to the conclusions we made in Sect. 6.3.1 with an interesting observation on the performance of MMVAE and mmJSD. As can be seen, the two models achieve the best performance in MNIST and Text generation; however, the accuracies significantly drop to 30%–48% when generating SVHN. Therefore, the MS learning framework of the two models becomes essential. On the other hand, BMVAE$_M$ and BMVAE$_P$ both avoid this issue and do not need additional learning algorithms.

6.4 MultiBench

In this subsection, we consider a broader class of models, modalities, and metrics for evaluations. We select MultiBench (Liang et al., 2021), which is a benchmark scoring generalization across modalities, training or testing complexity, and robustness against noisy or missing data. The benchmark was proposed with 15 datasets covering 10 modalities and 6 research areas. With a unified pipeline handling multi-modal data processing, models based on distinct paradigms are possible to be jointly evaluated. In our experiments, we select 5 publicly available datasets officially supporting generative models for training, and we compare BMVAE with 6 competitors including but not limited to MoE and PoE methods.

6.4.1 Datasets and models

We select datasets that do not have restricted access issues and have been officially tested by MultiBench MVAE. The selected datasets are CMU-MOSI (Zadeh et al., 2016), UR-FUNNY (Hasan et al., 2019), CMU-MOSEI (Bagher Zadeh et al., 2018), MUSTARD (Castro et al., 2019) and AV-MNIST (Vielzeuf et al., 2018). Modalities covered by the 5 datasets are language, image, video, and audio.

Besides MoE and PoE models, we additionally test MFM (Tsai et al., 2019), PVAE (Hsu & Glass, 2018) and late fusion (LF). As introduced in Sect. 2.1, MFM factorizes latent representations into modality-specific factors and discriminative factors encoding shared information, where the discriminative factors are learned from labels. Another model, PVAE, also learns to find modality-specific and shared factors but does not follow the MoE or PoE framework. Instead, PVAE transforms concatenated uni-modal embeddings into joint representations, requiring an additional hidden layer and separately learning uni-modal and multi-modal encoders. The third method, LF, is a baseline method adopted by MultiBench. It directly takes concatenation of uni-modal embeddings as the multi-modal representations. Despite being a simple method, it shows remarkable performance in MultiBench evaluation.

In the experiments, the architectures and parameter sizes of uni-modal encoders and decoders are the same across the tested methods, except that VAE-based methods require additional layers for reparameterization, and LF does not need decoders. The the architectures and parameters follow the released code.¹ The likelihoods we select are all Laplace. Regarding importance sampling, we do not set the sample size $K>1$ as no improved performance is observed. To obtain mean and variance of model performance, all the experiments are repeated 10 times, and the built-in early-stopping mechanism is always turned on.

6.4.2 Evaluation results

We follow the presentation proposed by MultiBench where the evaluation results are visualized to reveal trade-offs and provide deeper insights. The visualization results are plotted in Fig. 5a, b.

Fig. 5

Trade-off between performance and robustness or between performance and training speed. The size of circles in Fig. 5a represents variance of robustness. The size of circles in Fig. 5b represents variance of performance

Figure 5a is the result summarizing model performance and robustness. The performance scores correspond classification accuracies of predicting labels given latent representations. Robustness is tested by measuring model performance with increasingly noisy data. The robustness can be quantified via computing relative robustness and effective robustness proposed by MultiBench. Given noisy data, relative robustness directly measures model performance while effective robustness measures the rate of performance drops. We average relative and effective robustness scores as the final result, and represent variance of robustness via circle size. Figure 5b is the visualization presenting trade-off between performance and training speed. The circle size corresponds to variance of performance.

From Fig. 5a, b, we confirm that LF is a strong baseline as it shows decent performance and robustness in average, while we also note a potential weakness that the variances are relatively large. We can also observe trade-offs between LF and MFM in terms of performance, robustness, and training time. The MoE models we discussed in this work show good and similar performance and robustness. We also note that the MoE models have lower variances of robustness when compared to the PoE models, mmJSD and BMVAE$_P$. Finally, we confirm that although MMVAE can reach good performance and robustness, it requires a significantly long training time.

Finally, we report log-likelihood of the VAE-based models in Table 11 to examine performance of generation. We note that the differences are marginal except for PVAE. The reason for achieving higher log-likelihood could be the additional modality-specific representations. For example, to generate data with 3 modalities, PVAE takes joint and 3 sets of modality-specific representations for decoding, while other models only use joint representations. It can be observed that the additional representations effectively improve log-likelihood. while a potential issue would be handling unexpectedly noisy or missing data.

Table 11 Log likelihood of VAE-based models, where M$=10^6$ and K$=10^3$. The tested data are the 5 selected datasets and the covered modalities

7 Analysis of mixture weights

In this section, we analyze the learned mixture weights from multiple aspects. In Sect. 7.1, we provide observations and visualizations of the learning results. Sections 7.2 and 7.3 are quantitative and qualitative analyses of the weights. The weights we select for analyses in Sects. 7.1–7.3 are learned by BMVAE$_{M(k=1)}$; however, weights learned by BMVAE$_{M(k>1)}$ and BMVAE$_{P}$ also show similar characteristics and do not contradict conclusions we reach. In Sect. 7.4, we verify if BMVAE can be trained with fixed and uniform mixture weights. Takeaway messages summarizing our observations are provided in respective subsections.

7.1 Observations and visualizations

We take the weights learned from MNIST-SVHN-Text for analyses, since the data contain explainable attributes such as digit class, style or color scheme. The learned mixture weights are visualized in Fig. 6.

Fig. 6

Mixture weights learned from MNIST-SVHN-Text

In the figure, the learned $\alpha _{m,d}$ for $d=1,\ldots ,20$ are presented. Note that the values are normalized probabilities, namely, $\sum _{m=1}^3 \alpha _{m,d} = 1$. We can then judge whether a dimension tends to encode private or public information by observing the normalized values. For example, we may conclude that dimension 1, 2 and 11 encode information specific to MNIST, SVHN and Text respectively. In contrast, dimension 12 may be more like a shared dimension with a slight preference for SVHN. We note that the preference can also be meaningful. Let a dimension set $D_S$ be $\{2, 6, 12, 16, 17, 18, 19\}$. It can be observed that the 7 dimensions all prefer SVHN. Also, MNIST and Text are equally weak in $D_S$. With these observations we make two assumptions:

Assumption 1

$D_S$ is mainly responsible for encoding image styles specific to SVHN, which can explain why MNIST and Text are equally uninformative here. It may also imply that the specific styles are irrelevant to digit classes.

Assumption 2

Given that dimensions in $D_S$ are occupied, the information relevant to digit recognition tends to be encoded in the remaining 13 dimensions.

We denote the set of 13 dimensions as $D_{\bar{S}}$, and compare it with $D_S$ in Sects. 7.2 and 7.3 to verify the two assumptions.

7.2 Quantitative analysis

Here we conduct 10-class digit classification to check if digit information is mostly encoded in $D_{\bar{S}}$. The idea is that if $D_{\bar{S}}$ are more relevant to digit recognition, the values in $D_{\bar{S}}$ serve as better features for the classification task. To do this, we split vectors sampled from learned posteriors into sub-vectors by $D_{\bar{S}}$ and $D_S$. A set containing 13-dimensional vectors corresponding to $D_{\bar{S}}$ and sampled from MNIST, SVHN or Text encoders are denoted as $Z^M_{D_{\bar{S}}}$, $Z^S_{D_{\bar{S}}}$, or $Z^T_{D_{\bar{S}}}$ respectively. Likewise, we can define sub-vector sets $Z^M_{D_S}$, $Z^S_{D_S}$, and $Z^T_{D_S}$. Afterwards, we train a linear classifier and measure the accuracy for each sub-vector set. The results are shown in Table 12.

Table 12 Digit classification accuracy using sub-vectors. The results show that the digit information is aligned and encoded in dimension $D_{\bar{S}}$

The observations we have are as follows:

• $Z_{D_{\bar{S}}} = \{Z^M_{D_{\bar{S}}}, Z^S_{D_{\bar{S}}}, Z^T_{D_{\bar{S}}}\}$ significantly outperforms $Z_{D_S}$ on the classification task. Moreover, $Z_{D_{\bar{S}}}$ generally reproduces the accuracies reported in Table 9. It could indicate that digit classes are mainly encoded in $D_{\bar{S}}$.

• We can see that the three encoders all learn to encode digit information in $Z_{D_{\bar{S}}}$ instead of $Z_{D_S}$. It indicates that the three posteriors are successfully aligned with each other.

The second observation could be an expected result for BMVAE$_P$ as the $D_{KL}(q_{\phi _m}||\bar{q})$ objective encourages unifying posteriors. On the other hand, why does BMVAE$_M$ can still align the posteriors without the additional objective may be unclear.

To see the reason for alignment, let us tentatively assume $D_S$ indeed encodes SVHN-specific styles which are irrelevant to digit classes. It means that the SVHN decoder will learn to focus on $D_S$ for image reconstruction, while other decoders tend to ignore $D_S$. If the learned weights are positive in $D_S$, at some moments $Z^M_{D_S}$ or $Z^T_{D_S}$ will be selected to reconstruct SVHN images during training. Given that SVHN-specific styles are meaningless to MNIST and Text, the propagated gradients could be noise for the encoders. It may be similar to variational dropout which injects random noise to neurons to achieve sparsification. In our case, the MNIST and Text encoders learn to compress information to $D_{\bar{S}}$. It also explains why SVHN encoder learns digit classes well in $D_{\bar{S}}$. Since the digit classes are also meaningful to SVHN, the propagated gradients from MNIST or Text decoders would not be noise but beneficial information for learning.

In summary, the classification results confirm Assumption 2 that $D_{\bar{S}}$ encodes information relevant to digit recognition. The results could also lead to the following takeaway message.

Message 1 Despite no explicit objectives constraining alignment, BMVAE can learn to recognize and encode shared information in specific latent dimensions.

7.3 Qualitative analysis

Here we analyze the learned weights by image generation. In Sect. 7.2, we show $D_{\bar{S}}$ is responsible for the digit class. Here we attempt to show $D_S$ is relevant to SVHN-specific styles.

The idea is that given a latent vector sampled from the SVHN posterior, we explicitly replace the values in $D_{\bar{S}}$ with random values, then let the SVHN decoder generate an image based on the modified vector. Ideally, the generated image would depict a different digit while preserving the original style. Conversely, if we choose to replace values in $D_S$ with random noise, the expected result would be depicting the same digit with a different SVHN style. The results are shown in Fig. 7a, b.

Fig. 7

Results of conditional generation. Both BMVAE and mmJSD (MS) learns to disentangle digits and styles, while BMVAE is able to decide appropriate dimensions for encoding information without supervision

In Fig. 7a, each row is generated by replacing values in $D_S$ with random noise. The noise is sampled from the prior. As can be observed, digits in each row vary but image styles are well-preserved. In Fig. 7b, we change to replace values in $D_{\bar{S}}$. As expected, a sampled digit class can now be depicted in diverse styles.

The results of generation confirm Assumption 1 that information encoded in $D_S$ is relevant to style but not the digit labels. It implies that BMVAE can naturally disentangle modality-specific features without the need for explicitly designed algorithms such as mmJSD (MS). The takeaway messages are as follows.

Message 2 BMVAE can learn to disentangle shared and modality-specific information without supervision.

Message 3 The inferred mixture weights effectively indicates how BMVAE distributes learned features among latent dimensions.

7.4 BMVAE with uniform weights

We investigate whether the learnable mixture weights can be replaced by uniform weights when training BMVAE. To do this, we train BMVAE$_M$ and BMVAE$_P$ with constant weights $\frac{1}{M}$, denoted by BMVAE$^u_M$ and BMVAE$^u_P$, on the MNIST-SVHN-Text dataset. We conduct the latent classification and coherence evaluation tasks to examine the trained models.

From Table 13, it can be observed that classification performance is degraded if models are trained with uniform weights. The degradation is more obvious when multiple modalities are available, implying that the mixture method is not effective enough to preserve modality-specific information. From Table 14, it can be observed that BMVAE$^u_M$ has a significant drop in performance and may have the modality collapse issue. The PoE model BMVAE$^u_P$ is also weaker than BMVAE$_P$, while the degradation is relatively small.

Table 13 Classification accuracy of sampled latent vectors. Models with superscript u are trained by constant and uniform mixture weights. The dropped performance in the M,S and S,T columns could imply that models trained with uniform weights do not effectively preserve multi-modal information after merging

Table 14 Coherence evaluation for verifying the impact of learnable weights. The models with uniform weights have slight modality collapse issues such as BMVAE$^u_M$ on S$\mid$M and BMVAE$^u_P$ on M$\mid$S

We summarize the observations and provide the takeaway messages as follows.

Message 4 Adopting learnable and uneven weights improves model performance in general. The advantage is particularly significant on BMVAE$_M$.

Message 5 Forcing mixture weights to be uniform has negative effects on learning cross-modality information. In practice, one can observe less informative multi-modal latent representations and degraded performance in modality transferring.

Message 6 Learnable and uneven weights can help eliminate the modality collapse problem.

8 Conclusion

In this work, we propose dimension-wise Bayesian inference for multi-modal learning. We demonstrate the idea works on both MoE and PoE frameworks. The proposed MoE model, BMVAE$_M$, achieves state-of-the-art performance and is efficient to train. Therefore, computational cost is no longer an issue when we employ MoE methods. Regarding the proposed PoE model, BMVAE$_P$, we demonstrate that it achieves state-of-the-art performance as well and has theoretical connections to mmJSD and BMVAE$_M$.

In addition to data generation, we reveal that BMVAE does not need a specially-designed objective such as mmJSD (MS) to encode modal-specific information. Moreover, the private and shared features can be described by the inferred mixture weights. We also show that the inferred weights are beneficial to expert selection, improving data generation when multiple modalities are provided. Finally, we demonstrate that diverse mixture weights not only disentangle latent factors but also prevent degraded generation.