Abstract
Protecting ML classifiers from adversarial examples is crucial. We propose that the main threat is an attacker perturbing a confidently classified input to produce a confident misclassification. We consider in this paper the \(L_0\) attack in which a small number of inputs can be perturbed by the attacker at test-time. To quantify the risk of this form of attack we have devised a formal guarantee in the form of an adversarial bound (AB) for a binary, Gaussian process classifier using the EQ kernel. This bound holds for the entire input domain, bounding the potential of any future adversarial attack to cause a confident misclassification. We explore how to extend to other kernels and investigate how to maximise the bound by altering the classifier (for example by using sparse approximations). We test the bound using a variety of datasets and show that it produces relevant and practical bounds for many of them.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A machine learning (ML) classifier, given labelled training points \(\{{\textbf {X}}, \varvec{y}\}\), must classify a new test point, \(\varvec{x}_*\). It has been found that popular methods for performing this task are susceptible to small perturbations in the location of the test point (Dalvi et al., 2004; Biggio et al., 2013; Szegedy et al., 2014). By carefully crafting the perturbations, an attacker can cause an ML classifier to misclassify even with only a tiny alteration to the original data point. The bound in this paper considers \(L_0\) ‘norm’ attacks (such that a small number of dimensions are perturbed).
There is currently an absence of proven bounds on adversarial robustness that provide guarantees across the whole input domain. We find we can achieve this using Gaussian process (GP) classification. The two key features of GPs are that first, they allow one to specify priors, providing an equivalence to the smoothness mentioned by Ross and Doshi-Velez (2018). Second, the posterior latent mean can be expressed as a linear sum of observations. These two features allow us to bound the effect a perturbation can have on a prediction.
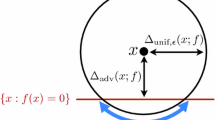
Typically, to obtain an adversarial example (AE), one might perturb some input to cause the ML algorithm to misclassify, while minimising a norm on the perturbation so the new input looks, to humans, largely indistinguishable from the original. We instead follow recent approaches of high-confidence adversarial examples (Carlini & Wagner, 2017b; Grosse et al., 2019), with the additional constraint that the starting point is also confidently classified. To motivate, we want self-driving cars to be very confident a traffic light is green before moving: If our self-driving car is only 55% confident the traffic light is green, we would expect it to stop. We are more interested in AEs in which the classification is moved from, say, 99% confident of a red light to 99% confident of a green. Unlike previous work, our guarantee holds for the whole domain and lower bounds the scale of a perturbation required to misclassify any confidently classified, as yet unknown, future test point. This guarantee we refer to as the adversarial bound (AB).
Other papers chose norms to reflect human perception, but we feel the choice should also consider the capacity of the attacker. We propose that the \(L_0\) norm reflects the most likely real-world attack, where the adversary is likely to only have access to a small portion of the domain. For example only being able to manipulate a subset of features used by a spam filter, or stickers on road-signs (Sitawarin et al., 2018) which modify a subset of dimensions. Su et al. (2019) even show single pixel perturbations can be sufficient to cause a misclassification with a typical DNN.
The algorithm in this paper provides a true mathematical lower bound on the scale of perturbation required to cause a (confident) misclassification, not an empirically derived result. We use Gaussian process classification (GPC), a powerful and widely adopted classifier, as the basis for our analysis and demonstrate the AB algorithm provides meaningful bounds for a variety of datasets.
1.1 Limitations
The AB algorithm described in this paper has several limitations.
-
It assumes the data (and test locations) lie within a restricted hyperrectangular domain. This might be defined by the problem (e.g. the range of values pixels can equal).
-
It is only applicable to binary classification. Extending it to multi-class classification poses a challenge, which we discuss in Sect. 5.2.
-
It has been principally developed for the EQ kernel. An extension to other kernels is described in Sect. 3.3.2 and demonstrated in Sect. 4.6 with the exponential kernel. However the approach is limited to stationary, isotropic kernels, and hasn’t been demonstrated with other kernels.
-
It doesn’t use the variance in the posterior latent distribution. This leads to looser bounds, but still bounds changes to predictions made using GPC integrating over the full distribution. Sect. 2.4 discusses this in more detail.
-
We used the Laplace approximation to move from a classification problem to a regression problem. Other approaches for inference in non-Gaussian likelihoods include expectation propagation and variational inference, but we leave applying the AB algorithm to these for future work (see Sect. 5.3).
-
It is arguably still quite loose, and depends on several tricks. One that really helped was the use of inducing points. We explored small numbers (e.g. up to 30) of inducing points. Clearly for some more complex datasets this might be insufficient.
1.2 Structure of the paper
Background
We start by reviewing Gaussian process regression (Sect. 2.1) and the Laplace approximation to perform Gaussian process classification (Sect. 2.2). We explain the vulnerability we are testing for (Sect. 2.3).
The adversarial bound (AB) algorithm
We then explain the AB algorithm, which involves first expressing the regression problem in such a way that one can bound the perturbation of the posterior mean (Sects. 3.2.2 and 3.2.3). This initial bound is restricted to low dimensions. We propose a method to allow higher input dimensions by projecting the space to a lower dimensionality (using PCA) and, to ensure the bound remains valid, handle the negative weights efficiently (Sects. 3.2.4 and 3.2.5 respectively).
Improvements to the algorithm
The bound is often still too loose to be practical, so two more refinements are explored: The domain is sliced so that a bound is found on smaller parts of the domain, then all the contiguous combinations of these parts are checked to find the largest perturbation (Sect. 3.3.1). We also find it worth revisiting those dimensions that have the largest possible perturbation and rerunning their analysis with more slices (Sect. 3.3.3).
We also propose a method for extending the algorithm to GPs with other kernels (Sect. 3.3.2. Section 4.6 demonstrates it).
Experiments
We then explore the method through a series of experiments and datasets. We look at MNIST (Sect. 4.1), a non-linearly-separably dataset (Sect. 4.2) and several other, real-world, datasets (Sect. 4.3). We then explore the effect of the number of slices and inducing points (Sect. 4.4).
Finally we look at the results of empirical attacks on the classifier to get an insight into how tight the bounds are (Sect. 4.5).
We conclude with a discussion of the results, the AB algorithm’s limitations and some proposals for future work.
2 Background
2.1 Gaussian process regression
2d example using logistic regression. a The logistic function, to move from 5% to 95% confidence requires a change of 2.94 in the latent function, \(w_0 + x_1 w_1 + x_2 w_2\). b Left plot, least regularisation: moving between thresholds is possible by changing just one input, \(x_2\) (as \(\vert w_2\vert >2.94\)), see dashed line. Middle plot: greater regularisation. It is only possible to move between the thresholds by altering both inputs (as \(\vert w_1\vert < 2.94\) & \(\vert w_2\vert < 2.94\)). Right plot: even more regularisation. It becomes impossible to move between the two thresholds (i.e. when \(\vert w_1\vert +\vert w_2\vert <2.94\)) even changing all inputs! We suggest rather than use fixed values for these trhresholds one should use the values of the 5th and 95th percentile training points (orange and blue lines) to assess the robustness of a classifier. C is inverse \(L_2\) regularisation (Color figure online)
We first, briefly review Gaussian process regression (GPR) before looking at GP classification (GPC) using the Laplace approximation.
A GP is a stochastic process defined such that any finite subset of output variables will have a multivariate normal distribution. The covariance between pairs of variables is defined by the kernel function, \(k({\textbf {x}},{\textbf {x}}')\) which describes how the covariance between pairs of points changes depending on their location and proximity. If the covariance only depends on the relative location of the two points it is called a stationary covariance. Because the values of a set of locations are assumed to be samples from a multivariate normal distribution, one can condition on some of these variables to make a closed-form prediction of the posterior latent mean for the remaining. This is a key advantage of using a GP, making prediction relatively trivial. To be specific: We are given a set of training input-output pairs, \({\textbf {X}} \in {\mathcal {R}}^{N \times D}\) and \({\textbf {y}} \in {\mathcal {R}}^{N}\). We wish to estimate the value of the latent function f at a test point \({\textbf {x}}_*\): \(f_* = f({\textbf {x}}_*)\). We assume that the training points have been generated with this function but with the addition of (independent) Gaussian noise,
This decides the likelihood model, i.e. it tells us how likely we consider an observation to be, given the value of f at the point’s location. By assuming the observations are Gaussian-noise-corrupted versions of the latent function, we can keep the solution in closed form:
The conditional distribution of \(f_* \vert {\textbf {y}}\) can be expressed analytically as a normal distribution with mean and covariance, \(\bar{f_*} = {\textbf {k}}_*^\top ({\textbf {K}} + \sigma ^2{\textbf {I}})^{-1} {\textbf {y}}\) and \({\mathbb {V}}[f_*] = {\textbf {k}}_{**} - {\textbf {k}}_*^\top ({\textbf {K}} + \sigma ^2{\textbf {I}})^{-1} {\textbf {k}}_*.\) Where \({\textbf {k}}_{**} = k({\textbf {x}}_*,{\textbf {x}}_*)\) is the kernel variance at the test point. \({\textbf {k}}_{*} = k({\textbf {X}},{\textbf {x}}_*)\) and \({\textbf {K}} = k({\textbf {X}},{\textbf {X}})\) are the covariances between test-training points and within training points respectively. The kernel used for most of this paper is the exponentiated Quadratic (EQ) kernel \(k(\varvec{x},\varvec{x}') = v \exp \left( -\frac{(\varvec{x}-\varvec{x}')^2}{2l^2}\right)\), where v and l are, respectively, the kernel’s variance and lengthscale. The posterior latent mean can be written as the sum of weighted kernels, letting \(\varvec{\alpha } = \varvec{K}^{-1} \varvec{y}\),
2.2 Binary Gaussian process classification using the Laplace approximation
To extend to classification, we consider binary observations, so \(y_i=+1\) or \(-1\). The likelihood will no longer be normal, but instead the probability of a point being of the positive class (given the latent function).
For binary classification our real-valued latent function (with GP prior) is transformed by a logistic link function, \(\sigma\), to give us a prior on the class probabilities, \(\pi ({\textbf {x}}) \equiv p(y=1 \vert {\textbf {x}}) = \sigma (f({\textbf {x}}))\).
To perform inference we need to consider two steps. First, the posterior distribution of the latent function is computed by combining the latent function and the likelihood and marginalising out the latent function; \(p(f_*\vert {\textbf {X}}, {\textbf {y}}, {\textbf {x}}_*) = \int p(f_*\vert {\textbf {X}}, {\textbf {x}}_*, {\textbf {f}}) p({\textbf {f}}\vert {\textbf {X}}, {\textbf {y}}) d{\textbf {f}}\). We then need to find the expected value of the transformed latent function’s distribution (i.e. after applying the link function) to give us the probability of being in class \(y_* = +1\), \(\pi ({\textbf {x}}_*) = \int \sigma (f_*)p(f_*\vert {\textbf {X}}, {\textbf {y}}, {\textbf {x}}_*) df_*.\)
Neither of the above integrals can be solved analytically. In this paper we use the Laplace approximation to the posterior distribution. Specifically, we place a Gaussian \({\mathcal {N}}\left( {\textbf {f}}\vert \hat{{\textbf {f}}},A^{-1}\right)\) on the mode \(\hat{{\textbf {f}}}\), of the posterior distribution \(p({\textbf {f}}\vert {\textbf {X}},{\textbf {y}})\) with a covariance \(A^{-1}\) that matches the posterior distribution’s second order curvature at that point. Finding the mode and covariance is mildly involved and is described in Williams and Rasmussen (2006), (pp. 42–43). The approximate mean of the latent function is then computed as for normal GP regression, but using \(\hat{\varvec{f}}\): \({\bar{f}}_* = \varvec{k}_*^\top {\textbf {K}}^{-1} \hat{\varvec{f}}\). Importantly, this is now a regression problem again, but with new training output values (\(\hat{\varvec{f}}\)). The second integral, to compute \(\pi ({\textbf {x}}_*)\), can either be ignored (if one wishes simply to report which class is most likely) or can be computed quickly using sampling or analytical approximation. The effect of including the latent predictive variance is to, ‘soften the prediction that would be obtained using the MAP prediction \({\hat{\pi }}_* = \sigma ({\bar{f}}_*)\), i.e. to move it towards 1/2’(Williams and Rasmussen 2006). Computing the variance requires an additional integration step but the AB-algorithm, for simplicity, ignores this source of uncertainty, and only considers the mean function. We discuss what this means for our bound in Sect. 2.4.
2.3 Confident misclassification
Rather than just produce a misclassification, we want to place a bound on the possibility of a confident misclassification, i.e. moving from a confidently classified point of one class to a confidently classified point of another class. The robustness of a Logistic Regression (LR) classifier is easy to quantify as one can simply cumulatively sum the sorted weight values associated with the inputs. One can determine the number of inputs that need altering to cause a confident misclassification by considering when the cumulative sum reaches a given threshold.
One can reduce the coefficients by simply increasing the regularisation, until the classifier can never reach the specified threshold output (Fig. 1). Clearly this makes little sense. Instead we propose that, to assess the quality of the bounds, one should use, as a heuristic, the value of the 5th and 95th percentile training points’ values, and report how many inputs need perturbing to pass between these two thresholds. This normalises the target of the adversarial attack by correcting for the scaling caused by regularisation.
Regularising can still help protect the classifier from adversarial examples even using this new way of framing the problem, as will be illustrated later.
2.4 Using just the latent mean
Returning to the issue of only using the mean latent function. An upper bound in the change in the posterior latent mean also allows us to compute, through the link function, upper bounds on the change in the predictive distribution: Adding any variance to the latent function’s posterior distribution will cause the prediction to move towards \(\frac{1}{2}\) (chance), as explained in the quote at the end of Sect. 2.2. Therefore the change in the prediction probabilities will be smaller than without the variance included in the calculation, so the bound we compute in this paper, on the effect a perturbation can cause on the predictions, remains applicable, even if one does integrate over the full variance of latent posterior’s distribution. The consequence is that the bound will be looser than it otherwise would need to be but a practitioner can still use the Bayesian approach (integrating over the distribution of \(f_*\)) for prediction (the bounds described will still apply to their predictions).
A separate issue that needs consideration is the effect of the variance in the posterior distribution on our use of training-point percentiles for evaluating the utility of the approach. To recap, this paper devises and proves a bound on the amount a prediction could change, for a certain number of input perturbations. But we also need to evaluate its utility: To demonstrate the approach we select the posterior latent mean values of the 5th and 95th percentile training points to evaluate the relevance of the bound. These percentiles provide a heuristic to allow us to assess the classifier in a way that allows us to control for the effect of regularisation (as discussed above). An issue is if some training points are in regions of the domain with high uncertainty. This would cause the prediction to lie nearer to the \(\frac{1}{2}\) (chance) line, while the posterior latent mean might be a long way from zero. The result would be a latent-mean threshold at the 5th or 95th percentile being unrealistically difficult to reach. However, given (for computing the percentiles) we are evaluating the posterior latent mean at training points, the variance is likely to be relatively small. So we suggest that using the 5th and 95th percentile training points is a good metric for assessing the utility and relevance of the bound and the robustness of a classifier to adversarial attack.
We emphasise that this issue looking for a ‘regularisation-corrected’, appropriate way to assess the robustness of a classifier doesn’t affect the bound result itself.
2.5 Related work
Much of the focus of the adversarial ML field has been on AEs with respect to deep neural network (DNN) classification. Overfitting, linearity and sharp decision boundaries associated with DNNs are hypothesised to be the cause of their susceptibility (Papernot et al., 2016b). Attempts have been made to regularise the DNN’s output. Ross and Doshi-Velez (2018) regularised the input gradients as they suggested a model with ‘smooth input gradients with fewer extreme values’ will be more robust (others, for example, Finlay and Oberman 2021, develop this further). Papernot et al. (2016b) used distillation (a method for crafting a smaller DNN) but this was later found to be insufficient (Carlini & Wagner, 2017b). The conclusions of Carlini and Wagner (2017a) were that adversarial perturbations are very challenging to detect or mitigate: attempts at mitigation quickly being compromised.
To move beyond the ‘arms-race’, researchers have begun providing formal guarantees on the scale of the perturbations required to cause a misclassification (Carlini et al., 2017; Hein & Andriushchenko, 2017; Huang et al., 2017; Madry et al., 2018; Wong & Kolter, 2018; Ruan et al., 2019; Bojchevski et al., 2020; Finlay & Oberman, 2021). These approaches only guarantee a ball around each training point is protected from AEs. For example Wong and Kolter (2018) proposed a method for producing a bound on the scale of adversarial examples if using a deep (ReLU) classifier. Hein and Andriushchenko (2017) also provided a formal proof for a minimum perturbation \(\delta\) which could create an AE around a particular training point, with a convex norm. Recently however, research has been conducted into the change that can be brought about due to perturbations anywhere in the domain. This ensures that future, unseen test data has guarantees regarding the minimum perturbation required to cause a misclassification. Peck et al. (2017) found a formal bound for DNNs in which one can start at any location, but produced bounds that were many orders of magnitude smaller than the true smallest perturbation. They also still require one chooses an initial test point. Blaas et al. (2020) proposed an approach for GPC, quantifying robustness in a ball around a test point. They do not however give robustness guarantees for the whole domain, something that our AB algorithm can provide. Cardelli et al. (2019) found bounds on the probability of a nearby point to a test point having a significantly different prediction. We found that the above results did not provide practical bounds for use across the whole domain, or with an \(L_0\) norm attack. The algorithm described in this paper achieves both.
3 Method
3.1 Threat model
We assume the GP classifier (with EQ kernel, for now) has been trained (both for hyperparameter optimisation and regression) using trusted data. At test-time, the attacker can manipulate a subset of input dimensions. We describe the attack by the number of dimensions that an attacker must manipulate to cause the classifier to confidently misclassify a test point it had previously confidently classified. We define ‘confident’ as having a posterior latent mean either greater than 95% or less than 5% of the training data labels. For simplicity in the derivations, the feature ranges of both the original unperturbed test data and the attacker perturbed adversarial example are defined to lie within the unit hypercube. This is w.l.o.g, as one can achieve this by simply scaling the data and lengthscales accordingly or including minor adjustments in the implementation. Using the ‘FAIL’ model (Suciu et al., 2018) we can formalise this: The attacker could have complete knowledge of the training data and the algorithm and complete access to the test point being manipulated (although we do motivate the \(L_0\) ‘norm’ by noting that in real situations this is less likely). This leads to full feature (F), algorithm (A) and instance (I) knowledge and full leverage (L).
3.2 The adversarial bound (AB) algorithm
3.2.1 Introduction
We wish to find a lower bound on the number of dimensions that need perturbing to cause the posterior mean to change more than t, the distance between the 5th and 95th percentile training points’ posterior latent means. Section 2.2 summarised how one ‘converts’ a classification problem into a regression problem using the Laplace approximation. This means we instead need to produce lower bounds for the number of dimensions that need altering for the regression case. Lemma 8 combines upper bounds on how much perturbing each dimension can increase the posterior mean, to allow us to lower bound the number of dimensions that are required to change the mean by t. These upper bounds for each dimension are provided by Lemma 1.
The trick to produce such an upper bound is to redefine the problem as finding an upper bound on the sum of weighted kernels in a \(D-1\) dimensional domain. This \(D-1\) dimensional domain is an upper bound on the amount the posterior mean can increase along a given dimension (fixing the \(D-1\) others). To find this upper bound over the sum of such weighted EQ kernels we use Lemma 2, which depends on Lemmas 3–7.
Finally, to further tighten the bound to a useful level we apply Lemma 9 which allows us to slice the domain and compute tighter upper bounds for the contribution from each dimension.
3.2.2 Upper bounding the posterior mean perturbation
The algorithm below computes an upper bound on the increase in the posterior mean due to an increase along one dimension \({\hat{d}}\). To find the increase in the opposite direction one can simply negate the training point values and rerun the algorithm (Lemma 7).
We are given training inputs, \(\varvec{X}\); training outputs, \(\varvec{y}\); the EQ kernel, \(k(\cdot , \cdot )\); and the weights, \(\varvec{\alpha }\), computed from the product of the precision matrix and the training outputs, \(\varvec{\alpha } = K^{-1} \varvec{y}\). We can compute the posterior mean, for Gaussian process regression (with no likelihood variance) using (3), reproduced here,
Where \(\varvec{x}_i\) is the location of training point i (a row in \(\varvec{X}\)). We also define \(\varvec{x}_i^\dagger\) as the vector \(\varvec{x}_i\) but with the \({\hat{d}}\) dimension removed:
Similarly \(\varvec{x}_*^\dagger\) is the vector \(\varvec{x}_*\) with the \({\hat{d}}\) dimension removed:
We define a function \(m(\cdot , \cdot , \cdot )\) that equals the largest increase in the latent mean moving along dimension \({\hat{d}}\) (constrained between a and b) for a given position in the remaining dimensions, specified by the \(D-1\) dimensional vector \(\varvec{x}_*^\dagger\):
Where we use a test point pair (\({\mathop {\varvec{x}}\limits ^{\vartriangle }}_*\) and \({\mathop {\varvec{x}}\limits ^{\triangledown }}_*\)) in which only one dimension, \({\hat{d}}\), differs. So, making the other dimensions all equal, \(0 \le [{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_j = [{\mathop {\varvec{x}}\limits ^{\triangledown }}_*]_j = [\varvec{x}_*]_j = [\varvec{x}_*^\dagger ]_l \le 1,\; \forall j \ne {\hat{d}}\), where the element of the \(\varvec{x_*}^\dagger\) vector is \(l=j\) if \(j<{\hat{d}}\), otherwise \(l=j-1\). The a and b limits on the \({\hat{d}}\) dimension apply to the test point pair: \(0 \le a \le b \le 1\); \(a \le [{\mathop {\varvec{x}}\limits ^{\triangledown }}_*]_{{\hat{d}}} \le b\) and \(a \le [{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}} \le b\).
Lemma 1
(Bounding posterior mean change) The largest increase in the latent mean as defined above can be bounded by a weighted sum of kernels,
where \(k(\cdot ,\cdot )\) is the EQ-kernel (with same hyperparameters as previously) and \(\beta _i = \alpha _i \left( k\left( [\varvec{x}_i]_{{\hat{d}}},[{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}\right) - k\left( \left[ \varvec{x}_i\right] _{{\hat{d}}},[{\mathop {\varvec{x}_*}\limits ^{\triangledown {(i)}}}]_{\hat{d}}\right) \right)\). Here \([{\mathop {\varvec{x}_*}\limits ^{\triangledown {(i)}}}]_{\hat{d}}\) and \([{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}\) are the positions along the \({\hat{d}}\) axis that maximise \(\beta _i\), for each training point, i. This depends on the the training point’s location and sign,
As explained, \([{\mathop {\varvec{x}_*}\limits ^{\triangledown {(i)}}}]_{\hat{d}}\) and \([{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}\) are simply the positions along the \({\hat{d}}\) axis that maximise \(\beta _i\), for each i. Note that we never use the rest of the \({\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}\) or \({\mathop {\varvec{x}_*}\limits ^{\triangledown {(i)}}}\) vectors in this proof, but we maintain the vector notation for consistency.
Proof
We can upper bound this by noting (e.g. using Jensen’s inequality) that in general, \(\max _{\theta } \left[ \sum _{i=1}^N f_i(\theta )\right] \le \sum _{i=1}^N [ \max _{\theta } f_i(\theta )]\). To this end we replace the pair of locations \({\mathop {\varvec{x}}\limits ^{\vartriangle }}_*\) and \({\mathop {\varvec{x}}\limits ^{\triangledown }}_*\) with specific pairs of locations, \({\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}\) and \({\mathop {\varvec{x}_*}\limits ^{\triangledown {(i)}}}\) which maximise each element of the summation, associated with each training point, to produce an upperbound;
The EQ kernel factorises across dimensions, as the exponent is the sum across dimensions. Specifically,
and
Substituting these two expressions into (10) and rearranging, noting that \(k(\varvec{x}_i^\dagger ,\varvec{x}_*^\dagger )\) remains constant with respect to \([{\mathop {\varvec{x}_*}\limits ^{\triangledown {(i)}}}]_{\hat{d}}\) and \([{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}\), we obtain
The value of \([{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}\) which maximises the \(\max\) term can be determined by considering the condition of the other two variables within the \(\max\) operation: the value of \(\alpha _i\) and the value of \([\varvec{x}_i]_{{\hat{d}}}\). If \(\alpha _i \ge 0\) then the expression is maximised if the (one-dimensional) kernel is maximised. The EQ kernel increases monotonically and symmetrically as the distance between the two inputs reduces. Hence the maximum will occur when \(\vert [\varvec{x}_i]_{{\hat{d}}}-[{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}\vert\) is minimised. (7) and (8) document the locations of the maxima and minima for all configurations. For example, if \([\varvec{x}_i]_{{\hat{d}}}<a\) then this distance is minimised when \([{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}=a\), if \([\varvec{x}_i]_{{\hat{d}}}>b\) this distance is minimised when \([{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}=b\) and if \(a \le [\varvec{x}_i]_{{\hat{d}}} \le b\) the distance is minimised if \([{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}= [\varvec{x}_i]_{{\hat{d}}}\). If \(\alpha _i\) is negative then the expression is maximised if the kernel term is as small as possible. Thus \(\vert [\varvec{x}_i]_{{\hat{d}}}-[{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}\vert\) should be maximised. This occurs by placing \([{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}\) on either a or b depending on which is furthest from \([\varvec{x}_i]_{{\hat{d}}}\) which can easily be determined by comparing \([\varvec{x}_i]_{{\hat{d}}}\) with the midpoint between a and b. A similar (but negated) logic applies to the \(\min\) term. Figure 2 shows some of the configurations of training point location and value to demonstrate where the expression is maximised and minimised.
Examples of three configurations of the training point’s location (\([\varvec{x}_i]_{{\hat{d}}}\)) and value (\(\alpha _i\)), to illustrate where \(\alpha _i k(\varvec{x}_i,{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*)\) is maximised. One can easily see the equivalent locations which minimise the expression. Here we have chosen \(a=0\) and \(b=1\). a If \(0 \le [\varvec{x}_i]_{{\hat{d}}} \le 1\) and \(a_i \ge 0, \alpha _i k(\varvec{x}_i, {\mathop {\varvec{x}}\limits ^{\vartriangle }}_*)\) is maximised if \([{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}} = [\varvec{x}_i]_{{\hat{d}}}\). b If \([\varvec{x}_i]_{{\hat{d}}} \ge 1\) and \(a_i \ge 0, \alpha _i k(\varvec{x}_i, {\mathop {\varvec{x}}\limits ^{\vartriangle }}_*)\) is maximised if \([{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}} = 1\). c If \([\varvec{x}_i]_{{\hat{d}}} \ge \frac{1}{2}\) and \(a_i \le 0, \alpha _i k(\varvec{x}_i, {\mathop {\varvec{x}}\limits ^{\vartriangle }}_*)\) is maximised if \([{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}} = 0\)
Once these values have been chosen, we can rewrite (11) without the \(\min\) and \(\max\) operations and with \(\alpha _i\) factored out.
\(\square\)
3.2.3 Bounding a weighted sum of EQ kernels
Lemma 1 defined an upper bound on the perturbation modifying one dimension can cause to the posterior mean, for any start point in the domain. The upper bound is in the form of a weighted sum of EQ kernels, which we need to upper bound instead. Research exists looking at heuristics and methods for approximating this sum (Carreira-Perpinan 2000; Pulkkinen et al., 2013) but we are interested in finding a strict bound on the peak. Specific to our problem, each EQ has the same, isotropic covariance, but the contribution weights for the EQs can be negative.
We propose below that one can compute such an upper bound by sampling from the domain on a regular grid, taking the maximum value and adding a term to account for the true maximum point lying between grid points.
For a low value of D this can be done with a simple grid search over the \(D-1\) dimensional domain, taking into account that the actual maximum will lie between grid points. For high dimensions this is intractable, so we project the training points to a low dimensional manifold using the principle components (from PCA), in Lemma 3. This holds only if the weights are non-negative. One could force the weights to be non-negative by simply setting the negative weights to zero, but this leads to a very loose bound. In Sect. 3.2.5, we improve on this by iteratively pairing each negative weighted kernel to its nearest positive counterpart and replace both with a new kernel that upper bounds their sum.
Lemma 2
(Grid bounded sum of positive-weighted EQ kernels)
Consider a positive-weighted sum of EQ kernels, with lengthscale, l, i.e. \(k\left( \varvec{x}_1,\varvec{x}_2\right) =\exp \left[ - \vert \varvec{x}_1-\varvec{x}_2\vert _2^2/(2l^2)\right]\), centred at points \(\{\varvec{x}_i\}_{i=1}^N\) with associated weights \(\{w_i\}_{i=1}^N\), \(w_i\ge 0 \;\forall i \in N\). For a given point \(\varvec{p}\), the weighted sum is \(\sum _{i=1}^N {w_ik(\varvec{x}_i, \varvec{p})}\). This sum is sampled on a regular, square, d-dimensional grid of points (with a spacing of s) fully spanning a hyperrectangular part, \({\mathcal {D}}\), of the domain. If \(\phi\) is the largest observed value at a grid vertex, then within the domain of the grid, \({\mathcal {D}}\), the sum is bounded by \(\sum _{i=1}^N {w_i k(\varvec{x}_i, \varvec{p})} \le \phi\; / \exp {\left( -\frac{s^2}{8l^2}d\right) }\;\forall \varvec{p} \in {\mathcal {D}}\).
Proof
To upper bound the function’s maximum we place the EQ kernels to maximise the ratio between the true maximum and the maximum evaluated at the grid points. Using Lemmas 5 and 6 we note that this occurs when all the kernels are colocated at the same point, and placed as far from the point being compared to as possible. We can extend the two lemmas to include lengthscale l in the kernels w.l.o.g. as one could scale the domain to make \(l=1\).
Consider placing \(\varvec{p}\) in \({\mathcal {D}}\): Placing the point equidistant from the nearest grid vertices, the largest \(L_2\) distance possible to \(\varvec{p}\), from any grid point (in the square grid, with spacing s) is \(\sqrt{\sum _{i=1}^d (s/2)^2} = \sqrt{d (s/2)^2} = s\sqrt{d}/2\). We can then compute the value of the EQ at this distance from its maximum, \(\exp \left[ - \left( s\sqrt{d}/2\right) ^2/\left( 2l^2\right) \right]\), and compute the ratio. This is the maximum ratio possible, between the maximum grid value and the true maximum. We thus multiply the actual measured value by this ratio, to give us an upper bound. \(\square\)
The above proof relied on the maximum difference between a grid point and the true maximum occurring when all kernels are co-located. We show this is true for identical positive kernels in Lemma 5 then elaborate for the positive weighted kernels on a grid in Lemma 6. These two lemmas are in Sect. 3.2.6.
3.2.4 Higher dimensions
Lemma 2 specifies how we can upper bound the sum of EQs in the the case of the low-(d)-dimensional input (we use \(d = D-1\)) with positive only weights, which we can exhaustively search with an evenly s-spaced grid. To summarise, we can evaluate the sum at each grid point but the actual peak is almost certain to lie between grid points. The furthest distance from a grid point is \(\frac{1}{2} s \sqrt{d}\). The worst case is that this consists of a Gaussian centred at that furthest point. Thus we assume this worst case contingency and assume that the actual peak is equal to the maximum grid value, \(\phi\), divided by \(\exp {\left( -\frac{s^2}{8l^2}d\right) }\), where l is the lengthscale of the kernel.
For higher dimensions the grid search becomes impractical, thus we apply Lemma 3 which allows us to find a (looser) bound by using a projection to lower dimensions.
Upper left, contour plot of the sum of three, two-dimensional EQs. Upper right, the values of the sum along the diagonal, one-dimensional line. Lower left, the effect on the contour plot if the three points are placed on the diagonal line to illustrate the effect of a principle component approximation. Lower right, the sum along the diagonal line. Note that this new function is never less than the function for when the EQ points are spaced in the full two-dimensional domain
Lemma 3
(Bounding the sum of a mixture of EQs in higher dimensions) Consider performing PCA on the d-dimensional, N locations of the EQs, \(\{\varvec{x}_i\}_{i=1}^N\), discarding all but the k principle components producing a series of equivalent low-rank vectors \(\{\varvec{x}_i'\}_{i=1}^N\) and then applying the grid upper bound algorithm (from Lemma 2) to the locations in the low-dimensional manifold. Any bound on the sum of inputs for the lower-dimensional manifold will hold for the full domain, assuming positive weights. For an illustration, see Fig. 3.
Proof
The proof is in two parts, first we show how the distance between pairs of points will never become larger in the low dimensional PCA manifold. Second we show that this means the upper bound on the low dimensional manifold applies to the full domain.
Consider how the distance between two points will differ in the k-(low)-dimensional manifold vs the (d-dimensional) full-domain. We can factorise the PCA transformation matrix, \(\varvec{W}\), into a rotation, \(\varvec{R}\), and a simple dimension removal matrix, \(\varvec{B}\). Without loss of generality we can chose the rotation to ensure that it is the first 1..k dimensions which are preserved (i.e. so \(\varvec{B}\) is a \(d \times k\) rectangular matrix, consisting of the \(k \times k\) identity matrix in the top sub matrix and zeros in the bottom sub matrix). Consider any pair of points, \(\varvec{x}_a\) and \(\varvec{x}_b\). The distance between any pair of points is invariant to the rotation. The distance between them in the full domain can be written \(\vert \vert \varvec{x}_a \varvec{R}-\varvec{x}_b \varvec{R}\vert \vert _2 = \sqrt{\sum _{j=1}^d\left[ (\varvec{x}_a-\varvec{x}_b) \varvec{R}\right] _{(j)}^2}\) and in the low-dimensional hyperplane \(\vert \vert (\varvec{x}_a-\varvec{x}_b) \varvec{R} \varvec{B}\vert \vert _2 = \sqrt{\sum _{j=1}^k[(\varvec{x}_a-\varvec{x}_b) \varvec{R}]_{(j)}^2}\). Where the \(\varvec{B}\) can be removed from the RHS as it is the identity for \(j \le k\) and the \([(\varvec{x}_a-\varvec{x}_b) \varvec{R}]_{(j)}^2\) terms then equal zero for \(j>k\), so are not included. We note that the terms in the two sums, \([(\varvec{x}_a-\varvec{x}_b) \varvec{R}]_{(j)}^2 \ge 0\) as they consist of the square of real numbers. So the sum over the k dimensions will necessarily be no greater than than the sum over the \(d \ge k\) dimensions. I.e. the distance between the two points will never be greater in the low-dimensional manifold.
We next note that the EQ decreases monotonically with increasing distance. For any location \(\varvec{x}_*\) the distance to any training point \(\varvec{x}_i\) will not increase when transformed to the k-dimensional manifold, and thus the associated EQ contribution to the (positive) weighted sum at \(\varvec{x}_*\) will not be reduced. As this is true for all test points and over all training points, we can see that the maximum of the weighted sum of EQs can not get smaller, when transformed to the k-dimensional manifold. Thus if we find an upper bound on the sum of the k-dimensional domain this will also hold for the full domain. There are no guarantees that the bound will be a close one, although, if the k principle components used capture sufficient variance in the data the residuals will not contribute as much to the distance between points. \(\square\)
3.2.5 Negative weights
We finally need to consider the negatively weighted EQ bases. One could set these to zero, and accept a looser bound. However, we found for this application there was a more efficient way to treat them.
A function f(x) equal to the sum of two (positive and negative weighted) Gaussians is upper bounded by a single EQ, placed at the peak of f(x), with a height equal to the height of the peak.
Lemma 4
(Combining a negative EQ kernel and a positive EQ kernel in 1d) Consider a one dimensional function f(x) equal to the sum of a positively weighted and a negatively weighted EQ (of equal lengthscale), w.l.o.g. placed at the origin and at \(a>0\), respectively. (Note that given these equal lengthscales, a can be scaled so that their lengthscales equal one).
We define the maximum of f(x) to be \(y_0\), at \(x=x_0\). This lemma states that f(x) is upper bounded by \({\mathop {f}\limits ^{\vartriangle }}(x)\), which consists of a single positive EQ, located at \(x_0\) and with weight \(y_0\). Note that we have negated w, so the weight of the negative EQ kernel is \(-w<0\). Figure 4 illustrates this combination of kernels and bound.
Proof
We proceed as follows. We first note that the gradient of f(x) should be zero (with respect to x) at the maximum (where \(x=x_0\)),
So,
This gives us an expression for w,
We note that \(y_0\) is simply (13) evaluated at \(x_0\), so \(y_0 = e^{-x_0^2} - w e^{-(x_0-a)^2}\).
Substituting in our expressions for w and \(y_0\) into inequality (13) we have,
and multiplying out the bracket,
Dividing both sides by \(\frac{x_0}{x_0-a} e^{-x^2}\) (this is always positive), and cancelling some exponential terms, we are left with;
Which finally results in,
We define a function g(x) which is simply the result of subtracting the right hand side of the inequality from the left,
We wish to show that g(x) is never greater than zero. To do this we shall show that (a) it has only two turning points (at \(x_0\) and a); (b) g(x) only has one (finite) point where it equals zero and that (c) this location is at \(x_0\); (d) the turning point at \(x_0\) is a maximum; (e) at this maximum g(x) is non-positive. The conclusion of these is that, as \(x_0\) is the only location where \(g(x)=0\), and the function must be negative everywhere else: \(g(x)\le 0\).
First we note that g(x)’s derivative with respect to x has only two zero-crossing points (for finite x). The gradient can be written as \(\frac{dg}{dx} = -2 a e^{-2 a x_0} e^{2 x a} + 2 a e^{-2 x_0^2} e^{2 x x_0}\). This expression equals zero (for non-zero a) in two cases. One at \(x=a\) and one where \(x=x_0\). The function g(x) only equals zero for one (finite) value of x. Setting the expression for \(g(x)=0\) in (21), then rearranging and solving for x gives us \(x=x_0\). Thus the turning point at \(x=x_0\) is the only (finite) location where \(g(x)=0\), too. We can disregard the other turning point and must now simply show that g(x) is at a maximum at \(x=x_0\) (and thus \(g(x) \le g(x_0)\) for all x). We do this by differentiating again, \(\frac{d^2g}{dx^2} = -4 a^2 e^{-2 a x_0} e^{2 x a} + 4 a x_0 e^{-2 x_0^2} e^{2 x x_0}\). Setting \(x=x_0\) means \(\frac{d^2g}{dx^2} = 4 a (x_0 - a)\). This expression is never positive (as \(x_0\) is never positive and a is non-negative). So this is a maximum location. We note again that using (21) we find that \(g(x_0)=0\). As this is a maximum and the only location where \(g(x)=0\) we can state that \(g(x) \le 0\) for all finite values of x. Thus our original inequality (13) holds too, i.e. an EQ function of scale \(y_0\) at location \(x_0\) is never less than f(x). \(\square\)
Remark 1
(Combining a negative and a positive kernel in higher dimensions) We can extend this to higher dimensions by considering this one dimension as lying on the line between two EQ centres in a high dimensional domain. Every parallel line in the domain has the same pair of summed functions, but scaled by some constant w: wf(x) and \(w {\mathop {f}\limits ^{\vartriangle }}(x)\). As the two functions are scaled equally the same bounds will apply.
3.2.6 Bound on true maximum using maximum from grid vertices
The two results in this Section are used by other proofs, and are relatively ‘self-evident’. If we want to bound the maximum of a sum of positive EQ kernels, we might evaluate the sum on a set of vertices in a grid, and then scale the maximum we find to bound the maximum we know probably lies somewhere between grid vertices - getting a bound by assuming a worst case that the maximum is as large as possible, given the largest sums we found on the vertices. Lemmas 5 and 6 simply show that the worst case is when the sum consists of all the kernels at the same location, at a point as far from a vertex as possible.
Lemma 5
(Kernel placement to maximise peak to test point ratio)Consider function \(S(x) = \sum _{i=1}^N e^{-(x-a_i)^2}\), the sum of positive, one dimensional EQ kernels, with equal width and height, centred at \(\{a_i\}_{i=1}^N\). The ratio of the maximum of this function to any other point is maximised if all kernels are placed at the maximum.
Proof
We assume w.l.o.g. that the maximum is at 0. Given that the gradient of S(x) at x is, \(\frac{dS(x)}{dx} = -2 \sum _{i=1}^N (x-a_i) e^{-(x-a_i)^2}\), we note that at \(x=0\), where the maximum is,
We wish to show that the ratio of S(x)/S(0) at any x, is smallest if all the kernels are placed at 0 (i.e. that all \(a_i=0\)). This means showing that,
The lhs is S(x)/S(0) for arbitrary \(a_i\). The rhs is S(x)/S(0) if all \(a_i=0\). We note the rhs can be simplified, leaving,
Multiplying out the numerator’s exponential and dividing through by \(e^{-x^2}\),
To show this is true, we apply Jensen’s inequality, noting that the exponential function is convex and the exponential terms are all positive,
The last expression’s numerator’s summation equals zero, from (22), Thus the inequality becomes,
\(\square\)
Lemma 6
(Placing all EQ kernels at same point as far from grid vertices as possible, maximises the ratio between the true maximum and the maximum at any grid vertex)Consider a function \(f(\varvec{x})\) equal to the sum of N, d-dimensional EQ-kernels, with positive, rational, weights, \(\{w_i\}_{i=1}^N\). A series of regularly spaced grid points G span the domain \({\mathcal {D}}\). The ratio of the function’s true maximum to its maximum at grid vertices, \(\max _{\varvec{x} \in {\mathcal {D}}} f(\varvec{x})/\max _{\varvec{x} \in G} f(\varvec{x})\), is maximised by placing all the kernel centres, \(\{\varvec{a}_i\}_{i=1}^N\) at a point \(\varvec{p}\), that has the greatest distance from the grid vertices.
Proof
The function evaluated along a straight line drawn through the sum of d-dimensional EQ-kernels, will equal the sum of 1-dimensional EQ-kernels, with new weights, due to the property of Gaussian conditioning. If one finds the greatest common measure (GCM) of these weights, one can construct the sum using a new sum of identical kernels, dividing the sum by the GCM. From (5) we know that for any such line, passing through the true maximum, the optimum placement of the EQ kernels is at the maximum: for the ratio of the maximum to any other point to be maximised. As this applies to all lines through the maximum and to all points on those lines, the kernels must all be placed at the maximum (in all dimensions) to maximise the ratio of the maximum to any point. One can write the sum of these EQ kernels as a single EQ at the maximum weighted by the sum of weights \(\sum _{i=1}^N{w_i}\). We finally note that, as the standard EQ kernel is monotonic and isotropic, the largest ratio of its maximum at \(\varvec{p}\) to a point \(\varvec{x}\) will occur when \(\vert \varvec{p}-\varvec{x}\vert _2\) is maximised. Thus one should place the maximum at a point furthest from any grid point. \(\square\)
3.2.7 Opposite direction
The entire algorithm will also need rerunning with the training point values negated, to account for paths moving in the negative direction along \({\hat{d}}\).
Lemma 7
(Reverse direction) Negating the training point values and applying Lemma 1 is equivalent to applying the Lemma but for travelling in a negative direction along dimension \({\hat{d}}\).
Proof
We simply note that if we can bound some change in a function \(f(a)-f(b) < c\) in which \(a>b\), then to upper bound the change in the opposite direction \(f(b)-f(a) < d\) one can negate the two functions, \((-f(b))-(-f(a)) = f(a)-f(b) < d\). This negation is equivalent to negating the training output values, as these are combined in a linear weighted sum: \(\varvec{\alpha } = K^{-1} \varvec{y}\). \(\square\)
3.2.8 Lower bound on number of dimensions
So far we have been finding a bound on the largest change a single perturbation (in dimension \({\hat{d}}\)) can cause to the posterior mean of a GP. We are actually interested in the number of inputs that need to change to cause the posterior mean to change more that a threshold, t. Lemma 8 cumulatively sums the single dimensional perturbation bounds to find how many need to be changed to reach the threshold.
Lemma 8
(Lower bound on the number of dimensions that need perturbing to cause the posterior mean to change more than t) We wish to find a lower bound, L, on the number of dimensions that will need to be perturbed to cause a change in the posterior mean more than a threshold, t. From Lemma 1, for N, d-dimensional training inputs \(\{\varvec{x}_i\}_{i=1}^N\) and outputs \(\{y_i\}_{i=1}^N\) and EQ kernel \(k(\cdot ,\cdot )\), we can find values \(v_{{\hat{d}}} = \sum _{i=1}^N \beta _i k(\varvec{x}_i^\dagger ,\varvec{x}_*^\dagger )\) which upper bound the largest change perturbing each dimension, \({\hat{d}}\), can cause to the posterior mean. We consider the sequence constructed of cumulatively summed bounds, presorted in descending order, such that the jth element of the sequence equals \(\sum _{i=1}^j v_{\hat{d_i}}\), where \(v_{{\hat{d}}_i} \ge v_{{\hat{d}}_{i+1}}\). The lower bound is simply the index of the first element of the sequence less than the threshold, t. I.e. the j in which \(\sum _{i=1}^j v_{\hat{d_i}} < t\).
Proof
The upper bound on the change in the posterior due to a perturbation in any given dimension \({\hat{d}}\) is \(v_{{\hat{d}}} = \sum _{i=1}^N \beta _i k(\varvec{x}_i^\dagger ,\varvec{x}_*^\dagger )\). If a series of perturbations are made in dimensions \(({\hat{d}}_{1},..{\hat{d}}_{L})\), with associated upper bounds \(v_{{\hat{d}}_{1}},..,v_{{\hat{d}}_{L}}\), the sum of the upper bounds, \(\sum _{i=1}^L v_{{\hat{d}}_{i}}\), will be a valid bound on the total perturbation of those selected dimensions. To see this, note that each upper bound value is for a perturbation starting at any location. Thus the bound for \({\hat{d}}_{i}\) is still valid, regardless what previous perturbations have been applied. Finally, we need to find a lower bound on the number of dimensions that need to be perturbed to change the posterior mean beyond a threshold amount. Given a list of upper bounds for all the dimensions, \(\{v_d\}_{d=1}^D\), maximising the sum of L items would be achieved by selecting the largest items. Hence we cumulatively sum the descended sorted bounds and find how many are needed to exceed the threshold. I.e., find the smallest L which leads to a sum \(\sum _{i=1}^L v_{{\hat{d}}_{i}} \ge t\). \(\square\)
Remark 2
The lower bound L, on the number of dimensions one needs to perturb, would be tighter if one explored two or more dimensions, by also slicing the domain into hyperrectangles along multiple dimensions. This will give a tighter bound, but at the cost of exponential computation, with \({d}\atopwithdelims (){S}\) combinations, which for small t is approximately \({\mathcal {O}}((dS^2)^t)\). Hence, we have used the looser bound approach described above.
3.3 Improvements to the AB algorithm
3.3.1 Slicing the Domain
This approach gives a very loose bound, as it combines the largest possible contribution of each term in (3) without taking into account that the increase associated with each one occurs at different locations along the \({\hat{d}}\) dimension. This was a necessary sacrifice to convert the problem back to a simple sum of weighted EQ kernels. To give an example of how this leads to a very loose bound, consider the sum of a line of four kernels (all with \(\alpha _i=+1\)) spaced with little overlap along the \({\hat{d}}\) dimension (Fig. 5). The largest possible increase in the posterior, when moving along \({\hat{d}}\), would be approximately 1 (e.g. point A to point B). However, the algorithm above would give an upper bound of 4 on that increase, as their location in the \({\hat{d}}\) direction has been lost in (6). It effectively will add together the largest increase each kernel can contribute (which is 1 for each). To tighten the bound we propose that one can slice the original domain orthogonal to \({\hat{d}}\) into S smaller hyperrectangle subdomains. The path between the initial and adversarial test point (travelling along \({\hat{d}}\)) may start, end, cross or be entirely within each subdomain. We can compute \(\beta _i^{(j)}\) for each \(\varvec{x}_i\) for each subdomain, j: \(\beta _i^{(j)} = k([{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}},[\varvec{x}_i]_{{\hat{d}}}) - k([{\mathop {\varvec{x}}\limits ^{\triangledown }}_*]_{{\hat{d}}},[\varvec{x}_i]_{{\hat{d}}}),\) then sum them, \(\beta _i = \alpha _i \sum _{j=1}^S \beta _i^{(j)}\). For the case of starting the path in a given subdomain, we constrain \([{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}}\) to equal the upper edge of the hyperrectangle. If we are ending in the subdomain, we set \([{\mathop {\varvec{x}}\limits ^{\triangledown }}_*]_{{\hat{d}}}\) equal to the lower edge. If we are crossing the entire subdomain, we set both \([{\mathop {\varvec{x}}\limits ^{\triangledown }}_*]_{{\hat{d}}}\) and \([{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}}\) to the lower and upper edges respectively. Finally, if the path is entirely within the subdomain then \([{\mathop {\varvec{x}}\limits ^{\triangledown }}_*]_{{\hat{d}}}\) and \([{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}}\) are unconstrained within the subdomain. We must consider all combinations of consecutive subdomains and perform the bound calculation separately for each. The more slices the tighter the bound will be, but at the cost of needing to bound quadratically more combinations.
To illustrate, we return to the example in Fig. 5. We will first consider a bound on the increase in the posterior mean when moving from the first subdomain, 1, across the whole of subdomain 2 to the last subdomain, 3. For each of these subdomains we need to compute the contribution of all training points. As an example, we start with the first training point, \(\varvec{x}_1\). For subdomain \(j=1\) (the starting subdomain) the path must end on the right edge of the subdomain’s hyperrectangle \(c_2\), so \([{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}} = c_2\), where \(k\left( [{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}},[\varvec{x}_1]_{{\hat{d}}}\right) \approx 0\). The \([{\mathop {\varvec{x}}\limits ^{\triangledown }}_*]_{{\hat{d}}}\) is placed to minimise \(k\left( [{\mathop {\varvec{x}}\limits ^{\triangledown }}_*]_{{\hat{d}}},[\varvec{x}_i]_{{\hat{d}}}\right)\), which happens also to lie at \(c_2\). So \(\beta _1^{(1)} = 0\). Similar calculations can be made for the other subdomains, leading to \(\beta _1 \approx 0\). To explain, remember we are bounding the increase in the posterior for a path that starts in the left subdomain and ends in the right subdomain. The contribution from \(\varvec{x}_1\) will be small. Running the calculation for all training points, one finds that just \(\varvec{x}_3\) and \(\varvec{x}_4\) contribute significantly and lead to an upper bound of approximately \(m(\varvec{x}_*)<1.5\), considerably better than the earlier bound of 4. The subdomain approach tightens the bound substantially. This is a bound on the path being in subdomains: {1,2,3}. We will need to perform the same calculation again, to test all combinations of contiguous subdomains ({1},{2},{3},{1,2},{2,3},{1,2,3}).
Lemma 9
(Slicing the domain) If we divide the domain, orthogonal to dimension \({\hat{d}}\), into several smaller hyperrectangles, then the bound is still valid by summing the appropriate contributions from these hyperrectangular subdomains.
Proof
From Lemma 1 we bound the largest increase in the latent mean with,
where \(\beta _i = \alpha _i \left( k\left( [\varvec{x}_i]_{{\hat{d}}},[{\mathop {\varvec{x}_*}\limits ^{\vartriangle {(i)}}}]_{\hat{d}}\right) - k\left( [\varvec{x}_i]_{{\hat{d}}},[{\mathop {\varvec{x}_*}\limits ^{\triangledown {(i)}}}]_{\hat{d}}\right) \right)\). If the domain were divided, orthogonal to dimension \({\hat{d}}\), into several smaller hyperrectangles, at \(a=c_1<c_2<...<c_S=b\) the perturbation that leads to the maximum change in the posterior will start, end and cross a contiguous sequence of these new hyperrectanglar subdomains. The bound in (28) still holds, but we can compute \(\beta _i\) more efficiently. Let us assume that the perturbation which causes the largest change travels from subdomain \({\mathcal {D}}_{(1)}\) to subdomain \({\mathcal {D}}_{(S)}\), where \({\mathcal {D}}_{(1)}\) may or may not equal \({\mathcal {D}}_{(S)}\). We note that one can write the sum as,
where simply the first kernel from each term cancels the second kernel from the following term. We define \(\beta _i^{(j)}\) equal to each term, times \(\alpha _i\). For example \(\beta _i^{(1)} = \alpha _i \left( k\left( [\varvec{x}_i]_{{\hat{d}}},c_1\right) - k\left( [\varvec{x}_i]_{{\hat{d}}},[{\mathop {\varvec{x}_*}\limits ^{\triangledown {(i)}}}]_{\hat{d}}\right) \right)\) such that we can write,
Although this has not changed the bound analytically, it has the effect of constraining the paths that can be taken to those from \({\mathcal {D}}_{(1)}\) to \({\mathcal {D}}_{(S)}\), which means, practically, the bound can be tighter. \(\square\)
Remark 3
As we do not know the (contiguous) sequence of one or more subdomains that the maximum perturbing path takes we must test all of them. To do this efficiently, we precompute the values of \(\beta _i^{(j)}\) for the four conditions, that the path,
-
Starts in that subdomain, i.e. \(\beta _i^{(j,\rightarrow )}\)
-
Starts and ends in that subdomain, i.e. \(\beta _i^{(j,-)}\)
-
Ends in that subdomain, i.e. \(\beta _i^{(j,\leftarrow )}\)
-
Crosses the entire subdomain, i.e. \(\beta _i^{(j,\leftrightarrow )}\)
To compute the four conditions we note that maxima and minima occur either at the boundaries of the domain (\(c_{j+1}\) and \(c_{j}\)) or where \([\varvec{x}_i]_{{\hat{d}}} = [\varvec{x}_*]_{{\hat{d}}}\). So we precompute the value at the start \({\mathop {v}\limits ^{s}}^{(j)}_{i}= \alpha _i k([\varvec{x}_i]_{{\hat{d}}},c_{j})\), end \({\mathop {v}\limits ^{e}}^{(j)}_{i}= \alpha _i k([\varvec{x}_i]_{{\hat{d}}},c_{j+1})\) of each subdomain and the middle of the kernel \({\mathop {v}\limits ^{m}}^{(j)}_{i}= \alpha _i \left( k([\varvec{x}_i]_{{\hat{d}}},[\varvec{x}_i]_{{\hat{d}}} \right)\) (iff it lies in the subdomain, otherwise this is assigned a ‘NaN’). The four expressions above become (with any ‘NaN’ terms being ignored):
-
Starts in the subdomain, \(\beta _i^{(j,\rightarrow )} = \text {max}\left( {\mathop {v}\limits ^{e}}^{(j)}_{i}-{\mathop {v}\limits ^{s}}^{(j)}_{i}, {\mathop {v}\limits ^{e}}^{(j)}_{i}-{\mathop {v}\limits ^{m}}^{(j)}_{i},0 \right)\).
-
Starts and ends in that subdomain, \(\beta _i^{(j,-)} = \text {max}\left( {\mathop {v}\limits ^{m}}^{(j)}_{i}-{\mathop {v}\limits ^{s}}^{(j)}_{i}, {\mathop {v}\limits ^{e}}^{(j)}_{i}-{\mathop {v}\limits ^{m}}^{(j)}_{i},{\mathop {v}\limits ^{e}}^{(j)}_{i}-{\mathop {v}\limits ^{s}}^{(j)}_{i},0 \right)\).
-
Ends in that subdomain, \(\beta _i^{(j,\leftarrow )} = \text {max}\left( {\mathop {v}\limits ^{m}}^{(j)}_{i}-{\mathop {v}\limits ^{s}}^{(j)}_{i},{\mathop {v}\limits ^{e}}^{(j)}_{i}-{\mathop {v}\limits ^{s}}^{(j)}_{i},0 \right)\).
-
Crosses the subdomain, \(\beta _i^{(j,\leftrightarrow )} = {\mathop {v}\limits ^{e}}^{(j)}_{i}-{\mathop {v}\limits ^{s}}^{(j)}_{i}\).
We then add up the appropriate sequence, for example: \(\beta _i = \beta _i^{(2,\rightarrow )} + \beta _i^{(3,\leftrightarrow )} + \beta _i^{(4,\leftarrow )}\) and use the earlier tools as before to bound the sum of weighted EQ kernels, \(m(\varvec{x}_*^\dagger ) \le \sum _{i=1}^N \beta _i k\left( \varvec{x}_i^\dagger ,\varvec{x}_*^\dagger \right)\).
3.3.2 Other Kernels
The algorithm and proofs all depend on the Gaussian process using the exponentiated quadratic (EQ) kernel. In particular the algorithm depends on the ability to write the expressions for the maximum and minimum over the \(D-1\) dimensions as the product of, \(k\left( [{\mathop {\varvec{x}}\limits ^{\vartriangle }}_*]_{{\hat{d}}},[\varvec{x}_i]_{{\hat{d}}}\right) \times k\left( \varvec{x}_*^\dagger ,\varvec{x}_i^\dagger \right) .\) Most other stationary kernels (for example the exponential) do not have this property.
To use AB mechanism for other kernels we propose that one can approximate an alternative, stationary, isotropic kernel \(k_t(r)\) with a weighted sum of EQ kernels (with a variety of lengthscales and weights).Footnote 1 To ensure we maintain a bound we generate two lists of weights, one that leads to a sum that is greater than our target kernel, \(k_t(r) \le \sum _{q=1}^Q {\mathop {w_q}\limits ^{\vartriangle }}k(r;l_q)\), and one that leads to a sum that is less, \(k_t(r) \ge \sum _{q=1}^Q {\mathop {w_q}\limits ^{\triangledown }}k(r;l_q)\).
If we want to approximate a kernel such as the exponential, with a sum of EQs, we can only do so up to a finite r as the tails of the exponential fall away slower than an EQs. So we state that this holds if r is no more than the length of the longest path \(\vert p\vert\) possible in the domain, i.e.;
For all \(0 \le r \le \vert p\vert\),
where \({\mathop {w_q}\limits ^{\vee }}\) and \({\mathop {w_q}\limits ^{\wedge }}\) have been chosen from \({\mathop {w_q}\limits ^{\vartriangle }}\) and \({\mathop {w_q}\limits ^{\triangledown }}\) to minimise and maximise each term (so need to be chosen, accounting for the sign of \(\alpha _i\) and k, we will return to this later).
To see how we can use this approximation we return to (9), substituting in our new definitions, where \(w_q\) and \(l_q\) are the weights and lengthscales of the Q contributing EQ kernels.
\({\mathop {w_q}\limits ^{\vee }}\) and \({\mathop {w_q}\limits ^{\wedge }}\) again need to be chosen from the two lists to minimise and maximise each term appropriately. Moving the sum over Q outside, and rearranging (using the Jensen-derived inequality \(\max _{\theta } \left[ \sum _{i=1}^N f_i(\theta )\right] \le \sum _{i=1}^N [ \max _{\theta } f_i(\theta )]\) again), we have a similar form to (12),
We again need to compute the four possible starting/ending combinations for each subdomain, as described in Remark 3, for example: If the path just starts in that subdomain \(\beta _i^{(j,\rightarrow )} = \alpha _i {\mathop {w_q}\limits ^{\wedge }}k\left( [\varvec{x}_i]_{{\hat{d}}},c_{j+1}\right) - \alpha _i {\mathop {w_q}\limits ^{\vee }}k\left( [\varvec{x}_i]_{{\hat{d}}},[{\mathop {\varvec{x}_*}\limits ^{\triangledown {(i)}}}]_{\hat{d}}\right)\). A simple approach would be to use \({\mathop {w_q}\limits ^{\wedge }}\) for the first term and \({\mathop {w_q}\limits ^{\vee }}\) for the latter. However we can be a little more efficient and consider the whole path. To do this and to resolve the issue of selecting which value to use for \({\mathop {w_q}\limits ^{\vee }}\) and \({\mathop {w_q}\limits ^{\wedge }}\), we use the notation and structure from Remark 3, but create an upper and lower version of \({\mathop {v}\limits ^{s}}^{(j)}_{i}\), \({\mathop {v}\limits ^{m}}^{(j)}_{i}\) and \({\mathop {v}\limits ^{e}}^{(j)}_{i}\) (which takes into account the sign of \(\alpha _i\), \(w_q\) and k), and compute a result for each weight in the approximation. So,
-
Largest and smallest values at start of subdomain,
$$\begin{aligned} {\mathop {v_{i}}\limits ^{s\vartriangle , q}}^{(j)}= \text {max} \left( \alpha _i {\mathop {w_q}\limits ^{\vartriangle }} k\left( [\varvec{x}_i]_{{\hat{d}}},c_{j}\right) , \alpha _i {\mathop {w_q}\limits ^{\triangledown }} k\left( [\varvec{x}_i]_{{\hat{d}}},c_{j}\right) \right) \end{aligned}$$(35)$$\begin{aligned} {\mathop {v_{i}}\limits ^{s\triangledown , q}}^{(j)}= \text {min} \left( \alpha _i {\mathop {w_q}\limits ^{\vartriangle }} k\left( [\varvec{x}_i]_{{\hat{d}}},c_{j}\right) , \alpha _i {\mathop {w_q}\limits ^{\triangledown }} k\left( [\varvec{x}_i]_{{\hat{d}}},c_{j}\right) \right) \end{aligned}$$(36) -
Largest and smallest values at end of subdomain,
$$\begin{aligned} {\mathop {v_{i}}\limits ^{e\vartriangle , q}}^{(j)}= \text {max} \left( \alpha _i {\mathop {w_q}\limits ^{\vartriangle }} k\left( [\varvec{x}_i]_{{\hat{d}}},c_{j+1}\right) , \alpha _i {\mathop {w_q}\limits ^{\triangledown }} k\left( [\varvec{x}_i]_{{\hat{d}}},c_{j+1}\right) \right) \end{aligned}$$(37)$$\begin{aligned} {\mathop {v_{i}}\limits ^{e\triangledown , q}}^{(j)}= \text {min} \left( \alpha _i {\mathop {w_q}\limits ^{\vartriangle }} k\left( [\varvec{x}_i]_{{\hat{d}}},c_{j+1}\right) , \alpha _i {\mathop {w_q}\limits ^{\triangledown }} k\left( [\varvec{x}_i]_{{\hat{d}}},c_{j+1}\right) \right) \end{aligned}$$(38) -
Largest and smallest values within subdomain,
$$\begin{aligned} \begin{aligned} \text {if} \;&c_{j} \le [\varvec{x}_i]_{{\hat{d}}} \le c_{j+1}\; \text {then}&\\&{\mathop {v_{i}}\limits ^{m\vartriangle , q}}^{(j)}= \text {max} \left( \alpha _i {\mathop {w_q}\limits ^{\vartriangle }} k\left( [\varvec{x}_i]_{{\hat{d}}},[\varvec{x}_i]_{{\hat{d}}}\right) , \alpha _i {\mathop {w_q}\limits ^{\triangledown }} k\left( [\varvec{x}_i]_{{\hat{d}}},[\varvec{x}_i]_{{\hat{d}}}\right) \right) \\&{\mathop {v_{i}}\limits ^{m\triangledown , q}}^{(j)}= \text {min} \left( \alpha _i {\mathop {w_q}\limits ^{\vartriangle }} k\left( [\varvec{x}_i]_{{\hat{d}}},[\varvec{x}_i]_{{\hat{d}}}\right) , \alpha _i {\mathop {w_q}\limits ^{\triangledown }} k\left( [\varvec{x}_i]_{{\hat{d}}},[\varvec{x}_i]_{{\hat{d}}}\right) \right) \\ \text {else}&\\&{\mathop {v_{i}}\limits ^{m\vartriangle , q}}^{(j)}= \text {NaN} \;\;\;\text {and}\;\;\; {\mathop {v_{i}}\limits ^{m\triangledown , q}}^{(j)}= \text {NaN}. \end{aligned} \end{aligned}$$(39)
We finally compute new versions of \(\beta _i\),
-
Starts in the subdomain,
$$\begin{aligned}\beta _i^{q(j,\rightarrow )} = \text {max}\left( {\mathop {v_{i}}\limits ^{e\triangledown , q}}^{(j)}-{\mathop {v_{i}}\limits ^{s\triangledown , q}}^{(j)}, {\mathop {v_{i}}\limits ^{e\triangledown , q}}^{(j)}-{\mathop {v_{i}}\limits ^{m\triangledown , q}}^{(j)},0 \right) .\end{aligned}$$ -
Starts and ends in that subdomain,
$$\begin{aligned} \begin{aligned}\beta _i^{q(j,-)} = \text {max}\Big (&{\mathop {v_{i}}\limits ^{m\vartriangle , q}}^{(j)}-{\mathop {v_{i}}\limits ^{s\triangledown , q}}^{(j)}, {\mathop {v_{i}}\limits ^{e\vartriangle , q}}^{(j)}-{\mathop {v_{i}}\limits ^{m\triangledown , q}}^{(j)},{\mathop {v_{i}}\limits ^{e\vartriangle , q}}^{(j)}-{\mathop {v_{i}}\limits ^{s\triangledown , q}}^{(j)}, \\&{\mathop {v_{i}}\limits ^{e\vartriangle , q}}^{(j)}-{\mathop {v_{i}}\limits ^{e\triangledown , q}}^{(j)}, {\mathop {v_{i}}\limits ^{s\vartriangle , q}}^{(j)}-{\mathop {v_{i}}\limits ^{s\triangledown , q}}^{(j)},{\mathop {v_{i}}\limits ^{m\vartriangle , q}}^{(j)}-{\mathop {v_{i}}\limits ^{m\triangledown , q}}^{(j)}, 0 \Big ).\end{aligned}\end{aligned}$$ -
Ends in that subdomain,
$$\begin{aligned}\beta _i^{q(j,\leftarrow )} = \text {max}\left( {\mathop {v_{i}}\limits ^{m\vartriangle , q}}^{(j)}-{\mathop {v_{i}}\limits ^{s\triangledown , q}}^{(j)},{\mathop {v_{i}}\limits ^{e\vartriangle , q}}^{(j)}-{\mathop {v_{i}}\limits ^{s\triangledown , q}}^{(j)},{\mathop {v_{i}}\limits ^{s\vartriangle , q}}^{(j)}-{\mathop {v_{i}}\limits ^{s\triangledown , q}}^{(j)},0 \right) .\end{aligned}$$ -
Crosses the subdomain,
$$\begin{aligned}\beta _i^{q(j,\leftrightarrow )} = {\mathop {v_{i}}\limits ^{e\triangledown , q}}^{(j)}-{\mathop {v_{i}}\limits ^{s\triangledown , q}}^{(j)}.\end{aligned}$$
We add up the appropriate sequence as before, e.g.: \(\beta ^q_i = \beta _i^{q(2,\rightarrow )} + \beta _i^{q(3,\leftrightarrow )} + \beta _i^{q(4,\leftarrow )}\). We then use the earlier tools to bound the sum of weighted EQ kernels, but this time we add up the contributions from the set of approximating EQ kernels, \(m(\varvec{x}_*^\dagger ) \le \sum _{q=1}^Q \sum _{i=1}^N \beta ^q_i k\left( \varvec{x}_i^\dagger ,\varvec{x}_*^\dagger ;l_q\right)\).
3.3.3 Enhancement
To improve the runtime we compute a fast initial pass, with few slices. We then run the algorithm on those combinations with the greatest bound (i.e. capable of changing the latent function the most), using a higher slice count. We refer to this procedure as ‘enhancement’.
3.4 Multiple dimensions and complexity
To find a lower bound on the number of dimensions that need to change in order for the posterior mean to change by more than t, one can run the above algorithm, assigning \({\hat{d}}\) as each of the D dimensions, then cumulatively sum the largest t of these upper bounds. This gives a lower bound on the number of perturbed dimensions required. We found that for the datasets used, this straightforward method achieved reasonable results. For a fixed number of training points, N, the time complexity, for S slices along each of the D dimensions, is \({\mathcal {O}}(DS^2)\).
3.5 Classification and the sparse approximation
The algorithm above is for regression, but we wish to consider GPC. For the Laplace approximation we find the mode and Hessian of the posterior. We can then use normal GP regression but with an alternative set of training values, \(\varvec{{\hat{f}}}\) in Williams and Rasmussen (2006)[p. 44].
The bound becomes increasingly loose as the number of training points increases, however one can use sparse approximation methods (Snelson and Ghahramani 2006) to mitigate this. Specifically, one replaces the original training data with a low-rank approximation using inducing inputs. First find suitable inducing point locations using gradient ascent to maximise the marginal log likelihood using the original \(\varvec{{\hat{f}}}\), then use the inducing inputs associated with the low-rank (e.g. deterministic training condition, DTC) approximation as the new training data for our classification. We then have \(\varvec{\alpha } = \sigma ^{-2} \varvec{\Sigma } \varvec{K}_{uf} \varvec{{\hat{f}}}\), where \(\varvec{\Sigma } = \left( \sigma ^{-2} \varvec{K}_{uf} \varvec{K}_{uf}^\top + \varvec{K}_{uu}\right) ^{-1}\) and \(\varvec{K}_{uu}\) is the covariance between inducing inputs, \(\varvec{K}_{uf}\) is the covariance between the inducing inputs and the original training points. We use this earlier expression, from Snelson and Ghahramani (2006), for inducing point approximation, instead of, for example the variational approach (in which induing points are integrated out) in Titsias (2009), as the AB algorithm only uses the posterior mean, which is equivalent in the two papers.
MNIST 3v5 test using 100 training points. GPC (left) and logistic regression (right). Upper plots: The bounded change in the posterior induced by changing 1, 2 or 3 input points (blue lines) for given values of the regulariser or lengthscale. The black line indicates the ‘confident misclassification’ threshold. Lower plot: how accuracy varies. The yellow/orange areas indicate regions in which two/three pixels need changing to cause a confident misclassification (Color figure online)
4 Results
We consider several classification problems, including three real datasets in which robustness against AEs is important for security (specifically credit-worthiness, spam-filtering and banknote-forgery). For each we compare the GPC results to LR, considering both accuracy and robustness. We investigate the effect of the number of splits and the number of inducing inputs on robustness, accuracy and runtime. We generate AEs that approach our new confident misclassification threshold to demonstrate bound tightness. We finally look at the approximation to allow us to use other kernels and apply it to the exponential kernel.
4.1 MNIST
We used a subset of 43 pixels from the \(8 \times 8\) MNIST(LeCun et al., 1998) (3 vs. 5, N = 100, not using a sparse approximation). Figure 6 shows the GPC has a greater accuracy (over 80%) than the LR algorithm (70%). The GPC (with \(l=2\)) achieves a bound of 3 pixel-changes and a higher accuracy than the LR solution, which can only achieve a two pixel-change bound. Thus the GPC solution is more robust and more accurate.
We then applied the GPC AB algorithm to the full resolution \(28 \times 28\) MNIST images (using 475 pixels) for 0 versus 1 (N = 1000). Four inducing points were used. The results are recorded in Table 1. For longer lengthscale configurations, dozens of pixels are required to change to achieve a confident misclassification.
4.2 Non-linearly-separable synthetic data
To demonstrate the AB algorithm on a dataset for which LR would fail, we generated an 8d linearly inseparable synthetic dataset (N = 50, not using a sparse approximation) placed in three Gaussian clusters (\(\sigma =0.1\)) within a unit hypercube, along its main diagonal, illustrated in Fig. 7. We confirm that, as expected, the LR classifier fails to classify beyond chance while the GPC achieves reasonable (96%) accuracy (\(l=0.7\), \(v=0.3\), \(\sigma ^2=1\)). With this configuration, the 5th and 95th percentile training points lie 0.321 apart. The AB algorithm (using enhancement) found the upper bound for a single input perturbation was 0.220. Thus at least two inputs need perturbing to cause a confident misclassification (Fig. 8). A brute-force search found a change as large as 0.144 was possible with a single dimension change. Thus the true value lies between 0.144 and 0.220.
Synthetic dataset using 50 training points and the GPC. The upper plot shows upper bounds (blue lines) on the change in the posterior induced by changing 1,2,3,4 or 5 input points. The black line indicates the ‘confident misclassification’ threshold. The lower plot shows the classifier’s accuracy versus lengthscale. The yellow and orange areas indicate regions in which two and three pixels respectively need changing to cause a confident misclassification. There is a trade off between accuracy and robustness (Color figure online)
4.3 Real world data: credit, spam and banknotes
The data used for these experiments was from the UCI Repository of Machine Learning Databases (Dua and Graff 2017). The ‘Australian Credit Approval’ dataset has 690 training points with 14 dimensions, consisting of categorical and continuous data (100 training points were used in all these examples, with no sparse approximation). The fairly high accuracy for LR (Fig. 9, upper plots) suggests the problem is mostly linearly separable, thus the long-lengthscale GP is able to maintain a good accuracy. The GPC is also provably more robust, compared to the linear classifier, with a lower bound of three inputs requiring perturbation, compared to one, for LR. It is unclear why it achieves more robustness compared to the linear classifier, the most likely explanation is that the two classes are somewhat compact such that single input changes can not move from one class to the other. We tested the algorithm on the 57 dimensional spam dataset (Cranor and LaMacchia 1998). Both the GPC and LR classifiers were non-robust, i.e. both had a bound less than one input, meaning a single dimension might be able to cause a confident misclassification. Both methods achieved over 85% accuracy (majority class 60%). We also tested the algorithm on 100 points from the four dimensional UCI banknote authentication dataset. For the GPC, at least two of the four inputs needed changing for some lengthscales, while LR only required one input change (Fig. 9, lower plots). Note that at the shortest lengthscale the GPC is not only more accurate but also more robust than at middle-lengthscales.
Credit (top set) and bank dataset (lower set) using GPC (left) and LR (right). Upper of each pair shows bounds on the impact on the latent function. Lower of each pair shows accuracy. Yellow/orange areas are where two/three pixels need changing to cause a confident misclassification. Black line indicates confident misclassification threshold (Color figure online)
4.4 Effect of number of slices and the sparse approximation
The contribution of each training point is assumed to be the ‘worst-case’ for a given hyperrectangle. By introducing more hyperrectangles we tighten this bound. To test this effect empirically, we consider again the \(8 \times 8\) MNIST (3 vs. 5) data (\(N=100\), 200 test, \(l=4\), \(v=1\), \(\text {accuracy} = 68.5\%\)). Left plots in Fig. 10 demonstrate how the number of slices, S, affect both the bound and computation. The runtime follows, as expected, an \(S^2\) time complexity and the bound does tighten with increasing S. This ignores the ‘enhancement’ approach of rerunning the algorithm with more slices on the most sensitive dimensions to use compute more efficiently.
Effect of (left) number of domain slices (right) number of inducing points. (upper) Cumulative effect of the first four most significant input dimensions are indicated by blue lines. Black line indicates confident misclassification threshold (distance between the 5th and 95th percentile training points). Lower plots show elapse times and accuracy. Dataset: \(8 \times 8\) MNIST (3 vs. 5) (Color figure online)
We also tested the effect of the number of slices on the credit dataset. With 400 training points, 200 test points, lengthscale of 2, 4 inducing points, we reach an accuracy of 80%. Table 2 summaries this for up to 100 slices. As for the MNIST example, more slices improve the bound but also take more computation. We also looked at the use of inducing points on this dataset (400 training points, 200 test points, lengthscale of 2, 100 slices). Table 3 details these results. These also follow the pattern of the MNIST data: having fewer inducing inputs is associated with a reduction in accuracy, but with improvements in the bound.
We compared this to the results of an empirical experiment, testing 5M pairs of points that differ by one, two or three dimensions. We found that for two inducing points, at least three dimensions needed changing. For the remaining rows in Table 3, the empirical number-of-dimensions equal those of the theoretical bounds: Our limited bound on robustness appears to be due to the classifier being vulnerable to single dimensional perturbation and not to our bounds being excessively loose.
We investigated using a sparse approximation using the \(8 \times 8\) MNIST data (3 vs. 5, N = 1000, l = 1, v = 1). Figure 10 shows, with more inducing points, the accuracy and computation time increase, as one would expect, while the algorithm’s upper bound increases (weakens). We suggest this is because increasing the number of inducing points leads to a looser bound directly, but also means the points must be closer together, leading to steeper gradients in the posterior. With just two inducing points, at least three inputs need to be altered to cause a confident misclassification (but the classifier has only a 78% accuracy). With five inducing points the accuracy is over 90% but now the algorithm only guarantees two inputs need to be modified.
We investigated the same question with the credit dataset. With more than four inducing points the classifier was bound such that only one input needed to change. With two inducing inputs it is close to needing three inputs to change. It would seem that a sparse approximation is a useful way to improve the strength of the bound on the scale of the perturbation required. However, this does seem to depend on the data. To explore a dataset with a more complex decision boundary we considered the 0,1,2,3,4 versus 5,6,7,8,9 8x8 MNIST task (keeping 33 pixels, 500 training points, 200 test points; number of inducing points: 4, 8, 16, 32, 64 or 128, \(l=4\)). In this we found, surprisingly, that the relationship between the number of inducing points and the bound wasn’t so clear and almost in the opposite direction, with the bound reaching two pixels only for 128 inducing points. This is probably partly due to the way inducing points are distributed. Possible future work could explore optimising the placement of inducing points for robustness (not just for model fit).
Demonstration of perturbation necessary from a confidently classified one, left; or zero, right; to become a confidently classified zero or one respectively. Crosses, pixels that were modified. Initial images are from test set. The AB algorithm found at least 3 pixels would need to be modified (to move from any confidently classified zero to a confidently classified one, or the reverse)
4.5 Bounds provided by empirical attack
The AB algorithm provides a lower bound on the number of dimensions that need perturbing, to cause a confident misclassification, while an empirical attack provides an upper bound. We build on the Jacobian-based Saliancy Map Attack (JSMA) by Papernot et al. (2016a) as it is easy to interpret and implement. It computes the gradient of the prediction with respect to each input, and sets the inputs with the largest gradients to their largest permitted value. The GP has a less monotonic relationship with its inputs than a DNN, so standard JSMA often placed the example away from the training data, causing the posterior to return to the prior mean, far from the 95% threshold. This may explain why shorter lengthscales are protective in the bank-note experiment. We initially developed a simple attack which, like Papernot et al. (2016a) produces a saliency map of gradients, but this time using the gradients of the GP latent mean function itself (with respect to the test inputs). We found however, as mentioned above, that simply perturbing each input to its extreme value often resulted in a near-prior mean posterior. Instead, we still choose the input with the largest absolute gradient but then we performed a search along the perturbed input’s axis to find the value that causes the largest change in the posterior. Figure 11 gives two examples of such a perturbation, causing a confidently classified zero or one to become a confidently classified one or zero. We applied this algorithm to all of the 470 confidently classified test points, and found examples in which just five pixels needed changing, providing an upper bound. The AB algorithm was applied to this model (\(l = 4\), \(v = 202\)). This found a lower bound of 3 pixels needing to be modified. Thus the true number is between 3 and 5.
Demonstration of perturbation necessary from a confidently classified zero, left column pair; or one, right column pair; to become a confidently classified one or zero respectively. Crosses mark the pixels that were modified. Initial images are from test set. Greyscale from zero (black) to one (white)
Figure 12 demonstrates 10 more adversarial examples. Note that these are generated by the empirical attack based on the JSMA algorithm and do not necessarily represent the least perturbation required. These plots are rather to illustrate what a ‘confident’ misclassification might look like. I.e. one in which a test point has been moved from being confidently labelled as one class to being confidently labelled of being in the opposite class.
We briefly experimented with the algorithm described in Carlini and Wagner (2017b) for the \(L_0\) attack, but found this produced looser bounds than the above approach. That algorithm chooses pixels to remove by using the gradient at the perturbed point, but this is ineffective for GPC, especially with a target threshold far from the 50% decision boundary.
4.6 Exponential kernel
The posterior mean for two kernels, with two training points (at 0.3 and 0.5 in the x-axis plotted). The dotted lines indicate the width of the bound (although absolute values are irrelevant). The solid lines are the posterior mean. Three values of lengthscale 0.1, 0.4 and 1.6 are shown, and three resolutions of slices are used (2, 8 and 32)
We finally, briefly, look at the result of using the approximation method described in 3.3.2 applied to the exponential kernel, \(k(r) = v e^{-\vert r/l\vert }\). In Fig. 13 we illustrate the approximation to the exponential kernel provided by summing seven EQ kernels. This provided bounds on the kernel for \(r<20\). To demonstrate, we construct a simple training set of two points (at [0.5,0.5], [0.3,0.5] with labels 1 and 0 respectively). Figure 14 illustrates the posterior mean for the two kernels along the \(x_2=0.5\) line. There is a complicated interaction between lengthscale and number of slices when looking at the tightness of the bounds, but at longer lengthscales the bound seems worse for the exponential kernel, even when more slices are used. Remember also the exponential kernel will take up to 7 times longer due to the summing of the approximation EQ kernels. The compute time is noted in each figure for the two kernels.
We applied both kernels to a scaled MNIST problem (300 balanced, randomly picked images were down-sampled to 1/4 size and those pixels that went over a value of 50 were used, leaving us with 35 dimensions. The GPC was applied using the EQ and exponential kernels, with \(l=4\), \(v=3\), 6 inducing points and 15 slices (the accuracy was comparable: 74% and 76.5% respectively). The 5% to 95% confident-classification interval, and bound on one pixel change for the two kernels was, respectively: EQ \(\text {CI} = 2.439\) and \(\text {bound} = 1.88\); exponential \(\text {CI} = 3.182\) and \(\text {bound} = 5.744\) (no enhancement was applied). The bound means that at least two pixels need to be changed in the EQ case, but the bound does not guarantee that for the exponential kernel case - the exponential kernel leads to a classifier less protected against adversarial attack. Part of the exponential kernel classifier’s looser bounds is due to the approximation, but we suspect it is mainly due to the steepness of parts of the posterior mean in the exponential-kernel case.
5 Discussion
The AB algorithm provides guaranteed limits on the ability of an attacker to cause a confident classification to be confidently misclassified. Specifically this allows us to prove that changing fewer than a certain number of inputs can not cause the classification to change from one threshold for classification confidence to another, given a set of hyperparameters and training data. This improves on previous efforts to evaluate the potential for adversarial attacks, as this AB algorithm holds for the whole domain, and not just a localised volume around each training point. Several interesting features are apparent. We find that for most of the datasets, more regularisation leads to more robust bounds. This is largely expected but probably depends on the type of regularisation used (Demontis et al., 2017; Grosse et al., 2018). There is an exception to this rule in the banknote dataset, where we see very short lengthscales also lead to robustness. With long-lengthscales it has more linear responses while at short lengthscales it may or may-not be robust, depending on where the training data lies. This reflects the findings of Grosse et al. (2018) who show empirically that both long and short lengthscales for a GPC can provide robustness against some attacks. We empirically looked at the tightness of the bound (in Sect. 4.5) by comparing generating AEs to the computed lower bound. The AB was fairly close to empirically generated AEs, suggesting our bound is quite tight. We considered examples of datasets that require protection from adversarial attack (credit-worthiness, spam-classification and banknote-forgery). The robustness of the classifiers in the different examples demonstrates that it is both the classifier’s parameters and the data distribution which will affect the utility of the bound. The use of a sparse approximation was found to improve the robustness of the bound, at the cost of some accuracy.
5.1 Future work: extending to deep architectures
For future work, extending this to a deep framework such as a deep GP (Damianou and Lawrence 2013) may be possible. The current AB algorithm allows one to bound the number of variables, for a given layer, required to cause a specific change in the layer’s output. With a slight modification one could consider the combinations of all paths in which each dimension has a limited perturbation (this would also open the way to a loose bound on the \(L_1\)-norm attack). Although potentially computationally intractable for high dimensionality, typical deep GPs have few dimensions beyond the input layer (Damianou and Lawrence 2013). Alternatively, if the approximation discussed in Sect. 3.3.2 could be applied to convolutional kernels then the AB algorithm might be applied to convolutional Gaussian processes (Van der Wilk et al., 2017). Finally, in the long term, work building equivalences between DNNs and GPs (e.g. Lee et al., 2018) might allow the AB Algorithm to provide bounds on some DNN classifiers.
5.2 Multi-class classification
One surprisingly challenging issue is how to extend the AB algorithm to the multi-class situation. In the binary classification problem, increasing the latent mean of one class will result in the posterior mean increasing (for a given variance). In the multi-class situation the softmax function that is usually used to compute the posterior will mean the posterior mean could reduce even if there is an increase in the latent mean, as the latent mean for the other classes could increase more. One approach might be to compute the bound for all the latent GPs for each slice and then computing the bound on the change to the softmax output (for each slice). This approach might also allow the variance of the latent distribution to be reintroduced. We hope to address these issues in future work.
5.3 Uncertainty in the latent posterior distribution
We decided against using the uncertainty estimates that the GP provides. It has been found (Grosse et al., 2019) that this uncertainty can assist in the detection of off-the-shelf adversarial attacks. However, the latent mean is usually near zero in highly uncertain locations anyway (for kernels like the EQ, as the posterior will return to the prior mean) so this would be of limited benefit. Another advantage of ignoring the GP variance is that it allows us to apply our bound to other stationary-kernel-based classifiers (i.e. that can be written in the form of (3)) for example after training, the expression for the posterior mean in (Hensman et al., 2015, Sect. 3.1) would be amenable to our bound approach.
5.4 Runtime
The runtime in our implementation was dominated (for large N) by the computation of \({\hat{f}}\), which did not take advantage of the sparse approximation. The algorithm scales to 100s of input dimensions (a typical limit of a GPC). Future computational improvements include the use of dynamic programming when summing path segments and iterative refinement of the grid when finding the bound on the mixture of EQs. The bound itself could be tightened by improving how the pairs of positive and negative EQs are selected when cancelling out the negative terms.
5.5 Other kernels
We were able to extend the approach to handle other stationary kernels by approximating them with the sum of EQ kernels. We demonstrated this with the exponential kernel, approximating it with seven EQ kernels. We found the bound on the classifier using the exponential kernel was weaker. This fits with our intuition: we expect that a smoother latent posterior prediction mean (driven by the prior) to lead to a classifier that is more robust to adversarial attack. The exponential kernel leads to a posterior latent mean that isn’t very smooth.
5.6 Optimising parameters
The AB algorithm has several parameters one needs to select, trading off robustness, computational time and accuracy. These choices will depend on the application, the data and the likely capacity of an attacker to perturb the input (and the consequences of poor classification vs successful attack). A search over parameters might be practical, or potentially using GP optimisation with a cost function combining the accuracy with the bound.
6 Conclusion
We believe that it is vital we can construct classifiers, confident that imperceptibly small changes will not cause large changes in classification. The presence of such vulnerabilities in classifiers used in safety critical applications is of concern. In particular is the danger of ‘blind spot attacks’ (Zhang et al., 2019) which are overlooked by the common certification methods that just work around the epsilon ball. Currently there are no extant practical global bounds for any (non-trivial) classifiers and it may even be that the true sensitivity of many classifiers is non-practical (i.e. are vulnerable to single-pixel changes). Having a practical global bound for a widely used classifier is a significant improvement given the lack of defences currently available. How one uses the bound to construct such classifiers is a more open question. We imagine that the designer of the classifier could run our algorithm on their classifier and training data and select model parameters to trade off the accuracy against this bound.
In summary, we have devised a framework for bounding the scale of an \(L_0\) adversarial attack leading to a confident misclassification, developed a method for applying the bound to GP classification and through a series of experiments tested this bound against similarly bounded LR and investigated the effect of classifier configuration parameters. We found our GP classifier could be accurate, practical and provably robust. This is the first paper to successfully find such a bound. The AB algorithm provides a foundation for future research — in particular for expanding to larger datasets and more complex classifiers.
Data availability
Not applicable. All the datasets used in this paper were from other sources, which have been cited appropriately.
Code availability
The code is split into two python modules, https://github.com/lionfish0/boundmixofgaussians is a module for finding an upper bound on a weighted sum of EQ kernels. https://github.com/lionfish0/GPAdversarialBound is the main module that computes a bound on the GP regression problem.
Notes
For isotropic, stationary kernel \(k(r) \equiv k(\varvec{x},\varvec{x}')\) where \(r=\vert \varvec{x}-\varvec{x}'\vert _2\).
References
Biggio, B., Corona, I., Maiorca, D. et al. (2013). Evasion attacks against machine learning at test time. In: Machine learning and knowledge discovery in databases - european conference, ECML PKDD 2013, Prague, Czech Republic, September 23–27, 2013, Proceedings, Part III, pp. 387–402
Blaas, A., Patane, A., Laurenti, L. et al. (2020). Robustness quantification for classification with Gaussian processes. In: 23rd international conference on artificial intelligence and statistics
Bojchevski, A., Klicpera, J., Günnemann, S. (2020). Efficient robustness certificates for discrete data: Sparsity-aware randomized smoothing for graphs, images and more. In: International conference on machine learning, PMLR, pp. 1003–1013
Cardelli, L., Kwiatkowska, M., Laurenti L. et al. (2019). Robustness guarantees for Bayesian inference with Gaussian processes. In: Proceedings of the AAAI conference on artificial intelligence, pp. 7759–7768
Carlini, N., Wagner, D. (2017a). Adversarial examples are not easily detected: Bypassing ten detection methods. In: Proceedings of the 10th ACM workshop on artificial intelligence and security, ACM, pp. 3–14
Carlini, N., Wagner, D. (2017b). Towards evaluating the robustness of neural networks. In: 2017 IEEE symposium on security and privacy (SP), IEEE, pp. 39–57
Carlini, N., Katz, G., Barrett, C. et al. (2017). Provably minimally-distorted adversarial examples. arXiv preprint arXiv:1709.10207
Carreira-Perpinan, M. A. (2000). Mode-finding for mixtures of Gaussian distributions. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(11), 1318–1323.
Cranor, L. F., & LaMacchia, B. A. (1998). Spam! Communications of the ACM, 41(8), 74–83.
Dalvi, N., Domingos, P., Sanghai, S. et al. (2004). Adversarial classification. In: Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining, pp. 99–108
Damianou, A., Lawrence, N. (2013). Deep Gaussian processes. In: Artificial intelligence and statistics, pp 207–215
Demontis, A., Melis, M., Biggio, B., et al. (2017). Yes, machine learning can be more secure! IEEE transactions on dependable and secure computing: A case study on Android malware detection.
Dua, D., Graff, C. (2017). UCI machine learning repository. http://archive.ics.uci.edu/ml
Finlay, C., & Oberman, A. M. (2021). Scaleable input gradient regularization for adversarial robustness. Machine Learning with Applications, 3(100), 017.
Grosse, K., Smith, M. T., Backes, M. (2018). Killing four birds with one Gaussian process: Analyzing test-time attack vectors on classification. arXiv preprint arXiv:1806.02032
Grosse, K., Pfaff, D., Smith, M.T., et al. (2019). The limitations of model uncertainty in adversarial settings. Bayesian Deep Learning Workshop @NeurIPS
Hein, M., Andriushchenko, M. (2017). Formal guarantees on the robustness of a classifier against adversarial manipulation. Advances in Neural Information Processing Systems, pp. 2266–2276
Hensman, J., Matthews, A., & Ghahramani, Z. (2015). Scalable variational Gaussian process classification. Journal of Machine Learning Research, 38, 351–360.
Huang, X., Kwiatkowska, M., Wang, S. et al. (2017). Safety verification of deep neural networks. In: International conference on computer aided verification, Springer, pp. 3–29
LeCun, Y., Bottou, L., Bengio, Y., et al. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324.
Lee, J., Bahri, Y., Novak, R., et al. (2018). Deep neural networks as gaussian processes. In: International conference on learning representations
Madry, A., Makelov, A., Schmidt, L. et al. (2018). Towards deep learning models resistant to adversarial attacks. In: 6th International conference on learning representations, ICLR 2018, Vancouver, BC, Canada, April 30–May 3, 2018, Conference Track Proceedings
Papernot, N., McDaniel, P., Jha, S., et al. (2016). (2016a) The limitations of deep learning in adversarial settings. Security and Privacy (EuroS &P) (pp. 372–387). IEEE: IEEE European Symposium on.
Papernot, N., McDaniel, P., Wu, X. et al. (2016b). Distillation as a defense to adversarial perturbations against deep neural networks. In: 2016 IEEE Symposium on Security and Privacy (SP), IEEE, pp. 582–597
Peck, J., Roels, J., Goossens, B., et al. (2017). Lower bounds on the robustness to adversarial perturbations. In: Advances in Neural Information Processing Systems, pp. 804–813
Pulkkinen, S., Mäkelä, M. M., & Karmitsa, N. (2013). A continuation approach to mode-finding of multivariate Gaussian mixtures and kernel density estimates. Journal of Global Optimization, 56(2), 459–487.
Ross, A. S., Doshi-Velez, F. (2018). Improving the adversarial robustness and interpretability of deep neural networks by regularizing their input gradients. In: Thirty-Second AAAI Conference on Artificial Intelligence
Ruan, W., Wu, M., Sun, Y., et al. (2019). Global robustness evaluation of deep neural networks with provable guarantees for the hamming distance. IJCAI
Sitawarin, C., Bhagoji, A. N., Mosenia, A. et al. (2018). Rogue signs: Deceiving traffic sign recognition with malicious ads and logos. arXiv preprint arXiv:1801.02780
Snelson, E., Ghahramani, Z. (2006). Sparse Gaussian processes using pseudo-inputs. In: Advances in neural information processing systems, pp. 1257–1264
Su, J., Vargas, D. V., & Sakurai, K. (2019). One pixel attack for fooling deep neural networks. IEEE Transactions on Evolutionary Computation, 23(5), 828–841.
Suciu, O., Marginean, R., Kaya, Y. et al. (2018). When does machine learning \(\{\)FAIL\(\}\)? generalized transferability for evasion and poisoning attacks. In: 27th \(\{\)USENIX\(\}\) Security Symposium (\(\{\)USENIX\(\}\) Security 18), pp. 1299–1316
Szegedy, C., Zaremba, W., Sutskever, I. et al. (2014). Intriguing properties of neural networks. ICLR
Titsias, M. (2009). Variational learning of inducing variables in sparse Gaussian processes. In: Artificial Intelligence and Statistics, pp. 567–574
Van der Wilk, M., Rasmussen, C. E., Hensman, J. (2017). Convolutional gaussian processes. arXiv preprint arXiv:1709.01894
Williams, C. K., & Rasmussen, C. E. (2006). Gaussian processes for machine learning. Cambridge: MIT Press.
Wong, E., Kolter, Z. (2018). Provable defenses against adversarial examples via the convex outer adversarial polytope. In: International conference on machine learning, pp. 5283–5292
Zhang, H., Chen, H., Song, Z. et al. (2019). The limitations of adversarial training and the blind-spot attack. In: 7th international conference on learning representations, ICLR 2019, New Orleans, LA, USA, May 6–9, 2019
Funding
This study was funded by the EPSRC (EP/N014162/1). Kathrin Grosse was supported by the German Federal Ministry of Education and Research (BMBF) through funding for the Center for IT-Security, Privacy and Accountability (CISPA) (FKZ: 16KIS0753).
Author information
Authors and Affiliations
Contributions
MS devised the approach, developed the mathematical proofs, coded and ran the experiments. KG proposed the initial concept and provided the background and approach. She also corrected many mistakes and improved the overall manuscript. MB acquired funding for the project. MA acquired funding and also provided useful suggestions and improvements to the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Additional information
Editors: Dana Drachsler Cohen, Javier Garcia, Mohammad Ghavamzadeh, Marek Petrik, Philip S. Thomas.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Smith, M.T., Grosse, K., Backes, M. et al. Adversarial vulnerability bounds for Gaussian process classification. Mach Learn 112, 971–1009 (2023). https://doi.org/10.1007/s10994-022-06224-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-022-06224-6