Learning with risks based on M-location

Abstract

In this work, we study a new class of risks defined in terms of the location and deviation of the loss distribution, generalizing far beyond classical mean-variance risk functions. The class is easily implemented as a wrapper around any smooth loss, it admits finite-sample stationarity guarantees for stochastic gradient methods, it is straightforward to interpret and adjust, with close links to M-estimators of the loss location, and has a salient effect on the test loss distribution, giving us control over symmetry and deviations that are not possible under naive ERM.

1 Introduction

In machine learning, the important yet ambiguous notion of “good off-sample generalization” (or “small test error”) is typically formalized in terms of minimizing the expected value of a random loss ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }{{\,\mathrm{L}\,}}(h)$, where h is a candidate decision rule and ${{\,\mathrm{L}\,}}(h)$ is a random variable on an underlying probability space $(\Omega ,\mathcal {F},\mu )$. This setup based on average off-sample performance has been famously called the “general setting of the learning problem” by Vapnik (1999), and is central to the decision-theoretic formulation of learning in the influential work of Haussler (1992). This is by no means a purely theoretical concern; when average performance dictates the ultimate objective of learning, the data-driven feedback used for training in practice will naturally be designed to prioritize average performance (Bottou et al. 2016; Johnson and Zhang 2014; Le Roux et al. 2013; Shalev-Shwartz and Zhang 2013). Take the default optimizers in popular software libraries such as PyTorch or TensorFlow; virtually without exception, these methods amount to efficient implementations of empirical risk minimization. While the minimal expected loss formulation is clearly an intuitive choice, the tacit emphasis on average performance represents an important and non-trivial value judgment, which may or may not be appropriate for any given real-world learning task.

1.1 Our basic motivation

Put simply, our goal is to develop learning algorithms that make risk function design an explicit part of the modern machine learning workflow, rather than the traditional tacit emphasis of average performance while ignoring all other properties of the (test) loss distribution that are inherent in traditional empirical risk minimization (ERM). More concretely, we want to design a transformation that can be applied to any loss function, which is flexible enough to express varying degrees of sensitivity to loss deviations and tail behavior, easy to implement using existing stochastic gradient-based frameworks (e.g., PyTorch), and ultimately leads to novel risks which are analytically tractable. In the following paragraphs, we will discuss the basic ideas underlying our approach at a high level, and touch on some of the key related literature. After some basic theoretical setup, we discuss the strengths and drawbacks of our proposed approach (relative to the existing literature) in more detail in Sect. 2.3.

1.2 Some statistical context

In order to make the value judgement of “how to define risk” an explicit part of the machine learning methodology, in this work we consider a generalized class of risk functions, designed to give the user much greater flexibility in terms of how they choose to evaluate performance, while still allowing for theoretical performance guarantees. One core statistical concept is that of the M-location of the loss distribution under a candidate h, defined by

$$\begin{aligned} {{\,\mathrm{M}\,}}(h) :=\mathop {\mathrm{arg\,min}}\limits _{\theta \in \mathbb {R}} \, {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho \left( \frac{{{\,\mathrm{L}\,}}(h)-\theta }{\sigma }\right) . \end{aligned}$$

(1)

Here $\rho :\mathbb {R}\rightarrow [0,\infty )$ is a function controlling how we measure deviations, and $\sigma > 0$ is a scaling parameter. Since the loss distribution $\mu$ is unknown, clearly ${{\,\mathrm{M}\,}}(h)$ is an ideal, unobservable quantity. If we replace $\mu$ with the empirical distribution induced by a sample $({{\,\mathrm{L}\,}}_1,\ldots ,{{\,\mathrm{L}\,}}_n)$, then for certain special cases of $\rho$ we get an M-estimator of the location of ${{\,\mathrm{L}\,}}(h)$, a classical notion dating back to Huber (1964), which justifies our naming. Ignoring integrability concerns for the moment, note that in the special case of $\rho (u) = u^{2}$, we get the classical risk ${{\,\mathrm{M}\,}}(h) = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }{{\,\mathrm{L}\,}}(h)$, and in the case of $\rho (u) = |u |$, we get ${{\,\mathrm{M}\,}}(h) = \inf \{u: \mu \{ {{\,\mathrm{L}\,}}(h) \le u \} \ge 0.5 \}$, namely the median of the loss distribution. This rich spectrum of evaluation metrics makes the notion of casting learning problems in terms of minimization of M-locations (via their corresponding M-estimators) very conceptually appealing. However, while the statistical properties of the minima of M-estimators in special cases are understood (Brownlees et al. 2015), the optimization involved is both costly and difficult, making the task of designing and studying ${{\,\mathrm{M}\,}}(\cdot )$-minimizing learning algorithms highly intractable. With these issues in mind, we study a closely related alternative which retains the conceptual appeal of raw M-locations, but is more computationally congenial.

1.3 Our approach

With $\sigma$ and $\rho$ as before, our generalized risks will be defined implicitly by

$$\begin{aligned} \min _{\theta \in \mathbb {R}} \left[ \theta + \eta {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho \left( \frac{{{\,\mathrm{L}\,}}(h)-\theta }{\sigma }\right) \right] , \end{aligned}$$

(2)

where $\eta > 0$ is a weighting parameter that controls the balance of priority between location and deviation. A more formal definition will be given in Sect. 2 (see Eqs. 3–5), including concrete forms for $\rho (\cdot )$ that are conducive to both fast computation and meaningful learning guarantees. In addition, we will show (cf. Proposition 3) that this new objective can be written as

$$\begin{aligned} {[}{{\,\mathrm{M}\,}}(h) - c_{{{\,\mathrm{M}\,}}}] + \eta {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho \left( \frac{{{\,\mathrm{L}\,}}(h)-[{{\,\mathrm{M}\,}}(h) - c_{{{\,\mathrm{M}\,}}}]}{\sigma }\right) , \end{aligned}$$

where the shift term $c_{{{\,\mathrm{M}\,}}} > 0$ can be simply characterized by the equality

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho ^{\prime }\left( \frac{{{\,\mathrm{L}\,}}(h)-[{{\,\mathrm{M}\,}}(h) - c_{{{\,\mathrm{M}\,}}}]}{\sigma }\right) = \frac{\sigma }{\eta }, \end{aligned}$$

noting that $c_{{{\,\mathrm{M}\,}}} \rightarrow 0_{+}$ as $\eta \rightarrow \infty$. By utilizing smoothness properties of loss functions typical to machine learning problems (e.g., squared error, cross-entropy, etc.), even though the generalized risks need not be convex, they can be shown to satisfy weak notions of convexity, which still admit finite-sample guarantees of near-stationary for stochastic gradient-based learning algorithms (details in Sect. 3). This approach has the additional benefit that implementation only requires a single wrapper around any given loss which can be set prior to training, making for easy integration with frameworks such as PyTorch and TensorFlow, while incurring negligible computational overhead.

1.4 Our contributions

The key contribution here is a new concrete class of risk functions, defined and analyzed in Sect. 2. These risks are statistically easy to interpret, their empirical counterparts are simple to implement in practice, and as we prove in Sect. 3, their design allows for standard stochastic gradient-based algorithms to be given competitive finite-sample excess risk guarantees. We also verify empirically (Sect. 4) that the proposed feedback generation scheme has a demonstrable effect on the test distribution of the loss, which as a side-effect can be easily leveraged to outperform traditional ERM implementations, a result which is in line with early insights from Breiman (1999) and Reyzin and Schapire (2006) regarding the impact of the loss distribution on generalization. More broadly, the choice of which risk to use plays a central role in pursuit of increased transparency in machine learning, and our results represent a first step towards formalizing this process.

1.5 Relation to existing literature

With respect to alternative notions of “risk” in machine learning, perhaps the most salient example is conditional value-at-risk (CVaR) (Prashanth et al. 2020; Holland and Haress 2021a), namely the expected loss conditioned on it exceeding a quantile at a pre-specified probability level. CVaR allows one to encode a sensitivity to extremely large losses, and admits convexity when the underlying loss is convex, though the conditioning often leaves the effective sample size very small. Other notions such as spectral risk and cumulative prospect theory (CPT) scores have also been considered (Bhat and Prashanth 2020; Holland and Haress 2021b; Khim et al. 2020; Leqi et al. 2019), but the technical difficulties involved with computation and analysis arguably outweigh the conceptual benefits of learning using such scores. These proposals can all be interpreted as “location” parameters of the underlying loss distribution; our risks take the form of a sum of a location and a deviation term, where the location is a shifted M-location, as described above. The basic notion of combining location and deviation information in evaluation is a familiar concept; the mean-variance objective ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }{{\,\mathrm{L}\,}}(\cdot )+{{\,\mathrm{var}\,}}_{\mu }{{\,\mathrm{L}\,}}(\cdot )$ dates back to classical work by Markowitz (1952); our proposed class includes this as a special case, but generalizes far beyond it. Mean-variance and other risk function classes are studied by Ruszczyński and Shapiro (2006, 2006b), who give minimizers a useful dual characterization, though our proposed class is not captured by their work (see also Remark 4). We note also that the recent (and independent) work of Lee et al. (2020) considers a form which is similar to (2) in the context of empirical risk minimizers; the critical technical difference is that their formulation is restricted to $\rho$ which is monotonic, an assumption which enforces convexity. The special case of mean-variance is also treated in depth in more recent work by Duchi and Namkoong (2019), who consider stochastic learning algorithms for doing empirical risk minimization with variance-based regularization. Finally, we note that our technical analysis in Sect. 3 makes crucial use of weak convexity properties of function compositions, an area of active research in recent years (Duchi and Ruan 2018; Drusvyatskiy and Paquette 2019; Davis and Drusvyatskiy 2019). Since our proposed objective can be naturally cast as a composition taking us from parameter space to a Banach space and finally to $\mathbb {R}$, leveraging the insights of these previous works, we extend the existing machinery to handle learning over Banach spaces, and give finite-sample guarantees for arbitrary Hilbert spaces. More details are provided in Sect. 3, plus the appendix.

1.6 Notation and terminology

To give the reader an approximate idea of the technical level of this paper, we assume some familiarity with probability spaces, the notion of sub-gradients and the sub-differential of convex functions, as well as special classes of vector spaces like Banach and Hilbert spaces, although the main text is written with a wide audience in mind. Strictly speaking, we will also deal with sub-differentials of non-convex functions, but these technical concepts are relegated to the appendix, where all formal proofs are given. In the main text, to improve readability, we write $\partial f(x)$ to denote the sub-differential of f at x, regardless of the convexity of f. When we refer to a function being $\lambda$-smooth, this refers to its gradient being $\lambda$-Lipschitz continuous, and weak smoothness just requires such continuity on directional derivatives; all these concepts are given a detailed introduction in the appendix. Throughout this paper, we use ${{\,\mathrm{\mathbf {E}}\,}}[\cdot ]$ for taking expectation, and ${{\,\mathrm{\mathbf {P}}\,}}$ as a general-purpose probability function. For indexing, we will write $[k] :=\{1,\ldots ,k\}$. Distance of a vector v from a set A will be denoted by ${{\,\mathrm{dist}\,}}(v;A) :=\inf \{\Vert v-v^{\prime }\Vert : v^{\prime } \in A \}$.

2 A concrete class of risk functions

Fig. 1

Left: graphs of $\rho$ defined in (3) (solid line), $\rho ^{\prime }$ (dashed line), and $\rho ^{\prime \prime }$ (dot-dash line). Middle–right: these are graphs of $\theta \mapsto \eta \rho _{\sigma }(1.0-\theta )$, with $\rho _{\sigma }$ defined in (4), where the minimizer is $\theta _{\min }=1.0$, the colors correspond to different $\sigma$ values, and $\eta$ is set following Remark 2. That is, for $0< \sigma < 1.0$, set $\eta = \sigma /{{\,\mathrm{atan}\,}}(\infty )$. For $\sigma = 0$, set $\eta = 1.05$. For $1.0 \le \sigma < \infty$, set $\eta = 2\sigma ^{2}$. For $\sigma = \infty$, set $\eta = 1.0$

The risks described by (2) are fairly intuitive as-is, but a bit more structure is needed to ensure they are well-defined and useful in practice. In this section, we introduce a concrete choice of $\rho$ for measuring deviations, consider a risk class modulated via re-scaling, establish basic theoretical properties and discuss both the utility and limitations of the proposed risk class.

2.1 Deviations and re-scaling

To make things more concrete, let us fix $\rho$ as

$$\begin{aligned} \rho (u) :=u {{\,\mathrm{atan}\,}}(u) - \frac{\log (1+u^2)}{2}, \quad u \in \mathbb {R}. \end{aligned}$$

(3)

This function is handy in that it behaves approximately quadratically around zero, and it is both $\pi /2$-Lipschitz and strictly convex on the real line.¹ Fixing this particular choice of $\rho$ and letting Z be a random variable (any $\mathcal {F}$-measurable function), we interpolate between mean- and median-centric quantities via the following class of functions, indexed by $\sigma \in [0,\infty ]$:

$$\begin{aligned} {{\,\mathrm{r}\,}}_{\sigma }(Z,\theta ) :=\theta + \eta {{\,\mathrm{\mathbf {E}}\,}}_{\mu } \rho _{\sigma }\left( Z-\theta \right) , \text { where } \rho _{\sigma }(u) :={\left\{ \begin{array}{ll} |u |, &{} \text {if } \sigma = 0\\ \rho \left( u/\sigma \right) , &{} \text {if } 0< \sigma < \infty \\ u^2, &{} \text {if } \sigma = \infty . \end{array}\right. } \end{aligned}$$

(4)

With this class of ancillary functions in hand, it is natural to define

$$\begin{aligned} {{\,\mathrm{R}\,}}_{\sigma }(Z) :=\inf _{\theta \in \mathbb {R}} \, {{\,\mathrm{r}\,}}_{\sigma }(Z,\theta ) \end{aligned}$$

(5)

to construct a class of risk functions. In the context of learning, we will use this risk function to derive a generalized risk, namely the composite function $h \mapsto {{\,\mathrm{R}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h))$. As a special case, clearly this includes risks of the form (2) given earlier. Visualizations of $\rho$ highlighting the role of re-scaling are given in Fig. 1. See also Fig. 5 in the appendix for visualizations of different loss functions transformed according to (4). Minimizing ${{\,\mathrm{R}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h))$ in h is our formal learning problem of interest.

2.2 Basic properties

Before considering learning algorithms, we briefly cover the basic properties of the functions ${{\,\mathrm{r}\,}}_{\sigma }$ and ${{\,\mathrm{R}\,}}_{\sigma }$. Without restricting ourselves to the specialized context of “losses,” note that if Z is any square-$\mu$-integrable random variable, this immediately implies that $|{{\,\mathrm{r}\,}}_{\sigma }(Z,\theta )|< \infty$ for all $\theta \in \mathbb {R}$, and thus ${{\,\mathrm{R}\,}}_{\sigma }(Z) < \infty$. Furthermore, the following result shows that it is straightforward to set the weight $\eta$ to ensure ${{\,\mathrm{R}\,}}_{\sigma }(Z) > -\infty$ also holds, and a minimum exists.

Proposition 1

Assuming that ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }Z^2 < \infty$, set $\eta$ based on $\sigma \in [0,\infty ]$ as follows: if $\sigma = 0$, take $\eta > 1$; if $0< \sigma < \infty$, take $\eta > 2\sigma /\pi$; if $\sigma = \infty$, take any $\eta > 0$. Under these settings, the function $\theta \mapsto {{\,\mathrm{r}\,}}_{\sigma }(Z,\theta )$ is bounded below and takes its minimum on $\mathbb {R}$. Thus, for each square-$\mu$-integrable Z, there always exists a (non-random) $\theta _{Z} \in \mathbb {R}$ such that

$$\begin{aligned} {{\,\mathrm{R}\,}}_{\sigma }(Z) = \theta _{Z} + \eta {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }\left( Z-\theta _{Z}\right) . \end{aligned}$$

(6)

Furthermore, when $\sigma > 0$, this minimum $\theta _{Z}$ is unique.

Remark 2

(Mean-median interpolation) In order to ensure that risk modulation via $\sigma \in [0,\infty ]$ smoothly transitions from a median-centric ($\sigma = 0$ case) to a mean-centric ($\sigma = \infty$ case) location, the parameter $\eta$ plays a key role. Noting that for any $u \in \mathbb {R}$, for $\rho$ defined by (3) we have $2\sigma ^2 \rho (u/\sigma ) \rightarrow u^2$ as $\sigma \rightarrow \infty$, and thus for large values of $\sigma > 0$ it is natural to set $\eta = 2\sigma ^2$. On the other end of the spectrum, since $\sigma \log (1+(u/\sigma )^2) \rightarrow 0_{+}$ whenever $\sigma \rightarrow 0_{+}$, it is thus natural to set $\eta = \sigma /{{\,\mathrm{atan}\,}}(\infty ) = 2\sigma /\pi$ when $\sigma > 0$ is small. Strictly speaking, in light of the conditions in Proposition 1, to ensure ${{\,\mathrm{R}\,}}_{\sigma }$ is finite one should take $\eta > 2\sigma /\pi$.

What can we say about our risk functions ${{\,\mathrm{R}\,}}_{\sigma }$ in terms of more traditional statistical risk properties? The form of ${{\,\mathrm{R}\,}}_{\sigma }$ given in (6) has a simple interpretation as a weighted sum of “location” and “deviation” terms. In the statistical risk literature, the seminal work of Artzner et al. (1999) gives an axiomatic characterization of location-based risk functions that can be considered coherent, while Rockafellar et al. (2006) characterize functions which capture the intuitive notion of “deviation,” and establish a lucid relationship between coherent risks and their deviation class. The following result describes key properties of the proposed risk functions, in particular highlighting the fact that while our location terms are monotonic, our risk functions are non-traditional in that they are non-monotonic.

Proposition 3

(Non-monotonic risk functions) Let $\mathcal {Z}$ be a Banach space of square-$\mu$-integrable functions. For any $\sigma \in [0,\infty ]$, let $\eta > 0$ be set as in Proposition 1. Then, the functions ${{\,\mathrm{r}\,}}_{\sigma }:\mathcal {Z}\times \mathbb {R}\rightarrow \mathbb {R}$ and ${{\,\mathrm{R}\,}}_{\sigma }:\mathcal {Z}\rightarrow \mathbb {R}$ satisfy the following properties:

• Both ${{\,\mathrm{r}\,}}_{\sigma }$ and ${{\,\mathrm{R}\,}}_{\sigma }$ are continuous, convex, and sub-differentiable.

• The location in (6) is monotonic (i.e., $Z_1 \le Z_2$ implies $\theta _{Z_1} \le \theta _{Z_2}$) and translation-equivariant (i.e., $\theta _{Z+a} = \theta _{Z} + a$ for any $a \in \mathbb {R}$), for any $0 < \sigma \le \infty$.

• The deviation in (6) is non-negative and translation-invariant, namely for any $a \in \mathbb {R}$, we have ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z+a-\theta _{Z+a}) = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z-\theta _{Z})$, for any $0 < \sigma \le \infty$.

• The risk ${{\,\mathrm{R}\,}}_{\sigma }$ is not monotonic, i.e., $\mu \{Z_1 \le Z_2\}=1$ need not imply ${{\,\mathrm{R}\,}}_{\sigma }(Z_1) \le {{\,\mathrm{R}\,}}_{\sigma }(Z_2)$.

In particular, the risk $h \mapsto {{\,\mathrm{R}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h))$ need not be convex, even if ${{\,\mathrm{L}\,}}(\cdot )$ is.

Remark 4

Since our risk function ${{\,\mathrm{R}\,}}_{\sigma }$ is not monotonic, standard results in the literature on optimizing generalized risks do not apply here. We remark that our proposed risk class does not appear among the comprehensive list of examples given in the works of Ruszczyński and Shapiro (2006, 2006b), aside from the special case of $\sigma = \infty$ with $\eta = 1$. While the continuity and sub-differentiability of any risk function which is convex and monotonic is well-known for a large class of Banach spaces (Ruszczyński and Shapiro 2006, Sec. 3), in Proposition 3 we obtain such properties without monotonicity by using square-$\mu$-integrability combined with properties of our function class $\rho _{\sigma }$.

Since our principal interest is the case where $Z = {{\,\mathrm{L}\,}}(h)$, the key takeaways from this section are that while the proposed risk $h \mapsto {{\,\mathrm{R}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h))$ is well-defined and easy to estimate given a random sample ${{\,\mathrm{L}\,}}_1(h),\ldots ,{{\,\mathrm{L}\,}}_n(h)$, the learning task is non-trivial since ${{\,\mathrm{R}\,}}_{\sigma }({{\,\mathrm{L}\,}}(\cdot ))$ is not differentiable (and thus non-smooth) when $\sigma = 0$, and for any $\sigma \in [0,\infty ]$ need not be convex, even when the underlying loss is both smooth and convex. Fortunately, smoothness properties of the losses typically used in machine learning can be leveraged to overcome these technical barriers, opening a path towards learning guarantees for practical algorithms, which is the topic of Sect. 3.

2.3 Strengths and limitations

Before diving further into the analysis of learning algorithms in the next section, let us pause for a moment to consider the following important question: when should we use the proposed risk class over more traditional alternatives? In addition, what kind of limitations or tradeoffs are faced when using this risk class? In the following paragraphs we attempt to provide an initial answer to these questions, in the context of traditional ERM and the alternative risk functions discussed in the literature review of Sect. 1.

2.3.1 Flexible control over deviations

The most obvious feature of the risk class defined in (4)–(5) is that it offers significant control over how we penalize deviations in the loss distribution. Unlike traditional ERM which simply requires that we minimize the location ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }{{\,\mathrm{L}\,}}(h)$, the proposed risk can only be made small when both the location and deviations are sufficiently small. It is well known that encouraging the (test) loss distribution to have small variance yields sharper bounds on the expected test loss than are available with naive ERM (Maurer and Pontil 2009). Furthermore, loss deviations are deeply linked to notions of fairness in machine learning (Williamson and Menon 2019), where an explicit design decision is made to ensure performance is similar across sensitive features (such as age, race, or gender), potentially at the cost of a larger expected loss. The alternative risks considered in this line of research are characterized by risks that add a deviation term to the expected loss ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }{{\,\mathrm{L}\,}}(h)$ (Hashimoto et al. 2018), and thus are always at least as sensitive to the loss distribution tails as the mean itself is. On the other hand, our deviation penalty based on $\sigma$ and $\rho$ can be used to enforce fairness with significant flexibility over the influence that errant observations have, since the location term is not fixed to the mean, but rather determined by the $\rho$ and $\sigma$ setting that we use; e.g., by taking $\sigma \rightarrow 0$ we obtain a location close to the median (often much lower than the mean), with deviations measured using a function that is insensitive to outliers. Please see Sect. 4 for empirical evidence that our risk class can be effectively used to control test loss deviations.

2.3.2 Symmetry

Another important feature of the risk class that we study here is the bidirectional nature of the function $\rho$ used to measure deviations. This is in stark contrast with existing alternative risk classes such as CVaR, entropic risk, and other so-called “optimal certainty equivalent” risks (Lee et al. 2020), as well as distributionally robust optimization (DRO) risks (Namkoong and Duchi 2016; Zhai et al. 2021), which all place a strong emphasis on the loss tails on the upside, while downplaying or completely ignoring tails on the downside. This difference becomes important for losses that are unbounded below and can take on negative values, such as in logistic regression or for more general negative log-likelihood minimization. When the loss distribution (during training) is asymmetric with heavy tails on the downside, risks such as CVaR will provide a much smaller penalty than our risk class, which by design picks up on deviations in both directions. This can be expected to encourage greater symmetry in the test loss distribution, a phenomenon that we have almost observed empirically (e.g., Fig. 4).

2.3.3 Drawbacks and workarounds

One of the key limitations to our approach is that the risk class proposed does not preserve convexity when the underlying loss ${{\,\mathrm{L}\,}}(h)$ is convex in h. One obvious limitation is that analysis of learning algorithms cannot in general yield (global) excess risk bounds, but rather must be limited to either analysis centered around an arbitrary local minimum or global analysis of stationarity (see Sect. 3 for more details). Another side to this is computational. For extremely computationally intensive tasks where production-class convex solvers are an essential ingredient, our risk class cannot be used as-is. One natural work-around is to replace $\rho (\cdot )$ with $\rho ((\cdot )_{+})$, which sacrifices the aforementioned symmetry of the deviation measure in exchange for monotonicity and convexity, while still retaining flexible control over the influence of tails on the upside. On the other hand, a great deal of modern machine learning applications are built upon non-linear models (e.g., most neural networks) which involve ${{\,\mathrm{L}\,}}(h)$ that is non-convex in h to begin with, so the drawbacks discussed here really only arise within the context of (large production-grade) linear models.

3 Learning algorithm analysis

Thus far, we have only been concerned with ideal quantities ${{\,\mathrm{R}\,}}_{\sigma }$ and ${{\,\mathrm{r}\,}}_{\sigma }$ used to define the ultimate formal goal of learning. In practice, the learner will only have access to noisy, incomplete information. In this work, we focus on iterative algorithms based on stochastic gradients, largely motivated by their practical utility and ubiquity in modern machine learning applications. For the rest of the paper, we overload our risk definitions to enhance readability, writing ${{\,\mathrm{r}\,}}_{\sigma }(h,\theta ) :={{\,\mathrm{r}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h),\theta )$ and ${{\,\mathrm{R}\,}}_{\sigma }(h) :={{\,\mathrm{R}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h))$. First note that we can break down the underlying joint objective as ${{\,\mathrm{r}\,}}_{\sigma }(h,\theta ) = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }(f_2 \circ F_1)(h,\theta )$, where we have defined

$$\begin{aligned} F_1(h,\theta ) :=({{\,\mathrm{L}\,}}(h),\theta ), \qquad f_2(u,\theta ) :=\theta + \eta \rho _{\sigma }(u-\theta ). \end{aligned}$$

(7)

From the point of view of the probability space $(\Omega ,\mathcal {F},\mu )$, the function $F_1$ is random, whereas $f_2$ is deterministic; our use of upper- and lower-case letters is just meant to emphasize this. Given some initial value $(h_0,\theta _0) \in \mathcal {H}\times \mathbb {R}$, one naively hopes to construct an efficient stochastic gradient algorithm using the update

$$\begin{aligned} (h_{t+1},\theta _{t+1})&= {{\,\mathrm{\Pi }\,}}_{C} \left[ (h_t,\theta _t) - \alpha _{t} G_t \right] , \end{aligned}$$

(8)

where $\alpha _t > 0$ is a step-size parameter, ${{\,\mathrm{\Pi }\,}}_{C}[\cdot ]$ denotes projection to some set $C \subset \mathcal {H}\times \mathbb {R}$, and the stochastic feedback $G_t$ is just a composition of sub-gradients, namely

$$\begin{aligned} G_t&\in \partial f_2({{\,\mathrm{L}\,}}(h_t),\theta _t) \circ \partial F_1(h_t,\theta _t). \end{aligned}$$

(9)

We call this approach “naive” since it is exactly what we would do if we knew a priori that the underlying objective was convex and/or smooth.² The precise learning algorithm studied here is summarized in Algorithm 1. Fortunately, as we describe below, this naive procedure actually enjoys lucid non-asymptotic guarantees, on par with the smooth case.

3.1 How to measure algorithm performance?

Before stating any formal results, we briefly discuss the means by which we evaluate learning algorithm performance. Since the sequence $({{\,\mathrm{R}\,}}_{\sigma }(h_t))$ cannot be controlled in general, a more tractable problem is that of finding a stationary point of ${{\,\mathrm{r}\,}}_{\sigma }$, namely any $(h^{*},\theta ^{*})$ such that $0 \in \partial {{\,\mathrm{r}\,}}_{\sigma }(h^{*},\theta ^{*})$. However, it is not practical to analyze ${{\,\mathrm{dist}\,}}(0;\partial {{\,\mathrm{r}\,}}_{\sigma }(h_t,\theta _t))$ directly, due to a lack of continuity. Instead, we consider a smoothed version of ${{\,\mathrm{r}\,}}_{\sigma }$:

$$\begin{aligned} {{\,\mathrm{\widetilde{r}}\,}}_{\sigma ,\beta }(h,\theta ) :=\inf _{h^{\prime },\theta ^{\prime }} \left[ {{\,\mathrm{r}\,}}_{\sigma }(h^{\prime },\theta ^{\prime }) + \frac{1}{2\beta }\Vert (h,\theta )-(h^{\prime },\theta ^{\prime })\Vert ^{2} \right] . \end{aligned}$$

(10)

This is none other than the Moreau envelope of ${{\,\mathrm{r}\,}}_{\sigma }$, with weighting parameter $\beta > 0$. A familiar concept from convex analysis on Hilbert spaces (Bauschke and Combettes 2017, Ch. 12 and 24), the Moreau envelope of non-smooth functions satisfying weak convexity properties has recently been shown to be a very useful metric for evaluating stochastic optimizers (Davis and Drusvyatskiy 2019; Drusvyatskiy and Paquette 2019). Our basic performance guarantees will first be stated in terms of the gradient of the smoothed function ${{\,\mathrm{\widetilde{r}}\,}}_{\sigma ,\beta }$. We will then relate this to the joint risk ${{\,\mathrm{r}\,}}_{\sigma }$ and subsequently the risk ${{\,\mathrm{R}\,}}_{\sigma }$.

3.2 Guarantees based on joint risk minimization

Within the context of the stochastic updates characterized by (8)–(9), we consider the case in which $\mathcal {H}$ is any Hilbert space. All Hilbert spaces are reflexive Banach spaces, and the stochastic sub-gradient $G_t \in (\mathcal {H}\times \mathbb {R})^{*}$ (the dual of $\mathcal {H}\times \mathbb {R}$) can be uniquely identified with an element of $\mathcal {H}\times \mathbb {R}$, for which we use the same notation $G_t$. Denoting the partial sequence $G_{[t]} :=(G_0,\ldots ,G_t)$, we formalize our assumptions as follows:

• A1. For all $h \in \mathcal {H}$, the random loss ${{\,\mathrm{L}\,}}(h)$ is square-$\mu$-integrable, locally Lipschitz, and weakly $\lambda$-smooth, with a gradient satisfying ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }|{{\,\mathrm{L}\,}}^{\prime }(h;\cdot ) |^{2} < \infty$.

• A2. $\mathcal {H}$ is a Hilbert space, and $C \subset \mathcal {H}\times \mathbb {R}$ is a closed convex set.

• A3. The feedback (9) satisfies ${{\,\mathrm{\mathbf {E}}\,}}[G_t \,\vert \,G_{[t-1]}] = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }G_t$ for all $t > 0$.³

• A4. For some $0< \kappa < \infty$, the second moments are bounded as ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }\Vert G_t\Vert ^{2} \le \kappa ^{2}$ for all t.

The following is a performance guarantee for Algorithm 1 in terms of the smoothed joint risk.

Theorem 5

(Nearly-stationary point of smoothed objective) If $0< \sigma < \infty$, set smoothing parameter $\gamma = (1+\eta \pi /(2\sigma ))\max \{1,\lambda \}$. Otherwise, if $\sigma = 0$, set $\gamma = (1+\eta )\max \{1,\lambda \}$. Under these $\sigma$-dependent settings and assumptions A1–A4, let $(\overline{h}_{[n]},\overline{\theta }_{[n]})$ denote the output of Algorithm 1, with ${{\,\mathrm{r}\,}}_{C}^{*} :=\inf \{{{\,\mathrm{r}\,}}_{\sigma }(h,\theta ): (h,\theta ) \in C\}$ denoting the minimum over the feasible set and $\Delta _0 :={{\,\mathrm{\widetilde{r}}\,}}_{\sigma ,\beta }(h_0,\theta _0) - {{\,\mathrm{r}\,}}_{C}^{*}$ denoting the initialization error. Then, for any choice of $n>1$, $\eta > 0$, and $\beta < 1/\gamma$, we have that

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}\Vert {{\,\mathrm{\widetilde{r}}\,}}_{\sigma ,\beta }^{\prime }(\overline{h}_{[n]},\overline{\theta }_{[n]})\Vert ^{2} \le \left( \frac{1}{1-\beta \gamma }\right) \frac{\Delta _0 + \gamma \kappa ^{2}\sum _{t=0}^{n-1}\alpha _{t}^{2}/2}{\sum _{t=0}^{n-1}\alpha _t}, \end{aligned}$$

where expectation is taken over all the feedback $G_{[n-1]}$.

Remark 6

(Sample complexity) Let us briefly describe a direct take-away from Theorem 5. If $\Delta _0$, $\gamma$, and $\kappa$ are known (upper bounds will of course suffice), then constructing step sizes as $\alpha _t^2 \ge \Delta _0/(n\gamma \kappa ^2)$, if we set $\beta = 1/(2\gamma )$, it follows immediately that

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}\Vert {{\,\mathrm{\widetilde{r}}\,}}_{\sigma ,\beta }^{\prime }(\overline{h}_{[n]},\overline{\theta }_{[n]})\Vert ^2 \le \sqrt{\frac{2\gamma \kappa ^{2}\Delta _0}{n}}. \end{aligned}$$

Fixing some desired precision level of $\sqrt{{{\,\mathrm{\mathbf {E}}\,}}\Vert {{\,\mathrm{\widetilde{r}}\,}}_{\sigma ,\beta }^{\prime }(\overline{h}_{[n]},\overline{\theta }_{[n]})\Vert ^2} \le \varepsilon$, the sample complexity is $\mathcal {O}(\varepsilon ^{-4})$. This matches guarantees available in the smooth (but non-convex) case (Ghadimi and Lan 2013), and suggests that the “naive” strategy implemented by Algorithm 1 in fact comes with a clear theoretical justification.

3.3 Implications in terms of the original objective

The results described in Theorem 5 and Remark 6 are with respect to a smoothed version of the joint risk function ${{\,\mathrm{r}\,}}_{\sigma }$. Linking these facts to insights in terms of the original proposed risk ${{\,\mathrm{R}\,}}_{\sigma }$ can be done as follows. Assuming we take $n \ge 2\gamma \kappa ^{2}\Delta _0/\varepsilon ^{4}$ to achieve the $\varepsilon$-precision discussed in Remark 6, the immediate conclusion is that the algorithm output is $(\varepsilon /2\gamma )$-close to a $\varepsilon$-nearly stationary point of ${{\,\mathrm{r}\,}}_{\sigma }$. More precisely, we have that there exists an ideal point $(h_{n}^{*},\theta _{n}^{*})$ such that

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}\left[ {{\,\mathrm{dist}\,}}\left( 0;\partial {{\,\mathrm{r}\,}}_{\sigma }(h_{n}^{*},\theta _{n}^{*})\right) \right] \le \varepsilon , \text { and } {{\,\mathrm{\mathbf {E}}\,}}\left\| (\overline{h}_{[n]},\overline{\theta }_{[n]})-(h_{n}^{*},\theta _{n}^{*}) \right\| = \frac{\varepsilon }{2\gamma }. \end{aligned}$$

(11)

The above fact follows from basic properties of the Moreau envelope (cf. Appendix 2.4). These non-asymptotic guarantees of being close to a “good” point extend to the function values of the risk ${{\,\mathrm{R}\,}}_{\sigma }$ since we are close to a candidate $h_{n}^{*}$ whose risk value can be no worse than

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}\left[ {{\,\mathrm{R}\,}}_{\sigma }(h_{n}^{*})\right] \le {{\,\mathrm{\mathbf {E}}\,}}\left[ {{\,\mathrm{r}\,}}_{\sigma }(h_{n}^{*},\theta _{n}^{*})\right] \le {{\,\mathrm{\mathbf {E}}\,}}\left[ {{\,\mathrm{r}\,}}_{\sigma }(\overline{h}_{[n]},\overline{\theta }_{[n]})\right] . \end{aligned}$$

We remark that these learning guarantees hold for a class of risks that are in general non-convex and need not even be differentiable, let alone satisfy smoothness requirements.

3.4 Key points in the proof of Theorem 5

Here we briefly highlight the key sub-results involved in proving Theorem 5; please see Appendix 3.2 for all the details. The key structure that we require is a smooth loss, reflected in assumption A1. This along with the Lipschitz property of our function $\rho _{\sigma }$ for all $0 \le \sigma < \infty$ allows us to prove that the underlying objective ${{\,\mathrm{r}\,}}_{\sigma }$ is weakly convex, where $\mathcal {H}$ can be any Banach space (Proposition 12); this generalizes a result of (Drusvyatskiy and Paquette 2019, Lem. 4.2) from Euclidean space to any Banach space. This alone is not enough to obtain the desired result. Note that the assumption A3 is very weak, and trivially satisfied in most traditional machine learning settings (e.g., where losses are based on a sequence of iid data points). The question of whether the feedback is unbiased or not, i.e., whether ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }G_t$ is in the sub-differential of ${{\,\mathrm{r}\,}}_{\sigma }$ at step t or not, is something that needs to be formally verified. In Proposition 14 we show that as long as the gradient has a finite expectation, this indeed holds for the feedback generated by (9), when $\mathcal {H}$ is any Banach space. With the two key properties of a weakly convex objective and unbiased random feedback in hand, we can leverage the techniques used in (Davis and Drusvyatskiy 2019, Thm. 3.1) for proximal stochastic gradient methods applied to weakly convex functions on $\mathbb {R}^{d}$, extending their core argument to the case of any Hilbert space. Combining this technique with the proof of weak convexity and unbiasedness lets us obtain Theorem 5.

4 Empirical analysis

In this section we introduce representative results for a series of experiments designed to investigate the quantitative and qualitative repercussions of modulating the underlying risk function class. We have prepared a GitHub repository that includes code for both re-creating the empirical tests and pre-processing all the benchmark data.⁴

4.1 Sanity check in one dimension

As a natural starting point, we use a toy example to ensure that Algorithm 1 takes us where we expect to go for a particular risk setting. Consider a loss on $\mathbb {R}$ with the form ${{\,\mathrm{L}\,}}(h) = h {{\,\mathrm{L}\,}}_{\text {wide}} + (1-h){{\,\mathrm{L}\,}}_{\text {thin}}$, where ${{\,\mathrm{L}\,}}_{\text {wide}}$ and ${{\,\mathrm{L}\,}}_{\text {thin}}$ are random variables independent of h and each other. As a simple example, we use a folded Normal distribution for both, namely ${{\,\mathrm{L}\,}}_{*}=|\text {Normal}(a_{*},b_{*}^{2}) |$, where $a_{\text {wide}}=0$, $a_{\text {thin}}=2.0$, $b_{\text {wide}}=1.0$, and $b_{\text {thin}}=0.1$. For simplicity, we fix $\alpha _t = 0.001$ throughout, and each step uses a mini-batch of size 8.⁵ Regarding the risk settings, we look in particular at the case of $\sigma = \infty$, where we modify the setting of $\eta = 2^k$ over $k=0,1,\ldots ,7$. Results averaged over 100 trials are given in Fig. 2. By modifying $\eta$, we can control whether the learning algorithm “prefers” candidates whose losses have a high degree of dispersion centered around a good location, or those whose losses are well-concentrated near a weaker location.

Fig. 2

A simple toy example using ${{\,\mathrm{L}\,}}(h) = h {{\,\mathrm{L}\,}}_{\text {wide}} + (1-h){{\,\mathrm{L}\,}}_{\text {thin}}$. Trajectories shown are the sequence $(h_t)$ generated by running (8) on $\mathbb {R}^{2}$, with $h_0 = 0.5$ and $\theta _0 = 0.5$, averaged over all trials. Densities of ${{\,\mathrm{L}\,}}_{\text {wide}}$ (red) and ${{\,\mathrm{L}\,}}_{\text {thin}}$ (blue) are also plotted, with additional details in the main text (Color figure online)

4.2 Impact of risk choice on linear regression

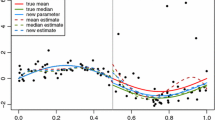
Next we consider how the key choice of $\sigma$ (and thus the underlying risk ${{\,\mathrm{R}\,}}_{\sigma }$) plays a role on the behavior of Algorithm 1. As another simple, yet more traditional example, consider linear regression in one dimension, where $Y = w_{0}^{*} + w_{1}^{*}X + \epsilon$, where X and $\epsilon$ are independent zero-mean random variables, and $(w_{0}^{*},w_{1}^{*}) \in \mathbb {R}^{2}$ are unknown to the learner. Using squared error ${{\,\mathrm{L}\,}}(h) = (Y - h(X))^{2}$, we run Algorithm 1 again with mini-batches of size 8 and $\alpha _t = 0.001$ fixed throughout, over a range of $\sigma \in [0, \infty ]$ settings, for the same number of iterations as in the previous experiment. The initial value $(h_0,\theta _0)$ is initialized at zero plus uniform noise on $[-0.05,0.05]$. We also consider multiple noise distributions; as a concrete example, letting $N = \text {Normal}(0,(0.8)^2)$, we consider both $\varepsilon = N$ (Normal case) and $\varepsilon = \mathrm {e}^{N} - {{\,\mathrm{\mathbf {E}}\,}}\mathrm {e}^{N}$ (log-Normal case). In Fig. 3, we plot the learned regression lines (averaged over 100 trials) for each choice of $\sigma$ and each noise setting. By modulating the target risk function, we can effectively choose between a self-imposed bias (smaller slope, lower intercept here), and a sensitivity to outlying values.

Fig. 3

Learned regression lines (solid; colors denote $\sigma \in [0,\infty ]$) are plotted along with the true model $(w_{0}^{*},w_{1}^{*}) = (1.0,1.0)$ (dashed; black). Histograms are of independent samples of $w_{0}^{*} + \varepsilon$. The left plots are the Normal case, and right plots are the log-Normal case

4.3 Tests using real-world data

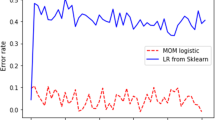
Finally, we consider an application to some well-known benchmark datasets for classification. At a high level, we run Algorithm 1 for multi-class logistic regression for 10 independent trials, where in each trial we randomly shuffle and re-split each full dataset (88% training, 12% testing), and randomly re-initialize the model weights identically to the previous paragraph, again with mini-batches of size 8, and step sizes fixed to $\alpha _t = 0.01/\sqrt{d}$, where d is the number of free parameters. Additional background on the datasets is given in Appendix 6. The key question of interest is how the test loss distribution changes as we modify the learner’s feedback to optimize a range of risks ${{\,\mathrm{R}\,}}_{\sigma }$. In Fig. 4, we see a stark difference between doing traditional empirical risk minimization (ERM, denoted “off”) and using ${{\,\mathrm{R}\,}}_{\sigma }$-based feedback, particularly for moderately large values of $\sigma$. The logistic losses are concentrated much more tightly (visible in the bottom row histograms), and this also leads to a better classification error (visible in the top row plots), an interesting trend that we observed across many distinct datasets.

Fig. 4

Top row: average test error (zero-one loss) as a function of epochs, for four datasets and five $\sigma$ levels, plus traditional ERM (denoted “off”). Middle and bottom rows: histograms of the test error (logistic loss) incurred after the final epoch for one trial under the covtype and emnist_balanced datasets

5 Concluding remarks

Moving forward, an appealing direction is to consider risk function classes which can encode properties going beyond location and deviation, such as explicit symmetry, multi-modality, tail properties, and so forth. The hope is to develop a flexible and highly expressive framework coupled with efficient and practical algorithms with guarantees, which encodes distributional properties that are not readily captured by the current framework or traditional risk classes such as spectral risks (Khim et al. 2020).

Taking the results of this paper together as a whole, we have obtained a generalized class of risk functions and a practical class of learning algorithms, which together effectively allow the user to encode the intuitive notions of location and deviation into the learning process. Of particular note is how changing the underlying risk has a lucid impact on the outcome of learning. In Sect. 4, we empirically verified that a simple modification of the scaling parameter of the underlying risk class (changing $\sigma$) was enough to result in a salient effect on the test loss distribution, using real-world datasets and typical stochastic gradient-based learning methods. While the importance of considering more properties of the loss distribution than just the expected value has been long understood (Breiman 1999; Reyzin and Schapire 2006), the key takeaway here is that we have seen how principled algorithmic modifications can bring about interpretable and meaningful effects on the test distribution, without having to abandon formal performance guarantees.

Appendices

Appendix 1 Overview of appendix contents

Our appendix is comprised of several sections, ordered as follows:

• 2 Background and setup

• 3 Detailed proofs

• 4 Helper results

• 5 Loss example

• 6 Empirical supplement

As with the main paper, we handle theoretical topics before diving into empirical topics. Section 2 gives a very detailed background including numerous formal definitions, supporting lemmas, and discussion on results used later in the detailed proofs (Sect. 3) for the main paper’s results. Additional numerical test results are at the very end of Sect. 6.

To provide additional visual intuition for the reader, we include several figures related to $\rho$ defined in (3), $\rho _{\sigma }$ defined in (4), and the resulting risk functions. In Fig. 1 we plot $\rho$ and its derivatives, plus $\rho _{\sigma }$ for a wide variety of $\sigma \in [0,\infty ]$ values. Additional details are given in the figure caption. In Fig. 5, we show how specific choices of standard loss functions lead two different forms of the function composition $h \mapsto {{\,\mathrm{L}\,}}(h) \mapsto \eta \rho _{\sigma }({{\,\mathrm{L}\,}}(h)-\theta )$.

Fig. 5

Graphs of $h \mapsto \eta \rho _{\sigma }({{\,\mathrm{L}\,}}(h)-\theta )$, with $h \in \mathbb {R}$, over different choices of $\sigma$ and ${{\,\mathrm{L}\,}}$, with $\theta = 3.0$ fixed, and $\eta$ set as in Fig. 1. Colors correspond to $\sigma$, and each plot corresponds to a choice of ${{\,\mathrm{L}\,}}(\cdot )$. Absolute: ${{\,\mathrm{L}\,}}(h) = |h-h^{*} |$. Squared: ${{\,\mathrm{L}\,}}(h) = (h-h^{*})^{2}$. Hinge: ${{\,\mathrm{L}\,}}(h) = \max \{0,1-hh^{*}\}$. Cross-entropy: ${{\,\mathrm{L}\,}}(h) = \log (1+\exp (-hh^{*}))$. In all cases, we have fixed $h^{*} = \pi$

Appendix 2 Background and setup

1.1 2.1 Preliminaries

General notation (probability) Underlying all our analysis is a probability space $(\Omega ,\mathcal {F},\mu )$.⁶ All random variables, unless otherwise specified, will be assumed to be $\mathcal {F}$-measurable functions with domain $\Omega$. Integration using $\mu$ will be denoted by ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }Z :=\int _{\Omega }Z(\omega )\,\mu (\mathop {}\!\mathrm {d}\omega )$, and ${{\,\mathrm{\mathbf {P}}\,}}$ will be used as a generic probability function, typically representing $\mu$ itself, or the product measure induced by a sample of random variables on $(\Omega ,\mathcal {F},\mu )$. We use $\mathcal {L}_{2} :=\mathcal {L}_{2}(\Omega ,\mathcal {F},\mu )$ to denote the set of all square-$\mu$-integrable functions.⁷

General notation (normed spaces) Let $\mathcal {V}$ denote an arbitrary vector space. When we call $\mathcal {V}$ a normed (linear) space, we are referring to $(\mathcal {V},\Vert \cdot \Vert )$, where $\Vert \cdot \Vert : \mathcal {V}\rightarrow \mathbb {R}$ denotes the relevant norm. For any normed space $\mathcal {V}$, we shall denote by $\mathcal {V}^{*}$ the usual dual space of $\mathcal {V}$, namely all continuous linear functionals defined on $\mathcal {V}$. The space $\mathcal {V}^{*}$ is equipped with the norm $\Vert v^{*}\Vert :=\sup \{ v^{*}(u): \forall \,u \in \mathcal {V}, \Vert u\Vert \le 1 \}$. We shall use the notation $\langle \cdot ,\cdot \rangle$ to represent the “coupling” function between $\mathcal {V}$ and $\mathcal {V}^{*}$, that is for any $u \in \mathcal {V}$ and $v^{*} \in \mathcal {V}^{*}$, we will write $\langle u, v^{*} \rangle :=v^{*}(u)$. For any sequence $(x_n)$ of elements $x_1,x_2,\ldots \in \mathcal {V}$, we denote convergence of $(x_n)$ to some element $x^{\prime }$ by $x_n \rightarrow x^{\prime }$. When we take limits and do not specify a particular sequence, for example writing $x \rightarrow x^{\prime }$, then this refers to any sequence (of elements from $\mathcal {V}$) that converges to $x^{\prime }$. In the special case of real-valued sequences (where $\mathcal {V}\subset \mathbb {R}$), if we write $x_n \rightarrow x^{\prime }_{+}$ (respectively $x_n \rightarrow x^{\prime }_{-}$), this refers to all sequences from above (resp. below), i.e., any convergent sequence such that $x_n \ge x^{\prime }$ (resp. $x_n \le x^{\prime }$) for all n. We denote the open ball of radius $r>0$ centered at $x_0 \in \mathcal {V}$ by $B(x_0;r) :=\{x \in \mathcal {V}: \Vert x_0-x\Vert < r\}$. We denote the extended real line by $\overline{\mathbb {R}}$. On normed space $\mathcal {V}$, we denote the interior of a set $U \subset \mathcal {V}$ by ${{\,\mathrm{int}\,}}U$ (all $x \in U$ such that $B(x;\delta ) \subset U$ for some $\delta$).

General terminology On any normed linear space $\mathcal {V}$, a set $A \subset \mathcal {V}$ is said to be compact if for any sequence of elements in A, there exists a sub-sequence which converges on A. We denote the effective domain of an extended real-valued function f by ${{\,\mathrm{dom}\,}}f :=\{x: f(x) < \infty \}$. We call a convex function $f:\mathcal {V}\rightarrow \overline{\mathbb {R}}$ proper if $f > -\infty$ and ${{\,\mathrm{dom}\,}}f \ne \emptyset$. We say that f is coercive if $\Vert x\Vert \rightarrow \infty$ implies $f(x) \rightarrow \infty$.⁸ For a function $f: \mathcal {X}\rightarrow \mathcal {Y}$, with $\mathcal {X}$ and $\mathcal {Y}$ being normed spaces, we say f is (locally) Lipschitz at $x_0 \in \mathcal {X}$ if there exists $\delta > 0$ and $\lambda > 0$ such that $x_1,x_2 \in B(x_0;\delta )$ implies $\Vert f(x_1)-f(x_2)\Vert \le \lambda \Vert x_1-x_2\Vert$. We say f is $\lambda$-Lipschitz on $\mathcal {X}$ if this property holds with a common coefficient $\lambda$ for all $x_0 \in \mathcal {X}$.

Semi-continuous functions We say that a function f is lower semi-continuous⁹ (LSC) at a point x if for each $\varepsilon > 0$, there exists $\delta > 0$ such that $\Vert x - x^{\prime }\Vert < \delta$ implies $f(x^{\prime }) > f(x) - \varepsilon$. If $-g$ is LSC, then we say g is upper semi-continuous (USC). The property that f is LSC at a point x is equivalent¹⁰ to the property that for any sequence $x_n \rightarrow x$, we have

$$\begin{aligned} f(x) \le \liminf _{n \rightarrow \infty } f(x_n). \end{aligned}$$

(12)

Ordinary continuity is equivalent to being both USC and LSC, but the added generality of these weaker notions of continuity is often useful.

Differentiability We start by introducing some common notions of directional differentiability at a high level of generality.¹¹ Let $\mathcal {X}$ and $\mathcal {Y}$ be normed linear spaces, $U \subset \mathcal {X}$ an open set, and $f:\mathcal {X}\rightarrow \mathcal {Y}$ a function of interest. The radial derivative of f at $x \in U$ in direction u is defined

$$\begin{aligned} f_{r}^{\prime }(x;u) :=\lim \limits _{\alpha \rightarrow 0_{+}} \frac{f(x + \alpha u)-f(x)}{\alpha }. \end{aligned}$$

(13)

A slight modification to this gives us the (Hadamard) directional derivative of f at $x \in U$ in direction u:

$$\begin{aligned} f^{\prime }(x;u) :=\lim \limits _{(\alpha ,u^{\prime })\rightarrow (0_{+},u)} \frac{f(x + \alpha u^{\prime })-f(x)}{\alpha } \end{aligned}$$

(14)

When $f_{r}^{\prime }(x;u)$ exists for all directions u, we say that f is radially differentiable at x. Identically, when $f^{\prime }(x;u)$ exists for all directions u, we say that f is directionally differentiable at x. When the map $u \mapsto f_{r}^{\prime }(x;u)$ is continuous and linear, we say that f is Gateaux differentiable at x. When the map $u \mapsto f^{\prime }(x;u)$ is continuous and linear, we say f is Hadamard differentiable at x. If f is Hadamard differentiable, then it is Gateaux differentiable. The converse does not hold in general, but if f is Lipschitz on a neighborhood of $x \in U$, then radial differentiability and directional differentiability (at x) are equivalent.¹²

When we simply say that a function $f:\mathcal {X}\rightarrow \mathcal {Y}$ is differentiable at $x \in U$, we mean that there exists a function $f^{\prime }(x)(\cdot ):\mathcal {X}\rightarrow \mathcal {Y}$ that is linear, continuous, and which satisfies

$$\begin{aligned} \lim \limits _{\Vert u\Vert \rightarrow 0} \frac{\Vert f(x+u)-f(u)-f^{\prime }(x)(u)\Vert }{\Vert u\Vert } = 0. \end{aligned}$$

(15)

This property is often referred to as Fréchet differentiability. When f is differentiable at x, the map $f^{\prime }(x)$ is uniquely determined.¹³ In the special case where $\mathcal {Y}\subset \mathbb {R}$, the linear functional represented by $f^{\prime }(x) \in \mathcal {X}^{*}$ is called the gradient of f at x. Differentiability is also closely related to directional differentiability; if f is Gateaux differentiable on U and the map $x \mapsto f^{\prime }(x;\cdot )$ is continuous at x, then f is differentiable at x.¹⁴

Sub-differentials Let $\mathcal {V}$ be any normed linear space. If $f:\mathcal {V}\rightarrow \overline{\mathbb {R}}$ is a (proper) convex function, the sub-differential of f at $x \in {{\,\mathrm{dom}\,}}f$ is defined

$$\begin{aligned} \partial f(x)&:=\left\{ v^{*} \in \mathcal {V}^{*}: f(u)-f(x) \ge \langle u-x, v^{*} \rangle , u \in \mathcal {V}\right\} \nonumber \\&= \left\{ v^{*} \in \mathcal {V}^{*}: f^{\prime }_{r}(x;u) \ge \langle u, v^{*} \rangle , u \in \mathcal {V}\right\} . \end{aligned}$$

(16)

The second characterization of $\partial f(x)$, given using the radial derivative (13), is useful and intuitive.¹⁵ Some authors refer to this as the Moreau-Rockafellar sub-differential to emphasize the context of convex analysis.

More generally, however, if f is not convex, then the strong global property used to define the MR sub-differential is so restrictive that most interesting functions are left out. A more general notion is that of the Fréchet sub-differential.¹⁶ Denoted $\partial _{F } f(x)$, the Fréchet sub-differential of f at x is the set of all bounded linear functionals $v^{*} \in \mathcal {V}^{*}$ such that for any $\varepsilon > 0$, there exists $\delta > 0$ such that

$$\begin{aligned} \Vert x-u\Vert \le \delta \implies f(u)-f(x) \ge \langle u-x, v^{*}\rangle - \varepsilon \Vert x-u\Vert . \end{aligned}$$

(17)

This local requirement is much weaker than the condition characterizing the MR-sub-differential, and clearly we have $\partial f(x) \subset \partial _{F } f(x)$. When f is assumed to be locally Lipschitz, another class of sub-differentials is often useful. Define the Clarke directional derivative of f at x in the direction u by

$$\begin{aligned} f_{C }^{\prime }(x;u) :=\limsup _{(\alpha ,x^{\prime }) \rightarrow (0_{+},x)} \frac{f(x^{\prime } + \alpha u ) - f(x^{\prime })}{\alpha }. \end{aligned}$$

(18)

The corresponding Clarke sub-differential is defined as

$$\begin{aligned} \partial _{C } f(x) :=\{ v^{*} \in \mathcal {V}^{*}: f_{C }^{\prime }(x;u) \ge \langle u, v^{*} \rangle , u \in \mathcal {V}\}. \end{aligned}$$

(19)

In the special case where f is convex, all the sub-differentials coincide, i.e., $\partial f(x) = \partial _{F } f(x) = \partial _{C } f(x)$.¹⁷ We say that a function f is sub-differentiable at x if its sub-differential (in any sense) at x is non-empty. Finally, a remark on notation when using set-valued functions like $x \mapsto \partial _{C } f(x)$. When we write something like “we have $\langle u, \partial _{C } f(x) \rangle \ge g(u)$,” it is the same as writing “we have $\langle u, v^{*} \rangle \ge g(u)$ for all $v^{*} \in \partial _{C } f(x)$.” This kind of notation will be used frequently.

1.2 2.2 Generalized convexity

Let $\mathcal {X}$ be a normed linear space. Take an open set $U \subset \mathcal {X}$ and fix some point $x_0 \in U$. For a function $f:\mathcal {X}\rightarrow \overline{\mathbb {R}}$ and parameter $\gamma \in \mathbb {R}$, say that there exists $\delta > 0$ such that for all $x,x^{\prime } \in B(x_0;\delta )$ and $\alpha \in (0,1)$, we have

$$\begin{aligned} f(\alpha x + (1-\alpha )x^{\prime }) \le \alpha f(x) + (1-\alpha )f(x^{\prime }) + \frac{\gamma \alpha (1-\alpha )}{2}\Vert x - x^{\prime }\Vert ^{2}. \end{aligned}$$

(20)

When $\gamma \ge 0$, we say f is $\gamma$ -weakly convex at $x_0$. When $\gamma \le 0$, we say f is $(-\gamma )$ -strongly convex at $x_0$. When (20) holds for all $x_0 \in U$, we say that f is $\gamma$-weakly/strongly convex on U. The special case of $\gamma = 0$ is the traditional definition of convexity on U.¹⁸

The ability to construct a quadratic lower-bounding function for f is closely related to notions of weak/strong convexity. Consider the following condition: given $\gamma \in \mathbb {R}$, there exists $\delta > 0$ such that for all $x,x^{\prime } \in B(x_0;\delta )$ we have

$$\begin{aligned} f(x^{\prime }) \ge f(x) + \langle x^{\prime }-x, \partial _{C }f(x) \rangle - \frac{\gamma }{2}\Vert x-x^{\prime }\Vert ^{2}. \end{aligned}$$

(21)

Here $\partial _{C }f$ denotes the Clarke sub-differential of f, defined by (19). Let us assume henceforth that $\mathcal {X}$ is Banach, f is locally Lipschitz, and $\partial _{C }f(x)$ is non-empty for all $x \in U$.¹⁹ For any $\gamma \in \mathbb {R}$, it is straightforward to show that (20) $\implies$ (21) holds.²⁰ Since (21) gives us a lower bound on both f(x) and $f(x^{\prime })$ for any x and $x^{\prime }$ close enough to $x_0$, adding up the inequalities immediately implies

$$\begin{aligned} \langle x-x^{\prime }, \partial _{C }f(x) - \partial _{C }f(x^{\prime }) \rangle \ge -\gamma \Vert x-x^{\prime }\Vert ^{2}. \end{aligned}$$

(22)

When $\mathcal {X}$ is Banach and f is locally Lipschitz, it is straightforward to show that (22) $\implies$ (20) is valid.²¹ As such, for Banach spaces and locally Lipschitz functions, we have that the conditions (20), (21), and (22) are all equivalent for the general case of $\gamma \in \mathbb {R}$.

Let us consider one more closely related property on the same open set $U \subset \mathcal {X}$:

$$\begin{aligned} x&\mapsto f(x) + \frac{\gamma }{2}\Vert x\Vert ^{2} \text { is convex on } U. \end{aligned}$$

(23)

In the special case where $\mathcal {X}$ is a real Hilbert space and the norm $\Vert \cdot \Vert$ is induced by the inner product as $\Vert \cdot \Vert = \sqrt{\langle \cdot ,\cdot \rangle }$, then for any $x,x^{\prime } \in U$ and $\alpha \in \mathbb {R}$, the equality

$$\begin{aligned} \alpha \Vert x\Vert ^{2} + (1-\alpha )\Vert x^{\prime }\Vert ^{2} = \Vert \alpha x + (1-\alpha )x^{\prime }\Vert ^{2} + \alpha (1-\alpha )\Vert x-x^{\prime }\Vert ^{2} \end{aligned}$$

(24)

is easily checked to be valid.²² In this case, the equivalence (20) $\iff$ (23) follows from direct verification using (24).²³

The facts above are summarized in the following result:

Proposition 7

(Characterization of generalized convexity) Consider a function $f:\mathcal {X}\rightarrow \overline{\mathbb {R}}$ on normed linear space $\mathcal {X}$. When $\mathcal {X}$ is Banach and f is locally Lipschitz, then with respect to open set $U \subset \mathcal {X}$ we have the following equivalence:

(20) $\Leftrightarrow$ (21) $\Leftrightarrow$ (22).

When $\mathcal {X}$ is Hilbert, this equivalence extends to (23).

1.3 2.3 Function composition on normed spaces

Next we consider the properties of compositions involving functions which are smooth and/or convex. Let $\mathcal {X}$ and $\mathcal {Y}$ be normed linear spaces. Let $g: \mathcal {X}\rightarrow \mathcal {Y}$ and $h: \mathcal {Y}\rightarrow \overline{\mathbb {R}}$ be the maps used in our composition, and denote by $f :=h \circ g$ the composition, i.e., $f(x) = h(g(x))$ for each $x \in \mathcal {X}$. Our goal will be to present sufficient conditions for the composition f to be weakly convex on an open set $U \subset \mathcal {X}$, in the sense of (20). If we assume simply that h is convex, fixing any point $x_0 \in U$ such that h is sub-differentiable at $g(x_0)$, it follows that for any choice of $x \in \mathcal {X}$ we have

$$\begin{aligned} f(x) = h(g(x))&\ge h(g(x_0)) + \langle g(x)-g(x_0), \partial h(g(x_0)) \rangle . \end{aligned}$$

(25)

Let us further assume that h is $\lambda _0$-Lipschitz, and g is smooth in the sense that it is differentiable on U and the map $x \mapsto g^{\prime }(x)$ is $\lambda _1$-Lipschitz. For readability, denote the derivative $g^{\prime }(x_0): \mathcal {X}\rightarrow \mathcal {Y}$ by $g_{0}^{\prime }(\cdot ) :=g^{\prime }(x_0)(\cdot )$. Taking any choice of $v_0 \in \partial h(g(x_0))$, we can write

$$\begin{aligned} \langle g(x)-g(x_0), v_0 \rangle&= \langle g_{0}^{\prime }(x-x_0), v_0 \rangle + \langle g(x)-g(x_0)-g_{0}^{\prime }(x-x_0), v_0 \rangle \nonumber \\&\ge \langle g_{0}^{\prime }(x-x_0), v_0 \rangle - \Vert g(x)-g(x_0)-g_{0}^{\prime }(x-x_0)\Vert \Vert v_0\Vert \nonumber \\&\ge \langle g_{0}^{\prime }(x-x_0), v_0 \rangle - \frac{\lambda _1}{2}\Vert x-x_0\Vert ^{2}\Vert v_0\Vert \nonumber \\&\ge \langle g_{0}^{\prime }(x-x_0), v_0 \rangle - \frac{\lambda _0\lambda _1}{2}\Vert x-x_0\Vert ^{2} \end{aligned}$$

(26)

The first inequality follows from the definition of the norm for linear functionals and the fact that $\partial h(g(x_0)) \subset \mathcal {Y}^{*}$. The second inequality follows from a Taylor approximation for Banach spaces (Proposition 16), using the smoothness of g. The final equality follows from the fact that for convex functions, the Lipschitz coefficient implies a bound on all sub-gradients, see (47). To deal with the remaining term, note that we can write

$$\begin{aligned} \langle g_{0}^{\prime }(x-x_0), \partial h(g(x_0)) \rangle = \langle x-x_0, (g_{0}^{\prime })^{*}(\partial h(g(x_0))) \rangle = \langle x-x_0, \partial h(g(x_0)) \circ g_{0}^{\prime } \rangle . \end{aligned}$$

(27)

To explain the notation here, we use $(\cdot )^{*}$ to denote the adjoint, namely $A^{*}(y^{*}) :=y^{*} \circ A$, induced by any continuous linear map $A: \mathcal {X}\rightarrow \mathcal {Y}$, defined for each $y^{*} \in \mathcal {Y}^{*}$.²⁴ The special case we have considered here is where $Au = g_{0}^{\prime }(u)$, noting that differentiability means that the map $u \mapsto g_{0}^{\prime }(u)$ is continuous and linear. Recalling the desired form of (21), we need to establish a connection with $\partial _{C }f(x_0)$. If we further assume that g is locally Lipschitz, then we have

$$\begin{aligned} \partial _{C }f(x_0) \subset \partial _{C }h(g(x_0)) \circ g_{0}^{\prime } = \partial h(g(x_0)) \circ g_{0}^{\prime }, \end{aligned}$$

(28)

where the equality follows from the coincidence of sub-differentials in the convex case, and the key inclusion follows from direct application of a generalized chain rule.²⁵ Taking these facts together yields the following result.

Proposition 8

(Weak convexity for composite functions) Let $\mathcal {X}$ and $\mathcal {Y}$ be Banach spaces. Let $g:\mathcal {X}\rightarrow \mathcal {Y}$ be locally Lipschitz and $\lambda _1$-smooth on an open set $U \subset \mathcal {X}$. Let $h:\mathcal {Y}\rightarrow \overline{\mathbb {R}}$ be convex and $\lambda _0$-Lipschitz on $g(U) \subset \mathcal {Y}$. Furthermore, let $g(U) \subset {{\,\mathrm{dom}\,}}h$. Then, the composite function $f :=h \circ g$ is $\gamma$-weakly convex on U, for $\gamma = \lambda _0\lambda _1$.

Proof

The desired result just requires us to piece together the key facts we have outlined in the main text. Local Lipschitz properties for g and h imply that f is locally Lipschitz, and thus $\partial _{C }f(x_0) \ne \emptyset$ for all $x_0 \in U$. Using (28), we have that $\partial h(g(x_0)) \ne \emptyset$ as well. With this in mind, linking up (25)–(27), under the assumptions stated, for each $x,x_0 \in U$ we have

$$\begin{aligned} f(x) \ge f(x_0) + \langle x-x_0, \partial h(g(x_0)) \circ g_{0}^{\prime } \rangle - \frac{\lambda _0\lambda _1}{2}\Vert x-x_0\Vert ^{2}. \end{aligned}$$

(29)

Using the inclusion (28) with (29), we have (21) for $\gamma = \lambda _0\lambda _1$, and the desired result holds since (21) implies (20). $\square$

Remark 9

We note that Proposition 8 extends a result of (Drusvyatskiy and Paquette 2019, Lem. 4.2) from the case where $\mathcal {X}$ and $\mathcal {Y}$ are finite-dimensional Euclidean spaces, to the general Banach space setting considered here. For the classical case of Euclidean spaces, exact chain rules are well-known (Rockafellar and Wets 1998, Ch. 10.B).

1.4 2.4 Proximal maps of weakly convex functions

For normed linear space $\mathcal {X}$ and function $f:\mathcal {X}\rightarrow \overline{\mathbb {R}}$, the Moreau envelope ${{\,\mathrm{env}\,}}_{\beta }f$ and proximal mapping (or proximity operator) ${{\,\mathrm{prox}\,}}_{\beta }f$ are respectively defined for each $x \in \mathcal {X}$ as follows:

$$\begin{aligned} {{\,\mathrm{env}\,}}_{\beta }f(x)&:=\inf \left\{ f(x^{\prime }) + \frac{1}{2\beta }\Vert x-x^{\prime }\Vert ^{2} : x^{\prime } \in \mathcal {X}\right\} \end{aligned}$$

(30)

$$\begin{aligned} {{\,\mathrm{prox}\,}}_{\beta }f(x)&:=\mathop {\mathrm{arg\,min}}\limits _{x^{\prime } \in \mathcal {X}} \left[ f(x^{\prime }) + \frac{1}{2\beta }\Vert x-x^{\prime }\Vert ^{2} \right] . \end{aligned}$$

(31)

Here $\beta > 0$ is a parameter. In the case where f is convex, the basic properties of the proximal map and envelope are well-understood, particularly when $\mathcal {X}$ is a Hilbert space.²⁶ These insights extend readily to the setting of weak convexity. Under the assumption that $\mathcal {X}$ is Hilbert, let f be $\gamma$-weakly convex on $\mathcal {X}$. Trivially we can write

$$\begin{aligned} f(x^{\prime }) + \frac{1}{2\beta }\Vert x-x^{\prime }\Vert ^{2} = \left( f(x^{\prime }) + \frac{\gamma }{2}\Vert x-x^{\prime }\Vert ^{2} \right) + \frac{1}{2}\left( \frac{1}{\beta }-\gamma \right) \Vert x-x^{\prime }\Vert ^{2}. \end{aligned}$$

If we write $f_{\gamma ,x}(u) :=f(u) + (\gamma /2)\Vert x-u\Vert ^{2}$ and $\beta _\gamma :=(\beta ^{-1}-\gamma )^{-1}$ for readability, then as long as $\beta _\gamma > 0$ we have for all $x \in \mathcal {X}$ that ${{\,\mathrm{env}\,}}_{\beta }f(x) = {{\,\mathrm{env}\,}}_{\beta _\gamma }f_{\gamma ,x}(x)$ and ${{\,\mathrm{prox}\,}}_{\beta }f(x) = {{\,\mathrm{prox}\,}}_{\beta _\gamma }f_{\gamma ,x}(x)$. By leveraging Proposition 7 under the Hilbert space assumption, we have that for any $x \in \mathcal {X}$, the function $f_{\gamma ,x}(\cdot )$ is convex. This means that as long as $\beta _\gamma > 0$, namely whenever $\gamma < \beta ^{-1}$, all the standard results available for the case of convex functions can be brought to bear on the problem.²⁷ Of particular importance to us is the fact that when f is LSC and $\gamma$-weakly convex, the Moreau envelope is differentiable, with gradient

$$\begin{aligned} ({{\,\mathrm{env}\,}}_{\beta }f)^{\prime }(x) = \frac{1}{\beta }\left( x - {{\,\mathrm{prox}\,}}_{\beta }f(x) \right) , \end{aligned}$$

(32)

well-defined for all $\beta < \gamma ^{-1}$ and $x \in \mathcal {X}$.²⁸ We will be interested in finding stationary points of f, namely those $x \in \mathcal {X}$ such that $0 \in \partial _{C }f(x)$. From the basic properties of the envelope and proximal mapping, for $\gamma$-weakly convex f we have

$$\begin{aligned} {{\,\mathrm{dist}\,}}(0;\partial _{C }f({{\,\mathrm{prox}\,}}_{\beta }f(x))) \le \Vert ({{\,\mathrm{env}\,}}_{\beta }f)^{\prime }(x)\Vert . \end{aligned}$$

(33)

That is, for any point $x \in \mathcal {X}$, the point ${{\,\mathrm{prox}\,}}_{\beta }f(x) \in \mathcal {X}$ is approximately stationary. The degree of precision is controlled by the gradient of ${{\,\mathrm{env}\,}}_{\beta }f$ evaluated at x. In addition, it follows immediately from (32) that

$$\begin{aligned} \Vert x - {{\,\mathrm{prox}\,}}_{\beta }f(x)\Vert = \beta \Vert ({{\,\mathrm{env}\,}}_{\beta }f)^{\prime }(x)\Vert . \end{aligned}$$

(34)

Since one trivially also has $f({{\,\mathrm{prox}\,}}_{\beta }f(x)) \le f(x)$, the norm of the gradient of ${{\,\mathrm{env}\,}}_{\beta }f$ evaluated at x also tells us how far we are from a point (namely ${{\,\mathrm{prox}\,}}_{\beta }f(x) \in \mathcal {X}$) which is no worse than x in terms of function value. These basic facts directly motivate the use of the Moreau envelope norm to quantify algorithm performance.²⁹

Appendix 3 Detailed proofs

1.1 3.1 Proofs for Sect. 2

Lemma 10

(Lower semi-continuity) Let $\mathcal {Z}$ be a linear space of $\mathcal {F}$-measurable random variables, and let $\rho :\mathbb {R}\rightarrow \overline{\mathbb {R}}$ be any non-negative LSC function that is Borel-measurable. Then we have that the functional $(Z,\theta ) \mapsto {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho (Z-\theta )$ is also LSC.

Proof of Lemma 10

Let $(Z_k)$ and $(\theta _k)$ respectively be convergent sequences on $\mathcal {Z}$ and $\mathbb {R}$. As we take $k \rightarrow \infty$, say $Z_k \rightarrow Z_{*}$ pointwise, for some $Z \in \mathcal {Z}$, and $\theta _k \rightarrow \theta _{*} \in \mathbb {R}$. Since by assumption $\rho$ is LSC on $\mathbb {R}$, using (12) we have (again, pointwise) that

$$\begin{aligned} \rho \left( Z_{*}-\theta _{*}\right) \le \liminf _{k \rightarrow \infty } \rho \left( Z_k-\theta _k\right) . \end{aligned}$$

Writing $\rho _k :=\rho (Z_k-\theta _k)$ for each $k \ge 1$ and $\rho _{*} = \rho (Z_{*}-\theta _{*})$, it follows that

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{*} \le {{\,\mathrm{\mathbf {E}}\,}}_{\mu } \left( \liminf _{k \rightarrow \infty } \rho _k\right) \le \liminf _{k \rightarrow \infty } \left( {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _k\right) . \end{aligned}$$

(35)

The former inequality follows from monotonicity of the integral, and the latter inequality follows from an application of Fatou’s inequality, which is valid since $\rho _k \ge 0$.³⁰ Taking both ends of (35) together, since the choice of sequences $(Z_k)$ and $(\theta _k)$ were arbitrary, it follows again from the equivalence (12) that the functional $(Z,\theta ) \mapsto {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho ((Z-\theta )/\sigma )$ is LSC on $\mathcal {Z}\times \mathbb {R}$. $\square$

Lemma 11

(Basic integration properties) Let ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }Z^{2} < \infty$ hold, and take any $\theta \in \mathbb {R}$. Then the following properties of integrals based on $\rho _{\sigma }$ defined in (5) hold:

• For all $\sigma \in [0,\infty ]$, we have $0 \le {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z-\theta ) < \infty$.

• For $0 < \sigma \le \infty$, $\rho _{\sigma }(\cdot )$ is differentiable, and we have ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }|\rho _{\sigma }^{\prime }(Z-\theta ) |< \infty$.

• For $0 < \sigma \le \infty$, $\rho _{\sigma }^{\prime }(\cdot )$ is differentiable, and we have $0 \le {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }^{\prime \prime }(Z-\theta ) < \infty$.

Furthermore, the Leibniz integration property holds for both derivatives, that is

$$\begin{aligned} \frac{d}{d\theta }{{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z-\theta ) = -\frac{{{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }^{\prime }(Z-\theta )}{\sigma }, \qquad \frac{d}{d\theta }{{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }^{\prime }(Z-\theta ) = -\frac{{{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }^{\prime \prime }(Z-\theta )}{\sigma } \end{aligned}$$

(36)

for any $0< \sigma < \infty$, and for the special case of $\sigma =\infty$, we have

$$\begin{aligned} \frac{d}{d\theta }{{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\infty }(Z-\theta ) = -2({{\,\mathrm{\mathbf {E}}\,}}_{\mu }Z-\theta ), \qquad \frac{d}{d\theta }{{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\infty }^{\prime }(Z-\theta ) = -2. \end{aligned}$$

(37)

These equalities hold for any $\theta \in \mathbb {R}$.

Proof of Lemma 11

Non-negativity of $\rho _{\sigma }$ implies $0 \le {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z-\theta )$ for all $\sigma$. Regarding finiteness, starting with $\sigma = 0$ we have ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{0}(Z-\theta ) = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }|Z-\theta |< \infty$, which follows from Hölder’s inequality and $\mu$-integrability of $Z^{2}$. For $0< \sigma < \infty$, first note that ${{\,\mathrm{atan}\,}}^{\prime }(u) \le 1$ for all $u \in \mathbb {R}$, and thus since ${{\,\mathrm{atan}\,}}(0)=0$, we have $|{{\,\mathrm{atan}\,}}(u) |\le |u |$ and $u{{\,\mathrm{atan}\,}}(u) \le u^{2}$ for all u. In particular, this means $\rho _{\sigma }(Z-\theta ) \le (Z-\theta )^{2}/\sigma ^{2}$, and thus square-$\mu$-integrability of Z implies ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z-\theta ) < \infty$. The $\sigma = \infty$ case follows identically.

Moving to $\rho _{\sigma }^{\prime }(\cdot )$, for $0< \sigma < \infty$ we have that $|\rho _{\sigma }^{\prime }(u) |< \pi /2$ for all $u \in \mathbb {R}$, and thus ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }|\rho _{\sigma }^{\prime }(Z-\theta ) |< \infty$. The exact same argument holds for $\rho _{\sigma }^{\prime \prime }(\cdot )$, since $0 < \rho _{\sigma }^{\prime \prime }(u) \le 1$ for all $u \in \mathbb {R}$. The $\sigma = \infty$ case follows analogously.

For the Leibniz property, let $(a_k)$ be any real sequence such that $a_k \rightarrow 0$. Using the fact that $\rho _{\sigma }^{\prime }$ is bounded, the dominated convergence theorem lets us deduce the following:

$$\begin{aligned} \lim \limits _{k \rightarrow \infty } \left[ \frac{{{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z-(\theta +a_k)) - {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z-\theta )}{a_k} \right]&= \lim \limits _{k \rightarrow \infty } {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\left[ \frac{\rho _{\sigma }(Z-(\theta +a_k)) - \rho _{\sigma }(Z-\theta )}{a_k} \right] \\&= {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\left[ \lim \limits _{k \rightarrow \infty } \frac{\rho _{\sigma }(Z-(\theta +a_k)) - \rho _{\sigma }(Z-\theta )}{a_k} \right] \\&= -\frac{{{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }^{\prime }(Z-\theta )}{\sigma }. \end{aligned}$$

We note that the first equality just uses $\mu$-integrability and linearity of the Lebesgue integral, the second equality uses boundedness and integrability of the derivative, plus dominated convergence (e.g., (Ash and Doléans-Dade 2000, Thm. 1.6.9)). The last equality is just the chain rule applied to the differentiable function $\rho _{\sigma }(\cdot )$. Since the sequence $(a_k)$ was arbitrary, we conclude that the first equality of (36) holds. The second equality of (36), as well as both equalities in (37) hold via an identical argument. $\square$

Proof of Proposition 1

First, note that the convexity of $\rho _{\sigma }(\cdot )$ implies that $\theta \mapsto {{\,\mathrm{r}\,}}_{\sigma }(Z,\theta )$ is convex. We start by showing that ${{\,\mathrm{r}\,}}_{\sigma }$ is also coercive, namely that $|\theta |\rightarrow \infty$ implies ${{\,\mathrm{r}\,}}_{\sigma }(Z,\theta ) \rightarrow \infty$. For all cases $\sigma \in [0,\infty ]$, the non-negativity of $\rho _{\sigma }$ and $\eta$ trivially implies that $\theta \rightarrow \infty$ implies ${{\,\mathrm{r}\,}}_{\sigma }(Z,\theta ) \rightarrow \infty$, and thus we need only consider the negative direction, where $\theta \rightarrow -\infty$.

For the case of $\sigma = 0$, note that

$$\begin{aligned} \theta + \eta {{\,\mathrm{\mathbf {E}}\,}}_{\mu }|Z-\theta |\ge \theta - \eta |\theta |+ \eta {{\,\mathrm{\mathbf {E}}\,}}_{\mu }|Z |. \end{aligned}$$

Clearly, with $\eta > 1$ the right-hand side grows without bound as $\theta \rightarrow -\infty$. For the case of $0 < \sigma = \infty$, writing $Z_{\theta } :=(Z-\theta )/\sigma$ for readability, the joint risk can be written conveniently as

$$\begin{aligned} {{\,\mathrm{r}\,}}_{\sigma }(Z,\theta ) = \theta \left( 1 - \frac{\eta }{\sigma }{{\,\mathrm{\mathbf {E}}\,}}_{\mu }{{\,\mathrm{atan}\,}}\left( Z_{\theta }\right) \right) + \frac{\eta }{\sigma }{{\,\mathrm{\mathbf {E}}\,}}_{\mu }Z{{\,\mathrm{atan}\,}}\left( Z_{\theta }\right) - \frac{\eta }{2}{{\,\mathrm{\mathbf {E}}\,}}_{\mu }\log \left( 1 + Z_{\theta }^{2}\right) . \end{aligned}$$

(38)

Since ${{\,\mathrm{atan}\,}}(\cdot )$ is monotonic (increasing) on $\mathbb {R}$, bounded as $|{{\,\mathrm{atan}\,}}(\cdot ) |< \pi /2$, and ${{\,\mathrm{atan}\,}}(u) \rightarrow \pi /2$ as $u \rightarrow \infty$, we have that ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }{{\,\mathrm{atan}\,}}(Z_{\theta }) \rightarrow \pi /2$ as $\theta \rightarrow -\infty$, by monotone convergence.³¹ Thus, taking $\eta > 2\sigma /\pi$ ensures that eventually as $\theta \rightarrow \infty$, the first term on the right-hand side of (38) will become positive. Since this term grows linearly, it dominates the other unbounded term (which is logarithmic), and thus we have shown that ${{\,\mathrm{r}\,}}_{\sigma }$ is coercive whenever $\sigma \ge 0$. Convexity and coercivity together imply that $\theta \mapsto {{\,\mathrm{r}\,}}_{\sigma }(Z,\theta )$ takes its minimum on $\mathbb {R}$; see (Bertsekas 2015, Sec. B.3.2) or (Barbu and Precupanu 2012, Thm. 2.11) for standard references.

The case of $\sigma = \infty$ is easy, since by direct inspection we can write

$$\begin{aligned} {{\,\mathrm{r}\,}}_{\infty }(Z,\theta ) = \theta (1 - 2\eta {{\,\mathrm{\mathbf {E}}\,}}_{\mu }Z) + \eta \theta ^{2} + \eta {{\,\mathrm{\mathbf {E}}\,}}_{\mu }Z^{2}. \end{aligned}$$

Since the sum of a strongly convex function and an affine function is strongly convex, we have that $\theta \mapsto {{\,\mathrm{r}\,}}_{\infty }(Z,\theta )$ has a unique minimum on $\mathbb {R}$.

It only remains to prove the uniqueness of $\theta _{Z}$ in the proposition statement for the case of $0< \sigma < \infty$. The most direct way of doing this is to use the Leibniz property (36) proved in our helper Lemma 11, which in particular tells us that

$$\begin{aligned} \frac{d^{2}}{d\theta ^{2}}{{\,\mathrm{r}\,}}_{\sigma }(Z,\theta ) = \frac{\eta }{\sigma }{{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho ^{\prime \prime }\left( \frac{Z-\theta }{\sigma }\right) > 0, \end{aligned}$$

where positivity follows from the fact that $\rho ^{\prime \prime }(\cdot ) = 1/(1+(\cdot )^{2}) > 0$. This implies strict convexity, and thus that the minimizer $\theta _{Z}$ is unique. $\square$

Proof of Proposition 3

We take the points in the statement of the proposition in order, one at a time. To being, the (joint) convexity of ${{\,\mathrm{r}\,}}_{\sigma }$ follows from direct inspection, using the convexity of $\rho _{\sigma }$ for any $\sigma \in [0,\infty ]$. With this fact in mind, note that the convexity of ${{\,\mathrm{R}\,}}_{\sigma }$ can be checked easily as follows. For any $Z_1,Z_2 \in \mathcal {Z}$ and $\theta _1,\theta _2 \in \mathbb {R}$, the definition and convexity of ${{\,\mathrm{r}\,}}_{\sigma }$ immediately implies that for any $\alpha \in (0,1)$ we have

$$\begin{aligned} {{\,\mathrm{R}\,}}_{\sigma }(\alpha Z_1 + (1-\alpha )Z_2)&\le {{\,\mathrm{r}\,}}_{\sigma }(\alpha Z_1 + (1-\alpha )Z_2, \alpha \theta _1 + (1-\alpha )\theta _2)\\&\le \alpha {{\,\mathrm{r}\,}}_{\sigma }(Z_1,\theta _1) + (1-\alpha ){{\,\mathrm{r}\,}}_{\sigma }(Z_2,\theta _2). \end{aligned}$$

Using the notation (and statement) of Proposition 1, we can set $\theta _1 = \theta _{Z_1} \in \mathbb {R}$ and $\theta _2 = \theta _{Z_2} \in \mathbb {R}$, and plugging this in to the above inequalities, we obtain

$$\begin{aligned} {{\,\mathrm{R}\,}}_{\sigma }(\alpha Z_1 + (1-\alpha )Z_2) \le \alpha {{\,\mathrm{R}\,}}_{\sigma }(Z_1) + (1-\alpha ){{\,\mathrm{R}\,}}_{\sigma }(Z_2), \end{aligned}$$

and thus both ${{\,\mathrm{r}\,}}_{\sigma }$ and ${{\,\mathrm{R}\,}}_{\sigma }$ are convex for any $\sigma \in [0,\infty ]$. Note that this does not require the minima $\theta _{Z_1}$ and $\theta _{Z_2}$ to be unique, and thus holds for the $\sigma = 0$ case without issue. From Lemma 11, we also have that $|{{\,\mathrm{r}\,}}_{\sigma }(\cdot ,\cdot ) |< \infty$ and $|{{\,\mathrm{R}\,}}_{\sigma }(\cdot ) |< \infty$, so both functions are proper convex. As for continuity, note that from Lemma 10 and the continuity of $\rho _{\sigma }(\cdot )$ for all $\sigma \in [0,\infty ]$, we can immediately infer that ${{\,\mathrm{r}\,}}_{\sigma }$ is LSC. It is well-known that on Banach spaces, any proper convex LSC function is continuous and sub-differentiable on the interior of the effective domain.³² Since our integrability assumptions imply ${{\,\mathrm{dom}\,}}{{\,\mathrm{r}\,}}_{\sigma } = \mathcal {Z}\times \mathbb {R}$, the continuity and sub-differentiability of ${{\,\mathrm{r}\,}}_{\sigma }$ is thus proved. To handle ${{\,\mathrm{R}\,}}_{\sigma }$, take any sequence $(Z_k)$ converging to an arbitrarily chosen point $Z_{*} \in \mathcal {Z}$. Let $(\theta _k)$ be any sequence converging to $\theta _{Z_{*}} \in \mathbb {R}$. Then by definition of ${{\,\mathrm{R}\,}}_{\sigma }$ and continuity of ${{\,\mathrm{r}\,}}_{\sigma }$, we have

$$\begin{aligned} \limsup _{k \rightarrow \infty } {{\,\mathrm{R}\,}}_{\sigma }(Z_k) \le \limsup _{k \rightarrow \infty } {{\,\mathrm{r}\,}}_{\sigma }(Z_k,\theta _k) = \lim \limits _{k \rightarrow \infty } {{\,\mathrm{r}\,}}_{\sigma }(Z_k,\theta _k) = {{\,\mathrm{R}\,}}_{\infty }(Z_{*},\theta _{Z_{*}}) = {{\,\mathrm{R}\,}}_{\sigma }(Z_{*}). \end{aligned}$$

(39)

The two ends of the inequality (39) imply that ${{\,\mathrm{R}\,}}_{\sigma }$ is USC, via (12) and the relation of USC to LSC functions. On the effective domain of any convex USC function, the function is in fact continuous.³³ Thus, we have that ${{\,\mathrm{R}\,}}_{\sigma }$ is continuous. Furthermore, the sub-differentiability of ${{\,\mathrm{R}\,}}_{\sigma }$ follows in the exact same fashion as for ${{\,\mathrm{r}\,}}_{\sigma }$.

Next, for the monotonicity of the location term $Z \mapsto \theta _{Z}$ in (6), with $0 < \sigma \le \infty$, recall that we can utilize the Leibniz properties (36)–(37) from the integration Lemma 11. To start, we know that for any Z, the corresponding $\theta _{Z}$ must satisfy the following first-order optimality condition:

$$\begin{aligned} \text {If }\sigma < \infty : \quad {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }^{\prime }(Z-\theta _{Z}) = \frac{\sigma }{\eta }. \qquad \text {If }\sigma = \infty : \quad \theta _{Z} = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }Z - \frac{1}{2\eta }. \end{aligned}$$

(40)

The desired monotonicity property is obvious for the $\sigma = \infty$ case using (40). As for the case of $0< \sigma < \infty$, it is evident from the second equality of (36) that the function $\theta \mapsto {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z-\theta )$ is monotonically decreasing on $\mathbb {R}$. Thus, if we assume $Z_1 \le Z_2$ almost surely but $\theta _{Z_1} > \theta _{Z_2}$, the first order optimality combined with monotonicity implies

$$\begin{aligned} \frac{\sigma }{\eta } = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z_1-\theta _{Z_1}) < {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z_1-\theta _{Z_2}) \le {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z_2-\theta _{Z_2}) = \frac{\sigma }{\eta }, \end{aligned}$$

which is a contradiction. Thus, $\theta _{Z_1} \le \theta _{Z_2}$ as desired for the $0< \sigma < \infty$ case as well.

The translation-equivariance property of $Z \mapsto \theta _{Z}$ follows from direct inspection using the condition (40), that is for $0< \sigma < \infty$, we trivially have

$$\begin{aligned} \frac{\sigma }{\eta } = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z-\theta _{Z}) = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }(Z+a-(\theta _{Z}+a)), \end{aligned}$$

and thus ${{\,\mathrm{r}\,}}_{\sigma }(Z+a,\theta _{Z}+a) = {{\,\mathrm{R}\,}}_{\sigma }(Z+a)$. Since Proposition 1 guarantees that the minimizer of $\theta \mapsto {{\,\mathrm{r}\,}}_{\sigma }(Z,\theta )$ is unique, we can safely write $\theta _{Z+a} = \theta _{Z}+a$. The proof for the $\sigma = \infty$ case is analogous.

Finally, to prove that ${{\,\mathrm{R}\,}}_{\sigma }$ is not in general monotonic, we give a concrete example of $Z_1$ and $Z_2$ such that $Z_1 \le Z_2$ almost surely, but ${{\,\mathrm{R}\,}}_{\sigma }(Z_1) > {{\,\mathrm{R}\,}}_{\sigma }(Z_2)$. For simplicity, consider the case of $\sigma = \infty$, where $\rho _{\infty }(\cdot ) = (\cdot )^{2}$, and for any $\eta > 0$ direct inspection shows that

$$\begin{aligned} {{\,\mathrm{R}\,}}_{\infty }(Z) = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }Z + \eta {{\,\mathrm{var}\,}}_{\mu }Z - \frac{1}{4\eta }. \end{aligned}$$

(41)

That is, the special case of $\sigma = \infty$ is equivalent to the mean-variance risk function of classical portfolio theory, dating back to Markowitz (1952). The random variables $Z_1$ and $Z_2$ are constructed as follows. Let $c_1$ and $c_2$ be the respective centers, $w_1$ and $w_2$ the respective widths, and $v_1 < w_{1}^{2}$ and $v_2 < w_{2}^{2}$ the respective scaling factors of $Z_1$ and $Z_2$, which are characterized as

$$\begin{aligned} {{\,\mathrm{\mathbf {P}}\,}}\left\{ Z_j = c_j-w_j\right\} = {{\,\mathrm{\mathbf {P}}\,}}\left\{ Z_j = c_j+w_j\right\} = \frac{v_j}{2w_{j}^{2}}, \qquad {{\,\mathrm{\mathbf {P}}\,}}\{Z_j = c_j\} = 1-{{\,\mathrm{\mathbf {P}}\,}}\{Z_j \ne c_j\} \end{aligned}$$

for each $j \in \{1,2\}$. Note that our assumptions imply $0< {{\,\mathrm{\mathbf {P}}\,}}\{Z_j = c_j\} < 1$, and direct inspection shows that ${{\,\mathrm{\mathbf {E}}\,}}Z_j = c_j$ and ${{\,\mathrm{var}\,}}Z_j = v_j$, again for each $j \in \{1,2\}$. As a simple concrete example, note that setting $c_2 = c_1 + w_1 + w_2$ guarantees $Z_1 \le Z_2$ with probability 1. From the equality (41) given above, the difference in risks can be written as

$$\begin{aligned} {{\,\mathrm{R}\,}}_{\infty }(Z_1)-{{\,\mathrm{R}\,}}_{\infty }(Z_2)&= {{\,\mathrm{\mathbf {E}}\,}}Z_1 - {{\,\mathrm{\mathbf {E}}\,}}Z_2 + \eta \left( {{\,\mathrm{var}\,}}Z_1 - {{\,\mathrm{var}\,}}Z_2 \right) \\&= -(w_1+w_2) + \eta (v_1 - v_2). \end{aligned}$$

Thus, ${{\,\mathrm{R}\,}}_{\infty }(Z_1) > {{\,\mathrm{R}\,}}_{\infty }(Z_2)$ holds whenever $v_1 - v_2 > w_1 + w_2$. For concreteness, say for some $\varepsilon > 0$, we fix the variance factors to $v_1 = w_{1}^{2} - \varepsilon$ and $v_2 = w_{2}^{2} - \varepsilon$ respectively. Then the condition simplifies to $w_{1}^{2} > w_1 + w_2 + w_{2}^{2}$. As an example, setting $w_1=2$ and $w_2 = 1/2$, the condition holds, implying ${{\,\mathrm{R}\,}}_{\infty }(Z_1) > {{\,\mathrm{R}\,}}_{\infty }(Z_2)$, despite the fact that $Z_1 \le Z_2$. This gives us a simple but intuitive example where monotonicity of ${{\,\mathrm{R}\,}}_{\sigma }$ does not hold, and concludes the proof. $\square$

1.2 3.2 Proofs for Sect. 3

Recall that our basic probabilistic setup for the learning problem has an underlying probability space $(\Omega ,\mathcal {F},\mu )$, a hypothesis class $\mathcal {H}$, and a random loss ${{\,\mathrm{L}\,}}(h)$ indexed by $\mathcal {H}$. That is, we consider any $\mathcal {F}$-measurable function ${{\,\mathrm{L}\,}}(h;\cdot ): \Omega \rightarrow \mathbb {R}$ as a loss. When a particular realization $\omega \in \Omega$ is important, we will write ${{\,\mathrm{L}\,}}(h;\omega )$, but otherwise, for readability we will typically write ${{\,\mathrm{L}\,}}(h) :={{\,\mathrm{L}\,}}(h;\cdot )$. Our basic integrability assumption, carried over from Sect. 2, is that of square-$\mu$-integrability, which in the context of losses is written explicitly as

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}_{\mu }|{{\,\mathrm{L}\,}}(h) |^{2} = \int _{\Omega }|{{\,\mathrm{L}\,}}(h;\omega ) |^{2} \, \mu (\mathop {}\!\mathrm {d}\omega ) < \infty \end{aligned}$$

for all $h \in \mathcal {H}$. This requirement is made in assumption A1 in the main text. It follows that $\{{{\,\mathrm{L}\,}}(h): h \in \mathcal {H}\} \subset \mathcal {L}_{2}(\Omega ,\mathcal {F},\mu )$. Thus the map $h \mapsto {{\,\mathrm{L}\,}}(h)$ takes us from $\mathcal {H}$ to $\mathcal {L}_{2}(\Omega ,\mathcal {F},\mu )$.

Loss-specific terminology To ensure our use of formal terms is clear, we apply the definitions of Sect. 2.1 to losses here. We shall typically suppress the dependence on $\omega \in \Omega$ in directional derivatives and gradients, writing ${{\,\mathrm{L}\,}}_{r}^{\prime }(h;g) :={{\,\mathrm{L}\,}}_{r}^{\prime }(h;g,\cdot )$, ${{\,\mathrm{L}\,}}^{\prime }(h;g) :={{\,\mathrm{L}\,}}^{\prime }(h;g,\cdot )$, and ${{\,\mathrm{L}\,}}^{\prime }(h) :={{\,\mathrm{L}\,}}^{\prime }(h;\cdot )$. Let $H \subset \mathcal {H}$ be an open set. We say that ${{\,\mathrm{L}\,}}$ is radially differentiable at $h \in H$ if the radial derivative ${{\,\mathrm{L}\,}}_{r}^{\prime }(h;g)$ exists for all directions $g \in \mathcal {H}$, $\mu$-almost surely. We say that ${{\,\mathrm{L}\,}}$ is directionally differentiable at $h \in H$ if the directional derivative ${{\,\mathrm{L}\,}}^{\prime }(h;g)$ exists for all directions $g \in \mathcal {H}$, $\mu$-almost surely. On this “good” event of probability 1, if the map $g \mapsto {{\,\mathrm{L}\,}}_{r}^{\prime }(h;g)$ is linear and continuous, we say ${{\,\mathrm{L}\,}}$ is Gateaux differentiable at h, and if the map $g \mapsto {{\,\mathrm{L}\,}}^{\prime }(h;g)$ is linear and continuous, we say ${{\,\mathrm{L}\,}}$ is Hadamard differentiable at h. When we say that ${{\,\mathrm{L}\,}}$ is (Fréchet) differentiable at $h \in H$, we mean that there exists a function ${{\,\mathrm{L}\,}}^{\prime }(h)(\cdot ):\mathcal {H}\rightarrow \mathbb {R}_{+}$ that is linear, continuous, and which satisfies (15) $\mu$-almost surely.³⁴ We say that ${{\,\mathrm{L}\,}}$ is $\lambda$ -Lipschitz at $h \in \mathcal {H}$ if there exists a $\delta > 0$ such that $\Vert h-h^{\prime }\Vert < \delta \implies \Vert {{\,\mathrm{L}\,}}(h)-{{\,\mathrm{L}\,}}(h^{\prime })\Vert \le \lambda \Vert h-h^{\prime }\Vert$. With the running assumption about second moments, this amounts to requiring

$$\begin{aligned} \Vert h-h^{\prime }\Vert < \delta \implies {{\,\mathrm{\mathbf {E}}\,}}_{\mu }|{{\,\mathrm{L}\,}}(h)-{{\,\mathrm{L}\,}}(h^{\prime }) |^{2} \le \lambda ^{2}\Vert h-h^{\prime }\Vert ^{2}. \end{aligned}$$

(42)

We say that ${{\,\mathrm{L}\,}}$ is weakly $\lambda$ -smooth at $h \in H$ if ${{\,\mathrm{L}\,}}$ is Gateaux differentiable and the map $h \mapsto {{\,\mathrm{L}\,}}_r^{\prime }(h;\cdot )$ is $\lambda$-Lipschitz $\mu$-almost surely at h. That is, if for small enough $\delta > 0$ we have

$$\begin{aligned} \Vert h-h^{\prime }\Vert < \delta \implies \Vert {{\,\mathrm{L}\,}}_r^{\prime }(h;\cdot )-{{\,\mathrm{L}\,}}_r^{\prime }(h^{\prime };\cdot ) \Vert \le \lambda \Vert h-h^{\prime }\Vert . \end{aligned}$$

(43)

Note that the norm used here is the operator norm applied to the linear map ${{\,\mathrm{L}\,}}_r^{\prime }(h;\cdot )-{{\,\mathrm{L}\,}}_r^{\prime }(h^{\prime };\cdot )$.

1.2.1 3.2.1 Weak convexity of joint composition function

The joint risk function ${{\,\mathrm{r}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h),\theta )$ can be written as a simple composition $(h,\theta ) \mapsto ({{\,\mathrm{L}\,}}(h),\theta ) \mapsto \theta + \eta {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\rho _{\sigma }({{\,\mathrm{L}\,}}(h)-\theta )$. For any $0 \le \sigma < \infty$ and any smooth loss, using the preliminary results established Sect. 2.3, it is straightforward to show the weak convexity of this composite function.

Proposition 12

Let the hypothesis class $\mathcal {H}$ be Banach. Let the loss ${{\,\mathrm{L}\,}}$ be locally Lipschitz and weakly $\lambda ^{\prime }$-smooth on $\mathcal {H}$. Then, for any $0 \le \sigma < \infty$, defining a $\sigma$-dependent factor $\lambda _{\sigma }$ as

$$\begin{aligned} \lambda _{\sigma } :={\left\{ \begin{array}{ll} 1, &{} \text {if } \sigma = 0\\ \pi /(2\sigma ), &{} \text {if } 0< \sigma < \infty \end{array}\right. } \end{aligned}$$

we have that $(h,\theta ) \mapsto {{\,\mathrm{r}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h),\theta )$ is $\gamma$-weakly convex with $\gamma = (1+\eta \lambda _{\sigma })\max \{1,\lambda ^{\prime }\}$.

Proof

Recall the generic result given in Proposition 8 for the weak convexity of generic composite functions. Our proof here amounts to checking that the assumptions of Proposition 8 are satisfied for the composition $f :={{\,\mathrm{r}\,}}_{\sigma } \circ f_1$, with $f_1: \mathcal {H}\times \mathbb {R}\rightarrow \mathcal {L}_{2}(\Omega ,\mathcal {F},\mu ) \times \mathbb {R}$ defined as $f_1(h,\theta ) :=({{\,\mathrm{L}\,}}(h),\theta )$.

To start, let us consider the properties of $f_1$. Since ${{\,\mathrm{L}\,}}$ is locally Lipschitz and Gateaux differentiable, it follows that ${{\,\mathrm{L}\,}}$ is also Hadamard differentiable.³⁵ Since the map $h \mapsto {{\,\mathrm{L}\,}}_r^{\prime }(h;\cdot ) = {{\,\mathrm{L}\,}}^{\prime }(h;\cdot )$ is continuous (by weak smoothness), it follows that ${{\,\mathrm{L}\,}}$ is (Fréchet) differentiable.³⁶ Since $(h,\theta ) \mapsto f_1(h,\theta )=({{\,\mathrm{L}\,}}(h),\theta )$ just passes $\theta$ through the identity, trivially the second component is also differentiable, and the differentiability of both components thus implies $f_1$ is differentiable.³⁷ Furthermore, the local Lipschitz property of ${{\,\mathrm{L}\,}}$ is clearly retained by $f_1$. Evaluating the gradients we have $f_1^{\prime }(h,\theta )(g,r) = ({{\,\mathrm{L}\,}}^{\prime }(h)(g),r)$, and thus using a typical product space norm we have

$$\begin{aligned} \Vert f_1^{\prime }(h_1,\theta _1)-f_1^{\prime }(h_2,\theta _2)\Vert = \Vert {{\,\mathrm{L}\,}}^{\prime }(h_1)-{{\,\mathrm{L}\,}}^{\prime }(h_2)\Vert + |\theta _1-\theta _2 |. \end{aligned}$$

By weak smoothness of ${{\,\mathrm{L}\,}}$, it follows that $f_1$ is $\max \{1,\lambda ^{\prime }\}$-smooth $\mu$-almost surely, where smoothness is in the sense defined in Sect. 2.3.

Next, let us look at properties of ${{\,\mathrm{r}\,}}_{\sigma }$. Note that $\rho _{\sigma }(\cdot )$ is trivially 1-Lipschitz in the case of $\sigma = 0$, and for $0< \sigma < \infty$, the $\pi /2$-Lipschitz property of $\rho$ defined in (3) implies that $\rho _{\sigma }(\cdot )$ is $\pi /(2\sigma )$-Lipschitz. With these basic facts in place, it follows that

$$\begin{aligned} |{{\,\mathrm{r}\,}}_{\sigma }(Z_1,\theta _1)-{{\,\mathrm{r}\,}}_{\sigma }(Z_2,\theta _2) |\le \left( 1 + \eta \lambda _{\sigma }\right) |\theta _1-\theta _2 |+ \eta \lambda _{\sigma }{{\,\mathrm{\mathbf {E}}\,}}_{\mu }|Z_1-Z_2 |, \end{aligned}$$

where the $\sigma$-dependent Lipschitz coefficient $\lambda _{\sigma }$ is as defined in the statement of the desired result. To obtain bounds in terms of the correct norm, note that

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}_{\mu }|Z_1 - Z_2 |\le \mu (\Omega )\sqrt{{{\,\mathrm{\mathbf {E}}\,}}_{\mu }|Z_1 - Z_2 |^{2}} = \sqrt{{{\,\mathrm{\mathbf {E}}\,}}_{\mu }|Z_1 - Z_2 |^{2}}, \end{aligned}$$

which follows from the fact that $\mu$ is a probability, and a simple application of Hölder’s inequality.³⁸ Plugging this into the previous inequality, and noting that it holds for any choice of $Z_1,Z_2 \in \mathcal {L}_2(\Omega ,\mathcal {F},\mu )$ and $\theta _1,\theta _2 \in \mathbb {R}$, it follows that ${{\,\mathrm{r}\,}}_{\sigma }$ is $(1+\eta \lambda _{\sigma })$-Lipschitz on $\mathcal {L}_2(\Omega ,\mathcal {F},\mu ) \times \mathbb {R}$, and $f_1(\mathcal {H}\times \mathbb {R}) \subset {{\,\mathrm{dom}\,}}{{\,\mathrm{r}\,}}_{\sigma }$. Furthermore, from Proposition 3, we have that ${{\,\mathrm{r}\,}}_{\sigma }$ is convex.

Taking the above points together, if we consider the good event of probability 1 where $f_1$ satisfies the desired properties, direct application of Proposition 8 to the map $(h,\theta ) \mapsto ({{\,\mathrm{r}\,}}_{\sigma } \circ f_1)(h,\theta )$ yields the desired result. $\square$

Remark 13

The result in the preceding Proposition 12 is rather useful, and it does not require the loss to be convex. When the loss is convex, the analysis becomes somewhat simpler and stronger arguments are naturally possible; composite risks under convex losses and convex, monotonic risk functions is the setting considered by (Ruszczyński and Shapiro 2006, Sec. 3.2), for example.

We have established conditions under which the intermediate joint objective ${{\,\mathrm{r}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h),\theta )$ is weakly convex, and characterized this weak convexity with respect to properties of the underlying risk function and data distribution. Since the data distribution $\mu$ is unknown, we can never actually compute ${{\,\mathrm{r}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h),\theta )$. Any learning algorithm will only have access to feedback of a stochastic nature which provides incomplete, noisy information. Our next task is to establish conditions under which the feedback available to the learner is “good enough” to ensure reasonable performance guarantees.

1.2.2 3.2.2 Unbiased stochastic feedback

In considering stochastic feedback, recall that ${{\,\mathrm{r}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h),\theta ) = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }(f_2 \circ F_1)(h,\theta )$, with $F_1$ and $f_2$ given by (7) in the main text. For each $h \in \mathcal {H}$ and $\theta \in \mathbb {R}$, the value $F_1(h,\theta )$ returned by $F_1$ is a random vector. We shall assume that for any $h \in \mathcal {H}$, the learner can obtain independent random samples of the loss ${{\,\mathrm{L}\,}}(h)$ and the associated gradient ${{\,\mathrm{L}\,}}^{\prime }(h)$. Since $F_{1}^{\prime }(h,\theta ) = ({{\,\mathrm{L}\,}}^{\prime }(h),1)$ by which we mean $F_{1}^{\prime }(h,\theta )(g,r) = ({{\,\mathrm{L}\,}}^{\prime }(h)(g),r)$ for all $g \in \mathcal {H}$ and $r \in \mathbb {R}$, clearly the learner can also independently sample from $F_1(h,\theta )$ and $F_{1}^{\prime }(h,\theta )$. Sub-differentiability is already guaranteed by Proposition 3, and since $\rho _{\sigma }$ and $\eta$ are by design known to the learner, they can readily acquire an element from $\partial f_2(u,\theta )$. Thus if $({{\,\mathrm{L}\,}}(h),\theta ) \in {{\,\mathrm{int}\,}}({{\,\mathrm{dom}\,}}f_2)=\mathbb {R}^{2}$ $\mu$-almost surely, it follows that the learner can sample from $\partial f_2({{\,\mathrm{L}\,}}(h),\theta ) \circ F_{1}^{\prime }(h,\theta )$. This is the stochastic feedback available to the learner, and when we ask that it be “good enough,” this means we require it to be an unbiased estimator of the (Clarke) sub-differential of ${{\,\mathrm{r}\,}}_{\sigma }$. The following result gives mild conditions under which this is achieved.

Proposition 14

Under the conditions of Proposition 12, for any $h \in \mathcal {H}$ and $\theta \in \mathbb {R}$, as long as ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }|{{\,\mathrm{L}\,}}^{\prime }(h;\cdot ) |< \infty$, the stochastic sub-differential is an unbiased estimator in that

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}_{\mu }\left[ \partial f_2({{\,\mathrm{L}\,}}(h),\theta ) \circ F_{1}^{\prime }(h,\theta ) \right] \subset \partial _{C }{{\,\mathrm{r}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h),\theta ), \end{aligned}$$

and this holds for any choice of $0 \le \sigma < \infty$.

Proof

Using the weak smoothness of ${{\,\mathrm{L}\,}}$, with probability 1, the map $(h,\theta ) \mapsto F_{1}^{\prime }(h,\theta )$ is continuous, plus $F_1$ is locally Lipschitz and $\partial _{C }F_{1}(h,\theta ) = \{F_{1}^{\prime }(h,\theta )\}$.³⁹ Furthermore, since $F_{1}^{\prime }(h,\theta )(g,r) = ({{\,\mathrm{L}\,}}^{\prime }(h)(g),r)$, the linearity of ${{\,\mathrm{L}\,}}^{\prime }(h)(\cdot )$ implies that $F_{1}^{\prime }(h,\theta )(\mathcal {H}\times \mathbb {R}) = \mathbb {R}^{2}$ $\mu$-almost surely. Since $F_1$ and $f_2$ are (locally) Lipschitz, the facts we have just laid out imply a strong chain rule.⁴⁰ That is, it holds $\mu$-almost surely that

$$\begin{aligned} \partial _{C }(f_2 \circ F_1)(h,\theta )&= \partial _{C }f_2({{\,\mathrm{L}\,}}(h),\theta ) \circ F_{1}^{\prime }(h,\theta )\nonumber \\&= \partial f_2({{\,\mathrm{L}\,}}(h),\theta ) \circ F_{1}^{\prime }(h,\theta ), \end{aligned}$$

(44)

where the second equality follows from the convexity of $f_2$.

Next, the Lipschitz property of $\rho _{\sigma }$ implies that $f_2$ is $\lambda$-Lipschitz for some $\lambda >0$; the actual value is not important for this proof. Using the Lipschitz continuity of $f_2$ and the fact that $\partial _{C }F_{1}(h,\theta ) = \{F_{1}^{\prime }(h,\theta )\}$ implies $\partial _{C }{{\,\mathrm{L}\,}}(h) = \{{{\,\mathrm{L}\,}}^{\prime }(h)\}$, we have

$$\begin{aligned} |(f_2 \circ F_1)_{C }^{\prime }(h,\theta )(g,r) |&\le \limsup _{(\alpha ,h^{\prime },\theta ^{\prime }) \rightarrow (0_{+},h,\theta )} \frac{|(f_2 \circ F_1)(h^{\prime }+\alpha g,\theta ^{\prime }+\alpha r)-(f_2 \circ F_1)(h^{\prime },\theta ^{\prime }) |}{\alpha }\\&\le \lambda \left( \limsup _{(\alpha ,h^{\prime }) \rightarrow (0_{+},h)}\frac{|{{\,\mathrm{L}\,}}(h^{\prime }+\alpha g)-{{\,\mathrm{L}\,}}(h^{\prime }) |}{\alpha } + \vert r |\right) \\&= \lambda \left( |{{\,\mathrm{L}\,}}^{\prime }(h)(g) |+ \vert r |\right) . \end{aligned}$$

Thus, using ${{\,\mathrm{r}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h),\theta ) = {{\,\mathrm{\mathbf {E}}\,}}_{\mu }(f_2 \circ F_1)(h,\theta )$ and ${{\,\mathrm{\mathbf {E}}\,}}_{\mu } |{{\,\mathrm{L}\,}}^{\prime }(h)(g) |< \infty$ for all $h,g \in \mathcal {H}$, we have

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}_{\mu } \left( f_2 \circ F_1 \right) _{C }^{\prime }(h,\theta ;\cdot ) = ({{\,\mathrm{r}\,}}_{\sigma })_{C }^{\prime }({{\,\mathrm{L}\,}}(h),\theta ;\cdot ) \end{aligned}$$

(45)

by a direct application of dominated convergence.⁴¹

To conclude, taking $G(h,\theta ) \in \partial f_2({{\,\mathrm{L}\,}}(h),\theta ) \circ F_{1}^{\prime }(h,\theta )$, by (44) it follows that we have $G(h,\theta ) \in \partial _{C }(f_2 \circ F_1)(h,\theta )$, and thus by definition of the Clarke sub-differential, monotonicity of the integral, and finally (45), we obtain

$$\begin{aligned} {{\,\mathrm{\mathbf {E}}\,}}_{\mu }G(h,\theta )(\cdot ) \le {{\,\mathrm{\mathbf {E}}\,}}_{\mu } (f_2 \circ F_1)_{C }^{\prime }(h,\theta ;\cdot ) = ({{\,\mathrm{r}\,}}_{\sigma })_{C }^{\prime }({{\,\mathrm{L}\,}}(h),\theta ;\cdot ). \end{aligned}$$

(46)

Linearity of ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }G(h,\theta )(\cdot )$ follows from the linearity of both $G(h,\theta )(\cdot )$ and the integral. Finally, applying (46) we have

$$\begin{aligned} \sup _{\Vert (u,r)\Vert =1} {{\,\mathrm{\mathbf {E}}\,}}_{\mu }G(h,\theta )(g,r) \le \sup _{\Vert (g,r)\Vert =1} ({{\,\mathrm{r}\,}}_{\sigma })_{C }^{\prime }({{\,\mathrm{L}\,}}(h),\theta ;u,r) < \infty , \end{aligned}$$

where finiteness holds because ${{\,\mathrm{r}\,}}_{\sigma }$ is locally Lipschitz.⁴² Thus ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }G(h,\theta ) \in (\mathcal {H}\times \mathbb {R})^{*}$, and with (46) we have ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }G(h,\theta ) \in \partial _{C }{{\,\mathrm{r}\,}}_{\sigma }({{\,\mathrm{L}\,}}(h),\theta )$ as desired. $\square$

Remark 15

The validity of interchanging the operations of (sub-)differentiation and expectation is a topic of fundamental importance in stochastic optimization and statistical learning theory. A useful, modern reference on this topic is included in (Ruszczyński and Shapiro 2003, Ch. 2). A classical reference is Rockafellar and Wets (1982); see also Rockafellar (1968) for a look at measurability of convex integrands. The interchangeability problem appears in various places in the literature over the years, see for example Shapiro (1994) as well as (Kall and Mayer 2005, Ch. 3, Rmk. 2.2). See also (Ruszczyński and Shapiro 2006, Eqn. (3.9)), who refer to generalized versions of a classic result due to Strassen (1965).

1.2.3 3.2.3 Proximity to a nearly-stationary point

Proof of Theorem 5

With all the results established thus far, this proof has just two simple parts. First, we need to show that the objective function of interest is weakly convex, and that we have access to unbiased estimates of the sub-differential; this is done here. This is done using the critical preparatory results in Propositions 12 and 14. Once this has been established, the remaining part just has us applying recent results from the literature for non-asymptotic control of the envelope gradient norm.

To begin, the assumptions of Proposition 12 are satisfied by A1, which ensures that ${{\,\mathrm{r}\,}}_{\sigma }$ is $\gamma$-weakly convex for $\gamma = (1+\eta \lambda _{\sigma })\max \{1,\lambda \}$. Furthermore, the $\mu$-integrability assumption on ${{\,\mathrm{L}\,}}^{\prime }(h)$ lets us use Proposition 14 to ensure that feedback drawn from (9) is such that ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }G_t \in \partial _{C }{{\,\mathrm{r}\,}}_{\sigma }(h_t,\theta _t)$ for all t. Furthermore, using A3 implies that ${{\,\mathrm{\mathbf {E}}\,}}[G_t \,\vert \,G_{[t-1]}] \in \partial _{C }{{\,\mathrm{r}\,}}_{\sigma }(h_t,\theta _t)$ for all t, since Algorithm 1 uses $G_t$ sampled via (9).

The desired result follows from an application of (Davis and Drusvyatskiy 2019, Thm. 3.1), where their objective function f corresponds to our ${{\,\mathrm{r}\,}}_{\sigma }$.⁴³ While their proof is given for the case of $\mathcal {H}= \mathbb {R}^{d}$, using assumption A2, if we leverage our characterization of weak convexity (Proposition 7), and replace their Lemma 2.2 with our (32), it is straightforward to see that their insights extend to arbitrary Hilbert spaces using the usual norm induced by the inner product. Thus with the moment bound A4 in hand, the generalized result can be applied to Algorithm 1, for objective function ${{\,\mathrm{r}\,}}_{\sigma }$, which has just been proved to be $\gamma$-weakly convex. The desired result follows immediately. $\square$

Appendix 4 Helper results

In this section, we provide some standard results that are leveraged in the main paper.

1.1 4.1 Useful results based on Lipschitz properties

Let $\mathcal {X}$ be a normed linear space, and let $f:\mathcal {X}\rightarrow \overline{\mathbb {R}}$ be convex and $\lambda$-Lipschitz. If f is sub-differentiable at a point x, then using the definition of the sub-differential, we have that

$$\begin{aligned} |\langle x^{\prime }-x, \partial f(x) \rangle |\le |f(x^{\prime })-f(x) |\le \lambda \Vert x^{\prime }-x\Vert . \end{aligned}$$

It immediately follows that

$$\begin{aligned} \Vert \partial f(x)\Vert \le \lambda . \end{aligned}$$

(47)

That is, all sub-gradients of f at x have norm no greater than the Lipschitz coefficient $\lambda$.

Let $\mathcal {X}$ and $\mathcal {Y}$ be Banach spaces, and let $f:\mathcal {X}\rightarrow \mathcal {Y}$ be differentiable on $U \subset \mathcal {X}$, an open set. Further, assume that the derivative is $\lambda$-Lipschitz on U, that is, for each $x, x^{\prime } \in U$, we have $\Vert f^{\prime }(x)-f^{\prime }(x^{\prime })\Vert \le \lambda \Vert x-x^{\prime }\Vert$. First-order Taylor approximations have direct analogues in this general setting, as the following result shows.⁴⁴

Proposition 16

Let $f:\mathcal {X}\rightarrow \mathcal {Y}$ be differentiable on an open set $U \subset \mathcal {X}$, with $\mathcal {X}$ and $\mathcal {Y}$ assumed to be Banach. If $f^{\prime }(\cdot )$ is $\lambda$-Lipschitz on U, then for any $x,u \in U$ such that $x+u \in U$, we have

$$\begin{aligned} \Vert f(x+u) - f(x) - f^{\prime }(x)(u)\Vert \le \frac{\lambda }{2}\Vert u\Vert ^{2}. \end{aligned}$$

1.2 4.2 Radial derivatives of convex functions

Say a function $f: \mathcal {V}\rightarrow \overline{\mathbb {R}}$ is convex. Take any $u, v \in {{\,\mathrm{dom}\,}}f$, and any scalar $c \ge 0$ such that $v + c(v-u) \in {{\,\mathrm{dom}\,}}f$. Then writing $u^{\prime } :=v + c(v-u)$, note that

$$\begin{aligned} v = \frac{1}{1+c}\left( u^{\prime }+cu\right) = (1-\beta )u^{\prime } + \beta u, \end{aligned}$$

where $\beta :=c/(1+c) \in [0,1)$. By convexity we have $f((1-\beta )u^{\prime } + \beta u) \le (1-\beta )f(u^{\prime }) + \beta f(u)$. Filling in definitions and rearranging we have

$$\begin{aligned} f(v + c(v-u)) - f(v) \ge c(f(v)-f(u)). \end{aligned}$$

(48)

Note that this can be done for any pair of u, v and scalar c that keeps the relevant points on the domain. Clearly this property is necessary for convexity, but it is in fact also sufficient.⁴⁵

For any function $f:\mathcal {V}\rightarrow \overline{\mathbb {R}}$ and open set $U \subset \mathcal {X}$, fix a point $x \in U$. We denote the difference quotient of f at x, incremented in the direction u, modulated by scalar $\alpha \ne 0$ as

$$\begin{aligned} q(\alpha ) :=q(\alpha ;f,x,u) :=\frac{f(x + \alpha u)-f(x)}{\alpha }. \end{aligned}$$

(49)

Consider the map $g(t) :=f(x + t u)-f(x)$, with all elements but $t \ge 0$ fixed. When f is convex, direct inspection immediately shows that $t \mapsto g(t)$ is convex. For any $0 \le t_{1} < t_{2}$, take some $t^{\prime } \in (t_1,t_2)$. Clearly, there exists a $\beta \in (0,1)$ such that $t^{\prime } = \beta t_1 + (1-\beta )t_2$. Then, we have

$$\begin{aligned} \frac{g(t^{\prime })-g(t_1)}{t^{\prime }-t_1} = \frac{g(\beta t_{1} + (1-\beta )t_2)-g(t_1)}{(1-\beta )(t_2-t_1)}&\le \frac{\beta g(t_1) + (1-\beta )g(t_2)-g(t_1)}{(1-\beta )(t_2-t_1)}\\&= \frac{g(t_2)-g(t_1)}{t_2-t_1}, \end{aligned}$$

where the inequality follows from convexity of g. If we use this inequality in the special case of $t_1 = 0$, alongside the basic relation $q(\alpha ) = (g(\alpha )-g(0))/\alpha$, it immediately follows that $\alpha \mapsto q(\alpha )$ is monotonic (non-decreasing) on the positive reals. Furthermore, the set $\{q(\alpha ): \alpha > 0\}$ is bounded below. To see this, take some $\gamma > 0$ small enough that $x - \gamma u \in {{\,\mathrm{dom}\,}}f$, and note that by direct application of convexity and the basic property (48), it follows that

$$\begin{aligned} \left( \frac{\alpha }{\gamma }\right) (f(x)-f(x-\gamma u)) \le f\left( x + \frac{\alpha }{\gamma }(x-(x-\gamma u)) \right) - f(x) = f(x + \alpha u) - f(x). \end{aligned}$$

That is, dividing both sides by $\alpha$, we have

$$\begin{aligned} \left( \frac{1}{\gamma }\right) (f(x)-f(x-\gamma u)) \le \frac{f(x + \alpha u) - f(x)}{\alpha } = q(\alpha ;f,u). \end{aligned}$$

(50)

Since the choice of $\gamma > 0$ depends only on x and u, and is free of $\alpha$, it follows that the set $\{q(\alpha ): \alpha > 0\}$ is bounded below, as desired. Using this boundedness alongside the monotonicity of $\alpha \mapsto q(\alpha )$, we have that the infimum is finite. Thus, recalling the definition (13) of the radial derivative of f at x in the direction u, since we have

$$\begin{aligned} f_{r}^{\prime }(x;u) = \lim \limits _{\alpha \rightarrow 0_{+}} \frac{f(x + \alpha u)-f(x)}{\alpha } = \inf \left\{ q(\alpha ;f,x,u) : \alpha > 0 \right\} , \end{aligned}$$

(51)

it follows immediately that the radial derivative always exists (i.e., $f^{\prime }(x;u) \in \mathbb {R}$). Note also that using convexity, direct inspection shows that for all u we have

$$\begin{aligned} f(u) - f(x) \ge f^{\prime }(x;u-x). \end{aligned}$$

(52)

Furthermore, it is easily verified that whenever $x \in {{\,\mathrm{dom}\,}}f$, the map $u \mapsto f^{\prime }(x;u)$ is sub-additive and positively homogeneous, i.e., a sub-linear functional.⁴⁶ The basic facts of interest here are summarized in the following proposition.

Proposition 17

(Difference quotients for convex functions) Let $\mathcal {V}$ be a vector space. If function $f: \mathcal {V}\rightarrow \overline{\mathbb {R}}$ is proper and convex, then it is radially differentiable on ${{\,\mathrm{int}\,}}({{\,\mathrm{dom}\,}}f)$.

Proof

The desired result follows immediately from previous discussion leading up to (51), and the fact that if x is an interior point of the effective domain of f, it follows that for any $u \in \mathcal {V}$, we can find a $\gamma > 0$ small enough that $x - \gamma u \in {{\,\mathrm{dom}\,}}f$, which means we can apply the lower bound of (50) to the difference quotients $q(\alpha ;f,x,u)$ indexed by $\alpha > 0$. $\square$

Appendix 5 Loss example

Example 18

While stated with a somewhat high degree of abstraction, let us give a concrete example to emphasize that the assumptions of Proposition 12 are readily satisfied under natural and important learning settings. Consider the regression problem, where we observe random pairs $(X,Y) \sim \mu$, assuming that X is a finite-dimensional real-valued random vector, and Y is a real-valued random variable, related to the inputs by the relation $Y = h^{*}(X) + \epsilon$, where $\epsilon$ is a zero-mean random noise term. For simplicity, let $h^{*}$ be a continuous linear map, and let $\mathcal {H}$ be the set of all continuous linear maps on the space that X is distributed over. Finally, let the loss by the squared error, such that

$$\begin{aligned} {{\,\mathrm{L}\,}}(h)&= (h(X)-Y)^{2} = (\langle X, h-h^{*} \rangle - \epsilon )^{2}\\ {{\,\mathrm{L}\,}}^{\prime }(h)(u)&= 2(\langle X, h-h^{*} \rangle - \epsilon )\langle u, X\rangle . \end{aligned}$$

Since we make almost no assumptions on the nature of the underlying noise distribution, clearly both the losses and the “gradients” can be unbounded and heavy-tailed. Fix any $h_0 \in \mathcal {H}$, and note that for any $h \in \mathcal {H}$, we have

$$\begin{aligned} {{\,\mathrm{L}\,}}(h)-{{\,\mathrm{L}\,}}(h_0)&= \langle X, h-h^{*} \rangle ^{2} - \langle X, h_0-h^{*} \rangle ^{2} - 2\epsilon \langle X, h-h_0 \rangle \\&= \langle X, h-h_0 \rangle \langle X, (h-h^{*}) + (h_0-h^{*}) \rangle - 2\epsilon \langle X, h-h_0 \rangle . \end{aligned}$$

Absolute values can be bounded above as

$$\begin{aligned} |{{\,\mathrm{L}\,}}(h)-{{\,\mathrm{L}\,}}(h_0) |\le \Vert X\Vert ^{2}\Vert h-h_0\Vert \left( \Vert h-h^{*}\Vert + \Vert h_0-h^{*}\Vert \right) + 2|\epsilon |\Vert X\Vert \Vert h-h_0\Vert . \end{aligned}$$

It follows immediately that as long as ${{\,\mathrm{\mathbf {E}}\,}}_{\mu }\Vert X\Vert ^{4} < \infty$, we have that the local Lipschitz property (42) of the loss is satisfied, for arbitrary choice of $h_0$.

As for the weak smoothness requirement on the loss, note that

$$\begin{aligned} \Vert {{\,\mathrm{L}\,}}^{\prime }(h)-{{\,\mathrm{L}\,}}^{\prime }(h_0)\Vert&= \sup _{\Vert u\Vert =1} \langle u, {{\,\mathrm{L}\,}}^{\prime }(h)-{{\,\mathrm{L}\,}}^{\prime }(h_0) \rangle \\&= \sup _{\Vert u\Vert =1} 2(\langle X, h-h_0 \rangle )\langle u, X\rangle \\&\le 2\Vert X\Vert ^{2}\Vert h-h_0\Vert . \end{aligned}$$

Thus, if the random inputs X are $\mu$-almost surely bounded, the desired smoothness condition (43) holds. Note that this does not preclude heavy-tailed losses and gradients since no additional assumptions have been made on the noise term.

Appendix 6 Empirical supplement

Due to limited space, we could only include key details and a few representative results in Sect. 4 of the main text. Here we fill in those additional details. To begin, all our numerical experiments have been implemented entirely in Python (v. 3.8) using the following additional open-source software: Jupyter notebook (for interactive demos),⁴⁷ matplotlib (v. 3.4.1, for all visuals),⁴⁸ PyTables (v. 3.6.1, for dataset handling),⁴⁹ NumPy (v. 1.20.0, for almost all computations),⁵⁰ and SciPy (v. 1.6.2, for random variable statistics and special functions). In the following paragraphs, we provide information about the benchmark datasets used, as well as several figures including additional experimental results.

Dataset description

The real-world benchmark datasets used in our classification tests are as follows: adult,⁵¹australian,⁵²cifar10,⁵³cod_rna,⁵⁴covtype,⁵⁵emnist_balanced,⁵⁶fashion_mnist,⁵⁷ and mnist.⁵⁸ See Table 1 for a summary. Further background on all datasets is available at the URLs provided in the footnotes. Dataset size reflects the size after removal of instances with missing values, where applicable. For all datasets with categorical features, the “input features” given in Table 1 represents the number of features after doing a one-hot encoding of all such features. The “model dimension” is just the product of the number of input features and the number of classes, since we are using multi-class logistic regression (one linear model for each class). All categorical features are given a one-hot representation. All input features are standardized to take values on the unit interval [0, 1]. As mentioned in the main text, we have prepared a GitHub repository that includes code for both re-creating the empirical tests and pre-processing the data (https://github.com/feedbackward/mrisk).

Table 1 A summary of the benchmark datasets used for performance evaluation

Additional results

In Figs. 6, 7 and 8, we give additional results that complement Fig. 4 in the main text. The trends in terms of the histograms of test loss distributions are essentially uniform across this wide variety of datasets. We also see that a sharply-concentrated logistic (test) loss tends to correlate with better classification error (average zero-one error), with cifar10 being the only exception to this trend. As another point not raised in the main text, intuitively we would hope that Algorithm 1 performs well in terms of the risk ${{\,\mathrm{R}\,}}_{\sigma }$ corresponding to its particular $\sigma$ setting; we have found this to be true across the benchmark datasets studied here. See Fig. 9 for an example from the adult dataset. Moving from top to bottom, the order of colors shows a rather clear reversal. Very similar trends can be observed on the other datasets as well. In estimating ${{\,\mathrm{R}\,}}_{\sigma }$ on the test set, we use an empirical mean estimate of ${{\,\mathrm{r}\,}}_{\sigma }$, and then minimize with respect to $\theta$ using the minimize_scalar function of the SciPy (v. 1.6.2) optimize module.

Fig. 6

Additional average classification error trajectories over epochs

Fig. 7

Additional test error histograms

Fig. 8

Additional test error histograms

Fig. 9

Empirical mean estimates of ${{\,\mathrm{R}\,}}_{\sigma }$ for a variety of $\sigma \in [0,\infty ]$ settings. The colored curves correspond to different $\sigma$ settings in running Algorithm 1, just as in previous plots, whereas the distinct plots correspond to the different $\sigma$ used in evaluation (Color figure online)