Stateless neural meta-learning using second-order gradients

Abstract

Meta-learning can be used to learn a good prior that facilitates quick learning; two popular approaches are MAML and the meta-learner LSTM. These two methods represent important and different approaches in meta-learning. In this work, we study the two and formally show that the meta-learner LSTM subsumes MAML, although MAML, which is in this sense less general, outperforms the other. We suggest the reason for this surprising performance gap is related to second-order gradients. We construct a new algorithm (named TURTLE) to gain more insight into the importance of second-order gradients. TURTLE is simpler than the meta-learner LSTM yet more expressive than MAML and outperforms both techniques at few-shot sine wave regression and 50% of the tested image classification settings (without any additional hyperparameter tuning) and is competitive otherwise, at a computational cost that is comparable to second-order MAML. We find that second-order gradients also significantly increase the accuracy of the meta-learner LSTM. When MAML was introduced, one of its remarkable features was the use of second-order gradients. Subsequent work focused on cheaper first-order approximations. On the basis of our findings, we argue for more attention for second-order gradients.

1 Introduction

Humans learn new tasks quickly. While deep neural networks have demonstrated human or even super-human performance on various tasks such as image recognition (Krizhevsky et al., 2012; He et al., 2015) and game-playing (Mnih et al., 2015; Silver et al., 2016), learning a new task is often slow and requires large amounts of data (LeCun et al., 2015). This limits their applicability in real-world domains where few data and limited computational resources are available.

Meta-learning (Schmidhuber, 1987; Schaul, 2010) is one approach to address this issue. The idea is to learn at two different levels of abstraction: at the outer-level (across tasks), we learn a prior that facilitates faster learning at the inner-level (single task) (Vilalta & Drissi, 2002; Vanschoren, 2018; Hospedales et al., 2020; Huisman et al., 2021). The prior that we learn at the outer-level can take on many different forms, such as the learning rule (Andrychowicz et al., 2016; Ravi & Larochelle, 2017) and the weight initialization (Nichol et al., 2018; Finn et al., 2017).

MAML Finn et al. (2017) and the meta-learner LSTM Ravi and Larochelle (2017) are two well-known techniques that focus on these two types of priors. More specifically, MAML aims to learn a good weight initialization from which it can learn new tasks quickly using regular gradient descent. In addition to learning a good weight initialization, the meta-learner LSTM Ravi and Larochelle (2017) attempts to learn the optimization procedure in the form of a separate LSTM network. The meta-learner LSTM is more general than MAML in the sense that the LSTM can learn to perform gradient descent (see Sect. 4) or something better.

This suggests that the performance of MAML can be mimicked by the meta-learner LSTM on few-shot image classification. However, our experimental results and those by Finn et al. (2017) show that this is not necessarily the case. The meta-learner LSTM fails to find a solution in the meta-landscape that learns as well as gradient descent.

In this work, we aim to investigate the performance gap between MAML and the meta-learner LSTM. We hypothesize that the underperformance of the meta-learner LSTM could be caused by (i) the lack of second-order gradients, or (ii) the fact that an LSTM is used as an optimizer. To investigate these hypotheses, we introduce TURTLE, which is similar to the meta-learner LSTM but uses a fully-connected feed-forward network as an optimizer instead of an LSTM and, in addition, uses second-order gradients. Although both MAML and the meta-learner LSTM are by now surpassed by other state-of-the-art techniques, such as LEO Rusu et al. (2019) and MetaOptNet (Lee et al., 2019) (see Sect. 2), they are still relevant and widely used. The aim of this paper is to gain insight into the performance gap between the meta-learner LSTM and MAML. Our contributions are:

• We formally show that the meta-learner LSTM subsumes MAML.

• We formulate a new meta-learning algorithm called TURTLE to overcome two potential shortcomings of the meta-learner LSTM. We demonstrate that TURTLE successfully closes the performance gap to MAML as it outperforms MAML (and the meta-learner LSTM) on sine wave regression, and various settings involving miniImageNet and CUB by at least 1% accuracy without any additional hyperparameter tuning. TURTLE requires roughly the same amount of computation time as second-order MAML.

• Based on the results of TURTLE, we enhance the meta-learner LSTM by using raw gradients as meta-learner input and second-order information and show these changes result in a performance boost of 1-6% accuracy, indicating the importance of second-order gradients.

2 Related work

The success of deep learning techniques has been largely limited to domains where abundant data and large compute resources are available (LeCun et al., 2015). The reason for this is that learning a new task requires large amounts of resources. Meta-learning is an approach that holds the promise of relaxing these requirements by learning to learn. The field has attracted much attention in recent years, resulting in many new techniques, which can be divided into metric-based, model-based, and optimization-based approaches (Huisman et al., 2021). In our work, we focus on an optimization-based approach, which includes both MAML and the meta-learner LSTM (see Fig. 1).

Fig. 1

An overview of the relationships between optimization-based meta-learning techniques (Huisman et al., 2021)

MAML Finn et al. (2017) aims to find a good weight initialization from which new tasks can be learned quickly within several gradient update steps. As shown in Fig. 1, many works build upon the key idea of MAML, for example, to decrease the computational costs (Nichol et al., 2018; Rajeswaran et al., 2019), increase the applicability to online and active learning settings (Grant et al., 2018; Finn et al., 2018), or increase the expressivity of the algorithm (Li et al., 2017; Park & Oliva, 2019; Lee & Choi, 2018). Despite its popularity, MAML does no longer yield state-of-the-art performance on few-shot learning benchmarks Lu et al. (2020), as it is surpassed by, for example, latent embedding optimization (LEO) Rusu et al. (2019) which optimizes the initial weights in a lower-dimensional latent space, and MetaOptNet Lee et al. (2019), which stacks a convex model on top of the meta-learned initialization of a high-dimensional feature extractor. Although these approaches achieve state-of-the-art techniques on few-shot benchmarks, MAML is elegant and generally applicable as it can also be used in reinforcement learning settings Finn et al. (2017).

While the meta-learner LSTM Ravi and Larochelle (2017) learns both an initialization and an optimization procedure, it is generally hard to properly train the optimizer (Metz et al., 2019). As a result, techniques that use hand-crafted learning rules instead of trainable optimizers may yield better performance. It is perhaps for this reason that most meta-learning algorithms use simple, hand-crafted optimization procedures to learn new tasks, such as regular gradient descent (Bottou, 2004), Adam (Kingma & Ba, 2015), or RMSprop (Tieleman & Hinton, 2017). Andrychowicz et al. (2016), show that learned optimizers may learn faster and yield better performance than gradient descent.

The goal of our work is to investigate why MAML often outperforms the meta-learner LSTM, while the latter is at least as expressive as the former (see Sect. 4.1).¹ Finn and Levine (2018) have shown that the reverse also holds: MAML can approximate any learning algorithm. However, this theoretical result only holds for sufficiently deep base-learner networks. Thus, for a given network depth, it does not say that MAML subsumes the meta-learner LSTM. In contrast, our result that the meta-learner LSTM subsumes MAML holds for any base-learner network and depth.

In order to investigate the performance gap between the meta-learner LSTM and MAML, we propose TURTLE which replaces the LSTM module from the meta-learner LSTM with a feed-forward neural network. Note that Metz et al. (2019) also used a regular feed-forward network as an optimizer. However, they were mainly concerned with understanding and correcting the difficulties that arise from training an optimizer and do not learn a weight initialization for the base-learner network as we do. Baik et al. (2020) also use a feed-forward network on top of MAML but its goal is to generate a per-step learning rate and weight decay coefficients. The feed-forward network in TURTLE, in contrast, generates direct weight updates.

3 Preliminaries

In this section, we explain the notation and the concepts of the works that we build upon.

3.1 Few-shot learning

In the context of supervised learning, the few-shot setup is commonly used as a testbed for meta-learning algorithms (Vinyals et al., 2016; Finn et al., 2017; Nichol et al., 2018; Ravi & Larochelle, 2017). One reason for this is the fact that tasks $\mathcal {T}_j$ are small, which makes learning a prior across tasks not overly expensive.

Every task $\mathcal {T}_j$ consists of a support (training) set $D^{tr}_{\mathcal {T}_j}$ and query (test) set $D^{te}_{\mathcal {T}_j}$ (Vinyals et al., 2016; Lu et al., 2020; Ravi & Larochelle, 2017). When a model is presented with a new task, it tries to learn the associated concepts from the support set. The success of this learning process is then evaluated on the query set. Naturally, this means that the query set contains concepts that were present in the support set.

In classification settings, a commonly used instantiation of the few-shot setup is called N-way k-shot learning (Finn et al., 2017; Vinyals et al., 2016). Here, given a task $\mathcal {T}_j$, every support set contains k examples for each of the N distinct classes. Moreover, the query set must contain examples from one of these N classes.

Suppose we have a dataset D from which we can extract J tasks. For meta-learning purposes, we split these tasks into three non-overlapping partitions: (i) meta-training, (ii) meta-validation, and (iii) meta-test tasks (Ravi & Larochelle, 2017; Sun et al., 2019). These partitions are used for training the meta-learning algorithm, hyperparameter tuning, and evaluation, respectively. Note that non-overlapping means that every partition is assigned some class labels which are unique to that partition.

3.2 MAML

As mentioned before, MAML Finn et al. (2017) attempts to learn a set of initial neural network parameters $\varvec{\theta }$ from which we can quickly learn new tasks within T steps of gradient descent, for a small value of T. Thus, given a task $\mathcal {T}_j = (D^{tr}_{\mathcal {T}_j}, D^{te}_{\mathcal {T}_j})$, MAML will produce a sequence of weights $(\varvec{\theta }_j^{(0)}, \varvec{\theta }^{(1)}_j, \varvec{\theta }^{(2)}_j,..., \varvec{\theta }^{(T)}_j)$, where

$$\begin{aligned} \varvec{\theta }^{(t+1)}_j = \varvec{\theta }_j^{(t)} - \alpha \nabla _{\varvec{\theta }^{(t)}_j} \mathcal {L}_{D^{tr}_{\mathcal {T}_j}}(\varvec{\theta }^{(t)}_j). \end{aligned}$$

(1)

Here, $\alpha$ is the inner learning rate and $\mathcal {L}_{D}(\varvec{\varphi })$ the loss of the network with weights $\varvec{\varphi }$ on dataset D. Note that the first set of weights in the sequence is equal to the initialization, i.e., $\varvec{\theta }_j^{(0)} = \varvec{\theta }$.

Given a distribution of tasks $p(\mathcal {T})$, we can formalize the objective of MAML as finding the initial parameters

$$\begin{aligned} {{\,\mathrm{arg\,min}\,}}_{\varvec{\theta }} \mathbb {E}_{\mathcal {T}_j \backsim p(\mathcal {T})} \left[ \mathcal {L}_{D^{te}_{\mathcal {T}_j}}(\varvec{\theta }^{(T)}_j) \right] . \end{aligned}$$

(2)

Note that the loss is taken with respect to the query set, whereas $\varvec{\theta }^{(T)}_j$ is computed on the support set $D^{tr}_{\mathcal {T}_J}$.

The initialization parameters $\varvec{\theta }$ are updated by optimizing this objective in Eq. (2), where the expectation over tasks is approximated by sampling a batch of tasks. Importantly, updating these initial parameters requires backpropagation through the optimization trajectories on the tasks from the batch. This implies the computation of second-order derivatives, which is computationally expensive. However, (Finn et al., 2017) have shown that first-order MAML, which ignores these higher-order derivatives and is computationally less demanding, works just as well as the complete, second-order MAML version.

3.3 Meta-learner LSTM

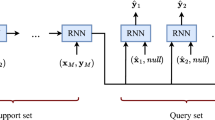
The meta-learner LSTM by Ravi and Larochelle (2017) can be seen as an extension of MAML as it does not only learn the initial parameters $\varvec{\theta }$ but also the optimization procedure which is used to learn a given task. Note that MAML only uses a single base-learner network, while the meta-learner LSTM uses a separate meta-network to update the base-learner parameters, as shown in Fig. 2. Thus, instead of computing $(\varvec{\theta }_j^{(0)}, \varvec{\theta }^{(1)}_j, \varvec{\theta }^{(2)}_j,\ldots , \varvec{\theta }^{(T)}_j)$ using regular gradient descent as done by MAML, the meta-learner LSTM learns a procedure that can produce such a sequence of updates, using a separate meta-network.

Fig. 2

The workflow of the meta-learner LSTM Ravi and Larochelle (2017). The base-learner parameters are updated by an LSTM meta-learner network. The base-learner is denoted as M. $(X_{t}, Y_{t})$ are support sets, whereas (X, Y) is the query set. Note that the figure uses subscripts to indicate time steps and not tasks, i.e., $\theta _T$ are the parameters at step T and not the initial parameters for task T

This trainable optimizer takes the form of a special LSTM module, which is applied to every weight in the base-learner network after the gradients and loss are computed on the support set. The idea is to embed the base-learner weights into the cell state $\varvec{c}$ of the LSTM module. Thus, for a given task $\mathcal {T}_j$, we start with cell state $\varvec{c}_j^{(0)} = \varvec{\theta }$. After this initialization phase, the base-learner parameters (which are now inside the cell state) are updated as

$$\begin{aligned} \varvec{c}_j^{(t+1)} =&\underbrace{\sigma \left( \varvec{W}_{\varvec{f}} \cdot [\nabla _{\varvec{\theta }^{(t)}_j}, \mathcal {L}_{D^{tr}_{\mathcal {T}_j}}, \varvec{\theta }^{(t)}_j, \varvec{f}^{(t-1)}_j ] + \varvec{b}_{\varvec{f}} \right) }_{\text {weight decay}} \odot \varvec{c}_j^{(t)} \nonumber \\&+\underbrace{\sigma \left( \varvec{W}_{\varvec{i}} \cdot [\nabla _{\varvec{\theta }^{(t)}_j}, \mathcal {L}_{D^{tr}_{\mathcal {T}_j}}, \varvec{\theta }^{(t)}_j, \varvec{i}^{(t-1)}_j ] + \varvec{b}_{\varvec{i}} \right) }_{\text {learning rate}} \odot \bar{\varvec{c}}^{(t)}_j, \end{aligned}$$

(3)

where $\odot$ is the element-wise product, the two sigmoid factors $\sigma$ are the parameterized forget gate $\varvec{f}^{(t)}_j$ and learning rate $\varvec{i}^{(t)}_j$ vectors that steer the learning process, $\nabla _{\varvec{\theta }^{(t)}_j} = \nabla _{\varvec{\theta }^{(t)}_j}\mathcal {L}_{D^{tr}_{\mathcal {T}_j}}(\varvec{\theta }^{(t)}_j)$, $\mathcal {L}_{D^{tr}_{\mathcal {T}_j}}=\mathcal {L}_{D^{tr}_{\mathcal {T}_j}}(\varvec{\theta }^{(t)}_j)$, and $\bar{\varvec{c}}^{(t)}_j = -\nabla _{\varvec{\theta }_j^{(t)}} \mathcal {L}_{D^{tr}_{\mathcal {T}_j}}(\varvec{\theta }^{(t)}_j)$. Both the learning rate and forget gate vectors are parameterized by weight matrices $\varvec{W}_f, \varvec{W}_i$ and bias vectors $\varvec{b}_{\varvec{f}}$ and $\varvec{b}_{\varvec{i}}$, respectively. These parameters steer the inner learning on tasks and are updated using regular, hand-crafted optimizers after every meta-training task. As noted by Ravi and Larochelle (2017), this is equivalent to gradient descent when $\varvec{c}^{(t)} = \varvec{\theta }^{(t)}_j$, and the sigmoidal factors are equal to $\varvec{1}$ and $\varvec{\alpha }$, respectively.

In spite of the fact that the LSTM module is applied to every weight individually to produce updates, it does maintain a separate hidden state for each of them. In a similar fashion to MAML, updating the initialization parameters (and LSTM parameters) would require propagating backwards through the optimization trajectory for each task. To circumvent the computational costs associated with this expensive operation, the meta-learner LSTM assumes that input gradients and losses are independent of the parameters in the LSTM.

4 Towards stateless neural meta-learning

In this section, we study the theoretical relationship between MAML and the meta-learner LSTM. Based on the resulting insight, we formulate a new meta-learning algorithm called TURTLE (stateless neural meta-learning) which is simpler than the meta-learner LSTM and more expressive than MAML.

4.1 Theoretical relationship

There is a subsumption relationship between MAML and the LSTM meta-learner. The gradient update rule used by MAML uses a fixed learning rate and no weight decay. The LSTM meta-learner, on the other hand, can learn a dynamic weight decay and learning rate schedule. These observations gives rise to the following theorem:

Theorem 1

The meta-learner LSTM subsumes MAML.

Proof

We prove this theorem by showing that there is a parameterization of the LSTM meta-learner such that it updates the base-learner weights using gradient descent with a fixed learning rate $\alpha$ and without weight decay. In other words, we show that there exist $\varvec{W}_f, \varvec{b_f}, \varvec{W_i}, \varvec{b_i}$ such that the update made by the LSTM meta-learner is equivalent to that made by MAML

$$\begin{aligned} \varvec{c}^{(t+1)}_j&= \varvec{\theta }_j^{(t)} - \alpha \nabla _{\varvec{\theta }^{(t)}_j} \mathcal {L}_{D^{tr}_{\mathcal {T}_j}}(\varvec{\theta }^{(t)}_j) \end{aligned}$$

(4)

$$\begin{aligned}&= \varvec{1} \odot \varvec{\theta }_j^{(t)} + \alpha \varvec{1} \odot - \nabla _{\varvec{\theta }^{(t)}_j} \mathcal {L}_{D^{tr}_{\mathcal {T}_j}}(\varvec{\theta }^{(t)}_j). \end{aligned}$$

(5)

The update of the meta-learner LSTM Eq. (3) satisfies this relationship when $\varvec{c}^{(0)}_j = \varvec{\theta }$ (satisfied by construction), the weight decay is equal a vector of ones $\varvec{1}$, and the learning rate to $\alpha \varvec{1}$. The weight decay condition condition can be met by setting $\varvec{W_f}$ to a matrix of zeros and $\mathbf {b}_f$ to vector of sufficiently large values to push the output of the sigmoid near its saturation point (1). Since the learning rate $0<\alpha < 1$ falls within the codomain of the sigmoid function, the learning rate condition can also be met by setting $\varvec{W_i}$ to a matrix of zeros and $\varvec{b}_f = - \ln (\frac{1-\alpha }{\alpha }) \varvec{1}$. Thus, we have shown that it is possible to parameterize the LSTM meta-learner so that it mimics gradient descent with any learning rate $0 < \alpha \le 1$. $\square$

4.2 Potential problems of the meta-learner LSTM

The theoretical insight that meta-learner LSTM subsumes MAML is not congruent with empirical findings which show that MAML outperforms the meta-learner LSTM on the miniImageNet image classification benchmark (Finn et al., 2017; Ravi & Larochelle, 2017), indicating that LSTM is unable to successfully navigate the error landscape to find a solution at least as good as the one found by MAML.

A potential cause is that the meta-learner LSTM attempts to learn a stateful optimization procedure, allowing it to employ dynamic weight decay and learning rate schedules for learning new tasks. While this gives the technique more flexibility in learning an optimization algorithm, it may also negatively affect meta-optimization as it may be harder to find a good dynamic optimization algorithm than a static one because the space of dynamic algorithms is less constrained. In addition, we conjecture that the loss landscape for dynamic algorithms is less smooth because the weight decay and learning rate schedules, which can have a large influence on the performance, depend on parameter trajectories (paths from initialization to task-specific parameters). We hypothesize that removing the stateful nature of the trainable optimizer may smoothen the meta-landscape as it constrains the space of possible solutions and removes the dependency of the learning rate on parameter trajectories, which can stabilize learning. For this reason, we replace the LSTM module in TURTLE with a regular fully-connected, feed-forward network, which is stateless.

Another potential cause of the underperformance could be the first-order assumption made by the meta-learner LSTM, which we briefly mentioned in Sect. 3.3. Effectively, this disconnects the computational graph by stating that weight updates made at time step t by the meta-network do not influence the inputs that this network receives at future time steps $t< t' < T$. Consequently, the algorithm ignores curvature information which can be important for stable training. While first-order MAML achieves similar performance to MAML, we think that the loss landscape of the LSTM meta-learner is less smooth (for reasons mentioned above), which can exacerbate the harmful effect of the first-order assumption. To overcome this issue, we use second-order gradients by default in TURTLE and investigate the effect of making the first-order assumption.

4.3 TURTLE

In an attempt to make the meta-landscape easier to navigate, we introduce a new algorithm, TURTLE, which trains a feed-forward meta-network to update the base-learner parameters. TURTLE is simpler than the meta-learner LSTM as it uses a stateless feed-forward neural network as a trainable optimizer, yet more expressive than MAML as its meta-network can learn to perform gradient descent.

The trainable optimizer in TURTLE is thus a fully-connected feed-forward neural network. We denote the batch of inputs that this network receives at time step t in the inner loop for task $\mathcal {T}_j$ as $I_j^{(t)} \in \mathbb {R}^{n \times d}$, where n and d are the number of base-learner parameters and the dimensionality of the inputs, respectively. The exact inputs that this network receives will be determined empirically, but two choices, inspired by the meta-learner LSTM, are: (i) the gradients with respect to all parameters and (ii) the current loss (repeated n times for each parameter in the base-network).

Moreover, we could mitigate the absence of a state in the meta-network by including a time step $t \in \{ 0,1,...,T-1 \}$ and/or historical information such as a moving average of previous gradients or updates made by the meta-network. We denote the latter by $\varvec{h}_j^{(t)}$ which is updated by

$$\begin{aligned} \varvec{h}_j^{(t+1)} = \beta \varvec{h}_j^{(t)} + (1 - \beta ) \varvec{v}_j^{(t)}, \end{aligned}$$

(6)

where $0 \le \beta \le 0$ is a constant that determines the time span over which previous inputs affect the new state $\varvec{h}_j^{(t+1)}$, and $\varvec{v}_j^{(t)} \in \mathbb {R}^n$ is the new information (either the updates or gradients at time step t). When using previous updates, we initialize $\varvec{h}_j^{(0)}$ by a vector of zeros.

Weight updates are then computed as follows

$$\begin{aligned} \varvec{\theta }^{(t+1)}_j = \varvec{\theta }_j^{(t)} + \varvec{\alpha } \odot g_{\varvec{\phi }}(I_j^{(t)}), \end{aligned}$$

(7)

where $\varvec{\alpha } \in \mathbb {R}^n$ is a vector of learning rates per parameter. Note that this weight update equation is simpler than the one used by the meta-learner LSTM (see Eq. (3)) as our meta-network $g_{\varvec{\phi }}$ is stateless. Therefore, we do not have parameterized forget and input gates. Moreover, the learning rates per parameter in $\varvec{\alpha }$ are not constrained to be within the interval [0, 1] as is the case for the meta-learner LSTM due to the use of the sigmoid function.

In Algorithm 1 we show, in different colors, the code for MAML (red), the meta-learner LSTM (blue), and TURTLE (green). Although the code structure of the three meta-learners is similar, the update rules are quite different. Both the base—and meta-learner parameters $\varvec{\theta }$ and $\varvec{\phi }$ are updated by backpropagation through the optimization trajectories (line 11).

5 Experiments

In this section, we describe our experimental setup and the results that we obtained.

5.1 Hyperparameter analysis on sine-wave regression

Here, we investigate the effect of the order of information (first- versus second-order), the number of updates T per task, and further increasing the number of layers of the meta-network on the performance of TURTLE on 5-shot sine wave regression. The results are displayed in Fig. 3. Note that in this experiment, we fixed the learning rate vector $\varvec{\alpha }$ to be a vector of ones, which means that the updates proposed by the meta-network are directly added to the base-learner parameters without any scaling. Moreover, the only input that the meta-network receives is the gradient of the loss on the support set with respect to a base-learner parameter, and every hidden layer of the meta-network consists of 20 nodes followed by ReLU nonlinearities.

Fig. 3

a $T = 1$ b $T = 5$ c $T = 10$ Influence of the order, number of update steps, and number of hidden layers (horizontal axis) on the meta-validation performance of TURTLE on 5-shot sine wave regression. We also plot the performance of first—and second-order MAML for comparison. Note that a lower MSE loss corresponds to better performance. The vertical bars indicate the 95% confidence intervals

As we can see, the difference between first—and second-order MAML is relatively small, which was also found by Finn et al. (2017). In contrast, this is not the case for TURTLE, where the first-order variant fails to achieve a similar performance as second-order TURTLE. Furthermore, we see that the stability of TURTLE decreases as T increases as the confidence intervals become larger and the performance with fewer hidden layers deteriorates. Lastly, we find that 5 or 6 hidden layers yield the best performance across different values of T. For this reason, all further TURTLE experiments will be conducted with a meta-network of 5 hidden layers.

5.2 Few-shot sine wave regression

First, we compare the performance of TURTLE to that of MAML and the meta-learner LSTM on sine wave regression, which was originally proposed by Finn et al. (2017). We follow their experimental setup and use 70K, 1K, and 2K tasks for training, validation, and testing respectively. All experiments are performed 30 times with different random weight initializations of the base—and meta-learner networks. We perform meta-validation every 2.5K tasks for hyperparameter tuning. The meta-test results of this experiment are displayed in Fig. 4. As we can see, TURTLE, which uses second-order gradients, systematically outperforms the meta-learner LSTM, which uses first-order gradients.

Fig. 4

Median meta-test performance of MAML, the meta-learner LSTM, and TURTLE on 5-shot sine wave regression. Note that a lower error indicates better performance. The vertical bars indicate the 95% confidence intervals

5.3 Few-shot image classification

Without additional hyperparameter tuning, we now investigate the performance of 5-step TURTLE on few-shot image classification tasks, following the setup used in Chen et al. (2019). In addition, we investigate the importance of second-order gradients in this setting. For this, we use miniImageNet (Vinyals et al., 2016) (with the class splits proposed by Ravi and Larochelle (2017)) and CUB Wah et al. (2011). We use the same base-learner network used by Snell et al. (2017) and Chen et al. (2019). Each algorithm is run with 5 different random weight initializations.

We compare the performance against three simple transfer-learning models, following (Chen et al., 2019): train from scratch, finetuning, and baseline++. Based on our hyperparameter experiments for TURTLE, we also investigate an enhanced version of the meta-learner LSTM which uses raw gradients as meta-learner input and second-order information. The meta-test accuracy scores on 5-way miniImageNet and CUB classification are displayed in Table 1. Note that we use the best-reported hyperparameters for MAML and the meta-learner LSTM on miniImageNet, while we use the best hyperparameters found on sine wave regression for TURTLE. Despite this, TURTLE and second-order meta-learner LSTM outperform MAML and other techniques in 50% of the tested scenarios while they yield the competitive performance in the other scenarios. As we can see, the performances of all models are better on 5-shot classification compared with 1-shot classification. Looking at the results for miniImageNet, we see that the addition of second-order gradients increases the performance of both the meta-learner LSTM and TURTLE. An overview of the exact hyperparameter values that were used for all techniques can be found in `Appendix A'.

Table 1 Median meta-test accuracy scores and 95% confidence intervals over 5 runs of 5-way image classification on miniImageNet (left) and CUB (right)

5.4 Cross-domain few-shot learning

We also investigate the robustness of the meta-learning algorithms when a task distribution shift occurs. For this, we train the techniques on miniImageNet and evaluate their performance on CUB tasks (and vice versa), following (Chen et al., 2019). This is a challenging setting that requires a more general learning ability than for the experiments above. The results are shown in Table 2. Also in these challenging scenarios, second-order gradients are important to increase the performance of both the meta-learner LSTM and TURTLE. More specifically, the omission of second-order gradients can lead to large performance penalties, ranging from 1 to 5% accuracy.

Table 2 Median meta-test accuracy scores in 5-way cross-domain classification (train on tasks from one dataset and evaluate on tasks from another dataset). The median accuracy and 95% confidence intervals were computed over 5 runs

5.5 Running time comparison

Lastly, we compare the running times of MAML, the meta-learner LSTM, and TURTLE on miniImageNet and CUB. A run comprises the time it costs to perform meta-training, meta-validation, and meta-testing on miniImageNet, and evaluation on CUB. We measure the average time in full hours across 5 runs on nodes with a Xeon Gold 6126 2.6GHz 12 core CPU and PNY GeForce RTX 2080TI GPU. The results are displayed in Fig. 5. As we can see, the first-order algorithms are the fastest, while the second-order algorithms are slower (so-MAML and TURTLE). However, the performance of the first-order meta-learner LSTM and first-order TURTLE is worse than that of the second-order variants, indicating the importance of second-order gradients. For MAML, we do not observe such a difference between the first—and second-order variants. TURTLE is, despite its name, not much slower than the second-order MAML (SO-MAML), indicating that the time complexity is dominated by learning the base-learner initialization parameters. In fact, we observe that TURTLE is slightly faster than MAML, indicating that our implementation of the latter is not optimally efficient. In addition, we note that TURTLE is faster than the second-order (enhanced) LSTM meta-learner.

Fig. 5

The running times and few-shot learning accuracy scores on 1-shot (left) and 5-shot (right) miniImageNet image classification of the different techniques for 5 runs with different random seeds

6 Discussion and future work

In this work, we have formally shown that the meta-learner LSTM Ravi and Larochelle (2017) subsumes MAML Finn et al. (2017). Experiments of Finn et al. (2017) and ourselves, however, show that MAML outperforms the meta-learner LSTM. We formulated two hypotheses for this surprising finding and, in turn, we formulated a new meta-learning algorithm named TURTLE, which is simpler than the meta-learner LSTM as it is stateless, yet more expressive than MAML because it can learn the weight update rule as it features a separate meta-network.

We empirically demonstrate that TURTLE is capable of outperforming both MAML and the (first-order) meta-learner LSTM on sine wave regression and—without additional hyperparameter tuning—on the frequently used miniImageNet benchmark. This shows that better update rules exist for fast adaptation than regular gradient descent, which is in line with findings by Andrychowicz et al. (2016). Moreover, we enhanced the meta-learner LSTM by using raw gradients as meta-learner input and second-order gradient information, as they were found to be important for TURTLE. Our results indicate that this enhanced version of the meta-learner LSTM systematically outperforms the original technique by 1–6% accuracy.

In short, these results show that second-order gradients are important for improving the few-shot image classification performance of the meta-learner LSTM and TURTLE, at the cost of additional runtime. In contrast, first-order MAML is a good approximation to second-order MAML as it yields similar performance Finn et al. (2017). This finding supports our hypothesis that the loss landscape of MAML is smoother than that of meta-learning techniques that learn both the initialization parameters and a gradient-based optimization procedure.

6.1 Limitations and open challenges

While TURTLE and the enhanced meta-learner LSTM were shown to yield good performance, it has to be noted that this comes at the cost of increased computational expenses compared with first-order algorithms. That is, these second-order algorithms perform backpropagation through the entire optimization trajectory which requires storing intermediate updates and the computation of second-order gradients. While this is also the case for MAML, it has been shown that first-order MAML achieves a similar performance whilst avoiding this expensive backpropagation process, yielding an excellent trade-off between performance and computational costs. For TURTLE, however, this is not the case, which means that other approaches should be investigated in order to reduce the computational costs. Future research may draw inspiration from Rajeswaran et al. (2019) who approximated second-order gradients in order to speed up MAML.

Our experiments also show that the training stability of TURTLE deteriorates as the number of inner updates increases. This is a known problem of meta-learning techniques that aim to learn the optimization algorithm. Metz et al. (2019) show that this instability is due to the fact that the meta-loss landscape becomes increasingly pathological as the number of inner updates increases. Future work is required to make it feasible to train such techniques for a large number of updates. Moreover, we note that we have only investigated the performances of MAML, TURTLE, and the LSTM meta-learner in 1—and 5-shot settings It would be interesting to investigate in future work how well MAML, TURTLE, and the LSTM meta-learner perform when more shots and ways (classes) are available per task. It may be possible that the performances of these techniques converge to the same point as the amount of available data increases. The intuition behind this is that given enough data, there is no need for a meta-learned prior to successfully learn the task.

Successfully using meta-learning algorithms in scenarios where task distribution shifts occur remains an important open challenge in the field of meta-learning. Our cross-domain experiment demonstrates that the learned optimization procedure by TURTLE generalizes to different tasks than the ones seen at training time, which is in line with findings by Andrychowicz et al. (2016). For this reason, we think that learned optimizers may be an important piece of the puzzle to broaden the applicability of meta-learning techniques to real-world problems. Future work can further investigate this hypothesis.

Our findings further show the benefit of learning an optimizer in addition to the initialization weights and highlight the importance of second-order gradients.

Appendix

1.1 Used hyperparameters

For all techniques mentioned below, we performed meta-validation after every 2,500 training tasks. The best-resulting configuration was evaluated at meta-test time.

For sine wave regression, we use the same base-learner network as Finn et al. (2017), i.e., a fully-connected feed-forward network consisting of a single input node followed by two hidden layers with 40 ReLU nodes each and a final single-node output layer.

For few-shot image classification problems, we use the same base-learner network as used by Snell et al. (2017) and Chen et al. (2019). This network is a stack of four identical convolutional blocks. Each block consists of 64 convolutions of size $3 \times 3$, batch normalization, a ReLU nonlinearity, and a 2D max-pooling layer with a kernel size of 2. The resulting embeddings of the $84 \times 84 \times 3$ input images are flattened and fed into a dense layer with N nodes (one for every class in a task). The base-learner is trained to minimize the cross-entropy loss on the query set, conditioned on the support set.

Transfer learning baselines Note that these models (TrainFromScratch, finetuning, baseline++) pre-trained on minibatches of size 16 sampled from the joint data obtained by merging all meta-training tasks. At test time, they were trained for 100 steps on mini-batches of size 4 sampled from new tasks following Chen et al. (2019). Every 25 steps, we evaluated their performance on the entire support set to select the best configuration to test on the query set.

LSTM meta-learner For selecting the hyperparameters of the LSTM meta-learner,² we followed Ravi and Larochelle (2017). That is, we use a 2-layer architecture, and Adam as meta-optimizer with a learning rate of 0.001. The batch size was set equal to the size of the task. Meta-gradients were clipped to have a norm of at most 0.25, following. The meta-network receives four inputs obtained by preprocessing the loss and gradients using in similar fashion to Andrychowicz et al. (2016) and Ravi and Larochelle (2017). On miniImageNet and CUB, the LSTM optimizer is set to perform 12 updates per task when the number of examples per class is $k=1$ and 5 updates when $k=5$.

MAML Again, we follow Finn et al. (2017) for selecting the hyperparameters, except for the meta-batch size on sine wave regression as we found it not to help performance. This means that the inner learning rate was set to 0.01 and the outer learning rate to 0.001, with Adam as meta-optimizer. These settings hold for both sine wave regression and image classification. When $T > 1$, we use gradient value clipping with a threshold of 10. On image classification, MAML was set to optimize the initial parameters based on $T=5$ update steps, but an additional 5 steps were made afterwards to further increase the performance. Moreover, we used a meta-batch size of 4 and 2 for 1- and 5-shot image classification respectively.

TURTLE We performed many experiments with the hyperparameters of TURTLE on sine wave regression. Here, we only report the settings that were found to give the best performance, which were also used on the image classification problems. That is, the meta-network consists of 5 hidden layers of 20 nodes each. Every hidden node is followed by a ReLU nonlinearity. The input consists of a raw gradient, a historical real-valued number indicating the moving average of the previous input gradients with a (with a beta decay of 0.9), and a time step integer $t \in \{0,...,T-1\}$. The output layer consists of a single node which corresponds to the proposed weight update. For training, we used meta-batches of size 2. Additionally, TURTLE maintains a separate learning rate for all weights in the base-learner network. Lastly, TURTLE uses second-order gradients and Adam as meta-optimizer with a learning rate of 0.001.