1 Introduction

Regression analysis seeks to find a relation between explanatory variables and an outcome variable. The most known linear regression estimator is the Ordinary Least Squares (OLS) which is the best linear unbiased estimator if the noise is i.i.d and Gaussian. Additional constraints on the OLS estimator can be added to ensure that it follows specific properties. For example, penalized regression such as the Ridge regression improves the efficiency of the estimation by introducing a bias and reducing the variance of the estimator in presence of collinearity (Hoerl and Kennard 1970). Another family of constrained regression is defined by the addition of hard constraints on the estimator, such as positivity constraints (Lawson and Hanson 1995) which can improve the estimation performance. Some applications in biology where the goal is to estimate cell proportions inside a tumor or the estimation of temperature in weather forecast justify the use of hard constraints on the estimator. The constrained OLS has been well studied, but the literature around the Support Vector Regression with additional constraints is scarcer.

Support Vector Machine. The Support Vector Machine (SVM) (Boser et al. 1992) is a class of supervised learning algorithms that have been widely used in the past 20 years for classification tasks and regression. These algorithms rely on two main ideas: the first one is the maximum margin hyperplane which consists in finding the hyperplane that maximises the distance between the vectors that are to be classified and the hyperplane. The second idea is the kernel method that allows the SVM to be used to solve non-linear problems. The technique is to map the vectors in a higher dimensional space which is done by using a positive definite kernel, then a maximum margin hyperplane is computed in this space which gives a linear classifier in the high dimensional space. In general, it leads to a non-linear classifier in the original input space.

From SVM to Support Vector Regression. Different implementations of the algorithms haven been proposed such as C-SVM, \(\nu\)-SVM (Schölkopf et al. 1999), Least-Squares SVM (Suykens and Vandewalle 1999), Linear Programming SVM (Friel and Harrison 1998) among others. Each of these versions have their strenghs and weaknesses depending on which application they are used. They differ in terms of constraints considered for the hyperplane (C-SVM and Least-Squares SVM), in terms of norm considered on the parameters (C-SVM and Linear Programming SVM) and in terms of optimization problem formulation (C-SVM and \(\nu\)-SVM). Overall, these algorithms are a great tool for classification tasks and they have been used in many different applications like facial recognition (Jia and Martinez 2009), image classification (Chapelle et al. 1999), cancer type classification (Haussler et al. 2000), text categorization (Joachims 1998) to only cite a few examples. Even though, SVM was first developped for classification, an adaptation for regression estimation was proposed in Drucker et al. (1997) under the name Support Vector Regression (SVR). In this case, the idea of maximum margin hyperplane is slightly changed into finding a tube around the regressors. The size of the tube is controlled by a hyperparameter chosen by the user: \(\epsilon\). This is equivalent to using an \(\epsilon\)-insensitive loss function, \(|y-f(x)|_{\epsilon } = \max \{0, |y-f(x)|-\epsilon \}\) which only penalizes the error above the chosen \(\epsilon\) level. As for the classification version of the algorithm, a \(\nu\)-SVR method exists. In this version, the hyperparameter \(\epsilon\) is computed automatically but a new hyperparameter \(\nu\) has to be chosen by the user which controls asymptotically the proportions of support vectors (Schölkopf et al. 1999). SVR has proven to be a great tool in the field of function estimation for many different applications: predicting times series in stock trades (Van Gestel et al. 2001), travel-time prediction (Chun-Hsin et al. 2004) and for estimating the amount of cells present inside a tumor (Newman et al. 2015).

Incorporating priors. In this last example of application, the authors used SVR to estimate a vector of proportions, however the classical SVR estimator does not take into account the information known about the space in which the estimator lives. Adding this prior information on the estimator may lead to better estimation performance. Incorporating information in the estimation process is a wide field of studies in statistical learning (we refer to Fig. 2 in Lauer and Bloch (2008) for a quick overview in the context of SVM). A growing interest in prior knowledge incorporated as regularization terms has emerged in the last decades. Lasso (Tibshirani 1996), Ridge (Hoerl and Kennard 1970), elastic-net (Zou and Hastie 2005) regression are examples of regularized problem where a prior information is used to fix an ill-posed problem or an overdetermined problem. The \(\ell _{1}\) regularization of the Lasso will force the estimator to be sparse and bring statistical guarantees of the Lasso estimator in high dimensional settings. Another common way to add prior knowledge on the estimator is to add constraints known a-priori on this estimator. The most common examples are the ones that constrain the estimator to live in a subspace such as Non Negative Least Squares Regression (NNLS) (Lawson and Hanson 1995), isotonic regression (Barlow and Brunk 1972). These examples belong to a more general type of constraints: linear constraints. Other types of constraints exist like constraints on the derivative of the function that is to be estimated, smoothness of the function for example. Adding those constraints on the Least Squares estimator has been widely studied (Barlow and Brunk 1972; Liew 1976; Bro and De Jong 1997) and similar work has been done for the Lasso estimator (Gaines et al. 2018). Concerning the SVR, inequality and equality constraints added as prior knowledge were studied in Lauer and Bloch (2008). In this paper, the authors described a method for adding linear constraints on the Linear Programming SVR (Friel and Harrison 1998). This implementation of the algorithm considers the \(\ell _{1}\) norm of the parameters in the optimization problem instead of the classical \(\ell _{2}\) norm which leads to a linear programming optimization problem to solve instead of a quadratic programming problem. They also described a method for using information about the derivative of the function that is estimated.

Sequential Minimal Optimization. One of the main challenges of adding these constraints is that it often increases the difficulty of solving the optimization problem related to the estimator. For example, the Least Squares optimization problem has a closed-form solution whereas the NNLS uses sophisticated algorithms (Bro and De Jong 1997) to approach the solution. SVM and SVR algorithms were extensively studied and used in practise because very efficient algorithms were developed to solve the underlying optimization problems. One of them is called Sequential Minimal Optimization (SMO) (Platt 1998) and is based on a well known optimization technique called coordinate descent. The idea of the coordinate descent is to break the optimization problem into sub-problems selecting a subset of coordinates at each step and minimizing the function only via this chosen subset. The development of parallel algorithms have increased the interest in these coordinate descent methods which show to be very efficient for large scale problems. One of the key settings for the coordinate descent is the choice of the coordinate at each step, the choice’s strategy will affect the efficiency of the algorithm. There exists three families of strategies for coordinate descent: cyclic (Tseng 2001), random (Nesterov 2012) and greedy. The SMO algorithm is a variant of a greedy coordinate descent (Wright 2015) and is the algorithm implemented in LibSVM (Chang and Lin 2011). It is very efficient to solve SVM/SVR optimization problems. In the context of linear kernel, other algorithm are used such as dual coordinate descent (Hsieh et al. 2008) or trust region newton methods (Lin et al. 2007).

Priors and SMO. In one of the application of SVR cited above, information a-priori about the estimator is not used in the estimation process and is only used in a post-processing step. This application comes from the cancer research field, where regression algorithms have been used to estimate the proportions of cell populations that are present inside a tumor (see Mohammadi et al. (2017) for a survey). Several estimators have been proposed in the biostatistics literature, most of them based on constrained least squares (Abbas et al. 2009; Qiao et al. 2012; Gong et al. 2011) but the gold standard is the estimator based on the Support Vector Regression (Newman et al. 2015). Our work is motivated by incorporating the fact that the estimator for this application belongs to the simplex: \({\mathcal {S}} = \{x \in {\mathbb {R}}^{n}: \sum _{i=1}^{n}x_{i}=1,\text { }x_{i}\ge 0\}\) in the SVR problem. We believe that for this application, it will lead to better estimation performance. From an optimization point of view, our motivation is to find an efficient algorithm that is able to solve the SVR optimization problem where generic linear constraints are added to the problem as prior knowledge, including simplex prior as described. This work follows the one from Lauer and Bloch (2008) except that in our case, we keep the \(\ell _{2}\) norm on the parameters in the optimization problem which is the most common version of the SVR optimization problem and we only focus on inequality and equality constraints as prior knowledge.

Contributions. In this paper, we study a linear SVR with linear constraints optimization problem. We show that the dual of this new problem shares similar properties with the classical \(\nu\)-SVR optimization problem (Proposition 2). We also prove that adding linear constraints to the SVR optimization problem does not change the nature of its dual problem, in the fact that the problem stays a semi-definite positive quadratic function subject to linear constraints. We propose a generalized SMO algorithm that allows the resolution of the new optimization problem. We show that the updates in the SMO algorithm keep a closed-form (Definition 5) and prove the convergence of the algorithm to a solution of the problem (Theorem 1). We illustrate on synthetic and real datasets the usefulness of our new regression estimator under different regression settings: non-negative regression, simplex regression and isotonic regression.

Outline. The article proceeds as follows: we introduce the optimization problem coming from the classical SVR and describe the modifications brought by adding linear constraints in Sect. 2. We then present the SMO algorithm, its generalization for solving constrained SVR and present our result on the convergence of the algorithm in Sect. 3. In Sect. 4, we use synthetic and real datasets on different regression settings to illustrate the practical performance of the new estimator.

Notations. We write ||.|| (resp. \(\langle .,.\rangle\)) for the euclidean norm (resp. inner product) on vectors. We use the notation \(X_{:i}\) (resp. \(X_{i:}\)) to denote the vector corresponding the the \(i^{th}\) column of the matrix X (resp. \(i^{th}\) row of the matrix X). Throughout this paper, the design matrix will be \(X\in {\mathbb {R}}^{n\times p}\) and \(y\in {\mathbb {R}}^{n}\) will be the response vector. \(X^{T}\) will be used for the transposed matrix of X. The vector e denotes the vector with only ones on each of its coordinates and \(e_{j}\) denotes the canonical vector with a one at the \(j^{\mathrm{th}}\) coordinate. \(\nabla _{x_{i}} f\) is the partial derivative \(\frac{\partial f}{\partial x_{i}}\).

2 Constrained support vector regression

We study the underlying optimization problem that arises when adding linear constraints to the SVR estimator. One way to solve the optimization problem is to perform coordinate descent algorithms variants in its dual. In this section, we derive the dual optimization problem of the constrained SVR in order to apply coordinate descent variants to solve the constrained version, as it will be shown in Sect. 3. We describe the similarities and the differences between the classical problem and the constrained one.

2.1 Previous work : \(\nu\)-support vector regression

The \(\nu\)-SVR estimator (Schölkopf et al. 1999) is obtained solving the following quadratic optimization problem:

$$\begin{aligned} \begin{array}{ll} \underset{\beta ,\beta _{0},\xi _{i},\xi _{i}^{*},\epsilon }{\min } & \frac{1}{2}||\beta ||^{2}+C\left( \nu \epsilon + \frac{1}{n} \displaystyle \sum _{i=1}^{n}(\xi _{i}+\xi _{i}^{*})\right) \\ \\ \text {subject to} & y_{i}-\beta ^{T}X_{i:}-\beta _{0}\le \epsilon + \xi _{i} \\ \\ & \beta ^{T}X_{i:}+\beta _{0} -y_{i}\le \epsilon +\xi _{i}^{*} \\ \\ & \xi _{i},\xi _{i}^{*}\ge 0,\epsilon \ge 0. \end{array} \end{aligned}$$
(SVR-P)

By solving Problem (SVR-P), we seek a linear function \(f(x)=\beta ^{T}x+\beta _{0}\) where \(\beta \in {\mathbb {R}}^{p}\) and \(\beta _{0}\in {\mathbb {R}}\), that is at most \(\epsilon\) deviating from the response vector coefficient \(y_{i}\). This function does not always exist which is why slack variables \(\xi \in {\mathbb {R}}^{n}\) and \(\xi ^{*}\in {\mathbb {R}}^{n}\) are introduced in the optimization problem to allow some observations to break the condition given before. C and \(\nu\) are two hyperparameters. \(C\in {\mathbb {R}}\) controls the tolerated error and \(\nu \in [0,1]\) controls the number of observations that will lay inside the tube of size \(2\epsilon\) given by the two first constraints in (SVR-P). It can be seen as an \(\epsilon\)-insensitive loss function where a linear penalization is put on the observations that lay outside the tube and the observations that lay inside the tube are not penalized (see Smola and Schölkopf (2004) for more details).

The different algorithms proposed to solve the primal Problem (SVR-P) often use its dual problem like in Platt (1998) and Hsieh et al. (2008). The dual problem is also a quadratic optimization problem with linear constraints but its structure allows an efficient resolution as we will see in more details in Sect. 3. The dual problem of (SVR-P) is the following optimization problem:

$$\begin{aligned} \begin{array}{ll} \underset{\alpha ,\alpha ^{*}}{\min } &\frac{1}{2}(\alpha -\alpha ^{*})^{T}Q(\alpha -\alpha ^{*})+y^{T}(\alpha -\alpha ^{*}) \\ \\ \text {subject to} & 0\le \alpha _{i},\alpha _{i}^{*}\le \frac{C}{n} \\ \\ & \mathbf{e} ^{T}(\alpha +\alpha ^{*})\le C\nu \\ \\ & \mathbf{e} ^{T}(\alpha -\alpha ^{*})=0 , \\ \end{array} \end{aligned}$$
(SVR-D)

where \(Q=XX^{T} \in {\mathbb {R}}^{n\times n}\). The equation link between (SVR-P) and (SVR-D) is given by the following formula: \(\beta =-\sum _{i=1}^{n}(\alpha _{i}-\alpha _{i}^{*})X_{i:} .\)

2.2 The constrained optimization problem

We propose a constrained version of Problem (SVR-P) that allows the addition of prior knowledge on the linear function f that we seek to estimate. The constrained estimator is obtained solving the optimization problem:

$$\begin{aligned} \begin{array}{ll} \underset{\beta ,\beta _{0},\xi _{i},\xi _{i}^{*},\epsilon }{\min } & \frac{1}{2}||\beta ||^{2}+C\left( \nu \epsilon +\frac{1}{n}\displaystyle \sum _{i=1}^{n}(\xi _{i}+\xi _{i}^{*})\right) \\ \\ \text {subject to} & \beta ^{T}X_{i:}+\beta _{0} -y_{i}\le \epsilon + \xi _{i} \\ \\ & y_{i}-\beta ^{T}X_{i:}-\beta _{0}\le \epsilon +\xi _{i}^{*} \\ \\ & \xi _{i},\xi _{i}^{*}\ge 0,\epsilon \ge 0 \\ \\ & A\beta \le b \\ \\ & \varGamma \beta = d, \\ \end{array} \end{aligned}$$
(LSVR-P)

where \(A\in {\mathbb {R}}^{k_{1}\times p}\), \(\varGamma \in {\mathbb {R}}^{k_{2}\times p}\), \(\beta \in {\mathbb {R}}^{p}\), \(\xi\), \(\xi ^{*} \in {\mathbb {R}}^{n}\) and \(\beta _{0}\), \(\epsilon\), \(\in {\mathbb {R}}\).

The algorithm that we propose in Sect. 3 also uses the structure of the dual problem of (LSVR-P). The next proposition introduces the dual problem and some of its properties.

Proposition 1

If the set \(\{ \beta \in {\mathbb {R}}^{n}, A\beta \le b, \varGamma \beta \ = d\}\) is not empty then,

  1. 1.

    Strong duality holds for (LSVR-P).

  2. 2.

    The dual problem of (LSVR-P) is

    $$\begin{aligned} \begin{array}{ll} \underset{\alpha ,\alpha ^{*},\gamma ,\mu }{\min } &\frac{1}{2}\left[ (\alpha -\alpha ^{*})^{T}Q(\alpha -\alpha ^{*}) +\gamma ^{T}AA^{T}\gamma \right. \\ \\ &+\mu ^{T}\varGamma \varGamma ^{T}\mu +2\displaystyle \sum ^{n}_{i=1}(\alpha _{i}-\alpha _{i}^{*})\gamma ^{T}AX_{i:}\\ \\ &\left. -2\displaystyle \sum ^{n}_{i=1}(\alpha _{i}-\alpha _{i}^{*})\mu ^{T}\varGamma X_{i:} -2\gamma ^{T}A\varGamma ^{T}\mu \right] \\ \\ &+y^{T}(\alpha -\alpha ^{*})+\gamma ^{T}b-\mu ^{T}d\\ \\ \text {subject to} & 0 \le \alpha _{i}^{(*)}\le \frac{C}{n} \\ \\ & \mathbf{e} ^{T}(\alpha +\alpha ^{*})\le C\nu \\ \\ & \mathbf{e} ^{T}(\alpha -\alpha ^{*})=0 \\ \\ & \gamma _{j}\ge 0, \\ \end{array} \end{aligned}$$
    (LSVR-D)
  3. 3.

    The equation link between primal and dual is

    $$\begin{aligned} \beta = -\sum _{i=1}^{n}(\alpha _{i}-\alpha _{i}^{*})X_{i:} - A^{T}\gamma +\varGamma ^{T}\mu . \end{aligned}$$

The proof of the first statement of the proposition is given in the discussion below whereas the proofs for the two other statements come from a straightforward derivation of the Lagragian dual of (LSVR-P). We have that \(\alpha\), \(\alpha ^{*}\in {\mathbb {R}}^{n}\), \(\gamma \in {\mathbb {R}}^{k_{1}}\) are the vector of Lagrange multipliers associated the the inequality constraint \(A\beta \le b\) which explains the non-negative constraints on its coefficients. \(\mu \in {\mathbb {R}}^{k_{2}}\) are the Lagrange multipliers associated to the equality constraint \(\varGamma \beta =d\) which also explains that there are no constraints in the dual problem on \(\mu\). The objective function f which we will write in the stacked form as:

$$\begin{aligned} f(\theta )=\theta ^{T}\bar{Q}\theta +l^{T}\theta , \end{aligned}$$

where

$$\begin{aligned} \theta= & \begin{bmatrix} \alpha \\ \alpha ^{*} \\ \gamma \\ \mu \end{bmatrix}, \quad l= \begin{bmatrix} y \\ -y \\ b \\ -d \end{bmatrix} \in {\mathbb {R}}^{2n+k_{1}+k_{2}},\\ \bar{Q}= & \begin{bmatrix} Q & -Q & XA^{T} & -X\varGamma ^{T} \\ -Q & Q & -XA^{T} & X\varGamma ^{T} \\ AX^{T} & -AX^{T} & AA^{T} & -A\varGamma ^{T} \\ -\varGamma X^{T} & \varGamma X^{T} & -\varGamma A^{T} & \varGamma \varGamma ^{T} \end{bmatrix} \end{aligned}$$

is a square matrix of size \(2n+k_{1}+k_{2}\).

An important observation is that this objective function is always convex. The matrix \(\bar{Q}\) is the product of the matrix \(\begin{bmatrix} X \\ -X \\ A \\ -\varGamma \end{bmatrix}\) and its transpose matrix. It means that \(\bar{Q}\) is a Gramian matrix and it is positive semi-definite which implies that f is convex. The problem (LSVR-D) is then a quadratic programming optimization problem which meets Slater’s condition if there exists a \(\theta\) that belongs to the feasible domain which we will denote by \({\mathcal {F}}\). If there is such a \(\theta\) we have strong duality holding between problem (LSVR-P) and (LSVR-D). The only condition we need to have on A and \(\varGamma\) is that they define a non-empty polyhedron in order to be able to solve the optimization problem.

Our second observation on problem (LSVR-D) is that the inequality constraints \(\mathbf{e} ^{T}(\alpha +\alpha ^{*})\le C\nu\) is replaced by an equality constraint in the same way that it was suggested in Chang and Lin (2002) for the classical problem (SVR-D).

Proposition 2

If \(\epsilon\) is strictly positive, all optimal solutions of (LSVR-D) satisfy

  1. 1.

    \(\alpha _{i}\alpha _{i}^{*}=0\), \(\forall i \le n\),

  2. 2.

    \(\mathbf{e} ^{T}(\alpha +\alpha ^{*})=C\nu\).

The proof is given in Appendix A. This observation will be important for the algorithm that we propose in Sect. 3.

3 Generalized sequential minimal optimization

In this section we propose a generalization of the SMO algorithm (Platt 1998) to solve problem (LSVR-D) and present our main result on the convergence of the proposed algorithm to the solution of (LSVR-D). The SMO algorithm is a variant of greedy coordinate descent taking into consideration non-separable constraints, which in our case are the two equality constraints. We start by describing the previous algorithm that solve (SVR-D).

3.1 Previous work: sequential minimal optimization

In this subsection, we define

$$\begin{aligned} f(\alpha ,\alpha ^{*})=\frac{1}{2}(\alpha -\alpha ^{*})^{T}Q(\alpha -\alpha ^{*}) +y^{T}(\alpha -\alpha ^{*}) \end{aligned}$$

and we note \(\nabla f\in {\mathbb {R}}^{2n}\) its gradient. From Keerthi and Gilbert (2002), we rewrite the Karush-Kuhn-Tucker (KKT) conditions in the following way:

$$\begin{aligned} \underset{i\in I_{\mathrm{up}}}{\min }\nabla _{\alpha _{i}} f \ge \underset{j\in I_{\mathrm{low}}}{\max }\nabla _{\alpha _{j}} f, \end{aligned}$$
(1)

where \(I_{\mathrm{up}}(\alpha )=\{i \in \{1,\ldots ,n\} : \alpha _{i}<\frac{C}{n}\}\) and \(I_{\mathrm{low}}(\alpha )=\{i \in \{1,\ldots ,n\} : \alpha _{i}>0\}\).

The same condition is written for the \(\alpha ^{*}\) variables replacing \(\alpha _{i}\) by \(\alpha _{i}^{*}\) above. These conditions leads to an important definition for the rest of this paper.

Definition 1

We will say that (i, j) is a violating pair of variables if one of these two conditions is satisfied:

$$\begin{aligned}&i\in I_{\mathrm{up}}(\alpha ), j\in I_{\mathrm{low}}(\alpha ) \text { and } \nabla _{\alpha _{i}}f< \nabla _{\alpha _{j}}f, \\&i\in I_{\mathrm{low}}(\alpha ), j\in I_{\mathrm{up}}(\alpha ) \text { and } \nabla _{\alpha _{i}}f> \nabla _{\alpha _{j}}f. \end{aligned}$$

Because the algorithm SMO does not provide in general an exact solution in a finite number of steps there is a need to relax the optimality conditions which gives a new definition.

Definition 2

We will say that (i, j) is a \(\tau\)-violating pair of variables if one of these two conditions is satisfied:

$$\begin{aligned}&i\in I_{\mathrm{up}}(\alpha ), j\in I_{\mathrm{low}}(\alpha ) \text { and } \nabla _{\alpha _{i}}f< \nabla _{\alpha _{j}}f -\tau , \\&i\in I_{\mathrm{low}}(\alpha ), j\in I_{\mathrm{up}}(\alpha ) \text { and } \nabla _{\alpha _{i}}f> \nabla _{\alpha _{j}}f +\tau . \end{aligned}$$

The SMO algorithm will then choose at each iteration a pair of violating variables in the \(\alpha\) block or in the \(\alpha ^{*}\) block. Once the choice is done, a subproblem of size two is solved, considering that only the two selected variables are to be minimized in problem (SVR-D). The outline of the algorithm is presented in Algorithm 1.

The choice of the violating pair of variables presented in Keerthi et al. (2001) was to always work with the most violating pairs of variables, which means the variables that leads to the largest gap compared to the optimality conditions given in (1). This choice is what makes a link with greedy coordinate descent, however greedy here is related to the largest gap with the optimality score and is not related to the largest decrease in the objective function.

The resolution of the subproblem of size two has a closed-form. The idea is to use the two equality constraints to go from a problem of size two to a problem of size one. Then, the goal is to minimize a quadratic function of one variable under box constraints which is done easily. We will give more details of the resolution of these subproblems in Sect. 3.3 for our proposed algorithm.

The proof of convergence of SMO algorithm was given in Keerthi and Gilbert (2002) without convergence rate. The proof relies on showing that the sequence defined by the algorithm \(f(\alpha ^{k},(\alpha ^{*})^{k})\) is a decreasing sequence and that there cannot be the same violating pair of variables infinitely many times. The linear convergence rate was proved later by She (2017) as well as the identification of the support vectors in finite time.

figure a

3.2 Optimality conditions for the constrained SVR

In this subsection we define f as the objective function of Problem (LSVR-D) and \(\nabla f\in {\mathbb {R}}^{2n+k_{1}+k_{2}}\) its gradient. We will now give the KKT conditions of (LSVR-D) for the different blocks. The results derive from classical Lagragian calculation.

The \(\alpha\) block   Case 1- \(\alpha _{i}=0\) then \(\beta _{i}=0\) and \(\lambda _{i}\ge 0\), we have that

$$\begin{aligned} \nabla _{\alpha _{i}} f-\sigma -\delta \ge 0. \end{aligned}$$

Case 2- \(\alpha _{i}=\frac{C}{n}\) then \(\lambda _{i}=0\) and \(\beta _{i}\ge 0\), we have that

$$\begin{aligned} \nabla _{\alpha _{i}} f-\sigma -\delta \le 0. \end{aligned}$$

Case 3- \(0<\alpha _{i}<\frac{C}{n}\) then \(\beta _{i}=0\), we have that

$$\begin{aligned} \nabla _{\alpha _{i}} f-\sigma -\delta =0. \end{aligned}$$

We then consider the sets of indices:

$$\begin{aligned}&I_{\mathrm{up}}(\alpha )=\left\{ i \in \{1,\ldots ,n\} : \alpha _{i}<\frac{C}{n}\right\} , \\&I_{\mathrm{low}}(\alpha )=\{i \in \{1,\ldots ,n\} : \alpha _{i}>0\}. \end{aligned}$$

The optimality conditions are satisfied if and only if

$$\begin{aligned} \underset{i\in I_{\mathrm{up}}}{\min }\nabla _{\alpha _{i}} f \ge \underset{j\in I_{\mathrm{low}}}{\max }\nabla _{\alpha _{j}} f. \end{aligned}$$

The \(\alpha ^{*}\) block    In this block, the conditions are very similar to the ones given for the block \(\alpha\), the only difference here is that we will have two new sets of indices:

$$\begin{aligned}&I_{\mathrm{up}}^{*}(\alpha ^{*}) =\left\{ i \in \{1,\ldots ,n\} : \alpha _{i}^{*}<\frac{C}{n}\right\} , \\&I_{\mathrm{low}}^{*}(\alpha )=\{i \in \{1,\ldots ,n\} : \alpha _{i}^{*}>0\}. \end{aligned}$$

which gives the following optimality condition:

$$\begin{aligned} \underset{i\in I_{\mathrm{up}}^{*}}{\min }\nabla _{\alpha _{i}^{*}} f \ge \underset{j\in I_{\mathrm{low}}^{*}}{\max }\nabla _{\alpha _{j}^{*}} f. \end{aligned}$$

The \(\gamma\) block

$$\begin{aligned} \nabla _{\gamma _{j}}L&= \nabla _{\gamma _{j}}f-\eta _{j}=0 \\ \eta _{j}\gamma _{j}&=0 \\ \eta _{j}&\ge 0. \end{aligned}$$

We will consider different possiblities of value for \(\gamma _{j}\).

Case 1- \(\gamma _{j}=0\) then \(\nabla _{\gamma _{j}} f\ge 0\).

Case 2- \(\gamma _{j}>0\) then \(\nabla _{\gamma _{j}} f= 0\).

Definition 3

We will say that j is a \(\tau\)-violating variable for the block \(\gamma\) if \(\nabla _{\gamma _{j}}f + \tau < 0\).

The \(\mu\) block

$$\begin{aligned} \nabla _{\mu _{j}}L= \nabla _{\mu _{j}}f=0. \end{aligned}$$

Definition 4

We will say that j is a \(\tau\)-violating variable for the block \(\mu\) if \(|\nabla _{\mu _{j}} f|> \tau\).

From these conditions on each block, we build an optimization strategy that follows the idea of the SMO described in Sect. 3.1. For each block of variables, we compute what we call a violating optimality score based on the optimality conditions given above. Once the scores are computed for each block, we select the block which has the largest score and solve an optimization subproblem in the block selected. If the block \(\alpha\) or the block \(\alpha ^{*}\) is selected, we will update a pair of variables by solving a minization problem of size two. However if the block \(\gamma\) or the block \(\mu\) is selected, we will update only one variable at a time. This is justified by the fact that the variables \(\alpha\) and \(\alpha ^{*}\) have non-separable equality constraints linking them together. The rest of this section will be dedicated to the presentation of our algorithm and to giving some interesting properties such as a closed-form for updates on each of the blocks and a convergence theorem.

figure b

3.3 Updates rules and convergence

The first definition describes the closed-form updates for the different blocks of variables.

Definition 5

The update between iterate k and iterate \(k+1\) of the generalized SMO algorithm has the following form:

  1. 1.

    if the block \(\alpha\) is selected and (i, j) is the most violating pair of variable then the update will be as follows:

    $$\begin{aligned}&\alpha _{i}^{k+1}=\alpha _{i}^{k}+t^{*}, \\&\alpha _{j}^{k+1}=\alpha _{j}^{k}-t^{*}, \end{aligned}$$

    where \(t^{*}=\min (\max (I_{1},-\frac{(\nabla _{\alpha _{i}}f -\nabla _{\alpha _{j}}f)}{(Q_{ii}-2Q_{ij}+Q_{jj})}),I_{2})\) with \(I_{1}=\max (-\alpha _{i}^{k},\alpha _{j}^{k}-\frac{C}{n})\) and \(I_{2}=\min (\alpha _{j}^{k},\frac{C}{n}-\alpha _{i}^{k})\).

  2. 2.

    if the block \(\alpha ^{*}\) is selected and \((i^{*},j^{*})\) is the most violating pair of variable then the update will be as follows:

    $$\begin{aligned}&(\alpha _{i}^{*})^{k+1} =(\alpha _{i}^{*})^{k}+t^{*}, \\&(\alpha _{j}^{*})^{k+1} =(\alpha _{j}^{*})^{k}-t^{*}, \end{aligned}$$

    where \(t^{*}=\min (\max (I_{1},-\frac{(\nabla _{\alpha _{i}^{*}}f -\nabla _{\alpha _{j}^{*}}f)}{(Q_{ii}-2Q_{ij}+Q_{jj})}),I_{2})\) with \(I_{1}=\max (-(\alpha _{i}^{*})^{k},(\alpha _{j}^{*})^{k}-\frac{C}{n})\) and \(I_{2}=\min ((\alpha _{j}^{*})^{k},\frac{C}{n} -(\alpha _{i}^{*}))^{k}\).

  3. 3.

    if the block \(\gamma\) is selected and i is the index of the most violating variable in this block then the update will be as follows:

    $$\begin{aligned} \gamma _{i}^{k+1}=\max \left( -\frac{\nabla _{\gamma _{i}}f}{(AA^{T})_{ii}}+\gamma _{i}^{k},0\right) . \end{aligned}$$
  4. 4.

    if the block \(\mu\) is selected and i is the index of the most violating variable in this block then the update will be as follows:

    $$\begin{aligned} \mu _{i}^{k+1}=-\frac{\nabla _{\mu _{i} f}}{(\varGamma \varGamma ^{T})_{ii}}+\mu _{i}^{k}. \end{aligned}$$

This choice of updates comes from solving the optimization problem (LSVR-D) considering that only one or two variables are updated at each step. One of the key elements of the algorithm is to make sure that at each step the iterate belongs to \({\mathcal {F}}\). Let us suppose that the block \(\alpha\) is selected as the block in which the update will happen and let (i, j) be the most violating pair of variables. The update is the resolution of a subproblem of size 2, considering that only \(\alpha _{i}\) and \(\alpha _{j}\) are the variables, the rest remains constant. The two equality constraints in (LSVR-D), \(\sum _{i=1}^{n}\alpha _{i}-\alpha _{i}^{*}=0\) and \(\sum _{i=1}^{n}\alpha _{i}+\alpha _{i}^{*}=C\nu\), lead to the two following equalities: \(\alpha _{i}^{k+1}+\alpha _{j}^{k+1} =\alpha _{i}^{k}+\alpha _{j}^{k}\). The later yields to using a parameter t for the update of the variables leading to \(\alpha _{i}^{k+1}=\alpha _{i}^{k}+t\) and \(\alpha _{j}^{k+1}=\alpha _{j}^{k}-t\).

Updating the variable in the block \(\alpha\) this way will force the iterates of Algorithm 1 to meet the two equalities constraints at each step. We find t by solving the dual problem (LSVR-D) considering that we minimize only over t. Let the vector \(u\in {\mathbb {R}}^{2n+p+k_{1}+k_{2}}\) which contains only zeros except at the \(i^{th}\) coordinate where it is equal to t and at \(j^{th}\) coordinate where it is equal to \(-t\). Therefore, we find t by minimizing the following optimization problem:

$$\begin{aligned} \begin{array}{ll} \underset{t \in {\mathbb {R}}}{\min } & \psi (t)=\frac{1}{2}\left[ (\theta ^{k}+u)^{T}\bar{Q}(\theta ^{k}+u)\right] +l^{T}(\theta ^{k}+u)\\ \\ \text {subject to} & 0 \le \alpha _{i}^{k+1},\alpha _{j}^{k+1}\le \frac{C}{n}. \\ \end{array} \end{aligned}$$

First we minimize the objective function without the constraints and since it is a quadratic function of one variable we just clip the solution of unconstrained problem to have the solution of the constrained problem. We will use the term “clipped update” or “clipping” when the update is projected unto the constraints space and is not the result of the unconstrainted optimization problem. As we only consider size one problem for the updates, it will mean that the update will be a bound of an interval. We will use the notation K as a term containing the terms that do not depend on t. We write that

$$\begin{aligned} \psi (t)&=\frac{1}{2}u^{T}\bar{Q}u +u^{T}\bar{Q}\theta ^{k}+l^{T}u+ K \\&= \frac{1}{2}t^{2}(\bar{Q}_{ii}+\bar{Q}_{jj}-2\bar{Q}_{ij}) +u^{T}\nabla f(\theta ^{k}) + K \\&= \frac{1}{2}t^{2}(\bar{Q}_{ii}+\bar{Q}_{jj}-2\bar{Q}_{ij}) +t(\nabla _{\alpha _{i}} f(\theta ^{k})\\&-\nabla _{\alpha _{j}} f(\theta ^{k})) + K. \end{aligned}$$

It follows that the unconstrained minimum of \(\psi (t)\) is \(t_{q}=\frac{-(\nabla _{\alpha _{i}} f(\theta ^{k})-\nabla _{\alpha _{j}} f(\theta ^{k}))}{(\bar{Q}_{ii}+\bar{Q}_{jj}-2\bar{Q}_{ij})}.\)

Taking the constraints into account we have that \(0\le \alpha _{i}^{k}+t\le \frac{C}{n}\) and \(0\le \alpha _{j}^{k}-t\le \frac{C}{n}\), which yields to \(t^{*}=\min (\max (I_{1},t_q),I_{2})\) with \(I_{1}=\max (-\alpha _{i},\alpha _{j}-\frac{C}{n})\) and \(I_{2}=\min (\alpha _{j},\frac{C}{n}-\alpha _{i})\). The definition of the updates for the block \(\alpha ^{*}\) relies on the same discussion.

Let us now make an observation that will explain the definition of the updates for the blocks \(\gamma\) and \(\mu\). Let i be the index of the variable that will be updated. Solving the problem; \(\theta _{i}^{k+1}=\underset{\theta _{i}}{\mathrm{argmin}}\frac{1}{2}\theta ^{T}\bar{Q}\theta +l^{T}\theta ,\) leads to the following solution \(\theta ^{k+1}_{i}=\frac{-\nabla _{i} f(\theta ^{k})}{\bar{Q}_{ii}}+\theta _{i}^{k}\).

Let us recall that the update for the block \(\gamma\) has to keep the coefficient of \(\gamma\) positive to stay in \({\mathcal {F}}\) hence we have to perform the following clipped update with \(i\in \{2n+p+1,\ldots ,2n+p+k_{1}\}\):

$$\begin{aligned} \theta _{i}^{k+1}=\max \left( \frac{-\nabla _{\gamma _{i}}f(\theta ^{k})}{\bar{Q}_{ii}}+\theta ^{k}_{i},0\right) . \end{aligned}$$

Then noticing that \(\bar{Q}_{ii} = AA^{T}_{ii}\) for this block, we obtain the update for the block \(\gamma\).

There are no constraints on the variables in the blok \(\mu\), so the update comes from the fact that \(\bar{Q}_{ii}=\varGamma \varGamma ^{T}_{ii}\) for \(i\in \{ 2n+p+k_{1}+1,\ldots ,2n+p+k_{1}+k_{2} \}\) which corresponds to the indices of the block \(\mu\).

From these updates we have to make sure that

$$\begin{aligned} Q_{ii}+Q_{jj}-2Q_{ij}\ne 0, \end{aligned}$$

let us recall that \(Q_{ij}=\langle X_{i:}, X_{j:}\rangle\) which means that

$$\begin{aligned} Q_{ii}+Q_{jj}-2Q_{ij}= ||X_{i:}-X_{j:}||^{2}. \end{aligned}$$

This quantity is zero only when \(X_{i:}=X_{j:}\) coordinate wise. It would mean that the same row appears two times in the design matrix which does not bring any new information for the regression and can be avoided easily. \((AA^{T})_{ii}=\langle A_{i:}, A_{i:}\rangle\) is zero if and only if \(A_{i:}=0\) which means that a row of the matrix A is zero, so there is no constraint on any variable of the optimization problem which will never happen. It is the same discussion for \((\varGamma \varGamma ^{T})_{ii}\).

The next proposition makes sure that once a variable (resp. pair of variables) is updated, it cannot be a violating variable (resp. pair of variables) at the next step. This proposition makes sure, for the two blocks \(\alpha\) and \(\alpha ^{*}\), that the update \(t^{*}\) cannot be 0.

Proposition 3

If (i, j) (resp.i) was the pair of most violating variable (resp. the most violating variable) in the block \(\alpha\) or \(\alpha ^{*}\) (resp. block \(\gamma\) or \(\mu\)) at iteration k then at iteration \(k+1\), (i, j) (resp. i) cannot be violating the optimality conditions.

The proof of this proposition is left in the Appendix B.

Finally, we show that the algorithm converges to a solution of (LSVR-D) and since strong duality holds it allows us to have a solution of (LSVR-P).

Theorem 1

For any given \(\tau >0\) the sequence of iterates \(\{\theta ^{k}\}\), defined by the generalized SMO algorithm, converges to an optimal solution of the optimization problem (LSVR-D)

The proof of this theorem relies on the same idea as the one proposed in Lopez and Dorronsoro (2012) for the classical SMO algorithm and is given in Appendix C. We show that it can be extended to our algorithm with some new observations. The general idea of the proof is to see that the distance between the primal vector generated by the SMO-algorithm and the optimal solution of the primal is controled by the following expression \(\frac{1}{2}||\beta ^{k}-\beta ^{\mathrm{opt}}||\le f(\theta ^{k})-f(\theta ^{\mathrm{opt}})\), where \(\beta ^{k}\) is the \(k^{th}\) primal iterate obtained via the relationship primal-dual and \(\theta ^{k}\) and where \(\beta ^{\mathrm{opt}}\) is a solution of (LSVR-P). From this observation, we show that we can find a subsequence of the SMO-algorithm \(\theta ^{k_{j}}\) that converges to some \(\bar{\theta }\), solution of the dual problem. Using the continuity of the objective function of the dual problem, we have that \(f(\theta ^{k_{j}})\rightarrow f(\bar{\theta })\). Finally, we show that the sequence \(\{f(\theta ^{k})\}\) is decreasing and bounded which implies its convergence and from the convergence monotone theorem we know that to \(f(\theta ^{k})\) converges to \(f(\bar{\theta })\) since one of its subsequences converges. This proves that \(||\beta ^{k}-\beta ^{\mathrm{opt}}||\rightarrow 0\) and finishes the proof. The convergence rate for the SMO algorithm is difficult to obtain considering the greedy choice of the blocks and the greedy choice inside the blocks. A proof for the classical SMO exists but with uniformly at random choice of the block (She 2017). Convergence rate for greedy algorithms in optimization can be found in Nutini et al. (2015) for example but the assumption that the constraints must be separable is a major issue for our case. The study of this convergence rate is out of scope of this paper.

4 Numerical experiments

The code for the different regression settings is available on a GitHub repositoryFootnote 1, each setting is wrapped up in a package and is fully compatible with scikit learn (Pedregosa et al. 2011) BaseEstimator class.

In order to compare the estimators, we worked with the Mean Absolute Error; \({{\,\mathrm{MAE}\,}}= \frac{1}{p}\sum _{i=1}^{p} |\beta ^{*}_{i}-\hat{\beta }_{i}|\) and the Root Mean Squared Error; \({{\,\mathrm{RMSE}\,}}=\sqrt{\frac{1}{p}||\beta ^{*}-\hat{\beta }||^{2}}\), where \(\beta ^{*}\) are the ground truth coefficients and \(\hat{\beta }\) are the estimated coefficients. We also used the Signal-To-Noise Ratio (SNR) to control the level noise simulated in the data defined as \({{\,\mathrm{SNR}\,}}=10\log 10(\frac{{\mathbb {E}}(X\beta (X\beta )^{T} )}{{{\,\mathrm{Var}\,}}(\epsilon )}).\)

4.1 Non negative regression

First, the constraints are set to force the coefficient of \(\beta\) to be positive and we compare our constrained-SVR estimator with the NNLS (Lawson and Hanson 1995) estimator which is the result of the following optimization problem

$$\begin{aligned} \begin{array}{ll} \underset{\beta }{\min } & \frac{1}{2}||y-X\beta || \\ \\ \text {subject to} & \beta _{i}\ge 0. \\ \end{array} \end{aligned}$$
(NNLS)

In this special case of non-negative regression, \(A=-I_{p}\), \(b=0\), \(\varGamma =0\), \(d=0\), the constrained-SVR optimization problem which we will call Non-Negative SVR (NNSVR) then becomes

$$\begin{aligned} \begin{array}{ll} \underset{\beta ,\beta _{0},\xi _{i},\xi _{i}^{*},\epsilon }{\min } & \frac{1}{2}||\beta ||^{2}+C\left( \nu \epsilon +\frac{1}{n}\displaystyle \sum _{i=1}^{n}(\xi _{i}+\xi _{i}^{*})\right) \\ \\ \text {subject to} & \beta ^{T}X_{i:}+\beta _{0} -y_{i}\le \epsilon + \xi _{i} \\ \\ & y_{i}-\beta ^{T}X_{i:}-\beta _{0}\le \epsilon +\xi _{i}^{*} \\ \\ & \xi _{i},\xi _{i}^{*}\ge 0,\epsilon \ge 0 \\ \\ & \beta _{i} \ge 0. \\ \end{array} \end{aligned}$$
(NNSVR)

Synthetic data. We generated the design matrix X from a Gaussian distribution \({\mathcal {N}}(0,1)\) with 500 samples and 50 features. The true coefficients to be found \(\beta ^{*}\) were gererated taking the exponential of a Gaussian distribution \({\mathcal {N}}(0,2)\) in order to have positive coefficients. Y was simply computed as the product between X and \(\beta ^{*}\). We wanted to test the robustness of our estimator compared to NNLS and variant of SVR estimators. To do so, we simulated noise in the data using different types of distributions, we tested Gaussian noise and Laplacian noise under different levels of noise. For this experiment, the noise distributions were generated to have an SNR equals to 10 and 20, for each type of noise we performed 50 repetitions. The noise was only added in the matrix Y, the design matrix X was left noiseless. The choice of the two hyperparameters C and \(\nu\) was done using 5-folds cross validation on a grid of possible pairs. The values of C were taken evenly spaced in the log10 base between \([-3,3]\), we considered 10 different values. The values of \(\nu\) were taken evenly spaced in the linear space between [0.05, 1.0] and we also considered 10 possible values.

We compared different estimators: NNLS, NNSVR, the Projected-SVR (P-SVR) which is simply the projection of the classical SVR estimator unto the positive orthant and also the classical SVR estimator without constraints. The results of this experiment are in Table 1. We see that for a low Gaussian noise level (\({{\,\mathrm{SNR}\,}}= 20\)) the NNLS has a lower RMSE and lower MAE. However, we see that the differences between the four compared methods are small. When the level of noise increases (\({{\,\mathrm{SNR}\,}}= 10\)), the NNSVR estimator is the one with the lowest RMSE and MAE. The NNLS estimator performs poorly in the presence of high level of noise in comparison to the SVR based estimator. When a Laplacian noise is added to the data, the NNSVR is the estimator that has the lowest RMSE and MAE for low level of noise \({{\,\mathrm{SNR}\,}}= 20\) and high level of noise \({{\,\mathrm{SNR}\,}}= 10\).

Table 1 Results for the support vector regression (SVR), projected support regression (P-SVR), non-negative support vector regression (NNSVR) and non-negative least squares (NNLS) for simulated data with \(n= 500\) and \(p=50\)
Full size table

4.2 Regression unto the simplex

In this subsection, we study the performance of our proposed estimator on simplex constraints Simplex Support Vector Regression (SSVR). In this case, \(A=-I_{p}\), \(b = 0\), \(\varGamma = \mathbf{e}\) and \(d=1\). The optimization problem that we seek to solve is:

$$\begin{aligned} \begin{array}{ll} \underset{\beta ,\beta _{0},\xi _{i},\xi _{i}^{*},\epsilon }{\min } & \frac{1}{2}||\beta ||^{2}+C\left( \nu \epsilon +\frac{1}{n}\displaystyle \sum _{i=1}^{n}(\xi _{i}+\xi _{i}^{*})\right) \\ \\ \text {subject to} & \beta ^{T}X_{i:}+\beta _{0} -y_{i}\le \epsilon + \xi _{i} \\ \\ & y_{i}-\beta ^{T}X_{i:}-\beta _{0}\le \epsilon +\xi _{i}^{*} \\ \\ & \xi _{i},\xi _{i}^{*}\ge 0,\epsilon \ge 0 \\ \\ & \beta _{i} \ge 0 \\ \\ & \sum _{i}\beta _{i} = 1. \\ \end{array} \end{aligned}$$
(SSVR)
Fig. 1
figure 1

The root mean squared error (RMSE) as a function of the signal to noise ration (SNR) is presented. Different dimensions for the design matrix X and the response vector y were considered. n represents the number of rows of X and p the number of columns. For each plot, the blue line represents the RMSE for the Linear Simplex SVR (LSSVR) estimator, the green one the Simplex Ordinary Least Squares (SOLS) estimator and the orange on the Cibersort estimator. Each point of the curve is the mean RMSE of 50 repetitions. The noise in the data has a Gaussian distribution

Full size image

Synthetic data. We first tested on simulated data generated by the function make_regression of scikit-learn. Once the design matrix X and the response vector y were generated using this function, we had access to the ground truth that we will write \(\beta ^{*}\). This function was not designed to generate data with a \(\beta ^{*}\) that belongs to the simplex so we first projected \(\beta ^{*}\) unto the simplex and then recomputed y multiplying the design matrix by the new projected \(\beta ^{*}_{{\mathcal {S}}}\). We added a centered Gaussian noise in the data with the standard deviation chosen such as the signal-to-noise ratio (SNR) was equal to a defined number, we used the following formula for a given SNR \(\sigma = \sqrt{\frac{{{\,\mathrm{Var}\,}}(y)}{10^{SNR/10}}}\), where \(\sigma\) is the standard deviation used to simulate the noise in the data. The choice of the two hyperparameters C and \(\nu\) was done using 5-folds cross validation on a grid of possible pairs. The values of C were taken evenly spaced in the log10 base between \([-3,3]\), we considered 10 different values. The values of \(\nu\) were taken evenly spaced in the linear space between [0.05, 1.0] and we also considered 10 possible values. We tested different size for the matrix \(X\in {\mathbb {R}}^{n\times p}\) to check the potential effects of the dimensions on the quality of the estimation and we did 50 repetitions for each point of the curves. The measure that was used to compare the different estimators is the RMSE between the true \(\beta\) and the estimated \(\hat{\beta }\).

We compared the RMSE of our estimator to the Simplex Ordinary Least Squares (SOLS) which is the result of the following optimization problem:

$$\begin{aligned} \begin{array}{ll} \underset{\beta }{\min } & \frac{1}{2}||y-X\beta ||^{2} \\ \\ \text {subject to} & \beta _{i}\ge 0, \\ \\ & \sum _{i=1}^{p} \beta _{i} = 1, \\ \end{array} \end{aligned}$$
(SOLS)

and to the estimator proposed in the biostatics litterature that is called Cibersort. This estimator is simply the result of using the classical SVR and project the obtained estimator unto the simplex. The RMSE curves as a function of the SNR are presented in Fig. 1. We observe that the SSVR is generally the estimator with the lowest RMSE, this observation becomes clearer as the level of noise increases in the data. We notice that when there is a low level of noise and when n is not too large in comparison to p, the three compared estimator perform equally. However, there is a setting when n is large in comparison to p (in this experiment for \(n = 250\) or 500 and \(p = 5\)) where the SSVR estimator has a higher RMSE than the Cibersort and SOLS estimator untill a certain level of noise (\({{\,\mathrm{SNR}\,}}<15\)). Overall, this simulation shows that there is a significant improvement in the estimation performance of the SSVR mainly when there is noise in the data.

Real dataset. In the cancer research field, regression algorithms have been used to estimate the proportions of cell populations that are present inside a tumor. Indeed, a tumor is composed of different types of cells such as cancer cells, immune cells, healthy cells among others. Having access to the information of the proportions of these cells could be a key to understanding the interactions between the cells and the cancer treatment called immunotherapy (Couzin-Frankel 2013). The modelization done is that the RNA extracted from the tumor is seen as a mixed signal composed of different pure signals coming from the different types of cells. This signal can be unmixed knowing the different pure RNA signal of the different types of cells. In other words, y will be the RNA signal coming from a tumor and X will be the design matrix composed of the RNA signal from the isolated cells. The number of rows represent the number of genes that we have access to and the number of columns of X is the number of cell populations that we would like to quantify. The hypothesis is that there is a linear relationship between X and y. As said above, we want to estimate proportions which means that the estimator has to belong to the probability simplex \(\mathscr {S}=\{x : x_{i}\ge 0\text { , }\sum _{i}x_{i}=1\}\).

Several estimators have been proposed in the biostatistics litterature most of them based on constrained least squares (Qiao et al. 2012; Gong et al. 2011; Abbas et al. 2009) but the gold standard is the estimator based on the SVR.

We compared the three same estimators on a real biological dataset where the real quantities of cells to obtain were known. The dataset can be found on the GEO website under the accession code GSE11103Footnote 2. For this example \(n=584\) and \(p=4\) and we have access to 12 different samples that are our repetitions. Following the same idea than previous benchmark performed in this field of application, we increased the level of noise in the data and compared the RMSE of the different estimators. Gaussian and Laplacian distributions of noise were added to the data. The choice of the two hyperparameters C and \(\nu\) was done using 5-folds cross validation on a grid of possible pairs. The values of C were taken evenly spaced in the \(\log _{10}\) base between \([-5,-3]\), we considered 10 different values. The interval of C is different than the simulated data because of the difference in the range value of the dataset. The values of \(\nu\) were taken evenly spaced in the linear space between [0.05, 1.0] and we also considered 10 possible values.

We see that when there is no noise in the data (\({{\,\mathrm{SNR}\,}}= \infty\)) both Cibersort and SSVR estimator perform equally. The SOLS estimator already has a higher RMSE than the two others estimator probably due to the noise already present in the data. As the level of noise increases, the SSVR estimator remains the estimator with the lowest RMSE in both Gaussian and Laplacian noise settings (Fig. 2).

Fig. 2
figure 2

The Root Mean Squared Error (RMSE) as a function of the Signal to Noise Ration (SNR) is presented on a real dataset where noise was manually added. Two different noise distribution were tested: Gaussian and laplacian. Each point of the curve is the mean RMSE of 12 different response vectors and we repeated the process four times for each level of noise. This would be equivalent to having 48 different repetitions

Full size image

4.3 Isotonic regression

In this subsection, we will consider constraints that impose an order on the variables. This type of regression is usually called isotonic regression. Such constraints appear when prior knowledge are known on a certain order on the variables. This partial order on the variables can also be seen as an acyclic directed graph. More formally, we note \(G = (V, E)\) a directed acyclic graph where V is the set of vertices and E is the set of nodes. On this graph, we define a partial order on the vertices. We will say for \(u, v\in V\) that \(u\le v\) if and only if there is a path joining u and v in G. This type of constraints seems natural in different applications such as biology, medicine, and weather forecast.

The most simple example of this type of constraints might be the monotonic regression where we force the variables to be in a increasing or decreasing order. It means that with our former notations that we would impose that \(\beta _{1}\le \beta _{2} \le \ldots \le \beta _{p}\) on the estimator. This type of constraints can be coded in a finite difference matrix (or more generally any incidence matrix of a graph) where \(A = (a_{i,j}) \in {\mathbb {R}}^{(p-1) \times p}\) defined by \(a_{i,i} = 1\), \(a_{i,i+1} = -1\), \(a_{i,j} = 0\) otherwise, and \(\varGamma = 0\), \(b=0\), \(d=0\) forming linear constraints as in the scope of this paper. The Isotonic Support Vector Regression (ISVR) optimization problem is written as follows:

$$\begin{aligned} \begin{array}{ll} \underset{\beta ,\beta _{0},\xi _{i},\xi _{i}^{*},\epsilon }{\min } & \frac{1}{2}||\beta ||^{2}+C\left( \nu \epsilon +\frac{1}{n}\displaystyle \sum _{i=1}^{n}(\xi _{i}+\xi _{i}^{*})\right) \\ \\ \text {subject to} & \beta ^{T}X_{i:}+\beta _{0} -y_{i}\le \epsilon + \xi _{i} \\ \\ & y_{i}-\beta ^{T}X_{i:}-\beta _{0}\le \epsilon +\xi _{i}^{*} \\ \\ & \xi _{i},\xi _{i}^{*}\ge 0,\epsilon \ge 0 \\ \\ & \beta _{1} \le \beta _{2}\le \ldots \le \beta _{n}. \\ \end{array} \end{aligned}$$
(ISVR)

We compare our proposed ISVR estimator with the classical least squares isotonic regression (IR) (Barlow and Brunk 1972) which is the solution of the following problem:

$$\begin{aligned} \begin{array}{ll} \underset{\beta }{\min } & \frac{1}{2}||\beta -y||^{2} \\ \\ \text {subject to} & \beta _{1} \le \beta _{2}\le \ldots \le \beta _{n}. \\ \end{array} \end{aligned}$$
(IR)

Synthetic dataset. We first generated data from a Gaussian distribution (\(\mu =0\), \(\sigma =1\)) that we sorted and then added noise in the data following the same process as described in Sect. 4.2 with different SNR values (10 and 20). We tested Gaussian noise and Laplacian noise. We compared the estimation quality of both methods using MAE and RMSE. In this experiment, the design matrix X is the identity matrix. We performed grid search selection via cross validation for the hyperparameters C and \(\nu\). C had 5 different possible values taken on the logscale from 0 to 3, and \(\nu\) had 5 different values taken between 0.05 and 1 on the linear scale. The dimension of the generated Gaussian vector was 50 and we did 50 repetitions. We present in Table 2 the results of the experiment, the value inside a cell is the mean RMSE or MAE over the 50 repetitions and the value between brackets is the standard deviation over the repetitions. Under a low level of Gaussian noise or Laplacian noise, both methods are close in term of RMSE and MAE with a little advantage for the classical isotonic regression estimator. When the level of noise is important (\({{\,\mathrm{SNR}\,}}= 10\)), our proposed ISVR has the lowest RMSE and MAE for the two noise distribution tested.

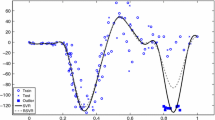
Table 2 Results for the isotonic support vector regression (ISVR), and the isotonic regression (IR) for simulated data with \(p=50\)
Full size table

Real dataset. Isotonic types of constraints can be found in different applications such as biology, ranking and weather forecast for example. Focusing on global warming type of data, researchers have studied the anomaly of the average temperature over a year in comparison to the years 1961-1990. These temperature anomalies have a monotenous trend and keep increasing since 1850 until 2015. Isotonic regression estimator was used on this datasetFootnote 3 in Gaines et al. (2018) and we compared our proposed ISVR estimator for anomaly prediction. The hyperparameter for the ISVR were set manually for this simulation. Figure 3 shows the result for the two estimators. The classical isotonic regression estimator perform better than our proposed estimator globally which is confirmed by the RMSE and MAE values of \({{\,\mathrm{RMSE}\,}}_{\mathrm{IR}} = 0.0067\) against \({{\,\mathrm{RMSE}\,}}_{\mathrm{ISVR}} = 0.083\) and \({{\,\mathrm{MAE}\,}}_{\mathrm{IR}} = 0.083\) against \({{\,\mathrm{MAE}\,}}_{\mathrm{ISVR}} = 0.116\). However, we notice that in the portions where there is a significant change like between 1910-1940 and 1980-2005, the IR estimation looks like a step function whereas the ISVR estimation follows an increasing trend without these piecewise constant portions. The bias induced by the use of constraints can be overcome with refitting methods such as Deledalle et al. (2017).

Fig. 3
figure 3

Global warming dataset. Annual temperature anomalies relative to 1961–1990 average, with estimated trend using Isotonic Support Vector Regression (ISVR) and the classical Isotonic Regression (IR) estimator

Full size image

4.4 Performance of the GSMO versus SMO

We compared the efficiency of the SMO algorithm to solve the classical SVR optimization problem and the SSVR optimization problem in Fig. 4. To do so, we used the same data simulation process described earlier in this subsection and set the number of rows of the matrix X, \(n = 200\) and the number of columns \(p=25\). Two different settings were considered here, one without any noise in the data and another one with Gaussian noise added such that the SNR would be equal to 30. The transparent trajectories represent the decrease of the objective function or the optimality score \(\varDelta\) for the classical SMO in blue and for the generalized SMO in red for the 50 repetitions considered. The average trajectory is represented in dense color. The first row of figures are the results for the noiseless setting and the second row for the setting with noise. When there is not noise in the data, the generalized SMO decreases faster than the classical SMO. It is important to remind that the true vector here belongs to the simplex so without any noise it is not surprising that our proposed algorithm goes faster than the classical SMO. However, when noise is adding to the data, it takes more iterations for the generalized SMO to find the solution of the optimization problem. Figure 4 illustrates the convergence towards a minimum the GSMO algorithm as stated in Theorem 1.

Fig. 4
figure 4

Plots of 50 trajectories of the dual objective function value (first column) and the optimality score (second column) in function of the number of iterations for the classical SMO algorithm in blue and the proposed generalized SMO in red. Two settings were used, one without noise and another one with additive Gaussian noise

Full size image

5 Conclusion

In this paper, we studied the optimization problem related to SVR with linear constraints. We showed that for this optimization problem, strong duality holds and that the dual problem is convex. We presented a generalized SMO algorithm that solve the dual problem and we proved its convergence to a solution. This algorithm uses a coordinate descent strategy where a closed-form of the updates were defined. The proposed algorithm is easy to implement and shows good performance in practise. We demonstrated the good performance of our proposed estimator on different regression settings. In presence of high level of noise, our estimator has shown to be robust and has better estimation performance in comparison to Least Squares based estimators or projected SVR estimators.

This work leaves several open questions for future works. The question of the convergence rate of the algorithm is very natural and will have to be address in the future. Another natural question rises about the possibility to extend our method on non-linear function estimation with linear constraints. From our point of view, it is a very challenging question because the dual optimization problem of the linearly constrained SVR loses its only dependence on the inner product between the columns of X, crossed terms appear in the objective function which makes it difficult to use the kernel trick as it would naturally be used for classical SVR.