Data scarcity, robustness and extreme multi-label classification

Abstract

The goal in extreme multi-label classification (XMC) is to learn a classifier which can assign a small subset of relevant labels to an instance from an extremely large set of target labels. The distribution of training instances among labels in XMC exhibits a long tail, implying that a large fraction of labels have a very small number of positive training instances. Detecting tail-labels, which represent diversity of the label space and account for a large fraction (upto 80%) of all the labels, has been a significant research challenge in XMC. In this work, we pose the tail-label detection task in XMC as robust learning in the presence of worst-case perturbations. This viewpoint is motivated by a key observation that there is a significant change in the distribution of the feature composition of instances of these labels from the training set to test set. For shallow classifiers, our robustness perspective to XMC naturally motivates the well-known $\ell _1$-regularized classification. Contrary to the popular belief that Hamming loss is unsuitable for tail-labels detection in XMC, we show that minimizing (convex upper bound on) Hamming loss with appropriate regularization surpasses many state-of-the-art methods. Furthermore, we also highlight the sub-optimality of the co-ordinate descent based solver in the LibLinear package, which, given its ubiquity, is interesting in its own right. We also investigate the spectral properties of label graphs for providing novel insights towards understanding the conditions governing the performance of Hamming loss based one-vs-rest scheme vis-à-vis label embedding methods.

1 Introduction

Extreme multi-label classification (XMC) refers to supervised learning with a large target label set where each training/test instance is labeled with small subset of relevant labels which are chosen from the large set of target labels. Machine learning problems consisting of hundreds of thousand labels are common in various domains such as annotating web-scale encyclopedia (Prabhu and Varma 2014), hash-tag suggestion in social media (Denton et al. 2015), and image-classification (Deng et al. 2010). For instance, all Wikipedia pages are tagged with a small set of relevant labels which are chosen from more than a million possible tags in the collection. It has been demonstrated that, in addition to automatic labelling, the framework of XMC can be leveraged to effectively address learning problems arising in recommendation systems, ranking and web-advertizing (Agrawal et al. 2013; Prabhu and Varma 2014). In the context of recommendation systems for example, by learning from similar users’ buying patterns in e-stores like Amazon and eBay, this framework can be used to recommend a small subset of relevant items from a large collection in the e-store. With applications in a diverse range, designing effective algorithms to solve XMC has become a key challenge for researchers in industry and academia alike.

In addition to large number of target labels, typical datasets in XMC consist of a similar scale for the number of instances in the training data and also for the dimensionality of the input feature space. For text datasets, each training instance is a sparse representation of a few hundred non-zero features from the input space having dimensionality of the order hundreds of thousand. An an example, a benchmark WikiLSHTC-325K dataset from the extreme classification repository (Bhatia et al. 2016) consists of 1.7 Million training instances which are distributed among 325,000 labels and each training instance sparsely spans a feature space of 1.6 Million dimensions. The challenge posed by the sheer scale of number of labels, training instances and features, makes the setup of XMC quite different from that tackled in classical literature in multi-label classification (Tsoumakas et al. 2009), and hence renders the direct and off-the-shelf application of some of the classical methods, such as Random Forests, Decision Trees and SVMs, non-applicable.

1.1 Tail labels

An important statistical characteristic of the datasets in XMC is that a large fraction of labels are tail labels, i.e., those which have very few training instances that belong to them (also referred to as power-law, fat-tailed distribution and Zipf’s law). This distribution is shown in Fig. 1 for two publicly available benchmark datasets from the XMC repository,¹WikiLSHTC-325K and Amazon-670K datasets, consisting of approximately 325,000 and 670,000 labels respectively. For Amazon-670K, only 100,000 out of 670,000 labels have more than 5 training instances in them.

Fig. 1

Power-law distribution. Y-axis is on log-scale, and X-axis represents the labels ranked according to decreasing number of training instances in them

Tail labels exhibit diversity of the label space, and contain informative content not captured by the head or torso labels. Indeed, by predicting well the head labels, an algorithm can achieve high accuracy and yet omit most of the tail labels. Such behavior is not desirable in many real world applications. For instance, in movie recommendation systems, the head labels correspond to popular blockbusters—most likely, the user has already watched these. In contrast, the tail corresponds to less popular yet equally favored films, like independent movies (Shani and Gunawardana 2013). These are the movies that the recommendation system should ideally focus on. A similar discussion applies to search engine development (Radlinski et al. 2009) and hash-tag recommendation in social networks (Denton et al. 2015), and hierarchical classification (Babbar et al. 2014).

From a statistical perspective, it has been conjectured in the recent works that Hamming loss is unsuitable for detection of tail-labels in XMC (Jain et al. 2016; Bhatia et al. 2015; Prabhu and Varma 2014). In particular, the work in Jain et al. (2016) proposes new propensity-scored loss functions (discussed in Sect. 3) which are sensitive towards the tail-labels by weighing them higher than the head/torso labels. In this work, we refute the above conjecture by motivating XMC from a robustness perspective.

1.2 Our contributions

In this work, our contributions are the following :

• Statistically, we model XMC as learning in the presence of worst-case perturbations, and demonstrate the efficacy of Hamming loss for tail-label prediction in XMC. This novel perspective stems from the observation that, for tail labels, there is a significant variation in the feature composition of instances in the test set as compared to the training set. We thus frame the learning problem as a robust optimization objective which accounts for this feature variation by considering perturbations $\tilde{\mathbf{x }}_i$ for each input training instance $\mathbf x _i$.

• Algorithmically, by exploiting the label-wise independence of Hamming loss among labels, our algorithm is amenable to distributed training across labels. As a result, our forward–backward proximal gradient algorithm can scale upto hundreds of thousand labels for benchmark datasets. Our investigation also shows that the corresponding solver in the LibLinear package (“−s 5” option) yields sub-optimal solutions because of severe under-fitting. Due to its widespread usage in machine learning packages such as scikit-learn, this finding is significant in its own right.

• Empirically, our robust optimization formulation of XMC naturally motivates the well-known $\ell _1$ regularized SVM, which is shown to surpass around one dozen state-of-the-art methods on benchmark datasets. For a Wikpedia dataset with 325,000 labels, we show 20% relative improvement over PFastreXML and Parabel—leading tree based approaches, and 60% over SLEEC—a leading label embedding method.

• Analytically, by drawing connections to spectral properties of label graphs, we also present novel insights to explain the conditions under which Hamming loss might be suited for XMC vis-à-vis label embedding methods. We show that the algebraic connectivity of label graph can be used to explain the variation in the relative performance of various methods as it varies from small datasets consisting of few hundred labels to the extreme regime consisting of hundreds of thousand labels.

Our robustness perspective also draws connections to recent advances in making deep networks robust to specifically designed perturbations.

2 Robust optimization for tail labels

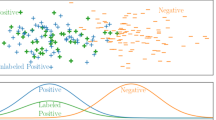
In the extreme classification scenario, the tail labels in the fat-tailed distribution have very few training instances that belong to them. Also, each training instance typically represents a document of about a few hundred words from a total vocabulary of hundreds of thousand or even millions of words. The training instance is, therefore, a sparse representation with only 0.1% or even lesser non-zero features. Due to sparsity, the non-zero features/words in one training instance differ significantly from the other training instance of the same label. Furthermore, since there are only a few training instance in the tail-labels, the union of feature composition of all the training instances for a particular label does not necessarily form a good representation of that label. As a result, the feature composition of the test instance may differ significantly from that of the training instances.

On the other hand, the head labels consist of few tens or even hundreds of training instances. Therefore, the union of words/features which appear in all the training instances is a reasonably good representation of the feature composition of that label. This can also be viewed from the perspective of density of sub-space spanned by the features for a label. For the head labels, this sub-space is much more densely spanned as compared to the tail labels where it is sparsely spanned.

The above observation for the change in the feature composition of tail labels motivates a robustness approach in order to account for the distribution shift. Robustness approach for handling adversarial perturbations to features has been a subject of resurgence particularly in the context of deep learning. In the white-box setting, i.e., with access to deep network and its parameters and their gradients, it has been shown that one can make the deep network predict any desired label for a given image (Goodfellow et al. 2014; Shaham et al. 2015; Szegedy et al. 2013). In the of image classification with deep learning, the benefit of taking a robustness perspective in the presence of less training data has been demonstrated in a very recent work in the upcoming ICLR 2019 (Tsipras et al. 2019). A game-theoretic approach for robustness to feature deletion or addition has also been studied in an earlier work (Globerson and Roweis 2006).

Before, we present our robust optimization framework for handling hundreds of thousand labels in the extreme classification set up, we would like to elucidate distribution shift phenomenon with a few case scenarios.

Table 1 Training and test instances for label 28503

2.1 Case scenarios

The distribution shift is demonstrated for two of the tail labels extracted from the raw data corresponding to Amazon-670K dataset [provided by the authors of Liu et al. (2017)]. The instances in the tail label in Table 1 refers to the book titles and editor reviews for books on computer vision and neuroscience, while the instances in the label in Table 2 provides similar descriptions for VHS tapes on action and adventure genre. Note that, in both cases, there is a significant variation in the features/vocabulary within training instances and also from training to test set instances. For instance, in the first example in Table 1, except the word ‘vision’, there is not much commonality between features of training instances, and those between training and test instances. Similarly, in the second instance, except for ‘vhs’, and the years ‘1942’ and ‘1943’, there is substantial variation in the vocabulary of instances. In other words, even though the underlying distribution generating the training and test set is same in principle, the typical assumption of the test set coming from the same distribution as the training distribution is violated substantially for tail-labels. Those features which were active in the training set might not appear in test set, and vice-versa.

2.2 Robust optimization

Let the training data, given by ${\mathcal {T}} = \left\{ (\mathbf x _1,\mathbf y _1), \ldots ,(\mathbf x _N,\mathbf y _N) \right\}$ consist of input feature vectors $\mathbf x _i \in {\mathcal {X}} \subseteq {\mathbb {R}}^D$ and respective output vectors $\mathbf y _i \in {\mathcal {Y}} \subseteq \{0,1\}^L$ such that $\mathbf y _{i_{\ell }}=1$ iff the $\ell$-th label belongs to the training instance $\mathbf x _i$. For each label $\ell$, sign vectors $\mathbf s ^{(\ell )} \in \{+1, -1\}^N$ can be constructed, such that $\mathbf s ^{(\ell )}_{i} = +1$ if and only if $\mathbf y _{i_\ell } = 1$, and −1 otherwise. The traditional goal in XMC is to learn a multi-label classifier in the form of a vector-valued output function $f : {\mathbb {R}}^D \mapsto \{0,1\}^L$. This is typically achieved by minimizing an empirical estimate of ${\mathbb {E}}_{(\mathbf x ,\mathbf y ) \sim {\mathcal {D}}}[{\mathcal {L}}(\mathbf W ;(\mathbf x ,\mathbf y ))]$ where ${\mathcal {L}}$ is a loss function, and samples $(\mathbf x ,\mathbf y )$ are drawn from some underlying distribution ${\mathcal {D}}$, and $\mathbf W$ denotes the desired parameters.

Accounting for feature variations demonstrated in the above examples in Tables 1 and 2, we consider a perturbation $\tilde{\mathbf{x }}_i \in \tilde{{\mathcal {X}}} \subseteq {\mathbb {R}}^D$ for instance $\mathbf x _i$. The corresponding robust optimization objective hence becomes

$$\begin{aligned} \min _\mathbf{W \in {\mathcal {W}}} {\mathbb {E}}[\sup _{\tilde{\mathbf{x }} \in \tilde{{\mathcal {X}}}}{\mathcal {L}}(\mathbf W ;(\mathbf x + \tilde{\mathbf{x }},\mathbf y ))] \end{aligned}$$

(1)

The above formulation is intractable to optimize over an arbitrary function class ${\mathcal {W}}$ even for convex loss function ${\mathcal {L}}$. For instance, in the context of deep learning methods which optimize over-parameterized non-convex function classes, the above problem in Eq. (1) cannot be solved exactly. Robustness against adversarial perturbations is therefore achieved by employing heuristics such as re-training the network to minimize the loss ${\mathcal {L}}(\mathbf W ;(\mathbf x +\tilde{\mathbf{x }}^* (\mathbf W ),\mathbf y ))$ instead of Eq. (1) (Szegedy et al. 2013; Goodfellow et al. 2014; Shaham et al. 2015). These adversarial perturbations are obtained by minimizing a linear approximation of the loss using Taylor series $\tilde{\mathbf{x }}^* (\mathbf W ) := \arg \max _{||r|| \le \epsilon }\{\nabla _\mathbf{x }{\mathcal {L}}(\mathbf W ;(\mathbf x ,\mathbf y ))^Tr\}$.

Table 2 Training and test instances for label 246910

For XMC problems, where N, D, and L lie in the range $10^4 - 10^6$, we restrict ourselves to Hamming loss for the loss function ${\mathcal {L}}$ and linear function class for ${\mathcal {W}}$. These have the following statistical and computational advantages: (i) the min-max optimization problem in Eq. (1) can be solved exactly without resorting to Taylor series approximation, (ii) Hamming loss function decomposes over individual labels, thereby enabling parallel training and hence linear speedup with number of cores, (iii) linear methods are computationally efficient and statistically comparable to kernel methods for large D (Huang and Lin 2016).

We first recall Hamming loss : for predicted output vector $\hat{\mathbf{y }}$ and the ground truth label vector $\mathbf y$, it is defined as ${\mathcal {L}}_H(\mathbf y , \hat{\mathbf{y }}) = \frac{1}{L}\sum _{\ell =1}^{L}I[\mathbf y _{\ell } \ne \hat{\mathbf{y }}_{\ell }]$, where I[.] is the indicator function. For linear function class, the classifier f is parameterized by $\mathbf W \in {\mathbb {R}}^{D \times L} := \left[ \mathbf w ^{(1)}, \ldots , \mathbf w ^{(L)}\right] , \mathbf w ^{(\ell )} \in {\mathbb {R}}^D$. For each label $\ell$, by replacing the indicator 0-1 loss function in Hamming loss by hinge loss as its convex upper bound, the weight vector $\mathbf w ^{(\ell )}$ for label $\ell$ with sign vector $\mathbf s ^{(\ell )} \in \{+1,-1 \}^N$, is learnt by minimizing the following robust optimization objective (without super-script ($\ell$) for clarity)

$$\begin{aligned} \min _\mathbf{w } \max _{(\tilde{\mathbf{x }}_1,\ldots ,\tilde{\mathbf{x }}_N)} \sum _{i=1}^N\max [1-\mathbf s _i (\langle \mathbf w ,\mathbf x _i - \tilde{\mathbf{x }}_i \rangle ), 0 ] \end{aligned}$$

(2)

such that $\tilde{\mathbf{x _i}} \in \tilde{{\mathcal {X}}}$. It has been shown in Xu et al. (2009) that if $\sum _{i=1}^N||\tilde{\mathbf{x }}_{i}|| < \lambda '$, then the objective in Eq. (2) is equivalent to regularizing with the dual norm without considering perturbations, and the correponding equivalent problem is:

$$\begin{aligned} \min _\mathbf{w } \lambda ' ||\mathbf w ||_* + \sum _{i=1}^N \max [1-\mathbf s _{i} ( \langle \mathbf{w },\mathbf{x }_i \rangle ), 0 ] \end{aligned}$$

(3)

where $||.||_*$ is the dual norm of ||.||, given by $||\mathbf w ||_* := \sup _\mathbf z \{\langle \mathbf z , \mathbf w \rangle , ||\mathbf z ||\le 1\}$.

From the equivalence between formulations in (2) and (3), the choice of norm in the bound on perturbations ($\sum _{i=1}^N||\tilde{\mathbf{x }}_{i}|| < \lambda '$) determines the regularizer in equivalent formulation in Eq. (3). For instance, considering $\ell _2$-bounded perturbations leads to $\ell _2$-regularized SVM, which is robust to spherical perturbations. It may be recalled that the dual of $||.||_1, ||.||_2$, and $||.||_\infty$ norms are $||.||_\infty , ||.||_2$, and $||.||_1$ respectively.

2.3 Choice of norm

As shown in the examples in Tables 1 and 2, there can be a significant variation in the features’ distribution from the training set to the test set instances. We therefore consider the worst case perturbations in the input, i.e., $||.||_\infty$ norm. This is given by $||\tilde{\mathbf{x }}_{i}||_\infty := \max _{d=1\ldots D}|\tilde{\mathbf{x }}_{i_d}|$. This choice of norm can be motivated from two perspectives.

Firstly, it may be noted that changing the input $\mathbf x$ by small perturbations along each dimension, such that $||\tilde{\mathbf{x }}||_\infty$ remains the same, can change the inner product evaluation of the decision function $\mathbf w ^T(\mathbf x +\tilde{\mathbf{x }})$ significantly. By accounting for such perturbations in the training data, the resulting weight vector is, therefore, robust to worst-case feature variations. This is not true for perturbations whose $||.||_1$ or $||.||_2$ norms are bounded.

Since the dual of $||.||_\infty$ is $||.||_1$ norm, this choice of norm for the perturbations in formulation (2) leads to the $\ell _1$ regularized SVM in the optimization problem in (3). As this is known to yield sparse solutions, the above choice of norm shows an equivalence between sparsity and robustness. Both of these are desirable properties in the context of XMC, since we want models which are robust to perturbations due to the tail-label effect, and also sparse which leads to compact models for fast prediction in real-times applications of XMC.

2.4 Optimization

However, both $\ell _1$-norm and hinge-loss $\max [1-\mathbf{s }_{i} ( \langle \mathbf{w },\mathbf x _i \rangle ), 0 ]$ are non-smooth, which is undesirable from the view-point of efficient optimization. In the following theorem, we prove that one can replace hinge loss by its squared version given by $(\max [1-\mathbf{s }_{i} ( \langle \mathbf{w },\mathbf{x }_i \rangle ), 0 ])^2$ for a different choice of the regularization parameter $\lambda$ instead of $\lambda '$. The statistically equivalent problem results in objective function in Eq. (5), which is easier optimize. The proof of the theorem follows the same technique as in Xu et al. (2010).

Theorem 1

The following objective function with hinge loss and regularization parameter $\lambda '$

$$\begin{aligned} \min _{\mathbf{w }} \lambda ' ||\mathbf{w }||_1 + \sum _{i=1}^N \max [1-\mathbf{s }_{i} ( \langle \mathbf{w },\mathbf{x }_i \rangle ), 0 ] \end{aligned}$$

(4)

is equivalent, upto a change in the regularization parameter, to the objective function below with squared hinge loss for some choice of $\lambda$

$$\begin{aligned} \min _{\mathbf{w }} \lambda ||\mathbf{w }||_1 + \sum _{i=1}^N (\max [1-\mathbf{s }_{i} ( \langle \mathbf{w },\mathbf{x }_i \rangle ), 0 ])^2 \end{aligned}$$

(5)

Proof

We first start with a definition. Let $g(.) : {\mathbb {R}}^D \mapsto {\mathbb {R}}$ and $h(.) : {\mathbb {R}}^D \mapsto {\mathbb {R}}$ be two functions. Then $\mathbf w ^*$ is called weakly efficient if atleast one of the following holds, (i) $\mathbf w ^* \in \arg \min _\mathbf{w \in {\mathbb {R}}^D} g(\mathbf w )$, (ii) $\mathbf w ^* \in \arg \min _\mathbf{w \in {\mathbb {R}}^D} h(\mathbf w )$, and (iii) $\mathbf w ^*$ is Pareto efficient, which means that $\not \exists$$\mathbf w '$ such that $g(\mathbf w ') \le g(\mathbf w ^*)$ and $h(\mathbf w ') \le h(\mathbf w ^*)$ with atleast one holding with strict inequality.

A standard result from convex analysis states that for convex functions $g(\mathbf w )$ and $h(\mathbf w )$, the set of optimal solutions for the weighted sum, $\min _\mathbf{w } (\lambda _1 g(\mathbf w ) + \lambda _2 h(\mathbf w ))$ where $\lambda _1, \lambda _2 \in [0,+\infty )$ and not being zero together, coincides with the set of weakly efficient solutions. This means that the set of optimal solutions of $\min _\mathbf{w } (\lambda ' ||\mathbf w ||_1 + \sum _{i=1}^N \max [1-\mathbf s _{i} (\langle \mathbf w ,\mathbf x _i \rangle ),0])$, where $\lambda '$ ranges in $[0,+\infty )$ is the set of weakly efficient solution of $||\mathbf w ||_1$ and $\sum _{i=1}^N \max [1-\mathbf s _{i} (\langle \mathbf w ,\mathbf x _i \rangle ), 0]$. On similar lines, the set of optimal solutions of $\min _\mathbf{w } ( \lambda ||\mathbf w ||_1 + \sum _{i=1}^N (\max [1-\mathbf s _{i} (\langle \mathbf w ,\mathbf x _i \rangle ), 0 ])^2)$ where $\lambda$ ranges in $[0,+\infty )$ is the set of weakly efficient solution of $||\mathbf w ||_1$ and $\sum _{i=1}^N (\max [1-\mathbf s _{i} ( \langle \mathbf w ,\mathbf x _i \rangle ), 0 ])^2$. Since taking the square for non-negatives is a monotonic function, it implies that these two sets are identical, and hence the two formulations given in Eqs. (4) and (5) are statistically equivalent upto change in the regularization parameter. $\square$

2.5 Sub-optimality of Liblinear solver (Fan et al. 2008)

The formulation in Eq. (5) lends itself to easier optimization and an efficient solution is implemented in the Liblinear package (as −s 5 argument) by using a cyclic co-ordinate descent (CCD) procedure. Liblinear has been included in machine learning packages such as scikit-learn and Cran LibLineaR for solving large-scale linear classification and regression tasks. A natural question to ask is - why not use this solver directly if the modeling of XMC under the worst-case perturbation setting and the resulting optimization problem are indeed correct.

We applied the CCD based implementation in LibLinear and found that it gives sub-optimal solution. In particular, the CCD solution, (i) underfits the training data, and (ii) does not give good generalization performance. For concreteness, let $\mathbf w _{CCD} \in {\mathbb {R}}^D$ be the minimizer of the objective function in Eq. (5) and $opt_{CCD} \in {\mathbb {R}}^+$ be the corresponding optimal value of the objective value attained. We demonstrate under-fitting by producing a certificate $\mathbf w _{Prox} \in {\mathbb {R}}^D$ with the corresponding objective function value $opt_{Prox} \in {\mathbb {R}}^+$ such that $opt_{Prox} < opt_{CCD}$. The construction of the certificate of sub-optimality is obtained by following a proximal gradient procedure in the next section. The inferior generalization performance of Liblinear is shown in Table 4, which among other methods, provides comparison on the test set of the models learnt by CCD and that learnt by our proximal gradient procedure in Algorithm 1.

2.6 Certificate construction by proximal gradient

Proximal methods have been effective in addressing large-scale non-smooth convex problems which can be written as sum of a differentiable function with Lipschtiz-continuous gradient and a non-differentiable function. We therefore use the forward–backward proximal procedure described in Algorithm 1 to construct the certificate $\mathbf w _{Prox}$ by solving the optimization problem in Eq. (5). The two main steps in the algorithm are in lines 3 and 4. In line 3 (called the forward step), gradient with respect to the differentiable part of the objective is taken, which we denote by ${\mathcal {H}}(\mathbf w )$ for squared hinge loss, i.e., ${\mathcal {H}}(\mathbf w ) := \sum _{i=1}^N (\max [1-\mathbf {s} _{i} ( \langle \mathbf {w} ,\mathbf {x} _i \rangle ), 0 ])^2$. The step size $\gamma _{t}$ in the forward step, which can be thought as inverse of the Lipshitz constant of ${\mathcal {H}}'(\mathbf w _t)$, is estimated for a new weight $\mathbf w '$ by starting at a high value and decreasing fractionally until the following condition is satisfied (Bach et al. 2011):

$$\begin{aligned} {\mathcal {H}}(\mathbf w ') \le {\mathcal {H}}(\mathbf w _t) + {\mathcal {H}}'(\mathbf w _t)^T(\mathbf w ' - \mathbf w _t) + 1/(2\gamma _t)||\mathbf w ' - \mathbf w _t||_2^2 \end{aligned}$$

Line 4 is the backward or proximal step in which minimization problem involving the computation of the proximal operator has a closed-form solution for $||\mathbf w ||_1$. It is given by the soft-thresholding operator, which for the j-th dimension at the t-th iterate is :

$$\begin{aligned} \mathbf w _{j_{t+1}} = sign\left( \mathbf u _{j_t}\right) \times \max \left[ \left( |\mathbf u _{j_t}| - \lambda \right) , 0\right] \end{aligned}$$

(6)

Note the forward–backward procedure detailed in Algorithm 1 learns the weight vector corresponding to each label. Similar to DiSMEC (Babbar and Schölkopf 2017), since the computations are independent for each label, it can be invoked in parallel over as many cores as are available for computation to learn $\mathbf W _{Prox} = \left[ \mathbf w ^{(1)}_{Prox}, \ldots , \mathbf w ^{(L)}_{Prox}\right]$. We call our proposed method PRoXML, which stands for parallel Robust extreme multi-label classification. The convergence of the forward–backward scheme for proximal gradient has been studied in Combettes and Pesquet (2007).

For EUR-Lex dataset, Fig. 2 compares the variation in the optimization objective for the weight $\mathbf w _{CCD}$ learnt by the LibLinear CCD solver and proximal gradient solver $\mathbf w _{Prox}$. For approximately 90% of the labels, the objective value obtained by Algorithm 1, was lower than that obtained by LibLinear, which in some cases could be as low as half for $\mathbf w _{Prox}$.

The outlier points with the corresponding optimal value among the highest ones correspond to the labels which mostly head labels. The head-labels are typically linearly non-separable from the others, and hence this leads to siginificant values for squared hinge loss $\sum _{i=1}^N (\max [1-\mathbf s _{i} ( \langle \mathbf w ,\mathbf x _i \rangle ), 0 ])^2$. Furthermore, the weight vectors for the head labels are relatively much less sparse compared to the tail labels which further adds to the contribution towards the overall objective value through the regularization term $\lambda ||\mathbf w ||_1$.

Fig. 2

Comparison of $opt_{CCD}$ and $opt_{Prox}$ over individual labels for EUR-Lex dataset

3 Experimental analysis

Dataset description and evaluation metrics We perform empirical evaluation on publicly available datasets from the XMC repository curated from sources such as Wikipedia and delicious (Mencia and Fürnkranz 2008; McAuley and Leskovec 2013). The detailed statistics of the datasets are shown in Table 3. The datasets exhibit a wide range of properties in terms of number of training instances, features, and labels. MediaMill and Bibtex datasets are small scale datasets and do not exhibit tail-label behavior. The last column shows the algebraic connectivity of label graph, which measures the degree of connectedness of labels based on their co-occurrences in the training data. The calculation of algebraic connectivity based on algebraic graph theoretic considerations, is described in Sect. 4.

Table 3 Multi-label datasets from XMC repository

With applications in recommendation systems, ranking and web-advertizing, the objective of the machine learning system in XMC is to correctly recommend/rank/advertize among the top-k slots. Propensity scored variants of precision@k and nDCG@k capture prediction accuracy of a learning algorithm at top-k slots of prediction, and also the diversity of prediction by giving higher score for predicting rarely occurring tail-labels. As detailed in Jain et al. (2016), the propensity $p_\ell$ of label $\ell$, is related to number of its positive training instances $N_\ell$ such that $p_\ell \approx 1$ for head-labels and $p_\ell<< 1$ for tail-labels. Let $\mathbf y \in \{0,1\}^L$ and $\hat{\mathbf{y }} \in {\mathbb {R}}^L$ denote the true and predicted label vectors respectively, then the propensity scored variants of P@k and nDCG are given by

$$\begin{aligned} PSP@k(\hat{\mathbf{y }},\mathbf y ):= & {} \frac{1}{k} \sum _{\ell \in rank_k{(\hat{\mathbf{y }})}}\mathbf{y _\ell }/p_\ell \end{aligned}$$

(7)

$$\begin{aligned} PSnDCG@k(\hat{\mathbf{y }},\mathbf y ):= & {} \frac{PSDCG@k}{\sum _{\ell =1}^{\min (k, ||\mathbf{y }||_0)}{\frac{1}{\log (\ell +1)}}} \end{aligned}$$

(8)

where $PSDCG@k := \sum _{\ell \in rank_k{(\hat{\mathbf{y }})}}{[\frac{\mathbf{y }_\ell }{p_\ell \log (\ell +1)}]}$ , and $rank_k(\mathbf{y })$ returns the k largest indices of $\mathbf y$.

To match against the ground truth, as suggested in Jain et al. (2016), we use $100*{\mathbb {G}}(\{\hat{\mathbf{y }}\})/{\mathbb {G}}(\{\mathbf{y }\})$ as the performance metric. For M test samples, ${\mathbb {G}}(\{\hat{\mathbf{y }}\}) = \frac{-1}{M}\sum _{i=1}^{M}{\mathbb {L}}(\hat{\mathbf{y }}_i,\mathbf y )$, where ${\mathbb {G}}(.)$ and ${\mathbb {L}}(.,.)$ signify gain and loss respectively. The loss ${\mathbb {L}}(.,.)$ can take two forms, (i)${\mathbb {L}}(\hat{\mathbf{y }}_i,\mathbf y ) = - PSnDCG@k$, and (ii) ${\mathbb {L}}(\hat{\mathbf{y }}_i,\mathbf y ) = - PSP@k$. This leads to the two metrics which are finally used in our comparison in Table 4 (denoted by N@k and P@k).

3.1 Methods for comparison

We compare PRoXML against eight algorithms including the state-of-the-art label-embedding, tree-based and linear methods:

Label embedding methods

• (I) LEML (Yu et al. 2014)—It learns a low-rank embedding of the label space and is shown to work well for datasets with high label correlation in the presence of moderate number of labels.

• (II) SLEEC (Bhatia et al. 2015)—It learns sparse locally low-rank embeddings and captures non-linear correlation among the labels. This method has been shown to scale for XMC problems by applying data clustering as an initialization step.

Tree-based methods

• (I) FastXML (Prabhu and Varma 2014)—This is a scalable tree-based method which partitions the feature space and optimizes vanilla nDCG metric at each node ($p_{\ell }=1$ in equation (8) above).

• (II) PFastreXML (Jain et al. 2016)—This method is designed for better classification of tail-labels. It learns an ensemble of PFastXML classifier which optimizes propensity-scored nDCG metric in Eq. 8 and Rocchio classifier (https://en.wikipedia.org/wiki/Rocchio_algorithm) applied on the top 1,000 labels predicted by PFastXML. It is shown to out-perform the production system used in Bing Search [c.f. Section 7 in Jain et al. (2016)] and reviewed in detail in Sect. 5.

• (III) Parabel (Prabhu et al. 2018)—This is recently proposed method which learns label partitions by a balanced 2-means algorithm, followed by learning one-vs-rest classifier at each node.

Linear methods

• (I) PD-Sparse (Yen et al. 2016)—It uses elastic net regularization with multi-class hinge loss and exploits the sparsity in the primal and dual problems for faster convergence.

• (II) DiSMEC (Babbar and Schölkopf 2017)—This is distributed one-vs-rest method which achieves state-of-the-art results on vanilla P@k and nDCG@k. It minimizes Hamming loss with $\ell _2$ regularization with weight pruning heuristic for model size reduction.

• (IV) CCD-L1—This is the in-built sparse solver as part of the LibLinear package which optimizes Eq. 5 using co-ordinate descent.

The proposed method PRoXML was implemented in C++ on 64-bit Linux system using openMP for parallelization. For PRoXML, the regularization parameter $\lambda$ was cross-validated for smaller datasets, MediaMill, Bibtex, and EUR-Lex and it was fixed to 0.1 for all bigger datasets. Due to computational constraints in XMC consisting of hundreds of thousand labels, keeping fixed values for hyper-parameters is quite standard [c.f. Hyper-parameters setting, Section 7 in Jain et al. (2016), and Section 3 in Bhatia et al. (2015), and Section 5 in Prabhu and Varma (2014)]. For all other approaches, the results were reproduced as suggested in the papers.

Table 4 Comparison of N@k for $\hbox {k}=1$,3 and 5

3.2 Prediction accuracy

The relative performance of various methods on propensity scored metrics for nDCG@k (denoted N@k) and precision@k (denoted P@k) is shown in Table 4. The important observations from these are summarized below:

(A) Larger datasets We first look at the results for the datasets falling in the extreme regime such as Amazon-670K, Wiki-500K and WikiLSHTC-325K with large number of labels, and a large fraction of them are tail-labels. Under this regime, PRoXML performs substantially better than both embedding-schemes and tree-based methods such as PFastreXML. For instance, for WikiLSHTC-325K, the improvement in P@5 and N@5 over SLEEC and PFastreXML is approx. 60% and 25% respectively. It is important to note that our method works better on propensity scored metrics than PFastreXML even though its training process is optimizing another metric, namely, a convex upper bound on Hamming loss. On the other hand, PFastreXML is minimizing the same metric on which the performance is evaluated. Due to its robustness properties, PRoXML also performs better than DiSMEC which also minimizes Hamming loss but employs $\ell _2$ regularization instead.

(B) Smaller datasets We now consider smaller datasets which consist of no tail-labels. These include Mediamill and Bibtex datasets consisting of 101 and 159 labels respectively. Under this regime, embedding based methods SLEEC and LEML perform better or at par with Hamming loss minimizing methods. As explained in Sect. 4, this is due to high algebraic connectivity of label graphs in smaller datasets, leading to high correlation between labels. This behavior is in stark contrast to datasets in the extreme regime such as WikiLSHTC-325K and Amazon-670K in which Hamming loss minimizing methods significantly outperform label-embedding methods. The above differences observed in the performance of small-scale problems vis-à-vis large-scale problems are indeed quite contrary to the remarks in recent works [c.f. abstract of Jain et al. (2016)].

(C) Label coverage This metric is a measure of the fraction of unique labels correctly predicted by an algorithm. It is shown in Fig. 3 (denoted by C@1, C@3, and C@5) for WikiLSHTC-325K and Amazon-670K. It is clear that PRoXML performs better than state-of-the-art methods in detecting more unique and correct labels. From Fig. 3, it may also be noted that Rocchio classifier applied on top-1000 labels short-listed by PFastXML, does better than PFastXML classifier itself. This indicates that the performance of PFastreXML depends heavily on the good performance of Rocchio classifier, which in turn is learnt from the top labels predicted by PFastXML classifier. On the other hand, our method despite not having any such ensemble effects, performs better than PFastreXML and its components PFastXML and Rocchio.

Fig. 3

Label Coverage for various methods on WikiLSHTC-325K and Amazon-670K datasets

(D) Vanilla metrics The results for vanilla precision@k and nDCG@k (in which the label propensity $p_{\ell }=1, \forall \ell$) are shown in the appendix. For these metrics, ProXML performs slightly worse than DiSMEC. However, this is expected since these metrics give equal weight to all the labels. As a result, those methods which are biased towards head-labels tend to perform better, but tend to yield less diverse predictions.

3.3 Model size, and training/prediction time

Due to the sparsity inducing $\ell _1$ regularization, the obtained models are quite sparse and light-weight. For instance, the model learnt by PRoXML is 3 GB in size for WikiLSHTC-325K, compared to 30 GB for PFastreXML on this dataset. In terms of training time, PRoXML uses a distributed training framework thereby exploiting any number of cores as are available for computation. The training can be done offline on a distributed/cloud based system for large datasets such as WikiLSHTC-325K and Amazon-670K. Faster convergence can be achieved by other methods such as sub-sampling negative examples or warm-starting the optimization with the weights learnt by DiSMEC algorithm to warm-start for faster convergence, via better initialization instead of initializing with an all-zeros solution in Algorithm 1.

Prediction speed is more critical for most applications of XMC which demand low latency in domains such as recommendation systems and web-advertizing. The compact model learnt by PRoXML can be easily evaluated for prediction on streaming test instances. This is further aided by distributed model storage which can exploit the parallel architecture for prediction. On WikiLSHTC-325K, it takes 2 ms per test instance on average which is thrice as fast as SLEEC, and at par with tree-based methods.

4 Discussion: what works, what doesn’t and why?

We now analyze the empirical results shown in the previous section by drawing connections to spectral properties of label graphs, and determine data-dependent conditions under which Hamming loss minimization is more suited compared to label embedding methods and vice-versa. This section also sheds light on qualitative differences between data properties when one moves from small-scale to the extreme regime.

4.1 Algebraic connectivity of label graphs

For the output vectors in the training data $\left\{ (\mathbf y _i)\right\} _{i=1}^{N}$ such that $\mathbf y _{i_{\ell }}=1$ iff the $\ell$-th label belongs to the training instance $\mathbf x _i$, and 0 otherwise. Consider the adjacency matrix A(G) corresponding to the label graph G, whose vertex set V(G) is the set of labels in training set, and the edge weights $a_{\ell , \ell ^{'}}$ are defined by $a_{\ell , \ell ^{'}} = \sum _{i=1}^N \left[ \left( \mathbf y _{i_{\ell }} = 1\right) \wedge \left( \mathbf y _{i_{\ell ^{'}}} = 1\right) \right]$, where $\wedge$ represents the logical and operator. The edge between labels $\ell$ and $\ell ^{'}$ is weighted by the number of times $\ell$ and $\ell ^{'}$ co-occur in the training data. By symmetry, $a_{\ell , \ell ^{'}} = a_{\ell ^{'}, \ell } \forall \ell , \ell {'} \in V(G)$. Let $d({\ell })$ denote the degree of label $\ell$, where $d({\ell }) = \sum _{\ell ^{'} \in V(G)} a_{\ell , \ell ^{'}}$, and D(G) be the diagonal degree matrix $d_{\ell , \ell } = d({\ell })$. The entries of normalized Laplacian matrix, L(G) is given by:

$$\begin{aligned} L_{\ell ,\ell '} = \left\{ \begin{array}{l l} 1-\frac{a_{\ell , \ell ^{'}}}{d_{\ell }} &{} \quad \hbox {if }\ell =\ell ' \hbox { and }d_{\ell } \ne 0\\ -\frac{a_{\ell , \ell ^{'}}}{\sqrt{d_{\ell } d_{\ell '}} } &{} \quad \hbox {if }\ell \hbox { and }\ell '\hbox { are adjacent}\\ 0 &{} \quad \hbox {otherwise}\ \end{array} \right. \end{aligned}$$

Let $\lambda _1(G), \ldots , \lambda _L(G)$ be the eigen-values of L(G). From spectral graph theory, $\lambda _2(G) \le \nu (G) \le \eta (G)$, where $\nu (G)$ and $\eta (G)$ are respectively the vertex and edge connectivity of G. i.e. minimum of vertices and edges to be removed from G to make it disconnected (Chung 1997). Being a lower bound on $\nu (G)$ and $\eta (G)$, $\lambda _2(G)$ gives an estimate on the connectivity of the label graph. The higher the algebraic connectivity, the more densely connected the labels are in the graph G. The last column of Table 3 shows algebraic connectivity for the normalized Laplacian matrix for various datasets. Higher values of algebraic connectivity, indicating high degree of connectivity and correlation between labels, are observed for smaller datasets such as MediaMill which consist of only a few hundreds labels. Lower value is observed for datasets in the extreme regime such as WikiLSHTC-325K, WikiLSHTC-500K and Amazon-670K.

Why Hamming loss works for extreme classification?

Contrary to the assertions in Jain et al. (2016), as shown in Table 4, Hamming loss minimizing one-vs-rest, which trains an independent classifier for every label, works well on datasets in the extreme regime such as WikiLSHTC-325K and Amazon-670K. In this regime, there is very little correlation between labels that could potentially be exploited in the first place by schemes such as LEML and SLEEC. The extremely weak correlation is indicated by crucial statistics shown in Table 3, which include: lower value of the algebraic connectivity of the label graph $\lambda _2(G)$, fat-tailed distribution of instances among labels and lower values of average number of labels per instance. The virtual non-existence of correlation indicates that the presence of a given label does not really imply the presence of other labels. It may be noted that though there may be underlying semantic similarity between labels, but there is not enough data, especially for tail-labels, to support that. This inherent separation in label graph for larger datasets leads to better performance of one-vs-rest scheme.

Why label-embedding is suitable for small datasets ?

For smaller datasets that consist of only a few hundred labels (such as MediaMill) and relatively large value for average number of labels per instance, the labels tend to co-occur more often than for datasets in extreme regime. In this situation, label correlation is much higher that can be easily exploited by label-embedding approaches leading to better performance compared to one-vs-rest approach. This scale of datasets, as is common in traditional multi-label problems, has been marked by the success of label-embedding methods. Therefore, it may be noted that conclusions drawn on this scale of problems, such as on the applicability of learning algorithms or suitability of loss functions for a given problem, may not necessarily apply to datasets in XMC.

What about PSP@k and PSPnDG@k?

Though PSP@k and PSPnDG@k are appropriate for performance evaluation, these may not right metrics to optimize over during training. For instance, if a training instance has fifteen positive labels and we are optimizing PSP@5, then as soon as it has correctly classified five out of the fifteen labels correctly, the training process will stop trying to change the decision hyper-plane for this training instance. As a result, the information regarding the remaining ten labels is not captured while optimizing the PSP@5 metric. It is possible that at test time, we get a similar instance which has some or all the remaining ten labels which were not optimized during training. On the other hand, one-vs-rest which minimizes Hamming loss would try to independently align the hyper-planes for all the fifteen labels until these are separated from the rest. Overall, the model learnt by optimizing is richer compared to that learnt by optimizing PSP@k and PSPnDG@k. Therefore, it leads to better performance on P@k and nDG@k as well as PSP@k and PSPnDG@k, when regularized properly.

5 Related work

To handle the large scale of labels in XMC, most methods have focused on two of the main strands, (i) Tree-based methods, and (ii) Label-embedding based methods.

Label-embedding approaches assume that the output space has an inherently low rank structure. These approaches have been at the fore-front in multi-label classification consisting of few hundred labels (Bhatia et al. 2015; Hsu et al. 2009; Yu et al. 2014; Tai and Lin 2012; Bi and Kwok 2013; Zhang and Schneider 2011; Chen and Lin 2012; Bengio et al. 2010; Lin et al. 2014; Tagami 2017). However, this assumption can break down in presence of large-scale power-law distributed category systems, and hence leading to high prediction error (Babbar et al. 2013, 2016).

Tree-based approaches (Jain et al. 2016; Prabhu and Varma 2014; Si et al. 2017; Niculescu-Mizil and Abbasnejad 2017; Daume III et al. 2016; Jernite et al. 2016; Jasinska et al. 2016) are aimed towards faster prediction which can be achieved by recursively dividing the space of labels or features. Due to the cascading effect, the prediction error made at a top-level cannot be corrected at lower levels. Typically, such techniques trade-off prediction accuracy for logarithmic prediction speed which might be desired in some applications.

Recently, there has been interest in developing distributed linear methods (Babbar and Schölkopf 2017; Yen et al. 2016) which can exploit distributed hardware, and deep learning methods (Liu et al. 2017; Nam et al. 2017). From a probabilistic view-point, bayesian approaches for multi-label classification have been developed in recent works such as Jain et al. 2017; Gaure et al. 2017 and Labeled LDA (Papanikolaou and Tsoumakas 2017). Here, we only discuss PFastreXML in detail here as this is the method designed specifically for better prediction of tail-labels.

Fig. 4

Variation of PSP@k with the trade-off parameter $\alpha$ for (i) EUR-Lex, (ii) WikiLSHTC-325K, and (iii) Amazon-670K datasets. For PFastreXML, $\alpha = 0.8$. On the left, ($\alpha =0$), represents $\texttt {Rocchio}_{1,000}$ classifier, and on the right ($\alpha =1$), represents PFastXML classifier without re-ranking step. PRoXML works better than PFastreXML for all ranges of $\alpha$ for PSP@3 and PSP@5. PSP@1 is not shown for clarity, and it is 44.3, 32.4, and 30.3 respectively

5.1 PFastreXML (Jain et al. 2016)

PFastreXML is a state-of-the-art tree-based method which outperformed a highly specialized production system for Bing search engine consisting of ensemble of a battery of ranking methods [cf. Section 7 in Jain et al. (2016)]. Learning the PFastreXML classifier primarily involves learning two components, (i) PFastXML classifier—which is an ensemble of trees which minimize propensity scored loss functions, and (ii) a re-ranker which attempts to recover the tail labels missed by PFastXML. The re-ranker is essentially Rocchio classifier, also called the nearest centroid classifier [Equation 7, Section 6.2 in Jain et al. (2016)], which assigns the test instance to the label with closest centroid among the top 1,000 labels predicted by PFastXML. The final score $s_{\ell }$ assigned to label $\ell$ for test instance $\mathbf x$ is given by a convex combination of scores PFastXML and the Rocchio classifier for top 1000 label (Equation 8, Section 6.2 in Jain et al. (2016)) as follows:

$$\begin{aligned} s_l = \alpha \log P_{PFast} (\mathbf y _l=1|\mathbf x ) + (1-\alpha ) \log P_{Roc_{1,000}}(\mathbf y _l=1|\mathbf x ) \end{aligned}$$

For PFastreXML, $\alpha$ is fixed to 0.8; setting $\alpha =1$ gives the scores from PFastXML classifier only and $\alpha =0$ gives the scores from $Rocchio_{1,000}$ classifier only. It may be recalled that, akin to FastXML, PFastXML is also an ensemble of a number of trees, which is typically set to 50. Some of its shortcomings in addition to the relatively poorer performance compared to PRoXML are:

• (I) Standalone PFastXML —Fig. 3 shows the variation of PSP@k of PFastreXML with change in $\alpha$ which includes the two extremes (PFastXML, $\alpha = 1$) and ($Rocchio_{1,000}$ classifier, $\alpha = 0$) on three datasets from Table 3. Clearly, the performance of PFastreXML depends heavily on good performance of $Rocchio_{1,000}$ classifier. It may be recalled that one of the main goals of propensity based metrics and PFastXML was better coverage of tail labels. However, PFastXML itself needs to be supported by the additional $Rocchio_{1,000}$ classifier for better tail label coverage. To the contrary, our method does not need additional such auxiliary classifier.

• (II) Need for propensity estimation from meta-data—To estimate propensities $p_\ell$ using $p_\ell := 1/\left( 1+C e^{-A\log (N_\ell +B)}\right)$, one needs to compute parameters A and B from some meta-information of the data-source such as Wikipedia or Amazon taxonomies. Furthermore, it might not even be possible on some datasets to have this side information, in which case the authors in Jain et al. (2016) set it to average of Wikipedia and Amazon datasets, which is quite ad-hoc. Our method does not need propensities for training and hence is also applicable to other metrics for tail-label coverage.

• (III) Large model sizes—PFastreXML leads to large model size such as 30 GB (for 50 trees) for WikiLSHTC-325K data, and 70 GB (for 20 trees) for Wiki-500K. Such large model sizes can be difficult to evaluate for making real-time predictions in recommendation systems and web-advertizing. For larger datasets such as WikiLSHTC-325K, the model sizes learnt by PRoXML is around 3 GB which is an order of magnitude smaller than PFastreXML.

• (IV) Lots of hyper-parameters—PFastreXML has around half a dozen hyper-parameters such as $\alpha$, number of trees in ensemble, and number of instances in the leaf node etc. Also, there is no reason apriori to fix $\alpha =0.8$ even though it gives better generalization performance as shown in Fig. 4. To the contrary, our method has just one hyper-parameter which is the regularization parameter.

Table 5 Comparison of N@k for $\hbox {k}=1$,3 and 5

Table 6 Comparison of N@k for $\hbox {k}=1$,3 and 5

6 Conclusion

In this work, we motivated the importance of effective tail-label discovery in XMC. We approached this problem from a novel perspective of robustness which has not been considered so far in the domain of XMC. We show that this view-point naturally motivates the well known $\ell _1$-regularized SVM, and demonstrate its surprising effectiveness over state-of-the-art methods while scaling to problems with millions of labels. To provide insights into the observations, we explain the performance gain of one-vs-rest scheme vis-à-vis label embedding methods, using tools from graph theory. We hope that synergizing with recent progress on robustness of deep learning methods will open new research avenues for future research.

Appendix: Further experimental results

In this section, we present results on the vanilla precision@k (Table 5) and nDCG@k (Table 6). Since these metrics weigh all labels equally, the prediction algorithms have an incentive to predict the head labels. The important observations are summarized below:

• DiSMEC which employs $\ell _2$-regularization tends to perform slightly better than ProXML on all datasets except for EURLex dataset.

• ProXML performs at par with Parabel which uses 2-means to hierarchically partition the data, and then employs $\ell _2$-regularized SVM at each node. However, as shown in Table 4 of the main paper, ProXML performs upto 25% better than Parabel on propensity scored metrics.

These results further reinforce the robustness properties introduced by our method, and its impact on effective prediction of tail-label-labels.