An accelerated variance reducing stochastic method with Douglas-Rachford splitting

Abstract

We consider the problem of minimizing the regularized empirical risk function which is represented as the average of a large number of convex loss functions plus a possibly non-smooth convex regularization term. In this paper, we propose a fast variance reducing (VR) stochastic method called Prox2-SAGA. Different from traditional VR stochastic methods, Prox2-SAGA replaces the stochastic gradient of the loss function with the corresponding gradient mapping. In addition, Prox2-SAGA also computes the gradient mapping of the regularization term. These two gradient mappings constitute a Douglas-Rachford splitting step. For strongly convex and smooth loss functions, we prove that Prox2-SAGA can achieve a linear convergence rate comparable to other accelerated VR stochastic methods. In addition, Prox2-SAGA is more practical as it involves only the stepsize to tune. When each loss function is smooth but non-strongly convex, we prove a convergence rate of ${\mathcal {O}}(1/k)$ for the proposed Prox2-SAGA method, where k is the number of iterations. Moreover, experiments show that Prox2-SAGA is valid for non-smooth loss functions, and for strongly convex and smooth loss functions, Prox2-SAGA is prominently faster when loss functions are ill-conditioned.

1 Introduction

In many artificial intelligence and machine learning applications, one needs to solve the following generic optimization problem in the form of regularized empirical risk minimization (Hastie et al. 2009)

$$\begin{aligned} \min \limits _{x\in {\mathbb {R}}^d} f(x) + h(x). \end{aligned}$$

(1)

Given n samples, f is the average of a set of convex loss functions

$$\begin{aligned} f(x) = \frac{1}{n}\sum \limits _{i=1}^{n} f_i (x), \end{aligned}$$

(2)

where $f_i: {\mathbb {R}}^d \rightarrow {\mathbb {R}}$ denotes the empirical loss of the i-th sample with regard to the parameters x, and h is the regularization term, which is convex but possibly non-smooth. The goal is to find the optimal solution of x that minimizes the regularized empirical loss over the whole dataset.

Numerous efforts have been devoted to solve this problem (Bottou et al. 2016; Johnson and Zhang 2013; Defazio et al. 2014; Shalev-Shwartz and Zhang 2013). When h is absent, stochastic gradient descent (SGD) (Robbins and Monro 1951) is a standard and effective method to solve (1), especially when the number of samples is very large. Specifically, stochastic gradient is utilized in SGD to update x in each step instead of calculating the full gradient, which yields lower per iteration cost. However, as a side effect, a rather large variance introduced by the stochastic gradient will slow down the convergence (Bottou et al. 2016).

To address the issue, a number of variance reducing (VR) stochastic methods have been developed in recent years, such as SVRG (Johnson and Zhang 2013), SAGA (Defazio et al. 2014) and SDCA (Shamir and Zhang 2013). As a key feature of the VR stochastic methods, the variance of the stochastic gradient goes to zero asymptotically along the iterative updates. Therefore, unlike SGD which needs a decaying step size to guarantee convergence, the step size can be fixed for these methods. As a result, the convergence rate can be improved from sub-linear in SGD to linear in the VR stochastic methods. Further, for the problem with the non-smooth regularization term h, a proximal operator of h is introduced at the end of each iteration of the VR stochastic methods, for example, Prox-SVRG (Xiao and Zhang 2014), Prox-SAGA (Defazio et al. 2014) and Prox-SDCA (Shalev-Shwartz and Zhang 2014). In addition, acceleration techniques such as Acc-SDCA (Shalev-Shwartz and Zhang 2014), Catalyst (Lin et al. 2015, 2017) and Katyusha (Allen-Zhu 2017), can boost these methods to faster convergence rates when the loss function is ill-conditioned. However, existing accelerated VR stochastic methods often involve mulitple parameters to tune, which brings difficulties to their implementations.

In this paper, we develop a simple accelerated VR stochastic method, named as Prox2-SAGA, to solve (1). Similar to most non-accelerated algorithms, Prox2-SAGA only has one parameter, the step size, to tune, and is hence easy to implement. Different from most stochastic algorithms which utilize the gradients of $f_i$, Prox2-SAGA uses the corresponding gradient mappings, through applying the proximal operator on each $f_i$. It is the proximal operator that enables Prox2-SAGA to achieve the accelerated rate when the loss functions are ill-conditioned. Prox2-SAGA can be regarded as the generalization of Point-SAGA (Defazio 2016) which considers a special case when the non-smooth regularizer h is absent. To handle h, Prox2-SAGA employs another proximal operator. The two proximal operators in one iteration of Prox2-SAGA essentially constitute a Douglas-Rachford splitting step. Our main contributions are listed below:

• We design Prox2-SAGA, a fast and simple VR stochastic method, to solve (1) with Douglas-Rachford splitting.

• When loss functions $f_i$ are convex and smooth, we prove that Prox2-SAGA can achieve a ${\mathcal {O}}(1/k)$ convergence rate, where k is the number of iterations. Further when $f_i$’s are strongly convex, we prove that Prox2-SAGA converges with an accelerated linear rate.

• Experiments are conducted to demonstrate the efficacy of the proposed algorithm, no matter whether the loss functions $f_i$ are smooth or not, in particular when the loss functions $f_i$ are ill-conditioned.

2 Definitions and assumptions

In this section, we introduce definitions and assumptions used in this paper.

2.1 Definitions

For a function f, the proximal operator at point x with step size $\gamma > 0$ is defined as

$$\begin{aligned} \text {prox}^{\gamma }_f(x) = \underset{y\in {\mathbb {R}}^d }{\text {argmin}} \Big ( f(y) + \frac{1}{2\gamma } \left\| y - x \right\| ^2 \Big ). \end{aligned}$$

(3)

For many functions f of interest, the proximal operator $\text {prox}^{\gamma }_f$ has a closed form solution or can be computed efficiently (Parikh and Boyd 2014).

Further, we define

$$\begin{aligned} \phi ^{\gamma }_{f}(x) = \frac{1}{\gamma } ( x - \text {prox}^{\gamma }_{f}(x) ) \end{aligned}$$

(4)

as the gradient mapping of f at point x with $\gamma > 0$. According to the definition of the proximal operator in (3), $\phi ^{\gamma }_{f}(x)$ is a subgradient of f at $\text {prox}^{\gamma }_{f}(x)$.

The subdifferential is introduced to facilitate the analysis of non-smoothness. The subdifferential $\partial f(x)$ of f at x is the set of all subgradient

Besides, the conjugate of a function f is defined as

2.2 Assumptions

In this paper, we may assume that each $f_i$ is $\mu$-strongly convex, namely, for any $x, y \in {\mathbb {R}}^d$ and any subgradient $g_i$ of $f_i$ at x, it holds that

$$\begin{aligned} f_i(y) \ge f_i(x) + \left<g_i, y-x\right> + \frac{\mu }{2}\left\| y-x\right\| ^2, \end{aligned}$$

where $\mu > 0$. The assumption can be easily satisfied by refining $f_i$ with a strongly-convex regularizer. For a general convex function, the above inequality always holds with $\mu = 0$.

We may also assume that each $f_i$ is L-smooth, namely, for any $x,y\in {\mathbb {R}}^{d}$, it holds that

$$\begin{aligned} f_i(y) \le f_i(x) + \left<\nabla f_i(x), y-x\right> + \frac{L}{2}\left\| y-x\right\| ^2 , \end{aligned}$$

where $L>0$ and $\nabla f_i(x)$ is the gradient of $f_i$ at x.

3 Related work

This section gives an overview of VR stochastic methods. In particular, we emphasize the accelertion techniques for ill-conditioned problems.

3.1 Variance reducing stochastic methods

To effectively reduce the variance of stochastic gradient in stochastic optimization, several statistical VR methods, such as importance sampling and stratified sampling (Owen 2013; Ross 2013), have been introduced. Although utilizing the internal structure of dataset to proceed importance sampling or stratified sampling, as considered in Zhao and Zhang (2014, 2015) and Needell et al. (2014), works quite well, it cannot asymptotically reduce the variance to zero.

Meanwhile, some other methods which employ control variates (Owen 2013, Chapter 8.9) have been considered in Johnson and Zhang (2013), Defazio et al. (2014), Shamir and Zhang (2013), Xiao and Zhang (2014) and Schmidt et al. (2017). SAGA (Defazio et al. 2014) and SVRG (Johnson and Zhang 2013) are two typical algorithms among them, which utilize the following VR stochastic gradient

$$\begin{aligned} \nabla f_j (x^k) - \nabla f_j ({\tilde{x}}) + \frac{1}{n}\sum _{i=1}^{n} \nabla f_i({\tilde{x}}), \end{aligned}$$

(5)

where ${\tilde{x}}$ is the saved “snapshot” of a previous x, to replace $\nabla f_j (x^k)$ in SGD. In SAGA and SVRG, $\nabla f_j ({\tilde{x}})$ can be regarded as the control variate of $\nabla f_j (x^k)$. The variance of the VR stochastic gradient goes to zero asymptotically along the iterative updates as $\nabla f_j (x^k)$ and $\nabla f_j ({\tilde{x}})$ become closer in expectation. This leads to a much faster convergence rate than that of SGD.

3.2 Acceleration for ill-conditioned problems

For an L-smooth and $\mu$-strongly convex function, $L/\mu$ is known as its condition number and we call a function ill-conditioned when $L/\mu$ is too large. Many gradient-based methods may perform poorly in handling ill-conditioned functions. Fortunately, the convergence rate can be boosted by some acceleration techniques. Specifically, for (1) where each $f_i$ is L-smooth and $\mu$-strongly convex while h is convex but possibly non-smooth, most VR stochastic methods such as Prox-SDCA, Prox-SAGA and Prox-SVRG require ${\mathcal {O}}\left( (n + L/\mu )\log (1/\epsilon )\right)$ steps to achieve an $\epsilon$-accurate solution. Nevertheless, if we apply some acceleration techniques, the numbers of iterations needed are ${\mathcal {O}}(( n+\sqrt{nL/\mu } )\log (L/\mu )\log (1/\epsilon ))$ in Catalyst (Woodworth and Srebro 2016) and ${\mathcal {O}}(( n+\sqrt{nL/\mu } )\log (1/\epsilon ))$ in Acc-SDCA (Shalev-Shwartz and Zhang 2014) and Katyusha (Allen-Zhu 2017). As a result, these accelerated methods will be significantly faster than the non-accelerated ones when $L/\mu \gg n$. In this paper, we shall show that our algorithm can also achieve an accelerated rate ${\mathcal {O}}(( n+\sqrt{n L/\mu } )\log (1/\epsilon ))$.

4 Algorithm

The proposed algorithm is outlined in Algorithm 1. It maintains four sequences, $x^k$, $y^k$, $g_j^k$ and $z_j^k$, where j stands for the j-th loss function. The starting point $x^0$ is set arbitrarily. Each $g_i^{0}$ can be chosen as any gradient/subgradient of $f_i$ at $x^0$. The algorithm has only one parameter, the step size $\gamma$. In the k-th iteration, a loss function $f_j$ is randomly chosen. Each $g_j$ is updated from $g_j^{k}$ to $g_j^{k+1}$ (see (9)) and x is updated from $x^{k}$ to $x^{k+1}$ (see (11)), while $z_j^{k}$ and $y^{k}$ can be regarded as the intermediate variables for the updates of $x^{k}$ and $g_j^{k}$. According to the definition of $z_j^{k}$ in (8) and update of $y^{k+1}$ in (10), the main steps can be written as

$$\begin{aligned} y^{k+1}= & {} x^{k} - \gamma \Big ( g_j^{k+1} - g_j^{k} + \frac{1}{n}\sum _{i=1}^{n}g_i^{k} \Big ), \end{aligned}$$

(6)

$$\begin{aligned} x^{k+1}= & {} \text {prox}_h^{\gamma }( y^{k} ), \end{aligned}$$

(7)

where $g_j^{k+1}$ is the gradient mapping of $f_j$ at $z_j^{k} +x^{k} - y^{k}$.

In every iteration of our algorithm, we make use of the proximal operator of $f_i$ to calculate the gradient mapping, in addition to the proximal operator of h. This setting enables the proposed algorithm to achieve the accelerated rate when the loss functions $f_i$’s are ill-conditioned. The main iteration steps in our algorithm are similar to those in Prox-SAGA, which, however, contains only one proximal operator to handle the non-smoothness of h. In this sense, we name our algorithm as Prox2-SAGA.

To be specific, the main difference between Prox2-SAGA and Prox-SAGA is the definition of $g_j$. In Prox2-SAGA, $g^{k+1}_j$ is a subgradient of $f_j$ at point $\text {prox}_{f_j}^{\gamma }(z_j^{k} +x^{k} - y^{k})$, while in Prox-SAGA $g_j^{k+1}$ is the gradient of $f_j$ at $x^{k}$. From (9) and (10), it holds that $\text {prox}_{f_j}^{\gamma }(z_j^{k} +x^{k} - y^{k}) = y^{k+1} + x^{k} - y^{k}$. That is to say, $\text {prox}_{f_j}^{\gamma }(z_j^{k} +x^{k} - y^{k})$ involves the “future” point $y^{k+1}$, which is analogous to the update in Point-SAGA (Defazio 2016). Therefore, compared to Prox-SAGA, our algorithm would achieve a faster convergence rate.

Like Prox-SAGA, we maintain a table of $g_i$ and update one element of the table in each iteration. The sum of gradient mappings $\sum _{i=1}^{n}g_i /n$ used in calculating $z_j^k$ can be cached and updated efficiently at each iteration by $\sum _{i=1}^{n}g_i^{k+1}/n = \sum _{i=1}^{n}g_i^{k}/n + (g_j^{k+1} -g_j^{k})/n$. Besides, for linearly parameterized models where $f_i(x)$ can be represented as the more structured form , following the routine of SAGA, we just need to store a single real value instead of a full vector for each $g_i$. Linear regression and binary classification with logistic or hinge losses both fall in this regime.

5 Connection with other methods

In this section, we show that Prox2-SAGA is essentially a Douglas-Rachford splitting algorithm, and is a generalization of Point-SAGA. Further, we also establish the relations between Prox2-SAGA and Prox-SDCA.

5.1 Connection with Douglas-Rachford splitting

When $n = 1$, since $g_j^{k} = \sum _{i=1}^{n}g_i^{k}/n$ in Prox2-SAGA, the main iterations can be simplified to

$$\begin{aligned} y^{k+1}= & {} -x^{k} + y^{k} + \text {prox}_f^{\gamma }(2x^{k} - y^{k}), \\ x^{k+1}= & {} \text {prox}_h^{\gamma }(y^{k+1}). \end{aligned}$$

These are the iterations of Douglas-Rachford splitting to minimize the composite cost function $f(x) + h(x)$ (Eckstein and Bertsekas 1992; Bauschke and Combettes 2017). In this sense, Prox2-SAGA is essentially a Douglas-Rachford splitting method, but aiming at solving the regularized empirical risk minimization problem when the number of samples n is larger than 1.

5.2 Generalization of point-SAGA

When $h = 0$, we have $x^k = y^{k}$ for Prox2-SAGA, and the main iterations can be simplified to

$$\begin{aligned} z_j^{k~~}= & {} x^{k} + \gamma \Big ( g_j^{k} - \frac{1}{n}\sum \limits _{i=1}^{n}g_i^{k} \Big ), \\ g_j^{k+1}= & {} \frac{1}{\gamma }(z_j^{k} - x^{k+1}), \\ x^{k+1}= & {} \text {prox}_{f_j}^{\gamma }(z_j^{k}). \end{aligned}$$

These are the iterations of Point-SAGA. Compared to Point-SAGA, Prox2-SAGA employs another proximal operator of h and uses Douglas-Rachford splitting to combine two proximal operators. Point-SAGA has been proven to have a ${\mathcal {O}}(1/k)$ convergence rate for non-smooth but strongly convex problems, and achieve an accelerated rate when each $f_i$ is smooth and strongly convex. Some convergence properties can also be inherited by Prox2-SAGA.

5.3 Relation to Prox-SDCA

Different from other VR stochastic methods such as Prox-SAGA and Prox-SVRG, Prox-SDCA considers the dual problem of (1). In this section, we show that Prox-SDCA is connected to Prox2-SAGA in the sense that it also involves calculating of gradient mappings and proximal operators. However, they are essentially different since Prox2-SAGA handles functions in the primal domain, while Prox-SDCA works in the dual domain.

The Prox-SDCA algorithm has been considered in Shalev-Shwartz and Zhang (2014). In order to unify notations, we work with $f_i(x)$ rather than the more structured $\psi _i (a_i x)$. Then the dual objective to maximize is:

where $f_i^{*}$, $h^{*}$ are the conjugate functions of $f_i$ and h, respectively; $\alpha _i$’s are d-dimension dual variables.

Adopting Option I of Prox-SDCA in Figure 1 of Shalev-Shwartz and Zhang (2012), for the selected index j in step k, we can represent the update of $\alpha _j$ as

$$\begin{aligned} \alpha _j^{k+1} = \alpha _j^{k} + \underset{\Delta \alpha _j \in {\mathbb {R}}^d}{\text {argmin}} \Big \{ f_j^{*}( -\alpha _j^{k} - \Delta \alpha _j ) + \frac{n}{2} \big \Vert x^{k} + \frac{1}{n} \Delta \alpha _j \big \Vert ^2 \Big \}, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \alpha ^{k+1}_j = \underset{y}{\text {argmin}} \Big \{ f_j^{*}(-y) + \frac{1}{2 n} \big \Vert y - \alpha ^{k}_j + n x^{k} \big \Vert ^2 \Big \}. \end{aligned}$$

(13)

Obviously, this update involves the calculation of the proximal operator of $f_j^{*}$. The relation between the proximal operator of a function and its convex conjugate can be established by the extended Moreau decomposition (Parikh and Boyd 2014):

$$\begin{aligned} \text {prox}_{f_j^{*}}^{1/\gamma }(u/\gamma ) = ( u - \text {prox}_{f_j}^{\gamma }(u) )/\gamma , \end{aligned}$$

which shows that $\text {prox}_{f_j^{*}}^{1/\gamma }(u/\gamma )$ is identical to the gradient mapping of $f_j$ at u. Therefore, the update of the dual variable $\alpha _j$ in (13) implies the calculation of the gradient mapping of $f_j$. It is the gradient mapping that allows Prox-SDCA to directly solve the problems with non-smooth loss functions. Next, we consider its update of the primal variable x.

The update of x in Prox-SDCA can be represented as

$$\begin{aligned} v^{k+1} = v^{k} + \frac{1}{n} \Delta \alpha _j, \end{aligned}$$

$$\begin{aligned} x^{k+1} = \nabla h^{*}( v^{k+1} ), \end{aligned}$$

(14)

where v is an auxiliary variable. As we optimize the strongly convex function, we can consider that there is an $L_2$ regularization in h(x). We represent h as: $h(x) = \frac{\lambda _2}{2} \left\| x \right\| ^2 + \lambda _1 r(x)$, where r(x) is the non-smooth part. Then, the conjugate function of h is

Therefore, it follows that

which is the proximal operator of r at $\frac{v^{k+1}}{\lambda _2}$. Thus, the update of x in (14) can be regarded as applying a proximal operator with step size $\frac{\lambda _1}{\lambda _2}$ on non-smooth r.

In conclusion, similar to Prox2-SAGA, Prox-SDCA involves computing the gradient mappings and proximal operators. Both (12) and (13) can be regarded as the calculation of the gradient mapping of $f_i$; the main difference is that in (13) the gradient mapping is calculated through the conjugate function of $f_i$, while in (12) the gradient mapping is calculated in the primal domain and by a rather straightforward way. Likewise, both (11) and (14) are the calculation of the proximal operator, except that (11) is more intuitive as it does not involve conjugate functions. Moreover, the gradient mapping in Prox2-SAGA involves the “future” point. Therefore, althrough both Prox2-SAGA and Prox-SDCA are able to converge linearly when each loss function is smooth and strongly convex, Prox2-SAGA would be faster than Prox-SDCA, as evidenced by the experiments.

6 Theory

In this section, we show that Prox2-SAGA converges to the optimal solution of (1) at a rate of ${\mathcal {O}}(1/k)$ when each $f_i$ is smooth, and achieves an accelerated linear rate when each $f_i$ is further assumed to be strongly convex. We begin with several useful propositions and lemmas.

6.1 Preliminaries

Our analysis is built upon the theory of Moreau envelope (Lemaréchal and Sagastizábal 1997). The Moreau envelope of a continuous function $f: {\mathbb {R}}^d \rightarrow {\mathbb {R}}$ with a regularization parameter $\gamma > 0$ is defined as

$$\begin{aligned} f^{\gamma }(x) = \inf \limits _{y}\Big \{ f(y) + \frac{1}{2\gamma }\left\| x-y \right\| ^2 \Big \}. \end{aligned}$$

(15)

The following proposition demonstrates the basic properties of Moreau envelope (Lemaréchal and Sagastizábal 1997).

Proposition 1

(Properties of Moreau envelope) Given a convex continuous function $f: {\mathbb {R}}^d \rightarrow {\mathbb {R}}$ and a regularization parameter $\gamma > 0$, we consider its Moreau envelope $f^{\gamma }$ defined in (15). Then

• 1. $f^{\gamma }$ is continuously differentiable even when f is non-differentiable, and

  $$\begin{aligned} \nabla f^{\gamma } (x) = \frac{1}{\gamma } (x - prox _f^{\gamma }(x)). \end{aligned}$$

  (16)

  Moreover, $f^{\gamma }$ is $\frac{1}{\gamma }$-smooth.

• 2. If f is $\mu$-strongly convex, then $f^{\gamma }$ is $\frac{\mu }{\mu \gamma + 1}$-strongly convex.

From the definition of the gradient mapping $\phi ^{\gamma }_f(x) = \frac{1}{\gamma }(x-\text {prox}^{\gamma }_f(x))$ in (4), we observe that $\nabla f^{\gamma }(x) = \phi ^{\gamma }_f(x)$. According to the fact that $f^{\gamma }$ is $\frac{1}{\gamma }$-smooth when f is convex and $\frac{\mu }{\mu \gamma + 1}$-strongly convex when f is $\mu$-strongly convex, we have the following lemma (Nesterov 2013).

Lemma 1

(Lower bounds of inner product) For any $x, y\in {\mathbb {R}}^d$, any convex function $f: {\mathbb {R}}^d \rightarrow {\mathbb {R}}$ and any regularization parameter $\gamma > 0$, we have

$$\begin{aligned} \left<\phi _f^{\gamma }(x) - \phi _f^{\gamma }(y), x-y \right> \ge \gamma \Vert \phi _f^{\gamma }(x) - \phi _f^{\gamma }(y) \Vert ^2. \end{aligned}$$

(17)

Further, if f is strongly convex with constant $\mu > 0$, we have

$$\begin{aligned} \left<\phi _f^{\gamma }(x) - \phi _f^{\gamma }(y), x-y \right> \ge \frac{\mu }{\mu \gamma + 1}\Vert x-y \Vert ^2. \end{aligned}$$

(18)

A direct corollary of Lemma 1 gives the following nonexpansiveness results, which are useful in the analysis.

Corollary 1

(Nonexpansiveness) For any $x, y\in {\mathbb {R}}^d$, any convex function $f: {\mathbb {R}}^d \rightarrow {\mathbb {R}}$ and any regularization parameter $\gamma > 0$, we have the firm nonexpansiveness of $prox _f^{\gamma }(x)$, given by

$$\begin{aligned} \Vert prox _f^{\gamma }(x) - prox _f^{\gamma }(y) \Vert ^2 \le \big < prox _f^{\gamma }(x) - prox _f^{\gamma }(y), x-y \big >, \,\, \end{aligned}$$

and the nonexpansiveness of $2 prox _f^{\gamma }(x) - x$, given by

$$\begin{aligned} \Vert 2 prox _f^{\gamma }(x) - x -(2 prox _f^{\gamma }(y) - y)\Vert \le \Vert x-y\Vert , \,\, \end{aligned}$$

Proof

The two inequalities follow from substituting $\phi ^{\gamma }_f(x) = \frac{1}{\gamma }(x-\text {prox}^{\gamma }_f(x))$ into (17) in Lemma 1 and reorganizing terms. $\square$

Lemma 1 gives lower bounds for the inner product $\big <\phi _f^{\gamma }(x) - \phi _f^{\gamma }(y), x-y \big>$ when f is convex or strongly convex, no matter whether f is smooth or not. When f is convex and smooth, we can deduce another lower bound for the inner product.

Lemma 2

(Another lower bound of inner product) For any $x, y \in {\mathbb {R}}^d$, any L-smooth function $f: {\mathbb {R}}^d \rightarrow {\mathbb {R}}$ and any regularization parameter $\gamma > 0$, we have

$$\begin{aligned} \left<\phi _f^{\gamma }(x) - \phi _f^{\gamma }(y), x-y \right> \ge \gamma \left( 1 + \frac{1}{L \gamma } \right) \Vert \phi _f^{\gamma }(x) - \phi _f^{\gamma }(y) \Vert ^2. \end{aligned}$$

(19)

Proof

Denote $f^*$ as the conjugate function of f. Note that L-smoothness of f implies $\frac{1}{L}$-strong convexity of $f^*$. According to (17) and (18) in Lemma 1, we have

$$\begin{aligned} \left<\phi _{f^*}^{\gamma }(x) - \phi _{f^*}^{\gamma }(y), x-y \right> \ge \frac{\frac{1}{L}}{2\frac{\gamma }{L} + 1}\Vert x - y \Vert ^2 + \frac{\gamma ( \frac{\gamma }{L} + 1 )}{2\frac{\gamma }{L} + 1} \Vert \phi _{f^*}^{\gamma }(x) - \phi _{f^*}^{\gamma }(y) \Vert ^2.\nonumber \\ \end{aligned}$$

(20)

Recalling the extended Moreau decomposition (Parikh and Boyd 2014)

$$\begin{aligned} \text {prox}_{f^*}^{\gamma }(x) = x - \gamma \,\text {prox}_{f}^{1/\gamma } (x/\gamma ), \end{aligned}$$

we have

$$\begin{aligned} \phi _{f^*}^{\gamma } (x) = \frac{1}{\gamma }\big ( x - \text {prox}_{f^*}^{\gamma }(x) \big ) = \text {prox}_f^{1/\gamma }(x/\gamma ) = \frac{1}{\gamma }\big ( x -\phi _f^{1/\gamma } (x/\gamma ) \big ). \end{aligned}$$

(21)

Plugging $\phi _{f^*}^{\gamma } (x) = \frac{1}{\gamma }\big ( x -\phi _f^{1/\gamma } (x/\gamma ) \big )$ into (20) and simplifying the terms lead to (19). $\square$

For the purpose of analysis, it is convenient to plug (9) into (9) to express Algorithm 1 in the form of

$$\begin{aligned} \left\{ \begin{array}{rcl} &{}&{}\!\!\!\! y^{k+1} = -x^{k} + y^{k} + \text {prox}_{f_j}^{\gamma }(u_j^k), \\ &{}&{}\!\!\!\! g_j^{k+1} = \frac{1}{\gamma }\big ( u_j^k - \text {prox}_{f_j}^{\gamma }(u_j^k)\big ). \end{array} \right. \end{aligned}$$

(22)

Here we define

$$\begin{aligned} u_j^{k} = z_j^{k} + x^{k} - y^{k}, \end{aligned}$$

(23)

while $z_j^{k} = x^{k} + \gamma \Big ( g_j^{k} - \frac{1}{n}\sum _{i=1}^{n}g_i^{k} \Big )$, $x^{k} = \text {prox}_h^{\gamma }(y^{k})$, as defined in (11) and (11), respectively. In these definitions, $j\in \{1,2,\dots ,n\}$.

Before giving the main results, we show that the fixed point of the Prox2-SAGA iteration, if it exists, is exactly a minimizer of (1).

Proposition 2

Suppose that $(y^{\infty },\{g_i^\infty \}_{i=1,\dots ,n})$ is the fixed point of the Prox2-SAGA iteration (22). Then $x^\infty = \mathrm{prox}_h^\gamma (y^\infty )$ is a minimizer of (1).

Proof

Define $z_j^{\infty } = x^{\infty } + \gamma \big ( g_j^{\infty } - \frac{1}{n}\sum _{i=1}^{n}g_i^{\infty } \big )$. Since $(y^{\infty },\{g_i^\infty \}_{i=1,\dots ,n})$ is the fixed point of (22), $y^{\infty } = -x^{\infty } + y^{\infty } + \text {prox}_{f_i}^{\gamma }(z_i^{\infty } + x^{\infty } - y^{\infty })$, which implies

$$\begin{aligned} (z_i^{\infty } - y^{\infty })/\gamma \in \partial f_i(x^{\infty }), \; i=1,\dots ,n. \end{aligned}$$

(24)

Meanwhile, because $x^{\infty } = \text {prox}_h^{\gamma }(y^{\infty })$, we have

$$\begin{aligned} (y^{\infty } - x^{\infty })/\gamma \in \partial h(x^{\infty }). \end{aligned}$$

(25)

Observing that

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n(z_i^\infty - y^\infty ) + (y^\infty -x^\infty ) = \frac{1}{n}\sum _{i=1}^n z_i^\infty - x^\infty = 0, \end{aligned}$$

from (24) and (25), we have $0 \in \partial f(x^{\infty }) + \partial h(x^{\infty })$, meaning that $x^{\infty }$ is a minimizer of (1). $\square$

Denote $x^*$ as a minimizer of (1). According to the first-order optimality condition of (1), there exist a set of subgradients $g_j^{*}$, one for each loss function $f_j$ at $x^{*}$, and a subgradient $\partial h(x^{*})$ for the regularization function h at $x^{*}$, such that $0 \in \frac{1}{n} \sum _{i=1}^{n} g_i^{*} + \partial h(x^{*})$. Define

$$\begin{aligned} g^{*} = \frac{1}{n} \sum _{i=1}^{n}g_i^{*},~y^{*} = z_j^{*} - \gamma g_j^{*},~z_j^{*} = x^{*} + \gamma \left( g_j^{*} - g^{*}\right) ,~u_j^* = z_j^* - x^* - y^*.\nonumber \\ \end{aligned}$$

(26)

It is not difficult to verify from these definitions and the properties of the proximal operator that

$$\begin{aligned} g_j^{*} = \frac{1}{\gamma }\big ( u_j^{*} - \mathrm{prox}_{f_j}^{\gamma }(u_j^{*}) \big ), ~ x^{*} = \text {prox}_h^{\gamma } (y^{*}). \end{aligned}$$

(27)

Throughout the analysis, all expectations are taken with respect to the choice of j at iteration k unless stated otherwise. Two particularly useful expectations are

$$\begin{aligned} {\mathbb {E}} [g_j^{k}] = \frac{1}{n} \sum _{i=1}^{n}g_i^{k}, ~ {\mathbb {E}} [g_j^{*}] = g^{*}. \end{aligned}$$

(28)

6.2 Main results

The proofs of the main results rely on a Lyapunov function, which at time $k+1$ is defined as

$$\begin{aligned} T^{k+1} = \frac{c}{n}\sum \limits _{i=1}^{n} \big \Vert \gamma (g_i^{k+1} - g_i^{*}) \big \Vert ^2 + \big \Vert y^{k+1} - y^* \big \Vert ^2, \end{aligned}$$

(29)

where $c > 0$ is a constant. We shall choose c as different values in the proofs of Theorems 1 and 2. The following lemma gives an upper bound for the expecation of the Lyapunov function.

Lemma 3

(Expectation of Lyapunov function) Assume that each loss functions $f_i$ is convex and L-smooth, while the regularization function h is convex. Then for Prox2-SAGA, at any time $k > 0$, the expectation of the Lyapunov function defined in (29) satisfies

$$\begin{aligned} {\mathbb {E}} [T^{k+1}]\le & {} \left( \frac{1}{2}+ \left( 1- \frac{1}{n} \right) c\right) \frac{1}{n}\sum \limits _{i=1}^{n} \big \Vert \gamma (g_i^{k} - g_i^*) \big \Vert ^2 + \left( 2+\frac{c}{n} \right) {\mathbb {E}} \big \Vert \gamma (g_j^{k+1} - g_j^*) \big \Vert ^2 \nonumber \\&+ \frac{1}{2}\Vert y^{k} - y^{*}\Vert ^2 + \frac{1}{2} {\mathbb {E}} \big \Vert u_j^{k} - u_j^{*} \big \Vert ^2 - 2{\mathbb {E}} \big <u_j^{k} - u_j^{*}, \gamma (g_j^{k+1} - g_j^{*}) \big >. \end{aligned}$$

(30)

Proof

Taking expectation over the first term of $T^{k+1}$, we have

$$\begin{aligned} \frac{c}{n}{\mathbb {E}}\sum \limits _{i=1}^{n} \big \Vert \gamma (g_i^{k+1} - g_i^*) \big \Vert ^2 = \left( 1- \frac{1}{n} \right) \frac{c}{n}\sum \limits _{i=1}^{n} \big \Vert \gamma (g_i^{k} - g_i^*) \big \Vert ^2 + \frac{c}{n}{\mathbb {E}} \big \Vert \gamma (g_j^{k+1} - g_j^*) \big \Vert ^2.\nonumber \\ \end{aligned}$$

(31)

To calculate the expectation for the second term of $T^{k+1}$, recall the definition of $z_j^{k}$ in (8) and $u_j^{k}$ in (23), we start by rewriting the iteration of $y^{k+1}$ in (22) as

$$\begin{aligned} y^{k+1} = \frac{1}{2}\Big ( y^{k} + \gamma \big (g_j^{k} - \frac{1}{n}\sum \limits _{i=1}^{n}g_i^{k}\big ) \Big ) + \frac{1}{2}\big ( 2\text {prox}_{f_j}^{\gamma }(u_j^{k}) - u_j^{k} \big ). \end{aligned}$$

(32)

Rewriting $y^{*}$ in the same way that $y^{*} = \frac{1}{2}\big ( y^{*} + \gamma (g_j^{*} - g^{*}) \big ) + \frac{1}{2} \big ( 2\text {prox}_{f_j}^{\gamma }(u_j^{*}) - u_j^{*} \big )$, then by Young’s inequality, we have

$$\begin{aligned} {\mathbb {E}} \big \Vert y^{k+1} - y^* \big \Vert ^2= & {} \frac{1}{4} {\mathbb {E}}\big \Vert y^k - y^* + \gamma \big ( g_j^{k} -\frac{1}{n}\sum \limits _{i=1}^{n}g_i^{k} - g_j^{*} + g^{*}\big ) \nonumber \\&+ \big ( 2\text {prox}_{f_j}^{\gamma }(u_j^{k}) - u_j^{k}\big ) - \big ( 2\text {prox}_{f_j}^{\gamma }(u_j^{*}) - u_j^{*} \big ) \big \Vert ^2 \nonumber \\\le & {} \frac{1}{2}{\mathbb {E}}\big \Vert y^k - y^* + \gamma \big ( g_j^{k} -\frac{1}{n}\sum \limits _{i=1}^{n}g_i^{k} - g_j^{*} + g^{*}\big ) \big \Vert ^2 \nonumber \\&+ \frac{1}{2}{\mathbb {E}} \big \Vert \big ( 2\text {prox}_{f_j}^{\gamma }(u_j^{k}) - u_j^{k}\big ) - \big ( 2\text {prox}_{f_j}^{\gamma }(u_j^{*}) - u_j^{*} \big )\big \Vert ^2. \end{aligned}$$

(33)

Because $y^{k} - y^{*}$ is independent with the selection of j, and ${\mathbb {E}} ( g_j^{k} - \frac{1}{n} \sum _{i=1}^{n}g_i^{k} - g_j^{*} + g^{*}) = 0$ according to (28), we have ${\mathbb {E}}\big <y^{k} - y^{*}, \gamma ( g_j^{k} - \frac{1}{n} \sum _{i=1}^{n}g_i^{k} - g_j^{*} + g^{*}) \big > = 0$. Then, for the first term at the right-hand side of (33), it holds

$$\begin{aligned}&{\mathbb {E}}\big \Vert y^k - y^* + \gamma \big ( g_j^{k} -\frac{1}{n}\sum \limits _{i=1}^{n}g_i^{k} - g_j^{*} + g^{*}\big ) \big \Vert ^2 \nonumber \\= & {} \Vert y^{k} - y^{*}\Vert ^2 + {\mathbb {E}}\Vert \gamma \big ( g_j^{k} -\frac{1}{n}\sum \limits _{i=1}^{n}g_i^{k} - g_j^{*} + g^{*}\big ) \big \Vert ^2 \nonumber \\\le & {} \Vert y^{k} - y^{*}\Vert ^2 + {\mathbb {E}}\Vert \gamma \big ( g_j^{k} - g_j^{*} \big ) \big \Vert ^2. \end{aligned}$$

(34)

The inequality comes from the variance formula ${\mathbb {E}}(X-{\mathbb {E}}X)^2 \le {\mathbb {E}}X^2$ applied to ${\mathbb {E}}\big \Vert \gamma \big ( g_j^{k} - g_j^{*} - \frac{1}{n} \sum _{i=1}^{n}g_i^{k} + g^{*}\big ) \big \Vert ^2$, since ${\mathbb {E}}(g_j^{k} - g_j^{*}) = \frac{1}{n} \sum _{i=1}^{n}g_i^{k} - g^{*}$.

We further manipulate the second term at the right-hand side of (33). Observe that $\gamma g_j^{k+1} = u_j^{k} - \text {prox}_{f_j}^{\gamma }(u_j^{k})$ by ((27)) and $\gamma g_j^* = u_j^* - \text {prox}_{f_j}^{\gamma }(u_j^*)$ by (27). Then we have

$$\begin{aligned}&{\mathbb {E}} \big \Vert \big ( 2\text {prox}_{f_j}^{\gamma }(u_j^{k}) - u_j^{k}\big ) - \big ( 2\text {prox}_{f_j}^{\gamma }(u_j^{*}) - u_j^{*} \big )\big \Vert ^2 \nonumber \\= & {} {\mathbb {E}} \Big \Vert u_j^{k} - 2 \gamma g_j^{k+1} - u_j^{*} + 2 \gamma g_j^* \Big \Vert ^2 \nonumber \\= & {} {\mathbb {E}} \big \Vert u_j^{k} - u_j^{*} \big \Vert ^2 + 4 {\mathbb {E}} \big \Vert \gamma (g_j^{k+1} - g_j^{*}) \big \Vert ^2 - 4{\mathbb {E}} \big <u_j^{k} - u_j^{*}, \gamma (g_j^{k+1} - g_j^{*}) \big >. \end{aligned}$$

(35)

Substituting (34) and (35) into (33) and combining with (31), we obtain the upper bound given by (30). $\square$

Theorem 1

(Non-strongly convex case) Assume that each loss function $f_i$ is convex and L-smooth, while the regularization function h is convex. Then for Prox2-SAGA with step size $\gamma \le 1/L$, at any time $k > 0$ it holds

$$\begin{aligned} {\mathbb {E}} \big \Vert {\bar{g}}_j^{k} - g_j^{*} \big \Vert ^2 \le \frac{1}{ k} \Big ( \sum \limits _{i=1}^{n} \big \Vert g_i^{0} - g_i^{*}\big \Vert ^2 + \Vert \frac{1}{\gamma } (y^{0} - y^{*}) \Vert ^2 \Big ), \end{aligned}$$

where ${\bar{g}}_j^{k} = \frac{1}{k}\sum _{t=1}^{k}g_j^{t}$. Here the expectation is taken over all choices of index j up to time k.

Proof

We further manipulate the upper bound of ${\mathbb {E}} [T^{k+1}]$ given by (30). Recalling the definitions of $u_j^{k} = z_j^{k} + x^{k} - y^{k}$ in (23) and $u_j^* = z_j^* + x^* - y^*$ in (26) as well as the definitions of $z_j^{k}$ in () and $z_j^{*}$ in (26), we bound ${\mathbb {E}} \Vert u_j^{k} - u_j^{*} \Vert ^2$ as

$$\begin{aligned} {\mathbb {E}} \Vert u_j^{k} - u_j^{*} \Vert ^2= & {} {\mathbb {E}} \Big \Vert 2x^k - y^k - (2x^{*} - y^{*}) + \gamma \big ( g_j^{k} -\frac{1}{n}\sum \limits _{i=1}^{n}g_i^{k} - g_j^{*} + g^{*}\big ) \Big \Vert ^2 \nonumber \\= & {} \big \Vert 2x^k - y^k - (2x^{*} - y^{*}) \big \Vert ^2 + {\mathbb {E}} \Big \Vert \gamma \big ( g_j^{k} -\frac{1}{n}\sum \limits _{i=1}^{n}g_i^{k} - g_j^{*} + g^{*}\big ) \Big \Vert ^2 \nonumber \\\le & {} \big \Vert y^{k} - y^{*} \big \Vert ^2 + {\mathbb {E}} \Big \Vert \gamma \big ( g_j^{k} -\frac{1}{n}\sum \limits _{i=1}^{n}g_i^{k} - g_j^{*} + g^{*}\big ) \Big \Vert ^2 \nonumber \\\le & {} \big \Vert y^{k} - y^{*} \big \Vert ^2 + {\mathbb {E}} \big \Vert \gamma \big ( g_j^{k} - g_j^{*} \big ) \big \Vert ^2. \end{aligned}$$

(36)

The first inequality is due to the nonexpansiveness of $2\text {prox}_h^{\gamma }(y) - y$ as stated in Corollary 1, since $x^{k}=\text {prox}_h^{\gamma }(y^{k})$ by (11) and $x^{*}=\text {prox}_h^{\gamma }(y^{*})$ by (27). The second inequality comes from the variance formula ${\mathbb {E}}(X-{\mathbb {E}}X)^2 \le {\mathbb {E}}X^2$ applied to ${\mathbb {E}}\big \Vert \gamma \big ( g_j^{k} - g_j^{*} - \frac{1}{n} \sum _{i=1}^{n}g_i^{k} + g^{*}\big ) \big \Vert ^2$, since ${\mathbb {E}}(g_j^{k} - g_j^{*}) = \frac{1}{n} \sum _{i=1}^{n}g_i^{k} - g^{*}$.

According to the definitions of $g_j^{k+1}$ by (9) and $g_j^{*}$ by (27), $g_j^{k+1}$ is the gradient mapping at $u_j^{k}$, while $g_j^{*}$ is the gradient mapping at $u_j^{*}$, we further apply Lemma 2 to bound $-\gamma \big <u^k_j - u^{*}_j, g_j^{k+1} - g_j^{*} \big >$ to deduce

$$\begin{aligned} - {\mathbb {E}} \big <u_j^{k} - u_j^{*}, \gamma (g_j^{k+1} - g_j^{*}) \big > \le - \big (1 +\frac{1}{L\gamma } \big ) {\mathbb {E}} \big \Vert \gamma (g_j^{k+1} - g_j^{*}) \big \Vert ^2. \end{aligned}$$

(37)

Plugging (36) and (37) into (30) and reorganizing terms, we obtain

$$\begin{aligned} {\mathbb {E}} [T^{k+1}]\le & {} T^{k} + \left( 1 - \frac{c}{n} \right) \frac{1}{n}\sum \limits _{i=1}^{n}\big \Vert \gamma (g_i^{k} - g_i^{*} )\big \Vert ^2 \\&+ \left( \frac{c}{n} - \frac{2}{L\gamma } + 1 \right) {\mathbb {E}}\big \Vert \gamma (g_j^{k+1} - g_j^{*} )\big \Vert ^2 - {\mathbb {E}}\big \Vert \gamma (g_j^{k+1} - g_j^{*} )\big \Vert ^2. \end{aligned}$$

In particular, we set $c=n$ and $\gamma \le 1/L$ to ensure that $1-\frac{c}{n}$ and $\frac{c}{n}-\frac{2}{L\gamma }+1$ are both non-positive, such that

$$\begin{aligned} {\mathbb {E}} [T^{k+1}] \le T^{k} - {\mathbb {E}}\big \Vert \gamma (g_j^{k+1} - g_j^{*} )\big \Vert ^2. \end{aligned}$$

(38)

Taking expectation on both sides of (38) and summing up over times from 0 to k, we have

$$\begin{aligned} \sum \limits _{t=1}^{k} {\mathbb {E}} \big \Vert \gamma (g_j^{t} - g_j^{*}) \big \Vert ^2 \le T^0 - {\mathbb {E}}[T^{k}]. \end{aligned}$$

Using Jensen’s inequality $\sum _{t=1}^{k} {\mathbb {E}} \big \Vert (g_j^{t} - g_j^{*}) \big \Vert ^2 \ge k {\mathbb {E}} \big \Vert {\bar{g}}_j^{k} - g_j^{*} \big \Vert ^2$ where ${\bar{g}}_j^{k} = \frac{1}{k}\sum _{t=1}^{k}g_j^{t}$, and throwing away the non-positive term $-{\mathbb {E}}[T^{k}]$, we further have

$$\begin{aligned} {\mathbb {E}} \big \Vert {\bar{g}}_j^{k} - g_j^{*} \big \Vert ^2 \le \frac{1}{\gamma ^{2} \cdot k} T^{0}. \end{aligned}$$

Substituting $c = n$ into $T^{0}$ completes the proof. $\square$

Theorem 2

(Strongly convex case) Assume that each loss functions $f_i$ is $\mu$-strongly convex convex and L-smooth, while the regularization function h is convex. Then for Prox2-SAGA with stepsize $\gamma = \min \Big \{\frac{1}{\mu n}, \frac{\sqrt{9L^{2} + 3 \mu L} - 3L}{2\mu L} \Big \}$, for any time $k>0$ it holds

$$\begin{aligned} {\mathbb {E}}\big \Vert x^{k} - x^{*} \big \Vert ^2 \le \big (1 - \frac{\mu \gamma }{2\mu \gamma + 2} \big )^{k} \cdot \frac{\mu \gamma - 2}{2 - n\mu \gamma }\Big \{\sum \limits _{i=1}^{n}\big \Vert \gamma (g_i^{0} - g_i^{*}) \big \Vert ^2 + \Vert y^{0} - y^{*} \Vert ^2 \Big \}.\nonumber \\ \end{aligned}$$

(39)

Here the expectation is taken over all choices of index j up to k.

Proof

We elaborate on the upper bound of ${\mathbb {E}} [T^{k+1}]$ given by (30) in a different way than that in the proof of Theorem 1. Since $f_j$ is $\mu$-strongly convex as well as $g_j^{k+1}$ and $g_j^{*}$ is the gradient mapping of $f_j$ at $u_j^{k}$ and $u_j^{*}$, respectively, from (18) in Lemma 1, it holds that

$$\begin{aligned} -\frac{1}{2}\big <u^k_j - u^{*}_j, \gamma (g_j^{k+1} - g_j^{*}) \big > \le - \frac{\mu \gamma }{2(1 + \mu \gamma )} \big \Vert u_j^{k} - u_j^{*} \big \Vert ^2. \end{aligned}$$

(40)

Plugging (40) and (37) into (30) in Lemma 3 and recalling the upper bound for ${\mathbb {E}} \Vert u_j^{k} - u_j^{*} \Vert ^2$ given by (36) in the proof of Theorem 1, we obtain

$$\begin{aligned} {\mathbb {E}} [T^{k+1}]\le & {} \left( 1 -\frac{\mu \gamma }{2\mu \gamma + 2} \right) T^{k} + \frac{1}{2} \left( \frac{\mu \gamma }{\mu \gamma + 1}c - \frac{2c}{n} + \frac{\mu \gamma + 2}{\mu \gamma + 1} \right) \frac{1}{n}\sum \limits _{i=1}^{n}\big \Vert \gamma (g_i^{k} - g_i^{*} )\big \Vert ^2 \nonumber \\&+ \frac{1}{2} \left( 1 - \frac{3}{L\gamma } + \frac{2c}{n} \right) {\mathbb {E}}\big \Vert \gamma (g_j^{k+1} - g_j^{*} )\big \Vert ^2. \end{aligned}$$

(41)

We choose proper values for c and $\gamma$ to ensure that the coefficients of the last two terms at the right-hand side of (41) are non-positive. Here we take

$$\begin{aligned} c = \frac{\mu \gamma + 2 }{2/n - \mu \gamma }, \;\;\gamma = \min \Big \{\frac{1}{\mu n}, \frac{\sqrt{9L^{2} + 3 \mu L} - 3L}{2\mu L} \Big \}. \end{aligned}$$

(42)

Dropping these two non-positive terms and then taking expectation for (41) with respect to all the previous steps give

$$\begin{aligned} {\mathbb {E}}[T^{k+1}] \le \left( 1 - \frac{\mu \gamma }{2\mu \gamma + 2} \right) {\mathbb {E}}[T^{k}]. \end{aligned}$$

Further chaining over k yields

$$\begin{aligned} {\mathbb {E}}[T^{k}] \le \left( 1 - \frac{\mu \gamma }{2\mu \gamma + 2} \right) ^{k} \cdot T^{0}. \end{aligned}$$

Due to the firm nonexpansiveness of $x^k = \text {prox}_h^{\gamma }(y^k)$, we have

$$\begin{aligned} {\mathbb {E}}\Vert x^{k} - x^{*} \Vert ^2 \le {\mathbb {E}}\Vert y^{k} - y^{*} \Vert ^2 \le {\mathbb {E}}[T^{k}] \le \left( 1 - \frac{\mu \gamma }{2\mu \gamma + 2} \right) ^{k} \cdot T^{0}. \end{aligned}$$

Substituting $c = \frac{\mu \gamma + 2 }{2/n - \mu \gamma }$ into $T^{0}$ completes the proof. $\square$

Remark 1

Under the step size rule $\gamma = \min \Big \{\frac{1}{\mu n}, \frac{\sqrt{9L^{2} + 3 \mu L} - 3L}{2\mu L} \Big \}$, to achieve an $\epsilon$-accurate solution $x^k$ such that ${\mathbb {E}}\big \Vert x^{k} - x^{*} \big \Vert ^2 \le \epsilon$, the number of required steps is ${\mathcal {O}}(n + L/\mu )\log (1/\epsilon )$, which is consistent with existing VR stochastic algorithms. Nevertheless, when $f_i$ is ill-conditioned, namely, $L/\mu \gg n$, we can use a different step size rule

$$\begin{aligned} \gamma = \min \Big \{\frac{1}{\mu n}, \frac{6L + \sqrt{36L^{2} - 6(n-2)\mu L}}{2(n-2)\mu L} \Big \}, \end{aligned}$$

under which the number of required steps to achieve an $\epsilon$-accurate solution is ${\mathcal {O}}(n + \sqrt{nL/\mu }) \log (1/\epsilon )$. This accelerated rate is consistent with the fastest accelerated methods such as Acc-SDCA and Katyusha.

7 Experiments

In this section, we conduct numerical experiments to validate the effectiveness and the theoretical properties of the proposed Prox2-SAGA algorithm. In the experiments, we focus on sparse SVMs:

(43)

and $\ell _1 \ell _2$-Logistic Regression (LR):

(44)

where $a_i \in {\mathbb {R}}^d$, $b_i \in \left\{ -1, +1\right\}$ and $\lambda _1, \lambda _2 \ge 0$. The first problem involves the non-smooth hinge loss, from which we verify the effectiveness of Prox2-SAGA to handle non-smooth loss functions. The $\ell _1 \ell _2$-logistic regression contains smooth logistic functions, from which we verify the acceleration effect of Prox2-SAGA and the performance of Prox2-SAGA for non-strongly convex problems.

Table 1 Summary of the datasets and models used in the experiments

We employ datasets from LIBSVM (Chang et al. 2011) which are summarized in Table 1. By referring to the previous works, we set the values of $\lambda _1$ and $\lambda _2$. Some values of $\lambda _1$ and $\lambda _2$ are also listed in Table 1. Prox-SAGA (Defazio et al. 2014), Prox-SDCA (Shalev-Shwartz and Zhang 2014), Prox-SGD (Duchi and Singer 2009; Langford et al. 2009) and Acc-SDCA (Shalev-Shwartz and Zhang 2014) are included in the experiments for comparison. In the k-th iteration, the step size of Prox-SGD is set as $\gamma ^{k}\! =\! \gamma ^{0}/ ( 1+\gamma ^{0} \eta k)$ with $\gamma ^{0}, \eta > 0$, and we take the fixed step size for other algorithms. We tune the step size and the other parameters for different algorithms so that they can achieve the best performance. To make a fair comparison, the initial value of x is set to zero in all algorithms. Denote the number of samples as n, we measure the objective gap at x as $f(x)-f(x^{*})+g(x)-g(x^{*})$ and the epoch as the evaluation of n component gradients to evaluate the performance of algorithms.

7.1 Sparse SVMs

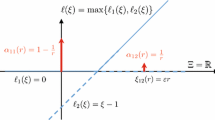
We first compare the performance of the proposed Prox2-SAGA with Prox-SGD, Prox-SAGA and Prox-SDCA for solving (43). For the non-smooth hinge loss $f_i(x) = \max \{0, 1-b_ia_ix\}$, we take its subgradient , and the proximal operator has a closed-form expression:

$$\begin{aligned} \text {prox}_{f_i}^\gamma (x) = x - \gamma b_i u a_i, \end{aligned}$$

where

Note that only Prox-SDCA and Prox-SGD can be theoretically guaranteed to converge to the minimizer of (1).

Fig. 1

Comparison of several algorithms with sparse SVMs

Fig. 2

Comparison of several algorithms with $\ell _1 \ell _2$-Logistic Regression

Experiments are conducted on four datasets, and the results are shown in Fig. 1. It can be seen that Prox2-SAGA works well with non-smooth loss functions. In contrast, the performance of the Prox-SGD algorithm is poor on all the datasets. Meanwhile, although Prox-SAGA may perform well in the beginning, it is possible to get stuck in the later iterations, which is particularly evident on the rcv1 dataset.

7.2 $\ell _1 \ell _2$-logistic regression

In the investigation here, we compare the performance of Prox2-SAGA with Prox-SGD, Prox-SAGA, Prox-SDCA and Acc-SDCA for solving (44). Prox2-SAGA and Acc-SDCA are the accelerated methods for Prox-SAGA and Prox-SDCA, respectively. For the log loss , the proximal operator can be computer efficiently by several Newton iterations. That is to say, we start from an initial point $c^0 \in {\mathbb {R}}$, and do the following iterations until convergence

Then the proximal operator is

Note that the Prox-SDCA and Acc-SDCA (Shalev-Shwartz and Zhang 2014) algorithms also need to employ such Newton iterations in practice. In order to understand the impacts of condition number on these algorithms, we set three different values of $\lambda _2$ for each dataset, which are marked in Fig. 2. Note that $\lambda _2 = 0$ corresponds to the non-strongly convex case, where Prox-SDCA and Acc-SDCA are not suitable. We use Acc-SDCA for comparison rather than other accelerated algorithms, since Acc-SDCA has less parameters to tune and is more practical.

Experiments are conducted on the datasets of mushrooms and w7a, and the results are shown in Fig. 2. One can observe that for relatively large $\lambda _2$, most VR stochastic methods perform similarly. On the other hand, when $\lambda _2$ gets smaller, the accelerated methods are significantly faster than the non-accelerated methods in most cases. This shows that as the accelerated algorithms, Prox2-SAGA and Acc-SDCA can resist the ill conditions well. Furthermore, Prox2-SAGA is more stable and performs better than Acc-SDCA according to Fig. 2.

8 Conclusion

In this paper, we propose a novel VR stochastic algorithm, Prox2-SAGA, to solve the regularized empirical risk minimization problem. At every iteration of Prox2-SAGA, we use two proximal operators, one on a randomly chosen loss function and the other on the regularization function. Accelerated convergence rate can be achieved when each loss function is strongly convex and smooth. Experimental results demonstrate its superiority over the other VR stochastic methods.