The online performance estimation framework: heterogeneous ensemble learning for data streams

Abstract

Ensembles of classifiers are among the best performing classifiers available in many data mining applications, including the mining of data streams. Rather than training one classifier, multiple classifiers are trained, and their predictions are combined according to a given voting schedule. An important prerequisite for ensembles to be successful is that the individual models are diverse. One way to vastly increase the diversity among the models is to build an heterogeneous ensemble, comprised of fundamentally different model types. However, most ensembles developed specifically for the dynamic data stream setting rely on only one type of base-level classifier, most often Hoeffding Trees. We study the use of heterogeneous ensembles for data streams. We introduce the Online Performance Estimation framework, which dynamically weights the votes of individual classifiers in an ensemble. Using an internal evaluation on recent training data, it measures how well ensemble members performed on this and dynamically updates their weights. Experiments over a wide range of data streams show performance that is competitive with state of the art ensemble techniques, including Online Bagging and Leveraging Bagging, while being significantly faster. All experimental results from this work are easily reproducible and publicly available online.

Introduction

Real-time analysis of data streams is a key area of data mining research. Many real world collected data are in fact streams where observations come in one by one, and algorithms processing these are often subject to time and memory constraints. The research community developed a large number of machine learning algorithms capable of online modelling general trends in stream data and make accurate predictions for future observations.

In many applications, ensembles of classifiers are the most accurate classifiers available. Rather than building one model, a variety of models are generated that all vote for a certain class label. One way to vastly improve the performance of ensembles is to build heterogeneous ensembles, consisting of models generated by different techniques, rather than homogeneous ensembles, in which all models are generated by the same technique. Both types of ensembles have been extensively analysed in classical batch data mining applications. As the underlying techniques upon which most heterogeneous ensemble techniques rely can not be trivially transferred to the data stream setting, there are currently no successful heterogeneous ensemble techniques in the data stream setting. State of the art heterogeneous ensembles in a data stream setting typically rely on meta-learning (van Rijn et al. 2014; Rossi et al. 2014). These approaches both require the extraction of computationally expensive meta-features and yield marginal improvements.

Fig. 1

Performance of four classifiers on intervals (size $1,000$) of the electricity dataset. Each data point represents the accuracy of a classifier on the most recent interval

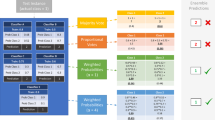
In this work we introduce a technique that natively combines heterogeneous models in the data stream setting. As data streams are constantly subject to change, the most accurate classifier for a given interval of observations also changes frequently, as illustrated by Fig. 1. In their seminal paper, Littlestone and Warmuth (1994) describe a strategy to weight the vote of ensemble members based on their performance on recent observations and prove certain error bounds. Although this work is of great theoretical value, it needs non-trivial adjustments to be applicable on practical data streams. Based on this approach, we propose a way to measure the performance of ensemble members on recent observations and combine their votes.

Our contributions are the following. We define Online Performance Estimation, a framework that provides dynamic weighting of the votes of individual ensemble members across the stream. Utilising this framework, we introduce a new ensemble technique that combines heterogeneous models. The members of the ensemble are selected based on their diversity in terms of the correlation of their errors, leveraging the Classifier Output Difference (COD) by Peterson and Martinez (2005). We conduct an extensive empirical study, covering 60 data streams and 25 classifiers, that shows that this technique is competitive with state of the art ensembles, while requiring significantly less resources. Our proposed methods are implemented in the data stream framework MOA and all our experimental results are made publicly available on OpenML.

The remainder of this paper is organised as follows. Section 2 surveys related work, and Sect. 3 introduces the proposed methods. We demonstrate the performance by two experiments. Section 4 describes the experimental setup, the selected data streams and the baselines. Section 5 compares the performance of the proposed methods against state of the art methods, and Sect. 6 surveys the effect of its parameters. Section 7 concludes.

Related work

It has been recognised that data stream mining differs significantly from conventional batch data mining (e.g., Domingos and Hulten 2003; Gama et al. 2009; Bifet et al. 2010a, b; Read et al. 2012). In the conventional batch setting, a finite amount of stationary data is provided and the goal is to build a model that fits the data as well as possible. When working with data streams, we should expect an infinite amount of data, where observations come in one by one and are being processed in that order. Furthermore, the nature of the data can change over time, known as concept drift. Classifiers should be able to detect when a learned model becomes obsolete and update it accordingly.

Common approaches Some batch classifiers can be trivially adapted to a data stream setting. Examples are k Nearest Neighbour (Beringer and Hüllermeier 2007; Zhang et al. 2011), Stochastic Gradient Descent (Bottou 2004) and SPegasos (Stochastic Primal Estimated sub-GrAdient SOlver for SVMs) (Shalev-Shwartz et al. 2011). Both Stochastic Gradient Descent and SPegasos are gradient descent methods, capable of learning a variety of linear models, such as Support Vector Machines and Logistic Regression, depending on the chosen loss function.

Other classifiers have been created specifically to operate on data streams. Most notably, Domingos and Hulten (2000) introduced the Hoeffding Tree induction algorithm, which inspects every example only once, and stores per-leaf statistics to calculate the information gain on which the split criterion is determined. The Hoeffding bound states that the true mean of a random variable of a given range will not differ from the estimated mean by more than a certain value. This provides statistical evidence that a certain split is superior over others. As Hoeffding Trees seem to work very well in practice, many variants have been proposed, such as Hoeffding Option Trees (Pfahringer et al. 2007), Adaptive Hoeffding Trees (Bifet and Gavaldà 2009) and Random Hoeffding Trees (Bifet et al. 2012).

Finally, a commonly used technique to adapt traditional batch classifiers to the data stream setting is training them on a window of w recent examples: after w new examples have been observed, a new model is built. This approach has the advantage that old examples are ignored, providing natural protection against concept drift. A disadvantage is that it doesn’t operate directly on the most recently observed data, not before w new observations are made and the model is retrained. Read et al. (2012) compare the performance of these batch-incremental classifiers with common data stream classifiers, and conclude that the overall performance is equivalent, although the batch-incremental classifiers generally use more resources.

Ensembles Ensemble techniques train multiple classifiers on a set of weighted training examples, and these weights can vary for different classifiers. In order to classify test examples, all individual models produce a prediction, also called a vote, and the final prediction is made according to a predefined voting schema, e.g., the class with the most votes is selected. Based on Condorcet’s jury theorem (Hansen and Salamon 1990; Ladha 1993) there is theoretical evidence that the error rate of an ensemble in the limit goes to zero if two conditions are met. First, the individual models must do better than random guessing, and second, the individual models must be diverse, i.e., their errors should not be correlated.

Classifier Output Difference (COD) is a metric which measures the number of observations on which a pair of classifiers yields a different prediction (Peterson and Martinez 2005). It is defined as:

$$\begin{aligned} { COD }_T(l_1,l_2) = \dfrac{\sum _{\mathbf {x} \in T}B(l_1(\mathbf {x}),l_2(\mathbf {x}))}{|T|} \end{aligned}$$

(1)

where T is the set of all test instances, $l_1$ and $l_2$ are the classifiers to compare and $l_1(\mathbf {x})$ and $l_2(\mathbf {x})$ is the label that the respective classifiers $l_1$ and $l_2$ give to test instance $\mathbf {x}$; finally, B is a binary function that returns 1 iff $l_1(\mathbf {x})$ and $l_2(\mathbf {x})$ are equal and 0 otherwise. Peterson and Martinez (2005) use this measure to ensure diversity among the ensemble members. A high value of COD indicates that two classifiers yield different predictions, hence they would be well suited to combine in an ensemble. Lee and Giraud-Carrier (2011) use Classifier Output Difference to build a hierarchical clustering among classifiers, resulting in classifiers that have similar predictions to be closely clustered, and vice versa.

In the data stream setting, ensembles can be either static or dynamic. Static ensembles contain a fixed set of ensemble members, whereas dynamic ensembles sometimes replace old models by new ones. Both approaches have advantages and disadvantages. Dynamic ensembles can actively replace obsolete models by new ones when concept drift occurs, whereas static ensembles need to rely on the individual members to recover from it. However, in order for dynamic ensembles to work properly, many parameters need to be set. For example, when to remove an old model, when to introduce a new model, which model should be introduced, and how long such new model should be trained before its vote will be considered. For these reasons, in this work we focus on static ensembles, in order to provide an off the shelf working method that does not require extensive parameter tuning. We will compare it with both static and dynamic ensemble methods.

Static ensembles Bagging (Breiman 1996) exploits the instability of classifiers by training them on different bootstrap replicates: resamplings (with replacement) of the training set. Effectively, the training sets for various classifiers differ by the weights of their training examples. Online Bagging (Oza 2005) operates on data streams by drawing the weight of each example from a $Poisson (1)$ distribution, which converges to the behaviour of the classical Bagging algorithm if the number of examples is large. As the Hoeffding bound gives statistical evidence that a certain split criteria is optimal, this makes them more stable and hence less suitable for the use in a Bagging scheme. However, in practise this yields good results. Boosting (Schapire 1990) is a technique that sequentially trains multiple classifiers, in which more weight is given to examples that where misclassified by earlier classifiers. Online Boosting (Oza 2005) applies this technique on data streams by assigning more weight to training examples that were misclassified by previously trained classifiers in the ensemble. Stacking (Wolpert 1992; Gama and Brazdil 2000) combines heterogeneous models in the classical batch setting. It trains multiple models on the training data. All base-learners output a prediction, and a meta-learner makes a final decision based on these. Caruana et al. (2004) propose a hill-climbing method to select an appropriate set of base-learners from a large library of models.

Dynamic ensembles Weighted Majority is an ensemble technique specific to data streams, where a meta-algorithm learns the weights of the ensemble members (Littlestone and Warmuth 1994). The authors also provide tight error bounds compared for the meta-algorithm compared to to the best ensemble member (under certain assumptions). Dynamic Weighted Majority is an extension of this work, specific to data streams with changing concepts (Kolter and Maloof 2007). It contains a set of classifiers, and measures the performance of these based on recent observations. Whenever an ensemble member classifies a new observation wrong, its weight gets decreased by a predefined factor. Whenever the ensemble misclassifies an instance, a new ensemble member gets added to the pool of learners. Members with a weight below a given threshold get removed from the ensemble.

Accuracy Weighted Ensemble is an ensemble technique that splits the stream into chunks of observations, and trains a classifier on each of these (Wang et al. 2003). Each created classifier votes for a class-label, and the votes are weighted according to the expected error of the individual models. Poorly performing ensemble members are replaced by new ones. As was remarked by Read et al. (2012), this makes them work particularly well in combination with batch-incremental classifiers. Once a new model is built upon a batch of data, the old model will not be eliminated, but instead it is also used in the ensemble.

Meta-learning Meta-learning aims to learn which learning techniques work well on what data. A common task, known as the Algorithm Selection Problem (Rice 1976), is to determine which classifier performs best on a given dataset. We can predict this by training a meta-model on data describing the performance of different methods on different datasets, characterised by meta-features (Brazdil et al. 1994). Meta-features are often categorised as either simple (number of examples, number of attributes), statistical (mean standard deviation of attributes, mean skewness of attributes), information theoretic (class entropy, mean mutual information), or landmarkers, performance evaluations of simple classifiers (Pfahringer et al. 2000). In the data stream setting, meta-learning techniques are often used to dynamically switch between classifiers at various points in the stream, effectively creating a heterogeneous ensemble (albeit at a certain cost in terms of resources).

Earlier approaches often train an ensemble of stream classifiers and a meta-model decides for each data point which of the base-learners will make a prediction. Rossi et al. (2014) dynamically choose between two regression techniques using meta-knowledge obtained earlier in the stream. van Rijn et al. (2014) select the best classifier among multiple classifiers, based on meta-knowledge from previously processed data streams. Online Performance Estimation was first introduced by van Rijn et al. (2015), which we will extend and improve in this paper. Gama and Kosina (2014) uses meta-learning on time series with recurrent concepts: when concept drift is detected, a meta-learning algorithm decides whether a model trained previously on the same stream could be reused, or whether the data is so different from before that a new model must be trained. Finally, Nguyen et al. (2012) propose a method that combines feature selection and heterogeneous ensembles; members that performed poorly can be replaced by a drift detector.

Concept drift One property of data streams is that the underlying concept that is being learned can change over time (e.g., Wang et al. 2003). This is called concept drift. Some of the aforementioned methods naturally deal with concept drift. For instance, k Nearest Neighbour maintains a number of w recent examples, substituting each example after w new examples have been observed. Change detectors, such as Drift Detection Method (DDM) (Gama et al. 2004a) and Adaptive Sliding Window Algorithm (ADWIN) (Bifet and Gavalda 2007) are stand-alone techniques that detect concept drift and can be used in combination with any stream classifier. Both rely on the assumption that classifiers improve (or at least maintain) their accuracy when trained on more data. When the accuracy of a classifier drops with respect to a reference window, this could mean that the learned concept is outdated, and a new classifier should be built. The main difference between DDM and ADWIN is the way they select the reference window. Furthermore, classifiers can have built-in drift detectors. For instance, Ultra Fast Forest of Trees (Gama et al. 2004b) are Hoeffding Trees with a built-in change detector for every node. When an earlier made split turns out to be obsolete, a new split can be generated.

It has been recognised that some classifiers recover faster from sudden changes of concepts than others. Shaker and Hüllermeier (2015) introduce recovery analysis, a framework to measure the ability of classifiers to recover from concept drift. They distinguish instance-based classifiers that operate directly on the data (e.g., k-NN) and model-based classifiers, that build and maintain a model (e.g., tree algorithms, fuzzy systems). Their experimental results suggest, quite naturally, that instance-based classifiers generally have a higher capability to recover from concept drift than model-based classifiers.

Evaluation As data from streams is non-stationary, the well-known cross-validation procedure for estimating model performance is not suitable. A commonly accepted estimation procedure is the prequential method (Gama et al. 2009), in which each example is first used to test the current model, and afterwards (either directly after testing or after a delay) becomes available for training. An advantage of this method is that it is tested on all data, and therefore no specific holdout set is needed.

Experiment databases Experiment databases facilitate the reproduction of earlier results for verification and reusability purposes, and make much larger studies (covering more classifiers and parameter settings) feasible. Above all, experiment databases allow a variety of studies to be executed by a database look-up, rather than setting up new experiments. An example of such an online experiment database is OpenML (Vanschoren et al. 2014). OpenML is an Open Science platform for Machine Learning, containing many datasets, algorithms, and experimental results (the result of an algorithm on a dataset). For each experimental result it stores all predictions and class confidences, making it possible to calculate a wide range of measures, such as predictive accuracy and COD. We use OpenML to obtain information about the performance and interplay between various base-classifiers and to store our experimental results.

Methods

Traditional Machine Learning problems consist of a number of examples that are observed in arbitrary order. In this work we consider classification problems. Each example $e = (\mathbf {x}, l(\mathbf {x}))$ is a tuple of p predictive attributes $\mathbf {x} = (x_1, \ldots , x_p)$ and a target attribute $l(\mathbf {x})$. A data set is an (unordered) set of such examples. The goal is to approximate a labelling function $l: \mathbf {x} \rightarrow l(\mathbf {x})$. In the data stream setting the examples are observed in a given order, therefore each data stream S is a sequence of examples $S = (e_1, e_2, e_3, \dots , e_n, \ldots )$, possibly infinite. Consequently, $e_i$ refers to the $i^{th}$ example in data stream S. The set of predictive attributes of that example is denoted by $PS _i$, likewise $l( PS _i)$ maps to the corresponding label. Furthermore, the labelling function that needs to be learned can change over time due to concept drift.

When applying an ensemble of classifiers, the most relevant variables are which base-classifiers (members) to use and how to weight their individual votes. This work mainly focuses on the latter question. Section 3.1 describes the Performance Estimation framework to weight member votes in an ensemble. In Sect. 3.2 we show how to use the Classifier Output Difference to select ensemble members. Section 3.3 describes an ensemble that employs these techniques.

Online performance estimation

In most common ensemble approaches all base-classifiers are given the same weight (as done in Bagging and Boosting) or their predictions are otherwise combined to optimise the overall performance of the ensemble (as done in Stacking). An important property of the data stream setting is often neglected: due to the possible occurrence of concept drift it is likely that in most cases recent examples are more relevant than older ones. Moreover, due to the fact that there is a temporal component in the data, we can actually measure how ensemble members have performed on recent examples, and adjust their weight in the voting accordingly. In order to estimate the performance of a classifier on recent data, van Rijn et al. (2015) proposed:

$$\begin{aligned} P_{win}(l',c,w,L) = 1 - \sum _{i=max(1,c-w)}^{c-1}\frac{L(l'( PS _i),l( PS _i))}{min(w,c-1)} \end{aligned}$$

(2)

where $l'$ is the learned labelling function of an ensemble member, c is the index of the last seen training example and w is the number of training examples over which we want to estimate the performance of ensemble members. Note that there is a certain start-up time (i.e., when w is larger than or equal to c) during which we can only calculate the performance estimation over a number of instances smaller than w. Also note that it can only be performed after several labels have been observed (i.e., $c > 1$). Finally, L is a loss function that compares the labels predicted by the ensemble member to the true labels. The most simple version is a zero/one loss function, which returns 0 when the predicted label is correct and 1 otherwise. More complicated loss functions can also be incorporated. The outcome of $P_ win$ is in the range [0, 1], with better performing classifiers obtaining a higher score. The performance estimates for the ensemble members can be converted into a weight for their votes, at various points over the stream. For instance, the best performing members at that point could receive the highest weights. Figure 2 illustrates this.

Fig. 2

Schematic view of Windowed Performance Estimation. For all classifiers, w flags are stored, each flag indicating whether it predicted a recent observation correctly

There are a few drawbacks to this approach. First, it requires the ensemble to store the $w \times n$ additional values, which is inconvenient in a data stream setting, where both time and memory are important factors. Second, it requires the user to tune a parameter which highly influences performance. Last, there is a hard cut-off point, i.e., an observations is either in or out of the window. What we would rather model is that the most recent observations are given most weight, and gradually lower this for less recent observations.

In order to address these issues, we propose an altered version of performance estimation, based on fading factors, as described by Gama et al. (2013). Fading factors give a high importance to recent predictions, whereas the importance fades away when they become older. This is illustrated by Fig. 3.

Fig. 3

The effect of a prediction after a number of observations, relative to when it was first observed (for various values of $\alpha$)

The red (solid) line shows a relatively fast fading factor, where the effect of a given prediction is already faded away almost completely after 500 predictions, whereas the blue (dashed) line shows a relatively slow fading factor, where the effect of an observation is still considerably high, even when $10,000$ observations have passed in the meantime. Note that even though all these functions start at 1, in practise we need to scale this down to $1 - \alpha$, in order to constrain the complete function within the range [0, 1]. Putting this all together, we propose:

$$\begin{aligned} P(l',c,\alpha ,L) = \left\{ \begin{array}{l l} 1 &{} {\mathrm {iff\ }} c = 0 \\ P(l',c-1,\alpha ,L) \cdot \alpha + (1 - L(l'( PS _c),l( PS _c))) \cdot (1 - \alpha ) &{} \mathrm {otherwise} \end{array} \right. \end{aligned}$$

(3)

where, similar to Eq. 2, $l'$ is the learned labelling function of an ensemble member, c is the index of the last seen training example and L is a loss function that compares the labels predicted by the ensemble member to the true labels. Fading factor $\alpha$ (range [0, 1]) determines at what rate historic performance becomes irrelevant, and is to be tuned by the user. A value close to 0 will allow for rapid changes in estimated performance, whereas a value close to 1 will keep them rather stable. The outcome of P is in the range [0, 1], with better performing classifiers obtaining a higher score. In Sect. 6 we will see that the fading factor parameter is more robust and easier to tune than the window size parameter. When building an ensemble based upon Online Performance Estimation, we can now choose between a Windowed approach (Eq. 2) and Fading Factors (Eq. 3).

Fig. 4

Online performance estimation, i.e. the estimated performance of each algorithm given previous examples, measured at the start of the electricity data stream. a Windowed, window size 1, 000. b Fading Factors, $\alpha = 0.999$

Figure 4 shows how the estimated performance for each base-classifier evolves at the start of the electricity data stream. Both figures expose similar trends: apparently, on this data stream the Hoeffding Tree classifier performs best and the Stochastic Gradient Descent algorithm performs worst. However, both approaches differ subtly in the way the performance of individual classifiers are measured. The Windowed approach contains many spikes, whereas the Fading Factor approach seems more stable.

Ensemble composition

In order for an ensemble to be successful, the individual classifiers should be both accurate and diverse. When employing a homogeneous ensemble, choosing an appropriate base-learner is an important decision. For heterogeneous ensembles this is even more true, as we have to choose a set of base-learners. We consider a set of classifiers from MOA 2016.04 (Bifet et al. 2010a). Furthermore, we consider some fast batch-incremental classifiers from Weka 3.7.12 (Hall et al. 2009) wrapped in the Accuracy Weighted Ensemble (Wang et al. 2003). Table 1 lists all classifiers and their parameter settings.

Table 1 Classifiers considered in this research

Figure 5 shows some basic results of the classifiers on 60 data streams. Figure 5a shows a violin plot of the predictive accuracy of all classifiers, with a box plot in the middle. Violin plots show the probability density of the data at different values (Hintze and Nelson 1998). The classifiers are sorted by median accuracy. Two common Data Stream baseline methods, the No Change classifier and the Majority Class classifier, end at the bottom of the ranking based on accuracy. This indicates that most of the selected data streams are both balanced (in terms of class labels) and do not have high auto-correlation. In general, tree-based methods seem to perform best.

Fig. 5

Performance of 25 data stream classifiers based on 60 data streams. a Predictive Accuracy. b Run time (seconds)

Figure 5b shows violin plots of the run time (in seconds) that the classifiers needed to complete the tasks. From the top-half performing classifiers in terms of accuracy, the Hoeffding Trees is the best ranked algorithm in terms of run time. Lazy algorithms (k-NN and its variations) turn out to be rather slow, despite the reasonable value of window size parameter (controlling the number of instances that are remembered). It also confirms some observation made by Read et al. (2012), that the batch-incremental classifiers generally take more resources than instance-incremental classifiers; all classifiers wrapped in the Accuracy Weighted Ensemble are on the right half of the figure.

Fig. 6

Results of Nemenyi test ($\alpha = 0.05$) on the predictive accuracy of the base-classifiers in this study

Figure 6 shows the result of a statistical test on the base-classifiers. Classifiers are sorted by their average rank (lower is better). Classifiers that are connected by a horizontal line are statistically equivalent. The results confirm some of the observations made based on the violin plots, e.g., the baseline models (Majority Class and No Change) perform worst; also other simple models such as the Decision Stumps and OneRule (which is essentially a Decision Stump) are inferior to the tree-based models. Oddly enough, the instance incremental Rule Classifier does not compete at all with the Batch-incremental counterpart (AWE(JRIP)).

When creating a heterogeneous ensemble, a diverse set of classifiers should be selected (Hansen and Salamon 1990). Classifier Output Difference is a metric that measures the difference in predictions between a pair of classifiers. We can use this to create a hierarchical agglomerative clustering of data stream classifiers in an identical way to Lee and Giraud-Carrier (2011). For each pair of classifiers involved in this study, we measure the number of observations for which the classifiers have different outputs, aggregated over all data streams involved. Hierarchical agglomerative clustering (HAC) converts this information into a hierarchical clustering. It starts by assigning each observation to its own cluster, and greedily joins the two clusters with the smallest distance (Rokach and Maimon 2005). The complete linkage strategy is used to measure the distance between two clusters. Formally, the distance between two clusters A and B is defined as $max \left\{ COD (a,b) : a \in A, b \in B\right\}$. Figure 7 shows the resulting dendrogram. There were 9 data streams on which several classifiers did not terminate. We left these out of the dendrogram.

Fig. 7

Hierarchical clustering of stream classifiers, averaged over 51 data streams from OpenML

We can use a dendrogram like the one in Fig. 7 to get a collection of diverse and well performing ensemble members. A COD-threshold is to be determined, selecting representative classifiers from all clusters with a distance lower than this threshold. A higher COD-threshold would result in a smaller set of classifiers, and vice versa. For example, if we set the COD-threshold to 0.2, we end up with an ensemble consisting of classifiers from 11 clusters. The ensemble will consist of one representative classifier from each cluster, which can be chosen based on accuracy, run time, a combination of the two (e.g., Brazdil et al. 2003) or any arbitrary other criteria. Which exact criteria to use is outside the scope of this research, however in this study we used a combination of accuracy and run time. Clearly, when using this technique in experiments, the dendrogram should be constructed in a leave-one-out setting: it can be created based on all data streams except for the one that is being tested.

Figure 7 can also be used to make some interesting observations. First, it confirms some well-established assumptions. The clustering seems to respect the taxonomy of classifiers provided by MOA. Many of the tree-based and rule-based classifiers are grouped together. There is a cluster of instance-incremental tree classifiers (Hoeffding Tree, AS Hoeffding Tree, Hoeffding Option Tree and Hoeffding Adaptive Tree), a cluster of batch-incremental tree-based and rule-based classifiers (REP Tree, J48 and JRip) and a cluster of simple tree-based and rule-based classifiers (Decision Stumps and One Rule). Also the Logistic and SVM models seem to produce similar predictions, having a sub-cluster of batch-incremental classifiers (SMO and Logistic) and a sub-cluster of instance incremental classifiers (Stochastic Gradient Descent and SPegasos with both loss functions).

The dendrogram also provides some surprising results. For example, the instance-incremental Rule Classifier seems to be fairly distant from the tree-based classifiers. As decision rules and decision trees work with similar decision boundaries and can easily be translated to each other, a higher similarity would be expected (Apté and Weiss 1997). Also the internal distances in the simple tree-based and rule-based classifiers seem rather high.

A possible explanation for this could be the mediocre performance of the Rule Classifier (see Fig. 5). Even though COD clusters are based on instance-level predictions rather than accuracy, well performing classifiers have a higher prior probability of being clustered together. As there are only few observations they predict incorrectly, naturally there are also few observations their predictions can disagree on.

BLAST

BLAST (short for best last) is an ensemble embodying the performance estimation framework. Ideally, it consists of a group of diverse base-classifiers. These are all trained using the full set of available training observations. For every test example, it selects one of its members to make the prediction. This member is referred to as the active classifier. The active classifier is selected based on Online Performance Estimation: the classifier that performed best over the set of w previous training examples is selected as the active classifier (i.e., it gets 100% of the weight), hence the name. Formally,

$$\begin{aligned} AC _c = \mathop {{{\mathrm{arg\,max}}}}\limits _{m_j \in M}{P(m_j,c-1,\alpha ,L)} \end{aligned}$$

(4)

where M is the set of models generated by the ensemble members, c is the index of the current example, $\alpha$ is a parameter to be set by the user (fading factor) and L is a zero/one loss function, giving a penalty of 1 to all misclassified examples. Note that the performance estimation function P can be replaced by any measure. For example, if we would replace it with Eq. 2, we would get the exact same predictions as reported by van Rijn et al. (2015). When multiple classifiers obtain the same estimated performance, any arbitrary classifier can be selected as active classifier. The details of this method are summarised in Algorithm 1.

Line 2 initialises a variable that keeps track of the estimated performance for each base-classifier. Everything that happens from lines 5–7 can be seen as an internal prequential evaluation method. At line 5 each training example is first used to test all individual ensemble members on. The predicted label is compared against the true label $l(\mathbf {x})$ on line 7. If it predicts the correct label then the estimated performance for this base-classifier will increase; if it predicts the wrong label, the estimated performance for this base-classifier will decrease (line 6). After this, base-classifier $m_j$ can be trained with the example (line 7). When, at any time, a test example needs to be classified, the ensemble looks up the highest value of $p_j$ and lets the corresponding ensemble member make the prediction.

The concept of an active classifier can also be extended to multiple active classifiers. Rather than selecting the best classifier on recent predictions, we can select the best k classifiers, whose votes for the specified class-label are all weighted according to some weighting schedule. First, we can weight them all equally. Indeed, when using this voting schedule and setting $k = |M|$, we would get the same behaviour as the Majority Vote Ensemble, as described by van Rijn et al. (2015), which performed only averagely. Alternatively, we can use Online Performance Estimation to weight the votes. This way, the best performing classifier obtains the highest weight, the second best performing classifier a bit less, and so on. Formally, for each $y \in Y$ (with Y being the set of all class labels):

$$\begin{aligned} votes _y = \sum _{m_j \in M} P(m_j,i,\alpha ,L) \times B(l_j'( PS _i),y) \end{aligned}$$

(5)

where M is the set of all models, $l_j'$ is the labelling function produced by model $m_j$ and B is a binary function, returning 1 iff $l_j'$ voted for class label y and 0 otherwise. Other functions regulating the voting process can also be incorporated, but are beyond the scope of this research. The label y that obtained the highest value $votes _y$ is then predicted. BLAST is available in the MOA framework as of version 2017.06.

Experimental setup

In order to establish the utility of BLAST and Online Performance Estimation, we conduct experiments using a large set of data streams. The data streams and results of all experiments are made publicly available in OpenML for the purposes of verifiability, reproducibility and generalizability.¹

Data streams The data streams are a combination of real world data streams (e.g., electricity, covertype, IMDB) and synthetically generated data (e.g., LED, Rotating Hyperplane, Bayesian Network Generator) commonly used in data stream research (e.g., Beringer and Hüllermeier 2007; Bifet et al. 2010a; van Rijn et al. 2014). Many contain a natural drift of concept. Table 2 shows a list of all data streams, the number of observations, features, classes and their default accuracy. We estimate the performance of the methods using the prequential method: each observation is used as a test example first and as a training example afterwards (Gama et al. 2009). As most data streams are fairly balanced, we will measure predictive accuracy in the experiments.

Table 2 Data streams used in the experiment

Baselines We compare the results of the defined methods with the Best Single Classifier. Each heterogeneous ensemble consists of n base-classifiers. The one that performs best on average over all data streams is considered the Best Single Classifier. This will allow to measure the potential accuracy gains of adding more classifiers (at the cost of using more computational resources). Which classifier should be considered the best single classifier is debatable. Based on the median scores depicted in Fig. 5a, Hoeffding Adaptive Tree is the best performing classifier. Based on the statistical test depicted in Fig. 6, the Hoeffding Option Tree is the best performing classifier. We selected the Hoeffding Option Tree as the single best classifier.

Furthermore, we compare against the Majority Vote Ensemble, which is a heterogeneous ensemble that predicts the label that is predicted by most ensemble members. This allows to measure the potential accuracy gain of using Online Performance Estimation over just naively combining the votes of individual classifiers. Finally, we also compare the techniques to state of the art homogeneous ensembles, such as Online Bagging, Leveraging Bagging, and Accuracy Weighted Ensemble. These are embodied with a Hoeffding Tree as base-classifier, because this is a good trade-off between predictive performance and run time. Amongst all classifiers that are considered statistically equivalent with the best classifier (Fig. 6 on page 14), it has the lowest median run time (Fig. 5b on page 13). This beneficial trade-off was also noted by Domingos and Hulten (2003), and Read et al. (2012), and allows for the use of a high number of base-classifiers. In order to understand the performance of these ensembles a bit better, we provide some results.

Fig. 8

Effect of the number of ensemble members on performance of Online Bagging and Leveraging Bagging. a Accuracy. b Run time (in seconds)

Figure 8 shows violin plots of the performance of Accuracy Weighted Ensemble (left bars, red), Leveraging Bagging (middle bars, green) and Online Bagging (right bars, blue), with an increasing number of ensemble members. Accuracy Weighted Ensemble (AWE) uses J48 trees as ensemble members, both Bagging schemes use Hoeffding Trees. Naturally, as the number of members increases, both accuracy and run time increase, however Leveraging Bagging performs eminently better than the others. Leveraging Bagging using 16 ensemble members already outperforms both AWE and Online Bagging using 128 ensemble members, based on median accuracy. This performance also comes at a cost, as it uses considerably more run time than both other techniques, even when containing the same number of members. Accuracy Weighted Ensemble performs pretty constant, regardless of the amount of ensemble members. As the ensemble size grows, both accuracy and run time slightly increase. We will compare BLAST against the heterogeneous ensembles containing 128 ensemble members.

Ensemble members We evaluate an instantiation of BLAST, using a set of differing classifiers. These are selected using the dendrogram from Fig. 7, setting the $COD$ threshold to 0.2. Using this threshold, it recommends a set of 12 classifiers. After omitting simple models such as No Change, Majority Class and Decision Stumps, we end up with the set of classifiers described in Table 3. One nice property is that all base-classifiers consist of different model types, making the resulting ensemble very heterogeneous. As for the baselines, Majority Vote Ensemble uses the same classifiers.

Table 3 Classifiers used in the experiment

Results

We ran all ensemble techniques on all data streams. BLAST was run both with fading factors ($\alpha = 0.999$) and Windowed ($w = 1,000$). For each prediction, one classifier was selected as the active classifier (i.e., $k = 1$). We explore the effect of other values for both parameters in Section 6.

Fig. 9

Performance of the proposed techniques averaged over 60 data streams. a Accuracy. b Run time (in seconds)

Figure 9a shows violin plots and box plots of the results in terms of accuracy. An important observation is that both versions of BLAST are competitive with state of the art ensembles. The highest median score is obtained by Leveraging Bagging, which performs very well in various empirical studies (Bifet et al. 2010b; Read et al. 2012; van Rijn 2016), closely followed by both versions of BLAST. Both versions of BLAST have less outliers at the bottom than Leveraging Bagging. As Leveraging Bagging solely relies on Hoeffding Trees as base-classifier, it will perform averagely on datasets that are not easily modelled by trees. Contrarily, BLAST easily selects an appropriate set of classifiers for each dataset, hence the fewer number of outliers.

As expected, both the Best Single Classifier and the Majority Vote Ensemble perform less than most other techniques. Clearly, combining heterogeneous ensemble members by simply counting votes does not work in this setup. It seems that poor results from some ensemble members outweigh the diversity. A peculiar observation is that the Accuracy Weighted Ensemble, which utilises historic performance data in a different way, does not manage to outperform the Best Single Classifier. Possibly, the window of $1,000$ instances on which the individual classifiers are trained is too small to make the individual models competitive.

Figure 9b shows plots of the results in terms of run time on a log scale. The results are as expected. The Best Single Classifier requires fewest resources, followed by AWE(J48). Although AWE(J48) consists of 128 ensemble members, it essentially feeds each training instance to just one ensemble member. The Majority Vote Ensemble and both versions of BLAST also require a similar amount of resources, as these already use the classifiers mentioned in Table 3. Finally, both Bagging ensembles require most resources, which was also observed by Bifet et al. (2010b) and Read et al. (2012). The fact that BLAST performs competitively with the Bagging ensemble, while it requires far fewer resources, suggests that Online Performance Estimation is a useful technique when applied to heterogeneous data stream ensembles.

Figure 10 shows the accuracy of the three heterogeneous ensemble techniques per data stream. In order to not overload the figure, we only show BLAST with fading factors (FF), Leveraging Bagging and the Best Single Classifier.

Fig. 10

Accuracy per data stream, sorted by accuracy of the best single classifier

Both BLAST (FF) and Leveraging Bagging consistently outperform the Best Single Classifier. Especially on data streams where the performance of the Best Single Classifier is mediocre (Fig. 10b), accuracy gains are eminent. The difference between Leveraging Bagging and BLAST is harder to assess. Although Leveraging Bagging seems to be slightly better in many cases, there are some clear cases where there is a big difference in favour of BLAST.

To assess statistical significance, we use the Friedman test with post-hoc Nemenyi test to establish the statistical relevance of our results. These tests are considered the state of the art when it comes to comparing multiple classifiers (Demšar 2006). The Friedman test checks whether there is a statistical difference between the classifiers; when this is the case the Nemenyi post-hoc test can be used to determine which classifiers are significantly better than others.

The results of the Nemenyi test ($\alpha = 0.05$) are shown in Fig. 11. It plots the average rank of all methods and the critical difference. Classifiers that are statistically equivalent are connected by a black line. For all other cases, there was a significant difference in performance, in favour of the classifier with the better average rank. We performed the test based on accuracy and run time.

Fig. 11

Results of Nemenyi test, $\alpha = 0.05$. Classifiers are sorted by their average rank (lower is better). Classifiers that are connected by a horizontal line are statistically equivalent. a Accuracy. b Run time

Figure 11a shows that there is no statistically significant difference in terms of accuracy between BLAST (FF) and the homogeneous ensembles (i.e., Leveraging Bagging and Online Bagging using 128 Hoeffding Trees). BLAST (Window) does perform significantly worse than Leveraging Bagging.² Similar to Fig. 9a, the Best Single Classifier, AWE(J48) and Majority Vote Ensemble are at the bottom of the ranking. These perform significantly less than the other techniques.

Figure 11b shows the results of the Nemenyi test on run time. The results are similar to Fig. 9b. The best single classifier (Hoeffding Option Tree) requires fewest resources. There is no significant difference in resources between BLAST (FF), BLAST (Window), Majority Vote Ensemble and Online Bagging. This makes sense, as these the first three operate on the same set of base-classifiers. Altogether, BLAST (FF) performs equivalent to both Bagging schemes in terms of accuracy, while using significantly fewer resources.

Parameter effect

In this section we study the effect of the various parameters of BLAST.

Window size and decay rate

First, for both versions of BLAST, there is a parameter that controls the rate of dismissal of old observations. For BLAST (FF) this is the $\alpha$ parameter (the fading factor); for BLAST (Windowed) this is the w parameter (the window size). The $\alpha$ parameter is always in the range [0, 1], and has no effect on the use of resources. The window parameter can be in the range [0, n], where n is the size of the data stream. Setting this value higher results in bigger memory requirements, although these are typically negligible compared to the memory usage of the base-classifiers.

Fig. 12

Effect of the decay rate and window parameter

Figure 12 shows violin plots and box plots of the effect of varying these parameters. The effect of the $\alpha$ (a) value on BLAST (FF) is displayed in the left (red) violin plots; the effect of the window (w) value on BLAST (Window) is displayed in the right (blue) violin plots. The trend over 60 data streams seems to be that setting this parameter too low results in sub-optimal accuracy. This is especially clear with BLAST (FF) with $\alpha = 0.9$ and BLAST (Window) with $w = 10$: there are more outliers at the bottom and the third quartile of the box plot is slightly larger. Arguably, this value performs well in highly volatile streams when concepts change rapidly, but in general we do not want to dismiss old information too quickly. In the other cases, the higher values seem to be slightly preferred, but it is hard to draw general conclusions from this. Altogether, BLAST (FF) seems to be slightly more robust, as the investigated values of the $\alpha$ parameter do not perceptibly influence performance.

Grace parameter

Prior work by Rossi et al. (2014) and van Rijn et al. (2015) introduced a grace parameter that controls the number of observations for which the active classifier was not changed. This potentially saves resources, especially when the algorithm selection process involves time consuming operations such as the calculation of meta-features. On the other hand, it can be seen that in a data stream setting where concept drift occurs, in terms of performance it is always optimal to act on changed behaviour as fast as possible. Although we have omitted this parameter from the formal definition of BLAST in Sect. 3, similar behaviour can be obtained by updating the active classifier only at certain intervals. Formally, a grace period can be enforced by only executing Eq. 4 when $c \mod g = 0$, where (following earlier definitions) c is the index of the current observation, and g is a grace period defined by the user.

Fig. 13

Effect of the grace parameter on accuracy. The x-axis denotes the grace, the y-axes the performance. BLAST (Window) was run with $w = 1,000$; BLAST (FF) was run with $\alpha = 0.999$

Figure 13 shows the effect of the (hypothetical) grace parameter on performance, averaged over 60 data streams. We observe two things from this plot. First, the difference in performance for various values of this parameter is quite small. Second, although this difference is very small, it seems that lower values are preferred.

The fact that the differences are small is supported by intuition. Although the performance ranking of the classifiers varies over the stream, it only happens occasionally that a new best classifier is selected. Even when BLAST is too slow in selecting the new active classifier, it is still the case that the old active classifier will probably not be entirely outdated. It will still predict with reasonable accuracy, until it is replaced. The fact that smaller values are preferable also makes sense. In data streams that contain concept drift, it is desirable to immediately act on the observed changes. Therefore, having a grace parameter can only affect performance in a negative way. Moreover, the algorithm selection phase of BLAST simply depends on finding the maximum element in an array. For these reasons, the grace period would not have any measurable influence on the required resources, and its default value can be fixed to 1.

Number of active classifiers

Rather than selecting one active classifier, multiple active classifiers can be selected that all vote for a class label. The votes of these classifiers can either contribute equally to the final vote, or be weighted according to their estimated performance. We used BLAST (FF) to explore the effect of this parameter. We varied the number of active classifiers k from one to five, and measured the performance according to both voting schemas. Figure 14 shows the results.

Fig. 14

Performance for various values of k, weighted votes versus unweighted votes. a Accuracy. b Root Mean Squared Error

Figure 14a shows how the various strategies perform when evaluated using predictive accuracy. We can make several observations to verify the correctness of the results. First, the results of both strategies are equal when $k = 1$, as the algorithm selects only one classifier, weights are obsolete. Second, the result of the Majority weighting schema for $k = 7$ is equal to the score of the Majority Weight Ensemble (from Fig. 9a), which is also correct, as these are the same by definition. Finally, when using the weighted strategy, setting $k = 2$ yields exactly the same scores for accuracy as setting $k = 1$. This also makes sense, as it is guaranteed that the second best base-classifier always has a lower weight as the best base-classifier, and thus it is incapable of changing any prediction.

In all, it seems that increasing the number of active classifiers is not beneficial for accuracy. Note that this is different from adding more classifiers in general, which clearly would not decrease performance results. This behaviour is different from the classical approach, where adding more classifiers (which inherently are all active) yield better results up to a certain point (Caruana et al. 2004). However, in the data stream setting we deal with a time component, and we can actually measure which classifiers performed well on recent intervals. By increasing the number of active classifiers, we would add classifiers to the vote of which we have empirical evidence that they performed worse on recent observations.

Similarly, Fig. 14b shows the Root Mean Squared Error (RMSE). RSME is typically used as an evaluation measure for regression, but can be used in classification problems to assess the quality of class confidences. For every prediction, the error is considered to be the difference between the class confidence for the correct label and 1. This means that if the classifier had a confidence close to 1 for the particular class label, a low error is recorded, and vice versa. The box plots indicate that adding more active classifiers can lead to a lower median error. This also makes sense, as the Root Mean Squared Error tends to punish classification errors harder when these are made with a high confidence. We observe this effect until $k = 3$, after which adding more active classifiers starts to lead to a higher RMSE. It is unclear why this effect holds until this particular value.

Altogether, from this experiment we conclude that adding more active classifiers in the context of Online Performance Estimation does not necessarily yields better results beyond selecting the expected best classifier at that point in the stream. This might be different when using more base-classifiers, as we would expect to have more similarly performing classifiers on each interval. As we expect to measure this effect when using orders of magnitude more classifiers, this is considered future work. Clearly, when using multiple active classifiers, weighting their votes using online performance estimation seems beneficial.

Conclusions

We introduced the Online Performance Estimation framework, which can be used in data stream ensembles to weight the votes of ensemble members, in particular when using fundamentally different model types. Online Performance Estimation measures the performance of all base-classifiers on recent training examples. We introduced two performance estimation functions. The first function is based on a window, and counts the number of incorrect predictions over this window. All are weighted equally. The second function is based on fading factors, which considers all predictions from the whole stream, but gives a higher weight to recent predictions.

BLAST is an heterogeneous ensemble technique based on Online Performance Estimation that selects the single best classifier on recent predictions to classify new observations. We have integrated both performance estimation functions into BLAST. Empirical evaluation shows that BLAST with fading factors performs better than BLAST using the windowed approach. This is most likely because Fading Factors are better able to capture typical data stream properties, such as changes of concepts. When this occurs, there will also be changes in the performances of ensemble members, and the fading factors adapt to this relatively fast.

We compared BLAST against state of the art ensembles over 60 data streams from OpenML. To the best of our knowledge, this is the largest data stream study to date. We observe that there is no statistical significant difference between the accuracy of the ensembles, although BLAST uses significantly fewer resources. Furthermore, we evaluated the effect of the method’s parameters on the performance. The most important parameter proves to be the one controlling the performance estimation function: $\alpha$ for the fading factor, controlling the decay rate, and w for the windowed approach, determining the window size. Our results show that the optimal value for these parameters is dependent on the given dataset, although setting this too low turns out to have a worse effect on accuracy than setting it too high.

To select the classifiers included in the heterogeneous ensemble, we created a hierarchical clustering of 25 commonly used data stream classifiers, based on Classifier Output Difference. We used this clustering to gain methodological justification for which classifiers to use, although the clustering is mainly a guideline. A human expert can still determine to deviate from the resulting set of algorithms, in order to save resources. The resulting dendrogram has also scientific value in itself. It confirms some well-established assumptions regarding the typically used classifier taxonomy in data streams, that have never been tested before. Many of the classifiers that were suspected to be similar were also clustered together, for example the various decision trees, support vector machines and gradient descent models all formed their own clusters. Moreover, some interesting observations were made that can be investigated in future work. For instance, the Rule Classifier used turns out to perform averagely, and was rather far removed from the decision trees, whereas we would expect it to perform better and be clustered closer to the decision trees.

Utilizing the Online Performance Estimation framework opens up a whole new line of data stream research. Rather than creating more data stream classifiers, combining them in a suitable way can elegantly lead to highly improved results that effortlessly adapt to changes in the data stream. More than in the classical batch setting, memory and time are of crucial importance. Experiments suggest that the selected set of base classifiers has a substantial influence on the performance of the ensemble. Research should be conducted to explore what model types best complement each other, and which work well together given a constraint on resources. We believe that by exploring these possibilities we can further push the state of the art in data stream ensembles.