Abstract
Copulas enable flexible parameterization of multivariate distributions in terms of constituent marginals and dependence families. Vine copulas, hierarchical collections of bivariate copulas, can model a wide variety of dependencies in multivariate data including asymmetric and tail dependencies which the more widely used Gaussian copulas, used in Meta-Gaussian distributions, cannot. However, current inference algorithms for vines cannot fit data with mixed—a combination of continuous, binary and ordinal—features that are common in many domains. We design a new inference algorithm to fit vines on mixed data thereby extending their use to several applications. We illustrate our algorithm by developing a dependency-seeking multi-view clustering model based on Dirichlet Process mixture of vines that generalizes previous models to arbitrary dependencies as well as to mixed marginals. Empirical results on synthetic and real datasets demonstrate the performance on clustering single-view and multi-view data with asymmetric and tail dependencies and with mixed marginals.
Similar content being viewed by others
1 Introduction
Modeling dependence in multivariate data is of fundamental importance in many machine learning problems. Copulas are increasingly popular in machine learning due to the modular parameterization of multivariate distributions they provide: the choice of arbitrary marginal distributions that are independent of the dependency models with different copula families. This flexibility of modeling multivariate (particularly non-Gaussian) distributions has been utilized in many common machine learning tasks such as classification (Han et al. 2013; Elidan 2012), clustering (Fujimaki et al. 2011), multi-task learning (Gonçalves et al. 2016), principal component analysis (Han and Liu 2013), time series modeling (Wu et al. 2013), feature selection (Chang et al. 2016), Bayesian network models (Elidan 2010), variational inference (Tran et al. 2015) and associated applications such as topic modeling (Amoualian et al. 2016), information retrieval Eickhoff et al. (2015), among others. Recent work has also led to more efficient inference (Kalaitzis and Silva 2013) and model selection (Tenzer and Elidan 2013), as well as more flexibility (Lopez-Paz et al. 2013) in copula-based models.
Bivariate Gaussian copula (left) and Clayton copula (right) samples, both with marginals T distribution with 5 degrees of freedom (Y1) and exponential distribution with rate 1 (Y2), illustrating symmetric and asymmetric dependencies respectively. The Gaussian Copula (with meta-Gaussian dependencies) on the left cannot model data with asymmetric dependencies shown on the right
With the Gaussian copula itself, using different marginals, many different joint distributions (even multimodal distributions) can be constructed, called meta-Gaussian distributions, that have been used in several applications (Letham et al. 2014; Eickhoff et al. 2015). However, meta-Gaussian dependencies from the Gaussian copula do not include asymmetric and tail dependencies that are captured by other copula families (Joe 2014): see Fig. 1. Vine copulas provide a flexible way of pair-wise dependency modeling using hierarchical collections of bivariate copulas, each of which can belong to any copula family thereby capturing a wide variety of dependencies (see Sect. 2 for details). Vines have been used in many applications such as time series analysis (Aas et al. 2009), domain adaptation (Lopez-Paz et al. 2012) and variational inference (Tran et al. 2015) in the machine learning literature.
Real world data often has mixed (continuous, binary and ordinal valued) features. While copulas have been useful for modeling continuous multivariate distributions their use with discrete data remains difficult—the copula is not margin-free and may not be identifiable—but they still provide usable dependence relationships (Genest and Neslehova 2007). In particular, there are no existing techniques to fit vine copulas on mixed data and the challenge lies mainly in parameter inference. Two previous approaches, both for only discrete (not mixed) features, require expensive estimation of marginals: one by Panagiotelis et al. (2012) and another by Smith and Khaled (2012). The latter can be extended to mixed data but their MCMC algorithm requires computations that are exponential in data dimensions per sampling step, making it practically infeasible. We address this problem, by designing a new efficient inference algorithm for vine copulas that can fit mixed data.
Our algorithm facilitates the extension of multivariate models—to arbitrary dependencies through the use of vines and to mixed data through our inference algorithm. We demonstrate such an extension in the context of multi-view learning. Multiple views of data refer to different measurement modalities or information sources for the same learning task, for example image and text (Chen et al. 2012) or text in two languages (Guo and Xiao 2012). The views could also be distinct information from the same source such as words and context (Pennington et al. 2014) or similar information from different measurement regimes (Wang et al. 2013) with potentially different noise characteristics. The multi-view learning paradigm involves simultaneously learning a model for each view, assuming the views are conditionally independent given the class label (or the cluster assignment, in a clustering scenario). Multi-view approaches utilize the dependencies within views and across views by co-learning, leading to improved learning, for example in multi-class classification (Minh et al. 2013), image de-noising (White et al. 2012) and co-clustering (Sun et al. 2015). Empirical (Wang et al. 2015; Minh et al. 2013) and theoretical (Chaudhuri et al. 2009) results show the effectiveness of such approaches, especially over methods that concatenate the features from multiple views.
Multi-view clustering based on Canonical Correlation Analysis (CCA) has been studied extensively (Chaudhuri et al. 2009; Kumar et al. 2011; Dhillon et al. 2011). The CCA-based dependency seeking clustering model of Klami and Kaski (2008) groups co-occurring samples in the combined space of the views, such that the views are independent given the clustering (see Sect. 3 for details). Through the use of Gaussian copulas, Rey and Roth (2012) eliminate two restrictive assumptions in Klami and Kaski’s model: Gaussian-only dependence structure and identical marginal distributions in all dimensions. However, as noted above, Gaussian copulas cannot capture many different kinds of dependencies prevalent in real-world datasets. For datasets with asymmetric and tail dependencies, Rey and Roth’s model that assumes meta-Gaussian distribution suffers from model mismatch and results in an erroneously large number of clusters (see Sect. 6). Another limitation of their method, as well as many other clustering methods, is the inability to fit mixed data. We overcome both these limitations by developing a dependency-seeking multi-view clustering model based on Dirichlet Process mixture of vines that generalizes to arbitrary dependencies as well as to mixed marginals.
Our Contributions
-
1.
We take the first step to fit vine copula for mixed data (with arbitrary continuous, ordinal and binary marginals) by designing a new MCMC inference algorithm with time complexity that is, per sampling step, quadratic in the data dimensions and linear in the number of bivariate copulas used. Our sampling scheme bypasses the costly estimation of marginals using a rank-based likelihood (Hoff 2007) to obtain approximate parameter estimates [Sect. 4]
Empirically, it is faster than the algorithm of Panagiotelis et al. (2012) for discrete marginals and it yields more accurate parameter estimates, in both the continuous and discrete case, than the current best estimators.
-
2.
We develop a Dirichlet Process mixture of vine copulas model for dependency seeking multi-view clustering, that generalizes the model of Rey and Roth (2012) to arbitrary dependencies (beyond meta-Gaussian) as well as to mixed marginals. The flexibility of the model comes with its challenges in fitting mixed data and non-conjugacy of priors for the latent variables in our model. We design an inference algorithm that overcomes both these hurdles by extending our inference algorithm for vines [Sect. 5].
-
3.
Our empirical results on synthetic and real datasets demonstrate (i) the scalability and accuracy of our inference algorithm and (ii) clustering performance on single-view and multi-view data with asymmetric and tail dependencies and with mixed marginals [Sect. 6].
The rest of the paper is organized as follows. We begin with a brief discussion on copulas, vines and non-parametric clustering in Sect. 2 to introduce the concepts used in this paper. In Sect. 3 we review related work in the problems that we address: parameter estimation methods for vines, multi-view dependency seeking clustering and clustering of mixed data. Section 4 describes our new algorithm to fit vines on mixed data. In the following Sect. 5 we detail our vine based model for dependency seeking clustering of multi-view data. All our experimental results are discussed in Sect. 6 and we conclude in Sect. 7.
2 Background
Copula An M-dimensional copula is a multivariate distribution function \(C: [0,1]^M \mapsto [0,1]\) with uniform margins. A theorem by Sklar (1959) proves that copulas can uniquely characterize continuous joint distributions. It shows that for every joint distribution, \(F(X_1, \ldots , X_M)\), with continuous marginals, \(F_j(X_j) ~~ \forall 1 \le j \le M\), there exists a unique copula function C such that \(F(X_1, \ldots , X_M) = C(F_1(X_1), \ldots , F_M(X_M) )\) as well as the converse. The joint density function p can be expressed as: \(p(X_1,\ldots ,X_M) = c(F_1(X_1), \ldots ,F_M(X_M)).p_1(X_1) \ldots p_M(X_M)\) for strictly increasing and continuous marginals \(F_j\) and copula density c. In the discrete case, the copula is uniquely determined, not in general, but on \(Ran(F_1) \times \ldots \times Ran(F_p)\), where \(Ran(F_j)\) is the range of marginal \(F_j\) and a copula based decomposition remains well defined. See Genest and Neslehova (2007) for a discussion on how dependence properties of copulas are valid for discrete data.
For example, the M-dimensional Gaussian copula, for a correlation matrix \({\varSigma } \in \mathbb {R}^{M\times M}\), is given by \(c(U_1, \ldots , U_M; {\varSigma }) = {\varPhi }_{{\varSigma }}\left( {\varPhi }^{-1}(U_1),\dots , {\varPhi }^{-1}(U_M) \right) \), where \(U_j = F_j(X_j)\), \({\varPhi }^{-1}\) is the inverse CDF of a standard normal and \({\varPhi }_{{\varSigma }}\) is the joint CDF of a multivariate normal with mean zero and correlation matrix \({\varSigma }\). A generative model of the Gaussian copula can be obtained by using normally distributed latent variables as follows (Hoff 2007):
where \(F_j^{-1}(U_{ij}) = \text {inf}\{X_{ij}: F_j(X_{ij}) \ge U_{ij}\}\) denotes the (pseudo) inverse or quantile function of the j th marginal CDF \(F_j\), \(X_{ij}\) denotes the j th dimension of the i th observation, \(\mathcal {N}\) and \({\varPhi }\) denote the normal and standard normal distributions respectively. The bivariate Clayton copula, given by \(C(U_1,U_2; \alpha ) = \max {((U_1^{-\alpha }+U_2^{-\alpha }-1)^{-1/\alpha },0)}\) exhibits lower tail dependence. Figure 1 illustrates the dependencies modeled by these two copulas. See Joe (2014) for a comprehensive treatment of copulas.
Vine Copula Vines are hierarchical collections that use bivariate copulas as their building blocks. Any multivariate density is decomposable into conditional densities: \(\small p(X_1,\ldots ,X_M) = p(X_M) . p(X_{M-1}| X_M) \ldots p(X_1| X_2, \ldots X_M)\), and can thereby be written as functions of bivariate copula densities by expanding the conditional density using the following identity for any set of random variables \(\tilde{Y}, Y_1, \ldots , Y_L\):
where \(Y_{-j}\) denotes the set \(\{Y_1, \ldots , Y_{j-1}, Y_{j+1}, \ldots , Y_L\}\). This forms the basis of the hierarchical vine structure. A detailed expansion of the joint density in terms of bivariate copula densities is explained in Aas et al. (2009). We note that in Eq. 2, it is a common practice to approximate \(c_{\tilde{Y},Y_j|Y_{-j}} ( F(\tilde{Y}|Y_{-j}) , F(Y_j|Y_{-j}) | Y_{-j})\) with \(c_{\tilde{Y},Y_j|Y_{-j}} ( F(\tilde{Y}|Y_{-j}) , F(Y_j|Y_{-j}))\) without conditioning on \(Y_{-j}\) for simplicity and computational tractability (refer to Lopez-Paz et al. (2013) for a more thorough treatment of this topic). Henceforth, we make this assumption through the rest of the paper.
Consider the example of expanding the joint density \(p(X_1,X_2,X_3,X_4 )\) in terms of bivariate copulas using the chain rule:
Expanding the second term of Eq. 3, \(p(X_3 | X_4) = c_{34} (F(X_3), F(X_4) ) p(X_3)\). Expanding the third term of Eq. 3, \(p(X_2 | X_3 X_4) = c_{24|3} (F(X_2 | X_3) , F(X_4 | X_3))\) \(p(X_2 | X_3)\), where, \(p(X_2 | X_3) = c_{23} (F(X_2), F(X_3) ) p (X_2)\). Expanding the fourth term of Eq. 3, \(p(X_1 | X_2, X_3, X_4) = c_{14 | 23} (F(X_1 | X_2 X_3) , F(X_4 | X_2, X_3) )\,p(X_1 | X_2 X_3)\), where, \(p(X_1 | X_2 X_3) = c_{13 | 2} (F(X_1 | X_2), F(X_3 | X_2) ) p(X_1 | X_2)\) and \(p(X_1 | X_2) = c_{12} (F(X_1), F(X_2) ) p(X_1)\). Hence, this leads us to the expansion of the joint density for four variables in terms of pair copulas:
Note that the density is expressed in terms of only univariate marginals and bivariate copulas. Since the number of bivariate copula decompositions is very large for high dimensions, special graphical models have been introduced that constrain the structure of the decompositions. A D-vine has \(M-1\) hierarchical trees and \(M \atopwithdelims ()2\) bivariate copulas for M dimensional data. The general expression for the density \(p(X_1,\ldots X_M)\) of a D-vine in terms of bivariate copulas is given by
comprising of \(M \atopwithdelims ()2\) bivariate copulas \(\{c_{s,s+t|s+1,\ldots ,s+t-1}\}\) where index s identifies the trees and t iterates over the edges in each tree; \(F^1_{s,t}=F(X_s|X_{s+1},\ldots , X_{s+t-1})\), \(F^2_{s,t}=F(X_{s+t}|X_{s+1},\ldots ,X_{s+t-1})\). The conditional distributions in the pair copula constructions, \(F^1_{s,t}\) and \(F^2_{s,t}\), can be recursively evaluated using h-functions (Aas et al. 2009) for any set of random variables \(\tilde{Y}, Y_1, Y_2,\ldots , Y_L\):
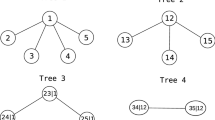
Figure 2 shows a D-Vine for the four dimensional case with density from equation 7.
At the lowest level, each input variable is associated with a node (1,2,3 and 4) and edges represent bivariate copulas (\(c_{12}, c_{23}, c_{34}\)). Nodes at subsequent level (12, 23 and 34) represent conditional distributions obtained from the nodes of the previous level and edges represent conditional copulas (\(c_{13|2}, c_{24|3}\)) which are evaluated using the appropriate h-functions. Nodes at the final level (\(c_{13|2}, c_{24|3}\)) once again represent conditional distributions obtained from the nodes of the previous level and edges represent conditional copulas (\(c_{14|23}\)) which is yet again evaluated using the appropriate h-functions.
During estimation the data at the lowest level are the transformed input data (transformed via rank or CDF transformations) and at each subsequent level they are obtained using h-functions.
Analytic expressions for h-functions have been derived for commonly used copulas; see Aas et al. (2009) for more details and an introduction to vines. The advantage of such a model is that not all the bivariate copulas have to belong to the same family thus enabling us to model different kinds of bivariate dependencies. In this paper we describe our models using D-Vines, but the techniques can easily be extended to other regular vines for a given configuration of pair-copulas. We note that the choice of D-vines is motivated by the ready availability of baselines for continuous data (Brechmann and Schepsmeier 2013) and discrete data (Panagiotelis et al. 2012) (though there is no available baseline for mixed data).
Non-Parametric Clustering Bayesian non-parametric models enable clustering with mixture models without having to fix the number of mixture components apriori, allowing the model to adapt based on the observed data. The Dirichlet Process (DP) serves as a prior for a mixture distribution over countably infinite components for a mixture model (Teh 2010). The DP is briefly described below, through a generative process, that produces countably infinite weights \({\pi _k}_{k=1}^{\infty }\) summing to one (refer to (Teh 2010) for alternate definitions). This generative process is also called the stick-breaking process (Aldous 1985), where the distribution of weights \({\pi _k}_{k=1}^{\infty }\) is often represented by GEM after its authors.
Formally, we define \( \pi \sim { GEM}(\alpha )\), with parameter \(\alpha \), if \(\pi _1 \sim { Beta}(1,\alpha )\) and \(\forall k \ge 2\), \(\pi _k = \eta _k \prod _{p=1}^{k-1}(1 - \eta _p)\; \eta _k \sim Beta(1,\alpha ) \). A probability distribution G is said to be sampled from a DP, i.e \(G \sim DP(\alpha , H)\) if:
where H is a suitably chosen base distribution of the DP, a prior for the parameters \(\phi _k\) of the cluster specific densities (for instance, in the case of D-Vine mixtures, H is the prior distribution for parameters and families of the D-Vine mixture components). Inference for DP-based models is commonly based on the Chinese restaurant process (CRP) (Aldous 1985), that gives the posterior predictive distribution of new cluster assignments, having observed samples from G.
3 Related work
Parameter Estimation for Discrete Vines For vines with discrete margins, Smith and Khaled (2012) propose an MCMC inference algorithm which uses a data augmentation approach to compute the probability mass function (PMF). It is extensible to mixed data, but requires, for a M-dimensional vine, \(\mathcal {O}(2^M)\) computations per sampling step. Panagiotelis et al. (2012) derive a decomposition of the PMF that requires only \(2M(M-1)\) evaluations of bivariate copula functions in the vine. But their method cannot be used with vines with mixed margins. Further, their recommended estimation method is the two-step IFM approach (Joe 2014; Panagiotelis et al. 2012) where the marginals are estimated first and then ML estimates of parameters are obtained using non-linear maximization methods such as gradient ascent that are fraught with problems due to local maxima.
Multi-view Dependency Seeking Clustering Finding linear inter-view dependencies through CCA has been extended in several ways in recent years to capture non-linear dependencies (eg. kernelized CCA (Shawe-Taylor and Cristianini 2004)) and non-normal distributions (eg. exponential CCA (Klami et al. 2010)).
Dependency-seeking multi-view clustering aims to cluster co-occurring samples in multiple views in a manner that enforces the cluster structure to capture the dependencies. The dependency seeking clustering model of Klami and Kaski (2008), for two views \(X^1\) and \(X^2\) with dimensions p and q respectively is given by:
where \(\mathcal {N}_{p+q}\) is a \((p+q)\)-dimensional normal distribution with mean \(\mu _z\) and covariance matrix \({\varPsi }_z = \left( \begin{array}{cc} {\varPsi }_{zx^1} &{} 0 \\ 0 &{} {\varPsi }_{zx^2} \\ \end{array} \right) \) and latent variable Z represents the clustering assignment, \(\pi \) being a multinomial distribution over clusters. The block diagonal structure of \({\varPsi }_z\) enforces independence of views given the cluster assignment. To address the problem of non-normally distributed data (that results in model mismatch and erroneously large number of uninterpretable clusters) this model is extended by Rey and Roth (2012) who use a Gaussian copula in place of \(\mathcal {N}_{p+q}\) thus enabling discovery of non-normally distributed clusters. This is done using normally distributed latent variables, \(\tilde{X}^1,\tilde{X}^2\), following the approach outlined in Hoff (2007) (also see Eq. 1). The complete model is given by:
where GEM is the stick breaking process (Aldous 1985) with parameter \(\alpha \), Z represents the clustering assignment and \({\varPsi }_z\) is a block diagonal covariance matrix of a standard normal distribution for the particular cluster generating latent variables \(\tilde{X}^1, \tilde{X}^2\). We denote the inverse CDF transformation for the j th dimension of the first view by \((F^1_j)^{-1}\) and the second view by \((F^2_j)^{-1}\), through which the final data \(X^1=\{X^1_j\}\) and \(X^2=\{X^2_j\}\) is obtained. Each marginal can be from any family of continuous distributions and we denote the parameters of the marginals for each view by \(\{\theta ^1_j\}\) and \(\{\theta ^2_j\}\) respectively. See Rey and Roth (2012) for more details. Thus their model is a DP mixture of Gaussian copulas that is limited to capturing meta-Gaussian dependencies. Further, the inference methods used for these models restricts them to continuous marginals, and cannot be used with mixed data.
Model-based clustering techniques such as that in Yerebakan et al. (2014) attempt to capture more complex continuous densities by modeling each mixture component with multimodal densities based on an Infinite Gaussian mixture, but cannot be used with multi-view data or mixed data.
Clustering mixed data Recent model-based clustering methods to fit mixed data have been designed by McParland and Gormley (2016) and Browne and McNicholas (2012) that use latent variable approaches, similar to ours, but assume Gaussian distribution; and by McParland et al. (2014) who use a mixture of factor analyzers model.
Recent copula-based models include a mixture of D-Vines by Kim et al. (2013) that can only fit continuous data. A more general mixture of copulas by Kosmidis and Karlis (2015) mentions possible extensions to discrete and mixed data. For several copula families their algorithm scales exponentially with dimensions rendering them impractical. For vines, that capture more complex dependencies and constitute our main focus, they do not discuss mixed data extensions and for discrete vines they suggest the same PMF decomposition of Panagiotelis et al. (2012) that we compare with in our experiments and significantly outperform.
Correlation clustering also attempts to find clusters based on dependencies and is typically PCA-based. E.g. INCONCO (Plant and Böhm 2011) that can be used with mixed data but models dependencies by distinct Gaussian distributions for each category of each discrete feature. While SCENIC (Plant 2012), that is empirically found to outperform INCONCO, is not as restrictive in the dependencies, it also is limited by the fact that it assumes a Gaussian distribution to find a low-dimensional embedding of the data. Note that these methods are not suited for multi-view clustering; we use SCENIC and ClustMD (McParland and Gormley 2016) as baselines in single-view settings only.
4 D-vines for mixed data
Our approach involves a generative formulation for D-vines where we explicitly introduce marginals for each datapoint as latent variables. Note that the model and inference algorithm can be readily extended to other regular vines but for ease of exposition we restrict ourselves to D-vines.
Generative formulation for D-vines Consider N observations of M dimensional data \(\mathbf {X}=\{X_{i,j} \}\). Let \(\mathbf {U}=\{U_{i,j} \} \in [0,1]^{N \times M}\) be a set of continuous latent variables. A generative formulation for D-vine can be defined as follows. We first sample \(U_{i,j},\forall i,j\) from a D-Vine, with pair-copula parameters \({\varSigma }\) and \({\varTheta }\). The observed data \(X_{i,j},\forall i,j\) is generated by invoking the quantile function of the corresponding marginal variable \(U_{i,j}\). We note that the actual marginal distributions \(\{F_j\}\) need not be continuous, which enables us to model mixed data. Further, to facilitate Bayesian inference on the parameters \({\varTheta }\) and \({\varSigma }\) of the D-vine, we introduce appropriate priors (summarized in Eq. 9.)
\({\varTheta }=\{\theta _{s,t} \in [T]: 1 \le s < t \le M \}\) denotes the set of \({M \atopwithdelims ()2}\) bivariate pair-copula families, chosen from a set of T families. Our technique is suitable for any set of bivariate copulas with invertible h-functions (This is discussed in more detail during the inference). We place a uniform prior on \(\theta _{s,t}, \forall s,t\) to select each copula family with a probability \(\frac{1}{T}\). We note that while the choice of uniform distribution for the selection of copula family is motivated by simplicity, one could alternately place a multinomial distribution to select the copula family, with a Dirichlet prior.
\({\varSigma }=\{\sigma _{s,t} : 1 \le s < t \le M \}\) is the collection of parameters of all the constituent bivariate copulas in the D-vine definition. We place a uniform prior over the support of the parameters in \({\varSigma }_{s,t} \forall s,t\), once again for simplicity. We also note that alternate priors exploiting conjugacy are preferable where permissible. For instance, for bivariate Gaussian copula, we place an inverse Wishart prior exploiting conjugacy. (Refer to sections 4.5 and 4.6 from Murphy (2012) for a discussion on Wishart distribution for Bayesian inference. The use of Inverse Wishart prior for Bayesian inference with the Gaussian copula is discussed in detail in Hoff 2007).
Inference Exact inference for this problem is intractable and we propose an approximate inference algorithm for vines for mixed data based on Gibbs sampling using the extended rank likelihood (Hoff 2007) approach that bypasses the estimation of margins and thus can accommodate both continuous and discrete ordinal margins. Further, due to the non-conjugacy of priors, our Gibbs Sampling steps are interspersed with Metropolis Hastings steps, similar to the sampling approaches found in Neal (2000) and Meeds et al. (2007).
Consider data \(\mathbf {X}=\{X_{i,j} \}\) and latent variables \(\{U_{i,j}\}\) introduced in our D-vine generative model. Without any knowledge of the marginals \(\{F_j\}\) and without observing \(\mathbf {U}\), (which may be discrete or continuous), observing \(\mathbf {X}\) tells us that \(\mathbf {U}\) must lie in the set (following the same rank constraints as in \(\mathbf {X}\)):
since marginals are non-decreasing. The occurrence of this event is considered as our data. The rank likelihood is given by:
Since the rank likelihood function is based on the marginal probability of an event that is a superset of observing the ranks (i.e. the event D), it is also referred to as the extended rank likelihood. For more details on the rank-likelihood approach, including clarifying illustrations, please see Hoff (2008).
Our Gibbs sampling scheme is as follows. The latent variables for which to compute Gibbs sampling updates during inference are \(\{U_{i,j}\}\), \({\varTheta }\) and \({\varSigma }\). Our strategy comprises of first sampling \(\{U_{i,j}\}\) from a D-vine subject to rank based constraints that follow from the extended rank likelihood methodology, followed by sampling \({\varSigma }\) and \( {\varTheta }\) conditioned on the \(\{U_{i,j}\}\) random variables.

An important aspect of this inference process is rank constrained sampler from a D-Vine, that we now discuss. Consider the set
Let \(D_{i,.}\) denote the set \(D_{i,1} \times D_{i,2} \times \cdots \times D_{i,M}\). We block sample the random variables \(U_{i,.}\) from \(p(U_{i,.} | {\varSigma }, {\varTheta }, U_{-i,.}, U_{i,.} \in D_{i,.})\) which is a truncated D-vine distribution due to rank constraints. However sampling directly from this distribution is hard, and so we use the Metropolis Hastings (MH) algorithm to draw a sample using a proposal that is a close approximation to this desired distribution. Our proposal distribution is \(p(U_{i,1} |{\varSigma }, {\varTheta }, U_{i,1} \in D_{i,1} ) \prod _{j=2}^M p(U_{i,j} |{\varSigma }, {\varTheta },U_{i,1} \ldots U_{i,j-1}, U_{i,j} \in D_{i,j} )\). To sample the random vector \(U_{i,.}\) from this proposal, we first sample \(U_{i,1}\) from \(p(U_{i,1} |{\varSigma }, {\varTheta }, U_{i,1} \in D_{i,1} )\), then sample from \(p(U_{i,2}| {\varSigma }, {\varTheta }, U_{i,1}, U_{i,2} \in D_{i,2})\) and so on, until we finally sample from conditional \(p(U_{i,M} | {\varSigma }, {\varTheta }, U_{i,1}, \ldots , U_{i,M-1}, U_{i,M} \in D_{i,M})\). The cumulative distributions for each conditional in this procedure are the h-functions (Aas et al. 2009) (see Eq. 6), that are invertible in closed form for most bivariate copula families. Hence we use inverse transform sampling to sample from these h-functions, subject to the rank constraint \(D_{i,j}\). Drawing a single sample \(U_{i,.}\) from the proposal for a single datapoint involves \(O(M^2)\) h-function inversions (as shown in Algorithm 1). We empirically observe a high acceptance ratio with this proposal leading to almost no rejected samples, thereby leading to a complexity of \(O(M^2)\) for the Gibbs update of \(U_{i,.}\). Details of this MH procedure are described in “Appendix 2”. Our algorithm is summarized in Algorithm 1.
To draw samples for latent variables \({\varTheta }\) and \({\varSigma }\), we use the Metropolis Hastings algorithm owing to the non-conjugacy of their priors. We also note that it is possible to collapse \({\varTheta }\) for faster mixing and work with a mixture of families for each pair copula. However, we do not encounter issues with convergence in our experiments for sampling \({\varTheta }\) and proceed as follows. We draw a sample of \(\{\sigma _{s,t}, \theta _{s,t}\}\), \(\forall 1\le s \le t\le M\) using random walk Metropolis Hastings (refer to “Appendix 2” for details) to sample from:
The conditioning set \(W^{s,t}\) is constructed as follows. When sampling \(\{\theta _{s,t},\sigma _{s,t}:t=s+1\}\), the parameters of the first level bivariate copulas depend directly on a subset of the sampled marginal variables \(\{U_{i,j}\}\) (refer Eq. 5). Hence, the update for \(\theta _{s,t},\sigma _{s,t}\) for the first level bivariate copulas is conditioned on the set of pairs \(W^{s,t}=\{U_{i,s}, U_{i,t} ,\forall i\}\). The parameters of higher level bivariate copulas \((t>s+1)\) depend on pairs of higher order conditionals (again, refer Eq. 5). Hence, for these, the set \(W^{s,t}\) is constructed as \(W^{s,t}=\{ F(U_{i,s} | U_{i,s+1}, \ldots , U_{i,s+t-1}), \) \(F(U_{i,t} | U_{i,s+1}, \ldots ,U_{i,s+t-1}), \forall i\}\). Note that the conditional distributions \(W^{s,t}, \forall t>s+1\) above are evaluated once again using the h-functions (Eq. 6) recursively.
Computational Complexity Drawing a single sample from a rank constrained D-vine with uniform marginals using Metropolis Hastings algorithm entails time complexity of \(O(M^2)\) with the chosen proposal. Hence, time complexity for a single Gibbs sweep in our algorithm is \(O(M^2 N)\) due to the quadratic complexity of sampling the \(U_{i,.}\) variables for each of the N samples and the sampling for parameters and families of \(M \atopwithdelims ()2\) pair copulas.
A popular technique to reduce the complexity of vine inference is truncation (Joe 2014) where all copulas beyond a certain level in the vine structure are assumed to be independence copulas. This can potentially lead to linear complexity per sampling step per data point. Our algorithm can be extended for truncated vines but we do not investigate this further in this paper.
5 Vines for multi-view dependency seeking clustering of mixed data
We now present a model for multi-view dependency seeking clustering using D-Vines. Consider data \(\{X_{i,v,j}\}\), N data points with \(i \in [N]\), collected from V views with \(v \in [V]\), where \(j \in [M_v]\) denotes the dimension in the specific view. Our goal is to cluster the data simultaneously from all the views, while modeling intra-view dependencies in each view. (Note that for better readability, we have slightly deviated from the superscript notation used in Sect. 3, to denote a view.)
We model the data in each view v in each cluster k with a D-Vine with the appropriate pair copula families denoted by \({\varTheta }=\{{\varTheta }_{k,v}\}\), and the corresponding parameters \({\varSigma }=\{{\varSigma }_{k,v}\}\) by extending the generative definition in Eq. 9 with a DP mixture model (Teh 2010) in Eq. 12. (Refer to Sect. 2 for more details on non-parametric clustering with the Dirichlet Process.) We note that each \({\varTheta }_{k,v}=\{\theta _{k,v,s,t} : 1 \le s < t \le M_v \}\), represents the families for set of all pair copulas for cluster k, view v. Similarly, we have \({\varSigma }_{k,v}=\{\sigma _{k,v,s,t} : 1 \le s < t \le M_v \}\), the corresponding set of pair copula parameters. To adaptively choose the number of mixture components from the data, we place a DP prior on our mixture distribution. Hence, we draw the mixture weights \(\pi \sim GEM(\alpha )\) using the stick breaking process (Aldous 1985; Teh 2010) with a concentration parameter \(\alpha \) in turn with a gamma prior. The generative process proceeds by selecting cluster indices \(\mathbf {Z}=\{Z_i\}\) for each observation i and generating the marginal latent variables \(\mathbf {U}=\{U_{i,v,j}\}\) from a D-Vine followed by the inverse transformation, to obtain \(\mathbf {X}=\{X_{i,v,j}\}\), similar to equation 9, in a multiview clustering setting. This generative process is shown in Eq. 12.
Inference Approximate inference for our model using Gibbs sampling is based on the D-vine inference technique outlined in Sect. 4. We sample random variables \(\mathbf {U}\), \({\varSigma }\), \(\theta \), \(\mathbf {Z}\) and \(\alpha \) while \(\pi \) is integrated out due to conjugacy (Aldous 1985).
Notation: A set with a subscript starting with a hyphen(−) indicates the set of all elements except the index following the hyphen. Let \(n_k = |\{ \mathbf {X}_i : Z_i=k\}|\).
For sampling \(\alpha \), we follow the standard technique in Escobar and West (1995). Sampling \(U, {\varSigma }, {\varTheta }\) follows from Sect. 4 due to our modeling assumption that data in each view and each cluster is independently generated from a D-vine. Hence, for each cluster k, for each view v, sampling the random variables corresponding to the marginal distributions \(\mathbf {U}^{k,v}=\{U_{i,v,.} :i\in [N],Z_i=k\}\), the pair copula parameters \({\varSigma }_{k,v}\) and the families \({\varTheta }_{k,v}\) independently follow the same steps as outlined in the Gibbs sampling iteration in Algorithm 1.
Sampling the cluster assignment, Z, is based on CRP (Aldous 1985), the predictive distribution arising from a DP. However, it differs from the standard approach due to the rank constraint in the algorithm. The probability of \(Z_i\) taking a particular value k can be expressed as a product of two terms, \(p(Z_i =k| Z_{-i})\) arising from the CRP and \(P(U_{i,.,.} | Z_i=k,{\varSigma },{\varTheta })\), the likelihood term (see Eq. 14). However the support for \(Z_i\) is constrained to the permissible set of clusters, \(C_i\) (defined below), for selecting an existing cluster that satisfies the rank constraints within the cluster. Hence, for any \(k \in [K]\), \(Z_i\) being set to k is permissible if \(\mathbf {U}^k \cup U_{i,.,.}\) meets the rank constraints. We define the set of permissible clusters as
The update for \(Z_i\) is given as follows.
Computing the probability of \(Z_i = k_{new}\), for a new component requires integrating over the prior distributions of the set of parameters \({\varSigma }_{k_{new},v}\) of the new component and the corresponding D-Vine families \({\varTheta }_{k_{new},v}\). We follow the technique proposed by Neal (2000), by finding a Monte Carlo estimate of the probability of selecting a new cluster.

6 Experiments
Parameter Estimation To evaluate how well our inference algorithm estimates parameters of a D-Vine, we simulate 500 samples from a 6-dimensional D-Vine with continuous marginals (Gaussian, exponential and gamma) with known parameters and estimate the parameters using our Algorithm Ext-DVine and the Maximum Likelihood method of Aas et al. (2009), MLE, as well as the method of Panagiotelis et al. (2012).
Table 1 shows the average RMSE of the original parameters with respect to the estimated parameters obtained by Ext-DVine and MLE. Our estimates are closer to the true parameters than those obtained by MLE. We repeat this experiment with mixed marginals (Gaussian, gamma, negative binomial, Poisson) and obtain a low RMSE of the estimated parameters from the original parameters (there are no available baselines for mixed data).
For continuous data, we also perform a goodness of fit test comparing Ext-DVine inference with the popular MLE technique of Aas et al. (2009), from the R package CDVine of Brechmann and Schepsmeier (2013), by estimating the parameters of the D-Vine and simulating new data with these parameters and comparing difference in correlations (measured by Kendall’s Tau, Spearman’s Rho and Pearson’s correlation coefficients) between the original dataset and the re-simulated dataset. Table 2 shows that the differences in correlations are lesser when parameters are estimated using our method thus implying a better fit with our Bayesian inference algorithm for Ext-DVine, as compared to the differences in correlations when simulation parameters are ML estimates.
Performance on discrete data: comparison with Panagiotelis et al. (2012), Ext-Dvine is much faster with higher accuracy: bars indicate 5 times sd over 25 runs. a Runtime. b Accuracy (RMSE)
Time Complexity We empirically evaluate the time complexity and accuracy for discrete marginals by plotting time taken for inference for varying dimensions (M), for a fixed datasize of N \(=\) 500 points with parameters generated from priors. Since there is no baseline for mixed data, we restrict this evaluation to discrete data and use the baseline of Panagiotelis et al. (2012), the most efficient method known for discrete vines. We use 15 sampling sweeps while the method of Panagiotelis et al. (2012) takes significantly more time to run till convergence (with between 10-20 iterations) and obtains less accurate parameter estimates. (Results shown over 25 runs with error bars in Fig. 3). While our inference method analytically leads to complexity quadratic in M (and linear in the number of pair-copulas), in Fig. 3, it almost looks linear in M, in comparison with Panagiotelis et al. (2012) due to significantly higher runtime of the baseline. In fact, the baseline did not complete its run to convergence after running for a day even for 20 dimensional data. In Fig. 4, we show a standalone plot of the runtime and accuracy of our technique (without the discrete baseline) for upto M \(=\) 50 dimensions. We observe quadratic complexity of O(\(M^2N\)), linear in the number of pair copulas, for a fixed datasize N \(=\) 500 as discussed.
6.1 Dependency seeking clustering
Multi-view Setting We evaluate our model for Multi-view dependency seeking clustering on synthetic datasets containing asymmetric and tail dependencies.
Baselines For continuous features, we compare with the model of Rey and Roth (2012), that uses Gaussian copulas (GC-MVC) and can only be used with continuous data. For mixed data, since there are no existing baselines, we implement an extended rank likelihood based inference on Rey and Roth’s model (Ext-GC-MVC). This method does not exist in previous literature, but inference follows the straightforward sampling scheme of Hoff (2007) and does not face the difficulties that we address, for inference with vines. Note that while this can fit mixed data, it can only model meta-Gaussian dependencies. Our vine-based algorithm to handle mixed data is denoted by Ext-Vine-MVC.
Histograms of number of clusters found by Ext-Vine-MVC (left) and GC-MVC (right). Above continuous marginals, Below: mixed marginals. We see that our D-vine based model infers the correct number of clusters (2) in most simulations. GC-MVC is unable to infer the correct number of clusters due to model mismatch. a Multiview-continuous. b Multiview-continuous. c Multiview-mixed. d Multiview-mixed
Evaluation Metrics We evaluate the ability of GC-MVC and our method Ext-Vine-MVC to identify the correct number of clusters. We also evaluate the clustering performance of Ext-Vine-MVC and Ext-GC-MVC when the number of clusters is given as input. Clustering performance is measured by Adjusted Rand Index (ARI) (Hubert and Arabie 1985), Variation of Information (VI) (Meilă 2007), Normalized Mutual Information (NMI) (Vinh et al. 2010) and the classification accuracy obtained by fixing the labels of the inferred clusters. Note that lower VI is better while higher values in other metrics indicate better performance. All results shown are averages over 25 simulations.
Simulations We generate data with two views, with three dimensions in each view. The pairwise dependencies for each view, with different dependency structures, is shown in Fig. 5. For mixed datasets we generate two datasets, one with continuous marginals (gamma, normal and exponential) in each view and one with mixed marginals (gamma, negative binomial and Poisson) in each view. Complete parameters of the simulations are detailed in “Appendix 1”.
Results Figure 6 shows the proportion of times, out of 25 runs, when algorithms Ext-Vine-MVC and GC-MVC obtain a specific number of clusters. We observe that GC-MVC does not infer the right number of clusters (Fig. 6b, d). In the continuous case, our method infers the right number 80% of the times and in the remaining cases, the deviation is not large—it infers 3 instead of 2 (Fig. 6a). In comparison, GC-MVC has to compensate for the model mismatch by increasing the number of clusters. In most cases, the number of clusters inferred is more than 6 (Fig. 6b). In the case of mixed data, the results of Ext-GC-MVC are worse. The inferred number of clusters range from 12 to 16 (Fig. 6d). Ext-Vine-MVC does much better, inferring the right number of clusters in 65% of cases and a low deviation of \(\le 2\) (Fig. 6c). Table 3 shows the clustering performance of Ext-Vine-MVC and GC-MVC for continuous data. Ext-Vine-MVC obtains better clustering performance than the other two methods. Table 4 shows the clustering performance of Ext-Vine-MVC and Ext-GC-MVC for mixed data. Note that Ext-GC–MVC is not able to discriminate between clusters with non-metaGaussian dependencies and hence has worse performance. Best results in both tables are in bold.
Single view setting—histograms of number of clusters found by Ext-Vine-MVC (left) and GC-MVC (right) on 25 simulations with continuous (a–b), mixed (c–d) marginals. We see that Ext-Vine-MVC infers the correct number of clusters (2) in most simulations. GC-MVC infers the wrong number of clusters in most cases due to model mismatch. a Continuous:Ext-Vine-MVC. b Continuous:GC-MVC. c Mixed:Ext-Vine-MVC. d Mixed:Ext-GC-MVC
Single-View Setting While our focus application is multiview dependency seeking clustering, we also run our algorithm in the special case of single-view setting to demonstrate our algorithm for datasets with more complex dependencies like combination of asymmetric and tail dependencies. We generate data with pairwise tail dependencies and asymmetric dependencies as shown in Fig. 7. In dataset 1 we use gamma, normal and exponential marginals and in dataset 2 we use gamma, negative binomial and Poisson marginals. Note that cluster 1 has asymmetric dependencies and cluster 2 has tail dependencies. We also use additional baselines of Gaussian Mixture Models (GMM) for continuous features and two state-of-the-art methods for mixed data: SCENIC (Plant 2012) and ClustMD (McParland and Gormley 2016).
Figure 8 shows the proportion of times, out of 25 runs, when algorithms Ext-Vine-MVC and GC-MVC obtain a specific number of clusters in the single view setting showing how our model fits the data compared to baseline for data generated from a known number of clusters. In the continuous case, our method infers the right number 80% of the times and in the remaining cases, the deviation is not large (Fig. 8a). GC-MVC has to compensate for the model mismatch by increasing the number of clusters (Fig. 8b). In the case of mixed data, Ext-GC-MVC erroneoulsy infers the number of clusters to be more than 5 in 90% of the cases (Fig. 8d). Ext-Vine-MVC does much better, inferring the right number of clusters in 80% of the cases and the deviation is \(\le 1\) (Fig. 8c). Table 5 shows the performance of Ext-Vine-MVC in comparison with GC-MVC and GMM for dependency seeking clustering on continuous data. Table 6 compares Ext-Vine-MVC versus baselines Ext-GC-MVC, SCENIC and ClustMD. Ext-Vine-MVC is found to consistently outperform the baselines in both continuous and mixed datasets.
Real Datasets We analyze two real world datasets—the mortality dataset and the abalone dataset.
Mortality Dataset This dataset from Physionet (MIMIC II database) Goldberger et al. (2000), comprises of 800 ICU patient records where each record contains the last collected readings for 8 features, from 2 views. (1) View 1 features: BUN, Creatinine, HCO3, PaO2 (2) View 2: GCS, HR, Weight, Age. View 1 contains measurements from blood tests and View 2 are other external measurements. Since the noise characteristics are different in these measurements, they can be considered as different views. The data also contains target binary label (mortality status) indicating whether or not the patient survived. Clustering of clinical data is a valuable tool to discover disease patterns, identify high-risk patients and has been done to study mortality-risk patterns (Marlin et al. 2012). We cluster this data with Ext-Vine-MVC and obtain two clusters that are indicative of patient mortality status with accuracy shown in Table 7. We outperform the baseline Ext–GC–MVC in all the clustering metrics and mortality prediction accuracy.
Abalone dataset This dataset, from the UCI repository (Bache and Lichman 2013), contains six continuous-valued attributes of abalones with different ages. Figure 9 shows pairwise correlations in older (age \({>}7\)) and younger abalones (age \(\le 7\)) which have different dependence structures. Younger abalones have asymmetric correlations where there is high correlation for smaller values and low correlation for larger values. Our algorithm finds two clusters, shown in Fig. 10, that meaningfully represents younger and older abalones. Our model accurately captures the asymmetric dependencies in younger abalones through bivariate Clayton copulas. We also show clustering results from our baseline GC-MVC that can only model meta-Gaussian dependencies in Fig. 10.
Abalone dataset: we show histograms of abalones by age for each cluster inferred by Ext-Vine-MVC (above) and GC-MVC (below). Each bar indicates the percentage of abalones in the specific cluster belonging to a particular age. a Ext-Vine-MVC infers 2 overlapping clusters: younger abalones (age \(\le 7\)) and older abalones (age \({>}7\)). This corresponds well with the difference in dependence structures in these age groups seen in Fig. 9. b GC-MVC infers 4 clusters which do not show discernible relation to age
6.2 Summary of results
-
Ext-Dvine obtains more accurate parameter estimates than the MLE method of Aas et al. (2009) for continuous margins as well as the method of Panagiotelis et al. (2012) for discrete margins. In runtime it is faster than the latter and is the first method to fit vines on mixed margins.
-
Ext-Vine-MVC, our DP mixture model for dependency seeking clustering in multi-view and single view settings, is evaluated on simulated continuous and mixed data containing asymmetric and tail dependencies. We show superior performance over baselines in
-
1.
clustering accuracy in a finite mixture setting,
-
2.
detecting the correct number of clusters in a non-parametric setting.
-
1.
-
Ext-Vine-MVC significantly outperforms GC-MVC and Ext-GC-MVC (that follow the model of Rey and Roth (2012) and are limited to modeling meta-Gaussian dependencies) on clustering real world datasets.
7 Conclusion
We design a new MCMC inference algorithm to fit vines on mixed data that runs in \(O(M^2 N)\) time per sampling step (M dimensions, N observations). Our model, a DP mixture of vines, can fit mixed margin distributions and arbitrary dependencies. Empirically we demonstrate the benefits of our model in dependency seeking clustering, extending state-of-the-art multi- and single- view models by modeling asymmetric and tail dependencies and fitting mixed data.
References
Aas, K., Czado, C., Frigessi, A., & Bakken, H. (2009). Pair-copula constructions of multiple dependence. Insurance: Mathematics and Economics, 44(2), 182–198.
Aldous, D. J. (1985). In École d’été de probabilités de Saint-Flour, XIII—1983. Lecture notes in mathematics (pp. 1–198). Springer.
Amoualian, H., Gaussier, E., Clausel, M., & Amini, M.-R. (2016). Streaming-lda: A copula-based approach to modeling topic dependencies in document streams. In Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining.
Bache, K., & Lichman, M. (2013). UCI Machine learning repository. http://archive.ics.uci.edu/ml.
Brechmann, E. C., & Schepsmeier, U. (2013). Modeling dependence with C- and D-vine copulas: The R package CDVine. Journal of Statistical Software, 52(3). doi:10.18637/jss.v052.i03.
Browne, R. P., & McNicholas, P. D. (2012). Model-based clustering, classification, and discriminant analysis of data with mixed type. Journal of Statistical Planning and Inference, 142(11), 2976–2984.
Chang, Y., Li, Y., Ding, A., & Dy, J. (2016). A robust-equitable copula dependence measure for feature selection. In Proceedings of the 19th international conference on artificial intelligence and statistics (AISTATS), (pp. 84–92).
Chaudhuri, K., Kakade, S. M., Livescu, K., & Sridharan, K. (2009). Multi-view clustering via canonical correlation analysis. In Proceedings of the 26th annual international conference on machine learning, (pp. 129–136). ACM.
Chen, N., Zhu, J., Sun, F., & Xing, E. P. (2012). Large-margin predictive latent subspace learning for multiview data analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 34(12), 2365–2378.
Dhillon, P., Foster, D. P., & Ungar, L. H. (2011). Multi-view learning of word embeddings via CCA. In Advances in Neural information processing systems (NIPS), (pp. 199–207).
Eickhoff, C., de Vries, A. P., & Hofmann, T. (2015). Modelling term dependence with copulas. In Proceedings of the 38th international ACM SIGIR conference on research and development in information retrieval, (pp. 783–786).
Elidan, G. (2010). Copula bayesian networks. In Advances in neural information processing systems (NIPS), (pp. 559–567).
Elidan, G. (2012). Copula network classifiers (cncs). In Proceedings of the seventeenth international conference on artificial intelligence and statistics (AISTATS), (pp. 346–354).
Escobar, M. D., & West, M. (1995). Bayesian density estimation and inference using mixtures. Journal of the American Statistical Association, 90, 577–588.
Fujimaki, R., Sogawa, Y., & Morinaga, S. (2011). Online heterogeneous mixture modeling with marginal and copula selection. In Proceedings of the 17th ACM SIGKDD international conference on knowledge discovery and data mining, (pp. 645–653).
Genest, C., & Neslehova, J. (2007). A primer on copulas for count data. Astin Bulletin, 37(2), 475.
Goldberger, A. L., Amaral, L. A. N., Glass, L., Hausdorff, J. M., Ivanov, P Ch., Mark, R. G., et al. (2000). PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation, 101(23), 215–220.
Gonçalves, A., Von Zuben, F. J., & Banerjee, A. (2016). Multi-task sparse structure learning with gaussian copula models. Journal of Machine Learning Research, 17(33), 1–30.
Guo, Y., & Xiao, M. (2012). Cross language text classification via subspace co-regularized multi-view learning. In Proceedings of the 29th international conference on machine learning (ICML).
Han, F., & Liu, H. (2013). Principal component analysis on non-gaussian dependent data. In Proceedings of the 30th international conference on machine learning (ICML), (pp. 240–248).
Han, F., Zhao, T., & Liu, H. (2013). Coda: High dimensional copula discriminant analysis. Journal of Machine Learning Research, 14, 629–671.
Hoff, P. D. (2007). Extending the rank likelihood for semiparametric copula estimation. The Annals of Applied Statistics, 1(1), 265–283.
Hoff, P. D. (2008). Rank likelihood estimation for continuous and discrete data. ISBA Bulletin, 15(1), 8–10.
Hubert, L., & Arabie, P. (1985). Comparing partitions. Journal of Classification, 2(1), 193–218.
Joe, H. (2014). Dependence Modeling with Copulas. Boca Raton: CRC Press.
Kalaitzis, A., & Silva, R. (2013). Flexible sampling of discrete data correlations without the marginal distributions. In Advances in neural information processing systems (NIPS).
Kim, D., Kim, J.-M., Liao, S.-M., & Jung, Y.-S. (2013). Mixture of D-vine copulas for modeling dependence. Computational Statistics & Data Analysis, 64, 1–19.
Klami, A., & Kaski, S. (2008). Probabilistic approach to detecting dependencies between data sets. Neurocomputing, 72(1), 39–46.
Klami, A., Virtanen, S., & Kaski, S. (2010). Bayesian exponential family projections for coupled data sources. In Proceedings of the twenty-sixth conference on uncertainty in artificial intelligence (UAI), (pp. 286–293).
Kosmidis, I., & Karlis, D. (2015). Model-based clustering using copulas with applications. In Statistics and computing. Springer.
Kumar, A., Rai, P., & Daume, H. (2011). Co-regularized multi-view spectral clustering. In Advances in neural information processing systems (NIPS), (pp. 1413–1421).
Letham, B., Sun, W., & Sheopuri, A. (2014). Latent variable copula inference for bundle pricing from retail transaction data. In Proceedings of the 31st international conference on machine learning (ICML), (pp. 217–225).
Lopez-Paz, D., Hernández-lobato, J. M, & Schölkopf, B. (2012). Semi-supervised domain adaptation with non-parametric copulas. In Advances in neural information processing systems (NIPS), (pp. 665–673).
Lopez-Paz, D., Hernández-Lobato, J. M., & Ghahramani, Z. (2013). Gaussian process vine copulas for multivariate dependence. In International conference on machine learning (ICML), (pp. 10–18).
Marlin, B. M., Kale, D. C., Khemani, R. G., & Wetzel, R. C. (2012). Unsupervised pattern discovery in electronic health care data using probabilistic clustering models. In Proceedings of the 2nd ACM SIGHIT international health informatics symposium, (pp. 389–398). ACM.
McParland, D., & Gormley, I. C. (2016). Model based clustering for mixed data: clustMD. Advances in Data Analysis and Classification,. doi:10.1007/s11634-016-0238-x.
McParland, D., Gormley, I. C., McCormick, T. H., Clark, S. J., Kabudula, C. W., & Collinson, M. A. (2014). Clustering South African households based on their asset status using latent variable models. The Annals of Applied Statistics, 8(2), 747.
Meeds, E., Ghahramani, Z., Neal, R., & Roweis, S. (2007). Modeling dyadic data with binary latent factors. In Advances in neural information processing systems (NIPS), 19.
Meilă, M. (2007). Comparing clusterings: an information based distance. Journal of Multivariate Analysis, 98(5), 873–895.
Minh, H. Q., Bazzani, L., & Murino, V. (2013). A unifying framework for vector-valued manifold regularization and multi-view learning. In Proceedings of the 30th international conference on machine learning (ICML), (pp. 100–108).
Murphy, K. P. (2012). Machine learning: A probabilistic perspective. Boston: MIT Press.
Neal, Radford M. (2000). Markov chain sampling methods for Dirichlet process mixture models. Journal of Computational and Graphical Statistics, 9(2), 249–265.
Panagiotelis, A., Czado, C., & Joe, H. (2012). Pair copula constructions for multivariate discrete data. Journal of the American Statistical Association, 107(499), 1063–1072.
Pennington, J., Socher, R., & Manning, C. D. (2014). Glove: Global vectors for word representation. In EMNLP, (Vol. 14, pp. 1532–1543).
Plant, C. (2012). Dependency clustering across measurement scales. In Proceedings of the 18th ACM SIGKDD international conference on knowledge discovery and data mining, (pp. 361–369).
Plant, C., & Böhm, C. (2011). INCONCO: Interpretable clustering of numerical and categorical objects. In Proceedings of the 17th ACM SIGKDD international conference on knowledge discovery and data mining, (pp. 1127–1135).
Rey, M., & Roth, V. (2012). Copula mixture model for dependency-seeking clustering. In International conference on machine learning (ICML).
Shawe-Taylor, John, & Cristianini, Nello. (2004). Kernel methods for pattern analysis. Cambridge: Cambridge University Press.
Sklar, A. (1959). Fonctions de rpartition n dimensions et leurs marges. Publications de l’Institut de statistique de l’Universite de Paris, 8, 229–231.
Smith, M. S., & Khaled, M. A. (2012). Estimation of copula models with discrete margins via Bayesian data augmentation. Journal of the American Statistical Association, 107(497), 290–303.
Sun, J., Lu, J., Xu, T., & Bi, J. (2015). Multi-view sparse co-clustering via proximal alternating linearized minimization. In Proceedings of the 32nd international conference on machine learning (ICML), (pp. 757–766).
Teh, Y. W. (2010). Dirichlet processes. In Encyclopedia of machine learning. Springer.
Tenzer, Y., & Elidan, G. (2013). Speedy model selection (sms) for copula models. In Proceedings of the 30th conference on uncertainty in artificial intelligence (UAI).
Tran, D., Blei, D., & Airoldi, E. M. (2015). Copula variational inference. In Advances in neural information processing systems (NIPS), (pp. 3564–3572).
Vinh, N. X., Epps, J., & Bailey, J. (2010). Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. The Journal of Machine Learning Research, 11, 2837–2854.
Wang, H., Nie, F., & Huang, H. (2013). Multi-view clustering and feature learning via structured sparsity. In Proceedings of the 30th international conference on machine learning (ICML), (pp. 352–360).
Wang, W., Arora, R., Livescu, K., & Bilmes, J. (2015). On deep multi-view representation learning. In Proceedings of the 32nd international conference on machine learning (ICML), (pp. 1083–1092).
White, M., Zhang, X., Schuurmans, D., & Yu, Y.-l. (2012). Convex multi-view subspace learning. In Advances in neural information processing systems (NIPS), (pp. 1673–1681).
Wu, Y., José Miguel, H.-L. & Ghahramani, Z. (2013). Dynamic covariance models for multivariate financial time series. In Proceedings of the 31st international conference on machine learning (ICML), (pp. 558–566).
Yerebakan, H. Z., Rajwa, B., & Dundar, M. (2014). The infinite mixture of infinite Gaussian mixtures. In Advances in neural information processing systems (NIPS).
Author information
Authors and Affiliations
Corresponding author
Additional information
Editors: Thomas Gärtner, Mirco Nanni, Andrea Passerini, and Celine Robardet.
Appendices
Appendix 1: Experiments: generation of simulated data
We generate synthetic data with pairwise tail dependencies. We do this by simulating data from a D-Vine with suitable dependency structure and performing the inverse transform with appropriate marginals. The data for each cluster is generated independently through this process.
Multiview Setting We generate two views for each cluster with three dimensions in each view. We use copula families Clayton, Gaussian and Student-T bivariate copulas with parameters shown in Table 8. For the discrete multiview dataset, we then generate the marginals with distributions and their parameters shown in Table 9. Similarly, for the continuous multiview dataset, we generate the parameters shown in Table 10.
Singleview Setting: The data generation process for the single view case is similar to the multi view case with only 1 view. We use copula families Clayton, Gaussian and Student-T bivariate copulas with parameters shown in Table 11. For the discrete single-view dataset, we then generate the marginals with distributions and their parameters shown in Table 12. Similarly, for the continuous multiview dataset, we generate the parameters shown in Table 13.
Appendix 2: Metropolis hastings for sampling parameters of pair-copulas
In this section, we briefly summarize the process of sampling the parameters \({\varTheta }\) and \({\varSigma }\). We place uniform priors on the parameters of the pair copulas (for simplicity), in the event there does not exist a ready conjugate prior. Where the parameters of the copulas are bounded, we place a uniform prior over the domain of these parameters. Where they are not bounded (for instance the degrees of freedom on a T distribution), we choose a reasonable bound during implementation and place a uniform prior. One could in principle experiment with other priors taking into account the characteristics of the specific copula functions. For instance, for the Gaussian pair copula, we have placed the inverse Wishart prior. The inverse Wishart distribution, a multidimensional generalization of the inverse Gamma distribution to positive definite matrices, is commonly used to model uncertainty in covariance matrices and their inverses (refer to Murphy 2012 for more details), and Hoff (2007) for its use for Bayesian inference with the Gaussian Copula.
We draw a sample of \(\{\sigma _{s,t}, \theta _{s,t}\}\), \(\forall 1\le s \le t\le M\) using random walk Metropolis Hastings to sample from Eq. 11 of the paper. The proposal distribution used in Metropolis Hastings is a Gaussian centered around the previous value in the case of continuous parameters, while we use a discrete uniform proposal centered at the previous sample for discrete parameters. Evaluating the conditional variables \(W^{s,t}\), is discussed in detail in the main text.
Appendix 3: Metropolis hastings for sampling from a rank constrained D-vine
An important step of our Gibbs sampling inference procedure in Sect. 4 comprises of sampling \(\{U_{i,.}\}\) from a D-vine subject to rank based constraints that follow from the extended rank likelihood methodology. Let \(D_{i,j} = \{u \in [0, 1]: max\left\{ U_{rj}: X_{rj}<X_{ij}, r\in [N]\right\}< u< min\left\{ U_{rj}: X_{ij}<X_{rj} , r\in [N]\right\} \}\). and \(D_{i,.}\) denote the set \(D_{i,1} \times D_{i,2} \times \ldots \times D_{i,M}\). Our target is to block sample the random variables \(U_{i,.}\) from a target distribution \(t(U_{i,.})\) that is a truncated D-vine with rank constraints \(p(U_{i,.} | {\varSigma }, {\varTheta }, U_{-i,.}, U_{i,.} \in D_{i,.})\). One way to sample from this distribution is to sample values from the unconstrained D-vine \(p(U_{i,.} | {\varSigma }, {\varTheta })\) and reject samples that do not satisfy rank constraints. However, this could lead to excessive rejections—instead we use Metropolis Hastings with a proposal that is an approximation of our target distribution, and satisfies the rank constraints.
Consider the following proposal distribution:
To sample the random vector \(U_{i,.}\) from this proposal, as mentioned in Sect. 4, we first sample \(U_{i,1}\) from \(p(U_{i,1} |{\varSigma }, {\varTheta }, U_{i,1} \in D_{i,1} )\), then sample from \(p(U_{i,2}| {\varSigma }, {\varTheta }, U_{i,1}, U_{i,2} \in D_{i,2})\) and so on, until we finally sample from conditional \(p(U_{i,M} | {\varSigma }, {\varTheta }, U_{i,1}, \ldots , U_{i,M-1}, U_{i,M} \in D_{i,M})\). The cumulative distributions for each step in this procedure are the h-functions (Aas et al. 2009) (see Eq. 6), that are invertible in closed form for most bivariate copula families. Hence we use inverse transform sampling to sample from these h-functions, subject to the rank constraint \(D_{i,j}\). Drawing a single sample \(U_{i,.}\) from the proposal for a single datapoint involves \(O(M^2)\) h-function inversions.
We now compute the acceptance ratio for this sampling scheme. Let \(t(U_{i,.})\) be the target distribution described above.
Now, consider a single term \(p(U_{i,j} |{\varSigma }, {\varTheta },U_{i,1} \ldots U_{i,j-1}, U_{i,j} \in D_{i,j} )\) in the proposal distribution from Eq. 15.
The acceptance ratio can be computed from Eqs. 18 and 16 as
We empirically observe a high acceptance ratio with this proposal leading to almost no rejected samples with our proposal. Table 14 shows the acceptance ratio averaged over 25 runs with datasets generated with 500 points with 6 dimensions. The complete inference algorithm is summarized in algorithm 1 of the main paper.
Rights and permissions
About this article
Cite this article
Tekumalla, L.S., Rajan, V. & Bhattacharyya, C. Vine copulas for mixed data : multi-view clustering for mixed data beyond meta-Gaussian dependencies. Mach Learn 106, 1331–1357 (2017). https://doi.org/10.1007/s10994-016-5624-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-016-5624-2